एरलांग वितरण: Difference between revisions
(Created page with "{{short description|Family of continuous probability distributions}} {{about|the mathematical / statistical distribution concept||Erlang (disambiguation){{!}}Erlang}} {{Probab...") |
No edit summary |
||
| (7 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Family of continuous probability distributions}} | {{short description|Family of continuous probability distributions}} | ||
{{Probability distribution | {{Probability distribution | ||
|name =Erlang | |name =Erlang | ||
| Line 21: | Line 20: | ||
|char =<math> \left(1 - \frac{it}{\lambda}\right)^{-k}</math>| | |char =<math> \left(1 - \frac{it}{\lambda}\right)^{-k}</math>| | ||
}} | }} | ||
एरलांग वितरण [[समर्थन (गणित)]] | एरलांग वितरण [[समर्थन (गणित)|समर्थन]] <math> x \in [0, \infty)</math> के साथ सतत प्रायिकता वितरण के दो-पैरामीटर वर्ग है। दो पैरामीटर इस प्रकार हैं: | ||
* एक | * एक धनात्मक पूर्णांक <math>k,</math> <nowiki>''आकार''</nowiki>, और | ||
* एक | * एक धनात्मक वास्तविक संख्या <math>\lambda,</math> <nowiki>''दर''</nowiki> और "मापक", <math>\beta,</math> दर का पारस्परिक, कभी-कभी इसके बदले प्रयोग किया जाता है। | ||
एरलांग वितरण | एरलांग वितरण प्रत्येक <math>1/\lambda</math> माध्य के साथ <math>k</math> स्वतंत्र घातीय चर के योग का वितरण है। समतुल्य रूप से, यह <math>\lambda</math> की दर के साथ प्वाइजन प्रक्रिया की kवीं घटना तक के समय का वितरण है। एरलांग और प्वाइजन वितरण पूरक हैं, जबकि प्वाइजन वितरण निश्चित समय में होने वाली घटनाओं की संख्या की गणना करते है, एरलांग वितरण घटनाओं की एक निश्चित संख्या के होने तक समय की मात्रा की गणना करते है। जब <math>k=1</math>, वितरण घातीय वितरण के लिए सरल हो जाता है। एरलांग वितरण [[गामा वितरण]] का एक विशेष प्रकरण है जिसमें वितरण का आकार भिन्न होता है। | ||
एरलांग वितरण को A. K. एरलांग द्वारा विकसित किया गया था ताकि स्विचिंग स्टेशनों के संचालक को एक ही समय में किए जाने वाले टेलीफोन कॉल की संख्या की जांच की जा सके। सामान्यतः क़तार प्रणाली में प्रतीक्षा समय पर विचार करने के लिए टेलीफोन [[टेलीट्रैफिक इंजीनियरिंग|ट्रैफ़िक अभियांत्रिकी]] पर यह काम विस्तृत किया गया है। वितरण का उपयोग प्रसंभाव्य प्रक्रियाओं के क्षेत्र में भी किया जाता है। | |||
== विशेषता == | == विशेषता == | ||
=== | === प्रायिकता घनत्व फलन === | ||
एरलांग वितरण का प्रायिकता घनत्व फलन है | |||
:<math>f(x; k,\lambda)={\lambda^k x^{k-1} e^{-\lambda x} \over (k-1)!}\quad\mbox{for }x, \lambda \geq 0,</math> | :<math>f(x; k,\lambda)={\lambda^k x^{k-1} e^{-\lambda x} \over (k-1)!}\quad\mbox{for }x, \lambda \geq 0,</math> | ||
पैरामीटर k को आकार | पैरामीटर k को आकार पैरामीटर कहा जाता है और पैरामीटर <math>\lambda</math> को दर पैरामीटर कहा जाता है। | ||
एक वैकल्पिक, लेकिन समतुल्य, | एक वैकल्पिक, लेकिन समतुल्य, प्राचलीकरण मापक पैरामीटर <math>\beta</math> का उपयोग करता है, जो दर पैरामीटर का पारस्परिक है (अर्थात, <math>\beta = 1/\lambda</math>): | ||
:<math>f(x; k,\beta)=\frac{ x^{k-1} e^{-\frac{x}{\beta}} }{\beta^k (k-1)!}\quad\mbox{for }x, \beta \geq 0.</math> | :<math>f(x; k,\beta)=\frac{ x^{k-1} e^{-\frac{x}{\beta}} }{\beta^k (k-1)!}\quad\mbox{for }x, \beta \geq 0.</math> | ||
जब | जब मापक पैरामीटर <math>\beta</math> 2 के समान है, तो वितरण 2k डिग्री स्वतंत्रता के साथ [[ची-वर्ग वितरण]] को सरल करता है। इसलिए इसे स्वतंत्रता की डिग्री की सम संख्याओं के लिए [[सामान्यीकृत ची-वर्ग वितरण]] के रूप में माना जा सकता है। | ||
=== संचयी वितरण | === संचयी वितरण फलन (सीडीएफ) === | ||
एरलांग वितरण का संचयी वितरण फलन है | |||
:<math>F(x; k,\lambda) = P(k, \lambda x) = \frac{\gamma(k, \lambda x)}{\Gamma(k)} = \frac{\gamma(k, \lambda x)}{(k-1)!},</math> | :<math>F(x; k,\lambda) = P(k, \lambda x) = \frac{\gamma(k, \lambda x)}{\Gamma(k)} = \frac{\gamma(k, \lambda x)}{(k-1)!},</math> | ||
जहाँ <math>\gamma</math> निम्न अपूर्ण गामा फलन है और <math>P</math> निम्न नियमित गामा फलन है। सीडीएफ को भी व्यक्त किया जा सकता है | |||
सीडीएफ को भी व्यक्त किया जा सकता है | |||
:<math>F(x; k,\lambda) = 1 - \sum_{n=0}^{k-1}\frac{1}{n!}e^{-\lambda x}(\lambda x)^n.</math> | :<math>F(x; k,\lambda) = 1 - \sum_{n=0}^{k-1}\frac{1}{n!}e^{-\lambda x}(\lambda x)^n.</math> | ||
=== एरलांग-k === | |||
एरलांग-k वितरण (जहाँ k एक धनात्मक पूर्णांक है) <math>E_k(\lambda)</math> को एरलांग वितरण के पीडीएफ में k समायोजन करके परिभाषित किया गया है।<ref>{{Cite web |title=h1.pdf|url=https://www.win.tue.nl/~iadan/sdp/h1.pdf}}</ref> उदाहरण के लिए, एरलांग-2 वितरण <math>E_2(\lambda) ={\lambda^2 x} e^{-\lambda x} \quad\mbox{for }x, \lambda \geq 0</math> है, जो <math>f(x; 2,\lambda)</math> समान हैं। | |||
=== एरलांग- | |||
=== मध्य === | === मध्य === | ||
एरलांग वितरण के माध्यिका के लिए एक उपगामी प्रसार जाना जाता है,<ref>{{Cite journal | last1 = Choi | first1 = K. P. | doi = 10.1090/S0002-9939-1994-1195477-8 | title = गामा बंटन की माध्यिकाओं पर और रामानुजन का एक समीकरण| journal = Proceedings of the American Mathematical Society | volume = 121 | pages = 245–251 | year = 1994 | jstor = 2160389| doi-access = free }}</ref> जिसके लिए गुणांकों की गणना की जा सकती है और सीमाएं ज्ञात हैं।<ref>{{Cite journal | last1 = Adell | first1 = J. A. | last2 = Jodrá | first2 = P. | doi = 10.1090/S0002-9947-07-04411-X | title = गामा बंटन की माध्यिका से जुड़े रामानुजन समीकरण पर| journal = Transactions of the American Mathematical Society | volume = 360 | issue = 7 | pages = 3631 | year = 2007 | doi-access = free }}</ref><ref>{{Cite journal | last1 = Jodrá | first1 = P. | title = Erlang बंटन के माध्यिका के स्पर्शोन्मुख विस्तार की गणना| doi = 10.3846/13926292.2012.664571 | journal = Mathematical Modelling and Analysis | volume = 17 | issue = 2 | pages = 281–292 | year = 2012 | doi-access = free }}</ref> एक सन्निकटन <math>\frac{k}{\lambda}\left(1-\dfrac{1}{3k+0.2}\right)</math>है, अर्थात माध्य <math>\frac{k}{\lambda}</math> से नीचे हैं। <ref name=Banneheka2009>{{cite journal | last1 = Banneheka | first1 = BMSG | last2 = Ekanayake | first2 = GEMUPD | year = 2009 | title = गामा वितरण के माध्यिका के लिए एक नया बिंदु अनुमानक| journal = Viyodaya J Science | volume = 14 | pages = 95–103 }}</ref> | |||
== एरलांग-वितरित यादृच्छिक चर उत्पन्न करना == | == एरलांग-वितरित यादृच्छिक चर उत्पन्न करना == | ||
निम्नलिखित सूत्र का उपयोग करके समान रूप से वितरित यादृच्छिक संख्या (<math>U \in [0,1]</math>) से एरलांग-वितरित यादृच्छिक चर उत्पन्न किए जा सकते हैं:<ref>{{cite web|url=http://www.xycoon.com/erlang_random.htm|title=सांख्यिकीय वितरण - एरलांग वितरण - यादृच्छिक संख्या जेनरेटर|last=Resa|website=www.xycoon.com|access-date=4 April 2018}}</ref> | |||
:<math>E(k,\lambda) = -\frac{1}\lambda \ln \prod_{i=1}^k U_{i} = -\frac{1}\lambda \sum_{i=1}^k \ln U_{i} </math> | :<math>E(k,\lambda) = -\frac{1}\lambda \ln \prod_{i=1}^k U_{i} = -\frac{1}\lambda \sum_{i=1}^k \ln U_{i} </math> | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
=== प्रतीक्षा समय === | === प्रतीक्षा समय === | ||
कुछ औसत दर के साथ स्वतंत्र रूप से घटित होने वाली घटनाओं को एक पॉइसन प्रक्रिया के साथ प्रतिरूपित किया जाता है। घटना की k घटनाओं के | कुछ औसत दर के साथ स्वतंत्र रूप से घटित होने वाली घटनाओं को एक पॉइसन प्रक्रिया के साथ प्रतिरूपित किया जाता है। घटना की k घटनाओं के मध्य प्रतीक्षा समय एरलांग वितरित किया जाता है। (किसी दिए गए समय में घटनाओं की संख्या से संबंधित प्रश्न [[पॉसों वितरण|प्वाइजन वितरण]] द्वारा वर्णित है।) | ||
एरलांग वितरण, जो आवक कॉल के मध्य के समय को मापता है, एरलांग में मापे गए ट्रैफ़िक भार के बारे में जानकारी उत्पन्न करने के लिए आने वाली कॉल की अपेक्षित अवधि के संयोजन के साथ उपयोग किया जा सकता है। इसका उपयोग पैकेट के हानि या विलंब की संभावना को निर्धारित करने के लिए किया जा सकता है, इस बारे में की गई विभिन्न धारणाओं के अनुसार कि क्या अवरूद्ध कॉल को निरस्त कर दिया गया है (एरलांग B सूत्र) या कतारबद्ध जब तक सेवा नहीं दी गई है (एरलांग C सूत्र)। [[कॉल सेंटर|कॉल केंद्रो]] के डिज़ाइन जैसे अनुप्रयोगों के लिए ट्रैफ़िक मॉडलिंग के लिए [[Erlang-B|एरलांग-B]] और C सूत्र अभी भी दैनिक के उपयोग में हैं। | |||
=== अन्य अनुप्रयोग === | === अन्य अनुप्रयोग === | ||
[[कैंसर]] रोग की | [[कैंसर]] रोग की घटनाओं का आयु वितरण प्रायः एरलांग वितरण का अनुसरण करता है, जबकि आकार और पैमाने के पैरामीटर क्रमशः चालक घटनाओं की संख्या और उनके मध्य समय अंतराल की भविष्यवाणी करते हैं।<ref>{{cite journal |last1=Belikov |first1=Aleksey V. |title=कैंसर की घटनाओं से प्रमुख कार्सिनोजेनिक घटनाओं की संख्या का अनुमान लगाया जा सकता है|journal=Scientific Reports |date=22 September 2017 |volume=7 |issue=1 |doi=10.1038/s41598-017-12448-7|pmc=5610194 |pmid=28939880 }}</ref><ref>{{Cite journal|last=Belikov|first=Aleksey V.|last2=Vyatkin|first2=Alexey|last3=Leonov|first3=Sergey V.|date=2021-08-06|title=Erlang वितरण बचपन और युवा वयस्कता के कैंसर की घटनाओं के आयु वितरण का अनुमान लगाता है|url=https://peerj.com/articles/11976|journal=PeerJ|language=en|volume=9|pages=e11976|pmid=34434669| doi=10.7717/peerj.11976| pmc=8351573|issn=2167-8359|doi-access=free}}</ref> अधिक सामान्यतः, बहुचरण मॉडल के परिणाम के रूप में, एरलांग वितरण को सेल आवर्तन समय वितरण के अच्छे सन्निकटन के रूप में सूचित किया गया है।<ref>{{cite journal |last1=Yates |first1=Christian A. |title=मार्कोव प्रक्रिया के रूप में सेल प्रसार का एक बहु-स्तरीय प्रतिनिधित्व|journal=Bulletin of Mathematical Biology |date=21 April 2017 |volume=79 |issue=1 |doi=10.1007/s11538-017-0356-4 |pages=2905–2928|doi-access=free }}</ref><ref>{{cite journal |last1=Gavagnin |first1=Enrico |title=यथार्थवादी सेल चक्र समय वितरण के साथ सेल माइग्रेशन मॉडल की आक्रमण गति|journal=Journal of Theoretical Biology |date=14 October 018 |volume=79 |issue=1 |doi=10.1016/j.jtbi.2018.09.010|arxiv=1806.03140 |pages=91–99 }}</ref> | ||
अंतरखरीद समय का वर्णन करने के लिए इसका उपयोग व्यावसायिक अर्थशास्त्र में भी किया गया है।<ref>C. Chatfield and G.J. Goodhardt: “A Consumer Purchasing Model with Erlang Interpurchase Times”; ''Journal of the American Statistical Association'', Dec. 1973, Vol.68, pp.828-835</ref> | |||
== गुण == | == गुण == | ||
*अगर <math> X \sim \operatorname{Erlang}(k, \lambda)</math> | *अगर <math> X \sim \operatorname{Erlang}(k, \lambda)</math> तो <math> a \cdot X \sim \operatorname{Erlang}\left(k, \frac{\lambda}{a}\right)</math> साथ में <math> a \in \mathbb{R}</math> | ||
*अगर <math> X \sim \operatorname{Erlang}(k_1, \lambda)</math> और <math> Y \sim \operatorname{Erlang}(k_2, \lambda)</math> | *अगर <math> X \sim \operatorname{Erlang}(k_1, \lambda)</math> और <math> Y \sim \operatorname{Erlang}(k_2, \lambda)</math> तो <math> X + Y \sim \operatorname{Erlang}(k_1 + k_2, \lambda)</math> अगर <math> X, Y </math> स्वतंत्र हैं | ||
== संबंधित वितरण == | == संबंधित वितरण == | ||
* | * एरलांग वितरण k [[स्वतंत्र और समान रूप से वितरित यादृच्छिक चर]] के योग का वितरण है, प्रत्येक में एक घातीय वितरण है। दीर्घसमयिक दर जिस पर घटनाएं घटित होती हैं, वह <math>X</math> की अपेक्षा का पारस्परिक है, अर्थात <math>\lambda/k</math> एरलांग वितरण की (आयु विशिष्ट घटना) दर, <math>k>1</math> के लिए, <math>x</math> में एकदिष्ट है, 0 से <math>x=0</math> पर बढ़ रहा है, <math>\lambda</math> के रूप में <math>x</math> अनंत की ओर जाता है।<ref>Cox, D.R. (1967) ''Renewal Theory'', p20, Methuen.</ref> | ||
* | *अर्थात्: अगर <math> X_i \sim \operatorname{Exponential}(\lambda),</math> तब <math display="block"> \sum_{i=1}^k{X_i} \sim \operatorname{Erlang}(k, \lambda)</math> | ||
* पीडीएफ और सीडीएफ के भाजक में क्रमगुणित फलन के कारण, एरलांग वितरण केवल तभी परिभाषित होता है जब पैरामीटर k एक धनात्मक पूर्णांक होता है। वास्तव में, इस वितरण को कभी-कभी एरलांग-k वितरण कहा जाता है (उदाहरण के लिए, एरलांग -2 वितरण <math>k=2</math> के साथ एरलांग वितरण है)। गामा वितरण क्रमगुणित फलन के बदले [[गामा समारोह|गामा फलन]] का उपयोग करके, किसी भी धनात्मक वास्तविक संख्या होने की अनुमति देकर एरलांग वितरण को सामान्यीकृत करता है। | |||
** अर्थात्: यदि k एक [[पूर्णांक]] है और <math> X \sim \operatorname{Gamma}(k, \lambda),</math> तब <math> X \sim \operatorname{Erlang}(k, \lambda)</math> | ** अर्थात्: यदि k एक [[पूर्णांक]] है और <math> X \sim \operatorname{Gamma}(k, \lambda),</math> तब <math> X \sim \operatorname{Erlang}(k, \lambda)</math> | ||
*अगर <math> U \sim \operatorname{Exponential}(\lambda)</math> और <math> V \sim \operatorname{Erlang}(n, \lambda)</math> तब <math> \frac{U}{V}+1 \sim \operatorname{Pareto}(1, n)</math> | *अगर <math> U \sim \operatorname{Exponential}(\lambda)</math> और <math> V \sim \operatorname{Erlang}(n, \lambda)</math> तब <math> \frac{U}{V}+1 \sim \operatorname{Pareto}(1, n)</math> | ||
* | *एरलांग वितरण पियर्सन प्रकार III वितरण का एक विशेष प्रकरण है{{citation needed|date=March 2016}} | ||
* | *एरलांग वितरण ची-वर्ग वितरण से संबंधित है। अगर <math> X \sim \operatorname{Erlang}(k,\lambda),</math> तब <math> 2\lambda X\sim \chi^2_{2k}</math>{{citation needed|date=March 2016}} | ||
* | *एरलांग वितरण प्वाइजन प्रक्रिया द्वारा प्वाइजन वितरण से संबंधित है: यदि <math> S_n = \sum_{i=1}^n X_i</math> ऐसा है कि <math> X_i \sim \operatorname{Exponential}(\lambda),</math> तब <math display="block"> S_n \sim \operatorname{Erlang}(n, \lambda)</math> और <math display="block"> \operatorname{Pr}(N(x) \leq n - 1) = \operatorname{Pr}(S_n > x) = 1 - F_X(x; n, \lambda) = \sum_{k=0}^{n-1} \frac{1}{k!}e^{-\lambda x} (\lambda x)^k.</math> <math>n</math> पर अंतर लेने से प्वाइजन वितरण प्राप्त होता है। | ||
== यह भी देखें == | == यह भी देखें == | ||
* | * कॉक्सियन वितरण | ||
* एंगसेट गणना | * एंगसेट गणना | ||
* [[एरलांग बी]] | * [[एरलांग बी]] सूत्र | ||
* [[एरलांग इकाई]] | * [[एरलांग इकाई]] | ||
* [[चरण-प्रकार वितरण]] | * [[चरण-प्रकार वितरण]] | ||
* [[यातायात उत्पादन मॉडल]] | * [[यातायात उत्पादन मॉडल|ट्रैफ़िक उत्पादन मॉडल]] | ||
==टिप्पणियाँ== | ==टिप्पणियाँ== | ||
| Line 111: | Line 100: | ||
==संदर्भ== | ==संदर्भ== | ||
* Ian Angus [http://www.tarrani.net/linda/ErlangBandC.pdf "An Introduction to | * Ian Angus [http://www.tarrani.net/linda/ErlangBandC.pdf "An Introduction to एरलांग B and एरलांग C"], Telemanagement #187 (PDF Document - Has terms and formulae plus short biography) | ||
* Stuart Harris [https://portagecommunications.com/a-primer-on-two-call-center-staffing-methods/ | * Stuart Harris [https://portagecommunications.com/a-primer-on-two-call-center-staffing-methods/ "एरलांग Calculations vs. Simulation"] | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
*[http://www.xycoon.com/erlang.htm | *[http://www.xycoon.com/erlang.htm एरलांग Distribution] | ||
*[http://www.eventhelix.com/RealtimeMantra/CongestionControl/resource_dimensioning_erlang_b_c.htm Resource Dimensioning Using | *[http://www.eventhelix.com/RealtimeMantra/CongestionControl/resource_dimensioning_erlang_b_c.htm Resource Dimensioning Using एरलांग-B and एरलांग-C] | ||
{{DEFAULTSORT:Erlang Distribution}} | |||
[[Category: | [[Category:All articles with unsourced statements|Erlang Distribution]] | ||
[[Category:Created On 21/03/2023]] | [[Category:Articles with unsourced statements from March 2016|Erlang Distribution]] | ||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:Created On 21/03/2023|Erlang Distribution]] | |||
[[Category:Lua-based templates|Erlang Distribution]] | |||
[[Category:Machine Translated Page|Erlang Distribution]] | |||
[[Category:Pages using infobox probability distribution with unknown parameters|scvएरलांग वितरण]] | |||
[[Category:Pages with script errors|Erlang Distribution]] | |||
[[Category:Short description with empty Wikidata description|Erlang Distribution]] | |||
[[Category:Templates Vigyan Ready|Erlang Distribution]] | |||
[[Category:Templates that add a tracking category|Erlang Distribution]] | |||
[[Category:Templates that generate short descriptions|Erlang Distribution]] | |||
[[Category:Templates using TemplateData|Erlang Distribution]] | |||
[[Category:असीम रूप से विभाज्य संभाव्यता वितरण|Erlang Distribution]] | |||
[[Category:घातीय परिवार वितरण|Erlang Distribution]] | |||
[[Category:निरंतर वितरण|Erlang Distribution]] | |||
Latest revision as of 13:08, 7 April 2023
|
Probability density function 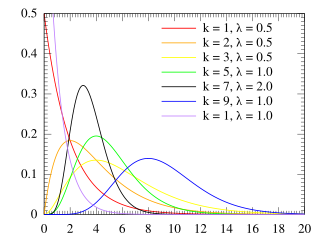 | |||
|
Cumulative distribution function  | |||
| Parameters |
shape rate alt.: scale | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean | |||
| Median | No simple closed form | ||
| Mode | |||
| Variance | |||
| Skewness | |||
| Ex. kurtosis | |||
| Entropy | |||
| MGF | for | ||
| CF | |||
एरलांग वितरण समर्थन के साथ सतत प्रायिकता वितरण के दो-पैरामीटर वर्ग है। दो पैरामीटर इस प्रकार हैं:
- एक धनात्मक पूर्णांक ''आकार'', और
- एक धनात्मक वास्तविक संख्या ''दर'' और "मापक", दर का पारस्परिक, कभी-कभी इसके बदले प्रयोग किया जाता है।
एरलांग वितरण प्रत्येक माध्य के साथ स्वतंत्र घातीय चर के योग का वितरण है। समतुल्य रूप से, यह की दर के साथ प्वाइजन प्रक्रिया की kवीं घटना तक के समय का वितरण है। एरलांग और प्वाइजन वितरण पूरक हैं, जबकि प्वाइजन वितरण निश्चित समय में होने वाली घटनाओं की संख्या की गणना करते है, एरलांग वितरण घटनाओं की एक निश्चित संख्या के होने तक समय की मात्रा की गणना करते है। जब , वितरण घातीय वितरण के लिए सरल हो जाता है। एरलांग वितरण गामा वितरण का एक विशेष प्रकरण है जिसमें वितरण का आकार भिन्न होता है।
एरलांग वितरण को A. K. एरलांग द्वारा विकसित किया गया था ताकि स्विचिंग स्टेशनों के संचालक को एक ही समय में किए जाने वाले टेलीफोन कॉल की संख्या की जांच की जा सके। सामान्यतः क़तार प्रणाली में प्रतीक्षा समय पर विचार करने के लिए टेलीफोन ट्रैफ़िक अभियांत्रिकी पर यह काम विस्तृत किया गया है। वितरण का उपयोग प्रसंभाव्य प्रक्रियाओं के क्षेत्र में भी किया जाता है।
विशेषता
प्रायिकता घनत्व फलन
एरलांग वितरण का प्रायिकता घनत्व फलन है
पैरामीटर k को आकार पैरामीटर कहा जाता है और पैरामीटर को दर पैरामीटर कहा जाता है।
एक वैकल्पिक, लेकिन समतुल्य, प्राचलीकरण मापक पैरामीटर का उपयोग करता है, जो दर पैरामीटर का पारस्परिक है (अर्थात, ):
जब मापक पैरामीटर 2 के समान है, तो वितरण 2k डिग्री स्वतंत्रता के साथ ची-वर्ग वितरण को सरल करता है। इसलिए इसे स्वतंत्रता की डिग्री की सम संख्याओं के लिए सामान्यीकृत ची-वर्ग वितरण के रूप में माना जा सकता है।
संचयी वितरण फलन (सीडीएफ)
एरलांग वितरण का संचयी वितरण फलन है
जहाँ निम्न अपूर्ण गामा फलन है और निम्न नियमित गामा फलन है। सीडीएफ को भी व्यक्त किया जा सकता है
एरलांग-k
एरलांग-k वितरण (जहाँ k एक धनात्मक पूर्णांक है) को एरलांग वितरण के पीडीएफ में k समायोजन करके परिभाषित किया गया है।[1] उदाहरण के लिए, एरलांग-2 वितरण है, जो समान हैं।
मध्य
एरलांग वितरण के माध्यिका के लिए एक उपगामी प्रसार जाना जाता है,[2] जिसके लिए गुणांकों की गणना की जा सकती है और सीमाएं ज्ञात हैं।[3][4] एक सन्निकटन है, अर्थात माध्य से नीचे हैं। [5]
एरलांग-वितरित यादृच्छिक चर उत्पन्न करना
निम्नलिखित सूत्र का उपयोग करके समान रूप से वितरित यादृच्छिक संख्या () से एरलांग-वितरित यादृच्छिक चर उत्पन्न किए जा सकते हैं:[6]
अनुप्रयोग
प्रतीक्षा समय
कुछ औसत दर के साथ स्वतंत्र रूप से घटित होने वाली घटनाओं को एक पॉइसन प्रक्रिया के साथ प्रतिरूपित किया जाता है। घटना की k घटनाओं के मध्य प्रतीक्षा समय एरलांग वितरित किया जाता है। (किसी दिए गए समय में घटनाओं की संख्या से संबंधित प्रश्न प्वाइजन वितरण द्वारा वर्णित है।)
एरलांग वितरण, जो आवक कॉल के मध्य के समय को मापता है, एरलांग में मापे गए ट्रैफ़िक भार के बारे में जानकारी उत्पन्न करने के लिए आने वाली कॉल की अपेक्षित अवधि के संयोजन के साथ उपयोग किया जा सकता है। इसका उपयोग पैकेट के हानि या विलंब की संभावना को निर्धारित करने के लिए किया जा सकता है, इस बारे में की गई विभिन्न धारणाओं के अनुसार कि क्या अवरूद्ध कॉल को निरस्त कर दिया गया है (एरलांग B सूत्र) या कतारबद्ध जब तक सेवा नहीं दी गई है (एरलांग C सूत्र)। कॉल केंद्रो के डिज़ाइन जैसे अनुप्रयोगों के लिए ट्रैफ़िक मॉडलिंग के लिए एरलांग-B और C सूत्र अभी भी दैनिक के उपयोग में हैं।
अन्य अनुप्रयोग
कैंसर रोग की घटनाओं का आयु वितरण प्रायः एरलांग वितरण का अनुसरण करता है, जबकि आकार और पैमाने के पैरामीटर क्रमशः चालक घटनाओं की संख्या और उनके मध्य समय अंतराल की भविष्यवाणी करते हैं।[7][8] अधिक सामान्यतः, बहुचरण मॉडल के परिणाम के रूप में, एरलांग वितरण को सेल आवर्तन समय वितरण के अच्छे सन्निकटन के रूप में सूचित किया गया है।[9][10]
अंतरखरीद समय का वर्णन करने के लिए इसका उपयोग व्यावसायिक अर्थशास्त्र में भी किया गया है।[11]
गुण
- अगर तो साथ में
- अगर और तो अगर स्वतंत्र हैं
संबंधित वितरण
- एरलांग वितरण k स्वतंत्र और समान रूप से वितरित यादृच्छिक चर के योग का वितरण है, प्रत्येक में एक घातीय वितरण है। दीर्घसमयिक दर जिस पर घटनाएं घटित होती हैं, वह की अपेक्षा का पारस्परिक है, अर्थात एरलांग वितरण की (आयु विशिष्ट घटना) दर, के लिए, में एकदिष्ट है, 0 से पर बढ़ रहा है, के रूप में अनंत की ओर जाता है।[12]
- अर्थात्: अगर तब
- पीडीएफ और सीडीएफ के भाजक में क्रमगुणित फलन के कारण, एरलांग वितरण केवल तभी परिभाषित होता है जब पैरामीटर k एक धनात्मक पूर्णांक होता है। वास्तव में, इस वितरण को कभी-कभी एरलांग-k वितरण कहा जाता है (उदाहरण के लिए, एरलांग -2 वितरण के साथ एरलांग वितरण है)। गामा वितरण क्रमगुणित फलन के बदले गामा फलन का उपयोग करके, किसी भी धनात्मक वास्तविक संख्या होने की अनुमति देकर एरलांग वितरण को सामान्यीकृत करता है।
- अर्थात्: यदि k एक पूर्णांक है और तब
- अगर और तब
- एरलांग वितरण पियर्सन प्रकार III वितरण का एक विशेष प्रकरण है[citation needed]
- एरलांग वितरण ची-वर्ग वितरण से संबंधित है। अगर तब [citation needed]
- एरलांग वितरण प्वाइजन प्रक्रिया द्वारा प्वाइजन वितरण से संबंधित है: यदि ऐसा है कि तब औरपर अंतर लेने से प्वाइजन वितरण प्राप्त होता है।
यह भी देखें
- कॉक्सियन वितरण
- एंगसेट गणना
- एरलांग बी सूत्र
- एरलांग इकाई
- चरण-प्रकार वितरण
- ट्रैफ़िक उत्पादन मॉडल
टिप्पणियाँ
- ↑ "h1.pdf" (PDF).
- ↑ Choi, K. P. (1994). "गामा बंटन की माध्यिकाओं पर और रामानुजन का एक समीकरण". Proceedings of the American Mathematical Society. 121: 245–251. doi:10.1090/S0002-9939-1994-1195477-8. JSTOR 2160389.
- ↑ Adell, J. A.; Jodrá, P. (2007). "गामा बंटन की माध्यिका से जुड़े रामानुजन समीकरण पर". Transactions of the American Mathematical Society. 360 (7): 3631. doi:10.1090/S0002-9947-07-04411-X.
- ↑ Jodrá, P. (2012). "Erlang बंटन के माध्यिका के स्पर्शोन्मुख विस्तार की गणना". Mathematical Modelling and Analysis. 17 (2): 281–292. doi:10.3846/13926292.2012.664571.
- ↑ Banneheka, BMSG; Ekanayake, GEMUPD (2009). "गामा वितरण के माध्यिका के लिए एक नया बिंदु अनुमानक". Viyodaya J Science. 14: 95–103.
- ↑ Resa. "सांख्यिकीय वितरण - एरलांग वितरण - यादृच्छिक संख्या जेनरेटर". www.xycoon.com. Retrieved 4 April 2018.
- ↑ Belikov, Aleksey V. (22 September 2017). "कैंसर की घटनाओं से प्रमुख कार्सिनोजेनिक घटनाओं की संख्या का अनुमान लगाया जा सकता है". Scientific Reports. 7 (1). doi:10.1038/s41598-017-12448-7. PMC 5610194. PMID 28939880.
- ↑ Belikov, Aleksey V.; Vyatkin, Alexey; Leonov, Sergey V. (2021-08-06). "Erlang वितरण बचपन और युवा वयस्कता के कैंसर की घटनाओं के आयु वितरण का अनुमान लगाता है". PeerJ (in English). 9: e11976. doi:10.7717/peerj.11976. ISSN 2167-8359. PMC 8351573. PMID 34434669.
- ↑ Yates, Christian A. (21 April 2017). "मार्कोव प्रक्रिया के रूप में सेल प्रसार का एक बहु-स्तरीय प्रतिनिधित्व". Bulletin of Mathematical Biology. 79 (1): 2905–2928. doi:10.1007/s11538-017-0356-4.
- ↑ Gavagnin, Enrico (14 October 018). "यथार्थवादी सेल चक्र समय वितरण के साथ सेल माइग्रेशन मॉडल की आक्रमण गति". Journal of Theoretical Biology. 79 (1): 91–99. arXiv:1806.03140. doi:10.1016/j.jtbi.2018.09.010.
{{cite journal}}: Check date values in:|date=(help) - ↑ C. Chatfield and G.J. Goodhardt: “A Consumer Purchasing Model with Erlang Interpurchase Times”; Journal of the American Statistical Association, Dec. 1973, Vol.68, pp.828-835
- ↑ Cox, D.R. (1967) Renewal Theory, p20, Methuen.
संदर्भ
- Ian Angus "An Introduction to एरलांग B and एरलांग C", Telemanagement #187 (PDF Document - Has terms and formulae plus short biography)
- Stuart Harris "एरलांग Calculations vs. Simulation"