मैक्सवेल सामग्री: Difference between revisions
mNo edit summary |
No edit summary |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 100: | Line 100: | ||
{{reflist}} | {{reflist}} | ||
{{DEFAULTSORT:Maxwell Material}} | {{DEFAULTSORT:Maxwell Material}} | ||
[[Category:CS1 maint]] | |||
[[Category:Created On 23/03/2023|Maxwell Material]] | |||
[[Category: | [[Category:Machine Translated Page|Maxwell Material]] | ||
[[Category:Created On 23/03/2023]] | [[Category:Pages with script errors|Maxwell Material]] | ||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Use dmy dates from November 2017|Maxwell Material]] | |||
[[Category:गैर-न्यूटोनियन तरल पदार्थ|Maxwell Material]] | |||
[[Category:जेम्स क्लर्क मैक्सवेल|Maxwell Material]] | |||
[[Category:पदार्थ विज्ञान|Maxwell Material]] | |||
Latest revision as of 15:52, 11 April 2023
मैक्सवेल सामग्री एक विशिष्ट तरल के गुण दिखाने वाला सबसे सरल प्रतिरूप श्यानप्रत्यास्थ सामग्री है। यह लंबे समय के स्तर पर चिपचिपा प्रवाह दिखाता है, लेकिन तेजी से विकृतियों के लिए अतिरिक्त लोचदार प्रतिरोध भी देता है [1] इसका नाम जेम्स क्लर्क मैक्सवेल के नाम पर रखा गया है जिन्होंने 1867 में प्रतिरूप का प्रस्ताव रखा था। इसे मैक्सवेल द्रव के रूप में भी जाना जाता है।
परिभाषा
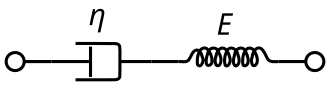
मैक्सवेल प्रतिरूप को विशुद्ध रूप से श्यानता अवमंदक और विशुद्ध रूप से लोच (भौतिकी) स्प्रिंग द्वारा श्रृंखला में जोड़ा जाता है,[2] जैसा कि आरेख में दिखाया गया है। इस विन्यास में, लागू अक्षीय प्रतिबल के नीचे, कुल प्रतिबल, और कुल विकृति, निम्नानुसार परिभाषित किया जा सकता है:[1]
जहां पादांक D डम्पर में प्रतिबल-विकृति को इंगित करता है और मूर्धांक S स्प्रिंग में प्रतिबल-विकृति को इंगित करता है। समय के संबंध में विकृति का व्युत्पन्न लेते हुए, हम प्राप्त करते हैं:
जहां E लोचदार मापांक है और η चिपचिपाहट का भौतिक गुणांक है। यह प्रतिरूप अवमंदक को न्यूटोनियन तरल पदार्थ के रूप में वर्णित करता है और स्प्रिंग को हुक के नियम के साथ प्रतिरूप करता है।
अगर, इसके विपरीत, हम इन दो तत्वों को समानांतर में जोड़ते हैं,[2] हमें एक ठोस केल्विन-वोइग सामग्री का सामान्यीकृत प्रतिरूप मिलता है।
मैक्सवेल सामग्री में, प्रतिबल (भौतिकी) σ, विकृति (सामग्री विज्ञान) ε और समय T के संबंध में परिवर्तन की उनकी दरें फॉर्म के समीकरणों द्वारा नियंत्रित होती हैं:[1]
या, डॉट नोटेशन में:
समीकरण या तो अपरूपण प्रतिबल या किसी सामग्री में समान दबाव के लिए लागू किया जा सकता है। पूर्व स्थिति में, चिक्कणता न्यूटोनियन द्रव के लिए संगत है। बाद की स्थिति में, प्रतिबल और विकृति की दर से संबंधित इसका थोड़ा अलग अर्थ है।
प्रतिरूप समान्यतः छोटे विरूपण की स्थिति में लागू होता है। बड़े विरूपण के लिए हमें कुछ ज्यामितीय गैर-रैखिकता समिलित करनी चाहिए। मैक्सवेल प्रतिरूप के सामान्यीकरण के सरलतम प्रकार के लिए, ऊपरी संवहन मैक्सवेल प्रतिरूप देखें।
अचानक विकृति का प्रभाव
यदि मैक्सवेल सामग्री अचानक विकृति हो जाती है और के प्रतिबल (सामग्री विज्ञान) में रखी जाती है तब प्रतिबल की एक विशिष्ट समय-सीमा पर क्षय होता है, जिसे शिथिलन अवधि के रूप में जाना जाता है। घटना को प्रतिबल विश्रांति के रूप में जाना जाता है।
चित्र आयाम रहित प्रतिबल की निर्भरता को समय पर दर्शाता है।
यदि हम सामग्री को समय पर मुक्त करते हैं, तो लोचदार तत्व के मान से वापस आ जाएगा
चूंकि चिपचिपा तत्व अपनी मूल लंबाई पर वापस नहीं आएगा, इसलिए विरूपण के अपरिवर्तनीय घटक को नीचे दी गई अभिव्यक्ति में सरल बनाया जा सकता है:
अचानक प्रतिबल का प्रभाव
यदि मैक्सवेल सामग्री अचानक प्रतिबल के अधीन है , तब लोचदार तत्व अचानक ख़राब हो जाएगा और चिपचिपा तत्व एक स्थिर दर से ख़राब हो जाएगा:
अगर किसी समय हम सामग्री जारी करेंगे, तो फिर लोचदार तत्व का विरूपण स्प्रिंग-बैक विरूपण होगा और चिपचिपा तत्व का विरूपण नहीं बदलेगा:
मैक्सवेल प्रतिरूप रेंगना (विकृति) प्रदर्शित नहीं करता है क्योंकि यह प्रतिबल को समय के रैखिक कार्य के रूप में दर्शाता है।
यदि पर्याप्त लंबे समय के लिए एक छोटा सा प्रतिबल लागू किया जाता है, तो अपरिवर्तनीय प्रतिबल बड़े हो जाते हैं। इस प्रकार, मैक्सवेल सामग्री एक प्रकार का तरल है।
निरंतर दबाव दर का प्रभाव
यदि मैक्सवेल सामग्री निरंतर प्रतिबल दर के अधीन है फिर प्रतिबल बढ़ जाता है, यह एक निम्न निरंतर मूल्य तक पहुँच जाता है
सामान्य रूप में
गतिक मापांक
मैक्सवेल सामग्री का जटिल गतिक मापांक होगा:
इस प्रकार, गतिक मापांक के घटक हैं:
और
चित्र मैक्सवेल सामग्री के लिए विश्रांति वर्णक्रम दिखाता है। विश्रांति का समय स्थिर . है।
| नीला वक्र | आयाम रहित लोचदार मापांक |
| गुलाबी वक्र | नुकसान का आयाम रहित मापांक |
| पीला वक्र | आयामहीन स्पष्ट चिपचिपाहट |
| X-अक्ष | आयाम रहित आवृत्ति . |
यह भी देखें
- सामान्यीकृत मैक्सवेल प्रतिरूप
- केल्विन–वोइगट सामग्री
- ओल्ड्रोयड-बी प्रतिरूप
- मानक रैखिक ठोस प्रतिरूप
- ऊपरी संवहन मैक्सवेल प्रतिरूप
संदर्भ
- ↑ 1.0 1.1 1.2 {{cite book|last=Roylance|first=David|title=इंजीनियरिंग विस्कोलेस्टिसिटी|year=2001|publisher=Massachusetts Institute of Technology|location=Cambridge, MA 02139|pages=8–11|url=http://web.mit.edu/course/3/3.11/www/modules/visco.pdf}
- ↑ 2.0 2.1 Christensen, R. M (1971). Viscoelasticity का सिद्धांत. London, W1X6BA: Academic Press. pp. 16–20. ISBN 9780121742508.
{{cite book}}: CS1 maint: location (link)