यूलर ईंट: Difference between revisions
(→उदाहरण) |
No edit summary |
||
| (24 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Cuboid whose edges and face diagonals have integer lengths}} | {{short description|Cuboid whose edges and face diagonals have integer lengths}} | ||
[[गणित]] में, एक ''' | [[गणित]] में, एक '''यूलर ईंट''', जिसका नाम '''<small>[[लियोनहार्ड ऑयलर|लियोनहार्ड यूलर]]</small>''' के नाम पर रखा गया है, एक [[आयताकार घनाभ]] है जिसके [[किनारों]] और [[फलक विकर्णों]] की लंबाई पूर्णांक होती है। एक '''अभाज्य यूलर ईंट''' एक यूलर ईंट होती है जिसके किनारों की लंबाई [[सापेक्षतः अभाज्य]] होती है। एक '''<small>[[पूर्ण ऑयलर ईंट|पूर्ण यूलर ईंट]]</small>''' वह है जिसका अंतरिक्ष विकर्ण भी एक पूर्णांक हो, लेकिन ऐसी ईंट अभी तक नहीं मिली है। | ||
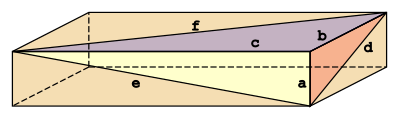
[[File:Euler_brick.svg|right|399x199px|अंगूठा|किनारे वाली यूलर ईंट {{math|''a'', ''b'', ''c''}} और विकर्णों का सामना करें {{math|''d'', ''e'', ''f''}}]] | [[File:Euler_brick.svg|right|399x199px|अंगूठा|किनारे वाली यूलर ईंट {{math|''a'', ''b'', ''c''}} और विकर्णों का सामना करें {{math|''d'', ''e'', ''f''}}]] | ||
== परिभाषा == | == '''परिभाषा''' == | ||
ज्यामितीय पदों में | ज्यामितीय पदों में यूलर ईंट की परिभाषा डायोफैंटिन समीकरणों की निम्नलिखित पद्धति के समाधान के बराबर है: | ||
:<math>\begin{cases} a^2 + b^2 = d^2\\ a^2 + c^2 = e^2\\ b^2 + c^2 = f^2\end{cases}</math> | :<math>\begin{cases} a^2 + b^2 = d^2\\ a^2 + c^2 = e^2\\ b^2 + c^2 = f^2\end{cases}</math> | ||
जहाँ {{math|''a'', ''b'', ''c''}} किनारे हैं और {{math|''d'', ''e'', ''f''}} विकर्ण हैं। | जहाँ {{math|''a'', ''b'', ''c''}} किनारे हैं और {{math|''d'', ''e'', ''f''}} विकर्ण हैं। | ||
== गुण == | == '''गुण''' == | ||
* यदि {{math|(''a'', ''b'', ''c'')}} एक समाधान है, तो {{math|(''ka'', ''kb'', ''kc'')}} भी किसी भी (''k'')का एक समाधान है। अतः,[[परिमेय संख्याओं]] में समाधान पूर्णांक समाधानों के सभी पुनर्विक्रय हैं। किनारे-लंबाई {{math|(''a'', ''b'', ''c'')}}के साथ एक यूलर ईंट को देखते हुए, त्रिक {{math|(''bc'', ''ac'', ''ab'')}} भी एक यूलर ईंट बनाता है।<ref name=Sierpinski>[[Wacław Sierpiński]], ''[[Pythagorean Triangles]]'', Dover Publications, 2003 (orig. ed. 1962).</ref>{{rp|p. 106}} | |||
* | * ''अभाज्य'' यूलर ईंट का ठीक एक किनारा और दो फलक विकर्ण विषम होते हैं। | ||
* | * यूलर ईंट के कम से कम दो किनारे 3 से विभाज्य होते हैं।<ref name=Sierpinski/>{{rp|p. 106}} | ||
* | * यूलर ईंट के कम से कम दो किनारे 4 से विभाज्य होते हैं।<ref name=Sierpinski/>{{rp|p. 106}} | ||
* | * यूलर ईंट का कम से कम एक किनारा 11 से विभाज्य है।<ref name=Sierpinski/>{{rp|p. 106}} | ||
== '''उदाहरण''' == | |||
1719 में [[पॉल हल्के|पॉल हाल्के]] द्वारा खोजी गई सबसे छोटी यूलर ईंट के किनारे {{math|(''a'', ''b'', ''c'') <nowiki>=</nowiki> (44, 117, 240)}} और फलक विकर्ण {{math|(''d'', ''e'', ''f'' ) <nowiki>=</nowiki> (125, 244, 267)}} हैं।<ref>''[https://books.google.com/books?id=S8SBBRNbj6cC&dq=smallest+Euler+brick%2C+discovered+by+Paul+Halcke&pg=PT219 Visions of Infinity: The Great Mathematical Problems]'' By Ian Stewart, Chapter 17</ref> किनारे {{math|(''a'', ''b'', ''c'')}} - फलक विकर्ण {{math|(''d'', ''e'', ''f'')}} के रूप में दिए गए कुछ अन्य छोटे ''प्राथमिक'' समाधान नीचे हैं: | |||
== उदाहरण == | [[File:Euler_brick_examples.svg|thumb|400px|1000 से कम आयामों वाली सभी पांच अभाज्य यूलर ईंटें]]: | ||
1719 में [[पॉल हल्के|पॉल हाल्के]] द्वारा खोजी गई सबसे छोटी | :{| style="border-collapse:collapse;text-align:right;white-space:nowrap;" | ||
[[File:Euler_brick_examples.svg|thumb|400px|1000 से कम आयामों वाली सभी पांच | |||
|(|| 85,|| 132,|| 720||) — (|| 157,|| 725,|| 732||) | |(|| 85,|| 132,|| 720||) — (|| 157,|| 725,|| 732||) | ||
|- | |- | ||
| Line 43: | Line 43: | ||
यूलर ने समस्या के कम से कम दो [[पैरामीट्रिक समाधान]] खोजे, लेकिन दोनों में से कोई भी सभी समाधान नहीं देता।<ref>{{mathworld|urlname=EulerBrick|title=Euler Brick}}</ref> | |||
[[निकोलस सौंडरसन]] के | |||
== '''सूत्र बनाना''' == | |||
यूलर ने समस्या के कम से कम दो [[पैरामीट्रिक समाधान|प्राचलिक समाधान]] खोजे, लेकिन दोनों में से कोई भी सभी समाधान नहीं देता।<ref>{{mathworld|urlname=EulerBrick|title=Euler Brick}}</ref> | |||
[[निकोलस सौंडरसन|सौंडरसन]] के [[पैरामीट्रिक समाधान|प्राचलिक]] सूत्र से यूलर ईंटों की अनंतता उत्पन्न की जा सकती है।<ref name="Saunderson">{{cite web |series=Math table |title=ट्रेजर हंटिंग परफेक्ट यूलर ब्रिक्स|date=February 24, 2009 |first=Oliver |last=Knill |url=http://www.math.harvard.edu/~knill/various/eulercuboid/lecture.pdf |publisher=[[Harvard University]]}}</ref> मान लीजिए {{math|(''u'', ''v'', ''w'')}} एक [[पायथागॉरियन ट्रिपल|पायथागॉरियन त्रिक]] है (यानी, {{math|''u''{{sup|2}} + ''v''{{sup|2}} {{=}} ''w''{{sup|2}}}}) तो<ref name="Sierpinski" />{{rp|105}} किनारे | |||
:<math> a=u|4v^2-w^2| ,\quad b=v|4u^2-w^2|, \quad c=4uvw </math> | :<math> a=u|4v^2-w^2| ,\quad b=v|4u^2-w^2|, \quad c=4uvw </math> | ||
दिया गया फलक विकर्ण | |||
:<math>d=w^3, \quad e=u(4v^2+w^2), \quad f=v(4u^2+w^2).</math> | :<math>d=w^3, \quad e=u(4v^2+w^2), \quad f=v(4u^2+w^2).</math> | ||
कई यूलर ईंटें हैं जो ऊपर की तरह | कई यूलर ईंटें हैं जो ऊपर की तरह प्राचलीकरण नहीं हैं, उदाहरण के लिए किनारों {{math|(''a'', ''b'', ''c'') <nowiki>=</nowiki> (240, 252, 275)}} और फलक विकर्ण {{math|(''d'', ''e'', ''f'' ) <nowiki>=</nowiki> (348, 365, 373)}} के साथ यूलर ईंटें। | ||
== | == परिपूर्ण घनाभ == | ||
{{unsolved|mathematics|Does a perfect cuboid exist?}} | {{unsolved|mathematics|Does a perfect cuboid exist?}} | ||
एक | एक '''परिपूर्ण घनाभ''' (जिसे एक '''पूर्ण यूलर ईंट''' या परिपूर्ण वर्ग भी कहा जाता है) एक यूलर ईंट है जिसका [[अंतरिक्ष विकर्ण]] भी पूर्णांक लंबाई का होता है। दूसरे शब्दों में, यूलर ईंट को परिभाषित करने वाले [[डायोफैंटाइन समीकरणों]] की पद्धति में निम्नलिखित समीकरण जोड़ा गया है: | ||
:<math>a^2 + b^2 + c^2 = g^2,</math> | :<math>a^2 + b^2 + c^2 = g^2,</math> | ||
जहाँ {{math|''g''}} अंतरिक्ष विकर्ण है। {{Asof|2020|September|df=}}, एक परिपूर्ण घनाभ का कोई उदाहरण नहीं मिला था और किसी ने यह सिद्ध नहीं किया है कि कोई अस्तित्व में नहीं है।<ref name=Matson/> | |||
[[File:Euler_brick_perfect.svg|right|thumb|किनारों | [[File:Euler_brick_perfect.svg|right|thumb|किनारों {{math|''a'', ''b'', ''c''}} और फलक विकर्ण {{math|''d'', ''e'', ''f''}} के साथ यूलर ईंट]]संपूर्ण कंप्यूटर खोजों से पता चलता है कि, यदि एक परिपूर्ण घनाभ मौजूद है, | ||
* विषम किनारा 2.5 × 10 से अधिक होना चाहिए<sup>13</sup>,<ref name=Matson>{{cite web |first=Robert D. |last=Matson |title=एक पूर्ण घनाभ के लिए कंप्यूटर खोज के परिणाम|url=http://unsolvedproblems.org/S58.pdf |work=unsolvedproblems.org |accessdate=February 24, 2020}}</ref> | * विषम किनारा 2.5 × 10<sup>13</sup> से अधिक होना चाहिए<sup>13</sup>,<ref name=Matson>{{cite web |first=Robert D. |last=Matson |title=एक पूर्ण घनाभ के लिए कंप्यूटर खोज के परिणाम|url=http://unsolvedproblems.org/S58.pdf |work=unsolvedproblems.org |accessdate=February 24, 2020}}</ref> | ||
* सबसे छोटा किनारा | * सबसे छोटा किनारा {{val|5e11}} से बड़ा होना चाहिए।<ref name=Matson/> *अंतरिक्ष विकर्ण 9 × 10<sup>15</sup> से अधिक होना चाहिए<sup>15</sup>.<ref name=Belogourov>Alexander Belogourov, Distributed search for a perfect cuboid, https://www.academia.edu/39920706/Distributed_search_for_a_perfect_cuboid</ref> | ||
[[मॉड्यूलर अंकगणित]] के आधार पर, गुणों के बारे में कुछ तथ्यों को जाना जाता है, जो एक | [[मॉड्यूलर अंकगणित|मापांक अंकगणित]] के आधार पर, गुणों के बारे में कुछ तथ्यों को जाना जाता है, जो एक अभाज्य पूर्ण घनाभ द्वारा संतुष्ट होना चाहिए, यदि कुछ मौजूद है:<ref>M. Kraitchik, On certain Rational Cuboids, Scripta Mathematica, volume 11 (1945).</ref> | ||
* एक किनारा, दो फलक विकर्ण और अंतरिक्ष विकर्ण विषम होना चाहिए, एक किनारा और शेष फलक विकर्ण 4 से विभाज्य होना चाहिए, और शेष किनारा 16 से विभाज्य होना चाहिए। | * एक किनारा, दो फलक विकर्ण और अंतरिक्ष विकर्ण विषम होना चाहिए, एक किनारा और शेष फलक विकर्ण 4 से विभाज्य होना चाहिए, और शेष किनारा 16 से विभाज्य होना चाहिए। | ||
* दो किनारों की लंबाई 3 से विभाज्य होनी चाहिए और उनमें से कम से कम एक किनारे की लंबाई 9 से विभाज्य होनी चाहिए। | * दो किनारों की लंबाई 3 से विभाज्य होनी चाहिए और उनमें से कम से कम एक किनारे की लंबाई 9 से विभाज्य होनी चाहिए। | ||
| Line 70: | Line 81: | ||
* एक किनारे की लंबाई 11 से विभाज्य होनी चाहिए। | * एक किनारे की लंबाई 11 से विभाज्य होनी चाहिए। | ||
* एक किनारे की लंबाई 19 से विभाज्य होनी चाहिए। | * एक किनारे की लंबाई 19 से विभाज्य होनी चाहिए। | ||
* एक | * एक किनारा या अंतरिक्ष विकर्ण 13 से विभाज्य होना चाहिए। | ||
* एक किनारा, | * एक किनारा, फलक विकर्ण या अंतरिक्ष विकर्ण 17 से विभाज्य होना चाहिए। | ||
* एक किनारा, | * एक किनारा, फलक विकर्ण या अंतरिक्ष विकर्ण 29 से विभाज्य होना चाहिए। | ||
* एक किनारा, | * एक किनारा, फलक विकर्ण या अंतरिक्ष विकर्ण 37 से विभाज्य होना चाहिए। | ||
इसके साथ ही: | इसके साथ ही: | ||
* अंतरिक्ष | * अंतरिक्ष विकर्ण न तो एक [[अभाज्य अगणित संख्या]] है और न ही दो [[अभाज्य संख्याओं का गुणन]] है।<ref name=Korec/>{{rp|p. 579}} | ||
* अंतरिक्ष विकर्ण में केवल अभाज्य विभाजक ≡ 1(mod 4) हो सकते हैं।<ref name=Korec>I. Korec, Lower bounds for Perfect Rational Cuboids, Math. Slovaca, 42 (1992), No. 5, p. 565-582.</ref>{{rp|p. 566}}<ref>Ronald van Luijk, On Perfect Cuboids, June 2000</ref> | * अंतरिक्ष विकर्ण में केवल अभाज्य विभाजक ≡ 1(mod 4) हो सकते हैं।<ref name=Korec>I. Korec, Lower bounds for Perfect Rational Cuboids, Math. Slovaca, 42 (1992), No. 5, p. 565-582.</ref>{{rp|p. 566}}<ref>Ronald van Luijk, On Perfect Cuboids, June 2000</ref> | ||
यदि एक | यदि एक परिपूर्ण घनाभ मौजूद है और <math>a, b, c</math> उसके किनारे हैं, <math>d, e, f</math> - संगत फलक विकर्ण और अंतरिक्ष विकर्ण <math>g</math>, फिर | ||
* भुजाओं की लंबाई वाला त्रिभुज <math>(d^2, e^2, f^2)</math> एक हेरोनियन त्रिभुज एक क्षेत्र है <math>abcg</math> तर्कसंगत कोण द्विभाजक के साथ।<ref name=Luca>Florian Luca (2000) "Perfect Cuboids and Perfect Square Triangles", Mathematics Magazine, 73:5, p. 400-401</ref> | * भुजाओं की लंबाई वाला त्रिभुज <math>(d^2, e^2, f^2)</math> एक [[हेरोनियन त्रिभुज]] एक क्षेत्र है, <math>abcg</math> तर्कसंगत कोण द्विभाजक के साथ।<ref name=Luca>Florian Luca (2000) "Perfect Cuboids and Perfect Square Triangles", Mathematics Magazine, 73:5, p. 400-401</ref> | ||
* | * भुजाओं की लंबाई के साथ न्यूनकोण त्रिभुज <math>(af, be, cd)</math>, भुजाओं की लंबाई के साथ अधिककोण त्रिभुज <math>(bf, ae, gd), (ad, cf, ge), (ce, bd, gf)</math> हेरोनियन त्रिभुज हैं, जिनका क्षेत्रफल <math>\frac{abcg}{2}</math> के बराबर है/ | ||
=== घनाभ अनुमान === | === घनाभ अनुमान === | ||
तीन घनाभ अनुमान तीन | तीन '''घनाभ अनुमान''' तीन [[गणितीय]] प्रस्ताव हैं जो कई [[पूर्णांक]] मापदंडों के आधार पर [[पूर्णांक गुणांक]] वाले तीन [[अविभाजित बहुपदों]] की [[अलघुकरणीय बहुपद|अलघुकरणीय]] का दावा करते हैं। अनुमान [[पूर्ण घनाभ]] समस्या से संबंधित हैं।<ref name=shr_01>{{cite journal |author=Sharipov R.A. |title=बिल्कुल सही घनाभ और अलघुकरणीय बहुपद|journal=Ufa Math Journal|year=2012 |volume=4 |issue=1 |pages=153–160|arxiv=1108.5348|bibcode=2011arXiv1108.5348S}}</ref><ref name=shr_02>{{cite journal |author=Sharipov R.A. |title=पूर्ण घनाभ समस्या के लिए स्पर्शोन्मुख दृष्टिकोण|journal=Ufa Math Journal|year=2015 |volume=7 |issue=3 |pages=100–113|doi=10.13108/2015-7-3-95 }</ref> हालांकि वे पूर्ण घनाभ समस्या के समतुल्य नहीं हैं, यदि ये तीनों अनुमान मान्य हैं, तो कोई भी पूर्ण घनाभ मौजूद नहीं है। वे न तो सिद्ध होते हैं और न ही असिद्ध। | ||
घनाभ अनुमान 1. '' | '''घनाभ अनुमान 1'''. ''किन्हीं दो धनात्मक [[सहअभाज्य]] पूर्णांक संख्याओं के लिए <math>a \neq u</math> आठवीं कोटि के बहुपद'' | ||
{{NumBlk|:|<math> | {{NumBlk|:|<math> | ||
P_{au}(t)=t^8+6\,(u^2-a^2)\,t^6+(a^4-4\,a^2\,u^2+u^4)\,t^4-6\,a^2\,u^2\,(u^2-a^2)\,t^2+u^4\,a^4</math>|{{EquationRef|1}}}} | P_{au}(t)=t^8+6\,(u^2-a^2)\,t^6+(a^4-4\,a^2\,u^2+u^4)\,t^4-6\,a^2\,u^2\,(u^2-a^2)\,t^2+u^4\,a^4</math>|{{EquationRef|1}}}} | ||
पूर्णांकों के वलय | पूर्णांकों के [[वलय]] पर अलघुकरणीय <math>\mathbb Z</math> है / | ||
'घनाभ अनुमान 2.' किन्हीं दो धनात्मक | '''घनाभ अनुमान 2.''' ''किन्हीं दो धनात्मक सहअभाज्य पूर्णांक संख्याओं के लिए <math>p \neq q</math> दसवीं कोटि के बहुपद'' | ||
{{NumBlk|:|<math>\begin{align} | {{NumBlk|:|<math>\begin{align} | ||
| Line 102: | Line 113: | ||
</math>|{{EquationRef|2}}}} | </math>|{{EquationRef|2}}}} | ||
पूर्णांकों के वलय पर अलघुकरणीय | पूर्णांकों के वलय पर अलघुकरणीय | ||
<math>\mathbb Z</math> है / | |||
'घनाभ अनुमान 3.' किन्हीं तीन धनात्मक | '''घनाभ अनुमान 3'''. ''किन्हीं तीन धनात्मक सहअभाज्य पूर्णांक संख्याओं के लिए <math>a</math>, <math>b</math>, <math>u</math> ऐसे हैं जैसे कि कोई पद नहीं है'' | ||
{{NumBlk|:|<math>\begin{array}{lcr} | {{NumBlk|:|<math>\begin{array}{lcr} | ||
| Line 111: | Line 125: | ||
\end{array}</math>|{{EquationRef|3}}}} | \end{array}</math>|{{EquationRef|3}}}} | ||
बारहवीं | ''बारहवीं कोटि का बहुपद पूरा हो गया है'' | ||
{{NumBlk|:|<math>\begin{align} | {{NumBlk|:|<math>\begin{align} | ||
| Line 121: | Line 135: | ||
\end{align}</math>|{{EquationRef|4}}}} | \end{align}</math>|{{EquationRef|4}}}} | ||
पूर्णांकों के वलय पर अलघुकरणीय | पूर्णांकों के वलय पर अलघुकरणीय | ||
== लगभग-परिपूर्ण घनाभ == | <math>\mathbb Z</math> है / | ||
लगभग | == '''लगभग-परिपूर्ण घनाभ''' == | ||
लगभग परिपूर्ण घनाभ की 7 में से 6 लम्बाई परिमेय है। इस तरह के घनाभों को तीन प्रकारों में बांटा जा सकता है, जिन्हें ''निकाय, किनारा और फलक'' घनाभ कहा जाता है।<ref>Rathbun R. L., Granlund Т., The integer cuboid table with body, edge, and face type of solutions // Math. Comp., 1994, Vol. 62, P. 441-442.</ref> समिति घनाभ की स्थिति में, समिति (अंतरिक्ष) विकर्ण {{math|''g''}} अपरिमेय है। किनारे वाले घनाभ के लिए, किनारों {{math|''a'', ''b'', ''c''}} में से एक अपरिमेय है। फलक घनाभ का एक विकर्ण {{math|''d'', ''e'', ''f''}} अपरिमेय है। | |||
समिति घनाभ को आमतौर पर लियोनहार्ड यूलर के सम्मान में ''यूलर घनाभ'' के रूप में जाना जाता है, जिन्होंने इस प्रकार के घनाभ पर चर्चा की।<ref>Euler, Leonhard, Vollst¨andige Anleitung zur Algebra, Kayserliche Akademie der Wissenschaften, St. Petersburg, 1771</ref> वह ''फलक'' घनाभों के बारे में भी जानते थे, और उन्होंने (104, 153, 672) उदाहरण प्रदान किया।<ref> Euler, Leonhard, Vollst¨andige Anleitung zur Algebra, 2, Part II, 236, English translation: Euler, Elements of Algebra, Springer-Verlag 1984</ref> तीन पूर्णांक घनाभ किनारे की लंबाई और एक फलक घनाभ की तीन पूर्णांक विकर्ण लंबाई को [[हेरोनियन टेट्राहेड्रॉन|हेरोनियन चतुष्फलक]] के किनारे की लंबाई के रूप में भी व्याख्या की जा सकती है जो कि [[श्लाफली ऑर्थोस्कीम]] भी है। असीम रूप से कई फलक वाले घनाभ हैं, और असीम रूप से कई हेरोनियन ऑर्थोस्केम हैं।<ref>{{citation | |||
| date = May 1985 | | date = May 1985 | ||
| department = Solutions | | department = Solutions | ||
| Line 135: | Line 150: | ||
| url = https://cms.math.ca/crux/backfile/Crux_v11n05_May.pdf | | url = https://cms.math.ca/crux/backfile/Crux_v11n05_May.pdf | ||
| volume = 11}}</ref> | | volume = 11}}</ref> | ||
किनारों, | किनारों, फलक विकर्ण और अंतरिक्ष विकर्ण (a, b, c, d, e, f, g) के रूप में दिए गए प्रत्येक प्रकार के लगभग '''परिपूर्ण''' घनाभों के लिए सबसे छोटे समाधान इस प्रकार हैं: | ||
* | * '''समिति घनाभ:''' {{math|(44, 117, 240, 125, 244, 267, {{sqrt|73225}})}} | ||
* किनारा घनाभ: {{math|(520, 576, {{sqrt|618849}}, 776, 943, 975, 1105)}} | * '''किनारा घनाभ:''' {{math|(520, 576, {{sqrt|618849}}, 776, 943, 975, 1105)}} | ||
* | * '''फलक घनाभ:''' {{math|(104, 153, 672, 185, 680, {{sqrt|474993}}, 697)}} | ||
{{Asof|2020|July}}, 200,000,000,027 से कम सबसे छोटे पूर्णांक किनारे वाले 167,043 पाए गए घनाभ हैं: 61,042 यूलर ( | {{Asof|2020|July}}, 200,000,000,027 से कम सबसे छोटे पूर्णांक किनारे वाले 167,043 पाए गए घनाभ हैं: 61,042 यूलर (समिति) घनाभ हैं, 16,612 एक सम्मिश्र संख्या किनारे की लंबाई वाले किनारे के घनाभ हैं, 32,286 किनारे के घनाभ थे, और 57,103 फलक घनाभ थे।<ref>{{cite arXiv |eprint=1705.05929v4 |class=math.NT |first=Randall L. |last=Rathbun |title=पूर्णांक घनाभ तालिका|date=14 Jul 2020}}</ref> | ||
{{Asof|2017|December}}, एक विस्तृत खोज ने 1,125,899,906,842,624: 194,652 से कम पूर्णांक अंतरिक्ष विकर्ण के साथ सभी किनारे और | {{Asof|2017|December}}, एक विस्तृत खोज ने 1,125,899,906,842,624: 194,652 से कम पूर्णांक अंतरिक्ष विकर्ण के साथ सभी किनारे और फलक घनाभों को गिना, 350,778 फलक घनाभ थे।<ref name=Belogourov/> | ||
== पूर्ण | == पूर्ण समान्तरषटफलक == | ||
एक पूर्ण | एक पूर्ण [[समान्तरषटफलक]] पूर्णांक-लंबाई वाले किनारों, फलक विकर्णों और निकाय के विकर्णों के साथ एक समान्तरषटफलक है, लेकिन जरूरी नहीं कि सभी समकोण हों; एक आदर्श घनाभ एक पूर्ण समान्तरषटफलक की एक विशेष स्थिति है। 2009 में, [[रिचर्ड गाइ]] के एक अनिर्णीत प्रश्न का उत्तर देते हुए,<ref>{{Cite journal|first1=Jorge F.|last1=Sawyer|first2=Clifford A.|last2=Reiter|year=2011|title=बिल्कुल सही समांतर चतुर्भुज मौजूद हैं|journal=[[Mathematics of Computation]]|volume=80|issue=274|pages=1037–1040|arxiv=0907.0220|doi=10.1090/s0025-5718-2010-02400-7|s2cid=206288198 }}.</ref> दर्जनों सटीक समान्तरषटफलकों का अस्तित्व दिखाया गया था। इनमें से कुछ पूर्ण समान्तरषटफलकों में दो आयताकार फलक होते हैं। सबसे छोटे पूर्ण समान्तरषटफलक के किनारे 271, 106 और 103 हैं; लघु फलक विकर्ण 101, 266 और 255; लंबे फलक विकर्ण 183, 312 और 323; और निकाय के विकर्ण 374, 300, 278 और 272 हैं। | ||
== यह भी देखें == | == यह भी देखें == | ||
* | * [[पाइथागोरियन]] [[चतुष्कोण]] | ||
== टिप्पणियाँ == | == टिप्पणियाँ == | ||
| Line 163: | Line 178: | ||
{{DEFAULTSORT:Euler Brick}} | {{DEFAULTSORT:Euler Brick}} | ||
[[Category: | [[Category:All articles containing potentially dated statements|Euler Brick]] | ||
[[Category:Created On 17/03/2023]] | [[Category:Articles containing potentially dated statements from December 2017|Euler Brick]] | ||
[[Category:Articles containing potentially dated statements from July 2020|Euler Brick]] | |||
[[Category:Articles containing potentially dated statements from September 2020|Euler Brick]] | |||
[[Category:Articles with invalid date parameter in template|Euler Brick]] | |||
[[Category:Created On 17/03/2023|Euler Brick]] | |||
[[Category:Lua-based templates|Euler Brick]] | |||
[[Category:Machine Translated Page|Euler Brick]] | |||
[[Category:Pages with script errors|Euler Brick]] | |||
[[Category:Short description with empty Wikidata description|Euler Brick]] | |||
[[Category:Template documentation pages|Short description/doc]] | |||
[[Category:Templates Vigyan Ready|Euler Brick]] | |||
[[Category:Templates that add a tracking category|Euler Brick]] | |||
[[Category:Templates that generate short descriptions|Euler Brick]] | |||
[[Category:Templates using TemplateData|Euler Brick]] | |||
[[Category:घनाभ|Euler Brick]] | |||
[[Category:ठोस ज्यामिति की अंकगणितीय समस्याएं|Euler Brick]] | |||
[[Category:डायोफैंटाइन समीकरण|Euler Brick]] | |||
[[Category:पाइथागोरस प्रमेय|Euler Brick]] | |||
[[Category:संख्या सिद्धांत विषयक अनसुलझी समस्याएं|Euler Brick]] | |||
Latest revision as of 11:03, 14 April 2023
गणित में, एक यूलर ईंट, जिसका नाम लियोनहार्ड यूलर के नाम पर रखा गया है, एक आयताकार घनाभ है जिसके किनारों और फलक विकर्णों की लंबाई पूर्णांक होती है। एक अभाज्य यूलर ईंट एक यूलर ईंट होती है जिसके किनारों की लंबाई सापेक्षतः अभाज्य होती है। एक पूर्ण यूलर ईंट वह है जिसका अंतरिक्ष विकर्ण भी एक पूर्णांक हो, लेकिन ऐसी ईंट अभी तक नहीं मिली है।
परिभाषा
ज्यामितीय पदों में यूलर ईंट की परिभाषा डायोफैंटिन समीकरणों की निम्नलिखित पद्धति के समाधान के बराबर है:
जहाँ a, b, c किनारे हैं और d, e, f विकर्ण हैं।
गुण
- यदि (a, b, c) एक समाधान है, तो (ka, kb, kc) भी किसी भी (k)का एक समाधान है। अतः,परिमेय संख्याओं में समाधान पूर्णांक समाधानों के सभी पुनर्विक्रय हैं। किनारे-लंबाई (a, b, c)के साथ एक यूलर ईंट को देखते हुए, त्रिक (bc, ac, ab) भी एक यूलर ईंट बनाता है।[1]: p. 106
- अभाज्य यूलर ईंट का ठीक एक किनारा और दो फलक विकर्ण विषम होते हैं।
- यूलर ईंट के कम से कम दो किनारे 3 से विभाज्य होते हैं।[1]: p. 106
- यूलर ईंट के कम से कम दो किनारे 4 से विभाज्य होते हैं।[1]: p. 106
- यूलर ईंट का कम से कम एक किनारा 11 से विभाज्य है।[1]: p. 106
उदाहरण
1719 में पॉल हाल्के द्वारा खोजी गई सबसे छोटी यूलर ईंट के किनारे (a, b, c) = (44, 117, 240) और फलक विकर्ण (d, e, f ) = (125, 244, 267) हैं।[2] किनारे (a, b, c) - फलक विकर्ण (d, e, f) के रूप में दिए गए कुछ अन्य छोटे प्राथमिक समाधान नीचे हैं:
:
( 85, 132, 720 ) — ( 157, 725, 732 ) ( 140, 480, 693 ) — ( 500, 707, 843 ) ( 160, 231, 792 ) — ( 281, 808, 825 ) ( 187, 1020, 1584 ) — ( 1037, 1595, 1884 ) ( 195, 748, 6336 ) — ( 773, 6339, 6380 ) ( 240, 252, 275 ) — ( 348, 365, 373 ) ( 429, 880, 2340 ) — ( 979, 2379, 2500 ) ( 495, 4888, 8160 ) — ( 4913, 8175, 9512 ) ( 528, 5796, 6325 ) — ( 5820, 6347, 8579 )
सूत्र बनाना
यूलर ने समस्या के कम से कम दो प्राचलिक समाधान खोजे, लेकिन दोनों में से कोई भी सभी समाधान नहीं देता।[3]
सौंडरसन के प्राचलिक सूत्र से यूलर ईंटों की अनंतता उत्पन्न की जा सकती है।[4] मान लीजिए (u, v, w) एक पायथागॉरियन त्रिक है (यानी, u2 + v2 = w2) तो[1]: 105 किनारे
दिया गया फलक विकर्ण
कई यूलर ईंटें हैं जो ऊपर की तरह प्राचलीकरण नहीं हैं, उदाहरण के लिए किनारों (a, b, c) = (240, 252, 275) और फलक विकर्ण (d, e, f ) = (348, 365, 373) के साथ यूलर ईंटें।
परिपूर्ण घनाभ
Does a perfect cuboid exist?
एक परिपूर्ण घनाभ (जिसे एक पूर्ण यूलर ईंट या परिपूर्ण वर्ग भी कहा जाता है) एक यूलर ईंट है जिसका अंतरिक्ष विकर्ण भी पूर्णांक लंबाई का होता है। दूसरे शब्दों में, यूलर ईंट को परिभाषित करने वाले डायोफैंटाइन समीकरणों की पद्धति में निम्नलिखित समीकरण जोड़ा गया है:
जहाँ g अंतरिक्ष विकर्ण है। As of September 2020[update], एक परिपूर्ण घनाभ का कोई उदाहरण नहीं मिला था और किसी ने यह सिद्ध नहीं किया है कि कोई अस्तित्व में नहीं है।[5]
संपूर्ण कंप्यूटर खोजों से पता चलता है कि, यदि एक परिपूर्ण घनाभ मौजूद है,
- विषम किनारा 2.5 × 1013 से अधिक होना चाहिए13,[5]
- सबसे छोटा किनारा 5×1011 से बड़ा होना चाहिए।[5] *अंतरिक्ष विकर्ण 9 × 1015 से अधिक होना चाहिए15.[6]
मापांक अंकगणित के आधार पर, गुणों के बारे में कुछ तथ्यों को जाना जाता है, जो एक अभाज्य पूर्ण घनाभ द्वारा संतुष्ट होना चाहिए, यदि कुछ मौजूद है:[7]
- एक किनारा, दो फलक विकर्ण और अंतरिक्ष विकर्ण विषम होना चाहिए, एक किनारा और शेष फलक विकर्ण 4 से विभाज्य होना चाहिए, और शेष किनारा 16 से विभाज्य होना चाहिए।
- दो किनारों की लंबाई 3 से विभाज्य होनी चाहिए और उनमें से कम से कम एक किनारे की लंबाई 9 से विभाज्य होनी चाहिए।
- एक किनारे की लंबाई 5 से विभाज्य होनी चाहिए।
- एक किनारे की लंबाई 7 से विभाज्य होनी चाहिए।
- एक किनारे की लंबाई 11 से विभाज्य होनी चाहिए।
- एक किनारे की लंबाई 19 से विभाज्य होनी चाहिए।
- एक किनारा या अंतरिक्ष विकर्ण 13 से विभाज्य होना चाहिए।
- एक किनारा, फलक विकर्ण या अंतरिक्ष विकर्ण 17 से विभाज्य होना चाहिए।
- एक किनारा, फलक विकर्ण या अंतरिक्ष विकर्ण 29 से विभाज्य होना चाहिए।
- एक किनारा, फलक विकर्ण या अंतरिक्ष विकर्ण 37 से विभाज्य होना चाहिए।
इसके साथ ही:
- अंतरिक्ष विकर्ण न तो एक अभाज्य अगणित संख्या है और न ही दो अभाज्य संख्याओं का गुणन है।[8]: p. 579
- अंतरिक्ष विकर्ण में केवल अभाज्य विभाजक ≡ 1(mod 4) हो सकते हैं।[8]: p. 566 [9]
यदि एक परिपूर्ण घनाभ मौजूद है और उसके किनारे हैं, - संगत फलक विकर्ण और अंतरिक्ष विकर्ण , फिर
- भुजाओं की लंबाई वाला त्रिभुज एक हेरोनियन त्रिभुज एक क्षेत्र है, तर्कसंगत कोण द्विभाजक के साथ।[10]
- भुजाओं की लंबाई के साथ न्यूनकोण त्रिभुज , भुजाओं की लंबाई के साथ अधिककोण त्रिभुज हेरोनियन त्रिभुज हैं, जिनका क्षेत्रफल के बराबर है/
घनाभ अनुमान
तीन घनाभ अनुमान तीन गणितीय प्रस्ताव हैं जो कई पूर्णांक मापदंडों के आधार पर पूर्णांक गुणांक वाले तीन अविभाजित बहुपदों की अलघुकरणीय का दावा करते हैं। अनुमान पूर्ण घनाभ समस्या से संबंधित हैं।[11][12] हालांकि वे पूर्ण घनाभ समस्या के समतुल्य नहीं हैं, यदि ये तीनों अनुमान मान्य हैं, तो कोई भी पूर्ण घनाभ मौजूद नहीं है। वे न तो सिद्ध होते हैं और न ही असिद्ध।
घनाभ अनुमान 1. किन्हीं दो धनात्मक सहअभाज्य पूर्णांक संख्याओं के लिए आठवीं कोटि के बहुपद
-
(1)
पूर्णांकों के वलय पर अलघुकरणीय है /
घनाभ अनुमान 2. किन्हीं दो धनात्मक सहअभाज्य पूर्णांक संख्याओं के लिए दसवीं कोटि के बहुपद
-
(2)
पूर्णांकों के वलय पर अलघुकरणीय
है /
घनाभ अनुमान 3. किन्हीं तीन धनात्मक सहअभाज्य पूर्णांक संख्याओं के लिए , , ऐसे हैं जैसे कि कोई पद नहीं है
-
(3)
बारहवीं कोटि का बहुपद पूरा हो गया है
-
(4)
पूर्णांकों के वलय पर अलघुकरणीय
है /
लगभग-परिपूर्ण घनाभ
लगभग परिपूर्ण घनाभ की 7 में से 6 लम्बाई परिमेय है। इस तरह के घनाभों को तीन प्रकारों में बांटा जा सकता है, जिन्हें निकाय, किनारा और फलक घनाभ कहा जाता है।[13] समिति घनाभ की स्थिति में, समिति (अंतरिक्ष) विकर्ण g अपरिमेय है। किनारे वाले घनाभ के लिए, किनारों a, b, c में से एक अपरिमेय है। फलक घनाभ का एक विकर्ण d, e, f अपरिमेय है।
समिति घनाभ को आमतौर पर लियोनहार्ड यूलर के सम्मान में यूलर घनाभ के रूप में जाना जाता है, जिन्होंने इस प्रकार के घनाभ पर चर्चा की।[14] वह फलक घनाभों के बारे में भी जानते थे, और उन्होंने (104, 153, 672) उदाहरण प्रदान किया।[15] तीन पूर्णांक घनाभ किनारे की लंबाई और एक फलक घनाभ की तीन पूर्णांक विकर्ण लंबाई को हेरोनियन चतुष्फलक के किनारे की लंबाई के रूप में भी व्याख्या की जा सकती है जो कि श्लाफली ऑर्थोस्कीम भी है। असीम रूप से कई फलक वाले घनाभ हैं, और असीम रूप से कई हेरोनियन ऑर्थोस्केम हैं।[16] किनारों, फलक विकर्ण और अंतरिक्ष विकर्ण (a, b, c, d, e, f, g) के रूप में दिए गए प्रत्येक प्रकार के लगभग परिपूर्ण घनाभों के लिए सबसे छोटे समाधान इस प्रकार हैं:
- समिति घनाभ: (44, 117, 240, 125, 244, 267, √73225)
- किनारा घनाभ: (520, 576, √618849, 776, 943, 975, 1105)
- फलक घनाभ: (104, 153, 672, 185, 680, √474993, 697)
As of July 2020[update], 200,000,000,027 से कम सबसे छोटे पूर्णांक किनारे वाले 167,043 पाए गए घनाभ हैं: 61,042 यूलर (समिति) घनाभ हैं, 16,612 एक सम्मिश्र संख्या किनारे की लंबाई वाले किनारे के घनाभ हैं, 32,286 किनारे के घनाभ थे, और 57,103 फलक घनाभ थे।[17]
As of December 2017[update], एक विस्तृत खोज ने 1,125,899,906,842,624: 194,652 से कम पूर्णांक अंतरिक्ष विकर्ण के साथ सभी किनारे और फलक घनाभों को गिना, 350,778 फलक घनाभ थे।[6]
पूर्ण समान्तरषटफलक
एक पूर्ण समान्तरषटफलक पूर्णांक-लंबाई वाले किनारों, फलक विकर्णों और निकाय के विकर्णों के साथ एक समान्तरषटफलक है, लेकिन जरूरी नहीं कि सभी समकोण हों; एक आदर्श घनाभ एक पूर्ण समान्तरषटफलक की एक विशेष स्थिति है। 2009 में, रिचर्ड गाइ के एक अनिर्णीत प्रश्न का उत्तर देते हुए,[18] दर्जनों सटीक समान्तरषटफलकों का अस्तित्व दिखाया गया था। इनमें से कुछ पूर्ण समान्तरषटफलकों में दो आयताकार फलक होते हैं। सबसे छोटे पूर्ण समान्तरषटफलक के किनारे 271, 106 और 103 हैं; लघु फलक विकर्ण 101, 266 और 255; लंबे फलक विकर्ण 183, 312 और 323; और निकाय के विकर्ण 374, 300, 278 और 272 हैं।
यह भी देखें
टिप्पणियाँ
- ↑ 1.0 1.1 1.2 1.3 1.4 Wacław Sierpiński, Pythagorean Triangles, Dover Publications, 2003 (orig. ed. 1962).
- ↑ Visions of Infinity: The Great Mathematical Problems By Ian Stewart, Chapter 17
- ↑ Weisstein, Eric W. "Euler Brick". MathWorld.
- ↑ Knill, Oliver (February 24, 2009). "ट्रेजर हंटिंग परफेक्ट यूलर ब्रिक्स" (PDF). Math table. Harvard University.
- ↑ 5.0 5.1 5.2 Matson, Robert D. "एक पूर्ण घनाभ के लिए कंप्यूटर खोज के परिणाम" (PDF). unsolvedproblems.org. Retrieved February 24, 2020.
- ↑ 6.0 6.1 Alexander Belogourov, Distributed search for a perfect cuboid, https://www.academia.edu/39920706/Distributed_search_for_a_perfect_cuboid
- ↑ M. Kraitchik, On certain Rational Cuboids, Scripta Mathematica, volume 11 (1945).
- ↑ 8.0 8.1 I. Korec, Lower bounds for Perfect Rational Cuboids, Math. Slovaca, 42 (1992), No. 5, p. 565-582.
- ↑ Ronald van Luijk, On Perfect Cuboids, June 2000
- ↑ Florian Luca (2000) "Perfect Cuboids and Perfect Square Triangles", Mathematics Magazine, 73:5, p. 400-401
- ↑ Sharipov R.A. (2012). "बिल्कुल सही घनाभ और अलघुकरणीय बहुपद". Ufa Math Journal. 4 (1): 153–160. arXiv:1108.5348. Bibcode:2011arXiv1108.5348S.
- ↑ {{cite journal |author=Sharipov R.A. |title=पूर्ण घनाभ समस्या के लिए स्पर्शोन्मुख दृष्टिकोण|journal=Ufa Math Journal|year=2015 |volume=7 |issue=3 |pages=100–113|doi=10.13108/2015-7-3-95 }
- ↑ Rathbun R. L., Granlund Т., The integer cuboid table with body, edge, and face type of solutions // Math. Comp., 1994, Vol. 62, P. 441-442.
- ↑ Euler, Leonhard, Vollst¨andige Anleitung zur Algebra, Kayserliche Akademie der Wissenschaften, St. Petersburg, 1771
- ↑ Euler, Leonhard, Vollst¨andige Anleitung zur Algebra, 2, Part II, 236, English translation: Euler, Elements of Algebra, Springer-Verlag 1984
- ↑ "Problem 930" (PDF), Solutions, Crux Mathematicorum, 11 (5): 162–166, May 1985
- ↑ Rathbun, Randall L. (14 Jul 2020). "पूर्णांक घनाभ तालिका". arXiv:1705.05929v4 [math.NT].
- ↑ Sawyer, Jorge F.; Reiter, Clifford A. (2011). "बिल्कुल सही समांतर चतुर्भुज मौजूद हैं". Mathematics of Computation. 80 (274): 1037–1040. arXiv:0907.0220. doi:10.1090/s0025-5718-2010-02400-7. S2CID 206288198..
संदर्भ
- Leech, John (1977). "The Rational Cuboid Revisited". American Mathematical Monthly. 84 (7): 518–533. doi:10.2307/2320014. JSTOR 2320014.
- Shaffer, Sherrill (1987). "Necessary Divisors of Perfect Integer Cuboids". Abstracts of the American Mathematical Society. 8 (6): 440.
- Guy, Richard K. (2004). Unsolved Problems in Number Theory. Springer-Verlag. pp. 275–283. ISBN 0-387-20860-7.
- Kraitchik, M. (1945). "On certain rational cuboids". Scripta Mathematica. 11: 317–326.
- Roberts, Tim (2010). "Some constraints on the existence of a perfect cuboid". Australian Mathematical Society Gazette. 37: 29–31. ISSN 1326-2297.