शुद्ध बल: Difference between revisions
No edit summary |
No edit summary |
||
| (17 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
[[यांत्रिकी]] में, शुद्ध बल कण या [[भौतिक वस्तु]] पर कार्य करने वाली शक्तियों का सदिश योग होता है। शुद्ध बल एक एकल बल है जो कण की [[गति]] पर मूल बलों के प्रभाव को प्रतिस्थापित करता है। यह कण को न्यूटन के गति के नियमों द्वारा वर्णित उन सभी वास्तविक बलों के समान [[त्वरण]] देता है | न्यूटन की गति का दूसरा नियम। | [[यांत्रिकी]] में, शुद्ध बल कण या [[भौतिक वस्तु]] पर कार्य करने वाली शक्तियों का सदिश योग होता है। शुद्ध बल एक एकल बल है जो कण की [[गति]] पर मूल बलों के प्रभाव को प्रतिस्थापित करता है। यह कण को न्यूटन के गति के नियमों द्वारा वर्णित उन सभी वास्तविक बलों के समान [[त्वरण]] देता है | न्यूटन की गति का दूसरा नियम। | ||
एक शुद्ध बल के | एक शुद्ध बल के अनुप्रयोग के बिंदु से जुड़े टॉर्क को निर्धारित करना संभव है इसलिए यह बल की मूल प्रणाली के अनुसार वस्तु के जेट की गति को बनाए रखे। इससे जुड़ा [[ टॉर्कः |टॉर्कः]] , शुद्ध बल, 'परिणामी बल' बन जाता है और वस्तु की घूर्णी गति पर वैसा ही प्रभाव पड़ता है जैसा कि सभी वास्तविक बलों को एक साथ लिया जाता है।<ref>Symon, Keith R. (1964), Mechanics, Addison-Wesley, {{LCCN|605164}}</ref> बलों की एक प्रणाली के लिए टॉर्क मुक्त परिणामी बल को परिभाषित करना संभव है। इस स्थिति में, शुद्ध बल, जब किये गये कार्य को उचित रेखा पर क्रियान्वित होता है, तो अनुप्रयोग के बिंदु पर सभी बलों के समान प्रभाव पड़ता है। टॉर्क-मुक्त परिणामी बल का पता लगाना सदैव संभव नहीं होता है। | ||
| Line 9: | Line 9: | ||
== संपूर्ण बल == | == संपूर्ण बल == | ||
[[File:Addition of forces.JPG|thumb|350px|A | [[File:Addition of forces.JPG|thumb|350px|A बलों को जोड़ने के लिए आरेखीय विधि।]]बल एक यूक्लिडियन सदिश राशि है, जिसका अर्थ है कि इसकी एक परिमाण और दिशा है, और इसे सामान्यतः '''F''' जैसे बोल्डफेस का उपयोग करके या प्रतीक पर रेखा का उपयोग करके दर्शाया जाता है, जैसे कि <math>\scriptstyle \vec F</math>. | ||
रेखांकन के रूप में, बल को उसके | रेखांकन के रूप में, बल को उसके अनुअनुप्रयोग बिंदु A से बिंदु B तक एक रेखा खंड के रूप में दर्शाया जाता है, जो इसकी दिशा और परिमाण को परिभाषित करता है। खंड AB की लंबाई बल के परिमाण को दर्शाती है। | ||
[[वेक्टर पथरी|वेक्टर गणना]] का विकास 1800 सदी के अंत और 1900 सदी के प्रारंभ में हुआ था। बलों को जोड़ने के लिए प्रयुक्त [[समांतर चतुर्भुज नियम]], | [[वेक्टर पथरी|वेक्टर गणना]] का विकास 1800 सदी के अंत और 1900 सदी के प्रारंभ में हुआ था। बलों को जोड़ने के लिए प्रयुक्त [[समांतर चतुर्भुज नियम]], यधपि, प्राचीन काल से है और गैलीलियो और न्यूटन द्वारा स्पष्ट रूप से चिन्हित किया गया है।<ref>Michael J. Crowe (1967). ''A History of Vector Analysis : The Evolution of the Idea of a Vectorial System''. Dover Publications (reprint edition; {{ISBN|0-486-67910-1}}).</ref> आरेख बलों के जोड़ को दर्शाता है <math>\scriptstyle \vec{F}_{1}</math> और <math>\scriptstyle \vec{F}_{2}</math>. योग <math>\scriptstyle \vec F</math> दो बलों में से प्रत्येक को दो बलों द्वारा परिभाषित समांतर चतुर्भुज के विकर्ण के रूप में खींचा जाता है। | ||
विस्तारित निकाय पर लगाए गए बलों के अनुप्रयोग के विभिन्न बिंदु हो सकते हैं। बल बद्ध सदिश होते हैं और इन्हें तभी जोड़ा जा सकता है जब वे एक ही बिंदु पर क्रियान्वित हों। पिंड पर कार्य करने वाली सभी शक्तियों से प्राप्त शुद्ध बल तब तक अपनी गति को संरक्षित नहीं करता है जब तक कि एक ही बिंदु पर क्रियान्वित नहीं किया जाता है, और अनुप्रयोग के नए बिंदु से जुड़े उपयुक्त टॉर्क के साथ निर्धारित किया जाता है। उपयुक्त बल आघूर्ण के साथ एक बिंदु पर लगाए गए पिंड पर कुल बल को परिणामी बल और बल आघूर्ण के रूप में जाना जाता है। | |||
विस्तारित निकाय पर लगाए गए बलों के | |||
== बलों के योग के लिए समानांतर चतुर्भुज नियम == | == बलों के योग के लिए समानांतर चतुर्भुज नियम == | ||
{{See also| | {{See also|बल का समांतर चतुर्भुज}}[[File:Parallelogram1.svg|right|समांतर चतुर्भुज एबीसीडी]]बल को एक बाध्य सदिश के रूप में जाना जाता है—जिसका अर्थ है कि इसकी एक दिशा और परिमाण और अनुप्रयोग का बिंदु है। बल को परिभाषित करने की सुविधाजनक विधि बिंदु A से बिंदु B तक एक रेखा खंड है। यदि हम इन बिंदुओं के निर्देशांक को 'A' = ( A<sub>''x''</sub>, A<sub>''y''</sub>, A<sub>''z''</sub>), और B = (B <sub>''x''</sub>, B <sub>''y''</sub>, B <sub>''z''</sub>), के रूप में निरूपित करते हैं तो A पर क्रियान्वित बल वेक्टर द्वारा दिया जाता है | ||
: <math>\mathbf{F}= \mathbf{B}-\mathbf{A} = (B_x-A_x, B_y-A_y, B_z-A_z).</math> | : <math>\mathbf{F}= \mathbf{B}-\mathbf{A} = (B_x-A_x, B_y-A_y, B_z-A_z).</math> | ||
वेक्टर B-A की लंबाई F के परिमाण को परिभाषित करती है और इसके द्वारा दिया जाता है | |||
: <math>|\mathbf{F}| = \sqrt{(B_x-A_x)^2+(B_y-A_y)^2+(B_z-A_z)^2}.</math> | : <math>|\mathbf{F}| = \sqrt{(B_x-A_x)^2+(B_y-A_y)^2+(B_z-A_z)^2}.</math> | ||
दो बलों का योग F<sub>1</sub> और | दो बलों का योग F<sub>1</sub> और F<sub>2</sub> A पर क्रियान्वित उन खंडों के योग से गणना की जा सकती है जो उन्हें परिभाषित करते हैं। चलो 'F'<sub>1</sub>= B−A और F<sub>2</sub>= D−A, तो इन दो सदिशों का योग है | ||
: <math>\mathbf{F}=\mathbf{F}_1+\mathbf{F}_2 = \mathbf{B}-\mathbf{A} + \mathbf{D}-\mathbf{A},</math> | : <math>\mathbf{F}=\mathbf{F}_1+\mathbf{F}_2 = \mathbf{B}-\mathbf{A} + \mathbf{D}-\mathbf{A},</math> | ||
जिसे इस रूप में लिखा जा सकता है | जिसे इस रूप में लिखा जा सकता है | ||
: <math>\mathbf{F}=\mathbf{F}_1+\mathbf{F}_2 = 2(\frac{\mathbf{B}+\mathbf{D}}{2}-\mathbf{A})=2(\mathbf{E}-\mathbf{A}),</math> | : <math>\mathbf{F}=\mathbf{F}_1+\mathbf{F}_2 = 2(\frac{\mathbf{B}+\mathbf{D}}{2}-\mathbf{A})=2(\mathbf{E}-\mathbf{A}),</math> | ||
जहां | जहां E खंड BD का मध्य बिंदु है जो बिंदु 'B' और 'D' से जुड़ता है। | ||
इस प्रकार, बलों का योग F<sub>1</sub> और | इस प्रकार, बलों का योग F<sub>1</sub> और F<sub>2</sub> दो बलों के अंतबिंदु B और D को मिलाने वाले खंड के मध्य बिंदु E से A को मिलाने वाला खंड दोगुना है। समानांतर ''ABCD'' को पूरा करने के लिए क्रमशः ' ''AD''<nowiki/>' और ' ''AB''<nowiki/>' के समानांतर '<nowiki/>''BC''<nowiki/>' और '''DC''<nowiki/>' खंडों को परिभाषित करके इस लंबाई का दोहरीकरण सरलता से प्राप्त किया जाता है। इस समांतर चतुर्भुज का विकर्ण 'AC' दो बल सदिशों का योग है। इसे बलों के योग के लिए समांतर चतुर्भुज नियम के रूप में जाना जाता है। | ||
== एक बल के कारण अनुवाद और घूर्णन == | == एक बल के कारण अनुवाद और घूर्णन == | ||
=== बिंदु बल === | === बिंदु बल === | ||
जब कोई बल किसी कण पर कार्य करता है, तो यह एक बिंदु पर | जब कोई बल किसी कण पर कार्य करता है, तो यह एक बिंदु पर क्रियान्वित होता है (कण का आयतन नगण्य होता है): यह एक बिंदु बल है और कण इसका अनुप्रयोग बिंदु है। लेकिन एक विस्तारित पिंड (वस्तु) पर एक बाह्य बल उसके कई घटक कणों पर लगाया जा सकता है, अर्थात पिंड के कुछ आयतन या सतह पर फैल सकता है। यधपि, अनुप्रयोग बिंदु पर इसके घूर्णी प्रभाव को निर्धारित करने के लिए आवश्यक है कि हम इसके अनुप्रयोग के बिंदु को निर्दिष्ट करें (वास्तव में, अनुप्रयोग बिंदु की रेखा, जैसा कि नीचे बताया गया है)। समस्या सामान्यतः निम्नलिखित विधियों से हल की जाती है: | ||
* | * अधिकांशतः, वह आयतन या सतह जिस पर बल कार्य करता है, अनुप्रयोग बिंदु के आकार की तुलना में अपेक्षाकृत छोटा होता है, इसलिए इसे एक बिंदु द्वारा आकलित किया जा सके। सामान्यतः यह निर्धारित करना कठिन नहीं है कि इस तरह के सन्निकटन के कारण होने वाली त्रुटि स्वीकार्य है या नहीं। | ||
* यदि यह स्वीकार्य नहीं है (स्पष्ट रूप से गुरुत्वाकर्षण बल के | * यदि यह स्वीकार्य नहीं है (स्पष्ट रूप से गुरुत्वाकर्षण बल के स्थिति में), तो ऐसे आयतन/सतही बल को बलों (घटकों) की एक प्रणाली के रूप में वर्णित किया जाना चाहिए, प्रत्येक एक कण पर कार्य करता है, और फिर प्रत्येक के लिए गणना की जानी चाहिए उनमें से अलग से। इस तरह की गणना सामान्यतः अनुप्रयोग बिंदु की मात्रा/सतह के अंतर तत्वों और अभिन्न कलन के उपयोग से सरल होती है। कई स्थितियों में, यधपि, यह प्रदर्शित किया जा सकता है कि वास्तविक गणना के बिना बलों की ऐसी प्रणाली को एकल बिंदु बल द्वारा प्रतिस्थापित किया जा सकता है (जैसा कि समान गुरुत्वाकर्षण बल के स्थिति में)। | ||
किसी भी | किसी भी स्थिति में, कठोर अनुप्रयोग बिंदु की गति का विश्लेषण बिंदु बल प्रतिरूप से प्रारम्भ होता है। और जब किसी पिंड पर कार्य करने वाले बल को रेखांकन के रूप में प्रदर्शित किया जाता है, तो बल का प्रतिनिधित्व करने वाला उन्मुख रेखा खंड सामान्यतः इस तरह खींचा जाता है कि अनुप्रयोग बिंदु पर प्रारम्भ (या अंत) हो। | ||
=== | === अनम्य अनुप्रयोग बिंदु === | ||
[[File:Free body acceleration.JPG|thumb|300px|कैसे एक बल एक | [[File:Free body acceleration.JPG|thumb|300px|कैसे एक बल एक अनुप्रयोग बिंदु को गति देता है।]]आरेख में प्रदर्शित किये गए उदाहरण में, एकल बल <math>\scriptstyle \vec F </math> एक मुक्त अनम्य अनुप्रयोग बिंदु पर अनुप्रयोग बिंदु H पर कार्य करता है। अनुप्रयोग बिंदु में द्रव्यमान <math>\scriptstyle m </math> होता है और इसका द्रव्यमान केंद्र बिंदु C है। निरंतर द्रव्यमान सन्निकटन में, बल निम्नलिखित भावों द्वारा वर्णित अनुप्रयोग बिंदु की गति में परिवर्तन का कारण बनता है: | ||
: <math> \vec a = {\vec F \over m} </math>द्रव्यमान त्वरण का केंद्र है; और | : <math> \vec a = {\vec F \over m} </math>द्रव्यमान त्वरण का केंद्र है; और | ||
: <math> \vec \alpha = {\vec \tau \over I} </math> | : <math> \vec \alpha = {\vec \tau \over I} </math>अनुप्रयोग बिंदु का [[कोणीय त्वरण]] है। | ||
दूसरी अभिव्यक्ति में, <math>\scriptstyle \vec \tau </math> टॉर्क या बल का क्षण है, जबकि <math>\scriptstyle I </math> | दूसरी अभिव्यक्ति में, <math>\scriptstyle \vec \tau </math> टॉर्क या बल का क्षण है, जबकि <math>\scriptstyle I </math> अनुप्रयोग बिंदु की जड़ता का क्षण है। एक बल के कारण से टॉर्क <math>\scriptstyle \vec F </math> किसी संदर्भ बिंदु के संबंध में परिभाषित एक वेक्टर मात्रा है: | ||
:<math> \vec \tau = \vec r \times \vec F </math>टॉर्क वेक्टर है, और | :<math> \vec \tau = \vec r \times \vec F </math>टॉर्क वेक्टर है, और | ||
| Line 63: | Line 53: | ||
:<math> \ \tau = Fk </math>टॉर्क की मात्रा है। | :<math> \ \tau = Fk </math>टॉर्क की मात्रा है। | ||
सदिश <math>\scriptstyle \vec r </math> बल अनुप्रयोग बिंदु का [[स्थिति वेक्टर]] है, और इस उदाहरण में इसे द्रव्यमान के केंद्र से संदर्भ बिंदु के रूप में खींचा गया है (आरेख देखें)। सीधी रेखा खंड <math>\scriptstyle k </math> बल की उत्तोलक भुजा है <math>\scriptstyle \vec F</math> द्रव्यमान के केंद्र के संबंध में। जैसा कि | सदिश <math>\scriptstyle \vec r </math> बल अनुप्रयोग बिंदु का [[स्थिति वेक्टर]] है,और इस उदाहरण में इसे द्रव्यमान के केंद्र से संदर्भ बिंदु के रूप में खींचा गया है (आरेख देखें)। सीधी रेखा खंड <math>\scriptstyle k </math> बल की उत्तोलक भुजा है <math>\scriptstyle \vec F</math> द्रव्यमान के केंद्र के संबंध में। जैसा कि आरेखण से पता चलता है, यदि बल के अनुप्रयोग की रेखा (बिंदीदार काली रेखा) के साथ अनुप्रयोग बिंदु को स्थानांतरित किया जाता है, तो टॉर्क नहीं बदलता है (उसी उत्तोलक भुजा)। अधिक औपचारिक रूप से, यह वेक्टर उत्पाद के गुणों से चलता है, और दिखाता है कि बल का घूर्णी प्रभाव केवल उसके अनुप्रयोग बिंदु की रेखा की स्थिति पर निर्भर करता है, न कि उस रेखा के साथ अनुप्रयोग बिंदु की विशेष चयन पर। | ||
टॉर्क वेक्टर बल | टॉर्क वेक्टर बल <math>\scriptstyle \vec r</math> और वेक्टर द्वारा परिभाषित सतह के लंबवत है, और इस उदाहरण में यह प्रेक्षक की ओर निर्देशित है; कोणीय त्वरण वेक्टर की एक ही दिशा होती है। [[दाहिने हाथ का नियम]] इस दिशा को रेखा-चित्र की सतह में दक्षिणावर्त या वामावर्त घूर्णन से संबंधित करता है। | ||
जड़त्व का क्षण <math>\scriptstyle I</math> द्रव्यमान के केंद्र के माध्यम से धुरी के संबंध में गणना की जाती है जो टॉर्क के समानांतर होती है। यदि रेखा-चित्र में प्रदर्शित गया अनुप्रयोग बिंदु एक सजातीय डिस्क है, तो यह जड़त्व का क्षण है <math>\scriptstyle I = m r^2/2</math>. यदि डिस्क का द्रव्यमान 0,5 kg और त्रिज्या 0,8 m है, तो जड़त्व का क्षण 0,16 kgm<sup>2 है | यदि बल की मात्रा 2 N है, और उत्तोलक भुजा 0,6 m है, तो टॉर्क की मात्रा 1,2 Nm है। दिखाए गए क्षण में, बल डिस्क को कोणीय त्वरण α = देता है {{math|''τ''}}/मैं = 7,5 rad/s2, और इसके द्रव्यमान के केंद्र को यह रैखिक त्वरण देता है a = F/m = 4 m/s<sup>2 | |||
== परिणामी बल == | == परिणामी बल == | ||
[[File:Rezultanta.JPG|thumb|500px|परिणामी बल का ग्राफिकल प्लेसमेंट।]]परिणामी बल और बलाघूर्ण कठोर पिंड की गति पर कार्य करने वाली शक्तियों की प्रणाली के प्रभावों को प्रतिस्थापित करता है। एक | [[File:Rezultanta.JPG|thumb|500px|परिणामी बल का ग्राफिकल प्लेसमेंट।]]परिणामी बल और बलाघूर्ण कठोर पिंड की गति पर कार्य करने वाली शक्तियों की प्रणाली के प्रभावों को प्रतिस्थापित करता है। एक रोचक विशेष स्थिति एक टॉर्क-मुक्त परिणामी है, जिसे निम्नानुसार पाया जा सकता है: | ||
# वेक्टर जोड़ का उपयोग शुद्ध बल खोजने के लिए किया जाता है; | # वेक्टर जोड़ का उपयोग शुद्ध बल खोजने के लिए किया जाता है; | ||
# शून्य टॉर्क के साथ | # शून्य टॉर्क के साथ अनुप्रयोग के बिंदु को निर्धारित करने के लिए समीकरण का प्रयोग करें: | ||
:<math> \vec r \times \vec F_\mathrm{R} = \sum_{i=1}^N ( \vec r_i \times \vec F_i ) </math> | :<math> \vec r \times \vec F_\mathrm{R} = \sum_{i=1}^N ( \vec r_i \times \vec F_i ) </math> | ||
जहाँ <math> \vec F_\mathrm{R} </math> शुद्ध बल है, <math> \vec r</math> इसके अनुप्रयोग के बिंदु का पता लगाता है, और व्यक्तिगत बल हैं <math> \vec F_i </math> अनुप्रयोग के बिंदुओं के साथ <math> \vec r_i </math>. ऐसा हो सकता है कि अनुप्रयोग के कोई बिंदु नहीं है जो टॉर्क मुक्त परिणाम उत्पन्न करता है। | |||
विपरीत आरेख सरल समतल प्रणाली के परिणामी बल के अनुप्रयोग के बिंदु की रेखा को खोजने के लिए सरल रेखा-चित्रीय विधियों को दिखाता है: | |||
# वास्तविक बलों के अनुप्रयोग के बिंदु की रेखाएँ <math>\vec{F}_{1}</math> और <math>\vec{F}_{2}</math> बाईं ओर आरेखण प्रतिच्छेद करता है। वेक्टर जोड़ के बाद "के स्थान पर" किया जाता है <math> \vec{F}_{1}</math>, प्राप्त शुद्ध बल का अनुवाद किया जाता है इसलिए इसके अनुप्रयोग के बिंदु की रेखा सामान्य अंतथप्रतिच्छेदन बिंदु से गुजरे। उस बिंदु के संबंध में सभी टॉर्क शून्य हैं, इसलिए परिणामी बल का टॉर्क <math>\vec{F}_\mathrm{R}</math> वास्तविक बलों के बलाघूर्णों के योग के बराबर है। | |||
विपरीत | # आरेख के बीच में आरेखण दो समानांतर वास्तविक बलों को दर्शाता है। के स्थान पर वेक्टर जोड़ के बाद <math>\vec{F}_{2}</math>, शुद्ध बल को अनुप्रयोग के बिंदु की उपयुक्त रेखा में अनुवादित किया जाता है, जहाँ यह <math>\scriptstyle \vec{F}_\mathrm{R}</math> परिणामी बल बन जाता है . प्रक्रिया घटकों में सभी बलों के अपघटन पर आधारित है, जिसके लिए अनुप्रयोग के बिंदु की रेखाएं (पीली बिंदीदार रेखाएं) एक बिंदु पर प्रतिच्छेद करती हैं (तथाकथित ध्रुव, आरेखण के दाईं ओर अव्यवस्थित रूप से स्थापित करना)। फिर बलाघूर्ण संबंधों को प्रदर्शित करने के लिए पिछले स्थिति के तर्कों को बलों और उनके घटकों पर क्रियान्वित किया जाता है। | ||
# वास्तविक बलों के | # सबसे सही आरेखण एक जोड़ी (यांत्रिकी) दिखाता है, दो समान लेकिन विपरीत बल जिनके लिए शुद्ध बल की मात्रा शून्य है, लेकिन वे शुद्ध टॉर्क का उत्पादन करते हैं <math> \scriptstyle \tau = Fd </math> जहाँ <math> \scriptstyle \ d </math>उनके अनुप्रयोग के बिंदु की रेखाओं के बीच की दूरी है। चूँकि कोई परिणामी बल नहीं है, यह बलाघूर्ण [है?] शुद्ध बलाघूर्ण के रूप में वर्णित किया जा सकता है। | ||
# आरेख के बीच में | |||
# सबसे सही | |||
== उपयोग == | == उपयोग == | ||
[[File:Non-parallel net force.svg|thumb|279px| | [[File:Non-parallel net force.svg|thumb|279px|असमानांतर बलों को जोड़ने के लिए वेक्टर आरेख।]]सामान्यतः, एक कठोर पिंड पर कार्यरत बलों की प्रणाली को सदैव बल और विशुद्ध (पिछला अनुभाग देखें) बलाघूर्ण द्वारा प्रतिस्थापित किया जा सकता है। बल विशुद्ध बल है, लेकिन अतिरिक्त बलाघूर्ण की गणना करने के लिए, विशुद्ध बल को क्रिया की रेखा सौंपी जानी चाहिए। क्रिया की रेखा की रेखा को असैद्धांतिक रूप से चुना जा सकता है, लेकिन अतिरिक्त शुद्ध टॉर्क इस विकल्प पर निर्भर करता है। एक विशेष स्थिति में, क्रिया की रेखा की ऐसी रेखा खोजना संभव है कि यह अतिरिक्त टॉर्क शून्य हो। | ||
बलों के किसी भी विन्यास के लिए परिणामी बल और बलाघूर्ण निर्धारित किया जा सकता है। | बलों के किसी भी विन्यास के लिए परिणामी बल और बलाघूर्ण निर्धारित किया जा सकता है। यधपि, एक रोचक विशेष स्थिति टॉर्क मुक्त परिणामी है। यह वैचारिक और व्यावहारिक दोनों तरह से उपयोगी है, क्योंकि अनुप्रयोग बिंदु बिना घुमाए चलता है जैसे कि वह एक कण था। | ||
कुछ लेखक परिणामी बल को शुद्ध बल से अलग नहीं करते हैं और शब्दों को समानार्थक शब्द के रूप में उपयोग करते हैं।<ref>Resnick, Robert and Halliday, David (1966), Physics, (Vol I and II, Combined edition), Wiley International Edition, Library of Congress Catalog Card No. 66-11527</ref> | |||
== यह भी देखें == | == यह भी देखें == | ||
* [[पेंच सिद्धांत]] | * [[पेंच सिद्धांत]] | ||
* | * घनत्व का केंद्र | ||
* [[गैर-समान क्षेत्रों में गुरुत्वाकर्षण के केंद्र]] | * [[गैर-समान क्षेत्रों में गुरुत्वाकर्षण के केंद्र|असमान क्षेत्रों में गुरुत्वाकर्षण के केंद्र]] | ||
== संदर्भ == | == संदर्भ == | ||
{{Reflist}} | {{Reflist}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Created On 23/03/2023]] | [[Category:Created On 23/03/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:गतिकी (यांत्रिकी)]] | |||
[[Category:ताकत]] | |||
Latest revision as of 18:42, 21 April 2023
यांत्रिकी में, शुद्ध बल कण या भौतिक वस्तु पर कार्य करने वाली शक्तियों का सदिश योग होता है। शुद्ध बल एक एकल बल है जो कण की गति पर मूल बलों के प्रभाव को प्रतिस्थापित करता है। यह कण को न्यूटन के गति के नियमों द्वारा वर्णित उन सभी वास्तविक बलों के समान त्वरण देता है | न्यूटन की गति का दूसरा नियम।
एक शुद्ध बल के अनुप्रयोग के बिंदु से जुड़े टॉर्क को निर्धारित करना संभव है इसलिए यह बल की मूल प्रणाली के अनुसार वस्तु के जेट की गति को बनाए रखे। इससे जुड़ा टॉर्कः , शुद्ध बल, 'परिणामी बल' बन जाता है और वस्तु की घूर्णी गति पर वैसा ही प्रभाव पड़ता है जैसा कि सभी वास्तविक बलों को एक साथ लिया जाता है।[1] बलों की एक प्रणाली के लिए टॉर्क मुक्त परिणामी बल को परिभाषित करना संभव है। इस स्थिति में, शुद्ध बल, जब किये गये कार्य को उचित रेखा पर क्रियान्वित होता है, तो अनुप्रयोग के बिंदु पर सभी बलों के समान प्रभाव पड़ता है। टॉर्क-मुक्त परिणामी बल का पता लगाना सदैव संभव नहीं होता है।
संपूर्ण बल
बल एक यूक्लिडियन सदिश राशि है, जिसका अर्थ है कि इसकी एक परिमाण और दिशा है, और इसे सामान्यतः F जैसे बोल्डफेस का उपयोग करके या प्रतीक पर रेखा का उपयोग करके दर्शाया जाता है, जैसे कि .
रेखांकन के रूप में, बल को उसके अनुअनुप्रयोग बिंदु A से बिंदु B तक एक रेखा खंड के रूप में दर्शाया जाता है, जो इसकी दिशा और परिमाण को परिभाषित करता है। खंड AB की लंबाई बल के परिमाण को दर्शाती है।
वेक्टर गणना का विकास 1800 सदी के अंत और 1900 सदी के प्रारंभ में हुआ था। बलों को जोड़ने के लिए प्रयुक्त समांतर चतुर्भुज नियम, यधपि, प्राचीन काल से है और गैलीलियो और न्यूटन द्वारा स्पष्ट रूप से चिन्हित किया गया है।[2] आरेख बलों के जोड़ को दर्शाता है और . योग दो बलों में से प्रत्येक को दो बलों द्वारा परिभाषित समांतर चतुर्भुज के विकर्ण के रूप में खींचा जाता है।
विस्तारित निकाय पर लगाए गए बलों के अनुप्रयोग के विभिन्न बिंदु हो सकते हैं। बल बद्ध सदिश होते हैं और इन्हें तभी जोड़ा जा सकता है जब वे एक ही बिंदु पर क्रियान्वित हों। पिंड पर कार्य करने वाली सभी शक्तियों से प्राप्त शुद्ध बल तब तक अपनी गति को संरक्षित नहीं करता है जब तक कि एक ही बिंदु पर क्रियान्वित नहीं किया जाता है, और अनुप्रयोग के नए बिंदु से जुड़े उपयुक्त टॉर्क के साथ निर्धारित किया जाता है। उपयुक्त बल आघूर्ण के साथ एक बिंदु पर लगाए गए पिंड पर कुल बल को परिणामी बल और बल आघूर्ण के रूप में जाना जाता है।
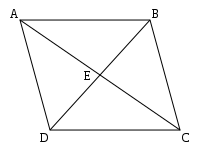
बलों के योग के लिए समानांतर चतुर्भुज नियम
बल को एक बाध्य सदिश के रूप में जाना जाता है—जिसका अर्थ है कि इसकी एक दिशा और परिमाण और अनुप्रयोग का बिंदु है। बल को परिभाषित करने की सुविधाजनक विधि बिंदु A से बिंदु B तक एक रेखा खंड है। यदि हम इन बिंदुओं के निर्देशांक को 'A' = ( Ax, Ay, Az), और B = (B x, B y, B z), के रूप में निरूपित करते हैं तो A पर क्रियान्वित बल वेक्टर द्वारा दिया जाता है
वेक्टर B-A की लंबाई F के परिमाण को परिभाषित करती है और इसके द्वारा दिया जाता है
दो बलों का योग F1 और F2 A पर क्रियान्वित उन खंडों के योग से गणना की जा सकती है जो उन्हें परिभाषित करते हैं। चलो 'F'1= B−A और F2= D−A, तो इन दो सदिशों का योग है
जिसे इस रूप में लिखा जा सकता है
जहां E खंड BD का मध्य बिंदु है जो बिंदु 'B' और 'D' से जुड़ता है।
इस प्रकार, बलों का योग F1 और F2 दो बलों के अंतबिंदु B और D को मिलाने वाले खंड के मध्य बिंदु E से A को मिलाने वाला खंड दोगुना है। समानांतर ABCD को पूरा करने के लिए क्रमशः ' AD' और ' AB' के समानांतर 'BC' और 'DC' खंडों को परिभाषित करके इस लंबाई का दोहरीकरण सरलता से प्राप्त किया जाता है। इस समांतर चतुर्भुज का विकर्ण 'AC' दो बल सदिशों का योग है। इसे बलों के योग के लिए समांतर चतुर्भुज नियम के रूप में जाना जाता है।
एक बल के कारण अनुवाद और घूर्णन
बिंदु बल
जब कोई बल किसी कण पर कार्य करता है, तो यह एक बिंदु पर क्रियान्वित होता है (कण का आयतन नगण्य होता है): यह एक बिंदु बल है और कण इसका अनुप्रयोग बिंदु है। लेकिन एक विस्तारित पिंड (वस्तु) पर एक बाह्य बल उसके कई घटक कणों पर लगाया जा सकता है, अर्थात पिंड के कुछ आयतन या सतह पर फैल सकता है। यधपि, अनुप्रयोग बिंदु पर इसके घूर्णी प्रभाव को निर्धारित करने के लिए आवश्यक है कि हम इसके अनुप्रयोग के बिंदु को निर्दिष्ट करें (वास्तव में, अनुप्रयोग बिंदु की रेखा, जैसा कि नीचे बताया गया है)। समस्या सामान्यतः निम्नलिखित विधियों से हल की जाती है:
- अधिकांशतः, वह आयतन या सतह जिस पर बल कार्य करता है, अनुप्रयोग बिंदु के आकार की तुलना में अपेक्षाकृत छोटा होता है, इसलिए इसे एक बिंदु द्वारा आकलित किया जा सके। सामान्यतः यह निर्धारित करना कठिन नहीं है कि इस तरह के सन्निकटन के कारण होने वाली त्रुटि स्वीकार्य है या नहीं।
- यदि यह स्वीकार्य नहीं है (स्पष्ट रूप से गुरुत्वाकर्षण बल के स्थिति में), तो ऐसे आयतन/सतही बल को बलों (घटकों) की एक प्रणाली के रूप में वर्णित किया जाना चाहिए, प्रत्येक एक कण पर कार्य करता है, और फिर प्रत्येक के लिए गणना की जानी चाहिए उनमें से अलग से। इस तरह की गणना सामान्यतः अनुप्रयोग बिंदु की मात्रा/सतह के अंतर तत्वों और अभिन्न कलन के उपयोग से सरल होती है। कई स्थितियों में, यधपि, यह प्रदर्शित किया जा सकता है कि वास्तविक गणना के बिना बलों की ऐसी प्रणाली को एकल बिंदु बल द्वारा प्रतिस्थापित किया जा सकता है (जैसा कि समान गुरुत्वाकर्षण बल के स्थिति में)।
किसी भी स्थिति में, कठोर अनुप्रयोग बिंदु की गति का विश्लेषण बिंदु बल प्रतिरूप से प्रारम्भ होता है। और जब किसी पिंड पर कार्य करने वाले बल को रेखांकन के रूप में प्रदर्शित किया जाता है, तो बल का प्रतिनिधित्व करने वाला उन्मुख रेखा खंड सामान्यतः इस तरह खींचा जाता है कि अनुप्रयोग बिंदु पर प्रारम्भ (या अंत) हो।
अनम्य अनुप्रयोग बिंदु
आरेख में प्रदर्शित किये गए उदाहरण में, एकल बल एक मुक्त अनम्य अनुप्रयोग बिंदु पर अनुप्रयोग बिंदु H पर कार्य करता है। अनुप्रयोग बिंदु में द्रव्यमान होता है और इसका द्रव्यमान केंद्र बिंदु C है। निरंतर द्रव्यमान सन्निकटन में, बल निम्नलिखित भावों द्वारा वर्णित अनुप्रयोग बिंदु की गति में परिवर्तन का कारण बनता है:
- द्रव्यमान त्वरण का केंद्र है; और
- अनुप्रयोग बिंदु का कोणीय त्वरण है।
दूसरी अभिव्यक्ति में, टॉर्क या बल का क्षण है, जबकि अनुप्रयोग बिंदु की जड़ता का क्षण है। एक बल के कारण से टॉर्क किसी संदर्भ बिंदु के संबंध में परिभाषित एक वेक्टर मात्रा है:
- टॉर्क वेक्टर है, और
- टॉर्क की मात्रा है।
सदिश बल अनुप्रयोग बिंदु का स्थिति वेक्टर है,और इस उदाहरण में इसे द्रव्यमान के केंद्र से संदर्भ बिंदु के रूप में खींचा गया है (आरेख देखें)। सीधी रेखा खंड बल की उत्तोलक भुजा है द्रव्यमान के केंद्र के संबंध में। जैसा कि आरेखण से पता चलता है, यदि बल के अनुप्रयोग की रेखा (बिंदीदार काली रेखा) के साथ अनुप्रयोग बिंदु को स्थानांतरित किया जाता है, तो टॉर्क नहीं बदलता है (उसी उत्तोलक भुजा)। अधिक औपचारिक रूप से, यह वेक्टर उत्पाद के गुणों से चलता है, और दिखाता है कि बल का घूर्णी प्रभाव केवल उसके अनुप्रयोग बिंदु की रेखा की स्थिति पर निर्भर करता है, न कि उस रेखा के साथ अनुप्रयोग बिंदु की विशेष चयन पर।
टॉर्क वेक्टर बल और वेक्टर द्वारा परिभाषित सतह के लंबवत है, और इस उदाहरण में यह प्रेक्षक की ओर निर्देशित है; कोणीय त्वरण वेक्टर की एक ही दिशा होती है। दाहिने हाथ का नियम इस दिशा को रेखा-चित्र की सतह में दक्षिणावर्त या वामावर्त घूर्णन से संबंधित करता है।
जड़त्व का क्षण द्रव्यमान के केंद्र के माध्यम से धुरी के संबंध में गणना की जाती है जो टॉर्क के समानांतर होती है। यदि रेखा-चित्र में प्रदर्शित गया अनुप्रयोग बिंदु एक सजातीय डिस्क है, तो यह जड़त्व का क्षण है . यदि डिस्क का द्रव्यमान 0,5 kg और त्रिज्या 0,8 m है, तो जड़त्व का क्षण 0,16 kgm2 है | यदि बल की मात्रा 2 N है, और उत्तोलक भुजा 0,6 m है, तो टॉर्क की मात्रा 1,2 Nm है। दिखाए गए क्षण में, बल डिस्क को कोणीय त्वरण α = देता है τ/मैं = 7,5 rad/s2, और इसके द्रव्यमान के केंद्र को यह रैखिक त्वरण देता है a = F/m = 4 m/s2
परिणामी बल
परिणामी बल और बलाघूर्ण कठोर पिंड की गति पर कार्य करने वाली शक्तियों की प्रणाली के प्रभावों को प्रतिस्थापित करता है। एक रोचक विशेष स्थिति एक टॉर्क-मुक्त परिणामी है, जिसे निम्नानुसार पाया जा सकता है:
- वेक्टर जोड़ का उपयोग शुद्ध बल खोजने के लिए किया जाता है;
- शून्य टॉर्क के साथ अनुप्रयोग के बिंदु को निर्धारित करने के लिए समीकरण का प्रयोग करें:
जहाँ शुद्ध बल है, इसके अनुप्रयोग के बिंदु का पता लगाता है, और व्यक्तिगत बल हैं अनुप्रयोग के बिंदुओं के साथ . ऐसा हो सकता है कि अनुप्रयोग के कोई बिंदु नहीं है जो टॉर्क मुक्त परिणाम उत्पन्न करता है।
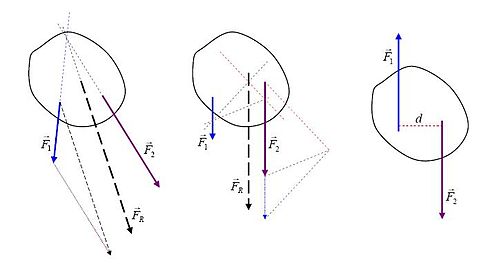
विपरीत आरेख सरल समतल प्रणाली के परिणामी बल के अनुप्रयोग के बिंदु की रेखा को खोजने के लिए सरल रेखा-चित्रीय विधियों को दिखाता है:
- वास्तविक बलों के अनुप्रयोग के बिंदु की रेखाएँ और बाईं ओर आरेखण प्रतिच्छेद करता है। वेक्टर जोड़ के बाद "के स्थान पर" किया जाता है , प्राप्त शुद्ध बल का अनुवाद किया जाता है इसलिए इसके अनुप्रयोग के बिंदु की रेखा सामान्य अंतथप्रतिच्छेदन बिंदु से गुजरे। उस बिंदु के संबंध में सभी टॉर्क शून्य हैं, इसलिए परिणामी बल का टॉर्क वास्तविक बलों के बलाघूर्णों के योग के बराबर है।
- आरेख के बीच में आरेखण दो समानांतर वास्तविक बलों को दर्शाता है। के स्थान पर वेक्टर जोड़ के बाद , शुद्ध बल को अनुप्रयोग के बिंदु की उपयुक्त रेखा में अनुवादित किया जाता है, जहाँ यह परिणामी बल बन जाता है . प्रक्रिया घटकों में सभी बलों के अपघटन पर आधारित है, जिसके लिए अनुप्रयोग के बिंदु की रेखाएं (पीली बिंदीदार रेखाएं) एक बिंदु पर प्रतिच्छेद करती हैं (तथाकथित ध्रुव, आरेखण के दाईं ओर अव्यवस्थित रूप से स्थापित करना)। फिर बलाघूर्ण संबंधों को प्रदर्शित करने के लिए पिछले स्थिति के तर्कों को बलों और उनके घटकों पर क्रियान्वित किया जाता है।
- सबसे सही आरेखण एक जोड़ी (यांत्रिकी) दिखाता है, दो समान लेकिन विपरीत बल जिनके लिए शुद्ध बल की मात्रा शून्य है, लेकिन वे शुद्ध टॉर्क का उत्पादन करते हैं जहाँ उनके अनुप्रयोग के बिंदु की रेखाओं के बीच की दूरी है। चूँकि कोई परिणामी बल नहीं है, यह बलाघूर्ण [है?] शुद्ध बलाघूर्ण के रूप में वर्णित किया जा सकता है।
उपयोग
सामान्यतः, एक कठोर पिंड पर कार्यरत बलों की प्रणाली को सदैव बल और विशुद्ध (पिछला अनुभाग देखें) बलाघूर्ण द्वारा प्रतिस्थापित किया जा सकता है। बल विशुद्ध बल है, लेकिन अतिरिक्त बलाघूर्ण की गणना करने के लिए, विशुद्ध बल को क्रिया की रेखा सौंपी जानी चाहिए। क्रिया की रेखा की रेखा को असैद्धांतिक रूप से चुना जा सकता है, लेकिन अतिरिक्त शुद्ध टॉर्क इस विकल्प पर निर्भर करता है। एक विशेष स्थिति में, क्रिया की रेखा की ऐसी रेखा खोजना संभव है कि यह अतिरिक्त टॉर्क शून्य हो।
बलों के किसी भी विन्यास के लिए परिणामी बल और बलाघूर्ण निर्धारित किया जा सकता है। यधपि, एक रोचक विशेष स्थिति टॉर्क मुक्त परिणामी है। यह वैचारिक और व्यावहारिक दोनों तरह से उपयोगी है, क्योंकि अनुप्रयोग बिंदु बिना घुमाए चलता है जैसे कि वह एक कण था।
कुछ लेखक परिणामी बल को शुद्ध बल से अलग नहीं करते हैं और शब्दों को समानार्थक शब्द के रूप में उपयोग करते हैं।[3]
यह भी देखें
- पेंच सिद्धांत
- घनत्व का केंद्र
- असमान क्षेत्रों में गुरुत्वाकर्षण के केंद्र
संदर्भ
- ↑ Symon, Keith R. (1964), Mechanics, Addison-Wesley, LCCN 60-5164
- ↑ Michael J. Crowe (1967). A History of Vector Analysis : The Evolution of the Idea of a Vectorial System. Dover Publications (reprint edition; ISBN 0-486-67910-1).
- ↑ Resnick, Robert and Halliday, David (1966), Physics, (Vol I and II, Combined edition), Wiley International Edition, Library of Congress Catalog Card No. 66-11527