इलेक्ट्रॉन प्रकाशिकी: Difference between revisions
(Created page with "{{Short description|Electron trajectories in electromagnetic fields}} thumb|चुंबकीय लेंसइलेक्ट्रॉन प्...") |
No edit summary |
||
| (10 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Electron trajectories in electromagnetic fields}} | {{Short description|Electron trajectories in electromagnetic fields}} | ||
[[File:Magnetic lens.jpg|thumb|चुंबकीय लेंस]]इलेक्ट्रॉन प्रकाशिकी [[विद्युत चुम्बकीय]] क्षेत्र के साथ इलेक्ट्रॉन | [[File:Magnetic lens.jpg|thumb|चुंबकीय लेंस]]इलेक्ट्रॉन प्रकाशिकी [[विद्युत चुम्बकीय]] क्षेत्र के साथ इलेक्ट्रॉन प्रक्षेप वक्र की गणना के लिए एक गणितीय रूपरेखा के रूप में होते है। प्रकाशिकी शब्द का प्रयोग इसलिए किया जाता है, क्योंकि [[चुंबकीय लेंस|चुंबकीय]] और [[इलेक्ट्रोस्टैटिक लेंस|स्थिर वैद्युत लेंस]] एक आवेशित कण प्रकाश किरण पर [[ऑप्टिकल लेंस]] के समान कार्य करते हैं। | ||
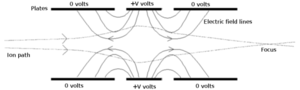
[[इलेक्ट्रॉन सूक्ष्मदर्शी]] और [[कण त्वरक]] के डिजाइन के लिए इलेक्ट्रॉन प्रकाशिकी गणना महत्वपूर्ण | [[इलेक्ट्रॉन सूक्ष्मदर्शी]] और [[कण त्वरक]] के डिजाइन के लिए इलेक्ट्रॉन प्रकाशिकी की गणना महत्वपूर्ण होती है। [[पैराएक्सियल सन्निकटन]] में, [[रे ट्रांसफर मैट्रिक्स विश्लेषण|किरण ट्रांसफर मैट्रिक्स विश्लेषण]] का उपयोग करके प्रक्षेप वक्र की गणना की जा सकती है।[[Image:Einzel lens.png|thumb|300px|एक [[एकल लेंस]], एक विशिष्ट प्रकार का स्थिर वैद्युत लेंस होता है। यह आंकड़ा इलेक्ट्रॉन पथ दिखाता है। एक विशेष क्षमता पर मध्य प्लेट के साथ छह प्लेटें उड़ान पथ के समानांतर होती हैं। यह आकिरण ख सकारात्मक आयनों के लिए बनाया गया था और केंद्रीय प्लेट पर सकारात्मक वोल्टेज दिखाता है। इलेक्ट्रॉनों के लिए यह वोल्टेज नकारात्मक होना चाहिए।]] | ||
[[Image:Einzel lens.png|thumb|300px|एक [[एकल लेंस]], एक विशिष्ट प्रकार का | |||
== इलेक्ट्रॉन गुण == | == इलेक्ट्रॉन गुण == | ||
{{main| | {{main|इलेक्ट्रॉन}} | ||
इलेक्ट्रॉन आवेशित कण | |||
इलेक्ट्रॉन आवेशित कण सामान्य द्रव्यमान वाले बिंदु आवेश [[स्पिन (भौतिकी)|स्पिन (भौतिकी]] 1/2 के साथ होते हैं, इसलिए वे [[फर्मियन]] रूप में होते है। इलेक्ट्रॉन उपयुक्त [[विद्युत क्षेत्र]] या [[चुंबकीय क्षेत्र]] क्षेत्रों द्वारा [[कण त्वरक]] के रूप में हो सकते हैं, जिससे [[गतिज ऊर्जा]] प्राप्त होती है। पर्याप्त वोल्टेज दिए जाने पर मापने योग्य सापेक्षतावादी प्रभावों को प्रदर्शित करने के लिए इलेक्ट्रॉन को पर्याप्त तेजी से त्वरित किया जाता है। [[तरंग कण द्वैत|तरंग कण डुअलिटी]] के अनुसार इलेक्ट्रॉनों को [[तरंग दैर्ध्य]] चरण तरंगों और [[आयाम]] जैसे गुणों के साथ पदार्थ तरंगों के रूप में भी जाना जा सकता है। | |||
== ज्यामितीय इलेक्ट्रॉन प्रकाशिकी == | == ज्यामितीय इलेक्ट्रॉन प्रकाशिकी == | ||
=== चुंबकीय क्षेत्र === | === चुंबकीय क्षेत्र === | ||
लोरेंत्ज़ बल की दूसरी अवधि के अनुसार | लोरेंत्ज़ बल की दूसरी अवधि के अनुसार चुंबकीय क्षेत्र और इलेक्ट्रॉन वेग के बीच एक क्रॉस उत्पाद के अनुसार इलेक्ट्रॉन चुंबकीय क्षेत्र के साथ क्रिया करते हैं। इस प्रकार एक अनंत समान क्षेत्र में इसका परिणाम क्षेत्र की दिशा के चारों ओर इलेक्ट्रॉन की एक गोलाकार गति के रूप में होता है, जिसके द्वारा दी गई त्रिज्या इस रूप में होती है | ||
:<math> r = \frac{mv_\perp}{eB}</math> | :<math> r = \frac{mv_\perp}{eB}</math> | ||
जहाँ r कक्षा की त्रिज्या है, m [[इलेक्ट्रॉन द्रव्यमान]] है, <math>v_\perp</math>क्षेत्र के लंबवत इलेक्ट्रॉन वेग का घटक है, ई इलेक्ट्रॉन आवेश है और बी लागू चुंबकीय क्षेत्र का परिमाण है। चुंबकीय क्षेत्र के समानांतर एक वेग घटक वाले इलेक्ट्रॉन [[ कुंडलित वक्रता ]] | जहाँ r कक्षा की त्रिज्या होती है, m [[इलेक्ट्रॉन द्रव्यमान]] होती है, <math>v_\perp</math>क्षेत्र के लंबवत इलेक्ट्रॉन वेग का घटक के रूप में होता है, ई इलेक्ट्रॉन आवेश है और बी लागू चुंबकीय क्षेत्र का परिमाण के रूप में है। चुंबकीय क्षेत्र के समानांतर एक वेग घटक वाले इलेक्ट्रॉन [[ कुंडलित वक्रता |कुंडलित वक्रता]] प्रक्षेप वक्र के साथ आगे बढ़ते है। | ||
=== विद्युत क्षेत्र === | === विद्युत क्षेत्र === | ||
एक | एक प्रयुक्त स्थिर वैद्युत क्षेत्र के स्थितियों में इलेक्ट्रॉन क्षेत्र के सकारात्मक ढाल की ओर विक्षेपित होता है। विशेष रूप से स्थिर वैद्युत फ़ील्ड लाइनों के इस क्रॉसिंग का अर्थ है कि स्थिर वैद्युत फ़ील्ड के माध्यम से चलने वाले इलेक्ट्रॉन अपने वेग के परिमाण को बदलते हैं, जबकि चुंबकीय क्षेत्र में, केवल वेग की दिशा को संशोधित किया जाता है। | ||
चूंकि इलेक्ट्रॉन [[विवर्तन]] जैसे गैर-कण | चूंकि इलेक्ट्रॉन [[विवर्तन]] जैसे गैर-कण तरंग जैसे, प्रभाव को प्रदर्शित करते हैं, मैक्सवेल के समीकरण के अनुसार इलेक्ट्रॉन पथों का एक पूर्ण विश्लेषण प्राप्त किया जा सकता है, चूंकि कई स्थितियों में कण व्याख्या जटिलता में बड़ी कमी के साथ पर्याप्त रूप में सन्निकटन मान प्रदान कर सकती है। | ||
इलेक्ट्रॉनों की एक और | इलेक्ट्रॉनों की एक और गुणधर्म यह है कि वे पदार्थ के साथ दृढ़ता से संपर्क करते हैं, क्योंकि वे न केवल नाभिक के प्रति संवेदनशील होते हैं, बल्कि पदार्थ के इलेक्ट्रॉन चार्ज क्लाउड के प्रति भी संवेदनशील होते हैं। इसलिए इलेक्ट्रॉनों को किसी भी उचित दूरी को प्रसारित करने के लिए [[ खालीपन |खालीपन]] की आवश्यकता होती है, जैसे इलेक्ट्रॉन ऑप्टिक प्रणाली में वांछनीय रूप में होता है। | ||
निर्वात में प्रवेश औसत मुक्त पथ द्वारा तय किया जाता है, इलेक्ट्रॉनों और पदार्थ के बीच टकराव की संभावना का एक उपाय | निर्वात में प्रवेश औसत मुक्त इलेक्ट्रॉन पथ द्वारा तय किया जाता है, इलेक्ट्रॉनों और पदार्थ के बीच टकराव की संभावना का एक उपाय अनुमानित मान जिसके लिए पॉइसन सांख्यिकी से प्राप्त किया जा सकता है। | ||
=== सापेक्षवादी सिद्धांत === | === सापेक्षवादी सिद्धांत === | ||
चूंकि, सापेक्षवादी सिद्धांत बहुत सामान्य नहीं है, [[डायराक समीकरण]] से प्रारंभ होने वाले आवेशित कणों पर चुंबकीय संरचनाओं के प्रभावों को प्राप्त करना भी संभव रूप में होता है।<ref>{{Cite journal | last1 = Jagannathan | first1 = R. | author-link1 = Ramaswamy Jagannathan| last2 = Simon | first2 = R. |author-link2 = Rajiah Simon| last3 = Sudarshan | first3 = E. C. G. |author-link3= George Sudarshan| last4 = Mukunda | first4 = N. |author-link4=N. Mukunda| title = डायराक समीकरण के आधार पर चुंबकीय इलेक्ट्रॉन लेंस का क्वांटम सिद्धांत| doi = 10.1016/0375-9601(89)90685-3 | journal = [[Physics Letters A]]| volume = 134 | issue = 8–9 | pages = 457 | year = 1989 |bibcode = 1989PhLA..134..457J | url = http://eprints.iisc.ac.in/964/1/Quantum_theory_of_magnetic_electron_lenses.pdf }}</ref> | |||
== विवर्तनिक इलेक्ट्रॉन प्रकाशिकी == | == विवर्तनिक इलेक्ट्रॉन प्रकाशिकी == | ||
निर्वात में प्रसार करने वाले | निर्वात में प्रसार करने वाले उप सापेक्षवादी मुक्त इलेक्ट्रॉन को एक [[ब्रोगली का]] पदार्थ तरंग के रूप में यथार्थ रूप से वर्णित किया जाता है, जिसकी तरंग दैर्ध्य इसके अनुदैर्ध्य संवेग के व्युत्क्रमानुपाती होती है। इस प्रकार इलेक्ट्रॉन द्वारा किए गए आवेश के परिणामस्वरूप विद्युत क्षेत्र, चुंबकीय क्षेत्र या स्थिर वैद्युत के रूप में होता है अर्थात पतली कमजोर रूप से परस्पर क्रिया करने वाली पदार्थ की आंतरिक क्षमता एक इलेक्ट्रॉन के तरंगाग्र में प्रावस्था विस्थापन कर सकती है।<ref> | ||
{{cite journal | {{cite journal | ||
|last = Pozzi | |last = Pozzi | ||
| Line 46: | Line 46: | ||
|url = https://cds.cern.ch/record/2128406 | |url = https://cds.cern.ch/record/2128406 | ||
}} | }} | ||
</ref> मोटाई | </ref> इस प्रकार मोटाई मॉडुलित [[सिलिकॉन नाइट्राइड]] झिल्ली और प्रोग्रामयोग्य फेज शिफ्ट उपकरण ने दूर क्षेत्र के स्थानिक तीव्रता के रूप में होते है और इलेक्ट्रॉन तरंग के चरण को नियंत्रित करने के लिए स्थानिक रूप से भिन्न चरण शिफ्टों को लागू करने के लिए इन गुणों का समुपयोजन किया जाता है। इस तरह के उपकरणों को इलेक्ट्रॉन तरंग यादृच्छिक प्रकार से आकार देने के लिए लागू किया गया है, इस प्रकार इलेक्ट्रॉन सूक्ष्मदर्शी में निहित [[ऑप्टिकल विपथन]] को [[मुक्त इलेक्ट्रॉनों की कक्षीय कोणीय गति]] में भेद करने के लिए तथा मुक्त इलेक्ट्रॉनों और चुंबकीय सामग्री या प्लास्मोनिक नैनोस्ट्रक्चर के बीच क्रिया में डुअलिटी को मापने के लिए लागू किया गया है।<ref name="ShilohLu2019"> | ||
{{cite journal|last1=Shiloh|first1=Roy|last2=Lu|first2=Peng-Han|last3=Remez|first3=Roei|last4=Tavabi|first4=Amir H|last5=Pozzi|first5=Giulio|last6=Dunin-Borkowski|first6=Rafal E|last7=Arie|first7=Ady|title=Nanostructuring of electron beams|journal=Physica Scripta|volume=94|issue=3|year=2019|pages=034004|issn=0031-8949|doi=10.1088/1402-4896/aaf258|bibcode=2019PhyS...94c4004S|doi-access=free}} | {{cite journal|last1=Shiloh|first1=Roy|last2=Lu|first2=Peng-Han|last3=Remez|first3=Roei|last4=Tavabi|first4=Amir H|last5=Pozzi|first5=Giulio|last6=Dunin-Borkowski|first6=Rafal E|last7=Arie|first7=Ady|title=Nanostructuring of electron beams|journal=Physica Scripta|volume=94|issue=3|year=2019|pages=034004|issn=0031-8949|doi=10.1088/1402-4896/aaf258|bibcode=2019PhyS...94c4004S|doi-access=free}} | ||
</ref> | </ref> | ||
== यह भी देखें == | == यह भी देखें == | ||
* आवेशित कण किरण | * आवेशित कण किरण के रूप में होता है | ||
* मजबूत फोकसिंग | * मजबूत फोकसिंग के रूप में होता है | ||
* [[इलेक्ट्रॉन | * [[इलेक्ट्रॉन किरण प्रौद्योगिकी]] के रूप में होती है | ||
* [[इलेक्ट्रॉन सूक्ष्मदर्शी]] | * [[इलेक्ट्रॉन सूक्ष्मदर्शी]] के रूप में होते है | ||
* [[ | * [[किरण उत्सर्जन]] के रूप में होता है | ||
* [[अर्नेस्ट रसा]] | * [[अर्नेस्ट रसा|एम्स्ट रुसका]] | ||
* अर्धगोल इलेक्ट्रॉन ऊर्जा विश्लेषक | * अर्धगोल इलेक्ट्रॉन ऊर्जा विश्लेषक के रूप में होते है | ||
==अग्रिम पठन== | ==अग्रिम पठन== | ||
* | * हॉक्स, पीडब्लू और कैस्पर, ई। (1994)। इलेक्ट्रॉन प्रकाशिकी के सिद्धांत के रूप में होते है। अकादमिक प्रेस के रूप में है। {{ISBN|9780080984162}}. | ||
* | * पॉज़ी, जी। (2016) इलेक्ट्रॉन प्रकाशिकी और माइक्रोस्कोपी में कण और तरंगो के रूप में होती है। अकादमिक प्रेस के रूप में है। {{ISBN|9780128048146}}. | ||
| Line 70: | Line 68: | ||
{{refend}} | {{refend}} | ||
{{DEFAULTSORT:Electron Optics}} | {{DEFAULTSORT:Electron Optics}} | ||
[[Category: Machine Translated Page]] | [[Category:Created On 31/03/2023|Electron Optics]] | ||
[[Category: | [[Category:Lua-based templates|Electron Optics]] | ||
[[Category:Machine Translated Page|Electron Optics]] | |||
[[Category:Pages with script errors|Electron Optics]] | |||
[[Category:Templates Vigyan Ready|Electron Optics]] | |||
[[Category:Templates that add a tracking category|Electron Optics]] | |||
[[Category:Templates that generate short descriptions|Electron Optics]] | |||
[[Category:Templates using TemplateData|Electron Optics]] | |||
[[Category:त्वरक भौतिकी|Electron Optics]] | |||
[[Category:विद्युत चुंबकत्व|Electron Optics]] | |||
Latest revision as of 16:19, 20 April 2023
इलेक्ट्रॉन प्रकाशिकी विद्युत चुम्बकीय क्षेत्र के साथ इलेक्ट्रॉन प्रक्षेप वक्र की गणना के लिए एक गणितीय रूपरेखा के रूप में होते है। प्रकाशिकी शब्द का प्रयोग इसलिए किया जाता है, क्योंकि चुंबकीय और स्थिर वैद्युत लेंस एक आवेशित कण प्रकाश किरण पर ऑप्टिकल लेंस के समान कार्य करते हैं। इलेक्ट्रॉन सूक्ष्मदर्शी और कण त्वरक के डिजाइन के लिए इलेक्ट्रॉन प्रकाशिकी की गणना महत्वपूर्ण होती है। पैराएक्सियल सन्निकटन में, किरण ट्रांसफर मैट्रिक्स विश्लेषण का उपयोग करके प्रक्षेप वक्र की गणना की जा सकती है।
इलेक्ट्रॉन गुण
इलेक्ट्रॉन आवेशित कण सामान्य द्रव्यमान वाले बिंदु आवेश स्पिन (भौतिकी 1/2 के साथ होते हैं, इसलिए वे फर्मियन रूप में होते है। इलेक्ट्रॉन उपयुक्त विद्युत क्षेत्र या चुंबकीय क्षेत्र क्षेत्रों द्वारा कण त्वरक के रूप में हो सकते हैं, जिससे गतिज ऊर्जा प्राप्त होती है। पर्याप्त वोल्टेज दिए जाने पर मापने योग्य सापेक्षतावादी प्रभावों को प्रदर्शित करने के लिए इलेक्ट्रॉन को पर्याप्त तेजी से त्वरित किया जाता है। तरंग कण डुअलिटी के अनुसार इलेक्ट्रॉनों को तरंग दैर्ध्य चरण तरंगों और आयाम जैसे गुणों के साथ पदार्थ तरंगों के रूप में भी जाना जा सकता है।
ज्यामितीय इलेक्ट्रॉन प्रकाशिकी
चुंबकीय क्षेत्र
लोरेंत्ज़ बल की दूसरी अवधि के अनुसार चुंबकीय क्षेत्र और इलेक्ट्रॉन वेग के बीच एक क्रॉस उत्पाद के अनुसार इलेक्ट्रॉन चुंबकीय क्षेत्र के साथ क्रिया करते हैं। इस प्रकार एक अनंत समान क्षेत्र में इसका परिणाम क्षेत्र की दिशा के चारों ओर इलेक्ट्रॉन की एक गोलाकार गति के रूप में होता है, जिसके द्वारा दी गई त्रिज्या इस रूप में होती है
जहाँ r कक्षा की त्रिज्या होती है, m इलेक्ट्रॉन द्रव्यमान होती है, क्षेत्र के लंबवत इलेक्ट्रॉन वेग का घटक के रूप में होता है, ई इलेक्ट्रॉन आवेश है और बी लागू चुंबकीय क्षेत्र का परिमाण के रूप में है। चुंबकीय क्षेत्र के समानांतर एक वेग घटक वाले इलेक्ट्रॉन कुंडलित वक्रता प्रक्षेप वक्र के साथ आगे बढ़ते है।
विद्युत क्षेत्र
एक प्रयुक्त स्थिर वैद्युत क्षेत्र के स्थितियों में इलेक्ट्रॉन क्षेत्र के सकारात्मक ढाल की ओर विक्षेपित होता है। विशेष रूप से स्थिर वैद्युत फ़ील्ड लाइनों के इस क्रॉसिंग का अर्थ है कि स्थिर वैद्युत फ़ील्ड के माध्यम से चलने वाले इलेक्ट्रॉन अपने वेग के परिमाण को बदलते हैं, जबकि चुंबकीय क्षेत्र में, केवल वेग की दिशा को संशोधित किया जाता है।
चूंकि इलेक्ट्रॉन विवर्तन जैसे गैर-कण तरंग जैसे, प्रभाव को प्रदर्शित करते हैं, मैक्सवेल के समीकरण के अनुसार इलेक्ट्रॉन पथों का एक पूर्ण विश्लेषण प्राप्त किया जा सकता है, चूंकि कई स्थितियों में कण व्याख्या जटिलता में बड़ी कमी के साथ पर्याप्त रूप में सन्निकटन मान प्रदान कर सकती है।
इलेक्ट्रॉनों की एक और गुणधर्म यह है कि वे पदार्थ के साथ दृढ़ता से संपर्क करते हैं, क्योंकि वे न केवल नाभिक के प्रति संवेदनशील होते हैं, बल्कि पदार्थ के इलेक्ट्रॉन चार्ज क्लाउड के प्रति भी संवेदनशील होते हैं। इसलिए इलेक्ट्रॉनों को किसी भी उचित दूरी को प्रसारित करने के लिए खालीपन की आवश्यकता होती है, जैसे इलेक्ट्रॉन ऑप्टिक प्रणाली में वांछनीय रूप में होता है।
निर्वात में प्रवेश औसत मुक्त इलेक्ट्रॉन पथ द्वारा तय किया जाता है, इलेक्ट्रॉनों और पदार्थ के बीच टकराव की संभावना का एक उपाय अनुमानित मान जिसके लिए पॉइसन सांख्यिकी से प्राप्त किया जा सकता है।
सापेक्षवादी सिद्धांत
चूंकि, सापेक्षवादी सिद्धांत बहुत सामान्य नहीं है, डायराक समीकरण से प्रारंभ होने वाले आवेशित कणों पर चुंबकीय संरचनाओं के प्रभावों को प्राप्त करना भी संभव रूप में होता है।[1]
विवर्तनिक इलेक्ट्रॉन प्रकाशिकी
निर्वात में प्रसार करने वाले उप सापेक्षवादी मुक्त इलेक्ट्रॉन को एक ब्रोगली का पदार्थ तरंग के रूप में यथार्थ रूप से वर्णित किया जाता है, जिसकी तरंग दैर्ध्य इसके अनुदैर्ध्य संवेग के व्युत्क्रमानुपाती होती है। इस प्रकार इलेक्ट्रॉन द्वारा किए गए आवेश के परिणामस्वरूप विद्युत क्षेत्र, चुंबकीय क्षेत्र या स्थिर वैद्युत के रूप में होता है अर्थात पतली कमजोर रूप से परस्पर क्रिया करने वाली पदार्थ की आंतरिक क्षमता एक इलेक्ट्रॉन के तरंगाग्र में प्रावस्था विस्थापन कर सकती है।[2] इस प्रकार मोटाई मॉडुलित सिलिकॉन नाइट्राइड झिल्ली और प्रोग्रामयोग्य फेज शिफ्ट उपकरण ने दूर क्षेत्र के स्थानिक तीव्रता के रूप में होते है और इलेक्ट्रॉन तरंग के चरण को नियंत्रित करने के लिए स्थानिक रूप से भिन्न चरण शिफ्टों को लागू करने के लिए इन गुणों का समुपयोजन किया जाता है। इस तरह के उपकरणों को इलेक्ट्रॉन तरंग यादृच्छिक प्रकार से आकार देने के लिए लागू किया गया है, इस प्रकार इलेक्ट्रॉन सूक्ष्मदर्शी में निहित ऑप्टिकल विपथन को मुक्त इलेक्ट्रॉनों की कक्षीय कोणीय गति में भेद करने के लिए तथा मुक्त इलेक्ट्रॉनों और चुंबकीय सामग्री या प्लास्मोनिक नैनोस्ट्रक्चर के बीच क्रिया में डुअलिटी को मापने के लिए लागू किया गया है।[3]
यह भी देखें
- आवेशित कण किरण के रूप में होता है
- मजबूत फोकसिंग के रूप में होता है
- इलेक्ट्रॉन किरण प्रौद्योगिकी के रूप में होती है
- इलेक्ट्रॉन सूक्ष्मदर्शी के रूप में होते है
- किरण उत्सर्जन के रूप में होता है
- एम्स्ट रुसका
- अर्धगोल इलेक्ट्रॉन ऊर्जा विश्लेषक के रूप में होते है
अग्रिम पठन
- हॉक्स, पीडब्लू और कैस्पर, ई। (1994)। इलेक्ट्रॉन प्रकाशिकी के सिद्धांत के रूप में होते है। अकादमिक प्रेस के रूप में है। ISBN 9780080984162.
- पॉज़ी, जी। (2016) इलेक्ट्रॉन प्रकाशिकी और माइक्रोस्कोपी में कण और तरंगो के रूप में होती है। अकादमिक प्रेस के रूप में है। ISBN 9780128048146.
संदर्भ
- ↑ Jagannathan, R.; Simon, R.; Sudarshan, E. C. G.; Mukunda, N. (1989). "डायराक समीकरण के आधार पर चुंबकीय इलेक्ट्रॉन लेंस का क्वांटम सिद्धांत" (PDF). Physics Letters A. 134 (8–9): 457. Bibcode:1989PhLA..134..457J. doi:10.1016/0375-9601(89)90685-3.
- ↑ Pozzi, Giulio; Peter Hawkes (2016). "Particles and waves in electron optics and microscopy". Advances in Imaging and Electron Physics. 194 (2): 1–336. doi:10.1016/bs.aiep.2016.02.001.
- ↑ Shiloh, Roy; Lu, Peng-Han; Remez, Roei; Tavabi, Amir H; Pozzi, Giulio; Dunin-Borkowski, Rafal E; Arie, Ady (2019). "Nanostructuring of electron beams". Physica Scripta. 94 (3): 034004. Bibcode:2019PhyS...94c4004S. doi:10.1088/1402-4896/aaf258. ISSN 0031-8949.
