जेरम प्लॉट: Difference between revisions

Latest revision as of 11:21, 27 April 2023

उदाहरण जेरम आरेख: समुद्र के अम्लीकरण से समुद्री जल के कार्बोनेट प्रणाली में परिवर्तन।

जेरम आरेख (नील्स जेरम के नाम पर; कभी-कभी सिलेन आरेख या हैग आरेख के रूप में भी जाना जाता है) विलयन में पॉलीप्रोटिक अम्ल की विभिन्न प्रजातियों की सांद्रता का आरेख है, पीएच (हाइड्रोजन की क्षमता) के कार्य के रूप में^[1] विलयन रासायनिक साम्यावस्था में होता है। अतः सांद्रता द्वारा विस्तृत परिमाण के कई क्रमों के कारण, वे सामान्य रूप से लघुगणकीय पैमाने पर आरेखित किए जाते हैं। कभी-कभी वास्तविक सांद्रता के अतिरिक्त सांद्रता के अनुपात को आरेख किया जाता है। और कभी-कभी H⁺ और OH⁻ भी आलेखित किए गए हैं।

सबसे अधिक बार कार्बोनेट प्रणाली को आरेखित किया जाता है, जहां पॉलीप्रोटिक अम्ल कार्बोनिक अम्ल (डिप्रोटिक अम्ल) होता है, और विभिन्न प्रजातियां कार्बन डाइऑक्साइड, कार्बोनिक अम्ल, बाइकार्बोनेट और कार्बोनेट में विलेय हो जाती हैं। अम्लीय स्थितियों में, प्रभावशाली रूप CO₂ और मूल (क्षारीय) स्थितियों में, प्रभावशाली रूप CO²⁻
₃ है; और बीच में, प्रभावशाली रूप HCO⁻
₃ है। प्रत्येक पीएच मान पर, कार्बोनिक अम्ल की सांद्रता घुलित CO₂ की सांद्रता की तुलना में नगण्य माना जाता है, और इसलिए इसे प्रायः जेरम आरेखों से विलोपित किया जाता है। ये आरेख विलयन रसायन और प्राकृतिक जल रसायन में अधिक सहायक होते हैं। यहाँ दिए गए उदाहरण में, यह जीवाश्म ईंधन के दहन द्वारा मानव निर्मित CO₂ उत्सर्जन के सहयोग के कारण समुद्री जल के पीएच और कार्बोनेट उपजातिकरण की प्रतिक्रिया को दर्शाता है।^[2]

सिलिकिक अम्ल, बोरिक अम्ल, सल्फ्यूरिक अम्ल और फॉस्फोरिक अम्ल अम्ल सहित अन्य पॉलीप्रोटिक अम्ल के लिए जेरम आरेख अन्य सामान्य रूप से उपयोग किए जाने वाले उदाहरण हैं।^[1]

कार्बोनेट प्रणाली के लिए जेरम आरेख समीकरण

यदि कार्बन डाइऑक्साइड, कार्बोनिक अम्ल, हाइड्रोन (रसायन विज्ञान), बाइकार्बोनेट और कार्बोनेट सभी पानी में विलेय हो जाते हैं, और रासायनिक साम्यावस्था पर उनकी साम्य सांद्रता को प्रायः निम्न अभिक्रिया द्वारा दिया जाता है:

{\begin{aligned}[]\left[{\textrm {CO}}_{2}\right]_{\text{eq}}&={\frac {\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}+K_{1}\left[{\textrm {H}}^{+}\right]_{\text{eq}}+K_{1}K_{2}}}\times {\textrm {DIC}},\\[3pt]\left[{\textrm {HCO}}_{3}^{-}\right]_{\text{eq}}&={\frac {K_{1}\left[{\textrm {H}}^{+}\right]_{\text{eq}}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}+K_{1}\left[{\textrm {H}}^{+}\right]_{\text{eq}}+K_{1}K_{2}}}\times {\textrm {DIC}},\\[3pt]\left[{\textrm {CO}}_{3}^{2-}\right]_{\text{eq}}&={\frac {K_{1}K_{2}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}+K_{1}\left[{\textrm {H}}^{+}\right]_{\text{eq}}+K_{1}K_{2}}}\times {\textrm {DIC}},\end{aligned}}

जहां पादांक 'eq' दर्शाता है कि ये साम्य सांद्रता हैं, K₁ प्रतिक्रिया के लिए साम्य CO
₂ + H
₂O ⇌ H⁺ + HCO⁻
₃ स्थिरांक है, अर्थात कार्बोनिक अम्ल के लिए पहला अम्ल पृथक्करण स्थिरांक है और K₂ प्रतिक्रिया के लिए HCO⁻
₃ ⇌ H⁺ + CO²⁻
₃ साम्य स्थिरांक (अर्थात कार्बोनिक अम्ल के लिए दूसरा अम्ल पृथक्करण स्थिरांक) है, और डीआईसी प्रणाली में कुल अकार्बनिक कार्बन की (अपरिवर्तनीय) समग्र सांद्रता [CO₂] + [HCO⁻
₃] + [CO²⁻
₃] होती है। अर्थात K₁, K₂ और डीआईसी प्रत्येक में सांद्रता की इकाइयां होती हैं, उदाहरण मोल (इकाई)/लीटर है।

इन तीन प्रजातियों के विपरीत आरेख करने के लिए इन तीन समीकरणों का उपयोग करके pH = −log₁₀ [H⁺]_eq जेरम आरेख प्राप्त किया जाता है, दिए गए K₁, K₂ और डीआईसी के लिए इन अभिक्रियाओ में भाग तीन प्रजातियों के सापेक्ष अनुपात देते हैं, और इसलिए यदि डीआईसी अज्ञात है, या वास्तविक सांद्रता नगण्य होती हैं, तो इसके अतिरिक्त इन अनुपातों को आरेख किया जा सकता है।

इन तीन समीकरणों से पता चलता है कि CO₂ और HCO⁻
₃ के लिए वक्र [H⁺]_eq = K₁, पर प्रतिच्छेद करता है, और HCO⁻
₃ और CO²⁻
₃ के वक्र [H⁺]_eq = K₂ पर प्रतिच्छेद करते हैं। इसलिए, K₁ और K₂ के मान जो किसी दिए गए जेरम आरेख को बनाने के लिए उपयोग किए गए थे, उस आरेख से परस्पर क्रिया के इन बिंदुओं पर सांद्रता का अध्ययन करके आसानी से प्राप्त किया जा सकता है। रेखीय Y अक्ष के साथ एक उदाहरण संलग्न आरेख में दिखाया गया है कि K₁ और K₂ के मान और इसलिए जेरम आरेख में वक्र, तापमान और लवणता के साथ अपेक्षाकृत अधिक भिन्न होते हैं।^[3]

कार्बोनेट प्रणाली के लिए जेरम आरेख समीकरणों की रासायनिक और गणितीय व्युत्पत्ति

मान लीजिए कि पानी में विलेय कार्बन डाइऑक्साइड, हाइड्रोन (रसायन विज्ञान), बाइकार्बोनेट और कार्बोनेट आयनों के बीच प्रतिक्रियाएँ इस प्रकार हैं:

CO
₂ + H
₂O ⇌ H⁺ + HCO⁻
₃

(1)

HCO⁻
₃ ⇌ H⁺ + CO²⁻
₃

(2)

ध्यान दें कि प्रतिक्रिया 1 वास्तव में दो प्राथमिक प्रतिक्रियाओं का संयोजन है:

CO
₂ + H
₂O ⇌ H
₂CO
₃ ⇌ H⁺ + HCO⁻
₃

यह मानते हुए कि द्रव्यमान क्रिया नियम इन दो प्रतिक्रियाओं पर प्रयुक्त होता है कि जल अधिकता (रसायन विज्ञान) है, और यह कि विभिन्न रासायनिक प्रजातियां सदैव अच्छी तरह से मिश्रित होती हैं, उनके दर समीकरण हैं

{\begin{aligned}{\frac {{\textrm {d}}\left[{\textrm {CO}}_{2}\right]}{{\textrm {d}}t}}&=-k_{1}\left[{\textrm {CO}}_{2}\right]+k_{-1}\left[{\textrm {H}}^{+}\right]\left[{\textrm {HCO}}_{3}^{-}\right],\\{\frac {{\textrm {d}}\left[{\textrm {H}}^{+}\right]}{{\textrm {d}}t}}&=k_{1}\left[{\textrm {CO}}_{2}\right]-k_{-1}\left[{\textrm {H}}^{+}\right]\left[{\textrm {HCO}}_{3}^{-}\right]+k_{2}\left[{\textrm {HCO}}_{3}^{-}\right]-k_{-2}\left[{\textrm {H}}^{+}\right]\left[{\textrm {CO}}_{3}^{2-}\right],\\{\frac {{\textrm {d}}\left[{\textrm {HCO}}_{3}^{-}\right]}{{\textrm {d}}t}}&=k_{1}\left[{\textrm {CO}}_{2}\right]-k_{-1}\left[{\textrm {H}}^{+}\right]\left[{\textrm {HCO}}_{3}^{-}\right]-k_{2}\left[{\textrm {HCO}}_{3}^{-}\right]+k_{-2}\left[{\textrm {H}}^{+}\right]\left[{\textrm {CO}}_{3}^{2-}\right],\\{\frac {{\textrm {d}}\left[{\textrm {CO}}_{3}^{2-}\right]}{{\textrm {d}}t}}&=k_{2}\left[{\textrm {HCO}}_{3}^{-}\right]-k_{-2}\left[{\textrm {H}}^{+}\right]\left[{\textrm {CO}}_{3}^{2-}\right]\end{aligned}}

जहाँ [ ] सांद्रता को दर्शाता है, t समय है, और K₁ और K₋₁ प्रतिक्रिया 1 के लिए उपयुक्त समानुपातिकता (गणित) स्थिरांक हैं, इस प्रतिक्रिया के लिए क्रमशः आगे और विपरीत प्रतिवर्ती दर स्थिरांक (इसी प्रकार K₂ और K₋₂ प्रतिक्रिया के लिए 2) कहा जाता है।

किसी भी साम्यावस्था पर, सांद्रता अपरिवर्तित होती है, इसलिए इन समीकरणों के बायीं ओर शून्य होते हैं। फिर, इन चार समीकरणों में से पहले से, प्रतिक्रिया का अनुपात 1 की दर स्थिरांक इसकी साम्य सांद्रता के अनुपात के समान होती है, और इस अनुपात को K₁ कहा जाता है, प्रतिक्रिया 1 के लिए साम्य स्थिरांक कहा जाता है, अर्थात

K_{1}={\frac {k_{1}}{k_{-1}}}={\frac {[{\textrm {H}}^{+}]_{\text{eq}}[{\textrm {HCO}}_{3}^{-}]_{\text{eq}}}{[{\textrm {CO}}_{2}]_{\text{eq}}}}

(3)

जहां पादांक 'eq' दर्शाता है कि ये साम्य सांद्रता हैं।

इसी प्रकार, साम्य स्थिरांक K₂ के लिए चतुर्थ समीकरण 2 से प्रतिक्रिया के लिए,

K_{2}={\frac {k_{2}}{k_{-2}}}={\frac {\left[{\textrm {H}}^{+}\right]_{\text{eq}}\left[{\textrm {CO}}_{3}^{2-}\right]_{\text{eq}}}{\left[{\textrm {HCO}}_{3}^{-}\right]_{\text{eq}}}}

(4)

3 को पुनर्व्यवस्थित करने पर प्राप्त होता है

\left[{\textrm {HCO}}_{3}^{-}\right]_{\text{eq}}={\frac {K_{1}\left[{\textrm {CO}}_{2}\right]_{\text{eq}}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}}}

(5)

और पुनर्व्यवस्थित 4, फिर प्रतिस्थापित करने पर 5 देता है

\left[{\textrm {CO}}_{3}^{2-}\right]_{\text{eq}}={\frac {K_{2}\left[{\textrm {HCO}}_{3}^{-}\right]_{\text{eq}}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}}}={\frac {K_{1}K_{2}\left[{\textrm {CO}}_{2}\right]_{\text{eq}}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}}}

(6)

प्रणाली में विलेय हुए अकार्बनिक कार्बन की कुल सांद्रता 5 और 6 में प्रतिस्थापित करके दी गई है:

{\begin{aligned}{\textrm {DIC}}&=\left[{\textrm {CO}}_{2}\right]+\left[{\textrm {HCO}}_{3}^{-}\right]+\left[{\textrm {CO}}_{3}^{2-}\right]\\&=\left[{\textrm {CO}}_{2}\right]_{\text{eq}}\left(1+{\frac {K_{1}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}}}+{\frac {K_{1}K_{2}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}}}\right)\\&=\left[{\textrm {CO}}_{2}\right]_{\text{eq}}\left({\frac {\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}+K_{1}\left[{\textrm {H}}^{+}\right]_{\text{eq}}+K_{1}K_{2}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}}}\right)\end{aligned}}

इसे पुनर्व्यवस्थित करने पर CO
₂ के लिए समीकरण प्राप्त होता है:

\left[{\textrm {CO}}_{2}\right]_{\text{eq}}={\frac {\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}+K_{1}\left[{\textrm {H}}^{+}\right]_{\text{eq}}+K_{1}K_{2}}}\times {\textrm {DIC}}

5 और 6 के लिए समीकरण HCO⁻
₃ और CO²⁻
₃ को इसमें प्रतिस्थापित करके प्राप्त किया जाता है

यह भी देखें

चार्लोट समीकरण
ग्रैन प्लॉट (ग्रैन अनुमापन या ग्रैन विधि के रूप में भी जाना जाता है)
हेंडरसन-हसलबल्च समीकरण
हिल समीकरण (जैव रसायन)
आयन प्रजाति
स्वच्छ जल
समुद्री जल
तापलवणीय संचरण

संदर्भ

↑ ^1.0 ^1.1 Andersen, C. B. (2002). "प्रायोगिक और प्राकृतिक प्रणालियों में क्षारीयता को मापकर कार्बोनेट संतुलन को समझना". Journal of Geoscience Education. 50 (4): 389–403. Bibcode:2002JGeEd..50..389A. doi:10.5408/1089-9995-50.4.389. S2CID 17094010.
↑ D.A. Wolf-Gladrow (2007). "Total alkalinity: the explicit conservative expression and its application to biogeochemical processes" (PDF). Marine Chemistry. 106 (1): 287–300. doi:10.1016/j.marchem.2007.01.006.
↑ Mook W (2000) Chemistry of carbonic acid in water. In 'Environmental Isotopes in the Hydrological Cycle: Principles and Applications' pp. 143-165. (INEA / UNESCO: Paris). [1] Retrieved 30 November 2013.

[Andersen-1] 1.0 ^1.1 Andersen, C. B. (2002). "प्रायोगिक और प्राकृतिक प्रणालियों में क्षारीयता को मापकर कार्बोनेट संतुलन को समझना". Journal of Geoscience Education. 50 (4): 389–403. Bibcode:2002JGeEd..50..389A. doi:10.5408/1089-9995-50.4.389. S2CID 17094010.

[wolfgladrow2007-2] D.A. Wolf-Gladrow (2007). "Total alkalinity: the explicit conservative expression and its application to biogeochemical processes" (PDF). Marine Chemistry. 106 (1): 287–300. doi:10.1016/j.marchem.2007.01.006.

[3] Mook W (2000) Chemistry of carbonic acid in water. In 'Environmental Isotopes in the Hydrological Cycle: Principles and Applications' pp. 143-165. (INEA / UNESCO: Paris). [1] Retrieved 30 November 2013.

[1]

[2]

[3]

@@ Line 1: / Line 1: @@
 {{short description|Graph of polyprotic acid concentration compared to pH}}
-[[File:Carbonate system of seawater.svg|thumb|upright=1.35|उदाहरण जेरम प्लाट: समुद्र के अम्लीकरण से समुद्री जल के कार्बोनेट सिस्टम में परिवर्तन।]]एक बेजरम प्लॉट ([[नील्स बजरम]] के नाम पर; कभी-कभी सिलेन डायग्राम या हैग डायग्राम के रूप में भी जाना जाता है) [[पीएच]] के एक कार्य के रूप में एक एसिड # पॉलीप्रोटिक एसिड इन सॉल्यूशन (रसायन विज्ञान) की विभिन्न प्रजातियों की सांद्रता का एक [[चार्ट]] है।<ref name=Andersen>{{Cite journal |last=Andersen|first=C. B.|year=2002 |title=प्रायोगिक और प्राकृतिक प्रणालियों में क्षारीयता को मापकर कार्बोनेट संतुलन को समझना| journal=Journal of Geoscience Education |volume=50 |issue=4 |pages=389–403 |doi=10.5408/1089-9995-50.4.389 |bibcode=2002JGeEd..50..389A|s2cid=17094010 }}</ref> जब विलयन रासायनिक साम्यावस्था में हो। सांद्रता द्वारा फैले परिमाण के कई आदेशों के कारण, वे आमतौर पर एक [[लघुगणकीय पैमाने]] पर प्लॉट किए जाते हैं। कभी-कभी वास्तविक सांद्रता के बजाय सांद्रता के अनुपात को प्लॉट किया जाता है। कभी-कभी एच<sup>+</sup> और ओह<sup>−</sup> भी प्लॉट किए गए हैं।
+[[File:Carbonate system of seawater.svg|thumb|upright=1.35|उदाहरण जेरम आरेख: समुद्र के अम्लीकरण से समुद्री जल के कार्बोनेट प्रणाली में परिवर्तन।]]'''''जेरम आरेख''''' ('''नील्स जेरम''' के नाम पर; कभी-कभी '''सिलेन आरेख''' या '''हैग आरेख''' के रूप में भी जाना जाता है) विलयन में पॉलीप्रोटिक अम्ल की विभिन्न प्रजातियों की सांद्रता का आरेख है, पीएच (हाइड्रोजन की क्षमता) के कार्य के रूप में<ref name=Andersen>{{Cite journal |last=Andersen|first=C. B.|year=2002 |title=प्रायोगिक और प्राकृतिक प्रणालियों में क्षारीयता को मापकर कार्बोनेट संतुलन को समझना| journal=Journal of Geoscience Education |volume=50 |issue=4 |pages=389–403 |doi=10.5408/1089-9995-50.4.389 |bibcode=2002JGeEd..50..389A|s2cid=17094010 }}</ref> विलयन रासायनिक साम्यावस्था में होता है। अतः सांद्रता द्वारा विस्तृत परिमाण के कई क्रमों के कारण, वे सामान्य रूप से [[लघुगणकीय पैमाने]] पर आरेखित किए जाते हैं। कभी-कभी वास्तविक सांद्रता के अतिरिक्त सांद्रता के अनुपात को आरेख किया जाता है। और कभी-कभी H<sup>+</sup> और OH<sup>−</sup> भी आलेखित किए गए हैं।
-सबसे अधिक बार, [[कार्बोनेट]] सिस्टम प्लॉट किया जाता है, जहां पॉलीप्रोटिक एसिड [[कार्बोनिक एसिड]] (एक [[डिप्रोटिक एसिड]]) होता है, और विभिन्न प्रजातियां [[ कार्बन डाईऑक्साइड ]], कार्बोनिक एसिड, [[ बिकारबोनिट ]] और कार्बोनेट में घुल जाती हैं। अम्लीय परिस्थितियों में, प्रमुख रूप है {{CO2}}; [[आधार (रसायन विज्ञान)]] (क्षारीय) स्थितियों में, प्रमुख रूप है {{chem|CO|3|2−}}; और बीच में, प्रमुख रूप है {{chem|HCO|3|−}}. प्रत्येक पीएच पर, भंग की एकाग्रता की तुलना में कार्बोनिक एसिड की एकाग्रता को नगण्य माना जाता है {{chem|CO|2}}, और इसलिए अक्सर बजेरम भूखंडों से छोड़ा जाता है। ये प्लॉट सॉल्यूशन केमिस्ट्री और नेचुरल वॉटर केमिस्ट्री में बहुत मददगार हैं। यहां दिए गए उदाहरण में, यह मानव निर्मित इनपुट के कारण समुद्री जल पीएच और कार्बोनेट प्रजाति की प्रतिक्रिया को दिखाता है {{chem|CO|2}} जीवाश्म ईंधन के दहन से उत्सर्जन।<ref name="wolfgladrow2007">{{cite journal | author=D.A. Wolf-Gladrow| title=Total alkalinity: the explicit conservative expression and its application to biogeochemical processes| journal=Marine Chemistry| year=2007| volume=106| issue=1| pages=287–300| doi=10.1016/j.marchem.2007.01.006| url=http://www.soest.hawaii.edu/oceanography/faculty/zeebe_files/Publications/WolfGladrowMarChem07.pdf}}</ref>
+सबसे अधिक बार कार्बोनेट प्रणाली को आरेखित किया जाता है, जहां पॉलीप्रोटिक अम्ल कार्बोनिक अम्ल (डिप्रोटिक अम्ल) होता है, और विभिन्न प्रजातियां कार्बन डाइऑक्साइड, कार्बोनिक अम्ल, बाइकार्बोनेट और कार्बोनेट में विलेय हो जाती हैं। अम्लीय स्थितियों में, प्रभावशाली रूप {{CO2}} और मूल (क्षारीय) स्थितियों में, प्रभावशाली रूप {{chem|CO|3|2−}} है; और बीच में, प्रभावशाली रूप {{chem|HCO|3|−}} है। प्रत्येक पीएच मान पर, कार्बोनिक अम्ल की सांद्रता घुलित CO<sub>2</sub> की सांद्रता की तुलना में नगण्य माना जाता है, और इसलिए इसे प्रायः जेरम आरेखों से विलोपित किया जाता है। ये आरेख विलयन रसायन और प्राकृतिक जल रसायन में अधिक सहायक होते हैं। यहाँ दिए गए उदाहरण में, यह जीवाश्म ईंधन के दहन द्वारा मानव निर्मित CO<sub>2</sub> उत्सर्जन के सहयोग के कारण समुद्री जल के पीएच और कार्बोनेट उपजातिकरण की प्रतिक्रिया को दर्शाता है।<ref name="wolfgladrow2007">{{cite journal | author=D.A. Wolf-Gladrow| title=Total alkalinity: the explicit conservative expression and its application to biogeochemical processes| journal=Marine Chemistry| year=2007| volume=106| issue=1| pages=287–300| doi=10.1016/j.marchem.2007.01.006| url=http://www.soest.hawaii.edu/oceanography/faculty/zeebe_files/Publications/WolfGladrowMarChem07.pdf}}</ref>
-[[सिलिकिक एसिड]], [[बोरिक एसिड]], [[सल्फ्यूरिक एसिड]] और [[फॉस्फोरिक एसिड]] एसिड सहित अन्य पॉलीप्रोटिक एसिड के लिए बजरम प्लॉट अन्य सामान्य रूप से उपयोग किए जाने वाले उदाहरण हैं।<ref name=Andersen />
+[[सिलिकिक एसिड|सिलिकिक अम्ल]], [[बोरिक एसिड|बोरिक अम्ल]], [[सल्फ्यूरिक एसिड|सल्फ्यूरिक अम्ल]] और [[फॉस्फोरिक एसिड|फॉस्फोरिक अम्ल]] अम्ल सहित अन्य पॉलीप्रोटिक अम्ल के लिए जेरम आरेख अन्य सामान्य रूप से उपयोग किए जाने वाले उदाहरण हैं।<ref name="Andersen" />
-== कार्बोनेट प्रणाली के लिए बेजरम प्लॉट समीकरण ==
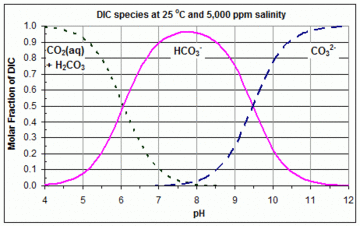
-[[File:Carbonate Bjerrum.gif|thumb|upright=1.2|alt=Distribution of DIC (कार्बोनेट) 25सी और 5,000 पीपीएम लवणता के लिए पीएच वाली प्रजातियां (जैसे नमक-पानी स्विमिंग पूल) - बेजरम प्लॉट]]यदि कार्बन डाइऑक्साइड, कार्बोनिक एसिड, [[हाइड्रोन (रसायन विज्ञान)]], बाइकार्बोनेट और कार्बोनेट सभी [[पानी]] में घुल जाते हैं, और रासायनिक संतुलन पर, उनकी संतुलन सांद्रता को अक्सर निम्न द्वारा दिया जाता है:
+== कार्बोनेट प्रणाली के लिए जेरम आरेख समीकरण ==
+[[File:Carbonate Bjerrum.gif|thumb|upright=1.2|alt=Distribution of DIC (कार्बोनेट) 25सी और 5,000 पीपीएम लवणता के लिए पीएच वाली प्रजातियां (जैसे नमक-पानी स्विमिंग पूल) - बेजरम प्लॉट]]यदि कार्बन डाइऑक्साइड, कार्बोनिक अम्ल, [[हाइड्रोन (रसायन विज्ञान)]], बाइकार्बोनेट और कार्बोनेट सभी [[पानी]] में विलेय हो जाते हैं, और रासायनिक साम्यावस्था पर उनकी साम्य सांद्रता को प्रायः निम्न अभिक्रिया द्वारा दिया जाता है:
 : <math>\begin{align}[]
@@ Line 14: / Line 16: @@
    \left[\textrm{CO}_3^{2-}\right]_\text{eq} &= \frac{K_1 K_2}{\left[\textrm{H}^+\right]_\text{eq}^2 + K_1\left[\textrm{H}^+\right]_\text{eq} + K_1 K_2} \times \textrm{DIC},
 \end{align}</math>
-जहां सबस्क्रिप्ट 'eq' दर्शाता है कि ये संतुलन सांद्रता हैं, K<sub>1</sub> प्रतिक्रिया के लिए संतुलन स्थिरांक है {{chem|CO|2}} + {{chem|H|2|O}} {{eqm}} एच<sup>+</sup> + {{chem|HCO|3|−}} (यानी कार्बोनिक एसिड के लिए पहला एसिड पृथक्करण स्थिरांक), के<sub>2</sub> प्रतिक्रिया के लिए संतुलन स्थिरांक है {{chem|HCO|3|−}} {{eqm}} एच<sup>+</sup> + {{chem|CO|3|2−}} (यानी कार्बोनिक एसिड के लिए दूसरा एसिड पृथक्करण स्थिरांक), और डीआईसी सिस्टम में [[कुल अकार्बनिक कार्बन]] की (अपरिवर्तनीय) कुल सांद्रता है, अर्थात [{{CO2}}] + [{{chem|HCO|3|−}}] + [{{chem|CO|3|2−}}]। क<sub>1</sub>, क<sub>2</sub> और डीआईसी प्रत्येक में एकाग्रता की इकाइयां होती हैं, उदा। मोल (यूनिट)/[[लीटर]]।
+जहां पादांक 'eq' दर्शाता है कि ये साम्य सांद्रता हैं, K<sub>1</sub> प्रतिक्रिया के लिए साम्य {{chem|CO|2}} + {{chem|H|2|O}} {{eqm}} H<sup>+</sup> + {{chem|HCO|3|−}} स्थिरांक है, अर्थात कार्बोनिक अम्ल के लिए पहला अम्ल पृथक्करण स्थिरांक है और K<sub>2</sub> प्रतिक्रिया के लिए {{chem|HCO|3|−}} {{eqm}} H<sup>+</sup> + {{chem|CO|3|2−}} साम्य स्थिरांक (अर्थात कार्बोनिक अम्ल के लिए दूसरा अम्ल पृथक्करण स्थिरांक) है, और डीआईसी प्रणाली में [[कुल अकार्बनिक कार्बन]] की (अपरिवर्तनीय) समग्र सांद्रता [{{CO2}}] + [{{chem|HCO|3|−}}] + [{{chem|CO|3|2−}}] होती है। अर्थात K<sub>1</sub>, K<sub>2</sub> और डीआईसी प्रत्येक में सांद्रता की इकाइयां होती हैं, उदाहरण मोल (इकाई)/[[लीटर]] है।
-इन तीन प्रजातियों के विरुद्ध प्लॉट करने के लिए इन तीन समीकरणों का उपयोग करके एक बजेरम प्लॉट प्राप्त किया जाता है {{nowrap|pH {{=}} −log<sub>10</sub> [H<sup>+</sup>]<sub>eq</sub>}}, दिए गए K के लिए<sub>1</sub>, क<sub>2</sub> और डीआईसी। इन समीकरणों में अंश तीन प्रजातियों के सापेक्ष अनुपात देते हैं, और इसलिए यदि डीआईसी अज्ञात है, या वास्तविक सांद्रता महत्वहीन हैं, तो इसके बजाय इन अनुपातों को प्लॉट किया जा सकता है।
+इन तीन प्रजातियों के विपरीत आरेख करने के लिए इन तीन समीकरणों का उपयोग करके {{nowrap|pH {{=}} −log<sub>10</sub> [H<sup>+</sup>]<sub>eq</sub>}} जेरम आरेख प्राप्त किया जाता है, दिए गए K<sub>1</sub>, K<sub>2</sub> और डीआईसी के लिए इन अभिक्रियाओ में भाग तीन प्रजातियों के सापेक्ष अनुपात देते हैं, और इसलिए यदि डीआईसी अज्ञात है, या वास्तविक सांद्रता नगण्य होती हैं, तो इसके अतिरिक्त इन अनुपातों को आरेख किया जा सकता है।
-इन तीन समीकरणों से पता चलता है कि के लिए घटता है {{CO2}} और {{chem|HCO|3|−}} पर प्रतिच्छेद करें {{nowrap|[H<sup>+</sup>]<sub>eq</sub> {{=}} ''K''<sub>1</sub>}}, और के लिए घटता है {{chem|HCO|3|−}} और {{chem|CO|3|2−}} पर प्रतिच्छेद करें {{nowrap|[H<sup>+</sup>]<sub>eq</sub> {{=}} ''K''<sub>2</sub>}}. इसलिए, K के मान<sub>1</sub> और के<sub>2</sub> इन चौराहों के इन बिंदुओं पर सांद्रता को पढ़कर, किसी दिए गए बजरम भूखंड को बनाने के लिए उपयोग किया गया था, उस भूखंड से आसानी से पाया जा सकता है। रेखीय Y अक्ष के साथ एक उदाहरण संलग्न ग्राफ में दिखाया गया है। K के मान<sub>1</sub> और के<sub>2</sub>, और इसलिए बजेरम प्लॉट में वक्र, तापमान और लवणता के साथ काफी भिन्न होते हैं।<ref>Mook W (2000) Chemistry of carbonic acid in water. In 'Environmental Isotopes in the Hydrological Cycle: Principles and Applications' pp. 143-165. (INEA / UNESCO: Paris). [http://www-naweb.iaea.org/napc/ih/documents/global_cycle/vol%20I/cht_i_09.pdf] Retrieved 30 November 2013.</ref>
+इन तीन समीकरणों से पता चलता है कि {{CO2}} और {{chem|HCO|3|−}} के लिए वक्र {{nowrap|[H<sup>+</sup>]<sub>eq</sub> {{=}} ''K''<sub>1</sub>}}, पर प्रतिच्छेद करता है, और {{chem|HCO|3|−}} और {{chem|CO|3|2−}} के वक्र {{nowrap|[H<sup>+</sup>]<sub>eq</sub> {{=}} ''K''<sub>2</sub>}} पर प्रतिच्छेद करते हैं। इसलिए, K<sub>1</sub> और K<sub>2</sub> के मान जो किसी दिए गए जेरम आरेख को बनाने के लिए उपयोग किए गए थे, उस आरेख से परस्पर क्रिया के इन बिंदुओं पर सांद्रता का अध्ययन करके आसानी से प्राप्त किया जा सकता है। रेखीय Y अक्ष के साथ एक उदाहरण संलग्न आरेख में दिखाया गया है कि K<sub>1</sub> और K<sub>2</sub> के मान और इसलिए जेरम आरेख में वक्र, तापमान और लवणता के साथ अपेक्षाकृत अधिक भिन्न होते हैं।<ref>Mook W (2000) Chemistry of carbonic acid in water. In 'Environmental Isotopes in the Hydrological Cycle: Principles and Applications' pp. 143-165. (INEA / UNESCO: Paris). [http://www-naweb.iaea.org/napc/ih/documents/global_cycle/vol%20I/cht_i_09.pdf] Retrieved 30 November 2013.</ref>
-==कार्बोनेट प्रणाली के लिए बेजरम प्लॉट समीकरणों की रासायनिक और गणितीय व्युत्पत्ति==
+==कार्बोनेट प्रणाली के लिए जेरम आरेख समीकरणों की रासायनिक और गणितीय व्युत्पत्ति==
-मान लीजिए कि पानी में घुले कार्बन डाइऑक्साइड, हाइड्रोन (रसायन विज्ञान), बाइकार्बोनेट और कार्बोनेट [[आयनों]] के बीच प्रतिक्रियाएँ इस प्रकार हैं:
+मान लीजिए कि पानी में विलेय कार्बन डाइऑक्साइड, हाइड्रोन (रसायन विज्ञान), बाइकार्बोनेट और कार्बोनेट [[आयनों]] के बीच प्रतिक्रियाएँ इस प्रकार हैं:
 {{NumBlk|:|{{chem|CO|2}} + {{chem|H|2|O}} {{eqm}} H<sup>+</sup> + {{chem|HCO|3|−}}|{{EquationRef|1}}}}
 {{NumBlk|:|{{chem|HCO|3|−}} {{eqm}} H<sup>+</sup> + {{chem|CO|3|2−}}|{{EquationRef|2}}}}
 ध्यान दें कि प्रतिक्रिया {{EquationNote|1}} वास्तव में दो [[प्राथमिक प्रतिक्रिया]]ओं का संयोजन है:
-: {{chem|CO|2}} + {{chem|H|2|O}} {{eqm}} {{chem|H|2|CO|3}} {{eqm}} एच<sup>+</sup> + {{chem|HCO|3|−}}
+: {{chem|CO|2}} + {{chem|H|2|O}} {{eqm}} {{chem|H|2|CO|3}} {{eqm}} H<sup>+</sup> + {{chem|HCO|3|−}}
-यह मानते हुए कि द्रव्यमान क्रिया कानून इन दो प्रतिक्रियाओं पर लागू होता है, कि पानी प्रचुरता (रसायन विज्ञान) है, और यह कि विभिन्न रासायनिक प्रजातियां हमेशा अच्छी तरह से मिश्रित होती हैं, उनके [[दर समीकरण]] हैं
+यह मानते हुए कि द्रव्यमान क्रिया नियम इन दो प्रतिक्रियाओं पर प्रयुक्त होता है कि जल अधिकता (रसायन विज्ञान) है, और यह कि विभिन्न रासायनिक प्रजातियां सदैव अच्छी तरह से मिश्रित होती हैं, उनके [[दर समीकरण]] हैं
 : <math>\begin{align}
         \frac{\textrm{d}\left[\textrm{CO}_2\right]}{\textrm{d}t} &= -k_1\left[\textrm{CO}_2\right] + k_{-1}\left[\textrm{H}^+\right]\left[\textrm{HCO}_3^-\right], \\
@@ Line 36: / Line 38: @@
    \frac{\textrm{d}\left[\textrm{CO}_3^{2-}\right]}{\textrm{d}t} &= k_2\left[\textrm{HCO}_3^-\right] - k_{-2}\left[\textrm{H}^+\right]\left[\textrm{CO}_3^{2-}\right]
 \end{align}</math>
-कहाँ {{nowrap|[&emsp;]}} एकाग्रता को दर्शाता है, t समय है, और K<sub>1</sub> और के<sub>−1</sub> प्रतिक्रिया के लिए उपयुक्त [[आनुपातिकता (गणित)]] स्थिरांक हैं {{EquationNote|1}}, इस प्रतिक्रिया के लिए क्रमशः आगे और विपरीत [[प्रतिक्रिया दर स्थिर]] कहा जाता है। (इसी प्रकार के<sub>2</sub> और के<sub>−2</sub> प्रतिक्रिया के लिए {{EquationNote|2}}.)
+जहाँ {{nowrap|[&emsp;]}} सांद्रता को दर्शाता है, t समय है, और K<sub>1</sub> और K<sub>−1</sub> प्रतिक्रिया {{EquationNote|1}} के लिए उपयुक्त [[आनुपातिकता (गणित)|समानुपातिकता (गणित)]] स्थिरांक हैं, इस प्रतिक्रिया के लिए क्रमशः आगे और विपरीत प्रतिवर्ती दर स्थिरांक (इसी प्रकार K<sub>2</sub> और K<sub>−2</sub> प्रतिक्रिया के लिए {{EquationNote|2}}) कहा जाता है।
-किसी भी संतुलन पर, सांद्रता अपरिवर्तित होती है, इसलिए इन समीकरणों के बाएँ हाथ शून्य होते हैं। फिर, इन चार समीकरणों में से पहले से, प्रतिक्रिया का अनुपात {{EquationNote|1}} की दर स्थिरांक इसकी संतुलन सांद्रता के अनुपात के बराबर होती है, और इस अनुपात को K कहा जाता है<sub>1</sub>, प्रतिक्रिया के लिए संतुलन स्थिरांक कहा जाता है {{EquationNote|1}}, अर्थात।
+किसी भी साम्यावस्था पर, सांद्रता अपरिवर्तित होती है, इसलिए इन समीकरणों के बायीं ओर शून्य होते हैं। फिर, इन चार समीकरणों में से पहले से, प्रतिक्रिया का अनुपात {{EquationNote|1}} की दर स्थिरांक इसकी साम्य सांद्रता के अनुपात के समान होती है, और इस अनुपात को K<sub>1</sub> कहा जाता है, प्रतिक्रिया {{EquationNote|1}} के लिए साम्य स्थिरांक कहा जाता है, अर्थात
 {{NumBlk|:|<math>K_1 = \frac{k_1}{k_{-1}} = \frac{[\textrm{H}^+]_\text{eq}[\textrm{HCO}_3^-]_\text{eq}}{[\textrm{CO}_2]_\text{eq}}</math>|{{EquationRef|3}}}}
-जहां सबस्क्रिप्ट 'eq' दर्शाता है कि ये संतुलन सांद्रता हैं।
+जहां पादांक 'eq' दर्शाता है कि ये साम्य सांद्रता हैं।
-इसी प्रकार, संतुलन स्थिरांक K के लिए चौथे समीकरण से<sub>2</sub> प्रतिक्रिया के लिए {{EquationNote|2}},
+इसी प्रकार, साम्य स्थिरांक K<sub>2</sub> के लिए चतुर्थ समीकरण {{EquationNote|2}} से प्रतिक्रिया के लिए,
 {{NumBlk|:|<math>K_2 = \frac{k_2}{k_{-2}} = \frac{\left[\textrm{H}^+\right]_\text{eq}\left[\textrm{CO}_3^{2-}\right]_\text{eq}}{\left[\textrm{HCO}_3^-\right]_\text{eq}}</math>|{{EquationRef|4}}}}
-उलटफेर करने पर {{EquationNote|3}} देता है
+{{EquationNote|3}} को पुनर्व्यवस्थित करने पर प्राप्त होता है
 {{NumBlk|:|<math>\left[\textrm{HCO}_3^-\right]_\text{eq} = \frac{K_1\left[\textrm{CO}_2\right]_\text{eq}}{\left[\textrm{H}^+\right]_\text{eq}}</math> {{space}} {{space}} {{space}} {{space}}|{{EquationRef|5}}}}
-और पुनर्व्यवस्थित {{EquationNote|4}}, फिर में प्रतिस्थापित करना {{EquationNote|5}} देता है
+और पुनर्व्यवस्थित {{EquationNote|4}}, फिर प्रतिस्थापित करने पर {{EquationNote|5}} देता है
 {{NumBlk|:|<math>\left[\textrm{CO}_3^{2-}\right]_\text{eq} = \frac{K_2\left[\textrm{HCO}_3^-\right]_\text{eq}}{\left[\textrm{H}^+\right]_\text{eq}} = \frac{K_1 K_2\left[\textrm{CO}_2\right]_\text{eq}}{\left[\textrm{H}^+\right]_\text{eq}^2}</math> {{space}} {{space}} {{space}} {{space}}|{{EquationRef|6}}}}
-सिस्टम में कुल अकार्बनिक कार्बन की कुल सांद्रता को प्रतिस्थापित करके दिया जाता है {{EquationNote|5}} और {{EquationNote|6}}:
+प्रणाली में विलेय हुए अकार्बनिक कार्बन की कुल सांद्रता 5 और 6 में प्रतिस्थापित करके दी गई है:
 : <math>\begin{align}
    \textrm{DIC}
@@ Line 59: / Line 61: @@
      &= \left[\textrm{CO}_2\right]_\text{eq} \left(\frac{\left[\textrm{H}^+\right]_\text{eq}^2 + K_1\left[\textrm{H}^+\right]_\text{eq} + K_1K_2}{\left[\textrm{H}^+\right]_\text{eq}^2}\right)
 \end{align}</math>
-इसे पुनर्व्यवस्थित करने पर के लिए समीकरण प्राप्त होता है {{chem|CO|2}}:
+इसे पुनर्व्यवस्थित करने पर {{chem|CO|2}} के लिए समीकरण प्राप्त होता है:
 : <math>\left[\textrm{CO}_2\right]_\text{eq} = \frac{\left[\textrm{H}^+\right]_\text{eq}^2}{\left[\textrm{H}^+\right]_\text{eq}^2 + K_1\left[\textrm{H}^+\right]_\text{eq} + K_1 K_2} \times \textrm{DIC}</math>
-के लिए समीकरण {{chem|HCO|3|−}} और {{chem|CO|3|2−}} को इसमें प्रतिस्थापित करके प्राप्त किया जाता है {{EquationNote|5}} और {{EquationNote|6}}.
+{{EquationNote|5}} और {{EquationNote|6}} के लिए समीकरण {{chem|HCO|3|−}} और {{chem|CO|3|2−}} को इसमें प्रतिस्थापित करके प्राप्त किया जाता है
 == यह भी देखें ==
 * [[चार्लोट समीकरण]]
-* [[ महान साजिश ]] (ग्रैन अनुमापन या ग्रैन विधि के रूप में भी जाना जाता है)
+* ग्रैन प्लॉट (ग्रैन अनुमापन या ग्रैन विधि के रूप में भी जाना जाता है)
 * हेंडरसन-हसलबल्च समीकरण
-* पहाड़ी समीकरण (जैव रसायन)
+* हिल समीकरण (जैव रसायन)
 * [[आयन प्रजाति]]
-* [[ताजा पानी]]
+* [[ताजा पानी|स्वच्छ जल]]
 * [[समुद्री जल]]
-* थर्मोहालाइन परिसंचरण
+* तापलवणीय संचरण
 == संदर्भ ==
 {{reflist}}
-[[Category: अम्ल-क्षार रसायन]] [[Category: जलीय पारिस्थितिकी]] [[Category: रासायनिक समुद्र विज्ञान]] [[Category: भू-रसायन शास्त्र]] [[Category: लींनोलोगु]] [[Category: औशेयनोग्रफ़ी]] [[Category: मृदा रसायन]] [[Category: ऊष्मप्रवैगिकी]] [[Category: जल रसायन]]
-[[Category: Machine Translated Page]]
 [[Category:Created On 27/03/2023]]
+[[Category:Lua-based templates]]
+[[Category:Machine Translated Page]]
+[[Category:Pages with script errors]]
+[[Category:Templates Vigyan Ready]]
+[[Category:Templates that add a tracking category]]
+[[Category:Templates that generate short descriptions]]
+[[Category:Templates using TemplateData]]
+[[Category:अम्ल-क्षार रसायन]]
+[[Category:ऊष्मप्रवैगिकी]]
+[[Category:औशेयनोग्रफ़ी]]
+[[Category:जल रसायन]]
+[[Category:जलीय पारिस्थितिकी]]
+[[Category:भू-रसायन शास्त्र]]
+[[Category:मृदा रसायन]]
+[[Category:रासायनिक समुद्र विज्ञान]]
+[[Category:लींनोलोगु]]

Anonymous

Search

जेरम प्लॉट: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 11:21, 27 April 2023

Contents

कार्बोनेट प्रणाली के लिए जेरम आरेख समीकरण

कार्बोनेट प्रणाली के लिए जेरम आरेख समीकरणों की रासायनिक और गणितीय व्युत्पत्ति

यह भी देखें

संदर्भ

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

जेरम प्लॉट: Difference between revisions

Latest revision as of 11:21, 27 April 2023

कार्बोनेट प्रणाली के लिए जेरम आरेख समीकरण

कार्बोनेट प्रणाली के लिए जेरम आरेख समीकरणों की रासायनिक और गणितीय व्युत्पत्ति

यह भी देखें

संदर्भ

Navigation

Wiki tools

Page tools

Other projects

Categories