समान अंतःवृत्त प्रमेय: Difference between revisions
No edit summary |
No edit summary |
||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 8: | Line 8: | ||
प्रमेय निम्नलिखित लेम्मा का प्रत्यक्ष परिणाम है: | प्रमेय निम्नलिखित लेम्मा का प्रत्यक्ष परिणाम है: | ||
मान लीजिए कि ''nवीं'' | मान लीजिए कि ''nवीं'' किरण आधाररेखा के अभिलम्ब के साथ एक कोण <math>\gamma_n</math> बनाती है। यदि <math>\gamma_n</math> को समीकरण <math>\tan \gamma_n = \sinh\theta_n</math> के अनुसार पैरामिट्रीकृत है, तो <math>\theta_n = a + nb</math> के मान जहां <math>a</math> और <math>b</math> वास्तविक स्थिरांक हैं, किरणों के क्रम को परिभाषित करते हैं जो समान अंतःवृत्तों की स्थिति को संतुष्ट करते हैं, और इसके अतिरिक्त किरणों के किसी भी अनुक्रम को संतुष्ट करते हैं स्थिरांक <math>a</math> और <math>b</math> के उपयुक्त विकल्प द्वारा स्थिति उत्पन्न की जा सकती है। | ||
== लेम्मा का प्रमाण == | == लेम्मा का प्रमाण == | ||
[[Image:equal incircles theorem.svg|600px|center]]रेखाचित्र में, रेखाएँ PS और PT आसन्न किरणें हैं जो | [[Image:equal incircles theorem.svg|600px|center]]रेखाचित्र में, रेखाएँ PS और PT आसन्न किरणें हैं जो <math>\gamma_n</math> और <math>\gamma_{n+1}</math> कोण को रेखा PR के साथ बनाती हैं, जो आधार रेखा, RST के लंबवत है। | ||
रेखा QXOY आधार रेखा के समानांतर है और <math>\triangle</math> PST, के अंतःवृत्त के केंद्र O से होकर गुजरती है, जो W और Z पर किरणों की स्पर्शरेखा है। साथ ही, रेखा PQ की लंबाई <math>h-r</math> है, और रेखा QR की लंबाई <math>r</math> अंतःवृत्त की त्रिज्या है। | |||
तब <math>\triangle</math> | तब <math>\triangle</math> OWX, <math>\triangle</math> PQX के समान है और <math>\triangle</math> OZY, <math>\triangle</math> PQY के समान है, और XY = XO + OY से हमें मिलता है | ||
: <math>(h-r) ( \tan \gamma_{n+1} - \tan \gamma_n ) = r ( \sec \gamma_n + \sec \gamma_{n+1} ).</math> | : <math>(h-r) ( \tan \gamma_{n+1} - \tan \gamma_n ) = r ( \sec \gamma_n + \sec \gamma_{n+1} ).</math> | ||
कोणों के | कोणों के समुच्चय पर यह संबंध, <math>\{ \gamma_m \}</math>, समान अंतःवृत्तों की स्थिति को व्यक्त करता है। | ||
लेम्मा को साबित करने के लिए, हम | लेम्मा को साबित करने के लिए, हम समुच्चय <math> \tan \gamma_n = \sinh (a+nb)</math> करते हैं, जो <math> \sec \gamma_n = \cosh(a+nb)</math> देता है। | ||
<math>a+(n+1)b = (a+nb)+b</math> का उपयोग करते हुए, हम इसके लिए अतिरिक्त नियम <math>\sinh</math> और <math>\cosh</math> प्रायुक्त करते हैं, और सत्यापित करें कि समान अंतःवृत्त संबंध समुच्चयिंग द्वारा संतुष्ट है | |||
: <math>\frac {r}{h-r} = \tanh\frac{b}{2}.</math> | : <math>\frac {r}{h-r} = \tanh\frac{b}{2}.</math> | ||
यह | यह ज्यामितीय मापों, <math>h</math> और <math>r</math> के संदर्भ में पैरामीटर <math>b</math> के लिए एक व्यंजक देता है। <math>b</math> की इस परिभाषा के साथ हम त्रिकोण | ||
: <math>\frac {r_N}{h-r_N} = \tanh\frac{Nb}{2}</math> | |||
के किनारों के रूप में प्रत्येक Nवीं किरण लेने के द्वारा गठित अंतःवृत्तों की त्रिज्या, <math>r_N</math> के लिए एक अभिव्यक्ति प्राप्त करते हैं। | |||
== यह भी देखें == | == यह भी देखें == | ||
* अतिशयोक्तिपूर्ण समारोह | * अतिशयोक्तिपूर्ण समारोह | ||
| Line 37: | Line 37: | ||
*[http://www.cut-the-knot.org/Curriculum/Geometry/AdjacentIncircles.shtml Equal Incircles Theorem] at [[cut-the-knot]] | *[http://www.cut-the-knot.org/Curriculum/Geometry/AdjacentIncircles.shtml Equal Incircles Theorem] at [[cut-the-knot]] | ||
*J. Tabov. A note on the five-circle theorem. ''Mathematics Magazine'' 63 (1989), 2, 92–94. | *J. Tabov. A note on the five-circle theorem. ''Mathematics Magazine'' 63 (1989), 2, 92–94. | ||
[[Category:Created On 10/04/2023]] | [[Category:Created On 10/04/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:जापानी गणित]] | |||
[[Category:त्रिकोण और वृत्त के बारे में प्रमेय]] | |||
[[Category:यूक्लिडियन ज्यामिति]] | |||
Latest revision as of 16:34, 27 April 2023
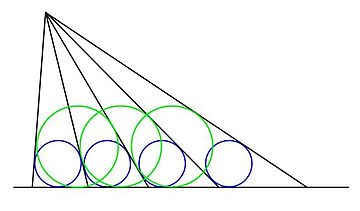
ज्यामिति में, समान अंतर्वृत्त प्रमेय जापानी संगकू से निकला है, और जो निम्नलिखित निर्माण से संबंधित है: किरणों की एक श्रृंखला एक दिए गए बिंदु से एक दी गई रेखा तक खींची जाती है, जैसे कि आसन्न किरणों और आधार रेखा द्वारा गठित त्रिभुजों के खुदे हुए घेरे बराबर हैं। चित्रण में समान नीले वृत्त किरणों के बीच की दूरी को परिभाषित करते हैं, जैसा कि वर्णित है।
प्रमेय में कहा गया है कि हर दूसरी किरण, हर तीसरी किरण आदि से बनने वाले त्रिकोण (किसी भी किरण से शुरू) के अंतःवृत्त और आधार रेखा भी बराबर होती है। हर दूसरी किरण की स्थिति हरे वृत्तों द्वारा ऊपर चित्रित की गई है, जो सभी समान हैं।
इस तथ्य से कि प्रमेय प्रारंभिक किरण के कोण पर निर्भर नहीं करता है, यह देखा जा सकता है कि प्रमेय ज्यामिति के अतिरिक्त गणितीय विश्लेषण से ठीक से संबंधित है, और निरंतर स्केलिंग फ़ंक्शन से संबंधित होना चाहिए जो किरणों के अंतर को परिभाषित करता है। वास्तव में, यह कार्य अतिशयोक्तिपूर्ण कार्य है।
प्रमेय निम्नलिखित लेम्मा का प्रत्यक्ष परिणाम है:
मान लीजिए कि nवीं किरण आधाररेखा के अभिलम्ब के साथ एक कोण बनाती है। यदि को समीकरण के अनुसार पैरामिट्रीकृत है, तो के मान जहां और वास्तविक स्थिरांक हैं, किरणों के क्रम को परिभाषित करते हैं जो समान अंतःवृत्तों की स्थिति को संतुष्ट करते हैं, और इसके अतिरिक्त किरणों के किसी भी अनुक्रम को संतुष्ट करते हैं स्थिरांक और के उपयुक्त विकल्प द्वारा स्थिति उत्पन्न की जा सकती है।
लेम्मा का प्रमाण
रेखाचित्र में, रेखाएँ PS और PT आसन्न किरणें हैं जो और कोण को रेखा PR के साथ बनाती हैं, जो आधार रेखा, RST के लंबवत है।
रेखा QXOY आधार रेखा के समानांतर है और PST, के अंतःवृत्त के केंद्र O से होकर गुजरती है, जो W और Z पर किरणों की स्पर्शरेखा है। साथ ही, रेखा PQ की लंबाई है, और रेखा QR की लंबाई अंतःवृत्त की त्रिज्या है।
तब OWX, PQX के समान है और OZY, PQY के समान है, और XY = XO + OY से हमें मिलता है
कोणों के समुच्चय पर यह संबंध, , समान अंतःवृत्तों की स्थिति को व्यक्त करता है।
लेम्मा को साबित करने के लिए, हम समुच्चय करते हैं, जो देता है।
का उपयोग करते हुए, हम इसके लिए अतिरिक्त नियम और प्रायुक्त करते हैं, और सत्यापित करें कि समान अंतःवृत्त संबंध समुच्चयिंग द्वारा संतुष्ट है
यह ज्यामितीय मापों, और के संदर्भ में पैरामीटर के लिए एक व्यंजक देता है। की इस परिभाषा के साथ हम त्रिकोण
के किनारों के रूप में प्रत्येक Nवीं किरण लेने के द्वारा गठित अंतःवृत्तों की त्रिज्या, के लिए एक अभिव्यक्ति प्राप्त करते हैं।
यह भी देखें
- अतिशयोक्तिपूर्ण समारोह
- चक्रीय बहुभुजों के लिए जापानी प्रमेय
- चक्रीय चतुर्भुजों के लिए जापानी प्रमेय
- वृत्तों की स्पर्श रेखाएँ
संदर्भ
- Equal Incircles Theorem at cut-the-knot
- J. Tabov. A note on the five-circle theorem. Mathematics Magazine 63 (1989), 2, 92–94.