अधिकतम बुलबुला दबाव विधि: Difference between revisions
(Created page with "{{Short description|Method of measuring surface tension}} भौतिकी में, अधिकतम बुलबुला दबाव विधि, या लघु...") |
No edit summary |
||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Method of measuring surface tension}} | {{Short description|Method of measuring surface tension}} | ||
भौतिकी में, अधिकतम बुलबुला दबाव विधि, या लघु बुलबुला दबाव विधि, एक [[तरल]] के सतही तनाव को मापने के लिए एक तकनीक है, जिसमें [[पृष्ठसक्रियकारक]] होते हैं। | भौतिकी में, '''''अधिकतम बुलबुला दबाव विधि''''', या लघु बुलबुला दबाव विधि, एक [[तरल]] के सतही-तनाव को मापने के लिए एक तकनीक है, जिसमें [[पृष्ठसक्रियकारक|आर्द्रक पृष्ठ संक्रियक]] होते हैं। | ||
__TOC__ | __TOC__ | ||
== पृष्ठभूमि == | == पृष्ठभूमि == | ||
जब तरल | जब तरल गैस प्रावस्था के साथ एक अंतराफलक बनाता है, तो सीमा पर एक अणु में समीप के अणुओं द्वारा बलों को आकर्षित करने के असंतुलित होने के कारण अपेक्षाकृत अधिक भिन्न भौतिक गुण होते हैं। तरल की साम्यावस्था में, आंतरिक अणु समान रूप से वितरित निकटवर्ती अणुओं के साथ संतुलित बलों के अधीन होते हैं। | ||
हालांकि, संघनन तरल | हालांकि, संघनन तरल प्रावस्था की तुलना में अंतराफलक के ऊपर गैस प्रावस्था में अणुओं की अपेक्षाकृत कम संख्या तरल के अंदर प्रत्यक्ष रूप से सतह के अणु पर प्रयुक्त होने वाली शक्तियों का समग्र योग बनाती है और इस प्रकार सतह के अणु अपने स्वयं के सतह क्षेत्र को कम करने की प्रवृत्ति रखते हैं। | ||
आणविक बलों की ऐसी असमानता अंदर से सतह की ओर अणुओं की निरंतर गति को प्रेरित करती है, जिसका अर्थ है कि सतह के अणुओं में अतिरिक्त [[ऊर्जा]] होती है, जिसे [[विशिष्ट सतह ऊर्जा]] या [[संभावित ऊर्जा]] कहा जाता है।{{which|date=April 2011}} और कम एकांक क्षेत्रफल पर कार्य करने वाली ऐसी ऊर्जा को | आणविक बलों की ऐसी असमानता अंदर से सतह की ओर अणुओं की निरंतर गति को प्रेरित करती है, जिसका अर्थ है कि सतह के अणुओं में अतिरिक्त [[ऊर्जा]] होती है, जिसे [[विशिष्ट सतह ऊर्जा]] या [[संभावित ऊर्जा|स्थितिज ऊर्जा]] कहा जाता है।{{which|date=April 2011}} और कम एकांक क्षेत्रफल पर कार्य करने वाली ऐसी ऊर्जा को सतही-तनाव के रूप में परिभाषित किया जाता है। | ||
यह प्रासंगिक घटना की व्याख्या करने के लिए एक | यह प्रासंगिक घटना की व्याख्या करने के लिए एक संरचना है जो पदार्थ की सतह या अंतराफलक में होती है और सतही-तनाव को मापने के लिए कई तरीके विकसित किए गए हैं।<ref name="Adamson-Gast">Adamson, Arthur W.; Alice P. Gast (1997). ''Physical Chemistry of Surfaces'' (6th ed.). Wiley Interscience.</ref> | ||
सतही-तनाव को निर्धारित करने के विभिन्न तरीकों में डू नोय वलय विधि और विल्हेल्मी स्लाइड (अवसर्पण) विधि तरल सतह से एक ठोस वस्तु के पृथक्करण पर आधारित हैं और लोलक बिन्दु विधि और अवरूद्ध बूंद या बुलबुला विधि एक द्रव बूंद के गोलीय आकृति के विरूपण पर निर्भर करती है।<ref name="Adamson-Gast" /> | |||
[[File:Bubble1.jpg]]: चित्र 1 - | तथापि ये विधियाँ अपेक्षाकृत सरल हैं और सामान्य रूप से [[ स्थिति-विज्ञान |स्थिर]] सतही-तनाव को निर्धारित करने के लिए उपयोग की जाती हैं, यदि अशुद्धियों को तरल में जोड़ा जाता है, तो [[गतिशील संतुलन|गतिक साम्यावस्था]] के आधार पर सतही-तनाव का माप प्रयुक्त किया जाना चाहिए क्योंकि पूरी तरह से गठित प्राप्त करने में अधिक समय लगता है सतह और इसका तात्पर्य है कि एक शुद्ध तरल के रूप में स्थैतिक साम्य प्राप्त करना कठिन है।<ref name="kruss-scientific.com">[https://www.kruss-scientific.com/services/education-theory/glossary/bubble-pressure-tensiometer/ Bubble Pressure Method] at kruss-scientific.com</ref> | ||
गतिशील (यांत्रिकी) सतही-तनाव [[माप]] को प्रेरित करने के लिए सबसे विशिष्ट अशुद्धता एक तल-सक्रिय-कारक अणु है जिसमें [[हाइड्रोफिलिक|जलरागी]] अनुभाग दोनों होते हैं, जिन्हें सामान्य रूप से "शीर्ष समूह" और [[ जल विरोधी |जल विरोधी]] अनुभाग कहा जाता है, जिसे सामान्य रूप से समान अणु में "पश्च समूह" कहा जाता है। विशिष्ट [[आणविक संरचना]] के कारण, तल-सक्रिय-कारक तरल सतह की सीमा गैस प्रावस्था में स्थानांतरित हो जाते हैं जब तक कि एक बाहरी बल अंतराफलक या सतह से संचित अणुओं को पूरी तरह से प्रसारित नहीं कर देता है और इस प्रकार अतिरिक्त अणुओं को समायोजित नहीं कर सकता है। इस प्रक्रिया के समय, सतही तनाव समय के कार्य के रूप में कम हो जाता है और अंत में साम्यावस्था सतही-तनाव (σ<sub>equilibrium</sub>) तक पहुंचता है।<ref name="lauda.de">[http://www.lauda.de/ Dynamic Methods] at lauda.de</ref> इस तरह की प्रक्रिया को चित्र 1 में दिखाया गया है। छवि को संदर्भ से पुन: प्रस्तुत किया गया था।<ref name="kruss-scientific.com" /> | |||
[[File:Bubble1.jpg]]: चित्र 1 - तल-सक्रिय-कारक अणुओं का प्रवासन और सतही-तनाव में परिवर्तन (σ<sub>t1</sub> >σ<sub>t2</sub> > σ<sub>equilibrium</sub>) | |||
== अधिकतम बुलबुला दबाव विधि == | == अधिकतम बुलबुला दबाव विधि == | ||
गतिशील | गतिशील सतही-तनाव को निर्धारित करने के लिए उपयोगी तरीकों में से एक अधिकतम बुलबुला दबाव विधि या, बुलबुला दबाव विधि को मापना है।<ref name="Adamson-Gast" /><ref name="kruss-scientific.com" /> | ||
बुलबुला दाब [[ टेन्सियोमीटर (सतह तनाव) |पृष्ठतनावमापी (सतही तनाव)]] स्थिर दर पर गैस के बुलबुले (जैसे- वायु) उत्पन्न करता है और उन्हें एक केशिका के माध्यम से बुलबुला बनाता है जो प्रतिदर्श तरल में निमज्जित है और इसकी त्रिज्या पहले से ही ज्ञात है। | |||
गैस बुलबुले के अंदर [[दबाव]] (P) बढ़ता रहता है और अधिकतम मान तब प्राप्त होता है जब बुलबुले में पूरी तरह से गोलार्द्ध का आकार होता है जिसका त्रिज्या केशिका के त्रिज्या के अनुरूप होता है।<ref name="lauda.de" /> | |||
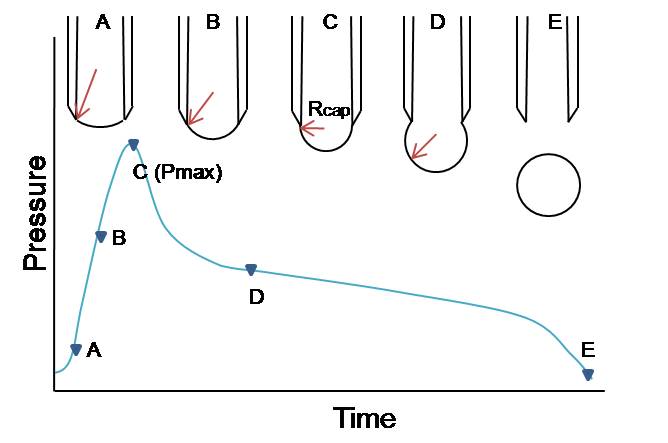
चित्रा 2 बुलबुला निर्माण के प्रत्येक प्रावस्था और बुलबुला त्रिज्या के इसी परिवर्तन को दर्शाता है और प्रत्येक प्रावस्था नीचे वर्णित है। छवि संदर्भ से पुन: प्रस्तुत की गई थी।<ref name="kruss-scientific.com" /><ref name="lauda.de" /> | |||
[[File:Bubble2.jpg]] | |||
चित्र 2 - समय के कार्य के रूप में आलेखित किए गए बुलबुले के निर्माण के समय दबाव में परिवर्तन। | |||
A, B: केशिका के सिरे में एक बुलबुला दिखाई देता है। जैसे-जैसे आकार बढ़ता है, बुलबुले की वक्रता की त्रिज्या कम होती जाती है। | |||
C: अधिकतम बुलबुला दाब पात पर, बुलबुले का एक पूर्ण गोलार्द्धीय आकार होता है जिसका त्रिज्या Rcap द्वारा निरूपित केशिका के त्रिज्या के समान होता है। द्रव के अंदर गोलाकार बुलबुले के आकार के लिए कम रूप में यंग-लाप्लास समीकरण का उपयोग करके सतही-तनाव को निर्धारित किया जा सकता है।<ref name="lauda.de" /> | |||
<math>\sigma=\frac{\Delta P_{\rm {max}} \times R_{\rm {cap}}}{2}</math> | <math>\sigma=\frac{\Delta P_{\rm {max}} \times R_{\rm {cap}}}{2}</math> | ||
(σ: सतही-तनाव, ΔP<sub>max</sub>: अधिकतम दाब पात, R<sub>cap</sub>: केशिका की त्रिज्या) | |||
वर्तमान में विकसित और व्यावसायीकृत | D, E: अधिकतम दबाव के बाद, बुलबुले का दबाव कम हो जाता है और बुलबुले की त्रिज्या बढ़ जाती है जब तक कि बुलबुला एक केशिका के अंत से अलग नहीं हो जाता है और एक नया चक्र प्रारंभ होता है। यह सतही-तनाव को निर्धारित करने के लिए प्रासंगिक नहीं है।<ref name="lauda.de" /> | ||
वर्तमान में विकसित और व्यावसायीकृत पृष्ठतनावमापी एक बुलबुला बनाने के लिए आवश्यक दबाव का संरक्षण करता है, बुलबुले के अंदर और बाहर दबाव अंतर, बुलबुले की त्रिज्या और प्रतिदर्श की सतही-तनाव की गणना एक बार में की जाती है और पीसी नियंत्रण के माध्यम से आंकड़ा अधिग्रहण किया जाता है। | |||
बुलबुला दबाव विधि का उपयोग सामान्य रूप से तल-सक्रिय-कारक या अन्य अशुद्धियों वाले प्रणाली के लिए गतिशील सतही-तनाव को मापने के लिए किया जाता है क्योंकि इसमें संपर्क कोण माप की आवश्यकता नहीं होती है और उच्च परिशुद्धता होती है, तथापि मापन तेजी से किया जाता है।<ref name="Adamson-Gast" /><ref name="lauda.de" /> "बुलबुला दाब विधि" को गतिशील सतही-तनाव को मापने के लिए प्रयुक्त किया जा सकता है, विशेष रूप से उन प्रणालियों के लिए जिनमें तल-सक्रिय-कारक होते हैं।<ref name="lauda.de" /> इसके अतिरिक्त, यह विधि जैविक तरल पदार्थ जैसे रक्त का जलीय अंश (सीरम) द्रव पर प्रयुक्त करने के लिए एक उपयुक्त तकनीक है{{which|date=April 2011}} क्योंकि इसे माप के लिए बड़ी मात्रा में द्रव प्रतिदर्श की आवश्यकता नहीं होती है।<ref name="Hubbard">Hubbard, Arthur T. (2002). ''Encyclopedia of Surface and Colloid Science'' (Vol. 1). CRC press, pp. 814–815</ref> अंत में, विधि का उपयोग औद्योगिक शोधन या विलेपन प्रक्षालन की सतही पदार्थ के अप्रत्यक्ष निर्धारण के लिए किया जाता है क्योंकि बुलबुला निर्माण दरों की एक विशेष श्रेणी में गतिशील सतही-तनाव सांद्रता के साथ एक प्रबल सहसंबंध दिखाता है।<ref name="kruss-scientific.com" /> | |||
| Line 53: | Line 59: | ||
* [http://www.sita-process.com/information-service/process-parameter-surface-tension/bubble-pressure-method-for-measuring-the-surface-tension/ Bubble pressure method for measuring the dynamic surface tension] | * [http://www.sita-process.com/information-service/process-parameter-surface-tension/bubble-pressure-method-for-measuring-the-surface-tension/ Bubble pressure method for measuring the dynamic surface tension] | ||
{{Refend}} | {{Refend}} | ||
[[Category: | [[Category:All articles with specifically marked weasel-worded phrases]] | ||
[[Category:Articles with invalid date parameter in template]] | |||
[[Category:Articles with specifically marked weasel-worded phrases from April 2011]] | |||
[[Category:Created On 03/04/2023]] | [[Category:Created On 03/04/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:द्रव यांत्रिकी]] | |||
Latest revision as of 14:22, 1 May 2023
भौतिकी में, अधिकतम बुलबुला दबाव विधि, या लघु बुलबुला दबाव विधि, एक तरल के सतही-तनाव को मापने के लिए एक तकनीक है, जिसमें आर्द्रक पृष्ठ संक्रियक होते हैं।
पृष्ठभूमि
जब तरल गैस प्रावस्था के साथ एक अंतराफलक बनाता है, तो सीमा पर एक अणु में समीप के अणुओं द्वारा बलों को आकर्षित करने के असंतुलित होने के कारण अपेक्षाकृत अधिक भिन्न भौतिक गुण होते हैं। तरल की साम्यावस्था में, आंतरिक अणु समान रूप से वितरित निकटवर्ती अणुओं के साथ संतुलित बलों के अधीन होते हैं।
हालांकि, संघनन तरल प्रावस्था की तुलना में अंतराफलक के ऊपर गैस प्रावस्था में अणुओं की अपेक्षाकृत कम संख्या तरल के अंदर प्रत्यक्ष रूप से सतह के अणु पर प्रयुक्त होने वाली शक्तियों का समग्र योग बनाती है और इस प्रकार सतह के अणु अपने स्वयं के सतह क्षेत्र को कम करने की प्रवृत्ति रखते हैं।
आणविक बलों की ऐसी असमानता अंदर से सतह की ओर अणुओं की निरंतर गति को प्रेरित करती है, जिसका अर्थ है कि सतह के अणुओं में अतिरिक्त ऊर्जा होती है, जिसे विशिष्ट सतह ऊर्जा या स्थितिज ऊर्जा कहा जाता है।[which?] और कम एकांक क्षेत्रफल पर कार्य करने वाली ऐसी ऊर्जा को सतही-तनाव के रूप में परिभाषित किया जाता है।
यह प्रासंगिक घटना की व्याख्या करने के लिए एक संरचना है जो पदार्थ की सतह या अंतराफलक में होती है और सतही-तनाव को मापने के लिए कई तरीके विकसित किए गए हैं।[1]
सतही-तनाव को निर्धारित करने के विभिन्न तरीकों में डू नोय वलय विधि और विल्हेल्मी स्लाइड (अवसर्पण) विधि तरल सतह से एक ठोस वस्तु के पृथक्करण पर आधारित हैं और लोलक बिन्दु विधि और अवरूद्ध बूंद या बुलबुला विधि एक द्रव बूंद के गोलीय आकृति के विरूपण पर निर्भर करती है।[1]
तथापि ये विधियाँ अपेक्षाकृत सरल हैं और सामान्य रूप से स्थिर सतही-तनाव को निर्धारित करने के लिए उपयोग की जाती हैं, यदि अशुद्धियों को तरल में जोड़ा जाता है, तो गतिक साम्यावस्था के आधार पर सतही-तनाव का माप प्रयुक्त किया जाना चाहिए क्योंकि पूरी तरह से गठित प्राप्त करने में अधिक समय लगता है सतह और इसका तात्पर्य है कि एक शुद्ध तरल के रूप में स्थैतिक साम्य प्राप्त करना कठिन है।[2]
गतिशील (यांत्रिकी) सतही-तनाव माप को प्रेरित करने के लिए सबसे विशिष्ट अशुद्धता एक तल-सक्रिय-कारक अणु है जिसमें जलरागी अनुभाग दोनों होते हैं, जिन्हें सामान्य रूप से "शीर्ष समूह" और जल विरोधी अनुभाग कहा जाता है, जिसे सामान्य रूप से समान अणु में "पश्च समूह" कहा जाता है। विशिष्ट आणविक संरचना के कारण, तल-सक्रिय-कारक तरल सतह की सीमा गैस प्रावस्था में स्थानांतरित हो जाते हैं जब तक कि एक बाहरी बल अंतराफलक या सतह से संचित अणुओं को पूरी तरह से प्रसारित नहीं कर देता है और इस प्रकार अतिरिक्त अणुओं को समायोजित नहीं कर सकता है। इस प्रक्रिया के समय, सतही तनाव समय के कार्य के रूप में कम हो जाता है और अंत में साम्यावस्था सतही-तनाव (σequilibrium) तक पहुंचता है।[3] इस तरह की प्रक्रिया को चित्र 1 में दिखाया गया है। छवि को संदर्भ से पुन: प्रस्तुत किया गया था।[2]
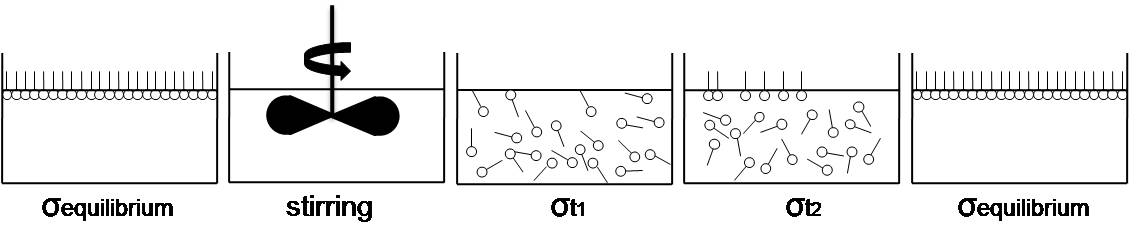: चित्र 1 - तल-सक्रिय-कारक अणुओं का प्रवासन और सतही-तनाव में परिवर्तन (σt1 >σt2 > σequilibrium)
अधिकतम बुलबुला दबाव विधि
गतिशील सतही-तनाव को निर्धारित करने के लिए उपयोगी तरीकों में से एक अधिकतम बुलबुला दबाव विधि या, बुलबुला दबाव विधि को मापना है।[1][2]
बुलबुला दाब पृष्ठतनावमापी (सतही तनाव) स्थिर दर पर गैस के बुलबुले (जैसे- वायु) उत्पन्न करता है और उन्हें एक केशिका के माध्यम से बुलबुला बनाता है जो प्रतिदर्श तरल में निमज्जित है और इसकी त्रिज्या पहले से ही ज्ञात है।
गैस बुलबुले के अंदर दबाव (P) बढ़ता रहता है और अधिकतम मान तब प्राप्त होता है जब बुलबुले में पूरी तरह से गोलार्द्ध का आकार होता है जिसका त्रिज्या केशिका के त्रिज्या के अनुरूप होता है।[3]
चित्रा 2 बुलबुला निर्माण के प्रत्येक प्रावस्था और बुलबुला त्रिज्या के इसी परिवर्तन को दर्शाता है और प्रत्येक प्रावस्था नीचे वर्णित है। छवि संदर्भ से पुन: प्रस्तुत की गई थी।[2][3]
चित्र 2 - समय के कार्य के रूप में आलेखित किए गए बुलबुले के निर्माण के समय दबाव में परिवर्तन।
A, B: केशिका के सिरे में एक बुलबुला दिखाई देता है। जैसे-जैसे आकार बढ़ता है, बुलबुले की वक्रता की त्रिज्या कम होती जाती है।
C: अधिकतम बुलबुला दाब पात पर, बुलबुले का एक पूर्ण गोलार्द्धीय आकार होता है जिसका त्रिज्या Rcap द्वारा निरूपित केशिका के त्रिज्या के समान होता है। द्रव के अंदर गोलाकार बुलबुले के आकार के लिए कम रूप में यंग-लाप्लास समीकरण का उपयोग करके सतही-तनाव को निर्धारित किया जा सकता है।[3]
(σ: सतही-तनाव, ΔPmax: अधिकतम दाब पात, Rcap: केशिका की त्रिज्या)
D, E: अधिकतम दबाव के बाद, बुलबुले का दबाव कम हो जाता है और बुलबुले की त्रिज्या बढ़ जाती है जब तक कि बुलबुला एक केशिका के अंत से अलग नहीं हो जाता है और एक नया चक्र प्रारंभ होता है। यह सतही-तनाव को निर्धारित करने के लिए प्रासंगिक नहीं है।[3]
वर्तमान में विकसित और व्यावसायीकृत पृष्ठतनावमापी एक बुलबुला बनाने के लिए आवश्यक दबाव का संरक्षण करता है, बुलबुले के अंदर और बाहर दबाव अंतर, बुलबुले की त्रिज्या और प्रतिदर्श की सतही-तनाव की गणना एक बार में की जाती है और पीसी नियंत्रण के माध्यम से आंकड़ा अधिग्रहण किया जाता है।
बुलबुला दबाव विधि का उपयोग सामान्य रूप से तल-सक्रिय-कारक या अन्य अशुद्धियों वाले प्रणाली के लिए गतिशील सतही-तनाव को मापने के लिए किया जाता है क्योंकि इसमें संपर्क कोण माप की आवश्यकता नहीं होती है और उच्च परिशुद्धता होती है, तथापि मापन तेजी से किया जाता है।[1][3] "बुलबुला दाब विधि" को गतिशील सतही-तनाव को मापने के लिए प्रयुक्त किया जा सकता है, विशेष रूप से उन प्रणालियों के लिए जिनमें तल-सक्रिय-कारक होते हैं।[3] इसके अतिरिक्त, यह विधि जैविक तरल पदार्थ जैसे रक्त का जलीय अंश (सीरम) द्रव पर प्रयुक्त करने के लिए एक उपयुक्त तकनीक है[which?] क्योंकि इसे माप के लिए बड़ी मात्रा में द्रव प्रतिदर्श की आवश्यकता नहीं होती है।[4] अंत में, विधि का उपयोग औद्योगिक शोधन या विलेपन प्रक्षालन की सतही पदार्थ के अप्रत्यक्ष निर्धारण के लिए किया जाता है क्योंकि बुलबुला निर्माण दरों की एक विशेष श्रेणी में गतिशील सतही-तनाव सांद्रता के साथ एक प्रबल सहसंबंध दिखाता है।[2]
संदर्भ
- ↑ 1.0 1.1 1.2 1.3 Adamson, Arthur W.; Alice P. Gast (1997). Physical Chemistry of Surfaces (6th ed.). Wiley Interscience.
- ↑ 2.0 2.1 2.2 2.3 2.4 Bubble Pressure Method at kruss-scientific.com
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 Dynamic Methods at lauda.de
- ↑ Hubbard, Arthur T. (2002). Encyclopedia of Surface and Colloid Science (Vol. 1). CRC press, pp. 814–815
