बिंदु-सेट त्रिभुज: Difference between revisions
No edit summary |
No edit summary |
||
| (12 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
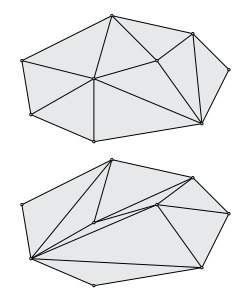
[[File:PointSetTriangulations.svg|समतल में 9 बिन्दुओं के समान समुच्चय के दो भिन्न त्रिभुज।|अंगूठा]] | [[File:PointSetTriangulations.svg|समतल में 9 बिन्दुओं के समान समुच्चय के दो भिन्न त्रिभुज।|अंगूठा]] | ||
[[यूक्लिडियन अंतरिक्ष]] | [[यूक्लिडियन अंतरिक्ष]] <math>\mathbb{R}^d</math> में बिंदुओं के सेट <math>\mathcal{P}</math> का त्रिभुज साधारण परिसर है जो <math>\mathcal{P}</math> के उत्तल पतवार को कवर करता है और जिनके शिखर <math>\mathcal{P}</math> से संबंधित हैं ।<ref name="DRS">{{cite book | ||
| last1 = De Loera | first1 = Jesús A. | author-link1 = Jesús A. De Loera | | last1 = De Loera | first1 = Jesús A. | author-link1 = Jesús A. De Loera | ||
| last2 = Rambau | first2 = Jörg | | last2 = Rambau | first2 = Jörg | ||
| Line 9: | Line 9: | ||
| series = Algorithms and Computation in Mathematics | | series = Algorithms and Computation in Mathematics | ||
| volume = 25 | | volume = 25 | ||
| publisher = Springer}}</ref> विमान में (ज्यामिति) (जब <math>\mathcal{P}</math> में बिंदुओं का | | publisher = Springer}}</ref> विमान में (ज्यामिति) (जब <math>\mathcal{P}</math> में बिंदुओं का सेट <math>\mathbb{R}^2</math> है ), त्रिभुज, उनके किनारों और शीर्षों सहित, त्रिभुजों से बने होते हैं। कुछ लेखकों की आवश्यकता है कि <math>\mathcal{P}</math> के सभी बिंदु इसके त्रिकोणासन के शीर्ष हैं।{{sfn |de Berg|van Kreveld|Overmars|Schwarzkopf|2008|loc=Section 9.1}} इस स्थितियों में, बिंदुओं के सेट का त्रिभुज <math>\mathcal{P}</math> विमान में वैकल्पिक रूप से बिंदुओं के बीच अ-रेखित किनारों के अधिकतम सेट के रूप में <math>\mathcal{P}</math> परिभाषित किया जा सकता है। समतल में, त्रिभुज तलीय सीधी-रेखा ग्राफ़ के विशेष स्थितियां हैं। | ||
विशेष रूप से रोचक प्रकार का त्रिकोण डेलाउने त्रिभुज है। वे [[वोरोनोई आरेख]] के दोहरे पॉलीटॉप हैं। बिंदुओं के | विशेष रूप से रोचक प्रकार का त्रिकोण डेलाउने त्रिभुज है। वे [[वोरोनोई आरेख]] के दोहरे पॉलीटॉप हैं। बिंदुओं के सेट का [[डेलाउने त्रिभुज]] <math>\mathcal{P}</math> विमान में [[गेब्रियल ग्राफ]], [[Index.php?title=निकटतम ग्राफ|निकटतम ग्राफ]] और <math>\mathcal{P}</math> न्यूनतम फैले पेड़ सम्मलित हैं । | ||
त्रिभुजों के कई अनुप्रयोग होते हैं और कुछ मानदंडों के अनुसार | त्रिभुजों के कई अनुप्रयोग होते हैं और कुछ मानदंडों के अनुसार दिए गए बिंदु सेट के अच्छे त्रिभुजों को खोजने में रुचि होती है, उदाहरण के लिए न्यूनतम-भार त्रिभुज । कभी-कभी विशेष गुणों के साथ त्रिभुज का होना वांछनीय होता है, उदाहरण के लिए, जिसमें सभी त्रिभुजों में बड़े कोण होते हैं (लंबे और संकीर्ण किरच त्रिकोण से बचा जाता है)।<ref name="deBerg">{{cite book | ||
| last = de Berg | | last = de Berg | ||
| first = Mark | | first = Mark | ||
| Line 25: | Line 25: | ||
| url = http://www.cs.uu.nl/geobook/interpolation.pdf | | url = http://www.cs.uu.nl/geobook/interpolation.pdf | ||
| isbn = 978-3-540-77973-5 | author2-link = Otfried Cheong | | isbn = 978-3-540-77973-5 | author2-link = Otfried Cheong | ||
}}</ref>समतल के बिंदुओं को जोड़ने वाले किनारों के | }}</ref>समतल के बिंदुओं को जोड़ने वाले किनारों के सेट को देखते हुए, यह निर्धारित करने की समस्या है कि क्या उनमें त्रिभुज है या नहीं, एनपी-पूर्ण है।{{sfn |Lloyd|1977}} | ||
== नियमित त्रिभुज == | == नियमित त्रिभुज == | ||
बिंदुओं के | बिंदुओं के सेट के कुछ त्रिभुज <math>\mathcal{P}\subset\mathbb{R}^d</math> के अंक उठाकर <math>\mathcal{P}</math> में <math>\mathbb{R}^{d+1}</math> प्राप्त किया जा सकता है (जो <math>x_{d+1}</math> समन्वय जोड़ने के लिए है <math>\mathcal{P}</math> के प्रत्येक बिंदु पर ), बिंदुओं के उठाए गए सेट के उत्तल पतवार की गणना करके और इस उत्तल पतवार <math>\mathbb{R}^d</math> के निचले चेहरों को वापस प्रक्षेपित किया जाता है । इस तरह से बनाए गए त्रिभुजों को नियमित त्रिकोणासन <math>\mathcal{P}</math> के रूप में संदर्भित किया जाता है । जब बिन्दुओं को समीकरण <math>x_{d+1} = x_1^2+\cdots+x_d^2</math> के परवलयज पर ले जाया जाता है , इस निर्माण का परिणाम डेलाउने त्रिभुज<math>\mathcal{P}</math> है। ध्यान दें कि, इस निर्माण के लिए त्रिभुज प्रदान करने के लिए, बिंदुओं के उठाए गए सेट के निचले उत्तल पतवार को [[साधारण पॉलीटॉप]] होना चाहिए। डेलाउने त्रिभुजों के स्थितियों में यह आवश्यक है कि नहीं <math>d+2</math> बिंदु <math>\mathcal{P}</math> एक ही गोले में न हो। | ||
== प्लेन में कॉम्बिनेटरिक्स == | == प्लेन में कॉम्बिनेटरिक्स == | ||
किसी भी सेट का हर त्रिकोण <math>\mathcal{P}</math> का <math>n</math> विमान में अंक है <math> 2n - h - 2</math> त्रिकोण और <math>3n - h - 3</math> किनारे कहाँ <math>h</math> | किसी भी सेट का हर त्रिकोण <math>\mathcal{P}</math> का <math>n</math> विमान में अंक है <math> 2n - h - 2</math> त्रिकोण और <math>3n - h - 3</math> किनारे कहाँ <math>h</math>, <math>\mathcal{P}</math> के उत्तल पतवार की सीमा में <math>\mathcal{P}</math> के बिंदुओं की संख्या है। यह सीधे [[यूलर विशेषता]] तर्क से आता है।<ref>{{citation | ||
| last1 = Edelsbrunner | first1 = Herbert | author1-link = Herbert Edelsbrunner | | last1 = Edelsbrunner | first1 = Herbert | author1-link = Herbert Edelsbrunner | ||
| last2 = Tan | first2 = Tiow Seng | | last2 = Tan | first2 = Tiow Seng | ||
| Line 43: | Line 43: | ||
| volume = 13 | | volume = 13 | ||
| year = 1992| citeseerx = 10.1.1.66.2895 }}.</ref> | | year = 1992| citeseerx = 10.1.1.66.2895 }}.</ref> | ||
== विमान में त्रिभुज बनाने के लिए एल्गोरिदम == | == विमान में त्रिभुज बनाने के लिए एल्गोरिदम == | ||
त्रिभुज | '''त्रिभुज विभाजन एल्गोरिथम''' : बिंदु सेट <math>\mathcal{P}</math> के उत्तल पतवार का पता लगाएं और इस पतवार को बहुभुज के रूप में त्रिकोणित करें। आंतरिक बिंदु चुनें और किनारों को उस त्रिकोण के तीन शीर्षों पर खींचें जिसमें यह सम्मलित है। इस प्रक्रिया को तब तक जारी रखें जब तक कि सभी आंतरिक बिंदु समाप्त न हो जाएं।<ref>Devadoss, O'Rourke ''Discrete and Computational Geometry''. Princeton University Press, 2011, p. 60.</ref> | ||
'''वृद्धिशील एल्गोरिथम''' : <math>\mathcal{P}</math> के बिंदुओं को क्रमबद्ध करें X-निर्देशांक के अनुसार। पहले तीन बिंदु त्रिभुज का निर्धारण करते हैं। <math>p</math> के अगले बिंदु पर विचार करें और आदेशित सेट में इसे पहले से विचार किए गए सभी बिंदुओं से जोड़ दें <math>\{p_1,..., p_k\}</math> जो p को दिखाई देते हैं। <math>\mathcal{P}</math> के बिंदु को जोड़ने की इस प्रक्रिया को जारी रखें समय में जब तक सभी <math>\mathcal{P}</math> संसाधित नहीं हो जाते।<ref>Devadoss, O'Rourke ''Discrete and Computational Geometry''. Princeton University Press, 2011, p. 62.</ref> | |||
== विभिन्न एल्गोरिदम की समय जटिलता == | == विभिन्न एल्गोरिदम की समय जटिलता == | ||
निम्न तालिका विभिन्न इष्टतमता मानदंडों के | निम्न तालिका विभिन्न इष्टतमता मानदंडों के अनुसार, विमान में बिंदु सेटों के त्रिभुजों के निर्माण के लिए समय जटिलता के परिणामों की रिपोर्ट करती है, जहां <math>n</math> बिंदुओं की संख्या है। | ||
{| class="wikitable" style="border:none;text-align:center;" | {| class="wikitable" style="border:none;text-align:center;" | ||
|- | |- | ||
! style="background:white;border:none;" colspan="2" | | ! style="background:white;border:none;" colspan="2" | | ||
! style="padding:1em;" | | ! style="padding:1em;" | न्यूनतम | ||
! style="padding:1em;" | | ! style="padding:1em;" | अधिकतम | ||
|- | |- | ||
! style="padding:1em;" | | ! style="padding:1em;" | न्यूनतम | ||
! rowspan="2" style="padding:1em;" | | ! rowspan="2" style="padding:1em;" | कोण | ||
| bgcolor="darkgray" | | | bgcolor="darkgray" | | ||
| <math>O(n \log n)</math> <br /> ([[Delaunay triangulation|डेलाउने | | <math>O(n \log n)</math> <br /> ([[Delaunay triangulation|डेलाउने त्रिकोण]]) | ||
|- | |- | ||
! style="padding:1em;" | | ! style="padding:1em;" | अधिकतम | ||
| <math>O(n^2 \log n)</math> {{sfn |Edelsbrunner|Tan|Waupotitsch|1990}} {{sfn |Bern|Edelsbrunner|Eppstein|Mitchell|1993}} | | <math>O(n^2 \log n)</math> {{sfn |Edelsbrunner|Tan|Waupotitsch|1990}} {{sfn |Bern|Edelsbrunner|Eppstein|Mitchell|1993}} | ||
| bgcolor="darkgray" | | | bgcolor="darkgray" | | ||
|- | |- | ||
! style="padding:1em;" | | ! style="padding:1em;" | न्यूनतम | ||
! rowspan="2" style="padding:1em;" | | ! rowspan="2" style="padding:1em;" | क्षेत्र | ||
| <math>O(n^2)</math> {{sfn |Chazelle|Guibas|Lee|1985}} | | <math>O(n^2)</math> {{sfn |Chazelle|Guibas|Lee|1985}} | ||
| <math>O(n^2 \log n)</math> {{sfn |Vassilev|2005}} | | <math>O(n^2 \log n)</math> {{sfn |Vassilev|2005}} | ||
|- | |- | ||
! style="padding:1em;" | | ! style="padding:1em;" | अधिकतम | ||
| <math>O(n^2 \log n)</math> {{sfn |Vassilev|2005}} | | <math>O(n^2 \log n)</math> {{sfn |Vassilev|2005}} | ||
| bgcolor="darkgray" | | | bgcolor="darkgray" | | ||
|- | |- | ||
! style="padding:1em;" | | ! style="padding:1em;" | अधिकतम | ||
! rowspan="1" style="padding:1em;" | | ! rowspan="1" style="padding:1em;" | डिग्री | ||
| [[ | | [[N P-सम्पूर्ण]] | ||
7 डिग्री के लिए {{sfn |Jansen|1992}} | |||
| bgcolor="darkgray" | | | bgcolor="darkgray" | | ||
|- | |- | ||
! style="padding:1em;" | | ! style="padding:1em;" | अधिकतम | ||
! rowspan="1" style="padding:1em;" | | ! rowspan="1" style="padding:1em;" | विलक्षणता | ||
| <math>O(n^3)</math> {{sfn |Bern|Edelsbrunner|Eppstein|Mitchell|1993}} | | <math>O(n^3)</math> {{sfn |Bern|Edelsbrunner|Eppstein|Mitchell|1993}} | ||
| bgcolor="darkgray" | | | bgcolor="darkgray" | | ||
|- | |- | ||
! style="padding:1em;" | | ! style="padding:1em;" | न्यूनतम | ||
! rowspan="3" style="padding:1em;" | | ! rowspan="3" style="padding:1em;" | किनारे की लम्बाई | ||
| <math>O(n \log n)</math> <br /> | | <math>O(n \log n)</math> <br /> [[(अंकों की निकटतम जोड़ी समस्या)]] | ||
| [[NP-complete]] {{sfn |Fekete|2012}} | | [[NP-complete|NP-सम्पूर्ण]] {{sfn |Fekete|2012}} | ||
|- | |- | ||
! style="padding:1em;" | | ! style="padding:1em;" | अधिकतम | ||
| <math>O(n^2)</math> {{sfn |Edelsbrunner|Tan|1991}} | | <math>O(n^2)</math> {{sfn |Edelsbrunner|Tan|1991}} | ||
| <math>O(n \log n)</math> <br /> ( | | <math>O(n \log n)</math> <br /> ([[उत्तल पतवार]] का उपयोग करना) | ||
|- | |- | ||
! style="padding:1em;" | | ! style="padding:1em;" | का योग | ||
| [[NP- | | [[NP-कठिन(न्यूनतम-भार त्रिकोणासन)|NP-कठिन]] | ||
[[NP-कठिन(न्यूनतम-भार त्रिकोणासन)|(न्यूनतम-भार त्रिकोणासन)]] | |||
| bgcolor="darkgray" | | | bgcolor="darkgray" | | ||
|- | |- | ||
! style="padding:1em;" | | ! style="padding:1em;" | न्यूनतम | ||
! rowspan="1" style="padding:1em;" | | ! rowspan="1" style="padding:1em;" | ऊंचाई | ||
| bgcolor="darkgray" | | | bgcolor="darkgray" | | ||
| <math>O(n^2 \log n)</math> {{sfn |Bern|Edelsbrunner|Eppstein|Mitchell|1993}} | | <math>O(n^2 \log n)</math> {{sfn |Bern|Edelsbrunner|Eppstein|Mitchell|1993}} | ||
|- | |- | ||
! style="padding:1em;" | | ! style="padding:1em;" | अधिकतम | ||
! rowspan="1" style="padding:1em;" | | ! rowspan="1" style="padding:1em;" | ढलान | ||
| <math>O(n^3)</math> {{sfn |Bern|Edelsbrunner|Eppstein|Mitchell|1993}} | | <math>O(n^3)</math> {{sfn |Bern|Edelsbrunner|Eppstein|Mitchell|1993}} | ||
| bgcolor="darkgray" | | | bgcolor="darkgray" | | ||
|} | |} | ||
== यह भी देखें == | == यह भी देखें == | ||
* | * [[मेष उत्पादन]] | ||
* [[बहुभुज त्रिभुज]] | * [[बहुभुज त्रिभुज]] | ||
| Line 243: | Line 240: | ||
{{refend}} | {{refend}} | ||
{{DEFAULTSORT:Point Set Triangulation}} | {{DEFAULTSORT:Point Set Triangulation}} | ||
[[de:Gitter (Geometrie)#Dreiecksgitter]] | [[de:Gitter (Geometrie)#Dreiecksgitter]] | ||
[[Category:Created On 05/05/2023|Point Set Triangulation]] | |||
[[Category:Machine Translated Page|Point Set Triangulation]] | |||
[[Category: Machine Translated Page]] | [[Category:Pages with script errors|Point Set Triangulation]] | ||
[[Category: | [[Category:Templates Vigyan Ready|Point Set Triangulation]] | ||
[[Category:त्रिकोणासन (ज्यामिति)|Point Set Triangulation]] | |||
Latest revision as of 17:15, 16 May 2023
यूक्लिडियन अंतरिक्ष में बिंदुओं के सेट का त्रिभुज साधारण परिसर है जो के उत्तल पतवार को कवर करता है और जिनके शिखर से संबंधित हैं ।[1] विमान में (ज्यामिति) (जब में बिंदुओं का सेट है ), त्रिभुज, उनके किनारों और शीर्षों सहित, त्रिभुजों से बने होते हैं। कुछ लेखकों की आवश्यकता है कि के सभी बिंदु इसके त्रिकोणासन के शीर्ष हैं।[2] इस स्थितियों में, बिंदुओं के सेट का त्रिभुज विमान में वैकल्पिक रूप से बिंदुओं के बीच अ-रेखित किनारों के अधिकतम सेट के रूप में परिभाषित किया जा सकता है। समतल में, त्रिभुज तलीय सीधी-रेखा ग्राफ़ के विशेष स्थितियां हैं।
विशेष रूप से रोचक प्रकार का त्रिकोण डेलाउने त्रिभुज है। वे वोरोनोई आरेख के दोहरे पॉलीटॉप हैं। बिंदुओं के सेट का डेलाउने त्रिभुज विमान में गेब्रियल ग्राफ, निकटतम ग्राफ और न्यूनतम फैले पेड़ सम्मलित हैं ।
त्रिभुजों के कई अनुप्रयोग होते हैं और कुछ मानदंडों के अनुसार दिए गए बिंदु सेट के अच्छे त्रिभुजों को खोजने में रुचि होती है, उदाहरण के लिए न्यूनतम-भार त्रिभुज । कभी-कभी विशेष गुणों के साथ त्रिभुज का होना वांछनीय होता है, उदाहरण के लिए, जिसमें सभी त्रिभुजों में बड़े कोण होते हैं (लंबे और संकीर्ण किरच त्रिकोण से बचा जाता है)।[3]समतल के बिंदुओं को जोड़ने वाले किनारों के सेट को देखते हुए, यह निर्धारित करने की समस्या है कि क्या उनमें त्रिभुज है या नहीं, एनपी-पूर्ण है।[4]
नियमित त्रिभुज
बिंदुओं के सेट के कुछ त्रिभुज के अंक उठाकर में प्राप्त किया जा सकता है (जो समन्वय जोड़ने के लिए है के प्रत्येक बिंदु पर ), बिंदुओं के उठाए गए सेट के उत्तल पतवार की गणना करके और इस उत्तल पतवार के निचले चेहरों को वापस प्रक्षेपित किया जाता है । इस तरह से बनाए गए त्रिभुजों को नियमित त्रिकोणासन के रूप में संदर्भित किया जाता है । जब बिन्दुओं को समीकरण के परवलयज पर ले जाया जाता है , इस निर्माण का परिणाम डेलाउने त्रिभुज है। ध्यान दें कि, इस निर्माण के लिए त्रिभुज प्रदान करने के लिए, बिंदुओं के उठाए गए सेट के निचले उत्तल पतवार को साधारण पॉलीटॉप होना चाहिए। डेलाउने त्रिभुजों के स्थितियों में यह आवश्यक है कि नहीं बिंदु एक ही गोले में न हो।
प्लेन में कॉम्बिनेटरिक्स
किसी भी सेट का हर त्रिकोण का विमान में अंक है त्रिकोण और किनारे कहाँ , के उत्तल पतवार की सीमा में के बिंदुओं की संख्या है। यह सीधे यूलर विशेषता तर्क से आता है।[5]
विमान में त्रिभुज बनाने के लिए एल्गोरिदम
त्रिभुज विभाजन एल्गोरिथम : बिंदु सेट के उत्तल पतवार का पता लगाएं और इस पतवार को बहुभुज के रूप में त्रिकोणित करें। आंतरिक बिंदु चुनें और किनारों को उस त्रिकोण के तीन शीर्षों पर खींचें जिसमें यह सम्मलित है। इस प्रक्रिया को तब तक जारी रखें जब तक कि सभी आंतरिक बिंदु समाप्त न हो जाएं।[6]
वृद्धिशील एल्गोरिथम : के बिंदुओं को क्रमबद्ध करें X-निर्देशांक के अनुसार। पहले तीन बिंदु त्रिभुज का निर्धारण करते हैं। के अगले बिंदु पर विचार करें और आदेशित सेट में इसे पहले से विचार किए गए सभी बिंदुओं से जोड़ दें जो p को दिखाई देते हैं। के बिंदु को जोड़ने की इस प्रक्रिया को जारी रखें समय में जब तक सभी संसाधित नहीं हो जाते।[7]
विभिन्न एल्गोरिदम की समय जटिलता
निम्न तालिका विभिन्न इष्टतमता मानदंडों के अनुसार, विमान में बिंदु सेटों के त्रिभुजों के निर्माण के लिए समय जटिलता के परिणामों की रिपोर्ट करती है, जहां बिंदुओं की संख्या है।
| न्यूनतम | अधिकतम | ||
|---|---|---|---|
| न्यूनतम | कोण | (डेलाउने त्रिकोण) | |
| अधिकतम | [8] [9] | ||
| न्यूनतम | क्षेत्र | [10] | [11] |
| अधिकतम | [11] | ||
| अधिकतम | डिग्री | N P-सम्पूर्ण
7 डिग्री के लिए [12] |
|
| अधिकतम | विलक्षणता | [9] | |
| न्यूनतम | किनारे की लम्बाई | (अंकों की निकटतम जोड़ी समस्या) |
NP-सम्पूर्ण [13] |
| अधिकतम | [14] | (उत्तल पतवार का उपयोग करना) | |
| का योग | NP-कठिन | ||
| न्यूनतम | ऊंचाई | [9] | |
| अधिकतम | ढलान | [9] | |
यह भी देखें
टिप्पणियाँ
- ↑ De Loera, Jesús A.; Rambau, Jörg; Santos, Francisco (2010). Triangulations, Structures for Algorithms and Applications. Algorithms and Computation in Mathematics. Vol. 25. Springer.
- ↑ de Berg et al. 2008, Section 9.1.
- ↑ de Berg, Mark; Otfried Cheong; Marc van Kreveld; Mark Overmars (2008). Computational Geometry: Algorithms and Applications (PDF). Springer-Verlag. ISBN 978-3-540-77973-5.
- ↑ Lloyd 1977.
- ↑ Edelsbrunner, Herbert; Tan, Tiow Seng; Waupotitsch, Roman (1992), "An O(n2 log n) time algorithm for the minmax angle triangulation", SIAM Journal on Scientific and Statistical Computing, 13 (4): 994–1008, CiteSeerX 10.1.1.66.2895, doi:10.1137/0913058, MR 1166172.
- ↑ Devadoss, O'Rourke Discrete and Computational Geometry. Princeton University Press, 2011, p. 60.
- ↑ Devadoss, O'Rourke Discrete and Computational Geometry. Princeton University Press, 2011, p. 62.
- ↑ Edelsbrunner, Tan & Waupotitsch 1990.
- ↑ 9.0 9.1 9.2 9.3 Bern et al. 1993.
- ↑ Chazelle, Guibas & Lee 1985.
- ↑ 11.0 11.1 Vassilev 2005.
- ↑ Jansen 1992.
- ↑ Fekete 2012.
- ↑ Edelsbrunner & Tan 1991.
संदर्भ
- Bern, M.; Edelsbrunner, H.; Eppstein, D.; Mitchell, S.; Tan, T. S. (1993), "Edge insertion for optimal triangulations", Discrete and Computational Geometry, 10 (1): 47–65, doi:10.1007/BF02573962, MR 1215322
- Chazelle, Bernard; Guibas, Leo J.; Lee, D. T. (1985). "The power of geometric duality" (PDF). BIT. BIT Computer Science and Numerical Mathematics. 25 (1): 76–90. doi:10.1007/BF01934990. ISSN 0006-3835. S2CID 122411548.
- de Berg, Mark; van Kreveld, Marc; Overmars, Mark; Schwarzkopf, Otfried (2008). Computational Geometry: Algorithms and Applications (3 ed.). Springer-Verlag.
- O'Rourke, Joseph; L. Devadoss, Satyan (2011). Discrete and Computational Geometry (1 ed.). Princeton University Press.
- Edelsbrunner, Herbert; Tan, Tiow Seng; Waupotitsch, Roman (1990). An O(n2log n) time algorithm for the MinMax angle triangulation. Proceedings of the sixth annual symposium on Computational geometry. SCG '90. ACM. pp. 44–52. CiteSeerX 10.1.1.66.2895. doi:10.1145/98524.98535. ISBN 0-89791-362-0.
- Edelsbrunner, Herbert; Tan, Tiow Seng (1991). A quadratic time algorithm for the minmax length triangulation. 32nd Annual Symposium on Foundations of Computer Science. pp. 414–423. CiteSeerX 10.1.1.66.8959. doi:10.1109/SFCS.1991.185400. ISBN 0-8186-2445-0.
- Fekete, Sándor P. (2012). "The Complexity of MaxMin Length Triangulation". arXiv:1208.0202v1 [cs.CG].
- Jansen, Klaus (1992). The Complexity of the Min-max Degree Triangulation Problem (PDF). 9th European Workshop on Computational Geometry. pp. 40–43.
- Lloyd, Errol Lynn (1977). On triangulations of a set of points in the plane. 18th Annual Symposium on Foundations of Computer Science. Switching and Automata Theory, 1974., IEEE Conference Record of 15Th Annual Symposium on. pp. 228–240. doi:10.1109/SFCS.1977.21. ISSN 0272-5428.
- Vassilev, Tzvetalin Simeonov (2005). Optimal Area Triangulation (PDF) (Ph.D.). University of Saskatchewan, Saskatoon. Archived from the original (PDF) on 2017-08-13. Retrieved 2013-06-15.