कतरनी तनाव: Difference between revisions
No edit summary |
No edit summary |
||
| (12 intermediate revisions by 3 users not shown) | |||
| Line 2: | Line 2: | ||
{{Infobox Physical quantity | {{Infobox Physical quantity | ||
| bgcolour = | | bgcolour = | ||
| name = | | name = अपरूपण तनाव | ||
| image = | | image = | ||
| caption = | | caption = | ||
| Line 9: | Line 9: | ||
| derivations = {{math|''τ'' {{=}} ''{{Sfrac|F|A}}''}} | | derivations = {{math|''τ'' {{=}} ''{{Sfrac|F|A}}''}} | ||
}} | }} | ||
[[File:Shear stress simple.svg|thumb|आयत के शीर्ष पर | [[File:Shear stress simple.svg|thumb|आयत के शीर्ष पर कर्तन बल लगाया जाता है, जबकि तल को स्थान पर रखा जाता है। परिणामी कतरनी तनाव, {{mvar|τ}}, आयत को समांतर [[चतुर्भुज]] में बदल देता है। इसमें सम्मिलित क्षेत्र समांतर चतुर्भुज का शीर्ष होगा।]]कतरनी तनाव (अधिकांशतः {{mvar|τ}} (ग्रीक: ताऊ) द्वारा निरूपित) [[सामग्री पार अनुभाग|पदार्थ पार अनुभाग]] के साथ [[तनाव (भौतिकी)]] [[समतलीय]] का घटक है। यह कतरनी बल से उत्पन्न होता है, पदार्थ अनुप्रस्थ काट के [[समानांतर (ज्यामिति)]] बल वेक्टर का घटक दूसरी ओर, 'सामान्य तनाव', बल सदिश घटक से उत्पन्न होता है, जो पदार्थ के अनुप्रस्थ काट पर लंबवत होता है, जिस पर यह कार्य करता है। | ||
== सामान्य कतरनी तनाव == | == सामान्य कतरनी तनाव == | ||
औसत कतरनी तनाव की गणना करने का सूत्र प्रति इकाई क्षेत्र पर बल है।<ref>{{cite book|last=Hibbeler|first=R.C.|title=सामग्री के यांत्रिकी|year=2004|publisher=Pearson Education|location=New Jersey USA|isbn=0-13-191345-X|pages=32}}</ref> | औसत कतरनी तनाव की गणना करने का सूत्र प्रति इकाई क्षेत्र पर बल है।<ref>{{cite book|last=Hibbeler|first=R.C.|title=सामग्री के यांत्रिकी|year=2004|publisher=Pearson Education|location=New Jersey USA|isbn=0-13-191345-X|pages=32}}</ref> | ||
:<math> \tau = {F \over A},</math> | :<math> \tau = {F \over A},</math> | ||
जहाँँ: | |||
:{{mvar|τ}} = कतरनी तनाव; | :{{mvar|τ}} = कतरनी तनाव; | ||
:{{mvar|F}} = लगाया गया बल; | :{{mvar|F}} = लगाया गया बल; | ||
:{{mvar|A}} = | :{{mvar|A}} = प्रयुक्त बल वेक्टर के समानांतर क्षेत्र के साथ पदार्थ का क्रॉस-आंशिक क्षेत्र है । | ||
: | |||
== अन्य रूप == | == अन्य रूप == | ||
===दीवार कतरनी तनाव=== | ===दीवार कतरनी तनाव=== | ||
दीवार कतरनी तनाव दीवार के बगल में बहने वाले द्रव की परतों में दीवार से मंदक बल (प्रति इकाई क्षेत्र) को व्यक्त करता है। इसे इस प्रकार परिभाषित किया गया है: | |||
<math>\tau_w:=\mu\left(\frac{\partial u}{\partial y}\right)_{y=0}</math> | <math>\tau_w:=\mu\left(\frac{\partial u}{\partial y}\right)_{y=0}</math> | ||
जहाँँ <math>\mu</math> गतिशील श्यानता, <math>u</math> प्रवाह वेग और <math>y</math> दीवार से दूरी है। | |||
इसका उपयोग, उदाहरण के लिए | इसका उपयोग, उदाहरण के लिए धमनी रक्त प्रवाह के विवरण में किया जाता है, जिसमें प्रमाण है कि यह [[ मेदार्बुदजनक |एथेरोजेनिक]] प्रक्रिया को प्रभावित करता है।<ref>{{cite journal |last1=Katritsis |first1=Demosthenes |title=Wall Shear Stress: Theoretical Considerations and Methods of Measurement |journal=Progress in Cardiovascular Diseases |year=2007 |volume=49 |issue=5 |pages=307–329 |doi=10.1016/j.pcad.2006.11.001|pmid=17329179 }}</ref> | ||
=== शुद्ध === | === शुद्ध === | ||
शुद्ध अपरूपण प्रतिबल शुद्ध अपरूपण विकृति से संबंधित है, जिसे | शुद्ध अपरूपण प्रतिबल शुद्ध अपरूपण विकृति से संबंधित है, जिसे {{mvar|γ}} निरूपित किया गया है, निम्नलिखित समीकरण द्वारा:<ref>{{cite web|url=http://www.eformulae.com/engineering/strength_materials.php#pureshear|title=सामग्री की ताकत|work=Eformulae.com|access-date=24 December 2011}}</ref> | ||
:<math>\tau = \gamma G\,</math> | :<math>\tau = \gamma G\,</math> | ||
जहाँँ {{mvar|G}} समदैशिक या पदार्थ विज्ञान पदार्थ का अपरूपण मापांक है, जिसके द्वारा दिया गया है | |||
:<math> G = \frac{E}{2(1+\nu)}. </math> | :<math> G = \frac{E}{2(1+\nu)}. </math> | ||
यहाँ {{mvar|E}} यंग का मापांक है और {{mvar|ν}} प्वासों का अनुपात है। | यहाँ {{mvar|E}} यंग का मापांक है और {{mvar|ν}} प्वासों का अनुपात है। | ||
| Line 40: | Line 41: | ||
बीम कतरनी को बीम पर लगाए गए कतरनी बल के कारण बीम के आंतरिक कतरनी तनाव के रूप में परिभाषित किया गया है। | बीम कतरनी को बीम पर लगाए गए कतरनी बल के कारण बीम के आंतरिक कतरनी तनाव के रूप में परिभाषित किया गया है। | ||
:<math> \tau := {fQ \over Ib},</math> | :<math> \tau := {fQ \over Ib},</math> | ||
जहाँँ | |||
:{{mvar|f}} = विचाराधीन स्थान पर कुल अपरूपण बल; | :{{mvar|f}} = विचाराधीन स्थान पर कुल अपरूपण बल; | ||
:{{mvar|Q}} = क्षेत्रफल का प्रथम आघूर्ण या क्षेत्रफल का स्थैतिक आघूर्ण; | :{{mvar|Q}} = क्षेत्रफल का प्रथम आघूर्ण या क्षेत्रफल का स्थैतिक आघूर्ण; | ||
:{{mvar|b}} = मोटाई (चौड़ाई) कतरनी के लंबवत | :{{mvar|b}} = मोटाई (चौड़ाई) कतरनी के लंबवत पदार्थ में; | ||
:{{mvar|I}} = पूरे क्रॉस-सेक्शनल क्षेत्र के क्षेत्रफल का दूसरा क्षण। | :{{mvar|I}} = पूरे क्रॉस-सेक्शनल क्षेत्र के क्षेत्रफल का दूसरा क्षण। | ||
[[दिमित्री इवानोविच ज़ुरावस्की]] के बाद बीम कतरनी सूत्र को ज़ुरावस्की कतरनी तनाव सूत्र के रूप में भी जाना जाता है, जिसने इसे 1855 में प्राप्त किया था।<ref>{{cite web|script-title=ru:Лекция Формула Журавского|url=http://sopromato.ru/pryamoy-izgib/formula-zhuravskogo.html |access-date=2014-02-26 |work=Сопромат Лекции |language=ru |trans-title=Zhuravskii's Formula}}</ref><ref>{{cite web|title=बीम का लचीलापन|url=http://www.eng.mcmaster.ca/civil/mechanicslectur-e/4flexurebeams1.pdf|work=Mechanical Engineering Lectures|publisher=[[McMaster University]]}}{{Dead link|date=February 2020 |bot=InternetArchiveBot |fix-attempted=yes }}</ref> | [[दिमित्री इवानोविच ज़ुरावस्की]] के बाद बीम कतरनी सूत्र को ज़ुरावस्की कतरनी तनाव सूत्र के रूप में भी जाना जाता है, जिसने इसे 1855 में प्राप्त किया था।<ref>{{cite web|script-title=ru:Лекция Формула Журавского|url=http://sopromato.ru/pryamoy-izgib/formula-zhuravskogo.html |access-date=2014-02-26 |work=Сопромат Лекции |language=ru |trans-title=Zhuravskii's Formula}}</ref><ref>{{cite web|title=बीम का लचीलापन|url=http://www.eng.mcmaster.ca/civil/mechanicslectur-e/4flexurebeams1.pdf|work=Mechanical Engineering Lectures|publisher=[[McMaster University]]}}{{Dead link|date=February 2020 |bot=InternetArchiveBot |fix-attempted=yes }}</ref> | ||
| Line 49: | Line 50: | ||
=== अर्ध-मोनोकोक कतरनी === | === अर्ध-मोनोकोक कतरनी === | ||
{{Further| | {{Further|अपरुपण प्रवाह}} | ||
अर्ध-मोनोकोक संरचना के | अर्ध-मोनोकोक संरचना के अंदर कतरनी तनाव की गणना संरचना के क्रॉस-सेक्शन को स्ट्रिंगर्स (केवल अक्षीय भार ले जाने वाले) और जाले (केवल कतरनी प्रवाह को ले जाने) में आदर्श बनाकर की जा सकती है। अर्ध-मोनोकोक संरचना के दिए गए भाग की मोटाई से कतरनी प्रवाह को विभाजित करने से कतरनी तनाव उत्पन्न होता है। इस प्रकार, अधिकतम कतरनी तनाव या तो अधिकतम कतरनी प्रवाह या न्यूनतम मोटाई के वेब में होगा | ||
कतरनी के कारण मिट्टी में निर्माण भी विफल हो सकता है; | कतरनी के कारण मिट्टी में निर्माण भी विफल हो सकता है; उदाहरण के लिए, मिट्टी से भरे बांध या डाइक का वजन छोटे से [[भूस्खलन]] की तरह, अवभूमि के ढहने का कारण बन सकता है। | ||
=== प्रभाव कतरनी === | === प्रभाव कतरनी === | ||
प्रभाव के अधीन | प्रभाव के अधीन ठोस गोल पट्टी में निर्मित अधिकतम कतरनी तनाव समीकरण द्वारा दिया गया है:<br /> | ||
:<math>\tau=\sqrt {2UG \over V},</math> | :<math>\tau=\sqrt {2UG \over V},</math> | ||
जहाँँ | |||
:{{mvar|U}} = गतिज ऊर्जा में परिवर्तन; | :{{mvar|U}} = गतिज ऊर्जा में परिवर्तन; | ||
:{{mvar|G}} = कतरनी मापांक; | :{{mvar|G}} = कतरनी मापांक; | ||
| Line 69: | Line 70: | ||
=== तरल पदार्थ में कतरनी तनाव === | === तरल पदार्थ में कतरनी तनाव === | ||
{{See also| | {{See also|श्यानता|कौएट प्रवाह|हेगन-पॉइज़्यूइल समीकरण|गहराई-ढलान उत्पाद|साधारण कतरनी}} | ||
ठोस सीमा के साथ चलने वाले किसी भी वास्तविक | ठोस सीमा के साथ चलने वाले किसी भी वास्तविक [[तरल]] पदार्थ (तरल पदार्थ और [[गैस]] सम्मिलित ) उस सीमा पर कतरनी तनाव उत्पन्न करेंगे। [[नो-स्लिप स्थिति]]<ref>{{Citation | last = Day | first = Michael A. | title = The no-slip condition of fluid dynamics | journal = Erkenntnis | publisher = Springer Netherlands | pages = 285–296 | year = 2004 | volume = 33 | issue = 3 | doi = 10.1007/BF00717588 | s2cid = 55186899 | url = https://doi.org/10.1007%2FBF00717588 | issn = 0165-0106}}.</ref> निर्धारित करता है कि सीमा पर द्रव की गति (सीमा के सापेक्ष) शून्य है; चूँकि सीमा से कुछ ऊँचाई पर प्रवाह की गति द्रव के सामान्य होनी चाहिए। इन दो बिंदुओं के बीच के क्षेत्र को [[सीमा परत]] जहाँ जाता है। लैमिनार प्रवाह में सभी [[न्यूटोनियन द्रव]] पदार्थों के लिए, कतरनी तनाव तरल पदार्थ में [[तनाव दर]] के समानुपाती होता है, जहां श्यानता आनुपातिकता का स्थिरांक होता है। गैर-न्यूटोनियन तरल पदार्थों के लिए श्यानता स्थिर नहीं है। वेग के इस हानि के परिणामस्वरूप कतरनी का तनाव सीमा पर लगाया जाता है। | ||
न्यूटोनियन तरल पदार्थ के लिए, बिंदु पर | न्यूटोनियन तरल पदार्थ के लिए, बिंदु {{mvar|y}} पर समतल प्लेट के समानांतर सतह तत्व पर कतरनी तनाव निम्न द्वारा दिया जाता है: | ||
:<math>\tau (y) = \mu \frac{\partial u}{\partial y}</math> | :<math>\tau (y) = \mu \frac{\partial u}{\partial y}</math> | ||
जहाँँ | |||
:{{mvar|μ}} प्रवाह की गतिशील | :{{mvar|μ}} प्रवाह की गतिशील श्यानता है; | ||
:{{mvar|u}} सीमा के साथ [[प्रवाह वेग]] है; | :{{mvar|u}} सीमा के साथ [[प्रवाह वेग]] है; | ||
:{{mvar|y}} सीमा से ऊपर की ऊंचाई है। | :{{mvar|y}} सीमा से ऊपर की ऊंचाई है। | ||
| Line 81: | Line 82: | ||
विशेष रूप से, दीवार कतरनी तनाव को इस प्रकार परिभाषित किया गया है: | विशेष रूप से, दीवार कतरनी तनाव को इस प्रकार परिभाषित किया गया है: | ||
:<math>\tau_\mathrm{w} := \tau(y=0)= \mu \left.\frac{\partial u}{\partial y}\right|_{y = 0}~~.</math> | :<math>\tau_\mathrm{w} := \tau(y=0)= \mu \left.\frac{\partial u}{\partial y}\right|_{y = 0}~~.</math> | ||
किसी भी सामान्य ज्यामिति (उपर्युक्त | किसी भी सामान्य ज्यामिति (उपर्युक्त समतल प्लेट सहित) के लिए न्यूटन का संवैधानिक नियम बताता है कि कतरनी टेन्सर ( दूसरे क्रम का टेंसर) प्रवाह वेग ढाल के समानुपाती होता है (वेग वेक्टर है, इसलिए इसका [[ ग्रेडियेंट |ग्रेडियेंट]] दूसरा क्रम है) टेन्सर): | ||
:<math>\overset \leftrightarrow \tau(\vec u) = \mu \vec \nabla \vec u</math> | :<math>\overset \leftrightarrow \tau(\vec u) = \mu \vec \nabla \vec u</math> | ||
और आनुपातिकता के स्थिरांक को गतिशील श्यानता कहा जाता है। आइसोट्रोपिक न्यूटोनियन प्रवाह के लिए यह | और आनुपातिकता के स्थिरांक को गतिशील श्यानता कहा जाता है। आइसोट्रोपिक न्यूटोनियन प्रवाह के लिए यह अदिश राशि है, जबकि अनिसोट्रोपिक न्यूटोनियन प्रवाह के लिए यह दूसरे क्रम का टेंसर भी हो सकता है। मौलिक पहलू यह है कि न्यूटोनियन द्रव के लिए गतिशील श्यानता प्रवाह वेग पर स्वतंत्र है (अर्थात, कतरनी तनाव संवैधानिक नियम रैखिक है), जबकि गैर-न्यूटोनियन प्रवाह यह सच नहीं है, और किसी को संशोधन की अनुमति देनी चाहिए: | ||
:<math>\overset \leftrightarrow\tau(\vec u) = \mu(\vec u) \vec \nabla \vec u</math> | :<math>\overset \leftrightarrow\tau(\vec u) = \mu(\vec u) \vec \nabla \vec u</math> | ||
यह अब न्यूटन का नियम नहीं है, | यह अब न्यूटन का नियम नहीं है, किंतु सामान्य तन्यता पहचान है: प्रवाह वेग के कार्य के रूप में कतरनी तनाव की किसी भी अभिव्यक्ति को प्रवाह वेग के कार्य के रूप में सदैव श्यानता की अभिव्यक्ति मिल सकती है। दूसरी ओर, प्रवाह वेग के कार्य के रूप में कतरनी तनाव दिया जाता है, यह न्यूटनियन प्रवाह का प्रतिनिधित्व करता है, यदि इसे प्रवाह वेग के ढाल के लिए स्थिर के रूप में व्यक्त किया जा सकता है। इस स्थितियों में जो स्थिर पाया जाता है वह प्रवाह की गतिशील श्यानता है। | ||
==== उदाहरण ==== | ==== उदाहरण ==== | ||
कार्तीय निर्देशांक (x, y) में | कार्तीय निर्देशांक (x, y) में 2D स्थान को ध्यान में रखते हुए (प्रवाह वेग घटक क्रमशः (u, v) हैं), फिर कतरनी तनाव आव्युह द्वारा दिया गया: | ||
:<math>\begin{pmatrix} | :<math>\begin{pmatrix} | ||
| Line 117: | Line 118: | ||
</math>, | </math>, | ||
अर्थात, विस्कोसिटी टेंसर के साथ अनिसोट्रोपिक प्रवाह: | |||
:<math>\begin{pmatrix} | :<math>\begin{pmatrix} | ||
| Line 128: | Line 129: | ||
\end{pmatrix} | \end{pmatrix} | ||
</math> | </math> | ||
जो असमान ( | जो असमान (स्थान निर्देशांक पर निर्भर करता है) और क्षणिक है, किन्तु प्रासंगिक रूप से यह प्रवाह वेग पर स्वतंत्र है: | ||
:<math>\overset \leftrightarrow \mu(x,t) = \begin{pmatrix} | :<math>\overset \leftrightarrow \mu(x,t) = \begin{pmatrix} | ||
| Line 134: | Line 135: | ||
0 & -t | 0 & -t | ||
\end{pmatrix} </math> | \end{pmatrix} </math> | ||
यह प्रवाह इसलिए न्यूटोनियन है। दूसरी ओर, | यह प्रवाह इसलिए न्यूटोनियन है। दूसरी ओर, प्रवाह जिसमें श्यानता थी: | ||
:<math>\begin{pmatrix} | :<math>\begin{pmatrix} | ||
| Line 145: | Line 146: | ||
\end{pmatrix} | \end{pmatrix} | ||
</math> | </math> | ||
गैर न्यूटनियन है क्योंकि | गैर न्यूटनियन है क्योंकि श्यानता प्रवाह वेग पर निर्भर करती है। यह गैर न्यूटोनियन प्रवाह समदैशिक है (आव्युह पहचान आव्युह के लिए आनुपातिक है), इसलिए श्यानता केवल स्केलर है: | ||
:<math>\mu (u) = \frac 1 u </math> | :<math>\mu (u) = \frac 1 u </math> | ||
| Line 153: | Line 154: | ||
=== डाइवर्जिंग फ्रिंज शियर स्ट्रेस सेंसर === | === डाइवर्जिंग फ्रिंज शियर स्ट्रेस सेंसर === | ||
दीवार कतरनी तनाव को मापने के लिए इस रिश्ते का | दीवार कतरनी तनाव को मापने के लिए इस रिश्ते का लाभ उठाया जा सकता है। यदि संवेदक सीधे दीवार पर वेग प्रोफ़ाइल के ढाल को माप सकता है, तो गतिशील श्यानता से गुणा करने से कतरनी तनाव उत्पन्न होगा। इस तरह के सेंसर का प्रदर्शन ए.ए. नकवी और डब्ल्यू.सी. रेनॉल्ड्स द्वारा किया गया था।<ref>{{citation | last1 = Naqwi |first1 = A. A. | last2 = Reynolds |first2 = W. C. | title = Dual cylindrical wave laser-Doppler method for measurement of skin friction in fluid flow | journal = NASA STI/Recon Technical Report N |date=Jan 1987 | volume = 87}}</ref> दो समानांतर स्लिट्स के माध्यम से प्रकाश की किरण भेजकर उत्पन्न हस्तक्षेप प्रतिरूप रैखिक रूप से अलग होने वाले फ्रिंज का नेटवर्क बनाता है जो दो स्लिट्स के विमान से उत्पन्न होता है ([[डबल-स्लिट प्रयोग]] देखें)। जैसे ही तरल पदार्थ का कण फ्रिन्जों से होकर गुजरता है, रिसीवर फ्रिन्ज प्रतिरूप के प्रतिबिंब का पता लगाता है। संकेत को संसाधित किया जा सकता है, और फ्रिंज कोण को जानकर, कण की ऊंचाई और वेग को सट्रपलेशन किया जा सकता है। दीवार वेग प्रवणता का मापा मान द्रव गुणों से स्वतंत्र है और इसके परिणामस्वरूप अंशांकन की आवश्यकता नहीं होती है। | ||
माइक्रो-ऑप्टिक फैब्रिकेशन प्रौद्योगिकियों में वर्तमान प्रगति ने हवा और तरल दोनों में उपयोग करने योग्य डाइवर्जिंग फ्रिंज कतरनी तनाव सेंसर बनाने के लिए एकीकृत विवर्तनिक ऑप्टिकल तत्व का उपयोग करना संभव बना दिया है।<ref>{microS Shear Stress Sensor, MSE}</ref> | |||
===सूक्ष्म स्तंभ कतरनी-तनाव सेंसर === | |||
और माप विधि लचीली बहुलक पीडीएमएस से बने पतले दीवार पर लगे सूक्ष्म स्तंभों की है, जो दीवार के आसपास के क्षेत्र में ड्रैग बलों को प्रयुक्त करने की प्रतिक्रिया में झुकते हैं। सेंसर अप्रत्यक्ष माप सिद्धांतों से संबंधित है जो निकट-दीवार वेग प्रवणता और स्थानीय दीवार-कतरनी तनाव के बीच संबंधों पर निर्भर करता है।<ref>{{citation | last1 = Große |first1 = S. | last2 = Schröder |first2 = W. | title = Two-Dimensional Visualization of Turbulent Wall Shear Stress Using Micropillars | journal = AIAA Journal | year = 2009 | doi = 10.2514/1.36892 | volume = 47 | issue=2 | pages = 314–321 |bibcode = 2009AIAAJ..47..314G }}</ref><ref>{{citation | last1 = Große |first1 = S. | last2 = Schröder |first2 = W. | title = Dynamic Wall-Shear Stress Measurements in Turbulent Pipe Flow using the Micro-Pillar Sensor MPS<sup>3</sup> | journal = International Journal of Heat and Fluid Flow | year = 2008 | doi = 10.1016/j.ijheatfluidflow.2008.01.008 | volume = 29 | issue=3 | pages = 830–840 }}</ref> | |||
== यह भी देखें == | ===इलेक्ट्रो-विसारक विधि === | ||
इलेक्ट्रो-डिफ्यूज़नल विधि सीमित प्रसार वर्तमान स्थिति के तहत माइक्रोइलेक्ट्रोड से तरल चरण में दीवार कतरनी दर को मापती है। व्यापक सतह के एनोड ( सामान्यतः मापने वाले क्षेत्र से दूर स्थित) और कैथोड के रूप में कार्य करने वाले छोटे कार्यरत इलेक्ट्रोड के बीच संभावित अंतर तेजी से रेडॉक्स प्रतिक्रिया की ओर जाता है। आयन विलुप्त होना केवल माइक्रोप्रोब सक्रिय सतह पर होता है, जिससे प्रसार सीमा परत का विकास होता है, जिसमें तेजी से विद्युत-प्रसार प्रतिक्रिया दर केवल प्रसार द्वारा नियंत्रित होती है। माइक्रोइलेक्ट्रोड के निकट दीवार क्षेत्र में संवहन-विसरित समीकरण का समाधान सूक्ष्म-जांच की विशेषताओं की लंबाई, विद्युत रासायनिक समाधान के प्रसार गुणों और दीवार कतरनी दर पर निर्भर विश्लेषणात्मक समाधानों की ओर ले जाता है।<ref>{{citation | last1 = Havlica |first1 = J. | last2 = Kramolis |first2 = D.| last3 = Huchet |first3 = F. | title = A revisit of the electro-diffusional theory for the wall shear stress measurement | journal = International Journal of Heat and Mass Transfer | year = 2021 | doi = 10.1016/j.ijheatmasstransfer.2020.120610 | volume = 165 | pages = 120610 |s2cid = 228876357 |url = https://hal.archives-ouvertes.fr/hal-03201637/file/doc00032676.pdf }}</ref> | |||
== यह भी देखें == | |||
* [[गंभीर समाधान कतरनी तनाव]] | * [[गंभीर समाधान कतरनी तनाव]] | ||
* [[प्रत्यक्ष कतरनी परीक्षण]] | * [[प्रत्यक्ष कतरनी परीक्षण]] | ||
| Line 180: | Line 181: | ||
{{Reflist|2}} | {{Reflist|2}} | ||
{{ | {{DEFAULTSORT:Shear Stress}} | ||
[[Category:All articles with dead external links]] | |||
[[Category:Articles with dead external links from February 2020]] | |||
[[Category:Articles with hatnote templates targeting a nonexistent page|Shear Stress]] | |||
[[Category:Articles with permanently dead external links]] | |||
[[Category: | [[Category:CS1 uses русский-language script (ru)]] | ||
[[Category:Created On 01/05/2023]] | [[Category:CS1 русский-language sources (ru)]] | ||
[[Category:Created On 01/05/2023|Shear Stress]] | |||
[[Category:Infobox templates|physical quantity]] | |||
[[Category:Lua-based templates|Shear Stress]] | |||
[[Category:Machine Translated Page|Shear Stress]] | |||
[[Category:Pages with script errors|Shear Stress]] | |||
[[Category:Templates Vigyan Ready|Shear Stress]] | |||
[[Category:Templates that add a tracking category|Shear Stress]] | |||
[[Category:Templates that generate short descriptions|Shear Stress]] | |||
[[Category:Templates using TemplateData|Shear Stress]] | |||
[[Category:सातत्यक यांत्रिकी|Shear Stress]] | |||
Latest revision as of 14:43, 23 May 2023
| अपरूपण तनाव | |
|---|---|
सामान्य प्रतीक | τ |
| Si इकाई | pascal |
अन्य मात्राओं से व्युत्पत्तियां | τ = F/A |
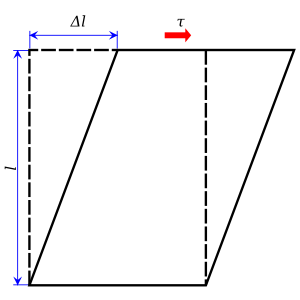
कतरनी तनाव (अधिकांशतः τ (ग्रीक: ताऊ) द्वारा निरूपित) पदार्थ पार अनुभाग के साथ तनाव (भौतिकी) समतलीय का घटक है। यह कतरनी बल से उत्पन्न होता है, पदार्थ अनुप्रस्थ काट के समानांतर (ज्यामिति) बल वेक्टर का घटक दूसरी ओर, 'सामान्य तनाव', बल सदिश घटक से उत्पन्न होता है, जो पदार्थ के अनुप्रस्थ काट पर लंबवत होता है, जिस पर यह कार्य करता है।
सामान्य कतरनी तनाव
औसत कतरनी तनाव की गणना करने का सूत्र प्रति इकाई क्षेत्र पर बल है।[1]
जहाँँ:
- τ = कतरनी तनाव;
- F = लगाया गया बल;
- A = प्रयुक्त बल वेक्टर के समानांतर क्षेत्र के साथ पदार्थ का क्रॉस-आंशिक क्षेत्र है ।
अन्य रूप
दीवार कतरनी तनाव
दीवार कतरनी तनाव दीवार के बगल में बहने वाले द्रव की परतों में दीवार से मंदक बल (प्रति इकाई क्षेत्र) को व्यक्त करता है। इसे इस प्रकार परिभाषित किया गया है:
जहाँँ गतिशील श्यानता, प्रवाह वेग और दीवार से दूरी है।
इसका उपयोग, उदाहरण के लिए धमनी रक्त प्रवाह के विवरण में किया जाता है, जिसमें प्रमाण है कि यह एथेरोजेनिक प्रक्रिया को प्रभावित करता है।[2]
शुद्ध
शुद्ध अपरूपण प्रतिबल शुद्ध अपरूपण विकृति से संबंधित है, जिसे γ निरूपित किया गया है, निम्नलिखित समीकरण द्वारा:[3]
जहाँँ G समदैशिक या पदार्थ विज्ञान पदार्थ का अपरूपण मापांक है, जिसके द्वारा दिया गया है
यहाँ E यंग का मापांक है और ν प्वासों का अनुपात है।
बीम कतरनी
बीम कतरनी को बीम पर लगाए गए कतरनी बल के कारण बीम के आंतरिक कतरनी तनाव के रूप में परिभाषित किया गया है।
जहाँँ
- f = विचाराधीन स्थान पर कुल अपरूपण बल;
- Q = क्षेत्रफल का प्रथम आघूर्ण या क्षेत्रफल का स्थैतिक आघूर्ण;
- b = मोटाई (चौड़ाई) कतरनी के लंबवत पदार्थ में;
- I = पूरे क्रॉस-सेक्शनल क्षेत्र के क्षेत्रफल का दूसरा क्षण।
दिमित्री इवानोविच ज़ुरावस्की के बाद बीम कतरनी सूत्र को ज़ुरावस्की कतरनी तनाव सूत्र के रूप में भी जाना जाता है, जिसने इसे 1855 में प्राप्त किया था।[4][5]
अर्ध-मोनोकोक कतरनी
अर्ध-मोनोकोक संरचना के अंदर कतरनी तनाव की गणना संरचना के क्रॉस-सेक्शन को स्ट्रिंगर्स (केवल अक्षीय भार ले जाने वाले) और जाले (केवल कतरनी प्रवाह को ले जाने) में आदर्श बनाकर की जा सकती है। अर्ध-मोनोकोक संरचना के दिए गए भाग की मोटाई से कतरनी प्रवाह को विभाजित करने से कतरनी तनाव उत्पन्न होता है। इस प्रकार, अधिकतम कतरनी तनाव या तो अधिकतम कतरनी प्रवाह या न्यूनतम मोटाई के वेब में होगा
कतरनी के कारण मिट्टी में निर्माण भी विफल हो सकता है; उदाहरण के लिए, मिट्टी से भरे बांध या डाइक का वजन छोटे से भूस्खलन की तरह, अवभूमि के ढहने का कारण बन सकता है।
प्रभाव कतरनी
प्रभाव के अधीन ठोस गोल पट्टी में निर्मित अधिकतम कतरनी तनाव समीकरण द्वारा दिया गया है:
जहाँँ
- U = गतिज ऊर्जा में परिवर्तन;
- G = कतरनी मापांक;
- V = छड़ का आयतन;
और
- U = Urotating + Uapplied;
- Urotating = 1/2Iω2;
- Uapplied = Tθdisplaced;
- I = जड़त्व का द्रव्यमान क्षण;
- ω = कोणीय गति।
तरल पदार्थ में कतरनी तनाव
ठोस सीमा के साथ चलने वाले किसी भी वास्तविक तरल पदार्थ (तरल पदार्थ और गैस सम्मिलित ) उस सीमा पर कतरनी तनाव उत्पन्न करेंगे। नो-स्लिप स्थिति[6] निर्धारित करता है कि सीमा पर द्रव की गति (सीमा के सापेक्ष) शून्य है; चूँकि सीमा से कुछ ऊँचाई पर प्रवाह की गति द्रव के सामान्य होनी चाहिए। इन दो बिंदुओं के बीच के क्षेत्र को सीमा परत जहाँ जाता है। लैमिनार प्रवाह में सभी न्यूटोनियन द्रव पदार्थों के लिए, कतरनी तनाव तरल पदार्थ में तनाव दर के समानुपाती होता है, जहां श्यानता आनुपातिकता का स्थिरांक होता है। गैर-न्यूटोनियन तरल पदार्थों के लिए श्यानता स्थिर नहीं है। वेग के इस हानि के परिणामस्वरूप कतरनी का तनाव सीमा पर लगाया जाता है।
न्यूटोनियन तरल पदार्थ के लिए, बिंदु y पर समतल प्लेट के समानांतर सतह तत्व पर कतरनी तनाव निम्न द्वारा दिया जाता है:
जहाँँ
- μ प्रवाह की गतिशील श्यानता है;
- u सीमा के साथ प्रवाह वेग है;
- y सीमा से ऊपर की ऊंचाई है।
विशेष रूप से, दीवार कतरनी तनाव को इस प्रकार परिभाषित किया गया है:
किसी भी सामान्य ज्यामिति (उपर्युक्त समतल प्लेट सहित) के लिए न्यूटन का संवैधानिक नियम बताता है कि कतरनी टेन्सर ( दूसरे क्रम का टेंसर) प्रवाह वेग ढाल के समानुपाती होता है (वेग वेक्टर है, इसलिए इसका ग्रेडियेंट दूसरा क्रम है) टेन्सर):
और आनुपातिकता के स्थिरांक को गतिशील श्यानता कहा जाता है। आइसोट्रोपिक न्यूटोनियन प्रवाह के लिए यह अदिश राशि है, जबकि अनिसोट्रोपिक न्यूटोनियन प्रवाह के लिए यह दूसरे क्रम का टेंसर भी हो सकता है। मौलिक पहलू यह है कि न्यूटोनियन द्रव के लिए गतिशील श्यानता प्रवाह वेग पर स्वतंत्र है (अर्थात, कतरनी तनाव संवैधानिक नियम रैखिक है), जबकि गैर-न्यूटोनियन प्रवाह यह सच नहीं है, और किसी को संशोधन की अनुमति देनी चाहिए:
यह अब न्यूटन का नियम नहीं है, किंतु सामान्य तन्यता पहचान है: प्रवाह वेग के कार्य के रूप में कतरनी तनाव की किसी भी अभिव्यक्ति को प्रवाह वेग के कार्य के रूप में सदैव श्यानता की अभिव्यक्ति मिल सकती है। दूसरी ओर, प्रवाह वेग के कार्य के रूप में कतरनी तनाव दिया जाता है, यह न्यूटनियन प्रवाह का प्रतिनिधित्व करता है, यदि इसे प्रवाह वेग के ढाल के लिए स्थिर के रूप में व्यक्त किया जा सकता है। इस स्थितियों में जो स्थिर पाया जाता है वह प्रवाह की गतिशील श्यानता है।
उदाहरण
कार्तीय निर्देशांक (x, y) में 2D स्थान को ध्यान में रखते हुए (प्रवाह वेग घटक क्रमशः (u, v) हैं), फिर कतरनी तनाव आव्युह द्वारा दिया गया:
न्यूटोनियन प्रवाह का प्रतिनिधित्व करता है, वास्तव में इसे इस रूप में व्यक्त किया जा सकता है:
- ,
अर्थात, विस्कोसिटी टेंसर के साथ अनिसोट्रोपिक प्रवाह:
जो असमान (स्थान निर्देशांक पर निर्भर करता है) और क्षणिक है, किन्तु प्रासंगिक रूप से यह प्रवाह वेग पर स्वतंत्र है:
यह प्रवाह इसलिए न्यूटोनियन है। दूसरी ओर, प्रवाह जिसमें श्यानता थी:
गैर न्यूटनियन है क्योंकि श्यानता प्रवाह वेग पर निर्भर करती है। यह गैर न्यूटोनियन प्रवाह समदैशिक है (आव्युह पहचान आव्युह के लिए आनुपातिक है), इसलिए श्यानता केवल स्केलर है:
सेंसर के साथ मापन
डाइवर्जिंग फ्रिंज शियर स्ट्रेस सेंसर
दीवार कतरनी तनाव को मापने के लिए इस रिश्ते का लाभ उठाया जा सकता है। यदि संवेदक सीधे दीवार पर वेग प्रोफ़ाइल के ढाल को माप सकता है, तो गतिशील श्यानता से गुणा करने से कतरनी तनाव उत्पन्न होगा। इस तरह के सेंसर का प्रदर्शन ए.ए. नकवी और डब्ल्यू.सी. रेनॉल्ड्स द्वारा किया गया था।[7] दो समानांतर स्लिट्स के माध्यम से प्रकाश की किरण भेजकर उत्पन्न हस्तक्षेप प्रतिरूप रैखिक रूप से अलग होने वाले फ्रिंज का नेटवर्क बनाता है जो दो स्लिट्स के विमान से उत्पन्न होता है (डबल-स्लिट प्रयोग देखें)। जैसे ही तरल पदार्थ का कण फ्रिन्जों से होकर गुजरता है, रिसीवर फ्रिन्ज प्रतिरूप के प्रतिबिंब का पता लगाता है। संकेत को संसाधित किया जा सकता है, और फ्रिंज कोण को जानकर, कण की ऊंचाई और वेग को सट्रपलेशन किया जा सकता है। दीवार वेग प्रवणता का मापा मान द्रव गुणों से स्वतंत्र है और इसके परिणामस्वरूप अंशांकन की आवश्यकता नहीं होती है।
माइक्रो-ऑप्टिक फैब्रिकेशन प्रौद्योगिकियों में वर्तमान प्रगति ने हवा और तरल दोनों में उपयोग करने योग्य डाइवर्जिंग फ्रिंज कतरनी तनाव सेंसर बनाने के लिए एकीकृत विवर्तनिक ऑप्टिकल तत्व का उपयोग करना संभव बना दिया है।[8]
सूक्ष्म स्तंभ कतरनी-तनाव सेंसर
और माप विधि लचीली बहुलक पीडीएमएस से बने पतले दीवार पर लगे सूक्ष्म स्तंभों की है, जो दीवार के आसपास के क्षेत्र में ड्रैग बलों को प्रयुक्त करने की प्रतिक्रिया में झुकते हैं। सेंसर अप्रत्यक्ष माप सिद्धांतों से संबंधित है जो निकट-दीवार वेग प्रवणता और स्थानीय दीवार-कतरनी तनाव के बीच संबंधों पर निर्भर करता है।[9][10]
इलेक्ट्रो-विसारक विधि
इलेक्ट्रो-डिफ्यूज़नल विधि सीमित प्रसार वर्तमान स्थिति के तहत माइक्रोइलेक्ट्रोड से तरल चरण में दीवार कतरनी दर को मापती है। व्यापक सतह के एनोड ( सामान्यतः मापने वाले क्षेत्र से दूर स्थित) और कैथोड के रूप में कार्य करने वाले छोटे कार्यरत इलेक्ट्रोड के बीच संभावित अंतर तेजी से रेडॉक्स प्रतिक्रिया की ओर जाता है। आयन विलुप्त होना केवल माइक्रोप्रोब सक्रिय सतह पर होता है, जिससे प्रसार सीमा परत का विकास होता है, जिसमें तेजी से विद्युत-प्रसार प्रतिक्रिया दर केवल प्रसार द्वारा नियंत्रित होती है। माइक्रोइलेक्ट्रोड के निकट दीवार क्षेत्र में संवहन-विसरित समीकरण का समाधान सूक्ष्म-जांच की विशेषताओं की लंबाई, विद्युत रासायनिक समाधान के प्रसार गुणों और दीवार कतरनी दर पर निर्भर विश्लेषणात्मक समाधानों की ओर ले जाता है।[11]
यह भी देखें
- गंभीर समाधान कतरनी तनाव
- प्रत्यक्ष कतरनी परीक्षण
- टकराव
- कतरनी और पल आरेख
- कट्टाई दर
- अपरूपण तनाव
- कतरनी ताकत
- तन्यता तनाव
- त्रिअक्षीय अपरूपण परीक्षण
संदर्भ
- ↑ Hibbeler, R.C. (2004). सामग्री के यांत्रिकी. New Jersey USA: Pearson Education. p. 32. ISBN 0-13-191345-X.
- ↑ Katritsis, Demosthenes (2007). "Wall Shear Stress: Theoretical Considerations and Methods of Measurement". Progress in Cardiovascular Diseases. 49 (5): 307–329. doi:10.1016/j.pcad.2006.11.001. PMID 17329179.
- ↑ "सामग्री की ताकत". Eformulae.com. Retrieved 24 December 2011.
- ↑ Лекция Формула Журавского [Zhuravskii's Formula]. Сопромат Лекции (in русский). Retrieved 2014-02-26.
- ↑ "बीम का लचीलापन" (PDF). Mechanical Engineering Lectures. McMaster University.[permanent dead link]
- ↑ Day, Michael A. (2004), "The no-slip condition of fluid dynamics", Erkenntnis, Springer Netherlands, 33 (3): 285–296, doi:10.1007/BF00717588, ISSN 0165-0106, S2CID 55186899.
- ↑ Naqwi, A. A.; Reynolds, W. C. (Jan 1987), "Dual cylindrical wave laser-Doppler method for measurement of skin friction in fluid flow", NASA STI/Recon Technical Report N, 87
- ↑ {microS Shear Stress Sensor, MSE}
- ↑ Große, S.; Schröder, W. (2009), "Two-Dimensional Visualization of Turbulent Wall Shear Stress Using Micropillars", AIAA Journal, 47 (2): 314–321, Bibcode:2009AIAAJ..47..314G, doi:10.2514/1.36892
- ↑ Große, S.; Schröder, W. (2008), "Dynamic Wall-Shear Stress Measurements in Turbulent Pipe Flow using the Micro-Pillar Sensor MPS3", International Journal of Heat and Fluid Flow, 29 (3): 830–840, doi:10.1016/j.ijheatfluidflow.2008.01.008
- ↑ Havlica, J.; Kramolis, D.; Huchet, F. (2021), "A revisit of the electro-diffusional theory for the wall shear stress measurement" (PDF), International Journal of Heat and Mass Transfer, 165: 120610, doi:10.1016/j.ijheatmasstransfer.2020.120610, S2CID 228876357