आइसोगोनल संयुग्म: Difference between revisions

From Vigyanwiki
No edit summary
No edit summary
 
(6 intermediate revisions by 3 users not shown)
Line 1: Line 1:
__नोटोक__
{{Short description|Geometric transformation applied to points with respect to a given triangle}}
{{Short description|Geometric transformation applied to points with respect to a given triangle}}
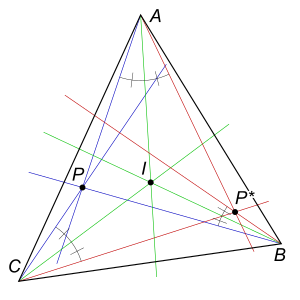
[[Image:Isogonal_Conjugate.svg|right|thumb|कोण समद्विभाजक (केन्द्र I पर संगत){{legend-line|solid blue|Lines from each vertex to {{mvar|P}}}}कोण समद्विभाजकों के बारे में परिलक्षित P की रेखाएँ (P * पर समवर्ती, P का समकोणीय संयुग्म)]]
[[Image:Isogonal_Conjugate.svg|right|thumb|कोण समद्विभाजक (केन्द्र I पर संगत) कोण समद्विभाजकों के बारे में परिलक्षित P की रेखाएँ (P * पर समवर्ती, P का समकोणीय संयुग्म)]]
  [[Image:Isogonal_Conjugate_transform.svg|right|thumb|त्रिभुज के अंदर बिंदुओं पर समकोणीय संयुग्म परिवर्तन।]][[ज्यामिति]] में, एक [[बिंदु (ज्यामिति)]] के समकोणीय संयुग्म {{mvar|P}} त्रिभुज के संबंध में {{math|△''ABC''}} का निर्माण रेखाओं के परावर्तन (गणित) द्वारा किया जाता है {{mvar|PA, PB, PC}} के [[कोण द्विभाजक]] के बारे में {{mvar|A, B, C}} क्रमश। ये तीन परावर्तित रेखाएँ {{mvar|P}} समकोणिक संयुग्म पर [[समवर्ती रेखाएँ]] हैं  (यह परिभाषा केवल उन बिंदुओं पर प्रयुक्त होती है जो त्रिभुज {{math|△''ABC''}} की विस्तारित भुजा पर नहीं हैं ) यह सेवा के प्रमेय के त्रिकोणमितीय रूप का प्रत्यक्ष परिणाम है।
  [[Image:Isogonal_Conjugate_transform.svg|right|thumb|त्रिभुज के अंदर बिंदुओं पर समकोणीय संयुग्म परिवर्तन।]][[ज्यामिति]] में, [[बिंदु (ज्यामिति)]] के समकोणीय संयुग्म {{mvar|P}} त्रिभुज के संबंध में {{math|△''ABC''}} का निर्माण रेखाओं के परावर्तन (गणित) द्वारा किया जाता है। {{mvar|PA, PB, PC}} के [[कोण द्विभाजक]] के बारे में {{mvar|A, B, C}} क्रमश ये तीन परावर्तित रेखाएँ {{mvar|P}} समकोणिक संयुग्म पर [[समवर्ती रेखाएँ]] हैं। (यह परिभाषा केवल उन बिंदुओं पर प्रयुक्त होती है जो त्रिभुज {{math|△''ABC''}} की विस्तारित भुजा पर नहीं हैं।) यह सेवा के प्रमेय के त्रिकोणमितीय रूप का प्रत्यक्ष परिणाम है।


एक बिंदु का समकोणीय संयुग्म {{mvar|P}} को कभी-कभी {{mvar|P*}} द्वारा निरूपित किया जाता है {{mvar|P*}} का समकोणीय संयुग्म {{mvar|P}} है '''{{mvar|P}}'''.
बिंदु का समकोणीय संयुग्म {{mvar|P}} को कभी-कभी {{mvar|P*}} द्वारा निरूपित किया जाता है {{mvar|P*}} का समकोणीय संयुग्म {{mvar|P}} है।


अंतःकेंद्र {{mvar|I}} का समकोणीय संयुग्म '''{{mvar|I}}''' ही है। [[लम्बकेन्द्र]] {{mvar|H}} का समकोणीय संयुग्म '''{{mvar|H}}''' परिकेन्द्र {{mvar|O}} है {{mvar|O}}. [[केन्द्रक]] {{mvar|G}} का समकोणीय संयुग्म '''{{mvar|G}}''' (परिभाषा के अनुसार) [[सिम्मेडियन बिंदु]] {{mvar|K}} है '''{{mvar|K}}'''. [[फर्मेट बिंदु]] के समकोणीय कॉन्जुगेट्स [[ आइसोडायनामिक बिंदु ]]्स हैं और इसके विपरीत। ब्रोकार्ड बिंदु एक दूसरे के समकोणीय संयुग्म हैं।
अंतःकेंद्र {{mvar|I}} का समकोणीय संयुग्म ही है। [[लम्बकेन्द्र]] {{mvar|H}} का समकोणीय संयुग्म परिकेन्द्र {{mvar|O}} है {{mvar|O}}. [[केन्द्रक]] {{mvar|G}} का समकोणीय संयुग्म (परिभाषा के अनुसार) [[सिम्मेडियन बिंदु]] {{mvar|K}} है [[फर्मेट बिंदु]] के समकोणीय कॉन्जुगेट्स [[ आइसोडायनामिक बिंदु |आइसोडायनामिक बिंदु]] हैं और इसके विपरीत ब्रोकार्ड बिंदु एक दूसरे के समकोणीय संयुग्म हैं।


[[ट्रिलिनियर निर्देशांक]] में, यदि <math>X=x:y:z</math> त्रिभुज {{math|△''ABC''}} की भुजा पर नहीं एक बिंदु है '''{{math|△''ABC''}}''', तो इसका समद्विबाहु संयुग्म है <math>\tfrac{1}{x} : \tfrac{1}{y} : \tfrac{1}{z}.</math> इस कारण {{mvar|X}} '''से''', का समकोणीय संयुग्म '''{{mvar|X}}''' को कभी-कभी निरूपित किया जाता है {{math|''X''{{sup| –1}}}}. '''[[सेट (गणित)]]<nowiki> {{mvar|S}</nowiki>'''त्रिरेखीय गुणनफल के अंतर्गत त्रिभुज केंद्रों के }, द्वारा परिभाषित किया गया है
[[ट्रिलिनियर निर्देशांक]] में, यदि <math>X=x:y:z</math> त्रिभुज {{math|△''ABC''}} की भुजा पर नहीं एक बिंदु है, तो इसका समद्विबाहु संयुग्म है <math>\tfrac{1}{x} : \tfrac{1}{y} : \tfrac{1}{z}.</math> इस कारण {{mvar|X}} का समकोणीय संयुग्म '''{{mvar|X}}''' को कभी-कभी निरूपित किया जाता है {{math|''X''{{sup| –1}}}} त्रिरेखीय गुणनफल के अंतर्गत त्रिभुज केंद्रों के द्वारा परिभाषित किया गया है।


: <math>(p:q:r)*(u:v:w) = pu:qv:rw,</math>
: <math>(p:q:r)*(u:v:w) = pu:qv:rw,</math>
[[क्रमविनिमेय समूह]] है, और {{mvar|S}} प्रत्येक {{mvar|X}} का व्युत्क्रम{{math|''X''{{sup| –1}}}} है '''{{mvar|X}} में {{mvar|S}} है {{math|''X''{{sup| –1}}}}.'''
[[क्रमविनिमेय समूह]] है, और {{mvar|S}} प्रत्येक {{mvar|X}} का व्युत्क्रम {{math|''X''{{sup| –1}}}} है।


जैसा कि समकोणीय संयुग्मन एक फलन (गणित) है, यह बिंदुओं के सेट, जैसे कि रेखाओं और वृत्तों के समकोणीय संयुग्मन के बारे में बात करने के लिए समझ में आता है। उदाहरण के लिए, एक रेखा का समकोणीय संयुग्म एक [[खतना और प्रतिष्ठित|सर्कमोनिक और प्रतिष्ठित]] है; विशेष रूप से, एक दीर्घवृत्त, [[परवलय]] या अतिपरवलय के अनुसार रेखा [[परिवृत्त]] को 0, 1, या 2 बिंदुओं में काटती है। परिवृत्त का समकोणीय संयुग्म [[अनंत पर रेखा]] है। कई प्रसिद्ध क्यूबिक समतल वक्र (जैसे, [[थॉमसन क्यूबिक]], डार्बौक्स क्यूबिक, [[ न्युबर्ग क्यूबिक ]]) स्व-समकोणीय-संयुग्मी हैं, इस अर्थ में कि यदि {{mvar|X}} क्यूबिक पर है, तो {{math|''X''{{sup| –1}}}} क्यूबिक पर भी है।
जैसा कि समकोणीय संयुग्मन फलन (गणित) है, यह बिंदुओं के सेट, जैसे कि रेखाओं और वृत्तों के समकोणीय संयुग्मन के बारे में बात करने के लिए समझ में आता है। उदाहरण के लिए रेखा का समकोणीय संयुग्म [[खतना और प्रतिष्ठित|सर्कमोनिक और प्रतिष्ठित]] है; विशेष रूप से दीर्घवृत्त, [[परवलय]] या अतिपरवलय के अनुसार रेखा [[परिवृत्त]] को 0, 1, या 2 बिंदुओं में काटती है। परिवृत्त का समकोणीय संयुग्म [[अनंत पर रेखा]] है। कई प्रसिद्ध क्यूबिक समतल वक्र (जैसे, [[थॉमसन क्यूबिक]], डार्बौक्स क्यूबिक, [[ न्युबर्ग क्यूबिक |न्युबर्ग क्यूबिक]] ) स्व-समकोणीय-संयुग्मी हैं, इस अर्थ में कि यदि {{mvar|X}} क्यूबिक पर है, तो {{math|''X''{{sup| –1}}}} क्यूबिक पर भी है।


=== == एक बिंदु == के समकोणीय संयुग्म के लिए एक और निर्माण ===
=== बिंदु के समकोणीय संयुग्म के लिए एक और निर्माण ===
[[File:A Second Definition Of Isogonal Conjugate.png|thumb|समकोणीय संयुग्म की दूसरी परिभाषा]]त्रिभुज {{math|△''ABC''}} के तल में '''{{math|△''ABC''}}'''किसी दिए गए बिंदु {{mvar|P}} के लिए '''{{mvar|P}} त्रिभुज के तल में {{math|△''ABC''}}''',माना की भुजाओं {{mvar|BC, CA, AB}} में {{mvar|P}}का प्रतिबिंब{{mvar|P{{sub|a}}, P{{sub|b}}, P{{sub|c}}}} है। '''प्रतिबिंब चलो {{mvar|P}} पार्श्व में {{mvar|BC, CA, AB}} होना {{mvar|P{{sub|a}}, P{{sub|b}}, P{{sub|c}}}}'''. तब वृत्त का केंद्र {{math|〇''P{{sub|a}}P{{sub|b}}P{{sub|c}}''}}, {{mvar|P}} का समकोणीय संयुग्म है '''{{mvar|P}}'''.<ref>{{cite web |last1=Steve Phelps |title=समकोणीय संयुग्मों का निर्माण|url=https://www.geogebra.org/m/sRVERPyd |website=GeoGebra |publisher=GeoGebra Team |access-date=17 January 2022}}</ref>
[[File:A Second Definition Of Isogonal Conjugate.png|thumb|समकोणीय संयुग्म की दूसरी परिभाषा]]त्रिभुज {{math|△''ABC''}} के तल में किसी दिए गए बिंदु {{mvar|P}} के लिए माना की भुजाओं {{mvar|BC, CA, AB}} में {{mvar|P}} का प्रतिबिंब {{mvar|P{{sub|a}}, P{{sub|b}}, P{{sub|c}}}} है। तब वृत्त का केंद्र {{math|〇''P{{sub|a}}P{{sub|b}}P{{sub|c}}''}}, {{mvar|P}} का समकोणीय संयुग्म है।<ref>{{cite web |last1=Steve Phelps |title=समकोणीय संयुग्मों का निर्माण|url=https://www.geogebra.org/m/sRVERPyd |website=GeoGebra |publisher=GeoGebra Team |access-date=17 January 2022}}</ref>




Line 33: Line 32:
*[http://mathworld.wolfram.com/IsogonalConjugate.html MathWorld]
*[http://mathworld.wolfram.com/IsogonalConjugate.html MathWorld]
* [http://www.cut-the-knot.org/Curriculum/Geometry/OrthologicPedal.shtml Pedal Triangle and Isogonal Conjugacy]
* [http://www.cut-the-knot.org/Curriculum/Geometry/OrthologicPedal.shtml Pedal Triangle and Isogonal Conjugacy]
[[Category: त्रिभुज ज्यामिति]]


 
[[Category:Commons category link is locally defined]]
 
[[Category: Machine Translated Page]]
[[Category:Created On 19/05/2023]]
[[Category:Created On 19/05/2023]]
[[Category:Lua-based templates]]
[[Category:Machine Translated Page]]
[[Category:Pages with broken file links]]
[[Category:Pages with maths render errors]]
[[Category:Pages with script errors]]
[[Category:Templates Vigyan Ready]]
[[Category:Templates that add a tracking category]]
[[Category:Templates that generate short descriptions]]
[[Category:Templates using TemplateData]]
[[Category:त्रिभुज ज्यामिति]]

Latest revision as of 16:00, 29 May 2023

कोण समद्विभाजक (केन्द्र I पर संगत) कोण समद्विभाजकों के बारे में परिलक्षित P की रेखाएँ (P * पर समवर्ती, P का समकोणीय संयुग्म)
त्रिभुज के अंदर बिंदुओं पर समकोणीय संयुग्म परिवर्तन।

ज्यामिति में, बिंदु (ज्यामिति) के समकोणीय संयुग्म P त्रिभुज के संबंध में △ABC का निर्माण रेखाओं के परावर्तन (गणित) द्वारा किया जाता है। PA, PB, PC के कोण द्विभाजक के बारे में A, B, C क्रमश ये तीन परावर्तित रेखाएँ P समकोणिक संयुग्म पर समवर्ती रेखाएँ हैं। (यह परिभाषा केवल उन बिंदुओं पर प्रयुक्त होती है जो त्रिभुज △ABC की विस्तारित भुजा पर नहीं हैं।) यह सेवा के प्रमेय के त्रिकोणमितीय रूप का प्रत्यक्ष परिणाम है।

बिंदु का समकोणीय संयुग्म P को कभी-कभी P* द्वारा निरूपित किया जाता है P* का समकोणीय संयुग्म P है।

अंतःकेंद्र I का समकोणीय संयुग्म ही है। लम्बकेन्द्र H का समकोणीय संयुग्म परिकेन्द्र O है O. केन्द्रक G का समकोणीय संयुग्म (परिभाषा के अनुसार) सिम्मेडियन बिंदु K है फर्मेट बिंदु के समकोणीय कॉन्जुगेट्स आइसोडायनामिक बिंदु हैं और इसके विपरीत ब्रोकार्ड बिंदु एक दूसरे के समकोणीय संयुग्म हैं।

ट्रिलिनियर निर्देशांक में, यदि त्रिभुज △ABC की भुजा पर नहीं एक बिंदु है, तो इसका समद्विबाहु संयुग्म है इस कारण X का समकोणीय संयुग्म X को कभी-कभी निरूपित किया जाता है X –1 त्रिरेखीय गुणनफल के अंतर्गत त्रिभुज केंद्रों के द्वारा परिभाषित किया गया है।

क्रमविनिमेय समूह है, और S प्रत्येक X का व्युत्क्रम X –1 है।

जैसा कि समकोणीय संयुग्मन फलन (गणित) है, यह बिंदुओं के सेट, जैसे कि रेखाओं और वृत्तों के समकोणीय संयुग्मन के बारे में बात करने के लिए समझ में आता है। उदाहरण के लिए रेखा का समकोणीय संयुग्म सर्कमोनिक और प्रतिष्ठित है; विशेष रूप से दीर्घवृत्त, परवलय या अतिपरवलय के अनुसार रेखा परिवृत्त को 0, 1, या 2 बिंदुओं में काटती है। परिवृत्त का समकोणीय संयुग्म अनंत पर रेखा है। कई प्रसिद्ध क्यूबिक समतल वक्र (जैसे, थॉमसन क्यूबिक, डार्बौक्स क्यूबिक, न्युबर्ग क्यूबिक ) स्व-समकोणीय-संयुग्मी हैं, इस अर्थ में कि यदि X क्यूबिक पर है, तो X –1 क्यूबिक पर भी है।

बिंदु के समकोणीय संयुग्म के लिए एक और निर्माण

समकोणीय संयुग्म की दूसरी परिभाषा

त्रिभुज △ABC के तल में किसी दिए गए बिंदु P के लिए माना की भुजाओं BC, CA, AB में P का प्रतिबिंब Pa, Pb, Pc है। तब वृत्त का केंद्र 〇PaPbPc, P का समकोणीय संयुग्म है।[1]


यह भी देखें

संदर्भ

  1. ↑ Steve Phelps. "समकोणीय संयुग्मों का निर्माण". GeoGebra. GeoGebra Team. Retrieved 17 January 2022.


बाहरी संबंध

Wikimedia Commons has media related to Isogonal Conjugates.
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=आइसोगोनल_संयुग्म&oldid=172167’