Latest revision as of 13:23, 15 June 2023

मैग्नेटोकेमिस्ट्री का संबंध रासायनिक यौगिकों के चुंबकीय गुणों से है। एक यौगिक में निहित इलेक्ट्रॉनों के स्पिन और कक्षीय कोणीय गति से चुंबकीय गुण उत्पन्न होते हैं। यौगिक प्रतिचुम्बकीय तब होते हैं जब उनमें कोई अयुगलित इलेक्ट्रॉन नहीं होता है। आणविक यौगिक जिनमें एक या एक से अधिक अयुग्मित इलेक्ट्रॉन होते हैं, अनुचुंबकीय होते हैं। अनुचुंबकत्व का परिमाण एक प्रभावी चुंबकीय क्षण, μ_eff के रूप में व्यक्त किया जाता है। प्रथम-पंक्ति संक्रमण धातुओं के लिए μ_eff का परिमाण, प्रथम सन्निकटन के लिए अयुग्मित इलेक्ट्रॉनों की संख्या का एक सरल कार्य है, स्पिन-केवल सूत्र सामान्यतः, स्पिन-ऑर्बिट कपलिंग μ_eff को स्पिन-केवल सूत्र से विचलित करने का कारण बनता है। भारी संक्रमण धातुओं लैंथेनाइड्स और एक्टिनाइड्स के लिए स्पिन-ऑर्बिट युग्मन को नजरअंदाज नहीं किया जा सकता है। परिवर्तन इंटरेक्शन रिजेक्शन और अनंत जाली में हो सकता है, जिसके परिणामस्वरूप फेरोमैग्नेटिज्म, एंटीफेरोमैग्नेटिज्म या फेरिमैग्नेटिज्म व्यक्तिगत स्पिन के सापेक्ष झुकाव के आधार पर होता है।

चुंबकीय संवेदनशीलता

मैग्नेटोकेमिस्ट्री में प्राथमिक माप चुंबकीय संवेदनशीलता है। यह पदार्थ को चुंबकीय क्षेत्र में रखने पर परस्पर क्रिया की ताकत को मापता है। मात्रा चुंबकीय संवेदनशीलता, प्रतीक द्वारा दर्शाया गया $\chi _{v}$ संबंध द्वारा परिभाषित किया गया है

{\vec {M}}=\chi _{v}{\vec {H}}

जहाँ, ${\vec {M}}$ पदार्थ का चुंबकीयकरण है (चुंबकीय द्विध्रुवीय क्षण प्रति इकाई आयतन), एम्पीयर प्रति मीटर (SI इकाइयों) में मापा जाता है और ${\vec {H}}$ चुंबकीय क्षेत्र की ताकत है, जिसे एम्पीयर प्रति मीटर में भी मापा जाता है . संवेदनशीलता एक आयाम रहित मात्रा है। रासायनिक अनुप्रयोगों के लिए मोलर चुंबकीय संवेदनशीलता (χ_mol) पसंदीदा मात्रा है। इसे m³·mol⁻¹ (SI) or cm³·mol⁻¹ (सीजीएस) में मापा जाता है और इसे इस रूप में परिभाषित किया जाता है

\chi _{\text{mol}}=M\chi _{v}/\rho

जहाँ ρ kg·m⁻³ (SI) या g·cm⁻³ (सीजीएस) में घनत्व है और M kg·mol⁻¹ (SI) या g·mol⁻¹ (सीजीएस) में मोलर द्रव्यमान है।

गौई संतुलन का योजनाबद्ध आरेख

चुंबकीय संवेदनशीलता को मापने के लिए कई विधि उपलब्ध हैं।

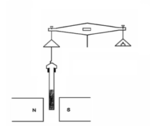
गौई संतुलन के साथ नमूने के वजन परिवर्तन को एक विश्लेषणात्मक संतुलन के साथ मापा जाता है जब नमूना एक सजातीय चुंबकीय क्षेत्र में रखा जाता है। मापों को एक ज्ञात मानक के विरुद्ध कैलिब्रेटेड किया जाता है, जैसे पारा कोबाल्ट थायोसाइनेट HgCo(NCS)₄.. अंशांकन नमूने के घनत्व को जानने की आवश्यकता को समाप्त करता है। नमूना को चुंबक के ध्रुव के टुकड़ों के बीच क्रायोस्टेट में रखकर चर तापमान मापन किया जा सकता है।^[1]
इवांस संतुलन^[2] एक मरोड़ संतुलन है जो चुम्बकों को उनकी प्रारंभिक स्थिति में वापस लाने के लिए एक निश्चित स्थिति में एक नमूना और एक चर माध्यमिक चुंबक का उपयोग करता है। यह भी HgCo(NCS)₄. के विपरीत कैलिब्रेट किया गया है
फैराडे तुला के साथ नमूना को निरंतर ढाल के चुंबकीय क्षेत्र में रखा जाता है, और एक मरोड़ संतुलन पर तौला जाता है। यह विधि चुंबकीय अनिसोट्रॉपी पर जानकारी प्राप्त कर सकती है।^[3]
स्क्विड एक बहुत ही संवेदनशील मैग्नेटोमीटर है।
समाधान में पदार्थों के लिए संवेदनशीलता को मापने के लिए परमाणु चुंबकीय अनुनाद का उपयोग किया जा सकता है।^[4]^[5]

चुंबकीय व्यवहार के प्रकार

जब एक पृथक परमाणु को चुंबकीय क्षेत्र में रखा जाता है तो एक अन्योन्य क्रिया होती है क्योंकि परमाणु में प्रत्येक इलेक्ट्रॉन चुंबक की तरह व्यवहार करता है अर्थात इलेक्ट्रॉन का एक चुंबकीय क्षण होता है। परस्पर क्रिया दो प्रकार की होती है।

प्रतिचुंबकत्व जब एक चुंबकीय क्षेत्र में रखा जाता है तो परमाणु चुंबकीय रूप से ध्रुवीकृत हो जाता है अर्थात यह एक प्रेरित चुंबकीय क्षण विकसित करता है। अंतःक्रिया का बल परमाणु को चुंबकीय क्षेत्र से बाहर धकेलता है। परिपाटी के अनुसार प्रतिचुम्बकीय संवेदनशीलता को ऋणात्मक चिह्न दिया जाता है। बहुधा प्रतिचुंबकीय परमाणुओं में कोई अयुगलित इलेक्ट्रॉन नहीं होता है अर्थात प्रत्येक इलेक्ट्रॉन एक ही परमाणु कक्षीय में दूसरे इलेक्ट्रॉन के साथ युग्मित होता है। दो इलेक्ट्रॉनों के क्षण एक दूसरे को समाप्त कर देते हैं इसलिए परमाणु का कोई शुद्ध चुंबकीय क्षण नहीं होता है। चूँकि आयन Eu³⁺के लिए जिसमें छह अयुग्मित इलेक्ट्रॉन होते हैं कक्षीय कोणीय संवेग इलेक्ट्रॉन कोणीय संवेग को समाप्त कर देता है और यह आयन शून्य केल्विन पर प्रतिचुंबकीय होता है।
पैरामैग्नेटिज्म कम से कम एक इलेक्ट्रॉन दूसरे के साथ युग्मित नहीं है। परमाणु का एक स्थायी चुंबकीय क्षण होता है। जब एक चुंबकीय क्षेत्र में रखा जाता है परमाणु क्षेत्र में आकर्षित होता है। परिपाटी द्वारा अनुचुंबकीय संवेदनशीलता को सकारात्मक संकेत दिया जाता है।

जब परमाणु किसी रासायनिक यौगिक में उपस्थित होता है तो उसका चुंबकीय व्यवहार उसके रासायनिक वातावरण द्वारा संशोधित होता है। चुंबकीय क्षण का मापन उपयोगी रासायनिक जानकारी दे सकता है।

कुछ क्रिस्टलीय पदार्थो में अलग-अलग चुंबकीय क्षणों को एक दूसरे के साथ संरेखित किया जा सकता है (चुंबकीय क्षण में परिमाण और दिशा दोनों होते हैं)। यह फेरोमैग्नेटिज्म, एंटीफेरोमैग्नेटिज्म या फेरिमैग्नेटिज्म को जन्म देता है। ये समग्र रूप से क्रिस्टल के गुण हैं जिनका रासायनिक गुणों पर बहुत कम प्रभाव पड़ता है।

प्रतिचुम्बकत्व

डायमैग्नेटिज्म रासायनिक यौगिकों की एक सार्वभौमिक संपत्ति है, क्योंकि सभी रासायनिक यौगिकों में इलेक्ट्रॉन जोड़े होते हैं। एक यौगिक जिसमें कोई अयुग्मित इलेक्ट्रॉन नहीं होता है, प्रतिचुम्बकीय कहलाता है। प्रभाव अशक्त है क्योंकि यह प्रेरित चुंबकीय क्षण के परिमाण पर निर्भर करता है। यह इलेक्ट्रॉन युग्मों की संख्या और उन परमाणुओं की रासायनिक प्रकृति पर निर्भर करता है जिनसे वे संबंधित हैं। इसका अर्थ है कि प्रभाव योज्य हैं और प्रतिचुंबकीय योगदानों की एक तालिका या पास्कल के स्थिरांक एक साथ रखे जा सकते हैं।^[6]^[7]^[8] अनुचुम्बकीय यौगिकों के साथ प्रेक्षित संवेदनशीलता को इसमें तथाकथित प्रतिचुंबकीय सुधार जोड़कर समायोजित किया जा सकता है, जो तालिका से मानो के साथ गणना की गई प्रतिचुंबकीय संवेदनशीलता है।^[9]

पैरामैग्नेटिज्म

तंत्र और तापमान निर्भरता

एक धातु आयन जिसमें एक एकल अयुग्मित इलेक्ट्रॉन होता है, जैसे Cu²⁺ एक समन्वय परिसर में अनुचुंबकत्व के तंत्र का सबसे सरल उदाहरण प्रदान करता है। अलग-अलग धातु आयनों को लिगेंड द्वारा दूर रखा जाता है, जिससे उनके बीच कोई चुंबकीय संपर्क न हो प्रणाली को चुंबकीय रूप से पतला कहा जाता है। परमाणुओं के चुंबकीय द्विध्रुव यादृच्छिक दिशाओं में इंगित करते हैं। जब एक चुंबकीय क्षेत्र प्रयुक्त किया जाता है, तो प्रथम-क्रम ज़िमान विभाजन होता है। स्पिन के साथ क्षेत्र में गठबंधन वाले परमाणु गैर-गठबंधन स्पिन वाले परमाणुओं से थोड़ा अधिक संख्या में हैं। पहले क्रम के ज़िमान प्रभाव में दो अवस्थाओ के बीच ऊर्जा अंतर प्रयुक्त क्षेत्र की ताकत के समानुपाती होता है। ΔE के रूप में ऊर्जा अंतर को नकारते हुए, बोल्टज़मान वितरण दो आबादी का अनुपात $e^{-\Delta E/kT}$ के रूप में देता है जहां k बोल्ट्जमैन स्थिरांक है और T केल्विन में तापमान है। अधिक्तर स्थितियों में ΔE kT से बहुत छोटा है और घातीय को 1 - ΔE/kT के रूप में विस्तारित किया जा सकता है। यह इस अभिव्यक्ति में 1/T की उपस्थिति से अनुसरण करता है कि संवेदनशीलता तापमान के व्युत्क्रमानुपाती होती है।^[10]

\chi ={C \over T}

इसे क्यूरी नियम के रूप में जाना जाता है और आनुपातिकता स्थिरांक सी, क्यूरी स्थिरांक के रूप में जाना जाता है, जिसका मान मोलर संवेदनशीलता के लिए गणना की जाती है^[11]

C={\frac {Ng^{2}S(S+1)\mu _{B}^{2}}{3k}}

जहाँ N अवोगाद्रो स्थिरांक है, g लैंडे g-कारक है, और μ_B है बोहर चुंबक है। इस उपचार में यह माना गया है कि इलेक्ट्रॉनिक जमीनी स्थिति पतित नहीं है, कि चुंबकीय संवेदनशीलता केवल इलेक्ट्रॉन स्पिन के कारण होती है और केवल जमीनी अवस्था ऊष्मीय रूप से आबाद होती है।

जबकि कुछ पदार्थ क्यूरी नियम का पालन करते हैं, अन्य क्यूरी-वीस नियम का पालन करते हैं।

\chi ={\frac {C}{T-T_{c}}}

T_cक्यूरी तापमान है। क्यूरी-वीस नियम तभी प्रयुक्त होगा जब तापमान क्यूरी तापमान से अधिक ऊपर हो। क्यूरी तापमान से कम तापमान पर पदार्थ लौह-चुंबकीय हो सकता है। भारी संक्रमण तत्वों के साथ अधिक जटिल व्यवहार देखा जाता है।

प्रभावी चुंबकीय क्षण

जब क्यूरी नियम का पालन किया जाता है, मोलर संवेदनशीलता और तापमान का उत्पाद स्थिर होता है। प्रभावी चुंबकीय क्षण, μ_eff तब परिभाषित किया जाता है^[12] जैसा

\mu _{\text{eff}}=\mathrm {constant} {\sqrt {T\chi }}

जहाँ C की सीजीएस इकाइयाँ cm³ mol⁻¹ K μ_eff है

\mu _{\text{eff}}={\sqrt {3k \over N\mu _{B}^{2}}}{\sqrt {T\chi }}\approx 2.82787{\sqrt {T\chi }}

जहाँ C का SI मात्रक m³ mol⁻¹ K μ_eff है

\mu _{\text{eff}}={\sqrt {3k \over N\mu _{0}\mu _{B}^{2}}}{\sqrt {T\chi }}\approx 797.727{\sqrt {T\chi }}

मात्रा μ_eff प्रभावी रूप से आयाम रहित है किंतु अधिकांशतः बोह्र मैग्नेटॉन (μ_B) की इकाइयों के रूप में कहा जाता है।^[12]

क्यूरी नियम का पालन करने वाले पदार्थों के लिए प्रभावी चुंबकीय क्षण तापमान से स्वतंत्र होता है। अन्य पदार्थों के लिए μ_eff तापमान पर निर्भर है किंतु यदि क्यूरी-वीस नियम प्रयुक्त होता है और क्यूरी तापमान कम होता है तो निर्भरता कम होती है।

तापमान स्वतंत्र अनुचुंबकत्व

जिन यौगिकों के प्रतिचुंबकीय होने की उम्मीद की जाती है वे इस प्रकार के अशक्त अनुचुंबकत्व को प्रदर्शित कर सकते हैं। यह दूसरे क्रम के ज़िमान प्रभाव से उत्पन्न होता है जिसमें अतिरिक्त विभाजन क्षेत्र की ताकत के वर्ग के अनुपात में होता है। यह निरीक्षण करना कठिन है क्योंकि यौगिक अनिवार्य रूप से चुंबकीय क्षेत्र के साथ प्रतिचुंबकीय अर्थ में भी संपर्क करता है। फिर भी परमैंगनेट आयन के लिए डेटा उपलब्ध हैं।^[13] भारी तत्वों के यौगिकों जैसे यूरेनिल यौगिकों में निरीक्षण करना आसान है।

एक्सचेंज इंटरैक्शन

कॉपर (II) एसीटेट डाइहाइड्रेट^[14]

2 आयामों में फेरिमैग्नेटिक ऑर्डरिंग

2 आयामों में एंटीफेरोमैग्नेटिक ऑर्डरिंग

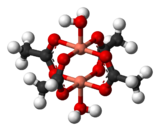
एक्सचेंज इंटरैक्शन तब होता है जब पदार्थ चुंबकीय रूप से पतला नहीं होता है और अलग-अलग चुंबकीय केंद्रों के बीच परस्पर क्रिया होती है। एक्सचेंज इंटरैक्शन के परिणाम को प्रदर्शित करने वाली सबसे सरल प्रणालियों में से एक क्रिस्टलीय कॉपर (II) एसीटेट Cu₂(OAc)₄(H₂O)₂. है जैसा कि सूत्र इंगित करता है, इसमें दो कॉपर (II) आयन होते हैं। Cu²⁺ आयनों को चार एसीटेट लिगेंड द्वारा एक साथ रखा जाता है, जिनमें से प्रत्येक तांबे के आयनों को बांधता है। प्रत्येक Cu²⁺ आयन में d⁹ है इलेक्ट्रॉनिक कॉन्फ़िगरेशन और इसलिए एक अयुग्मित इलेक्ट्रॉन होना चाहिए। यदि तांबे के आयनों के बीच एक सहसंयोजक बंधन होता तो इलेक्ट्रॉन जोड़े जाते और यौगिक प्रतिचुंबकीय होता। इसके अतिरिक्त एक एक्सचेंज इंटरेक्शन होता है जिसमें अयुग्मित इलेक्ट्रॉनों के स्पिन आंशिक रूप से एक-दूसरे से जुड़ जाते हैं। वास्तव में दो अवस्था बनते हैं एक समानांतर घुमावों के साथ और दूसरा विपरीत घुमावों के साथ दोनों अवस्थाओ के बीच ऊर्जा अंतर इतना कम है कि उनकी आबादी तापमान के साथ अधिक भिन्न होती है। परिणामस्वरूप सिग्मॉइड कार्य पैटर्न में चुंबकीय क्षण तापमान के साथ बदलता रहता है। स्पिन के विरोध वाले अवस्था में कम ऊर्जा होती है, इसलिए इस स्थिति में परस्पर क्रिया को एंटीफेरोमैग्नेटिक के रूप में वर्गीकृत किया जा सकता है।^[14] ऐसा माना जाता है कि यह सुपर एक्सचेंज का एक उदाहरण है जो एसीटेट लिगैंड्स के ऑक्सीजन और कार्बन परमाणुओं द्वारा मध्यस्थता करता है।^[15] अन्य डिमर और क्लस्टर विनिमय व्यवहार प्रदर्शित करते हैं।^[16]

एक्सचेंज इंटरैक्शन एक आयाम में अनंत श्रृंखलाओं दो आयामों में विमानों या तीन आयामों में पूरे क्रिस्टल पर कार्य कर सकता है। ये लंबी दूरी के चुंबकीय क्रम के उदाहरण हैं। वे फेरोमैग्नेटिज्म, एंटीफेरोमैग्नेटिज्म या फेरिमैग्नेटिज्म को जन्म देते हैं, जो कि अलग-अलग स्पिन की प्रकृति और सापेक्ष झुकाव पर निर्भर करता है।^[17]

क्यूरी तापमान से नीचे के तापमान पर यौगिक फेरोमैग्नेटिज्म के रूप में लंबी दूरी की चुंबकीय व्यवस्था प्रदर्शित करते हैं। एक अन्य महत्वपूर्ण तापमान नील तापमान है, जिसके नीचे एंटीफेरोमैग्नेटिज्म होता है। निकल क्लोराइड का हेक्साहाइड्रेट, NiCl₂·6H₂O, का तापमान 8.3 K है। इस तापमान पर संवेदनशीलता अधिकतम होती है। नील तापमान के नीचे संवेदनशीलता कम हो जाती है और पदार्थ एंटीफेरोमैग्नेटिक हो जाता है।^[18]

संक्रमण धातु आयनों के परिसरों

एक या एक से अधिक अयुग्मित इलेक्ट्रॉनों के साथ एक संक्रमण धातु आयन वाले यौगिक के लिए प्रभावी चुंबकीय क्षण अयुग्मित इलेक्ट्रॉनों के कुल कक्षीय और स्पिन कोणीय गति पर निर्भर करता है, ${\vec {L}}$ और ${\vec {S}}$ , क्रमश इस संदर्भ में कुल का अर्थ सदिश योग है। इस सन्निकटन में कि धातु आयनों की इलेक्ट्रॉनिक अवस्थाएँ कोणीय संवेग युग्मन रसेल-सॉन्डर्स युग्मन द्वारा निर्धारित की जाती हैं और वह स्पिन-ऑर्बिट युग्मन नगण्य है चुंबकीय क्षण द्वारा दिया जाता है^[19]

\mu _{\text{eff}}={\sqrt {{\vec {L}}({\vec {L}}+1)+4{\vec {S}}({\vec {S}}+1)}}\mu _{B}

स्पिन-केवल सूत्र

कक्षीय कोणीय संवेग तब उत्पन्न होता है जब कक्षकों के पतित समुच्चय के कक्षक में एक इलेक्ट्रॉन को घूर्णन द्वारा समुच्चय के किसी अन्य कक्षक में ले जाया जाता है। कम समरूपता वाले परिसरों में कुछ घूर्णन संभव नहीं होते हैं। उस स्थिति में कक्षीय कोणीय संवेग को "बुझाना" कहा जाता है और ${\vec {L}}$ अपेक्षा से छोटा होता है (आंशिक शमन), या शून्य (पूर्ण शमन)। निम्नलिखित स्थिति में पूर्ण शमन है। ध्यान दें कि d_x²–y² or d_z² कक्षकों के पतित युग्म में एक इलेक्ट्रॉन समरूपता के कारण अन्य कक्षकों में नहीं घूम सकता है।^[20]

बुझती कक्षीय कोणीय गति

dⁿ

ऑक्टाहेड्रल

टेट्राहेड्रल

उच्च-स्पिन

कम-स्पिन

d¹

e¹

d²

e²

d³

t_2g³

d⁴

t_2g³e_g¹

d⁵

t_2g³e_g²

d⁶

t_2g⁶

e³t₂³

d⁷

t_2g⁶e_g¹

e⁴t₂³

d⁸

t_2g⁶e_g²

d⁹

t_2g⁶e_g³

विख्यात: t_2g, t₂ = (d_xy, d_xz, d_yz). e_g, e = (d_x²–y², d_z²).

जब कक्षीय कोणीय संवेग पूरी तरह से बुझ जाता है, ${\vec {L}}=0$ और अनुचुंबकत्व को अकेले इलेक्ट्रॉन स्पिन के लिए उत्तरदाई ठहराया जा सकता है। कुल स्पिन कोणीय संवेग केवल अयुग्मित इलेक्ट्रॉनों की संख्या का आधा है और स्पिन-केवल सूत्र का परिणाम है।

\mu _{\text{eff}}={\sqrt {n(n+2)}}\mu _{B}

जहाँ n अयुग्मित इलेक्ट्रॉनों की संख्या है। स्पिन-केवल सूत्र पहली-पंक्ति संक्रमण धातुओं के उच्च-स्पिन परिसरों के लिए एक अच्छा पहला सन्निकटन है।^[21]

अयोन	की संख्या अयुगल इलेक्ट्रॉनों	सिर्फ घुमाव पल /μB	प्रेक्षित पल /μB
Ti³⁺	1	1.73	1.73
V⁴⁺	1	1.73	1.68–1.78
Cu²⁺	1	1.73	1.70–2.20
V³⁺	2	2.83	2.75–2.85
Ni²⁺	2	2.83	2.8–3.5
V²⁺	3	3.87	3.80–3.90
Cr³⁺	3	3.87	3.70–3.90
Co²⁺	3	3.87	4.3–5.0
Mn⁴⁺	3	3.87	3.80–4.0
Cr²⁺	4	4.90	4.75–4.90
Fe²⁺	4	4.90	5.1–5.7
Mn²⁺	5	5.92	5.65–6.10
Fe³⁺	5	5.92	5.7–6.0

स्पिन-केवल सूत्र से छोटे विचलन कक्षीय कोणीय गति या स्पिन-ऑर्बिट युग्मन की उपेक्षा के परिणामस्वरूप हो सकते हैं। उदाहरण के लिए टेट्राहेड्रल d³, d⁴, d⁸ और d⁹ कॉम्प्लेक्स एक ही आयन के ऑक्टाहेड्रल कॉम्प्लेक्स की तुलना में स्पिन-केवल सूत्र से बड़े विचलन दिखाते हैं, क्योंकि टेट्राहेड्रल स्थिति में कक्षीय योगदान की शमन कम प्रभावी होती है।^[22]

कम स्पिन कॉम्प्लेक्स

ऑक्टाहेड्रल कम स्पिन डी के लिए क्रिस्टल फील्ड आरेख⁵

ऑक्टाहेड्रल उच्च -स्पिन के लिए क्रिस्टल फील्ड डायग्राम d⁵

क्रिस्टल क्षेत्र सिद्धांत के अनुसार एक ऑक्टाहेडल परिसर में एक संक्रमण धातु आयन के डी ऑर्बिटल्स एक क्रिस्टल क्षेत्र में दो समूहों में विभाजित होते हैं। यदि विभाजन इतना बड़ा है कि इलेक्ट्रॉनों को एक ही कक्षीय में विपरीत स्पिन के साथ रखने के लिए आवश्यक ऊर्जा को दूर करने के लिए एक कम-स्पिन परिसर का परिणाम होगा।

उच्च और निम्न-स्पिन अष्टफलकीय परिसर
d-गणना	अयुग्मित इलेक्ट्रॉनों की संख्या		उदाहरण
d-गणना	उच्च घुमाव	कम घुमाव	उदाहरण
d⁴	4	2	Cr²⁺, Mn³⁺
d⁵	5	1	Mn²⁺, Fe³⁺
d⁶	4	0	Fe²⁺, Co³⁺
d⁷	3	1	Co²⁺

एक अयुगलित इलेक्ट्रॉन के साथ μ_eff मान 1.8 से 2.5 μ_B तक होता है और दो अयुग्मित इलेक्ट्रॉनों के साथ सीमा 3.18 से 3.3 μ_B होती है। ध्यान दें कि Fe²⁺ और Co³⁺ के कम स्पिन कॉम्प्लेक्स डायनामैग्नेटिक हैं। संकुलों का एक अन्य समूह जो प्रतिचुंबकीय है, d8 आयनों जैसे Ni²⁺ और Rh⁺ और Au³⁺ के वर्ग-तलीय संकुल हैं।

स्पिन क्रॉस-ओवर

जब उच्च -स्पिन और कम-स्पिन अवस्थाओं के बीच ऊर्जा का अंतर kT (k बोल्ट्जमैन स्थिरांक और T तापमान है) के समान होता है, तो स्पिन अवस्थाओं के बीच एक संतुलन स्थापित होता है, जिसमें "इलेक्ट्रॉनिक आइसोमर्स" कहा जाता है। ट्रिस-डाइथियोकार्बामेटो आयरन (III), Fe(S₂CNR₂)₃ एक अच्छी तरह से प्रलेखित उदाहरण है। प्रभावी क्षण 80 K पर 2.25 μ_B के सामान्य d⁵ कम स्पिन मान से 300 K से ऊपर 4 μ_B से अधिक भिन्न होता है।^[23]

दूसरी और तीसरी पंक्ति संक्रमण धातु

ऊपर चर्चा की गई संक्रमण धातुओं की तुलना में भारी संक्रमण धातुओं के परिसरों के लिए क्रिस्टल क्षेत्र विभाजन बड़ा है। इसका एक परिणाम यह है कि कम-स्पिन कॉम्प्लेक्स बहुत अधिक सामान्य हैं। स्पिन-ऑर्बिट युग्मन स्थिरांक, ζ, भी बड़े होते हैं और प्राथमिक उपचारों में भी इन्हें अनदेखा नहीं किया जा सकता है। डेटा की एक विस्तृत तालिका के साथ, चुंबकीय व्यवहार को संक्षेप में प्रस्तुत किया गया है।^[24]

d-गणना	kT/ζ=0.1 μ_eff	kT/ζ=0 μ_eff	बड़े स्पिन-ऑर्बिट युग्मन स्थिरांक के साथ सबंध, ζnd
d¹	0.63	0	^{μ_eff T1/2 के साथ बदलता रहता है}
d²	1.55	1.22	μ_eff लगभग T के साथ बदलता रहता है
d³	3.88	3.88	तापमान से स्वतंत्र
d⁴	2.64	0	μ_eff T^1/2 के साथ बदलता रहता है
d⁵	1.95	1.73	μ_eff लगभग T के साथ बदलता रहता है

लैंथेनाइड्स और एक्टिनाइड्स

रसेल-सॉन्डर्स युग्मन एलएस कपलिंग, लैंथेनाइड आयनों पर प्रयुक्त होता है क्रिस्टल क्षेत्र प्रभावों को अनदेखा किया जा सकता है किंतु स्पिन-ऑर्बिट युग्मन नगण्य नहीं है। परिणाम स्वरुप स्पिन और कक्षीय कोणीय संवेग को संयोजित करना पड़ता है

{\vec {L}}=\sum _{i}{\vec {l}}_{i}

{\vec {S}}=\sum _{i}{\vec {s}}_{i}

{\vec {J}}={\vec {L}}+{\vec {S}}

और परिकलित चुंबकीय क्षण द्वारा दिया जाता है

\mu _{\text{eff}}=g{\sqrt {{\vec {J}}({\vec {J}}+1)}};g={3 \over 2}+{\frac {{\vec {S}}({\vec {S}}+1)-{\vec {L}}({\vec {L}}+1)}{2{\vec {J}}({\vec {J}}+1)}}

त्रिकोणीय लैंथेनाइड यौगिकों के चुंबकीय गुण^[25]
लैंथेनाइड	Ce	Pr	Nd	Pm	Sm	Eu	Gd	Tb	Dy	Ho	Er	Tm	Yb
अयुग्मित इलेक्ट्रॉनों की संख्या	1	2	3	4	5	6	7	6	5	4	3	2	1
परिकलित क्षण /μ_B	2.54	3.58	3.62	2.68	0.85	0	7.94	9.72	10.65	10.6	9.58	7.56	4.54
प्रेक्षित क्षण /μ_B	2.3–2.5	3.4–3.6	3.5–3.6		1.4–1.7	3.3–3.5	7.9–8.0	9.5–9.8	10.4–10.6	10.4–10.7	9.4–9.6	7.1–7.5	4.3–4.9

एक्टिनाइड्स में स्पिन-ऑर्बिट युग्मन शसक्त होता है और युग्मन जे जे युग्मन के अनुमानित होता है।

{\vec {J}}=\sum _{i}{\vec {j}}_{i}=\sum _{i}({\vec {l}}_{i}+{\vec {s}}_{i})

इसका अर्थ है कि प्रभावी पल की गणना करना कठिन है। उदाहरण के लिए, यूरेनियम (IV), f², परिसर में [UCl₆]²⁻ का मापित प्रभावी आघूर्ण 2.2 μ_B है जिसमें तापमान-स्वतंत्र पैरामैग्नेटिज्म का योगदान सम्मिलित है।^[26]

मुख्य समूह तत्व और कार्बनिक यौगिक

CH का नकली इलेक्ट्रॉन पैरामैग्नेटिक अनुनाद स्पेक्ट्रम₃• मौलिक

MSTL स्पिन-लेबल

मुख्य वर्ग के तत्वों के बहुत कम यौगिक अनुचुम्बकीय होते हैं। उल्लेखनीय उदाहरणों में सम्मिलित हैं: ऑक्सीजन, O₂ नाइट्रिक ऑक्साइड, नहीं; नाइट्रोजन डाइऑक्साइड, NO₂ और क्लोरिन डाइऑक्साइड , ClO₂. कार्बनिक रसायन विज्ञान में, अयुग्मित इलेक्ट्रॉन वाले यौगिकों को मुक्त कण कहा जाता है। मुक्त कण कुछ अपवादों के साथ अल्पकालिक होते हैं क्योंकि एक मुक्त कण दूसरे के साथ तेजी से प्रतिक्रिया करेगा इसलिए उनके चुंबकीय गुणों का अध्ययन करना कठिन है। चूँकि यदि कम तापमान पर एक ठोस आव्यूह में एक तनु घोल में रेडिकल एक दूसरे से अच्छी तरह से अलग हो जाते हैं, तो उनका अध्ययन इलेक्ट्रॉन पैरामैग्नेटिक रेजोनेंस (ईपीआर ) द्वारा किया जा सकता है। ऐसे मूलक विकिरण द्वारा उत्पन्न होते हैं। व्यापक ईपीआर अध्ययनों ने मुक्त कणों में इलेक्ट्रॉन निरूपण के बारे में बहुत कुछ प्रकट किया है। CH₃का सिम्युलेटेड स्पेक्ट्रम• रैडिकल 3 समान हाइड्रोजन नाभिकों के साथ इलेक्ट्रॉन की परस्पर क्रिया के कारण अति सूक्ष्म विभाजन दिखाता है, जिनमें से प्रत्येक में 1/2 का स्पिन होता है।^[27]^[28]

स्पिन लेबल लंबे समय तक रहने वाले मुक्त कण होते हैं जिन्हें कार्बनिक अणुओं में डाला जा सकता है जिससे ईपीआर द्वारा उनका अध्ययन किया जा सकता है ।^[29] उदाहरण के लिए, साइट-निर्देशित स्पिन लेबलिंग में नाइट्रॉक्साइड एमटीएसएल, टेट्रा मिथाइल पाइपरिडीन ऑक्साइड, समय का एक कार्यात्मक व्युत्पन्न है।

अनुप्रयोग

गैडोलीनियम आयन, Gd³⁺, में f⁷ इलेक्ट्रॉनिक कॉन्फ़िगरेशन, सभी स्पिन समानांतर के साथ। Gd³⁺,के यौगिक आयन एमआरआई स्कैन के लिए एमआरआई कंट्रास्ट एजेंट के रूप में उपयोग करने के लिए सबसे उपयुक्त हैं।^[30] गैडोलीनियम यौगिकों के चुंबकीय क्षण किसी भी संक्रमण धातु आयन की तुलना में बड़े होते हैं। गैडोलिनियम है

अन्य लैंथेनाइड आयनों के लिए पसंद किया जाता है जिनमें से कुछ के पास बड़े प्रभावी क्षण होते हैं इसकी वजह यह है कि इसका ऊर्जा स्तर को कम करना नॉन-डीजेनरेट इलेक्ट्रॉनिक ग्राउंड स्टेट है।^[31]

कई वर्षों तक आक्सीहीमोग्लोबिन की प्रकृति, Hb-O₂, अत्यधिक विवादास्पद था। यह प्रयोगात्मक रूप से प्रतिचुंबकीय होने के लिए पाया गया था। डीऑक्सी-हीमोग्लोबिन को सामान्यतः +2 ऑक्सीकरण अवस्था में लोहे का एक जटिल माना जाता है, जो कि d⁶ है 4.9 μ_B के स्पिन-केवल मान के पास उच्च-स्पिन चुंबकीय आघूर्ण वाला प्रणाली यह प्रस्तावित किया गया था कि लोहे का ऑक्सीकरण होता है और ऑक्सीजन सुपरऑक्साइड में कम हो जाती है।

Fe(II)Hb (high-स्पिन) + O₂ ⇌ [Fe(III)Hb]O₂⁻

Fe³⁺ औरO₂⁻ से इलेक्ट्रॉनों की जोड़ी तब एक विनिमय तंत्र के माध्यम से होने का प्रस्ताव था। अब यह दिखाया गया है कि वास्तव में लोहा (II) उच्च -स्पिन से कम स्पिन में तब बदलता है जब एक ऑक्सीजन अणु लोहे को इलेक्ट्रॉनों की एक जोड़ी दान करता है। जबकि डीऑक्सी-हीमोग्लोबिन में लोहे का परमाणु हीम के तल के ऊपर स्थित होता है, कम-स्पिन परिसर में प्रभावी आयनिक त्रिज्या कम हो जाती है और लौह परमाणु हीम तल में स्थित होता है।^[32] :

Fe(II)Hb + O₂ ⇌ [Fe(II)Hb]O₂ (low-स्पिन)

कृत्रिम ऑक्सीजन वाहक खोजने के लिए अनुसंधान पर इस जानकारी का महत्वपूर्ण बेअरिंग है।

गैलियम (II) के यौगिक अभी हाल तक अज्ञात थे। चूंकि गैलियम की परमाणु संख्या एक विषम संख्या (31) है, Ga²⁺ में एक अयुग्मित इलेक्ट्रॉन होना चाहिए। यह मान लिया गया था कि यह एक मुक्त मूलक के रूप में कार्य करेगा और बहुत कम जीवनकाल होगा। गा (द्वितीय) यौगिकों का अस्तित्व तथाकथित निष्क्रिय-जोड़ी प्रभाव का हिस्सा था। जब आनुभविक सूत्र जैसे कि [GaCl₃]⁻ संश्लेषित किए गए थे, वे प्रतिचुंबकीय पाए गए थे। यह एक गा-गा बंधन और एक द्विमेरिक सूत्र, [Ga₂Cl₆]²⁻ के गठन को निहित करता है।.^[33]

यह भी देखें

संदर्भ

↑ Earnshaw, p. 89
↑ Magnetic Susceptibility Balances
↑ O'Connor, C.J. (1982). Lippard, S.J. (ed.). चुंबकीय संवेदनशीलता माप. Progress in Inorganic Chemistry. Vol. 29. Wiley. p. 203. ISBN 978-0-470-16680-2.
↑ Evans, D.F. (1959). "परमाणु चुंबकीय अनुनाद द्वारा समाधान में पदार्थों की अनुचुंबकीय संवेदनशीलता का निर्धारण". J. Chem. Soc.: 2003–2005. doi:10.1039/JR9590002003.
↑ Orchard, p. 15. Earnshshaw, p. 97
↑ Figgis&Lewis, p. 403
↑ Carlin, p. 3
↑ Bain, Gordon A.; Berry , John F. (2008). "प्रतिचुंबकीय सुधार और पास्कल के स्थिरांक". J. Chem. Educ. 85 (4): 532. Bibcode:2008JChEd..85..532B. doi:10.1021/ed085p532.
↑ Figgis&Lewis, p. 417
↑ Figgis&Lewis, p. 419
↑ Orchard, p. 48
↑ ^12.0 ^12.1 Hoppe, J.I. (1972). "प्रभावी चुंबकीय क्षण". J. Chem. Educ. 49 (7): 505. Bibcode:1972JChEd..49..505H. doi:10.1021/ed049p505.
↑ Orchard, p. 53
↑ ^14.0 ^14.1 Lawrence Que (March 2000). Physical methods in bioinorganic chemistry: spectroscopy and magnetism. University Science Books. pp. 345–348. ISBN 978-1-891389-02-3. Retrieved 22 February 2011.
↑ Figgis&Lewis, p. 435. Orchard, p. 67
↑ Carlin, sections 5.5–5.7
↑ Carlin, chapters 6 and 7, pp. 112–225
↑ Carin, p. 264
↑ Figgis&Lewis, p. 420
↑ Figgis&Lewis, pp. 424, 432
↑ Figgis&Lewis, p. 406
↑ Figgis&Lewis, Section 3, "Orbital contribution"
↑ Orchard, p. 125. Carlin, p. 270
↑ Figgis&Lewis, pp. 443–451
↑ Greenwood&Earnshaw p. 1243
↑ Orchard, p. 106
↑ Weil, John A.; Bolton, James R.; Wertz, John E. (1994). Electron paramagnetic resonance : elementary theory and practical applications. Wiley. ISBN 0-471-57234-9.
↑ Atkins, P. W.; Symons, M. C. R. (1967). The structure of inorganic radicals; an application of electron spin resonance to the study of molecular structure. Elsevier.
↑ Berliner, L.J. (1976). Spin labeling : theory and applications I. Academic Press. ISBN 0-12-092350-5.Berliner, L.J. (1979). Spin labeling II : theory and applications. Academic Press. ISBN 0-12-092352-1.
↑ Krause, W. (2002). Contrast Agents I: Magnetic Resonance Imaging: Pt. 1. Springer. ISBN 3540422471.
↑ Caravan, Peter; Ellison, Jeffrey J.; McMurry, Thomas J. ; Lauffer, Randall B., Jeffrey J.; McMurry, Thomas J.; Lauffer, Randall B. (1999). "Gadolinium(III) Chelates as MRI Contrast Agents: Structure, Dynamics, and Applications". Chem. Rev. 99 (9): 2293–2352. doi:10.1021/cr980440x. PMID 11749483.{{cite journal}}: CS1 maint: multiple names: authors list (link)
↑ Greenwood&Earnshaw, pp. 1099–1011
↑ Greenwood&Earnshaw, p. 240

ग्रन्थसूची

Carlin, R.L. (1986). Magnetochemistry. Springer. ISBN 978-3-540-15816-5.
Earnshaw, Alan (1968). Introduction to Magnetochemistry. Academic Press.
Figgis, B.N.; Lewis, J. (1960). "The Magnetochemistry of Complex Compounds". In Lewis. J. and Wilkins. R.G. (ed.). Modern Coordination Chemistry. New York: Wiley.
Greenwood, Norman N.; Earnshaw, Alan (1997). Chemistry of the Elements (2nd ed.). Butterworth-Heinemann. ISBN 978-0-08-037941-8.
Orchard, A.F. (2003). Magnetochemistry. Oxford Chemistry Primers. Oxford University Press. ISBN 0-19-879278-6.
Selwood, P.W. (1943). Magnetochemistry. Interscience Publishers Inc.
Vulfson, Sergey (1998). Molecular Magnetochemistry. Taylor & Francis. ISBN 90-5699-535-9.

बाहरी संबंध

[1] Earnshaw, p. 89

[2] Magnetic Susceptibility Balances

[3] O'Connor, C.J. (1982). Lippard, S.J. (ed.). चुंबकीय संवेदनशीलता माप. Progress in Inorganic Chemistry. Vol. 29. Wiley. p. 203. ISBN 978-0-470-16680-2.

[4] Evans, D.F. (1959). "परमाणु चुंबकीय अनुनाद द्वारा समाधान में पदार्थों की अनुचुंबकीय संवेदनशीलता का निर्धारण". J. Chem. Soc.: 2003–2005. doi:10.1039/JR9590002003.

[5] Orchard, p. 15. Earnshshaw, p. 97

[6] Figgis&Lewis, p. 403

[7] Carlin, p. 3

[8] Bain, Gordon A.; Berry , John F. (2008). "प्रतिचुंबकीय सुधार और पास्कल के स्थिरांक". J. Chem. Educ. 85 (4): 532. Bibcode:2008JChEd..85..532B. doi:10.1021/ed085p532.

[9] Figgis&Lewis, p. 417

[10] Figgis&Lewis, p. 419

[11] Orchard, p. 48

[HoppeJI-12] 12.0 ^12.1 Hoppe, J.I. (1972). "प्रभावी चुंबकीय क्षण". J. Chem. Educ. 49 (7): 505. Bibcode:1972JChEd..49..505H. doi:10.1021/ed049p505.

[13] Orchard, p. 53

[b1-14] 14.0 ^14.1 Lawrence Que (March 2000). Physical methods in bioinorganic chemistry: spectroscopy and magnetism. University Science Books. pp. 345–348. ISBN 978-1-891389-02-3. Retrieved 22 February 2011.

[15] Figgis&Lewis, p. 435. Orchard, p. 67

[16] Carlin, sections 5.5–5.7

[17] Carlin, chapters 6 and 7, pp. 112–225

[18] Carin, p. 264

[19] Figgis&Lewis, p. 420

[20] Figgis&Lewis, pp. 424, 432

[21] Figgis&Lewis, p. 406

[22] Figgis&Lewis, Section 3, "Orbital contribution"

[23] Orchard, p. 125. Carlin, p. 270

[24] Figgis&Lewis, pp. 443–451

[25] Greenwood&Earnshaw p. 1243

[26] Orchard, p. 106

[27] Weil, John A.; Bolton, James R.; Wertz, John E. (1994). Electron paramagnetic resonance : elementary theory and practical applications. Wiley. ISBN 0-471-57234-9.

[28] Atkins, P. W.; Symons, M. C. R. (1967). The structure of inorganic radicals; an application of electron spin resonance to the study of molecular structure. Elsevier.

[29] Berliner, L.J. (1976). Spin labeling : theory and applications I. Academic Press. ISBN 0-12-092350-5.Berliner, L.J. (1979). Spin labeling II : theory and applications. Academic Press. ISBN 0-12-092352-1.

[30] Krause, W. (2002). Contrast Agents I: Magnetic Resonance Imaging: Pt. 1. Springer. ISBN 3540422471.

[31] Caravan, Peter; Ellison, Jeffrey J.; McMurry, Thomas J. ; Lauffer, Randall B., Jeffrey J.; McMurry, Thomas J.; Lauffer, Randall B. (1999). "Gadolinium(III) Chelates as MRI Contrast Agents: Structure, Dynamics, and Applications". Chem. Rev. 99 (9): 2293–2352. doi:10.1021/cr980440x. PMID 11749483.{{cite journal}}: CS1 maint: multiple names: authors list (link)

[32] Greenwood&Earnshaw, pp. 1099–1011

[33] Greenwood&Earnshaw, p. 240

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

@@ Line 41: / Line 41: @@
 === तंत्र और तापमान निर्भरता ===
-[[File:Susceptibility.png|thumb|200px| तापमान के साथ चुंबकीय संवेदनशीलता की भिन्नता]]एक धातु आयन जिसमें एक एकल अयुग्मित इलेक्ट्रॉन होता है, जैसे Cu<sup>2+</sup> एक समन्वय परिसर में अनुचुंबकत्व के तंत्र का सबसे सरल उदाहरण प्रदान करता है। अलग-अलग धातु आयनों को लिगेंड द्वारा दूर रखा जाता है, जिससे उनके बीच कोई चुंबकीय संपर्क न हो प्रणाली को चुंबकीय रूप से पतला कहा जाता है। परमाणुओं के चुंबकीय द्विध्रुव यादृच्छिक दिशाओं में इंगित करते हैं। जब एक चुंबकीय क्षेत्र प्रयुक्त किया जाता है, तो प्रथम-क्रम [[Zeeman विभाजन|ज़िमान विभाजन]] होता है। स्पिन के साथ क्षेत्र में गठबंधन वाले परमाणु गैर-गठबंधन स्पिन वाले परमाणुओं से थोड़ा अधिक संख्या में हैं। पहले क्रम के ज़िमान प्रभाव में दो अवस्थाओ के बीच ऊर्जा अंतर प्रयुक्त क्षेत्र की ताकत के समानुपाती होता है। ΔE के रूप में ऊर्जा अंतर को नकारते हुए, बोल्टज़मान वितरण दो आबादी का अनुपात <math>e^{-\Delta E/kT}</math> के रूप में देता है जहां k [[बोल्ट्जमैन स्थिरांक]] है और T [[केल्विन]] में तापमान है। अधिक्तर स्थितियों में ΔE kT से बहुत छोटा है और घातीय को 1 - ΔE/kT के रूप में विस्तारित किया जा सकता है। यह इस अभिव्यक्ति में 1/T की उपस्थिति से अनुसरण करता है कि संवेदनशीलता तापमान के व्युत्क्रमानुपाती होती है।<ref>Figgis&Lewis, p. 419</ref>
+एक धातु आयन जिसमें एक एकल अयुग्मित इलेक्ट्रॉन होता है, जैसे Cu<sup>2+</sup> एक समन्वय परिसर में अनुचुंबकत्व के तंत्र का सबसे सरल उदाहरण प्रदान करता है। अलग-अलग धातु आयनों को लिगेंड द्वारा दूर रखा जाता है, जिससे उनके बीच कोई चुंबकीय संपर्क न हो प्रणाली को चुंबकीय रूप से पतला कहा जाता है। परमाणुओं के चुंबकीय द्विध्रुव यादृच्छिक दिशाओं में इंगित करते हैं। जब एक चुंबकीय क्षेत्र प्रयुक्त किया जाता है, तो प्रथम-क्रम ज़िमान विभाजन होता है। स्पिन के साथ क्षेत्र में गठबंधन वाले परमाणु गैर-गठबंधन स्पिन वाले परमाणुओं से थोड़ा अधिक संख्या में हैं। पहले क्रम के ज़िमान प्रभाव में दो अवस्थाओ के बीच ऊर्जा अंतर प्रयुक्त क्षेत्र की ताकत के समानुपाती होता है। ΔE के रूप में ऊर्जा अंतर को नकारते हुए, बोल्टज़मान वितरण दो आबादी का अनुपात <math>e^{-\Delta E/kT}</math> के रूप में देता है जहां k [[बोल्ट्जमैन स्थिरांक]] है और T [[केल्विन]] में तापमान है। अधिक्तर स्थितियों में ΔE kT से बहुत छोटा है और घातीय को 1 - ΔE/kT के रूप में विस्तारित किया जा सकता है। यह इस अभिव्यक्ति में 1/T की उपस्थिति से अनुसरण करता है कि संवेदनशीलता तापमान के व्युत्क्रमानुपाती होती है।<ref>Figgis&Lewis, p. 419</ref>
 :<math>\chi={C \over T}</math>
 इसे [[क्यूरी कानून|क्यूरी नियम]] के रूप में जाना जाता है और आनुपातिकता स्थिरांक सी, क्यूरी स्थिरांक के रूप में जाना जाता है, जिसका मान मोलर संवेदनशीलता के लिए गणना की जाती है<ref>Orchard, p. 48</ref>
@@ Line 314: / Line 314: @@
 {{Branches of chemistry}}
 {{Authority control}}
-[[Category: चुंबकत्व]] [[Category: रसायन विज्ञान]]
+[[Category:Articles with hatnote templates targeting a nonexistent page]]
+[[Category:CS1 maint]]
-[[Category: Machine Translated Page]]
+[[Category:Collapse templates]]
 [[Category:Created On 26/05/2023]]
+[[Category:Lua-based templates]]
+[[Category:Machine Translated Page]]
+[[Category:Navigational boxes| ]]
+[[Category:Navigational boxes without horizontal lists]]
+[[Category:Pages with script errors]]
+[[Category:Sidebars with styles needing conversion]]
+[[Category:Template documentation pages|Documentation/doc]]
+[[Category:Templates Vigyan Ready]]
+[[Category:Templates generating microformats]]
+[[Category:Templates that add a tracking category]]
+[[Category:Templates that are not mobile friendly]]
+[[Category:Templates that generate short descriptions]]
+[[Category:Templates using TemplateData]]
+[[Category:Wikipedia metatemplates]]
+[[Category:चुंबकत्व]]
+[[Category:रसायन विज्ञान]]

v t e Branches of chemistry
Glossary of chemical formulae List of biomolecules List of inorganic compounds Periodic table
Analytical	Instrumental chemistry Electroanalytical methods Spectroscopy IR Raman UV-Vis NMR Mass spectrometry EI ICP MALDI Separation process Chromatography GC HPLC Crystallography Characterization Titration Wet chemistry Calorimetry Elemental analysis
Theoretical	Quantum chemistry Computational chemistry Mathematical chemistry Molecular modelling Molecular mechanics Molecular dynamics
Physical	Electrochemistry Spectroelectrochemistry Photoelectrochemistry Thermochemistry Chemical thermodynamics Surface science Interface and colloid science Micromeritics Cryochemistry Sonochemistry Structural chemistry Chemical physics Femtochemistry Chemical kinetics Spectroscopy Photochemistry Spin chemistry Microwave chemistry Equilibrium chemistry
Inorganic	Coordination chemistry Magnetochemistry Organometallic chemistry Organolanthanide chemistry Cluster chemistry Solid-state chemistry Ceramic chemistry
Organic	Stereochemistry Alkane stereochemistry Physical organic chemistry Organic reactions Organic synthesis Retrosynthetic analysis Enantioselective synthesis Total synthesis / Semisynthesis Fullerene chemistry Polymer chemistry Petrochemistry Dynamic covalent chemistry
Biological	Biochemistry Molecular biology Cell biology Chemical biology Bioorthogonal chemistry Medicinal chemistry Pharmacology Clinical chemistry Neurochemistry Bioorganic chemistry Bioorganometallic chemistry Bioinorganic chemistry Biophysical chemistry
Interdisciplinarity	Nuclear chemistry Radiochemistry Radiation chemistry Actinide chemistry Cosmochemistry / Astrochemistry / Stellar chemistry Geochemistry Biogeochemistry Photogeochemistry Environmental chemistry Atmospheric chemistry Ocean chemistry Clay chemistry Carbochemistry Food chemistry Carbohydrate chemistry Food physical chemistry Agricultural chemistry Soil chemistry Chemistry education Amateur chemistry General chemistry Clandestine chemistry Forensic chemistry Forensic toxicology Post-mortem chemistry Nanochemistry Supramolecular chemistry Chemical synthesis Green chemistry Click chemistry Combinatorial chemistry Biosynthesis Chemical engineering Materials science Metallurgy Ceramic engineering Polymer science
See also	History of chemistry Nobel Prize in Chemistry Timeline of chemistry of element discoveries "The central science" Chemical reaction Catalysis Chemical element Chemical compound Atom Molecule Ion Chemical substance Chemical bond Alchemy Quantum mechanics
Category Commons Portal WikiProject

Anonymous

Search

मैग्नेटोकेमिस्ट्री: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 13:23, 15 June 2023

Contents

चुंबकीय संवेदनशीलता

चुंबकीय व्यवहार के प्रकार

प्रतिचुम्बकत्व

पैरामैग्नेटिज्म

तंत्र और तापमान निर्भरता

प्रभावी चुंबकीय क्षण

तापमान स्वतंत्र अनुचुंबकत्व

एक्सचेंज इंटरैक्शन

संक्रमण धातु आयनों के परिसरों

स्पिन-केवल सूत्र

कम स्पिन कॉम्प्लेक्स

स्पिन क्रॉस-ओवर

दूसरी और तीसरी पंक्ति संक्रमण धातु

लैंथेनाइड्स और एक्टिनाइड्स

मुख्य समूह तत्व और कार्बनिक यौगिक

अनुप्रयोग

यह भी देखें

संदर्भ

ग्रन्थसूची

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

मैग्नेटोकेमिस्ट्री: Difference between revisions

Latest revision as of 13:23, 15 June 2023

चुंबकीय संवेदनशीलता

चुंबकीय व्यवहार के प्रकार

प्रतिचुम्बकत्व

पैरामैग्नेटिज्म

तंत्र और तापमान निर्भरता

प्रभावी चुंबकीय क्षण

तापमान स्वतंत्र अनुचुंबकत्व

एक्सचेंज इंटरैक्शन

संक्रमण धातु आयनों के परिसरों

स्पिन-केवल सूत्र

कम स्पिन कॉम्प्लेक्स

स्पिन क्रॉस-ओवर

दूसरी और तीसरी पंक्ति संक्रमण धातु

लैंथेनाइड्स और एक्टिनाइड्स

मुख्य समूह तत्व और कार्बनिक यौगिक

अनुप्रयोग

यह भी देखें

संदर्भ

ग्रन्थसूची

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Categories