संख्यान प्रणाली: Difference between revisions
mNo edit summary |
No edit summary |
||
| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
== परिचय == | == परिचय == | ||
प्राचीन भारतीयों ने काव्य के माध्यम से गणित को सरल और रोचक बनाया है। कविता के माध्यम से प्रमेय या सूत्रों को याद रखना आसान है और दिलचस्प भी। भारतीय गणित का विज्ञान कविता के कई अलङ्कार (''छन्द'') में रचा गया था। प्राचीन भारतीयों ने कविता में संख्याओं को व्यक्त करने का एक अनूठा तरीका खोजा। इस | प्राचीन भारतीयों ने काव्य के माध्यम से [[गणित का विकास|गणित]] को सरल और रोचक बनाया है। कविता के माध्यम से प्रमेय या सूत्रों को याद रखना आसान है और दिलचस्प भी। भारतीय गणित का विज्ञान कविता के कई अलङ्कार (''[[छन्द]]'') में रचा गया था। प्राचीन भारतीयों ने कविता में संख्याओं को व्यक्त करने का एक अनूठा तरीका खोजा। इस प्रकार से संख्या निरूपण की निम्नलिखित दो प्रणालियों का जन्म हुआ। | ||
# भूत-सांख्य प्रणाली: | # भूत-सांख्य प्रणाली: | ||
| Line 6: | Line 6: | ||
== भूत-सांख्य == | == भूत-सांख्य == | ||
भूत-सांख्य संख्याओं के प्रतिनिधित्व की एक प्रणाली है जहाँ अंकों को कुछ शब्दों द्वारा व्यक्त किया जाता है। इन शब्दों के अर्थ या तो स्वाभाविक रूप से या लोकप्रिय भारतीय साहित्य में प्रसिद्ध संदर्भों द्वारा संख्याओं को इंगित करते हैं। भूत-सांख्य पिंगल के छन्दसूत्र में पाया जाता है जिसकी रचना तीसरी शताब्दी ईसा पूर्व में हुई थी।<ref>''A Primer to Bhāratīya Gaṇitam , Bhāratīya-Gaṇita-Praveśa- Part-1''. Delhi: Samskrit Promotion Foundation. 2021. [[ISBN (identifier)|ISBN]] [[Special:BookSources/978-81-951757-2-7|<bdi>978-81-951757-2-7</bdi>]].</ref> | भूत-सांख्य संख्याओं के प्रतिनिधित्व की एक प्रणाली है जहाँ अंकों को कुछ शब्दों द्वारा व्यक्त किया जाता है। इन शब्दों के अर्थ या तो स्वाभाविक रूप से या लोकप्रिय भारतीय साहित्य में प्रसिद्ध संदर्भों द्वारा संख्याओं को इंगित करते हैं। भूत-सांख्य पिंगल के छन्दसूत्र में पाया जाता है, जिसकी रचना तीसरी शताब्दी ईसा पूर्व में हुई थी।<ref>भारतीय गणितम के लिए एक प्राइमर, भारतीय-गणित-प्रवेश- भाग -1, दिल्ली: संस्कृत प्रमोशन फाउंडेशन।(''A Primer to Bhāratīya Gaṇitam , Bhāratīya-Gaṇita-Praveśa- Part-1''. Delhi: Samskrit Promotion Foundation.) 2021. [[ISBN (identifier)|ISBN]] [[Special:BookSources/978-81-951757-2-7|<bdi>978-81-951757-2-7</bdi>]].</ref> | ||
=== संख्याओं का प्रतिनिधित्व === | === संख्याओं का प्रतिनिधित्व === | ||
संख्या '1' को ''चंद्र'' द्वारा दर्शाया गया है, जिसका अर्थ है चंद्रमा। चंद्रमा पृथ्वी का एकमात्र प्राकृतिक उपग्रह है जो अद्वितीय है। ऐसी किसी भी अनूठी वस्तु का उपयोग संख्या '1' को दर्शाने के लिए किया जा सकता है। अन्य शब्द जो लोकप्रिय रूप से "1" का प्रतिनिधित्व करते हैं, वे हैं ''भूमि'' (पृथ्वी), ''रूप'' (रूप), आदि। | |||
संख्या '2' किसी भी लोकप्रिय जोड़ी द्वारा दर्शाया जाता है, जैसे आंखें, हाथ, या '' | संख्या '2' किसी भी लोकप्रिय जोड़ी द्वारा दर्शाया जाता है, जैसे आंखें, हाथ, या ''अश्विनी जुड़वां'' । | ||
संख्या '0' को ''आकाश'' (अंतरिक्ष) शब्द द्वारा दर्शाया गया है जो शून्य के लिए खड़ा है। | संख्या '0' को ''आकाश'' (अंतरिक्ष) शब्द द्वारा दर्शाया गया है, जो शून्य के लिए खड़ा है। | ||
संख्या '3' को ''गुण'' शब्द द्वारा दर्शाया गया है (त्रिगुण - तीन गुण अर्थात् ''सत्त्व, रजस'' और ''तमस'' )। | संख्या '3' को ''गुण'' शब्द द्वारा दर्शाया गया है (त्रिगुण - तीन गुण अर्थात् ''सत्त्व, रजस'' और ''तमस'' )। | ||
| Line 223: | Line 223: | ||
2. [[नीलकंठ सोमसुत्वन]], [[माधव]] द्वारा अपने आर्यभटीय -भाषा में दिए गए एक श्लोक को उद्धृत करते हैं। | 2. [[नीलकंठ सोमसुत्वन]], [[माधव]] द्वारा अपने आर्यभटीय -भाषा में दिए गए एक श्लोक को उद्धृत करते हैं। | ||
यह श्लोक भूत-सांख्य प्रणाली में (π जो वृत्त के व्यास का अनुपात है) π का मान निम्नानुसार प्रदान करता है: | यह श्लोक भूत-सांख्य प्रणाली में (π जो वृत्त के व्यास का अनुपात है), π का मान निम्नानुसार प्रदान करता है: | ||
''विबुधनेत्रगजाहिहुताशनत्रिगुणवेदभवारणबाहवः । नवनिखर्वमिते वृतिविस्तरे परिधिमानमिदं जगदुर्बुधाः ॥''<ref>''Āryabhaṭīya-bhāśya by Nīlakaṇṭha Somasutvan''. p. 42.</ref> | ''विबुधनेत्रगजाहिहुताशनत्रिगुणवेदभवारणबाहवः । नवनिखर्वमिते वृतिविस्तरे परिधिमानमिदं जगदुर्बुधाः ॥''<ref>नीलकण्ठ सोमसुत्वन द्वारा आर्यभटीय भाष्य,पृष्ठ. 42.(''Āryabhaṭīya-bhāśya by Nīlakaṇṭha Somasutvan''. p. 42.)</ref> | ||
"9 X 10<sup>11</sup> व्यास वाले वृत्त की परिधि 2827433388233 है।" | "9 X 10<sup>11</sup> व्यास वाले वृत्त की परिधि 2827433388233 है।" | ||
| Line 272: | Line 272: | ||
''अँकानां वामातो गति:'' के अनुसार संख्या उपरोक्त संख्या के विपरीत है जो कि 2827433388233 है। | ''अँकानां वामातो गति:'' के अनुसार संख्या उपरोक्त संख्या के विपरीत है जो कि 2827433388233 है। | ||
वृत्त की परिधि = 2827433388233 वृत्त का व्यास = 9 X 10<sup>11</sup> | वृत्त की परिधि = 2827433388233, वृत्त का व्यास = 9 X 10<sup>11</sup> | ||
<math>\frac{Circumference}{Diameter} =\frac{2827433388233}{9 \quad X \quad10^{11}} = 3.14159265359</math> | <math>\frac{Circumference}{Diameter} =\frac{2827433388233}{9 \quad X \quad10^{11}} = 3.14159265359</math> | ||
| Line 347: | Line 347: | ||
''नञौ अचः च शून्यानि सङ्ख्याः कटपयादयः मिश्रे तु उपान्त्यहल् सङ्ख्या न च चिन्त्यः हलः स्वरः।'' | ''नञौ अचः च शून्यानि सङ्ख्याः कटपयादयः मिश्रे तु उपान्त्यहल् सङ्ख्या न च चिन्त्यः हलः स्वरः।'' | ||
शंकरवर्मन द्वारा सदरत्नमाला (''सद्रत्नमाला'') के उपरोक्त श्लोक में पालन की जाने वाली विधि का वर्णन है। | शंकरवर्मन द्वारा [[सदरत्नमाला|सद्रत्नमाला]] (''सद्रत्नमाला'') के उपरोक्त श्लोक में पालन की जाने वाली विधि का वर्णन है। | ||
व्यंजन को ऊपर दी गई तालिका में दिए गए मान दिए गए हैं। | व्यंजन को ऊपर दी गई तालिका में दिए गए मान दिए गए हैं। | ||
| Line 353: | Line 353: | ||
स्वर, जैसे ''अ, आ, इ'', .. आदि, को मान 0 दिया जाता है। | स्वर, जैसे ''अ, आ, इ'', .. आदि, को मान 0 दिया जाता है। | ||
एक संयुक्त | एक संयुक्त अक्षर में, केवल अंतिम व्यंजन, जो एक स्वर के साथ प्रकट होता है, पर विचार किया जाना होता है। | ||
बिना स्वर वाले व्यंजन (''हलंत)'' को | बिना स्वर वाले व्यंजन (''हलंत)'' को नजर अंदाज करना चाहिए। | ||
एक सामान्य नियम है - ''"अक्कनाम् वामतो गतिः"'', यानी संख्याएं दाएं से बाएं जाती हैं। | एक सामान्य नियम है - ''"अक्कनाम् वामतो गतिः"'', यानी संख्याएं दाएं से बाएं ओर जाती हैं। | ||
=== कटपयादि प्रणाली के उदाहरण === | === कटपयादि प्रणाली के उदाहरण === | ||
| Line 390: | Line 390: | ||
सदरत्नमाला पाठ में 17 दशमलव स्थानों तक (π ) π के मान का उल्लेख है। | सदरत्नमाला पाठ में 17 दशमलव स्थानों तक (π ) π के मान का उल्लेख है। | ||
''स्याद् भद्राम्बुधिसिद्धजन्मगणितश्रद्धा स्म यद् भूपगीः'' । <ref>''Sadratnamālā''. pp. IV.2, p.26.</ref><small>(सदरत्नमाला IV.2, पृष्ठ 26)</small> | ''स्याद् भद्राम्बुधिसिद्धजन्मगणितश्रद्धा स्म यद् भूपगीः'' । <ref>सदरत्नमाला, पीपी। IV.2, पृष्ठ .26(''Sadratnamālā''. pp. IV.2, p.26.)</ref><small>(सदरत्नमाला IV.2, पृष्ठ 26)</small> | ||
कश्यपयादि प्रणाली का उपयोग करने के लिए संख्या । ''भद्राम्बुधिसिद्धजन्मगणितश्रद्धा स्म यद् भूपगीः'' | कश्यपयादि प्रणाली का उपयोग करने के लिए संख्या । ''भद्राम्बुधिसिद्धजन्मगणितश्रद्धा स्म यद् भूपगीः'' | ||
| Line 448: | Line 448: | ||
== संदर्भ == | == संदर्भ == | ||
<references /> | <references /> | ||
[[Category:Organic Articles]] | |||
[[Category:अंकगणित]] | [[Category:अंकगणित]] | ||
[[Category:गणित]] | |||
Latest revision as of 09:53, 18 October 2022
परिचय
प्राचीन भारतीयों ने काव्य के माध्यम से गणित को सरल और रोचक बनाया है। कविता के माध्यम से प्रमेय या सूत्रों को याद रखना आसान है और दिलचस्प भी। भारतीय गणित का विज्ञान कविता के कई अलङ्कार (छन्द) में रचा गया था। प्राचीन भारतीयों ने कविता में संख्याओं को व्यक्त करने का एक अनूठा तरीका खोजा। इस प्रकार से संख्या निरूपण की निम्नलिखित दो प्रणालियों का जन्म हुआ।
- भूत-सांख्य प्रणाली:
- कटपयादि प्रणाली:
भूत-सांख्य
भूत-सांख्य संख्याओं के प्रतिनिधित्व की एक प्रणाली है जहाँ अंकों को कुछ शब्दों द्वारा व्यक्त किया जाता है। इन शब्दों के अर्थ या तो स्वाभाविक रूप से या लोकप्रिय भारतीय साहित्य में प्रसिद्ध संदर्भों द्वारा संख्याओं को इंगित करते हैं। भूत-सांख्य पिंगल के छन्दसूत्र में पाया जाता है, जिसकी रचना तीसरी शताब्दी ईसा पूर्व में हुई थी।[1]
संख्याओं का प्रतिनिधित्व
संख्या '1' को चंद्र द्वारा दर्शाया गया है, जिसका अर्थ है चंद्रमा। चंद्रमा पृथ्वी का एकमात्र प्राकृतिक उपग्रह है जो अद्वितीय है। ऐसी किसी भी अनूठी वस्तु का उपयोग संख्या '1' को दर्शाने के लिए किया जा सकता है। अन्य शब्द जो लोकप्रिय रूप से "1" का प्रतिनिधित्व करते हैं, वे हैं भूमि (पृथ्वी), रूप (रूप), आदि।
संख्या '2' किसी भी लोकप्रिय जोड़ी द्वारा दर्शाया जाता है, जैसे आंखें, हाथ, या अश्विनी जुड़वां ।
संख्या '0' को आकाश (अंतरिक्ष) शब्द द्वारा दर्शाया गया है, जो शून्य के लिए खड़ा है।
संख्या '3' को गुण शब्द द्वारा दर्शाया गया है (त्रिगुण - तीन गुण अर्थात् सत्त्व, रजस और तमस )।
संख्या '4' शब्द वेद (ऋग्वेद, यजुर्वेद, अथर्ववेद, सामवेद) द्वारा दर्शाया गया है।
संख्याओं के निरूपण के लिए शब्दों का प्रयोग करते समय एक सामान्य परंपरा का प्रयोग किया जाता है। जिसमे, परंपरा "अङ्कानां वामतो गतिः" नियम का पालन करना है। इसका मतलब है कि संख्याओं को दाएं से बाएं पढ़ा जाना है। शब्दों के माध्यम से व्यक्त की जाने वाली संख्याएँ इकाई के स्थान से आगे बनती हैं।
अश्विनी आकाश गुण खा चंद्र रूप भूमि राम भूत बाण वायु महायज्ञ ऋतु वेदांग
भूत-सांख्य के रूप में प्रयुक्त शब्दों की सूची
| संख्यांक | भूत-सांख्य | अर्थ | विवरण |
|---|---|---|---|
| 0 | खा , आकाश | अंतरिक्ष, आसमान | अंतरिक्ष रिक्त का प्रतिनिधित्व करता है जिसका अर्थ शून्य है |
| 1 | चंद्र
रूप भूमि |
चंद्रमा
प्रपत्र धरती |
पृथ्वी मे एक ही चंद्रमा है
प्रपत्र प्रत्येक व्यक्ति के लिए अद्वितीय है पृथ्वी एक है |
| 2 | नेत्र
यमल अश्विनी |
आंख
जुड़वां जुड़वां देवता: |
इंसान की दो आंखें होती हैं
जुडवा नासत्य, दशरा - जुड़वां अश्विनी देवता। |
| 3 | गुण
राम |
गुणवत्ता
राम |
सत्व, रजस, तमस - 3 गुण
परशुराम, बलराम, दशरथी राम: |
| 4 | वेद | वेद | ऋग, यजुर, साम और अथर्व - 4 वेद: |
| 5 | भूत
महायज्ञ |
तत्व
त्याग |
पृथ्वी, जल, अग्नि, वायु और आकाश - 5 तत्वदेवयज्ञ, पितृयज्ञ, मनुयज्ञ, मनुष्ययज्ञ , भूतयज्ञ - पंचमहायज्ञ |
| 6 | महायज्ञ
वेदांग रस |
त्याग
हिंदू धर्म के 6 सहायक विषय स्वाद |
देवयज्ञ, पितृयज्ञ, मनुयज्ञ, मनुष्ययज्ञ, भूतयज्ञ - पंचमहायज्ञ
शिक्षा, व्याकरण, कल्प, निरुक्त, ज्योतिष, छन्द मीठा, नमक, खट्टा, तीखा, कसैला और कड़वा |
| 7 | मुनि, ऋषि
पर्वत स्वर |
संत
पहाड़ संगीतिक स्वर |
कश्यप अत्रि वशिष्ठ विश्वामित्र गौतम जमदग्नि भारध्वज
, |
| 8 | वासु
प्रकृति |
सृष्टि |
धारा, अनिल, अनल, आप, प्रत्यूष , प्रभास, सोम, ध्रुव।
पंचभूत, मानस, बुद्धि, अहंकार । |
| 9 | शरीर-द्वार
नंद |
शरीर में छिद्र
नंद वंश के राजा |
दो आँख, दो कान, दो नासिका, एक मुख और उत्सर्जन और जनन के अंग।
प्रसिद्ध नंद वंश के राजा - उग्रसेन, पाशुक, पांडुगती, भूतपाल, राष्ट्रपाल , गोविष्णक, दशसिद्धक, कैवर्त, धनानंद। |
| 10 | दिक | दिशा | दस दिशाएँ हैं - पूर्व, पश्चिम, उत्तर, दक्षिण, उत्तर-पूर्व, उत्तर-पश्चिम, दक्षिण-
पूर्व, दक्षिण-पश्चिम, ऊपर और नीचे। |
| 11 | रुद्र | देवता | ग्यारह रुद्र - मन्यु, मनु, महिन, महान, शिव, ऋतुध्वज, उग्रसेत , भव, काम, वामदेव, धृतव्रत। |
| 12 | सूर्य | रवि | मित्र, रवि, सूर्य, भानु, खग, पूष , हिरण्यगर्भ, मरचि, आदित्य, सवित्रि , अर्का, भास्कर। |
| 13 | विश्वेदेव | देवों का एक वर्ग | देवों का विशेष वर्ग जिनकी संख्या 13 है। |
| 14 | मनु | कल्प के प्रमुख | 14 मनु का उल्लेख पुराण साहित्य में मिलता है। वे हैं स्वायंभुव, स्वरचित्त, उत्तम, तपस, रैवत, चाक्षुण वैवस्वत, सावर्णी, दक्ष-सावर्णी, ब्रह्म-सावर्णी, धर्म-सावर्णी, देव-सावर्णी, रुद्र-सावर्णी, इंद्र-सावर्णी |
| 15 | तिथि | पक्ष के दिन | प्रथम से अमावस्या (अमावस्या का दिन) या पौर्णमी(पूर्णिमा के दिन) तक 15 तारीखें |
| 16 | अत्यास्ति | छंद के प्रकार | इसकी प्रत्येक तिमाही में 17 अक्षरों का एक काव्यात्मक छंद। |
| 18 | धृति | छंद के प्रकार | इसकी प्रत्येक तिमाही में 18 अक्षरों का एक काव्यात्मक छंद। |
| 27 | नक्षत्र | नक्षत्र-मंड़ल | भारतीय खगोल विज्ञान में, अण्डाकार के साथ 27 नक्षत्र या क्षेत्र हैं।[2] |
| 32 | दंत | दांत | मनुष्यों में दांतों की संख्या। |
| 33 | देव,
देवता |
आकाशीय प्राणी | पुराणों में 33 प्रकार के देवों का उल्लेख मिलता है। |
उपरोक्त शब्दों के किसी भी समानार्थी शब्द का उपयोग संबंधित अंकों को दर्शाने के लिए भी किया जा सकता है।
उदाहरण के लिए चंद्रमा (चंद्र) - सोम, इंदु, शशि।
भूत-सांख्य के उदाहरण
1. वर्ष 2022 को इस प्रकार व्यक्त किया जा सकता है।
| अश्विनी | नेत्र | आकाश | यमल | अंकानां वामतो गति: |
|---|---|---|---|---|
| 2 | 2 | 0 | 2 | 2022 |
2. नीलकंठ सोमसुत्वन, माधव द्वारा अपने आर्यभटीय -भाषा में दिए गए एक श्लोक को उद्धृत करते हैं।
यह श्लोक भूत-सांख्य प्रणाली में (π जो वृत्त के व्यास का अनुपात है), π का मान निम्नानुसार प्रदान करता है:
विबुधनेत्रगजाहिहुताशनत्रिगुणवेदभवारणबाहवः । नवनिखर्वमिते वृतिविस्तरे परिधिमानमिदं जगदुर्बुधाः ॥[3]
"9 X 1011 व्यास वाले वृत्त की परिधि 2827433388233 है।"
भूत-सांख्य प्रणाली के अनुसार:
| विबुध | नेत्र | गज | अहि | हुताशन | त्रि | गुण | वेद | भ | वारण | बाहवः |
| vibudha | netra | gaja | ahi | hutāśana | tri | guṇa | veda | bha | vāraṇa | bāhavaḥ |
| 33 | 2 | 8 | 8 | 3 | 3 | 3 | 4 | 27 | 8 | 2 |
संख्याएँ 33 2 8 8 3 3 3 4 27 8 2 हैं।
अँकानां वामातो गति: के अनुसार संख्या उपरोक्त संख्या के विपरीत है जो कि 2827433388233 है।
वृत्त की परिधि = 2827433388233, वृत्त का व्यास = 9 X 1011
इस श्लोक से π का मान 11 दशमलव स्थानों तक प्राप्त होता है। श्लोक के माध्यम से विद्यार्थी महत्वपूर्ण अंक आसानी से याद कर लेता है।
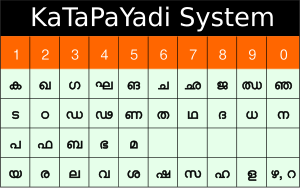
कटपयादि प्रणाली (अक्षर अंक)
कटपयादि संस्कृत वर्णमाला का उपयोग करके संख्याओं का प्रतिनिधित्व करने के लिए एक संकेतन प्रणाली है।
इस प्रणाली में संख्याओं को व्यक्त करने के लिए अंकों के स्थान पर व्यंजन का प्रयोग किया जाता है।
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| क | ख | ग | घ | ङ | च | छ | ज | झ | ञ |
| ट | ठ | ड | ढ | ण | त | थ | द | ध | न |
| प | फ | ब | भ | म | |||||
| य | र | ल | व | श | ष | स | ह | ळ | |
| अ, आ, इ, ई, उ, ऊ, ऋ, ॠ, ए, ऐ, ओ, औ | |||||||||
ध्यान देने योग्य महत्वपूर्ण तर्क :
नञौ अचः च शून्यानि सङ्ख्याः कटपयादयः मिश्रे तु उपान्त्यहल् सङ्ख्या न च चिन्त्यः हलः स्वरः।
शंकरवर्मन द्वारा सद्रत्नमाला (सद्रत्नमाला) के उपरोक्त श्लोक में पालन की जाने वाली विधि का वर्णन है।
व्यंजन को ऊपर दी गई तालिका में दिए गए मान दिए गए हैं।
स्वर, जैसे अ, आ, इ, .. आदि, को मान 0 दिया जाता है।
एक संयुक्त अक्षर में, केवल अंतिम व्यंजन, जो एक स्वर के साथ प्रकट होता है, पर विचार किया जाना होता है।
बिना स्वर वाले व्यंजन (हलंत) को नजर अंदाज करना चाहिए।
एक सामान्य नियम है - "अक्कनाम् वामतो गतिः", यानी संख्याएं दाएं से बाएं ओर जाती हैं।
कटपयादि प्रणाली के उदाहरण
राघवाय (राघवाय) (एपिग्रपहिया इंडिका खंड 6 पृष्ठ.121) र् + आ + घ + अ + व् + आ + य + अ
| र् | घ् | व् | य् | अङ्कानाम् वामतो गतिः |
|---|---|---|---|---|
| 2 | 4 | 4 | 1 | → 1442 |
भवति (भवति ) (भारतीय पुरातन खंड 2.2.p.60 भ् + अ + व् + अ + त् + इ
| भ् | व् | त् | अङ्कानाम् वामतो गतिः |
|---|---|---|---|
| 4 | 4 | 6 | → 644 |
सदरत्नमाला पाठ में 17 दशमलव स्थानों तक (π ) π के मान का उल्लेख है।
स्याद् भद्राम्बुधिसिद्धजन्मगणितश्रद्धा स्म यद् भूपगीः । [4](सदरत्नमाला IV.2, पृष्ठ 26)
कश्यपयादि प्रणाली का उपयोग करने के लिए संख्या । भद्राम्बुधिसिद्धजन्मगणितश्रद्धा स्म यद् भूपगीः
(भ्+अ+द्+र्+आ+म्+ब्+उ+ध्+इ+स्+इ+द्+ध्+अ+ज्+अ+न्+म्+अ+ग्+अ+ण्+इ+त्+अ+श्+र्+द्+ध+आ) (स्+म्+अ) (य्+अ+द्) (भ्+ऊ+प्+अ+ग्+ईः)
| भ् | र् | ब् | ध् | स् | ध् | ज् | म् | ग् | ण् | त् | र् | ध् | म् | य् | भ् | प् | ग् | अङ्कानाम् वामतो गतिः |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 2 | 3 | 9 | 7 | 9 | 8 | 5 | 3 | 5 | 6 | 2 | 9 | 5 | 1 | 4 | 1 | 3 | → 314159265358979324 |
पाठ के अनुसार इस संख्या (एक वृत्त की परिधि) को वृत्त के व्यास से 1017 से विभाजित करने पर, हमें (π) π का मान 3.14159265358979324 प्राप्त होता है
बाहरी संपर्क
यह भी देखें
संदर्भ
- ↑ भारतीय गणितम के लिए एक प्राइमर, भारतीय-गणित-प्रवेश- भाग -1, दिल्ली: संस्कृत प्रमोशन फाउंडेशन।(A Primer to Bhāratīya Gaṇitam , Bhāratīya-Gaṇita-Praveśa- Part-1. Delhi: Samskrit Promotion Foundation.) 2021. ISBN 978-81-951757-2-7.
- ↑ https://en.wikipedia.org/wiki/List_of_Nakshatras
- ↑ नीलकण्ठ सोमसुत्वन द्वारा आर्यभटीय भाष्य,पृष्ठ. 42.(Āryabhaṭīya-bhāśya by Nīlakaṇṭha Somasutvan. p. 42.)
- ↑ सदरत्नमाला, पीपी। IV.2, पृष्ठ .26(Sadratnamālā. pp. IV.2, p.26.)