बिटोनिक सॉर्टर: Difference between revisions
No edit summary |
No edit summary |
||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 25: | Line 25: | ||
चूँकि तुलनाओं की पूर्ण संख्या सामान्यतः बैचर के विषम-सम प्रकार से अधिक होती है, किन्तु बिटोनिक प्रकार में लगातार अनेक ऑपरेशन संदर्भ के स्थानीयता को बनाए रखते हैं, इस प्रकार जिससे कार्यान्वयन अधिक कैश-अनुकूल और सामान्यतः व्यवहार में अधिक कुशल हो जाता है। | चूँकि तुलनाओं की पूर्ण संख्या सामान्यतः बैचर के विषम-सम प्रकार से अधिक होती है, किन्तु बिटोनिक प्रकार में लगातार अनेक ऑपरेशन संदर्भ के स्थानीयता को बनाए रखते हैं, इस प्रकार जिससे कार्यान्वयन अधिक कैश-अनुकूल और सामान्यतः व्यवहार में अधिक कुशल हो जाता है। | ||
== एल्गोरिदम कैसे काम करता है == | == '''एल्गोरिदम कैसे काम करता है''' == | ||
निम्नलिखित 16 इनपुट वाला बिटोनिक सॉर्टिंग नेटवर्क है: | निम्नलिखित 16 इनपुट वाला बिटोनिक सॉर्टिंग नेटवर्क है: | ||
| Line 62: | Line 62: | ||
==यह भी देखें== | ==यह भी देखें== | ||
* बैचर विषम-सम मर्जसॉर्ट | * बैचर विषम-सम मर्जसॉर्ट | ||
* [[जोड़ीवार छँटाई नेटवर्क]] | * [[जोड़ीवार छँटाई नेटवर्क|जोड़ीवार सॉर्टिंग नेटवर्क]] | ||
== संदर्भ == | == संदर्भ == | ||
| Line 70: | Line 70: | ||
*[https://xlinux.nist.gov/dads/HTML/bitonicSort.html संदर्भ कोड] at [[NIST|एनआईएसटी]] | *[https://xlinux.nist.gov/dads/HTML/bitonicSort.html संदर्भ कोड] at [[NIST|एनआईएसटी]] | ||
*[https://www.tools-of-computing.com/tc/CS/Sorts/bitonic_sort.htm एनिमेटेड चित्रों और कामकाजी कोड के साथ ट्यूटोरियल] | *[https://www.tools-of-computing.com/tc/CS/Sorts/bitonic_sort.htm एनिमेटेड चित्रों और कामकाजी कोड के साथ ट्यूटोरियल] | ||
<references /> | |||
[[Category:Created On 07/07/2023]] | [[Category:Created On 07/07/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:छँटाई एल्गोरिदम]] | |||
Latest revision as of 10:53, 26 July 2023
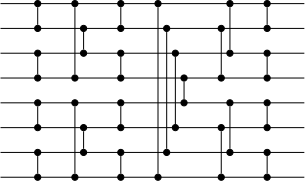 Bitonic sort network with eight inputs. | |
| Class | Sorting algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | parallel time |
| Best-case performance | parallel time |
| Average performance | parallel time |
| Worst-case space complexity | non-parallel time |
बिटोनिक मर्जसॉर्ट सॉर्टिंग के लिए समानांतर एल्गोरिदम है। इसका उपयोग सॉर्टिंग नेटवर्क के निर्माण के लिए निर्माण विधि के रूप में भी किया जाता है। एल्गोरिथ्म केन बैचर द्वारा तैयार किया गया था। इस प्रकार परिणामी सॉर्टिंग नेटवर्क से मिलकर बनता है तुलनित्र और की देरी है , कहाँ क्रमबद्ध की जाने वाली वस्तुओं की संख्या है।[1] इस प्रकार यह इसे आर्किटेक्चर पर बड़ी संख्या में तत्वों को सॉर्ट करने के लिए लोकप्रिय विकल्प बनाता है जिसमें लॉकस्टेप में चलने वाली बड़ी संख्या में समानांतर निष्पादन इकाइयां सम्मिलित होती हैं, जैसे कि विशिष्ट जीपीयू।
एक क्रमबद्ध अनुक्रम नीरस रूप से गैर-घटता (या गैर-बढ़ता) अनुक्रम है। बिटोनिक अनुक्रम अनुक्रम है कुछ के लिए , या ऐसे अनुक्रम का गोलाकार बदलाव।
जटिलता
होने देना और .
निर्माण एल्गोरिदम से यह स्पष्ट है कि समानांतर तुलनाओं के राउंड की संख्या दी गई है .
यह तुलनित्रों की संख्या का अनुसरण करता है घिरा है (जो इसके लिए त्रुटिहीन मान स्थापित करता है कब 2) की शक्ति है।
चूँकि तुलनाओं की पूर्ण संख्या सामान्यतः बैचर के विषम-सम प्रकार से अधिक होती है, किन्तु बिटोनिक प्रकार में लगातार अनेक ऑपरेशन संदर्भ के स्थानीयता को बनाए रखते हैं, इस प्रकार जिससे कार्यान्वयन अधिक कैश-अनुकूल और सामान्यतः व्यवहार में अधिक कुशल हो जाता है।
एल्गोरिदम कैसे काम करता है
निम्नलिखित 16 इनपुट वाला बिटोनिक सॉर्टिंग नेटवर्क है:
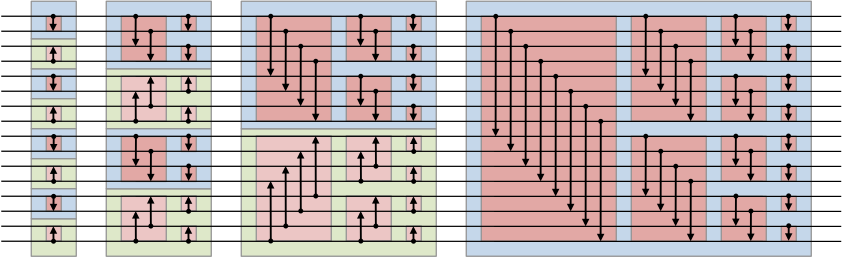 16 नंबर बाएं छोर पर इनपुट के रूप में प्रवेश करते हैं, 16 क्षैतिज तारों में से प्रत्येक के साथ स्लाइड करते हैं, और दाएं छोर पर आउटपुट पर बाहर निकलते हैं। नेटवर्क को तत्वों को क्रमबद्ध करने के लिए डिज़ाइन किया गया है, इस प्रकार जिसमें नीचे सबसे बड़ी संख्या है।
16 नंबर बाएं छोर पर इनपुट के रूप में प्रवेश करते हैं, 16 क्षैतिज तारों में से प्रत्येक के साथ स्लाइड करते हैं, और दाएं छोर पर आउटपुट पर बाहर निकलते हैं। नेटवर्क को तत्वों को क्रमबद्ध करने के लिए डिज़ाइन किया गया है, इस प्रकार जिसमें नीचे सबसे बड़ी संख्या है।
तीर तुलनित्र हैं. जब भी दो संख्याएँ तीर के दोनों सिरों तक पहुँचती हैं, तब उनकी तुलना यह सुनिश्चित करने के लिए की जाती है कि तीर बड़ी संख्या की ओर संकेत करता है। इस प्रकार यदि वह क्रम से बाहर हैं, तब उन्हें बदल दिया जाता है। रंगीन बक्से केवल चित्रण के लिए हैं और एल्गोरिदम पर उनका कोई प्रभाव नहीं पड़ता है।
प्रत्येक लाल बॉक्स की संरचना समान होती है: शीर्ष आधे में प्रत्येक इनपुट की तुलना नीचे के आधे भाग में संबंधित इनपुट से की जाती है, जिसमें सभी तीर नीचे (गहरा लाल) या सभी ऊपर (हल्का लाल) इंगित करते हैं। इस प्रकार यदि इनपुट बिटोनिक अनुक्रम बनाता है (एक एकल गैर-घटता क्रम जिसके पश्चात् एकल गैर-बढ़ता क्रम या इसके विपरीत), तब आउटपुट दो बिटोनिक अनुक्रम बनाएगा। आउटपुट का शीर्ष आधा भाग बिटोनिक होगा, और निचला आधा बिटोनिक होगा, शीर्ष आधे का प्रत्येक तत्व निचले आधे के प्रत्येक तत्व (गहरे लाल के लिए) या इसके विपरीत (हल्के लाल के लिए) से कम या उसके सामान्तर होगा। इस प्रकार यह प्रमेय स्पष्ट नहीं है, किन्तु शून्य-एक सिद्धांत का उपयोग करके विभिन्न इनपुट की तुलना कैसे की जा सकती है, इसके सभी स्थितियों पर सावधानीपूर्वक विचार करके सत्यापित किया जा सकता है, जहां बिटोनिक अनुक्रम 0s और 1s का अनुक्रम होता है जिसमें दो "10 से अधिक नहीं होते हैं " या "01" अनुवर्ती सम्मिलित हैं।
लाल डिब्बे मिलकर नीले और हरे डिब्बे बनाते हैं। ऐसे प्रत्येक बॉक्स की संरचना समान होती है: लाल बॉक्स पूरे इनपुट अनुक्रम पर प्रयुक्त होता है, फिर परिणाम के प्रत्येक आधे भाग पर, फिर उनमें से प्रत्येक परिणाम के प्रत्येक आधे पर, और इसी तरह। सभी तीर नीचे की ओर (नीला) या सभी ऊपर की ओर (हरा) इंगित करते हैं। इस प्रकार इस संरचना को तितली नेटवर्क के रूप में जाना जाता है। यदि इस बॉक्स में इनपुट बिटोनिक होता है, तब आउटपुट पूरी तरह से बढ़ते क्रम (नीला) या घटते क्रम (हरा) में सॉर्ट किया जाएगा। यदि कोई संख्या नीले या हरे बॉक्स में प्रवेश करती है, तब पहला लाल बॉक्स उसे सूची के सही आधे भाग में क्रमबद्ध कर देगा। इस प्रकार फिर यह छोटे लाल बॉक्स से होकर गुजरेगा जो इसे उस आधे भाग के अंदर सूची के सही तिमाही में क्रमबद्ध करता है। यह तब तक जारी रहता है जब तक इसे बिल्कुल सही स्थिति में क्रमबद्ध नहीं कर लिया जाता। इसलिए, हरे या नीले बॉक्स का आउटपुट पूरी तरह से सॉर्ट किया जाएगा।
हरे और नीले बक्से मिलकर संपूर्ण सॉर्टिंग नेटवर्क बनाते हैं। इनपुट के किसी भी मनमाने अनुक्रम के लिए, यह उन्हें सबसे नीचे सबसे बड़े के साथ, सही ढंग से क्रमबद्ध करेगा। इस प्रकार प्रत्येक हरे या नीले बॉक्स का आउटपुट क्रमबद्ध अनुक्रम होगा, इसलिए आसन्न सूचियों की प्रत्येक जोड़ी का आउटपुट बिटोनिक होगा, क्योंकि शीर्ष वाला नीला है और नीचे वाला हरा है। नीले और हरे बक्सों का प्रत्येक स्तंभ एन क्रमबद्ध अनुक्रम लेता है और उन्हें एन/2 बिटोनिक अनुक्रम बनाने के लिए जोड़े में जोड़ता है, जिसे एन/2 क्रमबद्ध अनुक्रम बनाने के लिए उस कॉलम के बक्सों द्वारा क्रमबद्ध किया जाता है। इस प्रकार यह प्रक्रिया प्रत्येक इनपुट के साथ प्रारंभ होती है जिसे तत्व की क्रमबद्ध सूची माना जाता है, और सभी कॉलमों के माध्यम से तब तक जारी रहता है जब तक कि अंतिम उन्हें एकल, क्रमबद्ध सूची में विलय नहीं कर देता। क्योंकि अंतिम चरण नीला था, इस अंतिम सूची में सबसे नीचे सबसे बड़ा तत्व होगा।
वैकल्पिक प्रतिनिधित्व
ऊपर दिए गए चित्र में प्रत्येक हरा बॉक्स, नीले बॉक्स के समान ही कार्य करता है, किन्तु विपरीत दिशा में सॉर्ट करता है। इस प्रकार इसलिए, प्रत्येक हरे बॉक्स को नीले बॉक्स से बदला जा सकता है और उसके पश्चात् क्रॉसओवर लगाया जा सकता है, जहां सभी तार विपरीत स्थिति में चले जाते हैं। यह सभी तीरों को ही दिशा इंगित करने की अनुमति देगा, किन्तु क्षैतिज रेखाओं को सीधा होने से रोकेगा। चूँकि, समान क्रॉसओवर को किसी भी लाल ब्लॉक से आउटपुट के निचले आधे भाग के दाईं ओर रखा जा सकता है, और सॉर्ट अभी भी सही ढंग से काम करेगा, क्योंकि बिटोनिक अनुक्रम का रिवर्स अभी भी बिटोनिक है। इस प्रकार यदि किसी लाल बॉक्स के पहले और पश्चात् में क्रॉसओवर है, तब इसे आंतरिक रूप से पुन: व्यवस्थित किया जा सकता है जिससे कि दोनों क्रॉसओवर रद्द हो जाएं, जिससे तार फिर से सीधे हो जाएं। इसलिए, निम्नलिखित आरेख ऊपर वाले के सामान्तर है, जहां प्रत्येक हरा बॉक्स नीला और क्रॉसओवर बन गया है, और प्रत्येक नारंगी बॉक्स लाल बॉक्स है जो दो ऐसे क्रॉसओवर को अवशोषित करता है:
 तीर के निशान नहीं खींचे गए हैं, क्योंकि प्रत्येक तुलनित्र ही दिशा में क्रमबद्ध होता है। नीले और लाल ब्लॉक पहले की तरह ही कार्य करते हैं। इस प्रकार नारंगी ब्लॉक लाल ब्लॉक के सामान्तर हैं जहां अनुक्रम क्रम इसके इनपुट के निचले आधे भाग और इसके आउटपुट के निचले आधे भाग के लिए उलटा होता है। इस प्रकार यह बिटोनिक सॉर्टिंग नेटवर्क का सबसे आम प्रतिनिधित्व है। पिछली व्याख्या के विपरीत, क्योंकि तत्व तार्किक रूप से क्रमबद्ध रहते हैं, इस प्रतिनिधित्व को गैर-शक्ति-दो स्थितियों में विस्तारित करना आसान है (जहां प्रत्येक तुलना-और-स्वैप किसी भी स्थितियों को अनदेखा करता है जहां बड़ा सूचकांक सीमा से बाहर है)।
तीर के निशान नहीं खींचे गए हैं, क्योंकि प्रत्येक तुलनित्र ही दिशा में क्रमबद्ध होता है। नीले और लाल ब्लॉक पहले की तरह ही कार्य करते हैं। इस प्रकार नारंगी ब्लॉक लाल ब्लॉक के सामान्तर हैं जहां अनुक्रम क्रम इसके इनपुट के निचले आधे भाग और इसके आउटपुट के निचले आधे भाग के लिए उलटा होता है। इस प्रकार यह बिटोनिक सॉर्टिंग नेटवर्क का सबसे आम प्रतिनिधित्व है। पिछली व्याख्या के विपरीत, क्योंकि तत्व तार्किक रूप से क्रमबद्ध रहते हैं, इस प्रतिनिधित्व को गैर-शक्ति-दो स्थितियों में विस्तारित करना आसान है (जहां प्रत्येक तुलना-और-स्वैप किसी भी स्थितियों को अनदेखा करता है जहां बड़ा सूचकांक सीमा से बाहर है)।
उदाहरण कोड
जब सरणी की लंबाई दो की शक्ति होती है, तब बिटोनिक मर्जसॉर्ट का रिकर्सन-मुक्त कार्यान्वयन निम्नलिखित है:[2]
// given an array arr of length n, this code sorts it in place
// all indices run from 0 to n-1
for (k = 2; k <= n; k *= 2) // k is doubled every iteration
for (j = k/2; j > 0; j /= 2) // j is halved at every iteration, with truncation of fractional parts
for (i = 0; i < n; i++)
l = bitwiseXOR (i, j); // in C-like languages this is "i ^ j"
if (l > i)
if ( (bitwiseAND (i, k) == 0) AND (arr[i] > arr[l])
OR (bitwiseAND (i, k) != 0) AND (arr[i] < arr[l]) )
swap the elements arr[i] and arr[l]
यह भी देखें
- बैचर विषम-सम मर्जसॉर्ट
- जोड़ीवार सॉर्टिंग नेटवर्क
संदर्भ
<संदर्भ />
बाहरी संबंध
- ↑ Bitonic sorting network for n not a power of 2
- ↑ The original source code in C was at https://www2.cs.duke.edu/courses/fall08/cps196.1/Pthreads/bitonic.c (the very last function in the file). It has been replaced with generic pseudocode syntax, not C-specific, for Wikipedia.