क्विकसेलेक्ट: Difference between revisions
No edit summary |
No edit summary |
||
| (13 intermediate revisions by 3 users not shown) | |||
| Line 12: | Line 12: | ||
}} | }} | ||
[[कंप्यूटर विज्ञान]] में, क्विकसेलेक्ट | [[कंप्यूटर विज्ञान]] में, '''क्विकसेलेक्ट''' अव्यवस्थित सूची में ''k''वें सबसे छोटे तत्व को खोजने के लिए चयन एल्गोरिदम है, जिसे ''k''वें क्रम के आंकड़ों के रूप में भी जाना जाता है। इस प्रकार संबंधित [[जल्दी से सुलझाएं|क्विकॉर्ट]] सॉर्टिंग एल्गोरिदम की तरह, इसे [[टोनी होरे]] द्वारा विकसित किया गया था, और इस प्रकार इसे '''होरे के चयन एल्गोरिदम''' के रूप में भी जाना जाता है।<ref>{{Cite journal | last1 = Hoare | title = Algorithm 65: Find | doi = 10.1145/366622.366647 | first1 = C. A. R. | author-link1 = Tony Hoare | journal = [[Communications of the ACM|Comm. ACM]] | volume = 4 | issue = 7 | pages = 321–322 | year = 1961 }}</ref> क्विकसॉर्ट की तरह, यह अभ्यास में कुशल है और इसका औसत-स्थितियों में प्रदर्शन अच्छा है, किन्तु सबसे खराब स्थिति में इसका प्रदर्शन खराब है। क्विकसेलेक्ट और इसके वेरिएंट चयन एल्गोरिदम हैं जिनका उपयोग अधिकांशतः कुशल वास्तविक विश्व के कार्यान्वयन में किया जाता है। | ||
क्विकसेलेक्ट क्विकॉर्ट के समान समग्र दृष्टिकोण का उपयोग करता है, | क्विकसेलेक्ट क्विकॉर्ट के समान समग्र दृष्टिकोण का उपयोग करता है, तत्व को धुरी के रूप में चुनता है और धुरी के आधार पर डेटा को दो भागों में विभाजित करता है, तदनुसार धुरी से कम या अधिक। चूँकि, क्विकसॉर्ट की तरह, दोनों तरफ पुनरावृत्ति करने के अतिरिक्त, क्विकसेलेक्ट केवल तरफ पुनरावृत्ति करता है - वह तत्व वाला पक्ष जिसे वह खोज रहा है। इससे औसत जटिलता कम हो जाती है <math>O(n\log n)</math> को <math>O(n)</math>, की सबसे खराब स्थिति के साथ <math>O(n^2)</math>. | ||
क्विकॉर्ट की तरह, क्विकसेलेक्ट को सामान्यतः [[इन-प्लेस एल्गोरिदम]] के रूप में और चयन से परे प्रयुक्त किया जाता है {{mvar|k}}वां तत्व, यह डेटा को आंशिक रूप से सॉर्ट भी करता है। सॉर्टिंग के साथ कनेक्शन की आगे की चर्चा के लिए चयन एल्गोरिदम देखें। | क्विकॉर्ट की तरह, क्विकसेलेक्ट को सामान्यतः [[इन-प्लेस एल्गोरिदम]] के रूप में और चयन से परे प्रयुक्त किया जाता है इस प्रकार {{mvar|k}}वां तत्व, यह डेटा को आंशिक रूप से सॉर्ट भी करता है। सॉर्टिंग के साथ कनेक्शन की आगे की चर्चा के लिए चयन एल्गोरिदम देखें। | ||
==एल्गोरिदम== | =='''एल्गोरिदम'''== | ||
क्विकसॉर्ट में, | क्विकसॉर्ट में, उपप्रक्रिया होती है जिसे <code>partition</code> कहा जाता है जो, रैखिक समय में, सूची को (सूचकांकों से बाएं से दाएं तक) दो भागों में समूहित कर सकता है। इस प्रकार जो निश्चित तत्व से कम हैं, और वे जो तत्व से बड़े या उसके सामान्तर हैं। यहां स्यूडोकोड है जो तत्व <code>सूची [pivotIndex]</code>:के बारे में विभाजन करता है | ||
'''function''' partition (list, left, right, pivotIndex) '''is''' | |||
pivotValue := list[pivotIndex] | |||
swap list[pivotIndex] and list[right] ''// Move pivot to end'' | |||
storeIndex := left | |||
'''for''' i '''from''' left '''to''' right − 1 '''do''' | |||
'''if''' list[i] < pivotValue '''then''' | |||
swap list[storeIndex] and list[i] | |||
increment storeIndex | |||
swap list[right] and list[storeIndex] ''// Move pivot to its final place'' | |||
'''return''' storeIndex | |||
इसे | इस प्रकार इसे लोमुटो विभाजन योजना के रूप में जाना जाता है, इस प्रकार जो होरे की मूल विभाजन योजना की तुलना में सरल किन्तु कम कुशल होते है। | ||
क्विकसॉर्ट में, हम दोनों शाखाओं को पुनरावर्ती रूप से क्रमबद्ध करते हैं, जिससे | क्विकसॉर्ट में, हम दोनों शाखाओं को पुनरावर्ती रूप से क्रमबद्ध करते हैं, जिससे <math>O(n\log n)</math> समय सर्वोत्तम स्थिति बनती है। चूँकि, चयन करते समय, हम पहले से ही जानते हैं कि हमारा वांछित तत्व किस विभाजन में है, क्योंकि धुरी अपनी अंतिम क्रमबद्ध स्थिति में है, इसके पहले वाले सभी तत्व अवर्गीकृत क्रम में हैं और इसके पश्चात् वाले सभी तत्व अवर्गीकृत क्रम में हैं। इसलिए, एकल पुनरावर्ती कॉल सही विभाजन में वांछित तत्व का पता लगाती है, और हम त्वरित चयन के लिए इस पर काम करते हैं: | ||
// | ''// Returns the k-th smallest element of list within left..right inclusive'' | ||
// ( | ''// (i.e. left <= k <= right).'' | ||
' | '''function''' select(list, left, right, k) '''is''' | ||
'''if''' left = right '''then''' ''// If the list contains only one element,'' | |||
'''return''' list[left] ''// return that element'' | |||
pivotIndexx:= ... ''// select a pivotIndex between left and right,'' | |||
''// e.g.,'' left + floor(rand() % (right − left + 1)) | |||
pivotIndexx:= partition(list, left, right, pivotIndex) | |||
''// The pivot is in its final sorted position'' | |||
'''if''' k = pivotIndex '''then''' | |||
'''return''' list[k] | |||
'''else if''' k < pivotIndex '''then''' | |||
'''return''' select(list, left, pivotIndex − 1, k) | |||
'''else''' | |||
'''return''' select(list, pivotIndex + 1, right, k) | |||
---- क्विकॉर्ट से समानता पर ध्यान दें: जिस तरह न्यूनतम-आधारित चयन एल्गोरिथ्म | ---- क्विकॉर्ट से समानता पर ध्यान दें: जिस तरह न्यूनतम-आधारित चयन एल्गोरिथ्म आंशिक चयन सॉर्ट है, यह आंशिक क्विकॉर्ट है, जो केवल उत्पन्न और विभाजन करता है <math>O(\log n)</math> उसके जैसा <math>O(n)</math> विभाजन. इस सरल प्रक्रिया में रैखिक प्रदर्शन की उम्मीद है, और, क्विकसॉर्ट की तरह, व्यवहार में इसका प्रदर्शन अधिक अच्छा है। इस प्रकार यह इन-प्लेस एल्गोरिदम भी है, यदि [[ पूंछ कॉल |टेल कॉल]] ऑप्टिमाइज़ेशन उपलब्ध है, या लूप के साथ [[ पूँछ प्रत्यावर्तन |टेल प्रत्यावर्तन]] को खत्म करने पर केवल निरंतर मेमोरी ओवरहेड की आवश्यकता होती है: | ||
'''function''' select(list, left, right, k) '''is''' | |||
'''loop''' | |||
'''if''' left = right '''then''' | |||
'''return''' list[left] | |||
pivotIndex := ... ''// select pivotIndex between left and right'' | |||
pivotIndex := partition(list, left, right, pivotIndex) | |||
'''if''' k = pivotIndex '''then''' | |||
'''return''' list[k] | |||
'''else if''' k < pivotIndex '''then''' | |||
right := pivotIndex − 1 | |||
'''else''' | |||
left := pivotIndex + 1 | |||
==समय जटिलता== | =='''समय जटिलता'''== | ||
क्विकसॉर्ट की तरह, क्विकसेलेक्ट का औसत प्रदर्शन अच्छा है, किन्तु चुनी गई धुरी के प्रति संवेदनशील है। यदि अच्छे पिवोट्स चुने जाते हैं, अर्थात वे जो किसी दिए गए अंश द्वारा खोज | क्विकसॉर्ट की तरह, क्विकसेलेक्ट का औसत प्रदर्शन अच्छा है, किन्तु चुनी गई धुरी के प्रति संवेदनशील है। इस प्रकार यदि अच्छे पिवोट्स चुने जाते हैं, अर्थात वे जो किसी दिए गए अंश द्वारा खोज समूह को लगातार कम करते हैं, तब खोज समूह आकार में तेजी से घटता है और प्रेरण (या ज्यामितीय श्रृंखला को संक्षेप में) से कोई देखता है कि प्रदर्शन रैखिक है, क्योंकि प्रत्येक चरण रैखिक है और कुल समय इसका स्थिर समय है '''(यह इस पर निर्भर करता है कि खोज समूह कितनी तेजी से कम होता है।)''' चूँकि, यदि खराब पिवोट्स को लगातार चुना जाता है, जैसे कि हर बार केवल ही तत्व कम होना, तब सबसे खराब स्थिति का प्रदर्शन द्विघात होता है: <math>O(n^2).</math> इस प्रकार उदाहरण के लिए, किसी समूह के अधिकतम तत्व की खोज करने, पहले तत्व को धुरी के रूप में उपयोग करने और डेटा को क्रमबद्ध करने में ऐसा होता है। इस प्रकार चूँकि, बेतरतीब ढंग से चुने गए पिवोट्स के लिए, यह सबसे खराब स्थिति बहुत ही असंभावित है: से अधिक का उपयोग करने की संभावना <math>Cn</math> किसी भी पर्याप्त बड़े स्थिरांक के लिए तुलना <math>C</math>, फलन के रूप में अतिघातीय रूप से <math>C</math> छोटा है .<ref>{{cite journal | ||
| last = Devroye | first = Luc | | last = Devroye | first = Luc | ||
| doi = 10.1016/0022-0000(84)90009-6 | | doi = 10.1016/0022-0000(84)90009-6 | ||
| Line 89: | Line 89: | ||
| volume = 31 | | volume = 31 | ||
| year = 2001}}</ref> | | year = 2001}}</ref> | ||
==वेरिएंट== | =='''वेरिएंट'''== | ||
सबसे आसान समाधान | सबसे आसान समाधान यादृच्छिक धुरी चुनना है, जो [[लगभग निश्चित]] रैखिक समय उत्पन्न करता है। इस प्रकार निश्चित रूप से, कोई मीडियन-ऑफ़-3 पिवट रणनीति (जैसे कि क्विकसॉर्ट में) का उपयोग कर सकता है, इस प्रकार जो आंशिक रूप से सॉर्ट किए गए डेटा पर रैखिक प्रदर्शन उत्पन्न करता है, जैसा कि वास्तविक विश्व में सामान्य है। चूँकि, काल्पनिक अनुक्रम अभी भी सबसे खराब स्थिति का कारण बन सकते हैं; [[डेविड मूसर]] ने '''"मीडियन-ऑफ-3 किलर"''' अनुक्रम का वर्णन किया है जो उस रणनीति के विरुद्ध हमले की अनुमति देता है, जो उनके [[ आत्मचयन |इंट्रोसेलेक्ट]] एल्गोरिदम के लिए प्रेरणा थी। | ||
अधिक परिष्कृत धुरी रणनीति का उपयोग करके सबसे खराब स्थिति में भी रैखिक प्रदर्शन सुनिश्चित किया जा सकता है; यह माध्यिका एल्गोरिदम के माध्यिका में किया जाता है। चूँकि, धुरी की गणना का ओवरहेड अधिक है, और इस प्रकार इसका उपयोग सामान्यतः व्यवहार में नहीं किया जाता है। तेज औसत | इस प्रकार अधिक परिष्कृत धुरी रणनीति का उपयोग करके सबसे खराब स्थिति में भी रैखिक प्रदर्शन सुनिश्चित किया जा सकता है; यह माध्यिका एल्गोरिदम के माध्यिका में किया जाता है। चूँकि, धुरी की गणना का ओवरहेड अधिक है, और इस प्रकार इसका उपयोग सामान्यतः व्यवहार में नहीं किया जाता है। इस प्रकार तेज औसत स्थितियों के प्रदर्शन और रैखिक सबसे खराब प्रदर्शन दोनों को प्राप्त करने के लिए फ़ॉलबैक के रूप में मध्यस्थों के माध्यिका के साथ मूलभूत त्वरित चयन को जोड़ा जा सकता है; यह इंट्रोसेलेक्ट में किया जाता है। | ||
औसत समय जटिलता की उत्तम गणना से सबसे खराब स्थिति उत्पन्न होती है <math>n(2+2\log 2+o(1)) \leq 3.4n + o(n)</math> यादृच्छिक पिवोट्स के लिए (माध्यिका के स्थितियोंमें; अन्य k तेज़ हैं)।<ref>[https://11011110.github.io/blog/2007/10/09/blum-style-analysis-of.html Blum-style analysis of Quickselect], [[David Eppstein]], October 9, 2007.</ref> अधिक जटिल धुरी रणनीति द्वारा स्थिरांक को 3/2 तक सुधारा जा सकता है, जिससे फ्लॉयड-रिवेस्ट एल्गोरिथ्म प्राप्त होता है, जिसकी औसत जटिलता है <math>1.5 n + O(n^{1/2})</math> | औसत समय जटिलता की उत्तम गणना से सबसे खराब स्थिति उत्पन्न होती है <math>n(2+2\log 2+o(1)) \leq 3.4n + o(n)</math> यादृच्छिक पिवोट्स के लिए (माध्यिका के स्थितियोंमें; अन्य k तेज़ हैं)।<ref>[https://11011110.github.io/blog/2007/10/09/blum-style-analysis-of.html Blum-style analysis of Quickselect], [[David Eppstein]], October 9, 2007.</ref> इस प्रकार अधिक जटिल धुरी रणनीति द्वारा स्थिरांक को 3/2 तक सुधारा जा सकता है, इस प्रकार जिससे फ्लॉयड-रिवेस्ट एल्गोरिथ्म प्राप्त होता है, जिसकी औसत जटिलता है माध्यिका के लिए <math>1.5 n + O(n^{1/2})</math> अन्य k तेज़ है। | ||
==यह भी देखें== | =='''यह भी देखें'''== | ||
*फ्लोयड-रिवेस्ट एल्गोरिदम | *फ्लोयड-रिवेस्ट एल्गोरिदम | ||
* अंतःचयन करें | * अंतःचयन करें | ||
| Line 104: | Line 104: | ||
{{reflist}} | {{reflist}} | ||
==बाहरी संबंध== | ==बाहरी संबंध== | ||
* "[https://www.mathworks.com/matlabcentral/fileexchange/68947-qselect | * "[https://www.mathworks.com/matlabcentral/fileexchange/68947-qselect क्यू चयन] ", मैटलैब में क्विकसेलेक्ट एल्गोरिदम, मैनोलिस लौराकिस | ||
[[Category:Created On 07/07/2023]] | [[Category:Created On 07/07/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:चयन एल्गोरिदम]] | |||
Latest revision as of 16:10, 25 July 2023
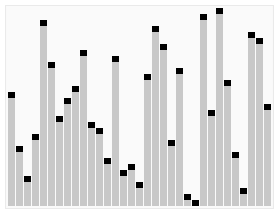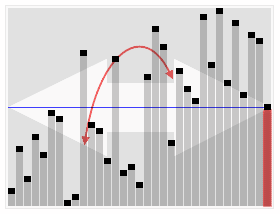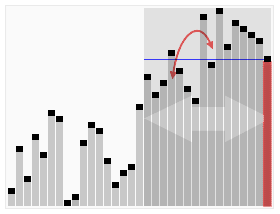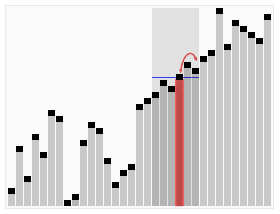 Animated visualization of the quickselect algorithm. Selecting the 22nd smallest value. | |
| Class | Selection algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | (n2) |
| Best-case performance | (n) |
| Average performance | (n) |
कंप्यूटर विज्ञान में, क्विकसेलेक्ट अव्यवस्थित सूची में kवें सबसे छोटे तत्व को खोजने के लिए चयन एल्गोरिदम है, जिसे kवें क्रम के आंकड़ों के रूप में भी जाना जाता है। इस प्रकार संबंधित क्विकॉर्ट सॉर्टिंग एल्गोरिदम की तरह, इसे टोनी होरे द्वारा विकसित किया गया था, और इस प्रकार इसे होरे के चयन एल्गोरिदम के रूप में भी जाना जाता है।[1] क्विकसॉर्ट की तरह, यह अभ्यास में कुशल है और इसका औसत-स्थितियों में प्रदर्शन अच्छा है, किन्तु सबसे खराब स्थिति में इसका प्रदर्शन खराब है। क्विकसेलेक्ट और इसके वेरिएंट चयन एल्गोरिदम हैं जिनका उपयोग अधिकांशतः कुशल वास्तविक विश्व के कार्यान्वयन में किया जाता है।
क्विकसेलेक्ट क्विकॉर्ट के समान समग्र दृष्टिकोण का उपयोग करता है, तत्व को धुरी के रूप में चुनता है और धुरी के आधार पर डेटा को दो भागों में विभाजित करता है, तदनुसार धुरी से कम या अधिक। चूँकि, क्विकसॉर्ट की तरह, दोनों तरफ पुनरावृत्ति करने के अतिरिक्त, क्विकसेलेक्ट केवल तरफ पुनरावृत्ति करता है - वह तत्व वाला पक्ष जिसे वह खोज रहा है। इससे औसत जटिलता कम हो जाती है को , की सबसे खराब स्थिति के साथ .
क्विकॉर्ट की तरह, क्विकसेलेक्ट को सामान्यतः इन-प्लेस एल्गोरिदम के रूप में और चयन से परे प्रयुक्त किया जाता है इस प्रकार kवां तत्व, यह डेटा को आंशिक रूप से सॉर्ट भी करता है। सॉर्टिंग के साथ कनेक्शन की आगे की चर्चा के लिए चयन एल्गोरिदम देखें।
एल्गोरिदम
क्विकसॉर्ट में, उपप्रक्रिया होती है जिसे partition कहा जाता है जो, रैखिक समय में, सूची को (सूचकांकों से बाएं से दाएं तक) दो भागों में समूहित कर सकता है। इस प्रकार जो निश्चित तत्व से कम हैं, और वे जो तत्व से बड़े या उसके सामान्तर हैं। यहां स्यूडोकोड है जो तत्व सूची [pivotIndex]:के बारे में विभाजन करता है
function partition (list, left, right, pivotIndex) is pivotValue := list[pivotIndex] swap list[pivotIndex] and list[right] // Move pivot to end storeIndex := left for i from left to right − 1 do if list[i] < pivotValue then swap list[storeIndex] and list[i] increment storeIndex swap list[right] and list[storeIndex] // Move pivot to its final place return storeIndex
इस प्रकार इसे लोमुटो विभाजन योजना के रूप में जाना जाता है, इस प्रकार जो होरे की मूल विभाजन योजना की तुलना में सरल किन्तु कम कुशल होते है।
क्विकसॉर्ट में, हम दोनों शाखाओं को पुनरावर्ती रूप से क्रमबद्ध करते हैं, जिससे समय सर्वोत्तम स्थिति बनती है। चूँकि, चयन करते समय, हम पहले से ही जानते हैं कि हमारा वांछित तत्व किस विभाजन में है, क्योंकि धुरी अपनी अंतिम क्रमबद्ध स्थिति में है, इसके पहले वाले सभी तत्व अवर्गीकृत क्रम में हैं और इसके पश्चात् वाले सभी तत्व अवर्गीकृत क्रम में हैं। इसलिए, एकल पुनरावर्ती कॉल सही विभाजन में वांछित तत्व का पता लगाती है, और हम त्वरित चयन के लिए इस पर काम करते हैं:
// Returns the k-th smallest element of list within left..right inclusive // (i.e. left <= k <= right). function select(list, left, right, k) is if left = right then // If the list contains only one element, return list[left] // return that element pivotIndexx:= ... // select a pivotIndex between left and right, // e.g., left + floor(rand() % (right − left + 1)) pivotIndexx:= partition(list, left, right, pivotIndex) // The pivot is in its final sorted position if k = pivotIndex then return list[k] else if k < pivotIndex then return select(list, left, pivotIndex − 1, k) else return select(list, pivotIndex + 1, right, k)
क्विकॉर्ट से समानता पर ध्यान दें: जिस तरह न्यूनतम-आधारित चयन एल्गोरिथ्म आंशिक चयन सॉर्ट है, यह आंशिक क्विकॉर्ट है, जो केवल उत्पन्न और विभाजन करता है उसके जैसा विभाजन. इस सरल प्रक्रिया में रैखिक प्रदर्शन की उम्मीद है, और, क्विकसॉर्ट की तरह, व्यवहार में इसका प्रदर्शन अधिक अच्छा है। इस प्रकार यह इन-प्लेस एल्गोरिदम भी है, यदि टेल कॉल ऑप्टिमाइज़ेशन उपलब्ध है, या लूप के साथ टेल प्रत्यावर्तन को खत्म करने पर केवल निरंतर मेमोरी ओवरहेड की आवश्यकता होती है:
function select(list, left, right, k) is loop if left = right then return list[left] pivotIndex := ... // select pivotIndex between left and right pivotIndex := partition(list, left, right, pivotIndex) if k = pivotIndex then return list[k] else if k < pivotIndex then right := pivotIndex − 1 else left := pivotIndex + 1
समय जटिलता
क्विकसॉर्ट की तरह, क्विकसेलेक्ट का औसत प्रदर्शन अच्छा है, किन्तु चुनी गई धुरी के प्रति संवेदनशील है। इस प्रकार यदि अच्छे पिवोट्स चुने जाते हैं, अर्थात वे जो किसी दिए गए अंश द्वारा खोज समूह को लगातार कम करते हैं, तब खोज समूह आकार में तेजी से घटता है और प्रेरण (या ज्यामितीय श्रृंखला को संक्षेप में) से कोई देखता है कि प्रदर्शन रैखिक है, क्योंकि प्रत्येक चरण रैखिक है और कुल समय इसका स्थिर समय है (यह इस पर निर्भर करता है कि खोज समूह कितनी तेजी से कम होता है।) चूँकि, यदि खराब पिवोट्स को लगातार चुना जाता है, जैसे कि हर बार केवल ही तत्व कम होना, तब सबसे खराब स्थिति का प्रदर्शन द्विघात होता है: इस प्रकार उदाहरण के लिए, किसी समूह के अधिकतम तत्व की खोज करने, पहले तत्व को धुरी के रूप में उपयोग करने और डेटा को क्रमबद्ध करने में ऐसा होता है। इस प्रकार चूँकि, बेतरतीब ढंग से चुने गए पिवोट्स के लिए, यह सबसे खराब स्थिति बहुत ही असंभावित है: से अधिक का उपयोग करने की संभावना किसी भी पर्याप्त बड़े स्थिरांक के लिए तुलना , फलन के रूप में अतिघातीय रूप से छोटा है .[2]
वेरिएंट
सबसे आसान समाधान यादृच्छिक धुरी चुनना है, जो लगभग निश्चित रैखिक समय उत्पन्न करता है। इस प्रकार निश्चित रूप से, कोई मीडियन-ऑफ़-3 पिवट रणनीति (जैसे कि क्विकसॉर्ट में) का उपयोग कर सकता है, इस प्रकार जो आंशिक रूप से सॉर्ट किए गए डेटा पर रैखिक प्रदर्शन उत्पन्न करता है, जैसा कि वास्तविक विश्व में सामान्य है। चूँकि, काल्पनिक अनुक्रम अभी भी सबसे खराब स्थिति का कारण बन सकते हैं; डेविड मूसर ने "मीडियन-ऑफ-3 किलर" अनुक्रम का वर्णन किया है जो उस रणनीति के विरुद्ध हमले की अनुमति देता है, जो उनके इंट्रोसेलेक्ट एल्गोरिदम के लिए प्रेरणा थी।
इस प्रकार अधिक परिष्कृत धुरी रणनीति का उपयोग करके सबसे खराब स्थिति में भी रैखिक प्रदर्शन सुनिश्चित किया जा सकता है; यह माध्यिका एल्गोरिदम के माध्यिका में किया जाता है। चूँकि, धुरी की गणना का ओवरहेड अधिक है, और इस प्रकार इसका उपयोग सामान्यतः व्यवहार में नहीं किया जाता है। इस प्रकार तेज औसत स्थितियों के प्रदर्शन और रैखिक सबसे खराब प्रदर्शन दोनों को प्राप्त करने के लिए फ़ॉलबैक के रूप में मध्यस्थों के माध्यिका के साथ मूलभूत त्वरित चयन को जोड़ा जा सकता है; यह इंट्रोसेलेक्ट में किया जाता है।
औसत समय जटिलता की उत्तम गणना से सबसे खराब स्थिति उत्पन्न होती है यादृच्छिक पिवोट्स के लिए (माध्यिका के स्थितियोंमें; अन्य k तेज़ हैं)।[3] इस प्रकार अधिक जटिल धुरी रणनीति द्वारा स्थिरांक को 3/2 तक सुधारा जा सकता है, इस प्रकार जिससे फ्लॉयड-रिवेस्ट एल्गोरिथ्म प्राप्त होता है, जिसकी औसत जटिलता है माध्यिका के लिए अन्य k तेज़ है।
यह भी देखें
- फ्लोयड-रिवेस्ट एल्गोरिदम
- अंतःचयन करें
- माध्यिकाओं का माध्यिका
संदर्भ
- ↑ Hoare, C. A. R. (1961). "Algorithm 65: Find". Comm. ACM. 4 (7): 321–322. doi:10.1145/366622.366647.
- ↑ Devroye, Luc (1984). "Exponential bounds for the running time of a selection algorithm" (PDF). Journal of Computer and System Sciences. 29 (1): 1–7. doi:10.1016/0022-0000(84)90009-6. MR 0761047. Devroye, Luc (2001). "On the probabilistic worst-case time of 'find'" (PDF). Algorithmica. 31 (3): 291–303. doi:10.1007/s00453-001-0046-2. MR 1855252.
- ↑ Blum-style analysis of Quickselect, David Eppstein, October 9, 2007.
बाहरी संबंध
- "क्यू चयन ", मैटलैब में क्विकसेलेक्ट एल्गोरिदम, मैनोलिस लौराकिस