बेलनाकार और गोलाकार निर्देशांक में सदिश फ़ील्ड: Difference between revisions
No edit summary |
No edit summary |
||
| (8 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Vector field representation in 3D curvilinear coordinate systems}} | {{Short description|Vector field representation in 3D curvilinear coordinate systems}} | ||
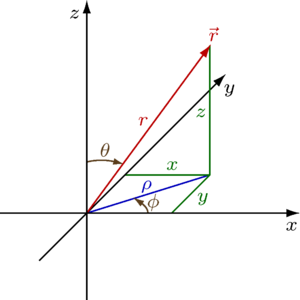
[[File:3D Spherical.svg|thumb|240px|right|गोलाकार निर्देशांक (r, θ, φ) जैसा कि | [[File:3D Spherical.svg|thumb|240px|right|गोलाकार निर्देशांक (r, θ, φ) जैसा कि सामान्यतः भौतिकी में उपयोग किया जाता है: रेडियल दूरी r, ध्रुवीय कोण θ ([[थीटा]]), और अज़ीमुथल कोण φ ([[phi]])। प्रतीक ρ ([[rho]]) का प्रयोग अक्सर r के स्थान पर किया जाता है।]]नोट: यह पृष्ठ गोलाकार निर्देशांक के लिए सामान्य भौतिकी संकेतन का उपयोग करता है, इस प्रकार जिसमें <math>\theta</math> z अक्ष और मूल बिंदु को विचाराधीन बिंदु से जोड़ने वाले त्रिज्या सदिश के मध्य का कोण है, जबकि <math>\phi</math> x-y तल और x अक्ष पर त्रिज्या सदिश के प्रक्षेपण के मध्य का कोण है। इस प्रकार कई अन्य परिभाषाएँ उपयोग में हैं, और इसलिए विभिन्न स्रोतों की तुलना करते समय सावधानी रखनी चाहिए।<ref name="wolfram">[http://mathworld.wolfram.com/CylindricalCoordinates.html Wolfram Mathworld, spherical coordinates]</ref> | ||
== बेलनाकार निर्देशांक प्रणाली == | |||
== बेलनाकार | |||
=== | === सदिश क्षेत्र === | ||
सदिशों को [[बेलनाकार निर्देशांक]] | सदिशों को [[बेलनाकार निर्देशांक]] में (ρ, φ, z) द्वारा परिभाषित किया जाता है, जहाँ | ||
* ρ xy-तल पर प्रक्षेपित | * ρ xy-तल पर प्रक्षेपित सदिश की लंबाई है, | ||
* φ, xy-तल ( | * φ, xy-तल (अर्थात ρ) और सकारात्मक x-अक्ष (0 ≤ φ < 2π) पर सदिश के प्रक्षेपण के मध्य का कोण है। | ||
* z नियमित z-निर्देशांक है। | * z नियमित z-निर्देशांक है। | ||
| Line 26: | Line 23: | ||
= A_x \mathbf{\hat x} + A_y \mathbf{\hat y} + A_z \mathbf{\hat z} | = A_x \mathbf{\hat x} + A_y \mathbf{\hat y} + A_z \mathbf{\hat z} | ||
= A_\rho \mathbf{\hat \rho} + A_\phi \boldsymbol{\hat \phi} + A_z \mathbf{\hat z}</math> | = A_\rho \mathbf{\hat \rho} + A_\phi \boldsymbol{\hat \phi} + A_z \mathbf{\hat z}</math> | ||
बेलनाकार इकाई | बेलनाकार इकाई सदिश कार्तीय इकाई सदिश से संबंधित हैं: | ||
<math display="block">\begin{bmatrix}\mathbf{\hat \rho} \\ \boldsymbol{\hat\phi} \\ \mathbf{\hat z}\end{bmatrix} | <math display="block">\begin{bmatrix}\mathbf{\hat \rho} \\ \boldsymbol{\hat\phi} \\ \mathbf{\hat z}\end{bmatrix} | ||
= \begin{bmatrix} | = \begin{bmatrix} | ||
| Line 34: | Line 31: | ||
\end{bmatrix} | \end{bmatrix} | ||
\begin{bmatrix} \mathbf{\hat x} \\ \mathbf{\hat y} \\ \mathbf{\hat z} \end{bmatrix}</math> | \begin{bmatrix} \mathbf{\hat x} \\ \mathbf{\hat y} \\ \mathbf{\hat z} \end{bmatrix}</math> | ||
ध्यान दें: | ध्यान दें: आव्यूह [[ऑर्थोगोनल मैट्रिक्स|ऑर्थोगोनल आव्यूह]] है, अर्थात इसका व्युत्क्रमणीय आव्यूह इसका स्थानान्तरण है। | ||
=== एक सदिश क्षेत्र का समय व्युत्पन्न === | === एक सदिश क्षेत्र का समय व्युत्पन्न === | ||
यह पता लगाने के लिए कि सदिश क्षेत्र A समय में कैसे | यह पता लगाने के लिए कि सदिश क्षेत्र A समय में कैसे परिवर्तित होते है, इस प्रकार समय व्युत्पन्न की गणना की जानी चाहिए। इस प्रयोजन के लिए समय व्युत्पन्न के लिए न्यूटन के अंकन (<math>\dot{\mathbf{A}}</math>) का उपयोग किया जाता है कार्तीय निर्देशांक में यह केवल है: | ||
इस प्रयोजन के लिए समय व्युत्पन्न के लिए न्यूटन के अंकन | |||
<math display="block">\dot{\mathbf{A}} = \dot{A}_x \hat{\mathbf{x}} + \dot{A}_y \hat{\mathbf{y}} + \dot{A}_z \hat{\mathbf{z}}</math> | <math display="block">\dot{\mathbf{A}} = \dot{A}_x \hat{\mathbf{x}} + \dot{A}_y \hat{\mathbf{y}} + \dot{A}_z \hat{\mathbf{z}}</math> | ||
चूँकि, बेलनाकार निर्देशांक में यह बन जाता है: | |||
<math display="block">\dot{\mathbf{A}} = \dot{A}_\rho \hat{\boldsymbol{\rho}} + A_\rho \dot{\hat{\boldsymbol{\rho}}} | <math display="block">\dot{\mathbf{A}} = \dot{A}_\rho \hat{\boldsymbol{\rho}} + A_\rho \dot{\hat{\boldsymbol{\rho}}} | ||
+ \dot{A}_\phi \hat{\boldsymbol{\phi}} + A_\phi \dot{\hat{\boldsymbol{\phi}}} | + \dot{A}_\phi \hat{\boldsymbol{\phi}} + A_\phi \dot{\hat{\boldsymbol{\phi}}} | ||
+ \dot{A}_z \hat{\boldsymbol{z}} + A_z \dot{\hat{\boldsymbol{z}}}</math> | + \dot{A}_z \hat{\boldsymbol{z}} + A_z \dot{\hat{\boldsymbol{z}}}</math> | ||
यूनिट | यूनिट सदिश के समय व्युत्पन्न की आवश्यकता है। वे इसके द्वारा दिए गए हैं: | ||
वे इसके द्वारा दिए गए हैं: | |||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
\dot{\hat{\mathbf{\rho}}} & = \dot{\phi} \hat{\boldsymbol{\phi}} \\ | \dot{\hat{\mathbf{\rho}}} & = \dot{\phi} \hat{\boldsymbol{\phi}} \\ | ||
| Line 58: | Line 52: | ||
+ \hat{\boldsymbol{\phi}} \left(\dot{A}_\phi + A_\rho \dot{\phi}\right) | + \hat{\boldsymbol{\phi}} \left(\dot{A}_\phi + A_\rho \dot{\phi}\right) | ||
+ \hat{\mathbf{z}} \dot{A}_z</math> | + \hat{\mathbf{z}} \dot{A}_z</math> | ||
=== सदिश क्षेत्र का दूसरी बार व्युत्पन्न === | === सदिश क्षेत्र का दूसरी बार व्युत्पन्न === | ||
दूसरी बार व्युत्पन्न भौतिकी में रुचि का है, क्योंकि यह [[शास्त्रीय यांत्रिकी]] प्रणालियों के लिए [[गति के समीकरण]] | दूसरी बार व्युत्पन्न भौतिकी में रुचि का है, क्योंकि यह [[शास्त्रीय यांत्रिकी|मौलिक यांत्रिकी]] प्रणालियों के लिए [[गति के समीकरण]] में पाया जाता है। इस प्रकार बेलनाकार निर्देशांक में सदिश क्षेत्र का दूसरी बार व्युत्पन्न निम्न द्वारा दिया गया है: | ||
बेलनाकार निर्देशांक में | |||
<math display="block">\mathbf{\ddot A} | <math display="block">\mathbf{\ddot A} | ||
= \mathbf{\hat \rho} \left(\ddot A_\rho - A_\phi \ddot\phi - 2 \dot A_\phi \dot\phi - A_\rho \dot\phi^2\right) | = \mathbf{\hat \rho} \left(\ddot A_\rho - A_\phi \ddot\phi - 2 \dot A_\phi \dot\phi - A_\rho \dot\phi^2\right) | ||
+ \boldsymbol{\hat\phi} \left(\ddot A_\phi + A_\rho \ddot\phi + 2 \dot A_\rho \dot\phi - A_\phi \dot\phi^2\right) | + \boldsymbol{\hat\phi} \left(\ddot A_\phi + A_\rho \ddot\phi + 2 \dot A_\rho \dot\phi - A_\phi \dot\phi^2\right) | ||
+ \mathbf{\hat z} \ddot A_z</math> | + \mathbf{\hat z} \ddot A_z</math> | ||
इस | इस एक्सप्रेशन को समझने के लिए, P के स्थान पर A प्रतिस्थापित किया जाता है, जहाँ P सदिश (''ρ'', ''φ'', ''z'') है। | ||
इस का | इस का कारण है कि <math>\mathbf{A} = \mathbf{P} = \rho \mathbf{\hat \rho} + z \mathbf{\hat z}</math>. | ||
प्रतिस्थापित करने के | प्रतिस्थापित करने के पश्चात , परिणाम दिया गया है: | ||
<math display="block">\ddot\mathbf{P} | <math display="block">\ddot\mathbf{P} | ||
= \mathbf{\hat \rho} \left(\ddot \rho - \rho \dot\phi^2\right) | = \mathbf{\hat \rho} \left(\ddot \rho - \rho \dot\phi^2\right) | ||
+ \boldsymbol{\hat\phi} \left(\rho \ddot\phi + 2 \dot \rho \dot\phi\right) | + \boldsymbol{\hat\phi} \left(\rho \ddot\phi + 2 \dot \rho \dot\phi\right) | ||
+ \mathbf{\hat z} \ddot z</math> | + \mathbf{\hat z} \ddot z</math> | ||
यांत्रिकी में, इस | यांत्रिकी में, इस एक्सप्रेशन के पदों को कहा जाता है: | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
\ddot \rho \mathbf{\hat \rho} &= \text{central outward acceleration} \\ | \ddot \rho \mathbf{\hat \rho} &= \text{central outward acceleration} \\ | ||
| Line 86: | Line 77: | ||
\end{align}</math> | \end{align}</math> | ||
{{See also| | {{See also|अभिकेन्द्रीय बल|कोणीय वेग|कॉरिओलिस प्रभाव}} | ||
==गोलाकार | ==गोलाकार निर्देशांक प्रणाली == | ||
=== | === सदिश क्षेत्र === | ||
सदिश को [[गोलाकार निर्देशांक]] में (r, θ, φ) द्वारा परिभाषित किया जाता है, जहां | |||
*r | *r सदिश की लंबाई है, | ||
* θ सकारात्मक Z-अक्ष और प्रश्न में | * θ सकारात्मक Z-अक्ष और प्रश्न में सदिश (0 ≤ θ ≤ π), के मध्य का कोण है और | ||
* φ xy-तल पर | * φ xy-तल पर सदिश के प्रक्षेपण और सकारात्मक X-अक्ष (0 ≤ φ < 2π) के मध्य का कोण है। | ||
(r, θ, φ) कार्तीय निर्देशांक में दिया गया है: | (r, θ, φ) कार्तीय निर्देशांक में दिया गया है: | ||
| Line 116: | Line 107: | ||
-\sin\phi & \cos\phi & 0 \end{bmatrix} | -\sin\phi & \cos\phi & 0 \end{bmatrix} | ||
\begin{bmatrix} \mathbf{\hat x} \\ \mathbf{\hat y} \\ \mathbf{\hat z} \end{bmatrix}</math> | \begin{bmatrix} \mathbf{\hat x} \\ \mathbf{\hat y} \\ \mathbf{\hat z} \end{bmatrix}</math> | ||
ध्यान दें: | ध्यान दें: आव्यूह ऑर्थोगोनल आव्यूह है, अर्थात इसका व्युत्क्रम केवल इसका स्थानान्तरण है। | ||
कार्तीय इकाई सदिश इस प्रकार गोलाकार इकाई सदिशों से संबंधित हैं: | कार्तीय इकाई सदिश इस प्रकार गोलाकार इकाई सदिशों से संबंधित हैं: | ||
| Line 124: | Line 115: | ||
\cos\theta & -\sin\theta & 0 \end{bmatrix} | \cos\theta & -\sin\theta & 0 \end{bmatrix} | ||
\begin{bmatrix} \boldsymbol{\hat{r}} \\ \boldsymbol{\hat\theta} \\ \boldsymbol{\hat\phi} \end{bmatrix}</math> | \begin{bmatrix} \boldsymbol{\hat{r}} \\ \boldsymbol{\hat\theta} \\ \boldsymbol{\hat\phi} \end{bmatrix}</math> | ||
=== एक सदिश क्षेत्र का समय व्युत्पन्न === | === एक सदिश क्षेत्र का समय व्युत्पन्न === | ||
यह पता लगाने के लिए कि सदिश क्षेत्र A समय में कैसे | यह पता लगाने के लिए कि सदिश क्षेत्र A समय में कैसे परिवर्तित है, इस प्रकार समय व्युत्पन्न की गणना की जानी चाहिए। कार्तीय निर्देशांक में यह पर्याप्त है: | ||
<math display="block">\mathbf{\dot A} = \dot A_x \mathbf{\hat x} + \dot A_y \mathbf{\hat y} + \dot A_z \mathbf{\hat z}</math> | <math display="block">\mathbf{\dot A} = \dot A_x \mathbf{\hat x} + \dot A_y \mathbf{\hat y} + \dot A_z \mathbf{\hat z}</math> | ||
चूँकि, गोलाकार निर्देशांक में यह बन जाता है: | |||
<math display="block">\mathbf{\dot A} = \dot A_r \boldsymbol{\hat r} + A_r \boldsymbol{\dot{\hat r}} | <math display="block">\mathbf{\dot A} = \dot A_r \boldsymbol{\hat r} + A_r \boldsymbol{\dot{\hat r}} | ||
+ \dot A_\theta \boldsymbol{\hat\theta} + A_\theta \boldsymbol{\dot{\hat\theta}} | + \dot A_\theta \boldsymbol{\hat\theta} + A_\theta \boldsymbol{\dot{\hat\theta}} | ||
+ \dot A_\phi \boldsymbol{\hat\phi} + A_\phi \boldsymbol{\dot{\hat\phi}}</math> | + \dot A_\phi \boldsymbol{\hat\phi} + A_\phi \boldsymbol{\dot{\hat\phi}}</math> | ||
यूनिट | यूनिट सदिश के समय व्युत्पन्न की आवश्यकता है। वे इसके द्वारा दिए गए हैं: | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
\boldsymbol{\dot{\hat r}} &= \dot\theta \boldsymbol{\hat\theta} + \dot\phi\sin\theta \boldsymbol{\hat\phi} \\ | \boldsymbol{\dot{\hat r}} &= \dot\theta \boldsymbol{\hat\theta} + \dot\phi\sin\theta \boldsymbol{\hat\phi} \\ | ||
| Line 146: | Line 134: | ||
+ \boldsymbol{\hat\theta} \left(\dot A_\theta + A_r \dot\theta - A_\phi \dot\phi \cos\theta\right) | + \boldsymbol{\hat\theta} \left(\dot A_\theta + A_r \dot\theta - A_\phi \dot\phi \cos\theta\right) | ||
+ \boldsymbol{\hat\phi} \left(\dot A_\phi + A_r \dot\phi \sin\theta + A_\theta \dot\phi \cos\theta\right)</math> | + \boldsymbol{\hat\phi} \left(\dot A_\phi + A_r \dot\phi \sin\theta + A_\theta \dot\phi \cos\theta\right)</math> | ||
== यह भी देखें == | |||
* विभिन्न निर्देशांक प्रणालियों में [[ ग्रेडियेंट |प्रवणता]] , [[ विचलन |विचलन]] , [[कर्ल (गणित)]], और [[लाप्लासियन]] के विनिर्देशन के लिए [[बेलनाकार और गोलाकार निर्देशांक में डेल]] का उपयोग किया जाता है। | |||
==संदर्भ == | |||
==संदर्भ== | |||
<references/> | <references/> | ||
{{DEFAULTSORT:Vector Fields In Cylindrical And Spherical Coordinates}} | {{DEFAULTSORT:Vector Fields In Cylindrical And Spherical Coordinates}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page|Vector Fields In Cylindrical And Spherical Coordinates]] | ||
[[Category:Created On 08/07/2023]] | [[Category:Created On 08/07/2023|Vector Fields In Cylindrical And Spherical Coordinates]] | ||
[[Category:Lua-based templates|Vector Fields In Cylindrical And Spherical Coordinates]] | |||
[[Category:Machine Translated Page|Vector Fields In Cylindrical And Spherical Coordinates]] | |||
[[Category:Pages with script errors|Vector Fields In Cylindrical And Spherical Coordinates]] | |||
[[Category:Templates Vigyan Ready|Vector Fields In Cylindrical And Spherical Coordinates]] | |||
[[Category:Templates that add a tracking category|Vector Fields In Cylindrical And Spherical Coordinates]] | |||
[[Category:Templates that generate short descriptions|Vector Fields In Cylindrical And Spherical Coordinates]] | |||
[[Category:Templates using TemplateData|Vector Fields In Cylindrical And Spherical Coordinates]] | |||
[[Category:वेक्टर कलन|Vector Fields In Cylindrical And Spherical Coordinates]] | |||
[[Category:सिस्टम संयोजित करें|Vector Fields In Cylindrical And Spherical Coordinates]] | |||
Latest revision as of 14:31, 28 July 2023
नोट: यह पृष्ठ गोलाकार निर्देशांक के लिए सामान्य भौतिकी संकेतन का उपयोग करता है, इस प्रकार जिसमें z अक्ष और मूल बिंदु को विचाराधीन बिंदु से जोड़ने वाले त्रिज्या सदिश के मध्य का कोण है, जबकि x-y तल और x अक्ष पर त्रिज्या सदिश के प्रक्षेपण के मध्य का कोण है। इस प्रकार कई अन्य परिभाषाएँ उपयोग में हैं, और इसलिए विभिन्न स्रोतों की तुलना करते समय सावधानी रखनी चाहिए।[1]
बेलनाकार निर्देशांक प्रणाली
सदिश क्षेत्र
सदिशों को बेलनाकार निर्देशांक में (ρ, φ, z) द्वारा परिभाषित किया जाता है, जहाँ
- ρ xy-तल पर प्रक्षेपित सदिश की लंबाई है,
- φ, xy-तल (अर्थात ρ) और सकारात्मक x-अक्ष (0 ≤ φ < 2π) पर सदिश के प्रक्षेपण के मध्य का कोण है।
- z नियमित z-निर्देशांक है।
(ρ, φ, z) कार्तीय निर्देशांक में दिया गया है:
या इसके विपरीत:
एक सदिश क्षेत्र का समय व्युत्पन्न
यह पता लगाने के लिए कि सदिश क्षेत्र A समय में कैसे परिवर्तित होते है, इस प्रकार समय व्युत्पन्न की गणना की जानी चाहिए। इस प्रयोजन के लिए समय व्युत्पन्न के लिए न्यूटन के अंकन () का उपयोग किया जाता है कार्तीय निर्देशांक में यह केवल है:
सदिश क्षेत्र का दूसरी बार व्युत्पन्न
दूसरी बार व्युत्पन्न भौतिकी में रुचि का है, क्योंकि यह मौलिक यांत्रिकी प्रणालियों के लिए गति के समीकरण में पाया जाता है। इस प्रकार बेलनाकार निर्देशांक में सदिश क्षेत्र का दूसरी बार व्युत्पन्न निम्न द्वारा दिया गया है:
इस का कारण है कि .
प्रतिस्थापित करने के पश्चात , परिणाम दिया गया है:
गोलाकार निर्देशांक प्रणाली
सदिश क्षेत्र
सदिश को गोलाकार निर्देशांक में (r, θ, φ) द्वारा परिभाषित किया जाता है, जहां
- r सदिश की लंबाई है,
- θ सकारात्मक Z-अक्ष और प्रश्न में सदिश (0 ≤ θ ≤ π), के मध्य का कोण है और
- φ xy-तल पर सदिश के प्रक्षेपण और सकारात्मक X-अक्ष (0 ≤ φ < 2π) के मध्य का कोण है।
(r, θ, φ) कार्तीय निर्देशांक में दिया गया है:
कार्तीय इकाई सदिश इस प्रकार गोलाकार इकाई सदिशों से संबंधित हैं:
एक सदिश क्षेत्र का समय व्युत्पन्न
यह पता लगाने के लिए कि सदिश क्षेत्र A समय में कैसे परिवर्तित है, इस प्रकार समय व्युत्पन्न की गणना की जानी चाहिए। कार्तीय निर्देशांक में यह पर्याप्त है:
यह भी देखें
- विभिन्न निर्देशांक प्रणालियों में प्रवणता , विचलन , कर्ल (गणित), और लाप्लासियन के विनिर्देशन के लिए बेलनाकार और गोलाकार निर्देशांक में डेल का उपयोग किया जाता है।