प्रायिकता वितरण: Difference between revisions
m (9 revisions imported from alpha:प्रायिकता_वितरण) |
|||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
संभाव्यता सिद्धांत और आंकड़ों में, संभाव्यता वितरण गणितीय फलन (गणित) है जो प्रयोग (संभाव्यता सिद्धांत) के लिए विभिन्न संभावित परिणामों की घटना की संभावना देता है।<ref name=":02">{{Cite book|title=कैम्ब्रिज डिक्शनरी ऑफ स्टैटिस्टिक्स|last=Everitt | first = Brian |date=2006|publisher=Cambridge University Press|isbn=978-0-511-24688-3 |edition=3rd|location=Cambridge, UK|oclc=161828328}}</ref><ref>{{Cite book|title=मूल संभावना सिद्धांत|last=Ash, Robert B.|date=2008|publisher=Dover Publications |isbn=978-0-486-46628-6 |edition=Dover |location=Mineola, N.Y. |pages=66–69|oclc=190785258}}</ref> यह इसके नमूना समष्टि और घटना की संभावना (संभाव्यता सिद्धांत) (नमूना समष्टि के उपसमुच्चय) के संदर्भ में यादृच्छिकता घटना का गणितीय विवरण है।<ref name=":1">{{cite book|title=संभाव्यता और सांख्यिकी: अनिश्चितता का विज्ञान|last1=Evans |first1=Michael |date=2010|publisher=W.H. Freeman and Co|last2=Rosenthal |first2=Jeffrey S. |isbn=978-1-4292-2462-8 |edition=2nd|location=New York|pages=38|oclc=473463742}}</ref> | |||
संभाव्यता सिद्धांत और आंकड़ों में, संभाव्यता वितरण गणितीय | |||
उदाहरण के लिए, यदि {{mvar|X}} सिक्का टॉस (प्रयोग) के परिणाम को निरूपित करने के लिए उपयोग किया जाता है, फिर {{mvar|X}} की संभावना वितरण {{math|1=''X'' = heads}} के लिए मान 0.5 (2 या 1/2 में 1) और 0.5 ले जाएगा {{math|1=''X'' = टेल}} (उस निष्पक्ष सिक्के को मानते हुए)। यादृच्छिक घटनाओं के उदाहरणों में कुछ भविष्य की तारीख में मौसम की स्थिति, यादृच्छिक रूप से चयनित व्यक्ति की ऊंचाई, स्कूल में पुरुष छात्रों का अंश, सर्वेक्षण पद्धति के परिणामों का संचालन करना, आदि सम्मिलित हैं।<ref name="ross" /> | उदाहरण के लिए, यदि {{mvar|X}} सिक्का टॉस (प्रयोग) के परिणाम को निरूपित करने के लिए उपयोग किया जाता है, फिर {{mvar|X}} की संभावना वितरण {{math|1=''X'' = heads}} के लिए मान 0.5 (2 या 1/2 में 1) और 0.5 ले जाएगा {{math|1=''X'' = टेल}} (उस निष्पक्ष सिक्के को मानते हुए)। यादृच्छिक घटनाओं के उदाहरणों में कुछ भविष्य की तारीख में मौसम की स्थिति, यादृच्छिक रूप से चयनित व्यक्ति की ऊंचाई, स्कूल में पुरुष छात्रों का अंश, सर्वेक्षण पद्धति के परिणामों का संचालन करना, आदि सम्मिलित हैं।<ref name="ross" /> | ||
== परिचय == | == परिचय == | ||
[[File:Dice Distribution (bar).svg|thumb|250px|right|संभावना द्रव्यमान | [[File:Dice Distribution (bar).svg|thumb|250px|right|संभावना द्रव्यमान फलन (पीएमएफ) <math>p(S)</math> योग के लिए संभावना वितरण निर्दिष्ट करता है <math>S</math> दो पासा से मायने रखता है।उदाहरण के लिए, आंकड़ा दिखाता है कि <math>p(11) = 2/36 = 1/18</math>।पीएमएफ इस तरह की घटनाओं की संभावनाओं की गणना की अनुमति देता है <math>P(X > 9) = 1/12 + 1/18 + 1/36 = 1/6</math>, और वितरण में अन्य सभी संभावनाएं।]]एक संभावना वितरण घटनाओं की संभावनाओं, नमूना समष्टि के उपसमुच्चय की संभावनाओं का गणितीय विवरण है।नमूना समष्टि, जिसे अधिकांशतः <math>\Omega</math> निरूपित किया जाता है , यादृच्छिक घटना के सभी संभावित परिणामों (संभावना) का समुच्चय (गणित) है;यह कोई भी समुच्चय हो सकता है: वास्तविक संख्याओं का समुच्चय, सदिश (गणित) का समुच्चय, इच्छानुसार गैर-नामांकित मूल्यों का समुच्चय, आदि। उदाहरण के लिए, सिक्का फ्लिप का नमूना समष्टि {{math|1=Ω = {heads, tails}<nowiki/>}} होगा । | ||
यादृच्छिक | यादृच्छिक चर के विशिष्ट स्थितियोंके लिए संभाव्यता वितरण को परिभाषित करने के लिए (इसलिए नमूना समष्टि को संख्यात्मक समुच्चय के रूप में देखा जा सकता है), असतत और बिल्कुल निरंतर यादृच्छिक चर के मध्य अंतर करना आम है।असतत स्थितियोंमें, यह संभावना द्रव्यमान फलन <math>p</math> को निर्दिष्ट करने के लिए पर्याप्त है प्रत्येक संभावित परिणाम के लिए संभावना प्रदान करना: उदाहरण के लिए, उचित पासा फेंकते समय, छह मान 1 से 6 में से प्रत्येक में संभावना 1/6 होती है।एक घटना की संभावना (संभाव्यता सिद्धांत) को तब उन परिणामों की संभावनाओं का योग माना जाता है जो घटना को संतुष्ट करते हैं;उदाहरण के लिए, घटना की संभावना भी मूल्य रोल करती है | ||
<math display="block">p(2) + p(4) + p(6) = 1/6 + 1/6 + 1/6 = 1/2.</math> | <math display="block">p(2) + p(4) + p(6) = 1/6 + 1/6 + 1/6 = 1/2.</math> | ||
इसके विपरीत, जब यादृच्छिक | इसके विपरीत, जब यादृच्छिक चर निरंतरता से मान लेता है तब सामान्यतः, किसी भी व्यक्तिगत परिणाम में संभावना शून्य होती है और केवल ऐसी घटनाएं होती हैं जिनमें असीम रूप से अनेक परिणाम सम्मिलित होते हैं, जैसे कि अंतराल, सकारात्मक संभावना हो सकती है। उदाहरण के लिए, सुपरमार्केट में हैम के टुकड़े के वजन को मापने पर विचार करें, और मान लें कि मापदंड में स्पष्टता के अनेक अंक हैं।संभावना है कि इसका वजन ठीक 500 & g शून्य है, क्योंकि इसमें कुछ गैर-शून्य दशमलव अंक होंगे।फिर भी, कोई भी गुणवत्ता नियंत्रण में मांग कर सकता है, कि 500 & g हैम के पैकेज;का वजन कम से कम 98% संभावना के साथ 490 & g और 510 & g के मध्य वजन होना चाहिए, और यह मांग माप उपकरणों की स्पष्टता के लिए कम संवेदनशील है। | ||
[[File:Combined Cumulative Distribution Graphs.png|thumb|455x455px | बाईं ओर संभावना घनत्व फलन दिखाता है।अधिकार संचयी वितरण फलन को दर्शाता है, जिसके लिए मूल्य पर के सामान्तर क्षेत्र के सामान्तर होता है।]]बिल्कुल निरंतर संभावना वितरण को अनेक तरीकों से वर्णित किया जा सकता है।संभाव्यता घनत्व फलन किसी भी मूल्य की इनफिनिटिमल्स संभावना का वर्णन करता है, और संभावना है कि किसी दिए गए अंतराल में परिणाम निहित है, एकीकरण (गणित) द्वारा उस अंतराल पर संभावना घनत्व फलन द्वारा गणना की जा सकती है।<ref name=":3" />वितरण का वैकल्पिक विवरण संचयी वितरण फलन के माध्यम से है, जो इस संभावना का वर्णन करता है कि यादृच्छिक | [[File:Combined Cumulative Distribution Graphs.png|thumb|455x455px | बाईं ओर संभावना घनत्व फलन दिखाता है।अधिकार संचयी वितरण फलन को दर्शाता है, जिसके लिए मूल्य पर के सामान्तर क्षेत्र के सामान्तर होता है।]]बिल्कुल निरंतर संभावना वितरण को अनेक तरीकों से वर्णित किया जा सकता है।संभाव्यता घनत्व फलन किसी भी मूल्य की इनफिनिटिमल्स संभावना का वर्णन करता है, और संभावना है कि किसी दिए गए अंतराल में परिणाम निहित है, एकीकरण (गणित) द्वारा उस अंतराल पर संभावना घनत्व फलन द्वारा गणना की जा सकती है।<ref name=":3" />वितरण का वैकल्पिक विवरण संचयी वितरण फलन के माध्यम से है, जो इस संभावना का वर्णन करता है कि यादृच्छिक चर किसी दिए गए मूल्य से बड़ा नहीं है (अर्थात, कुछ <math>x</math> के लिए <math>P(X < x)</math>)।संचयी वितरण फलन से संभावना घनत्व फलन के <math>-\infty</math> को <math>x</math> अनुसार क्षेत्र है, जैसा कि चित्र द्वारा दाईं ओर वर्णित है।<ref name='dekking'>{{Cite book|title=संभावना और सांख्यिकी के लिए एक आधुनिक परिचय: समझ में क्यों और कैसे|date=2005|publisher=Springer|others=Dekking, Michel, 1946-|isbn=978-1-85233-896-1|location=London|oclc=262680588}}</ref> | ||
| Line 19: | Line 16: | ||
== सामान्य संभाव्यता परिभाषा == | == सामान्य संभाव्यता परिभाषा == | ||
एक संभाव्यता वितरण को विभिन्न रूपों में वर्णित किया जा सकता है, जैसे कि संभावना द्रव्यमान | एक संभाव्यता वितरण को विभिन्न रूपों में वर्णित किया जा सकता है, जैसे कि संभावना द्रव्यमान फलन या संचयी वितरण फलन द्वारा।सबसे सामान्य विवरणों में से एक, जो बिल्कुल निरंतर और असतत चर के लिए प्रयुक्त होता है, संभाव्यता फलन के <math>P\colon \mathcal{A} \to \Reals</math> माध्यम से है जिसका इनपुट स्पेस <math>\mathcal{A}</math> संबंधित है नमूना समष्टि के लिए, और इसके आउटपुट के रूप में वास्तविक संख्या <math>{\displaystyle [0,1]\subseteq \mathbb {R} }.</math> संभावना देता है। | ||
संभाव्यता फलन <math>P</math> नमूना | संभाव्यता फलन <math>P</math> नमूना समष्टि के तर्क उपसमुच्चय के रूप में ले सकते हैं, जैसा कि सिक्का टॉस उदाहरण में, जहां फलन <math>P</math> ऐसा परिभाषित किया गया था {{math|1=''P''(heads) = 0.5}} और {{math|1=''P''(tails) = 0.5}}।चूंकि, यादृच्छिक चर के व्यापक उपयोग के कारण, जो नमूना समष्टि को संख्याओं के समुच्चय में बदल देते हैं (जैसे, <math>\R</math>, <math>\N</math>), संभावना वितरण का अध्ययन करना अधिक सामान्य है, जिनके तर्क इन विशेष प्रकार के समुच्चयों (संख्या समुच्चय) के उपसमुच्चय हैं,<ref>{{cite book| last1 = Walpole | first1 = R.E. | last2 = Myers | first2 = R.H. | last3 = Myers | first3 = S.L. | last4 = Ye | first4 = K.|year=1999|title=इंजीनियरों के लिए संभावना और सांख्यिकी|publisher=Prentice Hall}}</ref> और इस लेख में चर ्चा की गई सभी संभावना वितरण इस प्रकार के हैं।के रूप में निरूपित करना आम है <math>P(X \in E)</math> संभावना है कि चर <math>X</math> का निश्चित मूल्य निश्चित घटना से संबंधित है <math>E</math>.<ref name="ross" /><ref name="degroot" /> | ||
उपरोक्त संभाव्यता फलन केवल संभाव्यता वितरण की विशेषता है यदि यह सभी कोल्मोगोरोव स्वयंसिद्ध को संतुष्ट करता है, अर्थात: | उपरोक्त संभाव्यता फलन केवल संभाव्यता वितरण की विशेषता है यदि यह सभी कोल्मोगोरोव स्वयंसिद्ध को संतुष्ट करता है, अर्थात: | ||
| Line 27: | Line 24: | ||
# <math>P(X \in E) \le 1 \; \forall E \in \mathcal{A}</math>, इसलिए कोई संभावना <math>1</math> से अधिक नहीं है | # <math>P(X \in E) \le 1 \; \forall E \in \mathcal{A}</math>, इसलिए कोई संभावना <math>1</math> से अधिक नहीं है | ||
# <math>P(X \in \bigsqcup_{i} E_i ) = \sum_i P(X \in E_i)</math> समुच्चय <math>\{ E_i \}</math> के किसी भी असंतुष्ट परिवार के लिए उपयोग नही किया जाता है | # <math>P(X \in \bigsqcup_{i} E_i ) = \sum_i P(X \in E_i)</math> समुच्चय <math>\{ E_i \}</math> के किसी भी असंतुष्ट परिवार के लिए उपयोग नही किया जाता है | ||
संभाव्यता फलन की अवधारणा को संभाव्यता | संभाव्यता फलन की अवधारणा को संभाव्यता समष्टि <math>(X, \mathcal{A}, P)</math> के तत्व के रूप में परिभाषित करके अधिक कठोर बना दिया जाता है , जहाँ <math>X</math> संभावित परिणामों का समुच्चय है, <math>\mathcal{A}</math> सभी उपसमुच्चय का समुच्चय है <math>E \subset X</math> जिनकी संभावना को मापा जा सकता है, और <math>P</math> संभावना फलन, या संभाव्यता माप है, जो इन औसत अंकिते के उपसमुच्चय में से प्रत्येक के लिए संभावना प्रदान करता है <math>E \in \mathcal{A}</math>.<ref name="billingsley">{{cite book|author1=Billingsley, P.|year=1986|title=संभावना और माप| publisher=Wiley | isbn=9780471804789}}</ref> | ||
संभाव्यता वितरण सामान्यतः दो वर्गों में से संबंधित हैं। तथा असतत संभावना वितरण उन परिदृश्यों पर प्रयुक्त होता है जहां संभावित परिणामों का समुच्चय असतत संभावना वितरण है (जैसे कि सिक्का टॉस, मरने का रोल) और संभावनाओं को परिणामों की संभावनाओं की असतत सूची द्वारा एन्कोड किया जाता है; इस स्थितियों में असतत संभावना वितरण को संभावना द्रव्यमान | संभाव्यता वितरण सामान्यतः दो वर्गों में से संबंधित हैं। तथा असतत संभावना वितरण उन परिदृश्यों पर प्रयुक्त होता है जहां संभावित परिणामों का समुच्चय असतत संभावना वितरण है (जैसे कि सिक्का टॉस, मरने का रोल) और संभावनाओं को परिणामों की संभावनाओं की असतत सूची द्वारा एन्कोड किया जाता है; इस स्थितियों में असतत संभावना वितरण को संभावना द्रव्यमान फलन के रूप में जाना जाता है। दूसरी ओर, बिल्कुल निरंतर संभावना वितरण उन परिदृश्यों पर प्रयुक्त होते हैं जहां संभावित परिणामों का समुच्चय निरंतर सीमा (जैसे वास्तविक संख्या) में मूल्यों पर ले जा सकता है, जैसे कि किसी दिए गए दिन पर तापमान।अधिक बिल्कुल निरंतर स्थितियों में संभावनाएं संभाव्यता घनत्व फलन द्वारा वर्णित की जाती हैं, और संभावना वितरण संभावना घनत्व फलन के अभिन्न अंग की परिभाषा के अनुसार है।<ref name="ross" /><ref name=":3">{{cite web|title=1.3.6.1।एक संभावना वितरण क्या है|url=https://www.itl.nist.gov/div898/handbook/eda/section3/eda361.htm|access-date=2020-09-10 |website=www.itl.nist.gov}}</ref><ref name="degroot">{{cite book|last1=DeGroot|first1=Morris H. |last2=Schervish|first2=Mark J.|title=प्रायिकता अौर सांख्यिकी|publisher=Addison-Wesley|year=2002}}</ref> सामान्य वितरण सामान्यतः बिल्कुल निरंतर संभावना वितरण है।अधिक जटिल प्रयोग किये गये है, जैसे कि निरंतर समय में परिभाषित स्टोकेस्टिक प्रक्रियाओं को सम्मिलित करने वाले, अधिक सामान्य संभावना उपायों के उपयोग की मांग कर सकते हैं। | ||
एक संभाव्यता वितरण का उपयोग किया जाता है जिसका नमूना | एक संभाव्यता वितरण का उपयोग किया जाता है जिसका नमूना समष्टि एक-आयामी है और (उदाहरण के लिए वास्तविक संख्या, लेबल की सूची, ऑर्डर किए गए लेबल या बाइनरी) को अविभाज्य वितरण कहा जाता है, जबकि वितरण जिसका नमूना समष्टि आयाम 2 या 2 से अधिक का सदिश समष्टि है, जिसे मल्टीवेरेट वितरण कहा जाता है। अविभाज्य वितरण विभिन्न-विभिन्न मूल्यों पर एकल यादृच्छिक चर की संभावनाओं को देता है; एक बहुभिन्नरूपी वितरण (एक संयुक्त संभावना वितरण) यादृच्छिक सदिश की संभावनाएं देता है - दो या अधिक यादृच्छिक चर की सूची - मूल्यों के विभिन्न संयोजनों पर ले जाता है। महत्वपूर्ण और सामान्यतः सामना किए जाने वाले एकतरफा संभावना वितरण में द्विपद वितरण, हाइपरजोमेट्रिक वितरण और सामान्य वितरण सम्मिलित हैं। सामान्यतः सामना किया जाने वाला बहुभिन्नरूपी वितरण बहुभिन्नरूपी सामान्य वितरण है। | ||
संभाव्यता फलन, संचयी वितरण फलन, संभाव्यता द्रव्यमान फलन और संभाव्यता घनत्व फलन, क्षण उत्पन्न करने वाले फलन और विशेषता फलन (संभाव्यता सिद्धांत) के अतिरिक्त, संभावना वितरण की पहचान करने के लिए भी काम करते हैं, क्योंकि वे विशिष्ट रूप से अंतर्निहित संचयी वितरण फलन का निर्धारण करते हैं।<ref>{{cite journal|author1=Shephard, N.G.|year=1991|title=विशेषता फ़ंक्शन से वितरण फ़ंक्शन तक: सिद्धांत के लिए एक सरल ढांचा|journal=Econometric Theory|volume=7|issue=4|pages=519–529|doi=10.1017/S0266466600004746|s2cid=14668369 |url=https://ora.ox.ac.uk/objects/uuid:a4c3ad11-74fe-458c-8d58-6f74511a476c}}</ref>[[File:Standard deviation diagram.svg|right|thumb|250px|सामान्य वितरण की संभाव्यता घनत्व फलन (पीडीएफ), जिसे गाऊसी या बेल वक्र भी कहा जाता है, सबसे महत्वपूर्ण बिल्कुल निरंतर यादृच्छिक वितरण।जैसा कि आंकड़े पर ध्यान दिया गया है, मूल्यों के अंतराल की संभावनाएं वक्र के अनुसार क्षेत्र के अनुरूप हैं।]] | संभाव्यता फलन, संचयी वितरण फलन, संभाव्यता द्रव्यमान फलन और संभाव्यता घनत्व फलन, क्षण उत्पन्न करने वाले फलन और विशेषता फलन (संभाव्यता सिद्धांत) के अतिरिक्त, संभावना वितरण की पहचान करने के लिए भी काम करते हैं, क्योंकि वे विशिष्ट रूप से अंतर्निहित संचयी वितरण फलन का निर्धारण करते हैं।<ref>{{cite journal|author1=Shephard, N.G.|year=1991|title=विशेषता फ़ंक्शन से वितरण फ़ंक्शन तक: सिद्धांत के लिए एक सरल ढांचा|journal=Econometric Theory|volume=7|issue=4|pages=519–529|doi=10.1017/S0266466600004746|s2cid=14668369 |url=https://ora.ox.ac.uk/objects/uuid:a4c3ad11-74fe-458c-8d58-6f74511a476c}}</ref>[[File:Standard deviation diagram.svg|right|thumb|250px|सामान्य वितरण की संभाव्यता घनत्व फलन (पीडीएफ), जिसे गाऊसी या बेल वक्र भी कहा जाता है, सबसे महत्वपूर्ण बिल्कुल निरंतर यादृच्छिक वितरण।जैसा कि आंकड़े पर ध्यान दिया गया है, मूल्यों के अंतराल की संभावनाएं वक्र के अनुसार क्षेत्र के अनुरूप हैं।]] | ||
| Line 42: | Line 39: | ||
=== मूल शर्तें === | === मूल शर्तें === | ||
*यादृच्छिक | *यादृच्छिक चर : नमूना समष्टि से मान लेता है;संभावनाएं बताती हैं कि कौन से मान और मूल्यों के समुच्चय को अधिक संभावना है। | ||
*घटना (संभाव्यता सिद्धांत): यादृच्छिक | *घटना (संभाव्यता सिद्धांत): यादृच्छिक चर के संभावित मूल्यों (परिणामों) का समुच्चय जो निश्चित संभावना के साथ होता है। | ||
*संभाव्यता उपाय या संभाव्यता माप: संभावना <math>P(X \in E)</math> का वर्णन करता है वह घटना <math>E,</math> होता है।<ref name='vapnik'>Chapters 1 and 2 of {{harvp|Vapnik|1998}}</ref> | *संभाव्यता उपाय या संभाव्यता माप: संभावना <math>P(X \in E)</math> का वर्णन करता है वह घटना <math>E,</math> होता है।<ref name='vapnik'>Chapters 1 and 2 of {{harvp|Vapnik|1998}}</ref> | ||
*संचयी वितरण फलन : संभावना का मूल्यांकन करने वाले फलन <math>X</math> से कम या उसके सामान्तर मूल्य लेंगे <math>x</math> यादृच्छिक | *संचयी वितरण फलन : संभावना का मूल्यांकन करने वाले फलन <math>X</math> से कम या उसके सामान्तर मूल्य लेंगे <math>x</math> यादृच्छिक चर के लिए (केवल वास्तविक-मूल्यवान यादृच्छिक चर के लिए)। | ||
*क्वांटाइल फलन: संचयी वितरण फलन का उलटा।देता है <math>x</math> ऐसा, संभावना <math>q</math> के साथ , <math>X</math> <math>x</math> अधिक नहीं होगा । | *क्वांटाइल फलन: संचयी वितरण फलन का उलटा।देता है <math>x</math> ऐसा, संभावना <math>q</math> के साथ , <math>X</math> <math>x</math> अधिक नहीं होगा । | ||
=== असतत संभावना वितरण === | === असतत संभावना वितरण === | ||
*असतत संभावना वितरण: अनेक यादृच्छिक | *असतत संभावना वितरण: अनेक यादृच्छिक चर के लिए सूक्ष्म रूप से या गिनती से असीम रूप से अनेक मूल्यों के साथ। | ||
*'' प्रायिकता द्रव्यमान फलन'' ('' पीमफ ''): फलन जो संभावना देता है कि असतत यादृच्छिक | *'' प्रायिकता द्रव्यमान फलन'' ('' पीमफ ''): फलन जो संभावना देता है कि असतत यादृच्छिक चर कुछ मूल्य के सामान्तर है। | ||
*'' आवृत्ति वितरण '': तालिका जो विभिन्न परिणामों की आवृत्ति को {{em|एक नमूने में}} प्रदर्शित करती है । | *'' आवृत्ति वितरण '': तालिका जो विभिन्न परिणामों की आवृत्ति को {{em|एक नमूने में}} प्रदर्शित करती है । | ||
*सापेक्ष आवृत्ति वितरण: आवृत्ति वितरण जहां प्रत्येक मान को नमूना (आँकड़े) (अर्थात नमूना आकार) में अनेक परिणामों द्वारा विभाजित (सामान्यीकृत) किया गया है। | *सापेक्ष आवृत्ति वितरण: आवृत्ति वितरण जहां प्रत्येक मान को नमूना (आँकड़े) (अर्थात नमूना आकार) में अनेक परिणामों द्वारा विभाजित (सामान्यीकृत) किया गया है। | ||
*श्रेणीबद्ध वितरण: मूल्यों के परिमित समुच्चय के साथ असतत यादृच्छिक | *श्रेणीबद्ध वितरण: मूल्यों के परिमित समुच्चय के साथ असतत यादृच्छिक चर के लिए। | ||
=== बिल्कुल निरंतर संभावना वितरण === | === बिल्कुल निरंतर संभावना वितरण === | ||
*बिल्कुल निरंतर संभावना वितरण: अनेक यादृच्छिक | *बिल्कुल निरंतर संभावना वितरण: अनेक यादृच्छिक चर के लिए अधिकतम अनेक मूल्यों के साथ। | ||
*'' प्रायिकता घनत्व फलन ( पीडीफ )'' या ''प्रायिकता घनत्व '': फलन जिसका मूल्य किसी भी दिए गए नमूने (या बिंदु) पर नमूना | *'' प्रायिकता घनत्व फलन ( पीडीफ )'' या ''प्रायिकता घनत्व '': फलन जिसका मूल्य किसी भी दिए गए नमूने (या बिंदु) पर नमूना समष्टि (यादृच्छिक चर द्वारा लिए गए संभावित मूल्यों का समुच्चय) पर है। एक ''सापेक्ष संभावना 'प्रदान करने के रूप में व्याख्या की जा सकती है कि यादृच्छिक चर का मूल्य उस नमूने के सामान्तर होगा।'' | ||
=== संबंधित शब्द === | === संबंधित शब्द === | ||
*समर्थन (गणित): मान यादृच्छिक | *समर्थन (गणित): मान यादृच्छिक चर द्वारा गैर-शून्य संभावना के साथ मान लिया जा सकता है।एक यादृच्छिक चर <math>X</math> के लिए , इसे कभी -कभी <math>R_X</math>निरूपित किया जाता है । | ||
*टेल :<ref name='tail'>More information and examples can be found in the articles [[Heavy-tailed distribution]], [[Long-tailed distribution]], [[fat-tailed distribution]]</ref> यादृच्छिक | *टेल :<ref name='tail'>More information and examples can be found in the articles [[Heavy-tailed distribution]], [[Long-tailed distribution]], [[fat-tailed distribution]]</ref> यादृच्छिक चर की सीमा के करीब क्षेत्र, यदि पीएमएफ या पीडीएफ अपेक्षाकृत कम हैं। सामान्यतः रूप <math>X > a</math>, <math>X < b</math> या उसके पश्चात् संघ होता है। | ||
*हेड :<ref name='tail' /> वह क्षेत्र जहां पीएमएफ या पीडीएफ अपेक्षाकृत अधिक है। सामान्यतः <math>a < X < b</math> रूप होता है । | *हेड :<ref name='tail' /> वह क्षेत्र जहां पीएमएफ या पीडीएफ अपेक्षाकृत अधिक है। सामान्यतः <math>a < X < b</math> रूप होता है । | ||
*अपेक्षित मूल्य या मतलब: संभावित मूल्यों का भारित औसत है तथा उनकी संभावनाओं का उपयोग उनके वजन के रूप में;या निरंतर एनालॉग के उपयोग में किया जाता है । | *अपेक्षित मूल्य या मतलब: संभावित मूल्यों का भारित औसत है तथा उनकी संभावनाओं का उपयोग उनके वजन के रूप में;या निरंतर एनालॉग के उपयोग में किया जाता है । | ||
*माध्य: मूल्य जैसे कि माध्य से कम मानों का समुच्चय, और समुच्चय से अधिक समुच्चय, प्रत्येक में संभावनाएं हैं कि एक-आधा से अधिक नहीं है। | *माध्य: मूल्य जैसे कि माध्य से कम मानों का समुच्चय, और समुच्चय से अधिक समुच्चय, प्रत्येक में संभावनाएं हैं कि एक-आधा से अधिक नहीं है। | ||
*मोड (सांख्यिकी): असतत यादृच्छिक | *मोड (सांख्यिकी): असतत यादृच्छिक चर के लिए, उच्चतम संभावना के साथ मूल्य;एक बिल्कुल निरंतर यादृच्छिक चर के लिए, समष्टि जिस पर संभावना घनत्व फलन में समष्टिीय शिखर होता है। | ||
*क्वांटाइल: क्यू-क्वांटाइल मान है <math>x</math> ऐसा है कि <math>P(X < x) = q</math>। | *क्वांटाइल: क्यू-क्वांटाइल मान है <math>x</math> ऐसा है कि <math>P(X < x) = q</math>। | ||
*विचरण माध्य के बारे में पीएमएफ या पीडीएफ का दूसरा क्षण;वितरण के सांख्यिकीय फैलाव का महत्वपूर्ण उपाय। | *विचरण माध्य के बारे में पीएमएफ या पीडीएफ का दूसरा क्षण;वितरण के सांख्यिकीय फैलाव का महत्वपूर्ण उपाय। | ||
| Line 74: | Line 71: | ||
== संचयी वितरण फलन == | == संचयी वितरण फलन == | ||
एक वास्तविक-मूल्यवान यादृच्छिक | एक वास्तविक-मूल्यवान यादृच्छिक चर के विशेष स्थितियों में, संभाव्यता वितरण को संभावना माप के अतिरिक्त संचयी वितरण फलन द्वारा समान रूप से दर्शाया जा सकता है। एक यादृच्छिक चर का संचयी वितरण फलन <math>X</math> संभावना वितरण के संबंध में <math>p</math> की तरह परिभाषित किया गया है | ||
<math display="block">F(x) = P(X \leq x).</math> | <math display="block">F(x) = P(X \leq x).</math> | ||
किसी भी वास्तविक-मूल्यवान यादृच्छिक | किसी भी वास्तविक-मूल्यवान यादृच्छिक चर के संचयी वितरण फलन में गुण होते हैं: | ||
*<ली स्टाइल = मार्जिन: 0.7REM 0;><math>F(x)</math> गैर-डिसीजिंग है; </li> | *<ली स्टाइल = मार्जिन: 0.7REM 0;><math>F(x)</math> गैर-डिसीजिंग है; </li> | ||
*<ली स्टाइल = मार्जिन: 0.7REM 0;><math>F(x)</math> सही-निरंतर है; </li> | *<ली स्टाइल = मार्जिन: 0.7REM 0;><math>F(x)</math> सही-निरंतर है; </li> | ||
| Line 83: | Line 80: | ||
*<ली स्टाइल = मार्जिन: 0.7REM 0;><math>\Pr(a < X \le b) = F(b) - F(a)</math>। | *<ली स्टाइल = मार्जिन: 0.7REM 0;><math>\Pr(a < X \le b) = F(b) - F(a)</math>। | ||
इसके विपरीत, कोई भी | इसके विपरीत, कोई भी फलन <math>F:\mathbb{R}\to\mathbb{R}</math> यह उपरोक्त गुणों के पहले चार को संतुष्ट करता है, वास्तविक संख्याओं पर कुछ संभाव्यता वितरण का संचयी वितरण फलन है।<ref>{{Cite book|title=संभावना और स्टोकेस्टिक्स|last=Erhan|first=Çınlar|date=2011|publisher=Springer|isbn=9780387878584|location=New York|pages=57}}</ref> किसी भी संभावना वितरण को असतत संभावना वितरण के योग के रूप में विघटित किया जा सकता है, बिल्कुल निरंतर संभावना वितरण और विलक्षण उपाय,<ref>see [[Lebesgue's decomposition theorem]]</ref> और इस प्रकार कोई भी संचयी वितरण फलन संचयी वितरण फलनों के अनुसार तीनों के योग के रूप में अपघटन को स्वीकार करता है। | ||
== असतत संभावना वितरण == | == असतत संभावना वितरण == | ||
{{Main|जन समारोह की संभावना}} | {{Main|जन समारोह की संभावना}} | ||
[[File:Discrete probability distrib.svg|right|thumb|एक असतत संभावना वितरण की संभावना द्रव्यमान | [[File:Discrete probability distrib.svg|right|thumb|एक असतत संभावना वितरण की संभावना द्रव्यमान फलन।सिंगलटन (गणित) की संभावनाएं {1}, {3}, और {7} क्रमशः 0.2, 0.5, 0.3 हैं। इनमें से किसी भी बिंदु से युक्त समुच्चय में संभावना शून्य है।]] | ||
[[File:Discrete probability distribution.svg|right|thumb|एक असतत संभावना वितरण का संचयी वितरण | [[File:Discrete probability distribution.svg|right|thumb|एक असतत संभावना वितरण का संचयी वितरण फलन, ...]] | ||
[[File:Normal probability distribution.svg|right|thumb|... निरंतर संभावना वितरण की, ...]] | [[File:Normal probability distribution.svg|right|thumb|... निरंतर संभावना वितरण की, ...]] | ||
[[File:Mixed probability distribution.svg|right|thumb|... वितरण का जिसमें निरंतर हिस्सा और असतत हिस्सा दोनों है।]]एक असतत संभावना वितरण यादृच्छिक | [[File:Mixed probability distribution.svg|right|thumb|... वितरण का जिसमें निरंतर हिस्सा और असतत हिस्सा दोनों है।]]एक असतत संभावना वितरण यादृच्छिक चर की संभावना वितरण है जो केवल मानों की गिनती योग्य संख्या पर ले जा सकता है<ref>{{Cite book|title=संभावना और स्टोकेस्टिक्स|last=Erhan|first=Çınlar|date=2011|publisher=Springer| isbn=9780387878591| location=New York|pages=51|oclc=710149819}}</ref> (लगभग निश्चित रूप से)<ref>{{Cite book|title=माप सिद्धांत| last=Cohn|first=Donald L.|date=1993|publisher=Birkhäuser}}</ref> जिसका अर्थ है कि किसी भी घटना की संभावना <math>E</math> (परिमित या श्रृंखला (गणित)) योग के रूप में व्यक्त किया जा सकता है: | ||
<math display="block">P(X\in E) = \sum_{\omega\in A} P(X = \omega),</math> | <math display="block">P(X\in E) = \sum_{\omega\in A} P(X = \omega),</math> | ||
जहाँ <math>A</math> गिनती योग्य समुच्चय है। इस प्रकार असतत यादृच्छिक | जहाँ <math>A</math> गिनती योग्य समुच्चय है। इस प्रकार असतत यादृच्छिक चर वास्तव में संभावना द्रव्यमान <math>p(x) = P(X=x)</math> फलन के साथ हैं । उस स्थितियों में जहां मूल्यों की सीमा अनगिनत अनंत है, इन मानों को संभावनाओं के लिए पर्याप्त तेजी से शून्य तक गिरना होगा। उदाहरण के लिए, उदाहरण के लिए, यदि, यदि <math>p(n) = \tfrac{1}{2^n}</math> के लिए <math>n = 1, 2, ...</math>, संभावनाओं का योग होगा <math>1/2 + 1/4 + 1/8 + \dots = 1</math>। | ||
एक असतत यादृच्छिक | एक असतत यादृच्छिक चर यादृच्छिक चर है जिसका संभाव्यता वितरण असतत है। | ||
सांख्यिकीय मॉडलिंग में उपयोग किए जाने वाले प्रसिद्ध असतत संभावना वितरण में पॉइसन वितरण, बर्नौली वितरण, द्विपद वितरण, ज्यामितीय वितरण, ऋणात्मक द्विपद वितरण और श्रेणीबद्ध वितरण सम्मिलित हैं।<ref name=":1" /> जब नमूना (आँकड़े) (टिप्पणियों का समुच्चय) बड़ी जनसंख्या से खींचा जाता है, तब नमूना बिंदुओं में अनुभवजन्य वितरण फलन होता है जो असतत होता है, और जो जनसंख्या वितरण के बारे में जानकारी प्रदान करता है। इसके अतिरिक्त, यूनिफ़ॉर्म डिस्ट्रीब्यूशन (असतत) का उपयोग सामान्यतः कंप्यूटर प्रोग्रामों में किया जाता है जो अनेक विकल्पों के मध्य समान-संभाव्यता यादृच्छिक चयन बनाते हैं। | सांख्यिकीय मॉडलिंग में उपयोग किए जाने वाले प्रसिद्ध असतत संभावना वितरण में पॉइसन वितरण, बर्नौली वितरण, द्विपद वितरण, ज्यामितीय वितरण, ऋणात्मक द्विपद वितरण और श्रेणीबद्ध वितरण सम्मिलित हैं।<ref name=":1" /> जब नमूना (आँकड़े) (टिप्पणियों का समुच्चय) बड़ी जनसंख्या से खींचा जाता है, तब नमूना बिंदुओं में अनुभवजन्य वितरण फलन होता है जो असतत होता है, और जो जनसंख्या वितरण के बारे में जानकारी प्रदान करता है। इसके अतिरिक्त, यूनिफ़ॉर्म डिस्ट्रीब्यूशन (असतत) का उपयोग सामान्यतः कंप्यूटर प्रोग्रामों में किया जाता है जो अनेक विकल्पों के मध्य समान-संभाव्यता यादृच्छिक चयन बनाते हैं। | ||
=== संचयी वितरण फलन === | === संचयी वितरण फलन === | ||
एक वास्तविक-मूल्यवान असतत यादृच्छिक | एक वास्तविक-मूल्यवान असतत यादृच्छिक चर को समतुल्य रूप से यादृच्छिक चर के रूप में परिभाषित किया जा सकता है जिसका संचयी वितरण फलन केवल कूदने से बढ़ता है-अर्थात, इसका सीडीएफ केवल जहां यह उच्च मूल्य पर कूदता है, और बिना कूद के अंतराल में स्थिर होता है।जिन बिंदुओं पर छलांग लगती है, वे ठीक वे मान हैं जो यादृच्छिक चर ले सकते हैं। इस प्रकार संचयी वितरण फलन का रूप है | ||
<math display="block">F(x) = P(X \leq x) = \sum_{\omega \leq x} p(\omega).</math> | <math display="block">F(x) = P(X \leq x) = \sum_{\omega \leq x} p(\omega).</math> | ||
ध्यान दें कि वे बिंदु जहां सीडीएफ कूदता है सदैव गणना योग्य समुच्चय बनाता है; यह कोई भी गिनती करने योग्य समुच्चय हो सकता है और इस प्रकार वास्तविक संख्याओं में भी घना हो सकता है। | ध्यान दें कि वे बिंदु जहां सीडीएफ कूदता है सदैव गणना योग्य समुच्चय बनाता है; यह कोई भी गिनती करने योग्य समुच्चय हो सकता है और इस प्रकार वास्तविक संख्याओं में भी घना हो सकता है। | ||
=== DIRAC डेल्टा प्रतिनिधित्व === | === DIRAC डेल्टा प्रतिनिधित्व === | ||
एक असतत संभावना वितरण को अधिकांशतः डिराक उपायों पतित वितरण की संभावना वितरण के साथ दर्शाया जाता है। किसी भी परिणाम <math>\omega</math> के लिए , मान लीजिये <math>\delta_\omega</math> <math>\omega</math> डिराक उपाय पर केंद्रित हो । असतत संभावना वितरण को देखते हुए, <math>P(X \in A) = 1</math> के साथ गणना योग्य समुच्चय <math>A</math> है और संभावना द्रव्यमान | एक असतत संभावना वितरण को अधिकांशतः डिराक उपायों पतित वितरण की संभावना वितरण के साथ दर्शाया जाता है। किसी भी परिणाम <math>\omega</math> के लिए , मान लीजिये <math>\delta_\omega</math> <math>\omega</math> डिराक उपाय पर केंद्रित हो । असतत संभावना वितरण को देखते हुए, <math>P(X \in A) = 1</math> के साथ गणना योग्य समुच्चय <math>A</math> है और संभावना द्रव्यमान फलन <math>p</math> है।यदि <math>E</math> कोई घटना है, तब | ||
<math display="block">P(X \in E) = \sum_{\omega \in A} p(\omega) \delta_\omega(E),</math> या संक्षेप में, <math display="block">P_X = \sum_{\omega \in A} p(\omega) \delta_\omega.</math> | <math display="block">P(X \in E) = \sum_{\omega \in A} p(\omega) \delta_\omega(E),</math> या संक्षेप में, <math display="block">P_X = \sum_{\omega \in A} p(\omega) \delta_\omega.</math> | ||
इसी तरह, असतत वितरण को डिराक डेल्टा फलन के साथ सामान्यीकृत संभावना घनत्व फलन <math>f</math> के रूप में दर्शाया जा सकता है , जहाँ <math display="block">f(x) = \sum_{\omega \in A} p(\omega) \delta(x - \omega),</math> जिसका कारणहै | इसी तरह, असतत वितरण को डिराक डेल्टा फलन के साथ सामान्यीकृत संभावना घनत्व फलन <math>f</math> के रूप में दर्शाया जा सकता है , जहाँ <math display="block">f(x) = \sum_{\omega \in A} p(\omega) \delta(x - \omega),</math> जिसका कारणहै | ||
| Line 112: | Line 109: | ||
=== संकेतक-फलन प्रतिनिधित्व === | === संकेतक-फलन प्रतिनिधित्व === | ||
एक असतत यादृच्छिक | एक असतत यादृच्छिक चर <math>X</math> के लिए , मान लीजिये की <math>u_0, u_1, \dots</math> जो यह गैर-शून्य संभावना के साथ ले सकते हैं। निरूपित | ||
<math display="block">\Omega_i=X^{-1}(u_i)= \{\omega: X(\omega)=u_i\},\, i=0, 1, 2, \dots</math> | <math display="block">\Omega_i=X^{-1}(u_i)= \{\omega: X(\omega)=u_i\},\, i=0, 1, 2, \dots</math> | ||
| Line 121: | Line 118: | ||
<math display="block">X(\omega)=\sum_i u_i 1_{\Omega_i}(\omega)</math> | <math display="block">X(\omega)=\sum_i u_i 1_{\Omega_i}(\omega)</math> | ||
संभावना शून्य के समुच्चय को छोड़कर, जहां <math>1_A</math> <math>A</math> का संकेतक | संभावना शून्य के समुच्चय को छोड़कर, जहां <math>1_A</math> <math>A</math> का संकेतक फलन है । यह असतत यादृच्छिक चर की वैकल्पिक परिभाषा के रूप में काम कर सकता है। | ||
=== एक-बिंदु वितरण === | === एक-बिंदु वितरण === | ||
एक विशेष स्थितिया यादृच्छिक | एक विशेष स्थितिया यादृच्छिक चर का असतत वितरण है जो केवल निश्चित मूल्य पर ले सकता है;दूसरे शब्दों में, यह नियतात्मक वितरण है।औपचारिक रूप से व्यक्त किया गया, यादृच्छिक चर <math>X</math> यदि संभावित परिणाम है तब एक-बिंदु वितरण है <math>x</math> ऐसा है कि <math>P(X{=}x)=1.</math><ref>{{cite book |title=संभाव्यता सिद्धांत और गणितीय सांख्यिकी|first=Marek |last=Fisz |edition=3rd |publisher=John Wiley & Sons |year=1963 |isbn=0-471-26250-1 |page=129}}</ref> अन्य सभी संभावित परिणामों में संभावना 0. है। इसका संचयी वितरण फलन 0 से 1 तक तुरंत कूदता है। | ||
== बिल्कुल निरंतर संभावना वितरण == | == बिल्कुल निरंतर संभावना वितरण == | ||
{{Main|संभाव्यता सघनता फलन }} | {{Main|संभाव्यता सघनता फलन }} | ||
एक पूरी तरह से निरंतर संभावना वितरण वास्तविक संख्याओं के साथ वास्तविक संख्याओं पर संभावना वितरण है, जैसे कि वास्तविक रेखा में संपूर्ण अंतराल, और जहां किसी भी घटना की संभावना को अभिन्न के रूप में व्यक्त किया जा सकता है।<ref>{{Cite book|title=कठोर संभावना सिद्धांत पर एक पहला नज़र|author1=Jeffrey Seth Rosenthal|date=2000| publisher=World Scientific}}</ref> अधिक स्पष्ट रूप से, वास्तविक यादृच्छिक | एक पूरी तरह से निरंतर संभावना वितरण वास्तविक संख्याओं के साथ वास्तविक संख्याओं पर संभावना वितरण है, जैसे कि वास्तविक रेखा में संपूर्ण अंतराल, और जहां किसी भी घटना की संभावना को अभिन्न के रूप में व्यक्त किया जा सकता है।<ref>{{Cite book|title=कठोर संभावना सिद्धांत पर एक पहला नज़र|author1=Jeffrey Seth Rosenthal|date=2000| publisher=World Scientific}}</ref> अधिक स्पष्ट रूप से, वास्तविक यादृच्छिक चर <math>X</math> तब बिल्कुल निरंतर संभावना वितरण है यदि कोई फलन <math>f: \Reals \to [0, \infty]</math> है ऐसा कि प्रत्येक अंतराल <math>[a,b] \subset \mathbb{R}</math> के लिए <math>X</math> की से संबंधित <math>[a,b]</math> के संभावना <math>f</math> ऊपर <math>I</math>: अभिन्न अंग द्वारा दिया जाता है <ref>Chapter 3.2 of {{harvp|DeGroot|Schervish|2002}}</ref><ref>{{Cite web| last=Bourne|first=Murray|title=11. संभाव्यता वितरण - अवधारणाएं|url=https://www.intmath.com/counting-probability/11-probability-distributions-concepts.php|access-date=2020-09-10|website=www.intmath.com|language=en-us}}</ref> | ||
<math display="block">P\left(a \le X \le b \right) = \int_a^b f(x) \, dx .</math> | <math display="block">P\left(a \le X \le b \right) = \int_a^b f(x) \, dx .</math> | ||
| Line 135: | Line 132: | ||
यह संभाव्यता घनत्व फलन की परिभाषा है, जिससे पूरी तरह से निरंतर संभावना वितरण वास्तव में संभाव्यता घनत्व फलन के साथ हो। विशेष रूप से, <math>X</math> के लिए कोई एकल मूल्य लेने के लिए <math>a</math> (वह है, <math>a \le X \le a</math>) संभावना शून्य है, क्योंकि ऊपरी और निचली सीमाओं के साथ अभिन्न अंग सदैव शून्य के सामान्तर होता है।यदि अंतराल <math>[a,b]</math> किसी भी औसत अंकिते का समुच्चय <math>A</math> द्वारा प्रतिस्थापित किया जाता है , जो कि समानता के अनुसार अभी भी है: | यह संभाव्यता घनत्व फलन की परिभाषा है, जिससे पूरी तरह से निरंतर संभावना वितरण वास्तव में संभाव्यता घनत्व फलन के साथ हो। विशेष रूप से, <math>X</math> के लिए कोई एकल मूल्य लेने के लिए <math>a</math> (वह है, <math>a \le X \le a</math>) संभावना शून्य है, क्योंकि ऊपरी और निचली सीमाओं के साथ अभिन्न अंग सदैव शून्य के सामान्तर होता है।यदि अंतराल <math>[a,b]</math> किसी भी औसत अंकिते का समुच्चय <math>A</math> द्वारा प्रतिस्थापित किया जाता है , जो कि समानता के अनुसार अभी भी है: | ||
<math display="block"> P(X \in A) = \int_A f(x) \, dx .</math> | <math display="block"> P(X \in A) = \int_A f(x) \, dx .</math> | ||
एक बिल्कुल निरंतर यादृच्छिक | एक बिल्कुल निरंतर यादृच्छिक चर यादृच्छिक चर है जिसका संभाव्यता वितरण बिल्कुल निरंतर है। | ||
पूरी तरह से निरंतर संभावना वितरण के अनेक उदाहरण हैं: जो कि सामान्य वितरण, समान वितरण (निरंतर), ची-वर्ग वितरण | ची-स्क्वर्ड, और संभाव्यता वितरण की सूची या बिल्कुल निरंतर वितरण। | पूरी तरह से निरंतर संभावना वितरण के अनेक उदाहरण हैं: जो कि सामान्य वितरण, समान वितरण (निरंतर), ची-वर्ग वितरण | ची-स्क्वर्ड, और संभाव्यता वितरण की सूची या बिल्कुल निरंतर वितरण। | ||
=== संचयी वितरण फलन === | === संचयी वितरण फलन === | ||
ऊपर परिभाषित के रूप में बिल्कुल निरंतर संभावना वितरण ठीक पूर्ण निरंतरता संचयी वितरण फलन के साथ हैं। इस स्थितियों में, संचयी वितरण <math>F</math> | ऊपर परिभाषित के रूप में बिल्कुल निरंतर संभावना वितरण ठीक पूर्ण निरंतरता संचयी वितरण फलन के साथ हैं। इस स्थितियों में, संचयी वितरण <math>F</math> फलन प्रपत्र है | ||
<math display="block">F(x) = P(X \leq x) = \int_{-\infty}^x f(t)\,dt</math> | <math display="block">F(x) = P(X \leq x) = \int_{-\infty}^x f(t)\,dt</math> | ||
जहाँ <math>f</math> वितरण <math>P</math> के संबंध में यादृच्छिक | जहाँ <math>f</math> वितरण <math>P</math> के संबंध में यादृच्छिक चर <math>X</math> का घनत्व है | ||
शब्दावली पर ध्यान दें: बिल्कुल निरंतर वितरण को 'निरंतर वितरण' से अलग किया जाना चाहिए, जो निरंतर संचयी वितरण फलन वाले हैं।हर बिल्कुल निरंतर वितरण निरंतर वितरण है, किन्तुयह सच नहीं है, एकवचन वितरण उपस्थित हैं, जो न तब बिल्कुल निरंतर हैं और न ही असतत हैं और न ही उन का मिश्रण है, और कोई घनत्व नहीं है।एक उदाहरण कैंटर वितरण द्वारा दिया गया है।कुछ लेखक चूंकि सभी वितरणों को निरूपित करने के लिए सतत वितरण शब्द का उपयोग करते हैं, जिनके संचयी वितरण | शब्दावली पर ध्यान दें: बिल्कुल निरंतर वितरण को 'निरंतर वितरण' से अलग किया जाना चाहिए, जो निरंतर संचयी वितरण फलन वाले हैं।हर बिल्कुल निरंतर वितरण निरंतर वितरण है, किन्तुयह सच नहीं है, एकवचन वितरण उपस्थित हैं, जो न तब बिल्कुल निरंतर हैं और न ही असतत हैं और न ही उन का मिश्रण है, और कोई घनत्व नहीं है।एक उदाहरण कैंटर वितरण द्वारा दिया गया है।कुछ लेखक चूंकि सभी वितरणों को निरूपित करने के लिए सतत वितरण शब्द का उपयोग करते हैं, जिनके संचयी वितरण फलन बिल्कुल निरंतर फलन हैं, अर्थात निरंतर वितरण के रूप में बिल्कुल निरंतर वितरण को संदर्भित करते हैं।<ref name="ross">{{cite book|first=Sheldon M.|last=Ross|title=संभावना में पहला कोर्स|publisher=Pearson|year=2010}}</ref> घनत्व फलनों की अधिक सामान्य परिभाषा के लिए और समकक्ष बिल्कुल निरंतर उपायों को बिल्कुल निरंतर उपाय देखें। | ||
== kolmogorov परिभाषा == | == kolmogorov परिभाषा == | ||
{{Main|संभाव्यता | {{Main|संभाव्यता समष्टि|संभाव्यता माप}} | ||
माप सिद्धांत में | संभावना सिद्धांत के माप-सिद्धांतीय औपचारिकता, यादृच्छिक | माप सिद्धांत में | संभावना सिद्धांत के माप-सिद्धांतीय औपचारिकता, यादृच्छिक चर को औसत अंकिते का फलन के रूप में परिभाषित किया गया है <math>X</math> संभावना समष्टि से <math>(\Omega, \mathcal{F}, \mathbb{P})</math> औसत अंकिते के समष्टि के लिए <math>(\mathcal{X},\mathcal{A})</math>।फॉर्म की घटनाओं की संभावनाओं को देखते हुए <math>\{\omega\in\Omega\mid X(\omega)\in A\}</math> संतुष्ट संभाव्यता स्वयंसिद्ध <math>X</math>पुष्पक उपाय है <math>X_*\mathbb{P}</math> का <math>X</math> , जो संभावना उपाय है <math>(\mathcal{X},\mathcal{A})</math> संतुष्टि देने वाला <math>X_*\mathbb{P} = \mathbb{P}X^{-1}</math>.<ref>{{Cite book|title=संभाव्यता सिद्धांत: एक विश्लेषणात्मक दृष्टिकोण|last=W.|first=Stroock, Daniel|date=1999|publisher=Cambridge University Press|isbn=978-0521663496|edition= Rev.|location=Cambridge [England]|pages=11|oclc=43953136}}</ref><ref>{{Cite book|title=संभाव्यता के सिद्धांत की नींव|last=Kolmogorov|first=Andrey|publisher=Chelsea Publishing Company| year=1950|location=New York, USA|pages=21–24|orig-year=1933}}</ref><ref>{{Cite web|url=https://mathcs.clarku.edu/~djoyce/ma217/axioms.pdf|title=संभाव्यता के स्वयंसिद्ध|last=Joyce|first=David|date=2014|website=Clark University|access-date=December 5, 2019}}</ref> | ||
== अन्य प्रकार के वितरण == | == अन्य प्रकार के वितरण == | ||
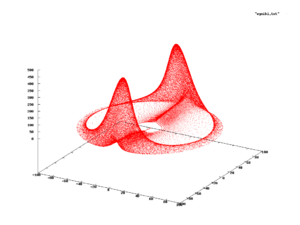
[[File:Rabinovich_Fabrikant_2314.png|right|thumb|300px|राबिनोविच -फब्रिकेंट समीकरणों के लिए समाधान।समर्थन के निश्चित | [[File:Rabinovich_Fabrikant_2314.png|right|thumb|300px|राबिनोविच -फब्रिकेंट समीकरणों के लिए समाधान।समर्थन के निश्चित समष्टि (अर्थात, लाल उपसमुच्चय) पर राज्य को देखने की संभावना क्या है?]]समर्थन के साथ बिल्कुल निरंतर और असतत वितरण <math>\mathbb{R}^k</math> या <math>\mathbb{N}^k</math> घटना के असंख्य को मॉडल करने के लिए बेहद उपयोगी हैं,<ref name='ross' /><ref name='dekking' />चूंकि अधिकांश व्यावहारिक वितरण अपेक्षाकृत सरल उपसमुच्चय पर समर्थित होते हैं, जैसे कि हाइपरक्यूब या बॉल (गणित)।चूंकि, यह सदैव स्थितिया नहीं होता है, और समर्थन के साथ घटनाएं उपस्थित हैं जो वास्तव में जटिल घटता हैं <math>\gamma: [a, b] \rightarrow \mathbb{R}^n</math> कुछ समष्टि के अंदर <math>\mathbb{R}^n</math> या इसी के समान।इन स्थितियोंं में, संभावना वितरण को इस तरह की वक्र की छवि पर समर्थित किया जाता है, और इसके लिए बंद सूत्र खोजने के अतिरिक्त अनुभवजन्य रूप से निर्धारित किए जाने की संभावना है।<ref name='alligood'>{{cite book|author1=Alligood, K.T.|author2=Sauer, T.D.|author3=Yorke, J.A.|year=1996|title=अराजकता: डायनेमिक सिस्टम का परिचय|publisher=Springer}}</ref> | ||
एक उदाहरण को दाईं ओर के आंकड़े में दिखाया गया है, जो विभेदक समीकरणों की प्रणाली के विकास को प्रदर्शित करता है (जिसे सामान्यतः राबिनोविच -फब्रिकेंट समीकरणों के रूप में जाना जाता है) का उपयोग प्लाज्मा (भौतिकी) में लैंगमुइर तरंगों के व्यवहार को मॉडल करने के लिए किया जा सकता है।<ref>{{cite journal|author1=Rabinovich, M.I.|author2=Fabrikant, A.L.|year=1979|title=कोई भी नहीं|journal=J. Exp. Theor. Phys.|volume=77|pages=617–629|bibcode=1979JETP...50..311R}}</ref> जब इस घटना का अध्ययन किया जाता है, तब उपसमुच्चय से देखे गए राज्यों को लाल रंग में इंगित किया जाता है।तब कोई यह पूछ सकता है कि लाल उपसमुच्चय की निश्चित स्थिति में राज्य को देखने की संभावना क्या है;यदि ऐसी संभावना उपस्थित है, तब इसे प्रणाली की संभावना माप कहा जाता है।<ref>Section 1.9 of {{cite book|author1=Ross, S.M.|author2=Peköz, E.A.|year=2007|title=A second course in probability|url=http://people.bu.edu/pekoz/A_Second_Course_in_Probability-Ross-Pekoz.pdf}}</ref><ref name='alligood' /> | एक उदाहरण को दाईं ओर के आंकड़े में दिखाया गया है, जो विभेदक समीकरणों की प्रणाली के विकास को प्रदर्शित करता है (जिसे सामान्यतः राबिनोविच -फब्रिकेंट समीकरणों के रूप में जाना जाता है) का उपयोग प्लाज्मा (भौतिकी) में लैंगमुइर तरंगों के व्यवहार को मॉडल करने के लिए किया जा सकता है।<ref>{{cite journal|author1=Rabinovich, M.I.|author2=Fabrikant, A.L.|year=1979|title=कोई भी नहीं|journal=J. Exp. Theor. Phys.|volume=77|pages=617–629|bibcode=1979JETP...50..311R}}</ref> जब इस घटना का अध्ययन किया जाता है, तब उपसमुच्चय से देखे गए राज्यों को लाल रंग में इंगित किया जाता है।तब कोई यह पूछ सकता है कि लाल उपसमुच्चय की निश्चित स्थिति में राज्य को देखने की संभावना क्या है;यदि ऐसी संभावना उपस्थित है, तब इसे प्रणाली की संभावना माप कहा जाता है।<ref>Section 1.9 of {{cite book|author1=Ross, S.M.|author2=Peköz, E.A.|year=2007|title=A second course in probability|url=http://people.bu.edu/pekoz/A_Second_Course_in_Probability-Ross-Pekoz.pdf}}</ref><ref name='alligood' /> | ||
| Line 162: | Line 159: | ||
== यादृच्छिक संख्या पीढ़ी == | == यादृच्छिक संख्या पीढ़ी == | ||
{{Main|छद्म-यादृच्छिक संख्या नमूनाकरण}} | {{Main|छद्म-यादृच्छिक संख्या नमूनाकरण}} | ||
अधिकांश एल्गोरिदम स्यूडोरेंडोम नंबर जनरेटर पर आधारित होते हैं जो संख्याओं का उत्पादन करता है <math>X</math> जो समान रूप से आधे-खुले अंतराल में वितरित किए जाते हैं {{closed-open|0, 1}}।ये यादृच्छिक | अधिकांश एल्गोरिदम स्यूडोरेंडोम नंबर जनरेटर पर आधारित होते हैं जो संख्याओं का उत्पादन करता है <math>X</math> जो समान रूप से आधे-खुले अंतराल में वितरित किए जाते हैं {{closed-open|0, 1}}।ये यादृच्छिक चर <math>X</math> फिर कुछ एल्गोरिथ्म के माध्यम से नया यादृच्छिक चर बनाने के लिए बदल दिया जाता है जो आवश्यक संभावना वितरण होता है।समान छद्म-यादृच्छिकता के इस स्रोत के साथ, किसी भी यादृच्छिक चर की वास्तविकता उत्पन्न की जा सकती है।<ref name=":0">{{Citation|last1=Dekking|first1=Frederik Michel| title=Why probability and statistics?|date=2005|work=A Modern Introduction to Probability and Statistics| pages=1–11| publisher =Springer London|isbn=978-1-85233-896-1|last2=Kraaikamp|first2=Cornelis| last3=Lopuhaä|first3=Hendrik Paul| last4=Meester| first4=Ludolf Erwin| doi=10.1007/1-84628-168-7_1}}</ref> | ||
उदाहरण के लिए, मान लीजिए <math>U</math> कुछ के लिए यादृच्छिक बर्नौली | उदाहरण के लिए, मान लीजिए <math>U</math> कुछ के लिए यादृच्छिक बर्नौली चर का निर्माण करने के लिए 0 और 1 के मध्य समान वितरण है <math>0 < p < 1</math>, हम परिभाषित करते हैं | ||
<math display="block">X = \begin{cases} | <math display="block">X = \begin{cases} | ||
1,& \text{if } U<p\\ | 1,& \text{if } U<p\\ | ||
| Line 171: | Line 168: | ||
<math display="block">\Pr(X=1) = \Pr(U<p) = p, \quad | <math display="block">\Pr(X=1) = \Pr(U<p) = p, \quad | ||
\Pr(X=0) = \Pr(U\geq p) = 1-p.</math> | \Pr(X=0) = \Pr(U\geq p) = 1-p.</math> | ||
इस यादृच्छिक | इस यादृच्छिक चर एक्स में पैरामीटर के साथ बर्नौली वितरण है <math>p</math>.<ref name=":0"/>ध्यान दें कि यह असतत यादृच्छिक चर का परिवर्तन है। | ||
एक वितरण फलन के लिए <math>F</math> बिल्कुल निरंतर यादृच्छिक | एक वितरण फलन के लिए <math>F</math> बिल्कुल निरंतर यादृच्छिक चर में से, बिल्कुल निरंतर यादृच्छिक चर का निर्माण किया जाना चाहिए। <math>F^{\mathit{inv}}</math>का उलटा फलन <math>F</math>, वर्दी चर से संबंधित है <math>U</math>: | ||
<math display="block">{U\leq F(x)} = {F^{\mathit{inv}}(U)\leq x}.</math> | <math display="block">{U\leq F(x)} = {F^{\mathit{inv}}(U)\leq x}.</math> | ||
उदाहरण के लिए, मान लें कि यादृच्छिक | उदाहरण के लिए, मान लें कि यादृच्छिक चर है जिसमें घातीय वितरण है <math>F(x) = 1 - e^{-\lambda x}</math> निर्माण किया जाना चाहिए। | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
| Line 186: | Line 183: | ||
इसलिए <math>F^{\mathit{inv}}(u) = \frac{-1}{\lambda}\ln(1-u)</math> और अगर <math>U</math> <math>U(0,1)</math> वितरण, फिर यादृच्छिक | इसलिए <math>F^{\mathit{inv}}(u) = \frac{-1}{\lambda}\ln(1-u)</math> और अगर <math>U</math> <math>U(0,1)</math> वितरण, फिर यादृच्छिक चर <math>X</math> द्वारा परिभाषित किया गया है <math>X = F^{\mathit{inv}}(U) = \frac{-1}{\lambda} \ln(1-U)</math>।यह घातीय वितरण है <math>\lambda</math>.<ref name=":0" /> | ||
सांख्यिकीय सिमुलेशन (मोंटे कार्लो विधि) में लगातार समस्या स्यूडोरेंडोमनेस की पीढ़ी है। छद्म-यादृच्छिक संख्या जो दिए गए तरीके से वितरित की जाती हैं। | सांख्यिकीय सिमुलेशन (मोंटे कार्लो विधि) में लगातार समस्या स्यूडोरेंडोमनेस की पीढ़ी है। छद्म-यादृच्छिक संख्या जो दिए गए तरीके से वितरित की जाती हैं। | ||
| Line 193: | Line 190: | ||
{{Main list|संभाव्यता वितरण की सूची}} | {{Main list|संभाव्यता वितरण की सूची}} | ||
संभाव्यता वितरण और यादृच्छिक | संभाव्यता वितरण और यादृच्छिक चर की अवधारणा जो वे वर्णन करते हैं कि संभाव्यता सिद्धांत के गणितीय अनुशासन और सांख्यिकी विज्ञान के विज्ञान को रेखांकित करता है।लगभग किसी भी मूल्य में प्रसार या परिवर्तनशीलता होती है जिसे जनसंख्या में मापा जा सकता है (जैसे लोगों की ऊंचाई, धातु की स्थायित्व, बिक्री वृद्धि, यातायात प्रवाह, आदि);लगभग सभी माप कुछ आंतरिक त्रुटि के साथ किए जाते हैं;भौतिकी में, अनेक प्रक्रियाओं को संभावित रूप से वर्णित किया जाता है, गैसों के गतिज सिद्धांत से मौलिक कणों के क्वांटम यांत्रिक विवरण तक।इन और अनेक अन्य कारणों के लिए, सरल संख्या अधिकांशतः मात्रा का वर्णन करने के लिए अपर्याप्त होती है, जबकि संभावना वितरण अधिकांशतः अधिक उपयुक्त होते हैं। | ||
निम्नलिखित कुछ सबसे सामान्य संभावना वितरणों की सूची है, जिसे वे संबंधित प्रक्रिया के प्रकार द्वारा समूहीकृत करते हैं।अधिक संपूर्ण सूची के लिए, संभाव्यता वितरण की सूची देखें, जो परिणाम की प्रकृति द्वारा माना जाता है (असतत, बिल्कुल निरंतर, बहुभिन्नरूपी, आदि) | निम्नलिखित कुछ सबसे सामान्य संभावना वितरणों की सूची है, जिसे वे संबंधित प्रक्रिया के प्रकार द्वारा समूहीकृत करते हैं।अधिक संपूर्ण सूची के लिए, संभाव्यता वितरण की सूची देखें, जो परिणाम की प्रकृति द्वारा माना जाता है (असतत, बिल्कुल निरंतर, बहुभिन्नरूपी, आदि) | ||
नीचे दिए गए सभी एकतरफा वितरण एकल रूप से | नीचे दिए गए सभी एकतरफा वितरण एकल रूप से चर म पर हैं;यही है, यह माना जाता है कि मान ही बिंदु के आसपास क्लस्टर करते हैं।व्यवहार में, वास्तव में देखी गई मात्रा अनेक मूल्यों के आसपास क्लस्टर हो सकती है।इस तरह की मात्रा को मिश्रण वितरण का उपयोग करके मॉडलिंग की जा सकती है। | ||
=== रैखिक विकास (जैसे त्रुटियां, ऑफसमुच्चय) === | === रैखिक विकास (जैसे त्रुटियां, ऑफसमुच्चय) === | ||
| Line 243: | Line 240: | ||
=== सामान्य रूप से वितरित मात्रा वर्गों के योग के साथ संचालित === | === सामान्य रूप से वितरित मात्रा वर्गों के योग के साथ संचालित === | ||
* ची-वर्ग वितरण, वर्ग मानक सामान्य | * ची-वर्ग वितरण, वर्ग मानक सामान्य चर के योग का वितरण उपयोगी उदा।सामान्य रूप से वितरित नमूनों के नमूना विचरण के बारे में अनुमान के लिए (ची-स्क्वर्ड परीक्षण देखें) | ||
* छात्र का टी वितरण, मानक सामान्य | * छात्र का टी वितरण, मानक सामान्य चर के अनुपात का वितरण और स्केल ची चुकता वितरण चर का वर्गमूल; अज्ञात विचरण के साथ सामान्य रूप से वितरित नमूनों के माध्य के बारे में अनुमान के लिए उपयोगी (छात्र का टी-टेस्ट देखें) | ||
* एफ-वितरण, दो स्केल ची चुकता वितरण | * एफ-वितरण, दो स्केल ची चुकता वितरण चर के अनुपात का वितरण उपयोगी उदा। ऐसे अनुमानों के लिए जिसमें वेरिएंट की तुलना करना या आर-स्क्वेयर सम्मिलित करना सम्मिलित है (चुकता पियर्सन उत्पाद-पल सहसंबंध गुणांक) | ||
=== के रूप में बायेसियन इनवेंशन में पूर्व वितरण के रूप में === | === के रूप में बायेसियन इनवेंशन में पूर्व वितरण के रूप में === | ||
| Line 258: | Line 255: | ||
* कैश लैंग्वेज मॉडल और अन्य सांख्यिकीय भाषा मॉडल प्राकृतिक भाषा प्रसंस्करण में उपयोग किए जाने वाले विशेष शब्दों और शब्द अनुक्रमों की घटना के लिए संभावनाएं प्रदान करने के लिए संभावना वितरण के माध्यम से ऐसा करते हैं। | * कैश लैंग्वेज मॉडल और अन्य सांख्यिकीय भाषा मॉडल प्राकृतिक भाषा प्रसंस्करण में उपयोग किए जाने वाले विशेष शब्दों और शब्द अनुक्रमों की घटना के लिए संभावनाएं प्रदान करने के लिए संभावना वितरण के माध्यम से ऐसा करते हैं। | ||
* क्वांटम यांत्रिकी में, किसी दिए गए बिंदु पर कण को खोजने की संभावना घनत्व उस बिंदु पर कण की तरंग के परिमाण के वर्ग के लिए आनुपातिक है (जन्म के नियम देखें)। इसलिए, कण की स्थिति की संभावना वितरण | * क्वांटम यांत्रिकी में, किसी दिए गए बिंदु पर कण को खोजने की संभावना घनत्व उस बिंदु पर कण की तरंग के परिमाण के वर्ग के लिए आनुपातिक है (जन्म के नियम देखें)। इसलिए, कण की स्थिति की संभावना वितरण फलन द्वारा वर्णित किया गया है <math display="inline">P_{a\le x\le b} (t) = \int_a^b d x\,|\Psi(x,t)|^2 </math>, संभावना है कि कण की स्थिति {{math|''x''}} अंतराल में होगा {{math|''a'' ≤ ''x'' ≤ ''b''}} आयाम में, और आयाम तीन में समान ट्रिपल अभिन्न।यह क्वांटम यांत्रिकी का प्रमुख सिद्धांत है।<ref>{{Cite book| title=रासायनिक विज्ञान के लिए भौतिक रसायन विज्ञान|last=Chang, Raymond.|others=Thoman, John W., Jr., 1960-| year=2014| isbn=978-1-68015-835-9 |location=[Mill Valley, California]|pages=403–406|oclc=927509011}}</ref> | ||
* पावर-फ्लो अध्ययन में संभाव्य लोड प्रवाह इनपुट | * पावर-फ्लो अध्ययन में संभाव्य लोड प्रवाह इनपुट चर की अनिश्चितताओं को संभाव्यता वितरण के रूप में बताता है और संभावना वितरण की अवधि में बिजली प्रवाह गणना भी प्रदान करता है।<ref>{{Cite book|title=2008 इलेक्ट्रिक यूटिलिटी डेरेग्यूलेशन और रिस्ट्रक्चरिंग एंड पावर टेक्नोलॉजीज पर तीसरा अंतर्राष्ट्रीय सम्मेलन|last1=Chen|first1=P.| last2=Chen|first2=Z.| last3=Bak-Jensen|first3=B.|date=April 2008|isbn=978-7-900714-13-8|pages=1586–1591|chapter=Probabilistic load flow: A review| doi=10.1109/drpt.2008.4523658|s2cid=18669309}}</ref> | ||
* पिछले आवृत्ति वितरण जैसे कि उष्णकटिबंधीय चक्रवात, ओले, घटनाओं के मध्य समय, आदि के आधार पर प्राकृतिक घटनाओं की भविष्यवाणी की ।<ref>{{Cite book|title=जल विज्ञान और जल विज्ञान में सांख्यिकीय विधियाँ|last=Maity | first = Rajib| isbn=978-981-10-8779-0|location=Singapore|oclc=1038418263|date = 2018-04-30}}</ref> | * पिछले आवृत्ति वितरण जैसे कि उष्णकटिबंधीय चक्रवात, ओले, घटनाओं के मध्य समय, आदि के आधार पर प्राकृतिक घटनाओं की भविष्यवाणी की ।<ref>{{Cite book|title=जल विज्ञान और जल विज्ञान में सांख्यिकीय विधियाँ|last=Maity | first = Rajib| isbn=978-981-10-8779-0|location=Singapore|oclc=1038418263|date = 2018-04-30}}</ref> | ||
| Line 304: | Line 301: | ||
*[http://threeplusone.com/FieldGuide.pdf Field Guide to Continuous Probability Distributions], Gavin E. Crooks. | *[http://threeplusone.com/FieldGuide.pdf Field Guide to Continuous Probability Distributions], Gavin E. Crooks. | ||
[[Category:Articles with excerpts|Probability Distribution]] | |||
[[Category:Articles with hatnote templates targeting a nonexistent page|Probability Distribution]] | |||
[[Category:CS1 English-language sources (en)|Probability Distribution]] | |||
[[Category:CS1 maint|Probability Distribution]] | |||
[[Category:Collapse templates|Probability Distribution]] | |||
[[Category:Created On 28/12/2022|Probability Distribution]] | |||
[[Category:Lua-based templates|Probability Distribution]] | |||
[[ | [[Category:Machine Translated Page|Probability Distribution]] | ||
[[Category:Navigational boxes| ]] | |||
[[ | [[Category:Navigational boxes without horizontal lists|Probability Distribution]] | ||
[[Category:Pages with empty portal template|Probability Distribution]] | |||
[[Category:Pages with maths render errors|Probability Distribution]] | |||
[[Category: | [[Category:Pages with script errors|Probability Distribution]] | ||
[[Category: | [[Category:Portal-inline template with redlinked portals|Probability Distribution]] | ||
[[Category:Vigyan Ready]] | [[Category:Portal templates with redlinked portals|Probability Distribution]] | ||
[[Category:Short description with empty Wikidata description|Probability Distribution]] | |||
[[Category:Sidebars with styles needing conversion|Probability Distribution]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready|Probability Distribution]] | |||
[[Category:Templates generating microformats|Probability Distribution]] | |||
[[Category:Templates that add a tracking category|Probability Distribution]] | |||
[[Category:Templates that are not mobile friendly|Probability Distribution]] | |||
[[Category:Templates that generate short descriptions|Probability Distribution]] | |||
[[Category:Templates using TemplateData|Probability Distribution]] | |||
[[Category:Wikipedia fully protected templates|Excerpt]] | |||
[[Category:Wikipedia metatemplates|Probability Distribution]] | |||
[[Category:Wikipedia page-section templates|Probability Distribution]] | |||
Latest revision as of 14:12, 6 September 2023
संभाव्यता सिद्धांत और आंकड़ों में, संभाव्यता वितरण गणितीय फलन (गणित) है जो प्रयोग (संभाव्यता सिद्धांत) के लिए विभिन्न संभावित परिणामों की घटना की संभावना देता है।[1][2] यह इसके नमूना समष्टि और घटना की संभावना (संभाव्यता सिद्धांत) (नमूना समष्टि के उपसमुच्चय) के संदर्भ में यादृच्छिकता घटना का गणितीय विवरण है।[3]
उदाहरण के लिए, यदि X सिक्का टॉस (प्रयोग) के परिणाम को निरूपित करने के लिए उपयोग किया जाता है, फिर X की संभावना वितरण X = heads के लिए मान 0.5 (2 या 1/2 में 1) और 0.5 ले जाएगा X = टेल (उस निष्पक्ष सिक्के को मानते हुए)। यादृच्छिक घटनाओं के उदाहरणों में कुछ भविष्य की तारीख में मौसम की स्थिति, यादृच्छिक रूप से चयनित व्यक्ति की ऊंचाई, स्कूल में पुरुष छात्रों का अंश, सर्वेक्षण पद्धति के परिणामों का संचालन करना, आदि सम्मिलित हैं।[4]
परिचय
एक संभावना वितरण घटनाओं की संभावनाओं, नमूना समष्टि के उपसमुच्चय की संभावनाओं का गणितीय विवरण है।नमूना समष्टि, जिसे अधिकांशतः निरूपित किया जाता है , यादृच्छिक घटना के सभी संभावित परिणामों (संभावना) का समुच्चय (गणित) है;यह कोई भी समुच्चय हो सकता है: वास्तविक संख्याओं का समुच्चय, सदिश (गणित) का समुच्चय, इच्छानुसार गैर-नामांकित मूल्यों का समुच्चय, आदि। उदाहरण के लिए, सिक्का फ्लिप का नमूना समष्टि Ω = {heads, tails} होगा ।
यादृच्छिक चर के विशिष्ट स्थितियोंके लिए संभाव्यता वितरण को परिभाषित करने के लिए (इसलिए नमूना समष्टि को संख्यात्मक समुच्चय के रूप में देखा जा सकता है), असतत और बिल्कुल निरंतर यादृच्छिक चर के मध्य अंतर करना आम है।असतत स्थितियोंमें, यह संभावना द्रव्यमान फलन को निर्दिष्ट करने के लिए पर्याप्त है प्रत्येक संभावित परिणाम के लिए संभावना प्रदान करना: उदाहरण के लिए, उचित पासा फेंकते समय, छह मान 1 से 6 में से प्रत्येक में संभावना 1/6 होती है।एक घटना की संभावना (संभाव्यता सिद्धांत) को तब उन परिणामों की संभावनाओं का योग माना जाता है जो घटना को संतुष्ट करते हैं;उदाहरण के लिए, घटना की संभावना भी मूल्य रोल करती है
बिल्कुल निरंतर संभावना वितरण को अनेक तरीकों से वर्णित किया जा सकता है।संभाव्यता घनत्व फलन किसी भी मूल्य की इनफिनिटिमल्स संभावना का वर्णन करता है, और संभावना है कि किसी दिए गए अंतराल में परिणाम निहित है, एकीकरण (गणित) द्वारा उस अंतराल पर संभावना घनत्व फलन द्वारा गणना की जा सकती है।[5]वितरण का वैकल्पिक विवरण संचयी वितरण फलन के माध्यम से है, जो इस संभावना का वर्णन करता है कि यादृच्छिक चर किसी दिए गए मूल्य से बड़ा नहीं है (अर्थात, कुछ के लिए )।संचयी वितरण फलन से संभावना घनत्व फलन के को अनुसार क्षेत्र है, जैसा कि चित्र द्वारा दाईं ओर वर्णित है।[6]
सामान्य संभाव्यता परिभाषा
एक संभाव्यता वितरण को विभिन्न रूपों में वर्णित किया जा सकता है, जैसे कि संभावना द्रव्यमान फलन या संचयी वितरण फलन द्वारा।सबसे सामान्य विवरणों में से एक, जो बिल्कुल निरंतर और असतत चर के लिए प्रयुक्त होता है, संभाव्यता फलन के माध्यम से है जिसका इनपुट स्पेस संबंधित है नमूना समष्टि के लिए, और इसके आउटपुट के रूप में वास्तविक संख्या संभावना देता है।
संभाव्यता फलन नमूना समष्टि के तर्क उपसमुच्चय के रूप में ले सकते हैं, जैसा कि सिक्का टॉस उदाहरण में, जहां फलन ऐसा परिभाषित किया गया था P(heads) = 0.5 और P(tails) = 0.5।चूंकि, यादृच्छिक चर के व्यापक उपयोग के कारण, जो नमूना समष्टि को संख्याओं के समुच्चय में बदल देते हैं (जैसे, , ), संभावना वितरण का अध्ययन करना अधिक सामान्य है, जिनके तर्क इन विशेष प्रकार के समुच्चयों (संख्या समुच्चय) के उपसमुच्चय हैं,[7] और इस लेख में चर ्चा की गई सभी संभावना वितरण इस प्रकार के हैं।के रूप में निरूपित करना आम है संभावना है कि चर का निश्चित मूल्य निश्चित घटना से संबंधित है .[4][8]
उपरोक्त संभाव्यता फलन केवल संभाव्यता वितरण की विशेषता है यदि यह सभी कोल्मोगोरोव स्वयंसिद्ध को संतुष्ट करता है, अर्थात:
- , इसलिए संभावना गैर-ऋणात्मक है
- , इसलिए कोई संभावना से अधिक नहीं है
- समुच्चय के किसी भी असंतुष्ट परिवार के लिए उपयोग नही किया जाता है
संभाव्यता फलन की अवधारणा को संभाव्यता समष्टि के तत्व के रूप में परिभाषित करके अधिक कठोर बना दिया जाता है , जहाँ संभावित परिणामों का समुच्चय है, सभी उपसमुच्चय का समुच्चय है जिनकी संभावना को मापा जा सकता है, और संभावना फलन, या संभाव्यता माप है, जो इन औसत अंकिते के उपसमुच्चय में से प्रत्येक के लिए संभावना प्रदान करता है .[9]
संभाव्यता वितरण सामान्यतः दो वर्गों में से संबंधित हैं। तथा असतत संभावना वितरण उन परिदृश्यों पर प्रयुक्त होता है जहां संभावित परिणामों का समुच्चय असतत संभावना वितरण है (जैसे कि सिक्का टॉस, मरने का रोल) और संभावनाओं को परिणामों की संभावनाओं की असतत सूची द्वारा एन्कोड किया जाता है; इस स्थितियों में असतत संभावना वितरण को संभावना द्रव्यमान फलन के रूप में जाना जाता है। दूसरी ओर, बिल्कुल निरंतर संभावना वितरण उन परिदृश्यों पर प्रयुक्त होते हैं जहां संभावित परिणामों का समुच्चय निरंतर सीमा (जैसे वास्तविक संख्या) में मूल्यों पर ले जा सकता है, जैसे कि किसी दिए गए दिन पर तापमान।अधिक बिल्कुल निरंतर स्थितियों में संभावनाएं संभाव्यता घनत्व फलन द्वारा वर्णित की जाती हैं, और संभावना वितरण संभावना घनत्व फलन के अभिन्न अंग की परिभाषा के अनुसार है।[4][5][8] सामान्य वितरण सामान्यतः बिल्कुल निरंतर संभावना वितरण है।अधिक जटिल प्रयोग किये गये है, जैसे कि निरंतर समय में परिभाषित स्टोकेस्टिक प्रक्रियाओं को सम्मिलित करने वाले, अधिक सामान्य संभावना उपायों के उपयोग की मांग कर सकते हैं।
एक संभाव्यता वितरण का उपयोग किया जाता है जिसका नमूना समष्टि एक-आयामी है और (उदाहरण के लिए वास्तविक संख्या, लेबल की सूची, ऑर्डर किए गए लेबल या बाइनरी) को अविभाज्य वितरण कहा जाता है, जबकि वितरण जिसका नमूना समष्टि आयाम 2 या 2 से अधिक का सदिश समष्टि है, जिसे मल्टीवेरेट वितरण कहा जाता है। अविभाज्य वितरण विभिन्न-विभिन्न मूल्यों पर एकल यादृच्छिक चर की संभावनाओं को देता है; एक बहुभिन्नरूपी वितरण (एक संयुक्त संभावना वितरण) यादृच्छिक सदिश की संभावनाएं देता है - दो या अधिक यादृच्छिक चर की सूची - मूल्यों के विभिन्न संयोजनों पर ले जाता है। महत्वपूर्ण और सामान्यतः सामना किए जाने वाले एकतरफा संभावना वितरण में द्विपद वितरण, हाइपरजोमेट्रिक वितरण और सामान्य वितरण सम्मिलित हैं। सामान्यतः सामना किया जाने वाला बहुभिन्नरूपी वितरण बहुभिन्नरूपी सामान्य वितरण है।
संभाव्यता फलन, संचयी वितरण फलन, संभाव्यता द्रव्यमान फलन और संभाव्यता घनत्व फलन, क्षण उत्पन्न करने वाले फलन और विशेषता फलन (संभाव्यता सिद्धांत) के अतिरिक्त, संभावना वितरण की पहचान करने के लिए भी काम करते हैं, क्योंकि वे विशिष्ट रूप से अंतर्निहित संचयी वितरण फलन का निर्धारण करते हैं।[10]
शब्दावली
संभावना वितरण के विषय पर साहित्य में व्यापक रूप से उपयोग किए जाने वाले कुछ प्रमुख अवधारणाओं और शब्द नीचे सूचीबद्ध हैं।[1]
मूल शर्तें
- यादृच्छिक चर : नमूना समष्टि से मान लेता है;संभावनाएं बताती हैं कि कौन से मान और मूल्यों के समुच्चय को अधिक संभावना है।
- घटना (संभाव्यता सिद्धांत): यादृच्छिक चर के संभावित मूल्यों (परिणामों) का समुच्चय जो निश्चित संभावना के साथ होता है।
- संभाव्यता उपाय या संभाव्यता माप: संभावना का वर्णन करता है वह घटना होता है।[11]
- संचयी वितरण फलन : संभावना का मूल्यांकन करने वाले फलन से कम या उसके सामान्तर मूल्य लेंगे यादृच्छिक चर के लिए (केवल वास्तविक-मूल्यवान यादृच्छिक चर के लिए)।
- क्वांटाइल फलन: संचयी वितरण फलन का उलटा।देता है ऐसा, संभावना के साथ , अधिक नहीं होगा ।
असतत संभावना वितरण
- असतत संभावना वितरण: अनेक यादृच्छिक चर के लिए सूक्ष्म रूप से या गिनती से असीम रूप से अनेक मूल्यों के साथ।
- प्रायिकता द्रव्यमान फलन ( पीमफ ): फलन जो संभावना देता है कि असतत यादृच्छिक चर कुछ मूल्य के सामान्तर है।
- आवृत्ति वितरण : तालिका जो विभिन्न परिणामों की आवृत्ति को एक नमूने में प्रदर्शित करती है ।
- सापेक्ष आवृत्ति वितरण: आवृत्ति वितरण जहां प्रत्येक मान को नमूना (आँकड़े) (अर्थात नमूना आकार) में अनेक परिणामों द्वारा विभाजित (सामान्यीकृत) किया गया है।
- श्रेणीबद्ध वितरण: मूल्यों के परिमित समुच्चय के साथ असतत यादृच्छिक चर के लिए।
बिल्कुल निरंतर संभावना वितरण
- बिल्कुल निरंतर संभावना वितरण: अनेक यादृच्छिक चर के लिए अधिकतम अनेक मूल्यों के साथ।
- प्रायिकता घनत्व फलन ( पीडीफ ) या प्रायिकता घनत्व : फलन जिसका मूल्य किसी भी दिए गए नमूने (या बिंदु) पर नमूना समष्टि (यादृच्छिक चर द्वारा लिए गए संभावित मूल्यों का समुच्चय) पर है। एक सापेक्ष संभावना 'प्रदान करने के रूप में व्याख्या की जा सकती है कि यादृच्छिक चर का मूल्य उस नमूने के सामान्तर होगा।
संबंधित शब्द
- समर्थन (गणित): मान यादृच्छिक चर द्वारा गैर-शून्य संभावना के साथ मान लिया जा सकता है।एक यादृच्छिक चर के लिए , इसे कभी -कभी निरूपित किया जाता है ।
- टेल :[12] यादृच्छिक चर की सीमा के करीब क्षेत्र, यदि पीएमएफ या पीडीएफ अपेक्षाकृत कम हैं। सामान्यतः रूप , या उसके पश्चात् संघ होता है।
- हेड :[12] वह क्षेत्र जहां पीएमएफ या पीडीएफ अपेक्षाकृत अधिक है। सामान्यतः रूप होता है ।
- अपेक्षित मूल्य या मतलब: संभावित मूल्यों का भारित औसत है तथा उनकी संभावनाओं का उपयोग उनके वजन के रूप में;या निरंतर एनालॉग के उपयोग में किया जाता है ।
- माध्य: मूल्य जैसे कि माध्य से कम मानों का समुच्चय, और समुच्चय से अधिक समुच्चय, प्रत्येक में संभावनाएं हैं कि एक-आधा से अधिक नहीं है।
- मोड (सांख्यिकी): असतत यादृच्छिक चर के लिए, उच्चतम संभावना के साथ मूल्य;एक बिल्कुल निरंतर यादृच्छिक चर के लिए, समष्टि जिस पर संभावना घनत्व फलन में समष्टिीय शिखर होता है।
- क्वांटाइल: क्यू-क्वांटाइल मान है ऐसा है कि ।
- विचरण माध्य के बारे में पीएमएफ या पीडीएफ का दूसरा क्षण;वितरण के सांख्यिकीय फैलाव का महत्वपूर्ण उपाय।
- मानक विचलन: विचरण का वर्गमूल, और इसलिए फैलाव का और उपाय।
- सममित संभावना वितरण: कुछ वितरणों की संपत्ति जिसमें वितरण का हिस्सा विशिष्ट मूल्य के बाईं ओर (सामान्यतः माध्यिका) के हिस्से की दर्पण छवि है, जो इसके दाईं ओर है।
- तिरछापन: जिस सीमा तक पीएमएफ या पीडीएफ अपने माध्य के तरफ से झुकता है, उसका उपाय।वितरण का तीसरा मानकीकृत क्षण।
- कर्टोसिस: पीएमएफ या पीडीएफ की पूंछ के मोटापे का उपाय।वितरण का चौथा मानकीकृत क्षण।
संचयी वितरण फलन
एक वास्तविक-मूल्यवान यादृच्छिक चर के विशेष स्थितियों में, संभाव्यता वितरण को संभावना माप के अतिरिक्त संचयी वितरण फलन द्वारा समान रूप से दर्शाया जा सकता है। एक यादृच्छिक चर का संचयी वितरण फलन संभावना वितरण के संबंध में की तरह परिभाषित किया गया है
- <ली स्टाइल = मार्जिन: 0.7REM 0;> गैर-डिसीजिंग है;
- <ली स्टाइल = मार्जिन: 0.7REM 0;> सही-निरंतर है;
- <ली स्टाइल = मार्जिन: 0.7REM 0;>;
- <ली स्टाइल = मार्जिन: 0.7REM 0;> और ;और
- <ली स्टाइल = मार्जिन: 0.7REM 0;>।
इसके विपरीत, कोई भी फलन यह उपरोक्त गुणों के पहले चार को संतुष्ट करता है, वास्तविक संख्याओं पर कुछ संभाव्यता वितरण का संचयी वितरण फलन है।[13] किसी भी संभावना वितरण को असतत संभावना वितरण के योग के रूप में विघटित किया जा सकता है, बिल्कुल निरंतर संभावना वितरण और विलक्षण उपाय,[14] और इस प्रकार कोई भी संचयी वितरण फलन संचयी वितरण फलनों के अनुसार तीनों के योग के रूप में अपघटन को स्वीकार करता है।
असतत संभावना वितरण
एक असतत संभावना वितरण यादृच्छिक चर की संभावना वितरण है जो केवल मानों की गिनती योग्य संख्या पर ले जा सकता है[15] (लगभग निश्चित रूप से)[16] जिसका अर्थ है कि किसी भी घटना की संभावना (परिमित या श्रृंखला (गणित)) योग के रूप में व्यक्त किया जा सकता है:
एक असतत यादृच्छिक चर यादृच्छिक चर है जिसका संभाव्यता वितरण असतत है।
सांख्यिकीय मॉडलिंग में उपयोग किए जाने वाले प्रसिद्ध असतत संभावना वितरण में पॉइसन वितरण, बर्नौली वितरण, द्विपद वितरण, ज्यामितीय वितरण, ऋणात्मक द्विपद वितरण और श्रेणीबद्ध वितरण सम्मिलित हैं।[3] जब नमूना (आँकड़े) (टिप्पणियों का समुच्चय) बड़ी जनसंख्या से खींचा जाता है, तब नमूना बिंदुओं में अनुभवजन्य वितरण फलन होता है जो असतत होता है, और जो जनसंख्या वितरण के बारे में जानकारी प्रदान करता है। इसके अतिरिक्त, यूनिफ़ॉर्म डिस्ट्रीब्यूशन (असतत) का उपयोग सामान्यतः कंप्यूटर प्रोग्रामों में किया जाता है जो अनेक विकल्पों के मध्य समान-संभाव्यता यादृच्छिक चयन बनाते हैं।
संचयी वितरण फलन
एक वास्तविक-मूल्यवान असतत यादृच्छिक चर को समतुल्य रूप से यादृच्छिक चर के रूप में परिभाषित किया जा सकता है जिसका संचयी वितरण फलन केवल कूदने से बढ़ता है-अर्थात, इसका सीडीएफ केवल जहां यह उच्च मूल्य पर कूदता है, और बिना कूद के अंतराल में स्थिर होता है।जिन बिंदुओं पर छलांग लगती है, वे ठीक वे मान हैं जो यादृच्छिक चर ले सकते हैं। इस प्रकार संचयी वितरण फलन का रूप है
DIRAC डेल्टा प्रतिनिधित्व
एक असतत संभावना वितरण को अधिकांशतः डिराक उपायों पतित वितरण की संभावना वितरण के साथ दर्शाया जाता है। किसी भी परिणाम के लिए , मान लीजिये डिराक उपाय पर केंद्रित हो । असतत संभावना वितरण को देखते हुए, के साथ गणना योग्य समुच्चय है और संभावना द्रव्यमान फलन है।यदि कोई घटना है, तब
संकेतक-फलन प्रतिनिधित्व
एक असतत यादृच्छिक चर के लिए , मान लीजिये की जो यह गैर-शून्य संभावना के साथ ले सकते हैं। निरूपित
एक-बिंदु वितरण
एक विशेष स्थितिया यादृच्छिक चर का असतत वितरण है जो केवल निश्चित मूल्य पर ले सकता है;दूसरे शब्दों में, यह नियतात्मक वितरण है।औपचारिक रूप से व्यक्त किया गया, यादृच्छिक चर यदि संभावित परिणाम है तब एक-बिंदु वितरण है ऐसा है कि [18] अन्य सभी संभावित परिणामों में संभावना 0. है। इसका संचयी वितरण फलन 0 से 1 तक तुरंत कूदता है।
बिल्कुल निरंतर संभावना वितरण
एक पूरी तरह से निरंतर संभावना वितरण वास्तविक संख्याओं के साथ वास्तविक संख्याओं पर संभावना वितरण है, जैसे कि वास्तविक रेखा में संपूर्ण अंतराल, और जहां किसी भी घटना की संभावना को अभिन्न के रूप में व्यक्त किया जा सकता है।[19] अधिक स्पष्ट रूप से, वास्तविक यादृच्छिक चर तब बिल्कुल निरंतर संभावना वितरण है यदि कोई फलन है ऐसा कि प्रत्येक अंतराल के लिए की से संबंधित के संभावना ऊपर : अभिन्न अंग द्वारा दिया जाता है [20][21]
यह संभाव्यता घनत्व फलन की परिभाषा है, जिससे पूरी तरह से निरंतर संभावना वितरण वास्तव में संभाव्यता घनत्व फलन के साथ हो। विशेष रूप से, के लिए कोई एकल मूल्य लेने के लिए (वह है, ) संभावना शून्य है, क्योंकि ऊपरी और निचली सीमाओं के साथ अभिन्न अंग सदैव शून्य के सामान्तर होता है।यदि अंतराल किसी भी औसत अंकिते का समुच्चय द्वारा प्रतिस्थापित किया जाता है , जो कि समानता के अनुसार अभी भी है:
पूरी तरह से निरंतर संभावना वितरण के अनेक उदाहरण हैं: जो कि सामान्य वितरण, समान वितरण (निरंतर), ची-वर्ग वितरण | ची-स्क्वर्ड, और संभाव्यता वितरण की सूची या बिल्कुल निरंतर वितरण।
संचयी वितरण फलन
ऊपर परिभाषित के रूप में बिल्कुल निरंतर संभावना वितरण ठीक पूर्ण निरंतरता संचयी वितरण फलन के साथ हैं। इस स्थितियों में, संचयी वितरण फलन प्रपत्र है
शब्दावली पर ध्यान दें: बिल्कुल निरंतर वितरण को 'निरंतर वितरण' से अलग किया जाना चाहिए, जो निरंतर संचयी वितरण फलन वाले हैं।हर बिल्कुल निरंतर वितरण निरंतर वितरण है, किन्तुयह सच नहीं है, एकवचन वितरण उपस्थित हैं, जो न तब बिल्कुल निरंतर हैं और न ही असतत हैं और न ही उन का मिश्रण है, और कोई घनत्व नहीं है।एक उदाहरण कैंटर वितरण द्वारा दिया गया है।कुछ लेखक चूंकि सभी वितरणों को निरूपित करने के लिए सतत वितरण शब्द का उपयोग करते हैं, जिनके संचयी वितरण फलन बिल्कुल निरंतर फलन हैं, अर्थात निरंतर वितरण के रूप में बिल्कुल निरंतर वितरण को संदर्भित करते हैं।[4] घनत्व फलनों की अधिक सामान्य परिभाषा के लिए और समकक्ष बिल्कुल निरंतर उपायों को बिल्कुल निरंतर उपाय देखें।
kolmogorov परिभाषा
माप सिद्धांत में | संभावना सिद्धांत के माप-सिद्धांतीय औपचारिकता, यादृच्छिक चर को औसत अंकिते का फलन के रूप में परिभाषित किया गया है संभावना समष्टि से औसत अंकिते के समष्टि के लिए ।फॉर्म की घटनाओं की संभावनाओं को देखते हुए संतुष्ट संभाव्यता स्वयंसिद्ध पुष्पक उपाय है का , जो संभावना उपाय है संतुष्टि देने वाला .[22][23][24]
अन्य प्रकार के वितरण
समर्थन के साथ बिल्कुल निरंतर और असतत वितरण या घटना के असंख्य को मॉडल करने के लिए बेहद उपयोगी हैं,[4][6]चूंकि अधिकांश व्यावहारिक वितरण अपेक्षाकृत सरल उपसमुच्चय पर समर्थित होते हैं, जैसे कि हाइपरक्यूब या बॉल (गणित)।चूंकि, यह सदैव स्थितिया नहीं होता है, और समर्थन के साथ घटनाएं उपस्थित हैं जो वास्तव में जटिल घटता हैं कुछ समष्टि के अंदर या इसी के समान।इन स्थितियोंं में, संभावना वितरण को इस तरह की वक्र की छवि पर समर्थित किया जाता है, और इसके लिए बंद सूत्र खोजने के अतिरिक्त अनुभवजन्य रूप से निर्धारित किए जाने की संभावना है।[25]
एक उदाहरण को दाईं ओर के आंकड़े में दिखाया गया है, जो विभेदक समीकरणों की प्रणाली के विकास को प्रदर्शित करता है (जिसे सामान्यतः राबिनोविच -फब्रिकेंट समीकरणों के रूप में जाना जाता है) का उपयोग प्लाज्मा (भौतिकी) में लैंगमुइर तरंगों के व्यवहार को मॉडल करने के लिए किया जा सकता है।[26] जब इस घटना का अध्ययन किया जाता है, तब उपसमुच्चय से देखे गए राज्यों को लाल रंग में इंगित किया जाता है।तब कोई यह पूछ सकता है कि लाल उपसमुच्चय की निश्चित स्थिति में राज्य को देखने की संभावना क्या है;यदि ऐसी संभावना उपस्थित है, तब इसे प्रणाली की संभावना माप कहा जाता है।[27][25]
इस तरह का जटिल समर्थन गतिशील प्रणालियों में काफी बार दिखाई देता है।यह स्थापित करना सरल नहीं है कि प्रणाली में संभावना उपाय है, और मुख्य समस्या निम्नलिखित है।होने देना समय में इंस्टेंट हो और समर्थन का उपसमुच्चय;यदि प्रणालीके लिए संभावना उपाय उपस्थित है, तब कोई समुच्चय के अंदर राज्यों को देखने की आवृत्ति की उम्मीद करेगा अंतराल में समान होगा और , जो नहीं हो सकता है;उदाहरण के लिए, यह साइन के समान दोलन कर सकता है, , किसकी सीमा कब अभिसरण नहीं करता है।औपचारिक रूप से, माप केवल तभी उपस्थित होता है जब सापेक्ष आवृत्ति की सीमा तब होती है जब प्रणालीको अनंत भविष्य में देखा जाता है।[28] डायनेमिक प्रणाली की शाखा जो संभाव्यता माप के अस्तित्व का अध्ययन करती है वह है एर्गोडिक सिद्धांत।
ध्यान दें कि इन स्थितियोंं में भी, संभावना वितरण, यदि यह उपस्थित है, तब भी इस बात पर निर्भर करता है कि समर्थन क्रमशः या गिनती योग्य है या नहीं, इस पर निर्भर करता है।
यादृच्छिक संख्या पीढ़ी
अधिकांश एल्गोरिदम स्यूडोरेंडोम नंबर जनरेटर पर आधारित होते हैं जो संख्याओं का उत्पादन करता है जो समान रूप से आधे-खुले अंतराल में वितरित किए जाते हैं [0, 1)।ये यादृच्छिक चर फिर कुछ एल्गोरिथ्म के माध्यम से नया यादृच्छिक चर बनाने के लिए बदल दिया जाता है जो आवश्यक संभावना वितरण होता है।समान छद्म-यादृच्छिकता के इस स्रोत के साथ, किसी भी यादृच्छिक चर की वास्तविकता उत्पन्न की जा सकती है।[29] उदाहरण के लिए, मान लीजिए कुछ के लिए यादृच्छिक बर्नौली चर का निर्माण करने के लिए 0 और 1 के मध्य समान वितरण है , हम परिभाषित करते हैं
एक वितरण फलन के लिए बिल्कुल निरंतर यादृच्छिक चर में से, बिल्कुल निरंतर यादृच्छिक चर का निर्माण किया जाना चाहिए। का उलटा फलन , वर्दी चर से संबंधित है :
इसलिए और अगर वितरण, फिर यादृच्छिक चर द्वारा परिभाषित किया गया है ।यह घातीय वितरण है .[29]
सांख्यिकीय सिमुलेशन (मोंटे कार्लो विधि) में लगातार समस्या स्यूडोरेंडोमनेस की पीढ़ी है। छद्म-यादृच्छिक संख्या जो दिए गए तरीके से वितरित की जाती हैं।
सामान्य संभावना वितरण और उनके अनुप्रयोग
संभाव्यता वितरण और यादृच्छिक चर की अवधारणा जो वे वर्णन करते हैं कि संभाव्यता सिद्धांत के गणितीय अनुशासन और सांख्यिकी विज्ञान के विज्ञान को रेखांकित करता है।लगभग किसी भी मूल्य में प्रसार या परिवर्तनशीलता होती है जिसे जनसंख्या में मापा जा सकता है (जैसे लोगों की ऊंचाई, धातु की स्थायित्व, बिक्री वृद्धि, यातायात प्रवाह, आदि);लगभग सभी माप कुछ आंतरिक त्रुटि के साथ किए जाते हैं;भौतिकी में, अनेक प्रक्रियाओं को संभावित रूप से वर्णित किया जाता है, गैसों के गतिज सिद्धांत से मौलिक कणों के क्वांटम यांत्रिक विवरण तक।इन और अनेक अन्य कारणों के लिए, सरल संख्या अधिकांशतः मात्रा का वर्णन करने के लिए अपर्याप्त होती है, जबकि संभावना वितरण अधिकांशतः अधिक उपयुक्त होते हैं।
निम्नलिखित कुछ सबसे सामान्य संभावना वितरणों की सूची है, जिसे वे संबंधित प्रक्रिया के प्रकार द्वारा समूहीकृत करते हैं।अधिक संपूर्ण सूची के लिए, संभाव्यता वितरण की सूची देखें, जो परिणाम की प्रकृति द्वारा माना जाता है (असतत, बिल्कुल निरंतर, बहुभिन्नरूपी, आदि)
नीचे दिए गए सभी एकतरफा वितरण एकल रूप से चर म पर हैं;यही है, यह माना जाता है कि मान ही बिंदु के आसपास क्लस्टर करते हैं।व्यवहार में, वास्तव में देखी गई मात्रा अनेक मूल्यों के आसपास क्लस्टर हो सकती है।इस तरह की मात्रा को मिश्रण वितरण का उपयोग करके मॉडलिंग की जा सकती है।
रैखिक विकास (जैसे त्रुटियां, ऑफसमुच्चय)
- सामान्य वितरण (गौसियन वितरण), ऐसी मात्रा के लिए;सबसे अधिक उपयोग किया जाने वाला बिल्कुल निरंतर वितरण
घातीय वृद्धि (जैसे कीमत, आय, आबादी)
- लॉग-सामान्य वितरण, ऐसी एकल मात्रा के लिए जिसका लॉग सामान्य वितरण वितरित है
- Pareto वितरण, ऐसी एकल मात्रा के लिए जिसका लॉग घातांक वितरण वितरित है;प्रोटोटाइप पावर लॉ डिस्ट्रीब्यूशन
समान रूप से वितरित मात्रा
- असतत वर्दी वितरण, मूल्यों के परिमित समुच्चय के लिए (जैसे कि मेला मरने का परिणाम)
- निरंतर समान वितरण, बिल्कुल लगातार वितरित मूल्यों के लिए
बर्नौली परीक्षण (हाँ/नहीं घटना, किसी दिए गए संभाव्यता के साथ)
- मूलभूत वितरण:
- बर्नौली वितरण, एकल बर्नौली परीक्षण के परिणाम के लिए (जैसे सफलता/विफलता, हाँ/नहीं)
- द्विपद वितरण, सकारात्मक घटनाओं की संख्या (जैसे सफलताओं, हाँ वोट, आदि) के लिए स्वतंत्र (सांख्यिकी) घटनाओं की निश्चित कुल संख्या दी गई है
- ऋणात्मक द्विपद वितरण, द्विपद-प्रकार की टिप्पणियों के लिए, किन्तु जहां ब्याज की मात्रा निश्चित संख्या में होने से पहले विफलताओं की संख्या है
- ज्यामितीय वितरण, द्विपद-प्रकार की टिप्पणियों के लिए किन्तु जहां ब्याज की मात्रा पहली सफलता से पहले विफलताओं की संख्या है; ऋणात्मक द्विपद वितरण का विशेष स्थितिया
- एक परिमित जनसंख्या पर नमूना योजनाओं से संबंधित:
- हाइपरजोमेट्रिक वितरण, सकारात्मक घटनाओं की संख्या (जैसे सफलताओं, हाँ वोट, आदि) के लिए कुल घटनाओं की निश्चित संख्या को देखते हुए, प्रतिस्थापन के बिना नमूने का उपयोग करना
- बीटा-बिनोमियल वितरण, सकारात्मक घटनाओं की संख्या (जैसे सफलताओं, हाँ वोट, आदि) के लिए कुल घटनाओं की निश्चित संख्या दी गई, प्लायला कलश मॉडल का उपयोग करके नमूनाकरण (कुछ अर्थों में, प्रतिस्थापन के बिना नमूने के विपरीत)
श्रेणीबद्ध परिणाम (के साथ घटनाएं) K संभावित परिणाम)
- श्रेणीबद्ध वितरण, एकल श्रेणीगत परिणाम के लिए (जैसे सर्वेक्षण में हाँ/नहीं/संभवतः); बर्नौली वितरण का सामान्यीकरण
- बहुराष्ट्रीय वितरण, प्रत्येक प्रकार के श्रेणीबद्ध परिणामों की संख्या के लिए, कुल परिणामों की निश्चित संख्या को देखते हुए; द्विपद वितरण का सामान्यीकरण
- बहुभिन्नरूपी हाइपरजोमेट्रिक वितरण, बहुराष्ट्रीय वितरण के समान, किन्तु प्रतिस्थापन के बिना नमूने का उपयोग करना हाइपरजोमेट्रिक वितरण का सामान्यीकरण
पॉइसन प्रक्रिया (किसी दिए गए दर के साथ स्वतंत्र रूप से होने वाली घटनाएं)
- पॉइसन वितरण, समय की अवधि में पॉइसन-प्रकार की घटनाओं की संख्या के लिए
- घातीय वितरण, अगले पॉइसन-प्रकार की घटना से पहले के समय के लिए
- गामा वितरण, अगले पॉइसन K - प्रकार की घटनाओं से पहले के समय के लिए
सामान्य रूप से वितरित घटकों के साथ सदिश का निरपेक्ष मान
- रेले वितरण, गॉसियन वितरित ऑर्थोगोनल घटकों के साथ सदिश परिमाण के वितरण के लिए। गॉसियन वास्तविक और काल्पनिक घटकों के साथ आरएफ संकेत में रेले वितरण पाए जाते हैं।
- राइस वितरण, रेले वितरण का सामान्यीकरण जहां स्थिर पृष्ठभूमि संकेत घटक है। मल्टीपैथ प्रसार के कारण और गैर-शून्य एनएमआर संकेत पर ध्वनि भ्रष्टाचार के साथ एमआर छवियों में रेडियो सिग्नल के रेनियन लुप्त होने में पाया गया।
सामान्य रूप से वितरित मात्रा वर्गों के योग के साथ संचालित
- ची-वर्ग वितरण, वर्ग मानक सामान्य चर के योग का वितरण उपयोगी उदा।सामान्य रूप से वितरित नमूनों के नमूना विचरण के बारे में अनुमान के लिए (ची-स्क्वर्ड परीक्षण देखें)
- छात्र का टी वितरण, मानक सामान्य चर के अनुपात का वितरण और स्केल ची चुकता वितरण चर का वर्गमूल; अज्ञात विचरण के साथ सामान्य रूप से वितरित नमूनों के माध्य के बारे में अनुमान के लिए उपयोगी (छात्र का टी-टेस्ट देखें)
- एफ-वितरण, दो स्केल ची चुकता वितरण चर के अनुपात का वितरण उपयोगी उदा। ऐसे अनुमानों के लिए जिसमें वेरिएंट की तुलना करना या आर-स्क्वेयर सम्मिलित करना सम्मिलित है (चुकता पियर्सन उत्पाद-पल सहसंबंध गुणांक)
के रूप में बायेसियन इनवेंशन में पूर्व वितरण के रूप में
- बीटा वितरण, एकल संभावना के लिए (0 और 1 के मध्य वास्तविक संख्या) बर्नौली वितरण और द्विपद वितरण के लिए संयुग्मन
- गामा वितरण, गैर-ऋणात्मक स्केलिंग पैरामीटर के लिए एक पॉइसन वितरण या घातीय वितरण के दर पैरामीटर के लिए संयुग्मन, सामान्य वितरण, आदि के स्पष्ट (सांख्यिकी) (उलटा विचरण), आदि।
- डिरिचलेट वितरण, संभावनाओं के सदिश के लिए जो 1 के लिए राशि होनी चाहिए; श्रेणीबद्ध वितरण और बहुराष्ट्रीय वितरण के लिए संयुग्म बीटा वितरण का सामान्यीकरण
- विशार्ट वितरण, सममित गैर-ऋणात्मक निश्चित आव्युह के लिए; बहुभिन्नरूपी सामान्य वितरण के सहसंयोजक आव्युह के व्युत्क्रम के लिए संयुग्म गामा वितरण का सामान्यीकरण[30]
संभावना वितरण के कुछ विशेष अनुप्रयोग
- कैश लैंग्वेज मॉडल और अन्य सांख्यिकीय भाषा मॉडल प्राकृतिक भाषा प्रसंस्करण में उपयोग किए जाने वाले विशेष शब्दों और शब्द अनुक्रमों की घटना के लिए संभावनाएं प्रदान करने के लिए संभावना वितरण के माध्यम से ऐसा करते हैं।
- क्वांटम यांत्रिकी में, किसी दिए गए बिंदु पर कण को खोजने की संभावना घनत्व उस बिंदु पर कण की तरंग के परिमाण के वर्ग के लिए आनुपातिक है (जन्म के नियम देखें)। इसलिए, कण की स्थिति की संभावना वितरण फलन द्वारा वर्णित किया गया है , संभावना है कि कण की स्थिति x अंतराल में होगा a ≤ x ≤ b आयाम में, और आयाम तीन में समान ट्रिपल अभिन्न।यह क्वांटम यांत्रिकी का प्रमुख सिद्धांत है।[31]
- पावर-फ्लो अध्ययन में संभाव्य लोड प्रवाह इनपुट चर की अनिश्चितताओं को संभाव्यता वितरण के रूप में बताता है और संभावना वितरण की अवधि में बिजली प्रवाह गणना भी प्रदान करता है।[32]
- पिछले आवृत्ति वितरण जैसे कि उष्णकटिबंधीय चक्रवात, ओले, घटनाओं के मध्य समय, आदि के आधार पर प्राकृतिक घटनाओं की भविष्यवाणी की ।[33]
फिटिंग
संभाव्यता वितरण फिटिंग या पूर्णतः वितरण फिटिंग एक चर घटना के बार-बार माप से संबंधित डेटा की एक श्रृंखला के लिए संभाव्यता वितरण की फिटिंग है। वितरण फिटिंग का उद्देश्य किसी निश्चित अंतराल में घटना की भयावहता की संभावना की भविष्यवाणी करना या घटित होने की आवृत्ति का पूर्वानुमान लगाना है।
कई संभाव्यता वितरण हैं (संभाव्यता वितरण की सूची देखें) जिनमें से कुछ को घटना और वितरण की विशेषताओं के आधार पर, दूसरों की तुलना में डेटा की देखी गई आवृत्ति के अधिक समीप से उपयुक्त किया जा सकता है। यह माना जाता है कि वितरण एक करीबी उपयुक्त देता है जिससे अच्छी भविष्यवाणियाँ होती हैं। इसलिए, वितरण फिटिंग में, किसी को ऐसे वितरण का चयन करने की आवश्यकता होती है जो डेटा के लिए उपयुक्त हो।
यह भी देखें
- सशर्त संभाव्यता वितरण
- संयुक्त संभावना वितरण
- अर्धसंभाव्यता वितरण
- अनुभवजन्य संभावना
- हिस्टोग्राम
- रीमैन-स्टिल्टजे इंटीग्रल या एप्लिकेशन टू प्रोबेबिलिटी थ्योरी | रीमैन-स्टिल्टजेस इंटीग्रल एप्लिकेशन टू प्रोबेबिलिटी थ्योरी
सूची
- संभाव्यता वितरण की सूची
- सांख्यिकीय विषयों की सूची
संदर्भ
उद्धरण
- ↑ 1.0 1.1 Everitt, Brian (2006). कैम्ब्रिज डिक्शनरी ऑफ स्टैटिस्टिक्स (3rd ed.). Cambridge, UK: Cambridge University Press. ISBN 978-0-511-24688-3. OCLC 161828328.
- ↑ Ash, Robert B. (2008). मूल संभावना सिद्धांत (Dover ed.). Mineola, N.Y.: Dover Publications. pp. 66–69. ISBN 978-0-486-46628-6. OCLC 190785258.
- ↑ 3.0 3.1 Evans, Michael; Rosenthal, Jeffrey S. (2010). संभाव्यता और सांख्यिकी: अनिश्चितता का विज्ञान (2nd ed.). New York: W.H. Freeman and Co. p. 38. ISBN 978-1-4292-2462-8. OCLC 473463742.
- ↑ 4.0 4.1 4.2 4.3 4.4 Ross, Sheldon M. (2010). संभावना में पहला कोर्स. Pearson.
- ↑ 5.0 5.1 "1.3.6.1।एक संभावना वितरण क्या है". www.itl.nist.gov. Retrieved 2020-09-10.
- ↑ 6.0 6.1 संभावना और सांख्यिकी के लिए एक आधुनिक परिचय: समझ में क्यों और कैसे. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ↑ Walpole, R.E.; Myers, R.H.; Myers, S.L.; Ye, K. (1999). इंजीनियरों के लिए संभावना और सांख्यिकी. Prentice Hall.
- ↑ 8.0 8.1 DeGroot, Morris H.; Schervish, Mark J. (2002). प्रायिकता अौर सांख्यिकी. Addison-Wesley.
- ↑ Billingsley, P. (1986). संभावना और माप. Wiley. ISBN 9780471804789.
- ↑ Shephard, N.G. (1991). "विशेषता फ़ंक्शन से वितरण फ़ंक्शन तक: सिद्धांत के लिए एक सरल ढांचा". Econometric Theory. 7 (4): 519–529. doi:10.1017/S0266466600004746. S2CID 14668369.
- ↑ Chapters 1 and 2 of Vapnik (1998)
- ↑ 12.0 12.1 More information and examples can be found in the articles Heavy-tailed distribution, Long-tailed distribution, fat-tailed distribution
- ↑ Erhan, Çınlar (2011). संभावना और स्टोकेस्टिक्स. New York: Springer. p. 57. ISBN 9780387878584.
- ↑ see Lebesgue's decomposition theorem
- ↑ Erhan, Çınlar (2011). संभावना और स्टोकेस्टिक्स. New York: Springer. p. 51. ISBN 9780387878591. OCLC 710149819.
- ↑ Cohn, Donald L. (1993). माप सिद्धांत. Birkhäuser.
- ↑ Khuri, André I. (March 2004). "सांख्यिकी में Dirac के डेल्टा फ़ंक्शन के अनुप्रयोग". International Journal of Mathematical Education in Science and Technology (in English). 35 (2): 185–195. doi:10.1080/00207390310001638313. ISSN 0020-739X. S2CID 122501973.
- ↑ Fisz, Marek (1963). संभाव्यता सिद्धांत और गणितीय सांख्यिकी (3rd ed.). John Wiley & Sons. p. 129. ISBN 0-471-26250-1.
- ↑ Jeffrey Seth Rosenthal (2000). कठोर संभावना सिद्धांत पर एक पहला नज़र. World Scientific.
- ↑ Chapter 3.2 of DeGroot & Schervish (2002)
- ↑ Bourne, Murray. "11. संभाव्यता वितरण - अवधारणाएं". www.intmath.com (in English). Retrieved 2020-09-10.
- ↑ W., Stroock, Daniel (1999). संभाव्यता सिद्धांत: एक विश्लेषणात्मक दृष्टिकोण (Rev. ed.). Cambridge [England]: Cambridge University Press. p. 11. ISBN 978-0521663496. OCLC 43953136.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ Kolmogorov, Andrey (1950) [1933]. संभाव्यता के सिद्धांत की नींव. New York, USA: Chelsea Publishing Company. pp. 21–24.
- ↑ Joyce, David (2014). "संभाव्यता के स्वयंसिद्ध" (PDF). Clark University. Retrieved December 5, 2019.
- ↑ 25.0 25.1 Alligood, K.T.; Sauer, T.D.; Yorke, J.A. (1996). अराजकता: डायनेमिक सिस्टम का परिचय. Springer.
- ↑ Rabinovich, M.I.; Fabrikant, A.L. (1979). "कोई भी नहीं". J. Exp. Theor. Phys. 77: 617–629. Bibcode:1979JETP...50..311R.
- ↑ Section 1.9 of Ross, S.M.; Peköz, E.A. (2007). A second course in probability (PDF).
- ↑ Walters, Peter (2000). एर्गोडिक थ्योरी का परिचय. Springer.
- ↑ 29.0 29.1 29.2 Dekking, Frederik Michel; Kraaikamp, Cornelis; Lopuhaä, Hendrik Paul; Meester, Ludolf Erwin (2005), "Why probability and statistics?", A Modern Introduction to Probability and Statistics, Springer London, pp. 1–11, doi:10.1007/1-84628-168-7_1, ISBN 978-1-85233-896-1
- ↑ Bishop, Christopher M. (2006). पैटर्न मान्यता और मशीन प्रवीणता. New York: Springer. ISBN 0-387-31073-8. OCLC 71008143.
- ↑ Chang, Raymond. (2014). रासायनिक विज्ञान के लिए भौतिक रसायन विज्ञान. Thoman, John W., Jr., 1960-. [Mill Valley, California]. pp. 403–406. ISBN 978-1-68015-835-9. OCLC 927509011.
{{cite book}}: CS1 maint: location missing publisher (link) - ↑ Chen, P.; Chen, Z.; Bak-Jensen, B. (April 2008). "Probabilistic load flow: A review". 2008 इलेक्ट्रिक यूटिलिटी डेरेग्यूलेशन और रिस्ट्रक्चरिंग एंड पावर टेक्नोलॉजीज पर तीसरा अंतर्राष्ट्रीय सम्मेलन. pp. 1586–1591. doi:10.1109/drpt.2008.4523658. ISBN 978-7-900714-13-8. S2CID 18669309.
- ↑ Maity, Rajib (2018-04-30). जल विज्ञान और जल विज्ञान में सांख्यिकीय विधियाँ. Singapore. ISBN 978-981-10-8779-0. OCLC 1038418263.
{{cite book}}: CS1 maint: location missing publisher (link)
स्रोत
- den Dekker, A. J.; Sijbers, J. (2014). "चुंबकीय अनुनाद छवियों में डेटा वितरण: एक समीक्षा". Physica Medica. 30 (7): 725–741. doi:10.1016/j.ejmp.2014.05.002. PMID 25059432.
- Vapnik, Vladimir Naumovich (1998). सांख्यिकीय शिक्षण सिद्धांत. John Wiley and Sons.
इस पृष्ठ में गुम आंतरिक लिंक की सूची
बाहरी कड़ियाँ
- "Probability distribution", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Field Guide to Continuous Probability Distributions, Gavin E. Crooks.