प्रक्रिया क्षमता सूचकांक: Difference between revisions

From Vigyanwiki
(Created page with "{{Short description|Statistical measure of process capability}} {{redirect|Cpk||CPK (disambiguation){{!}}CPK}} {{context|date=May 2015}} प्रक्रिया क्...")
 
No edit summary
 
(7 intermediate revisions by 4 users not shown)
Line 1: Line 1:
{{Short description|Statistical measure of process capability}}
{{Short description|Statistical measure of process capability}}
{{redirect|Cpk||CPK (disambiguation){{!}}CPK}}
'''प्रक्रिया क्षमता सूचकांक''', या प्रक्रिया क्षमता अनुपात, प्रक्रिया क्षमता का एक सांख्यिकीय माप है: [[विशिष्टता (तकनीकी मानक)]] सीमा के भीतर उत्पादन उत्पन्न करने के लिए एक इंजीनियरिंग प्रक्रिया की क्षमता है।<ref>{{Cite web|url=http://www.itl.nist.gov/div898/handbook/pmc/section1/pmc16.htm|title=What is Process Capability?|accessdate=2008-06-22|work=[http://www.itl.nist.gov/div898/handbook/index.htm NIST/Sematech Engineering Statistics Handbook]|publisher=[[National Institute of Standards and Technology]]}}</ref> प्रक्रिया क्षमता की अवधारणा केवल उन प्रक्रियाओं के लिए अर्थ रखती है जो सांख्यिकीय नियंत्रण की स्थिति में हैं। इसका मतलब यह है कि यह उन विचलनों का विवरण नहीं दे सकता है जिनकी अपेक्षा नहीं की जाती है, जैसे कि गलत तरीके से संरेखित, क्षतिग्रस्त, या घिसे हुए उपकरण। प्रक्रिया क्षमता सूचकांक मापते हैं कि एक प्रक्रिया अपनी विशिष्टता सीमाओं के सापेक्ष कितनी "प्राकृतिक भिन्नता" का अनुभव करती है, और विभिन्न प्रक्रियाओं की तुलना इस बात से करने की अनुमति देती है कि कोई संगठन उन्हें कितनी अच्छी तरह नियंत्रित करता है। कुछ हद तक विपरीत रूप से, उच्च सूचकांक मान बेहतर प्रदर्शन का संकेत देते हैं, जबकि शून्य उच्च विचलन का संकेत देता है।
{{context|date=May 2015}}
[[प्रक्रिया क्षमता]] सूचकांक, या प्रक्रिया क्षमता अनुपात, प्रक्रिया क्षमता का एक सांख्यिकीय माप है: [[विशिष्टता (तकनीकी मानक)]] सीमा के भीतर आउटपुट उत्पन्न करने के लिए एक इंजीनियरिंग प्रक्रिया (इंजीनियरिंग) की क्षमता।<ref>{{Cite web|url=http://www.itl.nist.gov/div898/handbook/pmc/section1/pmc16.htm|title=What is Process Capability?|accessdate=2008-06-22|work=[http://www.itl.nist.gov/div898/handbook/index.htm NIST/Sematech Engineering Statistics Handbook]|publisher=[[National Institute of Standards and Technology]]}}</ref> प्रक्रिया क्षमता की अवधारणा केवल उन प्रक्रियाओं के लिए अर्थ रखती है जो [[सांख्यिकीय नियंत्रण]] की स्थिति में हैं। इसका मतलब यह है कि यह उन विचलनों का हिसाब नहीं दे सकता है जिनकी अपेक्षा नहीं की जाती है, जैसे कि गलत तरीके से संरेखित, क्षतिग्रस्त, या घिसे हुए उपकरण। प्रक्रिया क्षमता सूचकांक मापते हैं कि सामान्य-कारण और विशेष-कारण कितना है| एक प्रक्रिया अपनी विशिष्टता सीमाओं के सापेक्ष प्राकृतिक भिन्नता का अनुभव करती है, और विभिन्न प्रक्रियाओं की तुलना इस बात से करने की अनुमति देती है कि कोई संगठन उन्हें कितनी अच्छी तरह नियंत्रित करता है। कुछ हद तक विपरीत रूप से, उच्च सूचकांक मान बेहतर प्रदर्शन का संकेत देते हैं, जबकि शून्य उच्च विचलन का संकेत देता है।


==गैर-विशेषज्ञों के लिए उदाहरण==
==गैर-विशेषज्ञों के लिए उदाहरण==
एक कंपनी एक खराद पर नाममात्र व्यास 20 मिमी के साथ धुरी का उत्पादन करती है। चूँकि कोई भी धुरी बिल्कुल 20 मिमी तक नहीं बनाई जा सकती है, डिज़ाइनर अधिकतम स्वीकार्य विचलन (जिन्हें सहनशीलता या विनिर्देश सीमा कहा जाता है) निर्दिष्ट करता है। उदाहरण के लिए, आवश्यकता यह हो सकती है कि धुरी 19.9 और 20.2 मिमी के बीच होनी चाहिए। प्रक्रिया क्षमता सूचकांक एक माप है कि यह कितनी संभावना है कि एक उत्पादित धुरी इस आवश्यकता को पूरा करती है। सूचकांक केवल सांख्यिकीय (प्राकृतिक) विविधताओं से संबंधित है। ये ऐसी विविधताएँ हैं जो बिना किसी विशेष कारण के स्वाभाविक रूप से घटित होती हैं। जिन त्रुटियों पर ध्यान नहीं दिया गया उनमें ऑपरेटर त्रुटियां, या लेथ तंत्र में गड़बड़ी शामिल है जिसके परिणामस्वरूप उपकरण की गलत या अप्रत्याशित स्थिति उत्पन्न हो जाती है। यदि बाद वाले प्रकार की त्रुटियां होती हैं, तो प्रक्रिया सांख्यिकीय नियंत्रण की स्थिति में नहीं है। जब यह मामला है, तो प्रक्रिया क्षमता सूचकांक अर्थहीन है।
एक कंपनी खराद पर नाममात्र व्यास 20 मिमी के साथ धुरी का उत्पादन करती है। चूँकि कोई भी धुरी बिल्कुल 20 मिमी तक नहीं बनाई जा सकती है, रूपकार अधिकतम स्वीकार्य विचलन (जिन्हें सहनशीलता या विनिर्देश सीमा कहा जाता है) निर्दिष्ट करता है। उदाहरण के लिए, आवश्यकता यह हो सकती है कि धुरी 19.9 और 20.2 मिमी के बीच होनी चाहिए। प्रक्रिया क्षमता सूचकांक एक माप है कि यह कितनी संभावना है कि एक उत्पादित धुरी इस आवश्यकता को पूरा करती है। सूचकांक केवल सांख्यिकीय (प्राकृतिक) विविधताओं से संबंधित है। ये ऐसी विविधताएँ हैं जो बिना किसी विशेष कारण के स्वाभाविक रूप से घटित होती हैं। जिन त्रुटियों पर ध्यान नहीं दिया गया उनमें संचालक त्रुटियां, या लेथ तंत्र में गड़बड़ी सम्मिलित है जिसके परिणामस्वरूप उपकरण की गलत या अप्रत्याशित स्थिति उत्पन्न हो जाती है। यदि बाद वाले प्रकार की त्रुटियां होती हैं, तो प्रक्रिया सांख्यिकीय नियंत्रण की स्थिति में नहीं है। जब यह मामला है, तो प्रक्रिया क्षमता सूचकांक अर्थहीन है।


==परिचय==
==परिचय==
यदि प्रक्रिया की ऊपरी और निचली विशिष्टता (तकनीकी मानक) सीमाएं यूएसएल और एलएसएल हैं, तो लक्ष्य प्रक्रिया माध्य टी है, प्रक्रिया का अनुमानित माध्य है <MATH>\hat{\mu}</MATH> और प्रक्रिया की अनुमानित परिवर्तनशीलता ([[मानक विचलन]] के रूप में व्यक्त) है <MATH>\hat{\sigma}</MATH>, तो आम तौर पर स्वीकृत प्रक्रिया क्षमता सूचकांकों में शामिल हैं:
यदि प्रक्रिया की ऊपरी और निचली विनिर्देश (तकनीकी मानक) सीमाएं यूएसएल और एलएसएल हैं, तो लक्ष्य प्रक्रिया माध्य T है, प्रक्रिया का अनुमानित माध्य <math>\hat{\mu}</math> है और प्रक्रिया की अनुमानित परिवर्तनशीलता ([[मानक विचलन]] के रूप में व्यक्त) <math>\hat{\sigma}</math> है, तो आम तौर पर स्वीकृत प्रक्रिया क्षमता सूचकांकों में सम्मिलित हैं:


{| class="wikitable"
{| class="wikitable"
Line 15: Line 13:
|-
|-
| <MATH>\hat{C}_p = \frac{\text{USL - LSL}} {6 \hat{\sigma}}</MATH>
| <MATH>\hat{C}_p = \frac{\text{USL - LSL}} {6 \hat{\sigma}}</MATH>
| Estimates what the process is capable of producing if the process mean were to be centered between the specification limits.  Assumes process output is approximately normally distributed.
| यह अनुमान लगाता है कि यदि प्रक्रिया माध्य को विनिर्देश सीमाओं के बीच केंद्रित किया जाए तो प्रक्रिया क्या उत्पादन करने में सक्षम है। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।
|-
|-
| <MATH>\hat{C}_{p,\text{lower}} = {\hat{\mu} - \text{LSL} \over 3 \hat{\sigma}}</MATH>
| <MATH>\hat{C}_{p,\text{lower}} = {\hat{\mu} - \text{LSL} \over 3 \hat{\sigma}}</MATH>
| Estimates process capability for specifications that consist of a lower limit only (for example, strength).  Assumes process output is approximately normally distributed.
| उन विशिष्टताओं के लिए प्रक्रिया क्षमता का अनुमान लगाता है जिनमें केवल निचली सीमा निहित होती है (उदाहरण के लिए, ताकत)। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।
|-
|-
| <MATH>\hat{C}_{p,\text{upper}} = {\text{USL} - \hat{\mu} \over 3 \hat{\sigma}}</MATH>
| <MATH>\hat{C}_{p,\text{upper}} = {\text{USL} - \hat{\mu} \over 3 \hat{\sigma}}</MATH>
| Estimates process capability for specifications that consist of an upper limit only (for example, concentration).  Assumes process output is approximately normally distributed.
| उन विशिष्टताओं के लिए प्रक्रिया क्षमता का अनुमान लगाता है जिनमें केवल ऊपरी सीमा होती है (उदाहरण के लिए, एकाग्रता)। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।
|-
|-
| <MATH>\hat{C}_{pk} = \min \Bigg[ {\text{USL} - \hat{\mu} \over 3 \hat{\sigma}}, { \hat{\mu} - \text{LSL} \over 3 \hat{\sigma}} \Bigg]</MATH>
| <MATH>\hat{C}_{pk} = \min \Bigg[ {\text{USL} - \hat{\mu} \over 3 \hat{\sigma}}, { \hat{\mu} - \text{LSL} \over 3 \hat{\sigma}} \Bigg]</MATH>
| Estimates what the process is capable of producing, considering that the process mean may not be centered between the specification limits.  (If the process mean is not centered, <MATH>\hat{C}_p</MATH> overestimates process capability.) <MATH>\hat{C}_{pk} < 0</MATH> if the process mean falls outside of the specification limits.  Assumes process output is approximately normally distributed.
| अनुमान लगाता है कि प्रक्रिया क्या उत्पादन करने में सक्षम है, यह ध्यान में रखते हुए कि प्रक्रिया माध्य विनिर्देश सीमाओं के बीच केंद्रित नहीं हो सकता है। (यदि प्रक्रिया माध्य केन्द्रित नहीं है, तो <MATH>\hat{C}_p</MATH> प्रक्रिया क्षमता को अधिक महत्व देता है।) <MATH>\hat{C}_{pk} < 0</MATH> यदि प्रक्रिया माध्य विनिर्देश सीमा से बाहर आता है। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।
|-
|-
| <MATH>\hat{C}_{pm} = \frac{ \hat{C}_p } { \sqrt{ 1 + \left ( \frac{\hat{\mu} - T} {\hat{\sigma}} \right )^2 } }</MATH>
| <MATH>\hat{C}_{pm} = \frac{ \hat{C}_p } { \sqrt{ 1 + \left ( \frac{\hat{\mu} - T} {\hat{\sigma}} \right )^2 } }</MATH>
| Estimates process capability around a target, T.  <MATH>\hat{C}_{pm}</MATH> is always greater than zero.  Assumes process output is approximately normally distributed.  <MATH>\hat{C}_{pm}</MATH> is also known as the [[Taguchi methods|Taguchi]] capability index.<ref>{{Cite news| last = Boyles | first = Russell | year = 1991 | title = The Taguchi Capability Index | periodical = Journal of Quality Technology | publication-place = [[Milwaukee, Wisconsin]] | publisher = [[American Society for Quality|American Society for Quality Control]] | volume = 23 | issue = 1 | pages = 17–26 | url = http://www.asq.org/pub/jqt/ | issn = 0022-4065 | oclc = 1800135 }}</ref>
| लक्ष्य T के आसपास प्रक्रिया क्षमता का अनुमान लगाता है। <MATH>\hat{C}_{pm}</MATH> हमेशा शून्य से बड़ा होता है। यह मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित होता है। <MATH>\hat{C}_{pm}</MATH> को तागुची क्षमता सूचकांक के रूप में भी जाना जाता है।<ref>{{Cite news| last = Boyles | first = Russell | year = 1991 | title = The Taguchi Capability Index | periodical = Journal of Quality Technology | publication-place = [[Milwaukee, Wisconsin]] | publisher = [[American Society for Quality|American Society for Quality Control]] | volume = 23 | issue = 1 | pages = 17–26 | url = http://www.asq.org/pub/jqt/ | issn = 0022-4065 | oclc = 1800135 }}</ref>
|-
|-
| <MATH>\hat{C}_{pkm} = \frac{ \hat{C}_{pk} } { \sqrt{ 1 + \left ( \frac{\hat{\mu} - T} {\hat{\sigma}} \right )^2 } }</MATH>
| <MATH>\hat{C}_{pkm} = \frac{ \hat{C}_{pk} } { \sqrt{ 1 + \left ( \frac{\hat{\mu} - T} {\hat{\sigma}} \right )^2 } }</MATH>
| Estimates process capability around a target, T, and accounts for an off-center process mean.  Assumes process output is approximately normally distributed.
| किसी लक्ष्य, T के आसपास प्रक्रिया क्षमता का अनुमान लगाता है, और केन्द्र के बाहर प्रक्रिया माध्य का हिसाब रखता है। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।
|}
|}


Line 36: Line 34:


==अनुशंसित मान==
==अनुशंसित मान==
प्रक्रिया क्षमता सूचकांकों का निर्माण तेजी से उच्च मूल्यों के साथ अधिक वांछनीय क्षमता को व्यक्त करने के लिए किया जाता है। शून्य के करीब या नीचे के मान लक्ष्य से बाहर चल रही प्रक्रियाओं को दर्शाते हैं (<MATH>\hat{\mu}</MATH> T से दूर) या उच्च भिन्नता के साथ।
प्रक्रिया क्षमता सूचकांकों का निर्माण तेजी से उच्च मूल्यों के साथ अधिक वांछनीय क्षमता को व्यक्त करने के लिए किया जाता है। शून्य के निकट या नीचे के मान लक्ष्य से दूर (T से <math>\hat{\mu}</math> दूर) या उच्च भिन्नता के साथ संचालित होने वाली प्रक्रियाओं को दर्शाते हैं।


न्यूनतम स्वीकार्य प्रक्रिया क्षमता लक्ष्यों के लिए मूल्य तय करना व्यक्तिगत राय का मामला है, और जो सर्वसम्मति मौजूद है वह उद्योग, सुविधा और विचाराधीन प्रक्रिया के अनुसार भिन्न होती है। उदाहरण के लिए, ऑटोमोटिव उद्योग में, [[ऑटोमोटिव इंडस्ट्री एक्शन ग्रुप]] अनुशंसित सी के लिए उत्पादन भाग अनुमोदन प्रक्रिया, चौथे संस्करण में दिशानिर्देश निर्धारित करता है।<SUB>pk</SUB> महत्वपूर्ण-से-गुणवत्ता प्रक्रिया विशेषताओं के लिए न्यूनतम मान। हालाँकि, ये मानदंड बहस योग्य हैं और कई प्रक्रियाओं का मूल्यांकन क्षमता के लिए नहीं किया जा सकता है क्योंकि उनका उचित मूल्यांकन नहीं किया गया है।
न्यूनतम "स्वीकार्य" प्रक्रिया क्षमता लक्ष्यों के लिए मूल्य तय करना व्यक्तिगत राय का विषय है, और जो सर्वसम्मति मौजूद है वह उद्योग, सुविधा और विचाराधीन प्रक्रिया के अनुसार भिन्न होती है। उदाहरण के लिए, ऑटोमोटिव उद्योग में, [[ऑटोमोटिव इंडस्ट्री एक्शन ग्रुप]] महत्वपूर्ण-से-गुणवत्ता प्रक्रिया विशेषताओं के लिए अनुशंसित C<SUB>pk</SUB> न्यूनतम मूल्यों के लिए उत्पादन भाग अनुमोदन प्रक्रिया, चौथे संस्करण में दिशानिर्देश निर्धारित करता है। महत्वपूर्ण-से-गुणवत्ता प्रक्रिया विशेषताओं के लिए न्यूनतम मान। हालाँकि, ये मानदंड विवादास्पद योग्य हैं और कई प्रक्रियाओं का मूल्यांकन क्षमता के लिए नहीं किया जा सकता है क्योंकि उनका उचित मूल्यांकन नहीं किया गया है।


चूँकि प्रक्रिया क्षमता विनिर्देश का एक कार्य है, प्रक्रिया क्षमता सूचकांक केवल विनिर्देश जितना ही अच्छा है। उदाहरण के लिए, यदि विनिर्देश भाग के कार्य और आलोचनात्मकता पर विचार किए बिना एक इंजीनियरिंग दिशानिर्देश से आया है, तो प्रक्रिया क्षमता के बारे में चर्चा बेकार है, और यदि इस पर ध्यान केंद्रित किया जाए कि विनिर्देश के बाहर एक भाग की सीमा रेखा होने के वास्तविक जोखिम क्या हैं, तो अधिक लाभ होंगे। . तागुची विधियों का हानि कार्य इस अवधारणा को बेहतर ढंग से दर्शाता है।
चूँकि प्रक्रिया क्षमता विनिर्देश का एक कार्य है, प्रक्रिया क्षमता सूचकांक केवल विनिर्देश जितना ही अच्छा है। उदाहरण के लिए, यदि विनिर्देश भाग के कार्य और आलोचनात्मकता पर विचार किए बिना इंजीनियरिंग दिशानिर्देश से आया है, तो प्रक्रिया क्षमता के बारे में चर्चा बेकार है, और यदि इस पर ध्यान केंद्रित किया जाए कि विनिर्देश के बाहर भाग की सीमा रेखा होने के वास्तविक विपत्ति क्या हैं, तो अधिक लाभ होंगे। तागुची विधियों का हानि प्रकार्य इस अवधारणा को बेहतर ढंग से दर्शाता है।


कम से कम एक अकादमिक विशेषज्ञ अनुशंसा करता है<ref>{{Cite book | last = Montgomery | first = Douglas | title = सांख्यिकीय गुणवत्ता नियंत्रण का परिचय| publisher = John Wiley & Sons, Inc. | year = 2004 | location = [[New York, New York]] | url = http://www.eas.asu.edu/~masmlab/montgomery/ | isbn = 978-0-471-65631-9 | oclc = 56729567 | page = 776 | url-status = dead | archiveurl = https://web.archive.org/web/20080620095346/http://www.eas.asu.edu/~masmlab/montgomery/ | archivedate = 2008-06-20 }}</ref> निम्नलिखित:
कम से कम एक शैक्षणिक विशेषज्ञ निम्नलिखित की अनुशंसा करता है<ref>{{Cite book | last = Montgomery | first = Douglas | title = सांख्यिकीय गुणवत्ता नियंत्रण का परिचय| publisher = John Wiley & Sons, Inc. | year = 2004 | location = [[New York, New York]] | url = http://www.eas.asu.edu/~masmlab/montgomery/ | isbn = 978-0-471-65631-9 | oclc = 56729567 | page = 776 | url-status = dead | archiveurl = https://web.archive.org/web/20080620095346/http://www.eas.asu.edu/~masmlab/montgomery/ | archivedate = 2008-06-20 }}</ref>:


{| class="wikitable"
{| class="wikitable"
  ! Situation
  ! परिस्थिति
  ! Recommended minimum process capability for two-sided specifications
  ! दोतरफा विशिष्टताओं के लिए अनुशंसित न्यूनतम प्रक्रिया क्षमता
  ! Recommended minimum process capability for one-sided specification
  ! एकतरफ़ा विशिष्टता के लिए अनुशंसित न्यूनतम प्रक्रिया क्षमता
|-
|-
| Existing process
| विद्यमान प्रक्रिया
| 1.33
| 1.33
| 1.25
| 1.25
|-
|-
| New process
| नई प्रक्रिया
| 1.50
| 1.50
| 1.45
| 1.45
|-
|-
| Safety or critical parameter for existing process
| विद्यमान प्रक्रिया के लिए सुरक्षा या महत्वपूर्ण प्राचल
| 1.50
| 1.50
| 1.45
| 1.45
|-
|-
| Safety or critical parameter for new process
| नई प्रक्रिया के लिए सुरक्षा या महत्वपूर्ण प्राचल
| 1.67
| 1.67
| 1.60
| 1.60
|-
|-
| [[Six Sigma]] quality process
| [[Six Sigma|सिक्स सिग्मा]] गुणवत्ता प्रक्रिया
| 2.00
| 2.00
| 2.00
| 2.00
|}
|}
हालाँकि, जहां एक प्रक्रिया 2.5 से अधिक क्षमता सूचकांक के साथ एक विशेषता उत्पन्न करती है, अनावश्यक परिशुद्धता महंगी हो सकती है।<ref>{{Cite book|author1=Booker, J. M. |author2=Raines, M. |author3=Swift, K. G. | title=सक्षम और विश्वसनीय उत्पाद डिज़ाइन करना| year=2001 | publisher=[[Butterworth-Heinemann]] | location=[[Oxford]] | isbn=978-0-7506-5076-2 | oclc=47030836}}</ref>
तथापि, जहां एक प्रक्रिया 2.5 से अधिक क्षमता सूचकांक के साथ एक विशेषता उत्पन्न करती है, अनावश्यक परिशुद्धता महंगी हो सकती है।<ref>{{Cite book|author1=Booker, J. M. |author2=Raines, M. |author3=Swift, K. G. | title=सक्षम और विश्वसनीय उत्पाद डिज़ाइन करना| year=2001 | publisher=[[Butterworth-Heinemann]] | location=[[Oxford]] | isbn=978-0-7506-5076-2 | oclc=47030836}}</ref>
 
 
==प्रक्रिया के नतीजों के उपायों से संबंध==
==प्रक्रिया के नतीजों के उपायों से संबंध==
प्रक्रिया क्षमता सूचकांकों से मैपिंग, जैसे सी<SUB>pk</SUB>, प्रक्रिया के नतीजों के उपाय सीधे हैं। प्रोसेस फॉलआउट यह निर्धारित करता है कि एक प्रक्रिया कितने दोष पैदा करती है और इसे [[प्रति मिलियन अवसरों में दोष]] या प्रति मिलियन पार्ट्स में मापा जाता है। प्रक्रिया उपज प्रक्रिया परिणाम का पूरक है और संभाव्यता घनत्व फ़ंक्शन के तहत क्षेत्र के लगभग बराबर है <MATH>\Phi(\sigma) = \frac{1}{\sqrt{2\pi>< प्रक्रिया आउटपुट लगभग [[सामान्य रूप से वितरित]] होता है।
प्रक्रिया क्षमता सूचकांकों, जैसे C<SUB>pk</SUB>, से प्रक्रिया परिणाम के माप तक मैपिंग सीधी है। प्रक्रिया परिणाम यह निर्धारित करता है कि एक प्रक्रिया कितने दोष पैदा करती है और इसे [[प्रति मिलियन अवसरों में दोष]] या प्रति मिलियन पार्ट्स में मापा जाता है। प्रक्रिया उपज, प्रक्रिया परिणाम का पूरक है और यदि प्रक्रिया उत्पादन लगभग सामान्य रूप से वितरित किया जाता है, तो यह प्रायिकता घनत्व फलन '''<math>\Phi(\sigma) = \frac{1}{\sqrt{2\pi}} \int_{-\sigma}^\sigma e^{-t^2/2} \, dt</math>''' के तहत क्षेत्र के लगभग बराबर है।


अल्पावधि (शॉर्ट सिग्मा) में, रिश्ते हैं:
अल्पावधि ("लघु सिग्मा") में, संबंध हैं:
{| class="wikitable"
{| class="wikitable"
!C<sub>p</sub>
!सिग्मा स्तर (σ)
!संभाव्यता घनत्व फ़ंक्शन के अंतर्गत क्षेत्र
<math>\Phi(\sigma)</math>
!प्रक्रिया प्राप्ति
!प्रक्रिया का परिणाम
(डीपीएमओ/पीपीएम के संदर्भ में)
|-
|-
! C<sub>p</sub>
|0.33
! Sigma level (σ)
|1
! Area under the
|0.6826894921
[[probability density function]] <math>\Phi(\sigma)</math>
|68.27%
! Process yield
|317311
! Process fallout
(in terms of DPMO/PPM)
|-
|-
| 0.33 || 1 ||0.6826894921||68.27%||317311
|0.67
|2
|0.9544997361
|95.45%
|45500
|-
|-
| 0.67 || 2 ||0.9544997361||95.45%||45500
|1.00
|3
|0.9973002039
|99.73%
|2700
|-
|-
| 1.00 || 3 ||0.9973002039||99.73%||2700
|1.33
|4
|0.9999366575
|99.99%
|63
|-
|-
| 1.33 || 4 ||0.9999366575||99.99%||63
|1.67
|5
|0.9999994267
|99.9999%
|1
|-
|-
| 1.67 || 5 ||0.9999994267||99.9999%||1
|2.00
|-
|6
| 2.00 || 6 ||0.9999999980||99.9999998%||0.002
|0.9999999980
|99.9999998%
|0.002
|}
|}
लंबी अवधि में, प्रक्रियाएं महत्वपूर्ण रूप से स्थानांतरित या बहाव कर सकती हैं (अधिकांश [[नियंत्रण चार्ट]] केवल प्रक्रिया आउटपुट में 1.5σ या उससे अधिक के परिवर्तनों के प्रति संवेदनशील होते हैं)। यदि प्रक्रियाओं में लक्ष्य से 1.5 सिग्मा शिफ्ट 1.5σ दूर था (सिक्स सिग्मा#सिग्मा स्तर देखें), तो यह इन रिश्तों का उत्पादन करेगा:<ref>{{Cite web|url=http://bmgi.org/tools-templates/sigma-conversion-calculator|title=Sigma Conversion Calculator {{!}} BMGI.org|website=bmgi.org|access-date=2016-03-17|archive-url=https://web.archive.org/web/20160316152655/http://bmgi.org/tools-templates/sigma-conversion-calculator|archive-date=2016-03-16|url-status=dead}}</ref>
लंबी अवधि में, प्रक्रियाएं महत्वपूर्ण रूप से स्थानांतरित या प्रवाहित हो सकती हैं (अधिकांश [[नियंत्रण चार्ट]] केवल प्रक्रिया उत्पादन में 1.5σ या उससे अधिक के परिवर्तनों के प्रति संवेदनशील होते हैं)। यदि प्रक्रियाओं में लक्ष्य से 1.5 सिग्मा शिफ्ट 1.5σ दूर था (सिक्स सिग्मा देखें), तो यह इन सम्बन्ध का उत्पादन करेगा:<ref>{{Cite web|url=http://bmgi.org/tools-templates/sigma-conversion-calculator|title=Sigma Conversion Calculator {{!}} BMGI.org|website=bmgi.org|access-date=2016-03-17|archive-url=https://web.archive.org/web/20160316152655/http://bmgi.org/tools-templates/sigma-conversion-calculator|archive-date=2016-03-16|url-status=dead}}</ref>
{| class="wikitable"
{| class="wikitable"
!C<sub>p</sub>
!C<sub>p</sub>
!Adjusted
!समायोजित
Sigma level (σ)
सिग्मा स्तर (σ)
!Area under the
!संभाव्यता घनत्व फलन के अंतर्गत क्षेत्र <math>\Phi(\sigma)</math>
[[probability density function]] <math>\Phi(\sigma)</math>
!प्रक्रिया उपज
!Process yield
!प्रक्रिया का नतीजा (डीपीएमओ/पीपीएम के संदर्भ में)
!Process fallout
(in terms of DPMO/PPM)
|-
|-
|0.33
|0.33
Line 145: Line 163:
|3.40
|3.40
|}
|}
चूँकि प्रक्रियाएँ लंबे समय तक महत्वपूर्ण रूप से स्थानांतरित या बहाव कर सकती हैं, प्रत्येक प्रक्रिया में एक अद्वितीय सिग्मा शिफ्ट मान होगा, इस प्रकार प्रक्रिया क्षमता सूचकांक कम लागू होते हैं क्योंकि उन्हें सांख्यिकीय नियंत्रण की आवश्यकता होती है।
चूँकि प्रक्रियाएँ लंबे समय तक महत्वपूर्ण रूप से स्थानांतरित या प्रवाहित हो सकती हैं, प्रत्येक प्रक्रिया में एक अद्वितीय सिग्मा शिफ्ट मान होगा, इस प्रकार प्रक्रिया क्षमता सूचकांक कम लागू होते हैं क्योंकि उन्हें सांख्यिकीय नियंत्रण की आवश्यकता होती है।


==उदाहरण==
==उदाहरण==
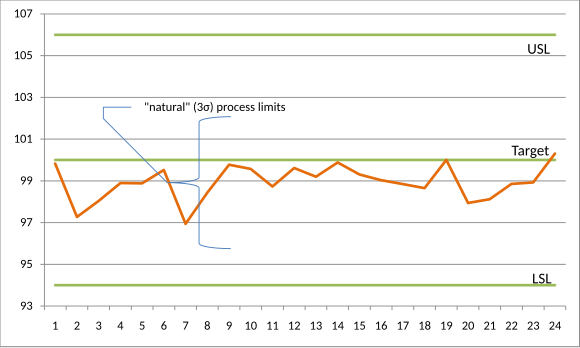
100.00 माइक्रोमीटर|μm के लक्ष्य और क्रमशः 106.00 μm और 94.00 μm की ऊपरी और निचली विनिर्देश सीमा के साथ एक गुणवत्ता विशेषता पर विचार करें। यदि, कुछ समय तक प्रक्रिया की सावधानीपूर्वक निगरानी करने के बाद, यह प्रतीत होता है कि प्रक्रिया नियंत्रण में है और अनुमानित रूप से आउटपुट दे रही है (जैसा कि नीचे [[रन चार्ट]] में दर्शाया गया है), तो हम इसके माध्य और मानक विचलन का सार्थक अनुमान लगा सकते हैं।
100.00 μm के लक्ष्य और क्रमशः 106.00 μm और 94.00 μm की ऊपरी और निचली विनिर्देश सीमा के साथ एक गुणवत्ता विशेषता पर विचार करें। यदि, कुछ समय तक प्रक्रिया की सावधानीपूर्वक निगरानी करने के बाद, यह प्रतीत होता है कि प्रक्रिया नियंत्रण में है और अनुमानित रूप से उत्पादन दे रही है (जैसा कि नीचे [[रन चार्ट]] में दर्शाया गया है), तो हम इसके माध्य और मानक विचलन का सार्थक अनुमान लगा सकते हैं।


[[File:ProcessCapabilityExample.svg]]अगर <MATH>\hat{\mu}</MATH> और <MATH>\hat{\sigma}</MATH> का अनुमान क्रमशः 98.94 μm और 1.03 μm है, तो
[[File:ProcessCapabilityExample.svg]]
 
 
यदि <math>\hat{\mu}</math> और <math>\hat{\sigma}</math> का अनुमान क्रमशः 98.94 μm और 1.03 μm है, तो
{| class="wikitable"
{| class="wikitable"
  ! Index
  ! अनुक्रमणिका
|-
|-
| <MATH>\hat{C}_p = \frac{\text{USL - LSL}} {6 \hat{\sigma}} = \frac{106.00 - 94.00} {6 \times 1.03} = 1.94</MATH>
| <math>\hat{C}_p = \frac{\text{USL - LSL}} {6 \hat{\sigma}} = \frac{106.00 - 94.00} {6 \times 1.03} = 1.94</math>
|-
|-
| <MATH>\hat{C}_{pk} = \min \Bigg[ {\text{USL} - \hat{\mu} \over 3 \hat{\sigma}}, { \hat{\mu} - \text{LSL} \over 3 \hat{\sigma}} \Bigg] = \min \Bigg[ {106.00 - 98.94 \over 3 \times 1.03}, { 98.94 - 94 \over 3 \times 1.03} \Bigg] = 1.60</MATH>
| <math>\hat{C}_{pk} = \min \Bigg[ {\text{USL} - \hat{\mu} \over 3 \hat{\sigma}}, { \hat{\mu} - \text{LSL} \over 3 \hat{\sigma}} \Bigg] = \min \Bigg[ {106.00 - 98.94 \over 3 \times 1.03}, { 98.94 - 94 \over 3 \times 1.03} \Bigg] = 1.60</math>
|-
|-
| <MATH>\hat{C}_{pm} = \frac{ \hat{C}_p } { \sqrt{ 1 + \left ( \frac{\hat{\mu} - T} {\hat{\sigma}} \right )^2 } } = \frac{ 1.94 } { \sqrt{ 1 + \left ( \frac{98.94 - 100.00} {1.03} \right )^2 } } = 1.35</MATH>
| <math>\hat{C}_{pm} = \frac{ \hat{C}_p } { \sqrt{ 1 + \left ( \frac{\hat{\mu} - T} {\hat{\sigma}} \right )^2 } } = \frac{ 1.94 } { \sqrt{ 1 + \left ( \frac{98.94 - 100.00} {1.03} \right )^2 } } = 1.35</math>
|-
|-
| <MATH>\hat{C}_{pkm} = \frac{ \hat{C}_{pk} } { \sqrt{ 1 + \left ( \frac{\hat{\mu} - T} {\hat{\sigma}} \right )^2 } } = \frac{ 1.60 } { \sqrt{ 1 + \left ( \frac{98.94 - 100.00} {1.03} \right )^2 } } = 1.11</MATH>
| <math>\hat{C}_{pkm} = \frac{ \hat{C}_{pk} } { \sqrt{ 1 + \left ( \frac{\hat{\mu} - T} {\hat{\sigma}} \right )^2 } } = \frac{ 1.60 } { \sqrt{ 1 + \left ( \frac{98.94 - 100.00} {1.03} \right )^2 } } = 1.11</math>
|}
|}
तथ्य यह है कि प्रक्रिया ऑफ-सेंटर (अपने लक्ष्य से लगभग 1σ नीचे) चल रही है, सी के लिए स्पष्ट रूप से भिन्न मूल्यों में परिलक्षित होता है<SUB>पी</उप>, सी<SUB>पीके</उप>, सी<SUB>pm</SUB>, और सी<SUB>पीकेएम</उप>.
तथ्य यह है कि प्रक्रिया केन्द्र के बाहर (अपने लक्ष्य से लगभग 1σ नीचे) चल रही है, जो C<sub>p</sub>, C<sub>pk</sub>, C<sub>pm</sub>, और C<sub>pkm</sub> के लिए स्पष्ट रूप से भिन्न मूल्यों में परिलक्षित होती है।


==यह भी देखें==
==यह भी देखें==
Line 172: Line 193:
{{Reflist}}
{{Reflist}}


{{DEFAULTSORT:Process Capability Index}}[[Category: सूचकांक संख्या]] [[Category: गुणवत्ता नियंत्रण]]
{{DEFAULTSORT:Process Capability Index}}
 
 


[[Category: Machine Translated Page]]
[[Category:CS1 errors]]
[[Category:Created On 09/07/2023]]
[[Category:Created On 09/07/2023|Process Capability Index]]
[[Category:Lua-based templates|Process Capability Index]]
[[Category:Machine Translated Page|Process Capability Index]]
[[Category:Pages with script errors|Process Capability Index]]
[[Category:Templates Vigyan Ready|Process Capability Index]]
[[Category:Templates that add a tracking category|Process Capability Index]]
[[Category:Templates that generate short descriptions|Process Capability Index]]
[[Category:Templates using TemplateData|Process Capability Index]]
[[Category:गुणवत्ता नियंत्रण|Process Capability Index]]
[[Category:सूचकांक संख्या|Process Capability Index]]

Latest revision as of 12:37, 28 July 2023

प्रक्रिया क्षमता सूचकांक, या प्रक्रिया क्षमता अनुपात, प्रक्रिया क्षमता का एक सांख्यिकीय माप है: विशिष्टता (तकनीकी मानक) सीमा के भीतर उत्पादन उत्पन्न करने के लिए एक इंजीनियरिंग प्रक्रिया की क्षमता है।[1] प्रक्रिया क्षमता की अवधारणा केवल उन प्रक्रियाओं के लिए अर्थ रखती है जो सांख्यिकीय नियंत्रण की स्थिति में हैं। इसका मतलब यह है कि यह उन विचलनों का विवरण नहीं दे सकता है जिनकी अपेक्षा नहीं की जाती है, जैसे कि गलत तरीके से संरेखित, क्षतिग्रस्त, या घिसे हुए उपकरण। प्रक्रिया क्षमता सूचकांक मापते हैं कि एक प्रक्रिया अपनी विशिष्टता सीमाओं के सापेक्ष कितनी "प्राकृतिक भिन्नता" का अनुभव करती है, और विभिन्न प्रक्रियाओं की तुलना इस बात से करने की अनुमति देती है कि कोई संगठन उन्हें कितनी अच्छी तरह नियंत्रित करता है। कुछ हद तक विपरीत रूप से, उच्च सूचकांक मान बेहतर प्रदर्शन का संकेत देते हैं, जबकि शून्य उच्च विचलन का संकेत देता है।

गैर-विशेषज्ञों के लिए उदाहरण

एक कंपनी खराद पर नाममात्र व्यास 20 मिमी के साथ धुरी का उत्पादन करती है। चूँकि कोई भी धुरी बिल्कुल 20 मिमी तक नहीं बनाई जा सकती है, रूपकार अधिकतम स्वीकार्य विचलन (जिन्हें सहनशीलता या विनिर्देश सीमा कहा जाता है) निर्दिष्ट करता है। उदाहरण के लिए, आवश्यकता यह हो सकती है कि धुरी 19.9 और 20.2 मिमी के बीच होनी चाहिए। प्रक्रिया क्षमता सूचकांक एक माप है कि यह कितनी संभावना है कि एक उत्पादित धुरी इस आवश्यकता को पूरा करती है। सूचकांक केवल सांख्यिकीय (प्राकृतिक) विविधताओं से संबंधित है। ये ऐसी विविधताएँ हैं जो बिना किसी विशेष कारण के स्वाभाविक रूप से घटित होती हैं। जिन त्रुटियों पर ध्यान नहीं दिया गया उनमें संचालक त्रुटियां, या लेथ तंत्र में गड़बड़ी सम्मिलित है जिसके परिणामस्वरूप उपकरण की गलत या अप्रत्याशित स्थिति उत्पन्न हो जाती है। यदि बाद वाले प्रकार की त्रुटियां होती हैं, तो प्रक्रिया सांख्यिकीय नियंत्रण की स्थिति में नहीं है। जब यह मामला है, तो प्रक्रिया क्षमता सूचकांक अर्थहीन है।

परिचय

यदि प्रक्रिया की ऊपरी और निचली विनिर्देश (तकनीकी मानक) सीमाएं यूएसएल और एलएसएल हैं, तो लक्ष्य प्रक्रिया माध्य T है, प्रक्रिया का अनुमानित माध्य है और प्रक्रिया की अनुमानित परिवर्तनशीलता (मानक विचलन के रूप में व्यक्त) है, तो आम तौर पर स्वीकृत प्रक्रिया क्षमता सूचकांकों में सम्मिलित हैं:

Index Description
यह अनुमान लगाता है कि यदि प्रक्रिया माध्य को विनिर्देश सीमाओं के बीच केंद्रित किया जाए तो प्रक्रिया क्या उत्पादन करने में सक्षम है। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।
उन विशिष्टताओं के लिए प्रक्रिया क्षमता का अनुमान लगाता है जिनमें केवल निचली सीमा निहित होती है (उदाहरण के लिए, ताकत)। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।
उन विशिष्टताओं के लिए प्रक्रिया क्षमता का अनुमान लगाता है जिनमें केवल ऊपरी सीमा होती है (उदाहरण के लिए, एकाग्रता)। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।
अनुमान लगाता है कि प्रक्रिया क्या उत्पादन करने में सक्षम है, यह ध्यान में रखते हुए कि प्रक्रिया माध्य विनिर्देश सीमाओं के बीच केंद्रित नहीं हो सकता है। (यदि प्रक्रिया माध्य केन्द्रित नहीं है, तो प्रक्रिया क्षमता को अधिक महत्व देता है।) यदि प्रक्रिया माध्य विनिर्देश सीमा से बाहर आता है। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।
लक्ष्य T के आसपास प्रक्रिया क्षमता का अनुमान लगाता है। हमेशा शून्य से बड़ा होता है। यह मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित होता है। को तागुची क्षमता सूचकांक के रूप में भी जाना जाता है।[2]
किसी लक्ष्य, T के आसपास प्रक्रिया क्षमता का अनुमान लगाता है, और केन्द्र के बाहर प्रक्रिया माध्य का हिसाब रखता है। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।

का अनुमान मानक विचलन के निष्पक्ष अनुमान का उपयोग करके लगाया जाता है।

अनुशंसित मान

प्रक्रिया क्षमता सूचकांकों का निर्माण तेजी से उच्च मूल्यों के साथ अधिक वांछनीय क्षमता को व्यक्त करने के लिए किया जाता है। शून्य के निकट या नीचे के मान लक्ष्य से दूर (T से दूर) या उच्च भिन्नता के साथ संचालित होने वाली प्रक्रियाओं को दर्शाते हैं।

न्यूनतम "स्वीकार्य" प्रक्रिया क्षमता लक्ष्यों के लिए मूल्य तय करना व्यक्तिगत राय का विषय है, और जो सर्वसम्मति मौजूद है वह उद्योग, सुविधा और विचाराधीन प्रक्रिया के अनुसार भिन्न होती है। उदाहरण के लिए, ऑटोमोटिव उद्योग में, ऑटोमोटिव इंडस्ट्री एक्शन ग्रुप महत्वपूर्ण-से-गुणवत्ता प्रक्रिया विशेषताओं के लिए अनुशंसित Cpk न्यूनतम मूल्यों के लिए उत्पादन भाग अनुमोदन प्रक्रिया, चौथे संस्करण में दिशानिर्देश निर्धारित करता है। महत्वपूर्ण-से-गुणवत्ता प्रक्रिया विशेषताओं के लिए न्यूनतम मान। हालाँकि, ये मानदंड विवादास्पद योग्य हैं और कई प्रक्रियाओं का मूल्यांकन क्षमता के लिए नहीं किया जा सकता है क्योंकि उनका उचित मूल्यांकन नहीं किया गया है।

चूँकि प्रक्रिया क्षमता विनिर्देश का एक कार्य है, प्रक्रिया क्षमता सूचकांक केवल विनिर्देश जितना ही अच्छा है। उदाहरण के लिए, यदि विनिर्देश भाग के कार्य और आलोचनात्मकता पर विचार किए बिना इंजीनियरिंग दिशानिर्देश से आया है, तो प्रक्रिया क्षमता के बारे में चर्चा बेकार है, और यदि इस पर ध्यान केंद्रित किया जाए कि विनिर्देश के बाहर भाग की सीमा रेखा होने के वास्तविक विपत्ति क्या हैं, तो अधिक लाभ होंगे। तागुची विधियों का हानि प्रकार्य इस अवधारणा को बेहतर ढंग से दर्शाता है।

कम से कम एक शैक्षणिक विशेषज्ञ निम्नलिखित की अनुशंसा करता है[3]:

परिस्थिति दोतरफा विशिष्टताओं के लिए अनुशंसित न्यूनतम प्रक्रिया क्षमता एकतरफ़ा विशिष्टता के लिए अनुशंसित न्यूनतम प्रक्रिया क्षमता
विद्यमान प्रक्रिया 1.33 1.25
नई प्रक्रिया 1.50 1.45
विद्यमान प्रक्रिया के लिए सुरक्षा या महत्वपूर्ण प्राचल 1.50 1.45
नई प्रक्रिया के लिए सुरक्षा या महत्वपूर्ण प्राचल 1.67 1.60
सिक्स सिग्मा गुणवत्ता प्रक्रिया 2.00 2.00

तथापि, जहां एक प्रक्रिया 2.5 से अधिक क्षमता सूचकांक के साथ एक विशेषता उत्पन्न करती है, अनावश्यक परिशुद्धता महंगी हो सकती है।[4]

प्रक्रिया के नतीजों के उपायों से संबंध

प्रक्रिया क्षमता सूचकांकों, जैसे Cpk, से प्रक्रिया परिणाम के माप तक मैपिंग सीधी है। प्रक्रिया परिणाम यह निर्धारित करता है कि एक प्रक्रिया कितने दोष पैदा करती है और इसे प्रति मिलियन अवसरों में दोष या प्रति मिलियन पार्ट्स में मापा जाता है। प्रक्रिया उपज, प्रक्रिया परिणाम का पूरक है और यदि प्रक्रिया उत्पादन लगभग सामान्य रूप से वितरित किया जाता है, तो यह प्रायिकता घनत्व फलन के तहत क्षेत्र के लगभग बराबर है।

अल्पावधि ("लघु सिग्मा") में, संबंध हैं:

Cp सिग्मा स्तर (σ) संभाव्यता घनत्व फ़ंक्शन के अंतर्गत क्षेत्र

प्रक्रिया प्राप्ति प्रक्रिया का परिणाम

(डीपीएमओ/पीपीएम के संदर्भ में)

0.33 1 0.6826894921 68.27% 317311
0.67 2 0.9544997361 95.45% 45500
1.00 3 0.9973002039 99.73% 2700
1.33 4 0.9999366575 99.99% 63
1.67 5 0.9999994267 99.9999% 1
2.00 6 0.9999999980 99.9999998% 0.002

लंबी अवधि में, प्रक्रियाएं महत्वपूर्ण रूप से स्थानांतरित या प्रवाहित हो सकती हैं (अधिकांश नियंत्रण चार्ट केवल प्रक्रिया उत्पादन में 1.5σ या उससे अधिक के परिवर्तनों के प्रति संवेदनशील होते हैं)। यदि प्रक्रियाओं में लक्ष्य से 1.5 सिग्मा शिफ्ट 1.5σ दूर था (सिक्स सिग्मा देखें), तो यह इन सम्बन्ध का उत्पादन करेगा:[5]

Cp समायोजित

सिग्मा स्तर (σ)

संभाव्यता घनत्व फलन के अंतर्गत क्षेत्र प्रक्रिया उपज प्रक्रिया का नतीजा (डीपीएमओ/पीपीएम के संदर्भ में)
0.33 1 0.3085375387 30.85% 691462
0.67 2 0.6914624613 69.15% 308538
1.00 3 0.9331927987 93.32% 66807
1.33 4 0.9937903347 99.38% 6209
1.67 5 0.9997673709 99.9767% 232.6
2.00 6 0.9999966023 99.99966% 3.40

चूँकि प्रक्रियाएँ लंबे समय तक महत्वपूर्ण रूप से स्थानांतरित या प्रवाहित हो सकती हैं, प्रत्येक प्रक्रिया में एक अद्वितीय सिग्मा शिफ्ट मान होगा, इस प्रकार प्रक्रिया क्षमता सूचकांक कम लागू होते हैं क्योंकि उन्हें सांख्यिकीय नियंत्रण की आवश्यकता होती है।

उदाहरण

100.00 μm के लक्ष्य और क्रमशः 106.00 μm और 94.00 μm की ऊपरी और निचली विनिर्देश सीमा के साथ एक गुणवत्ता विशेषता पर विचार करें। यदि, कुछ समय तक प्रक्रिया की सावधानीपूर्वक निगरानी करने के बाद, यह प्रतीत होता है कि प्रक्रिया नियंत्रण में है और अनुमानित रूप से उत्पादन दे रही है (जैसा कि नीचे रन चार्ट में दर्शाया गया है), तो हम इसके माध्य और मानक विचलन का सार्थक अनुमान लगा सकते हैं।

ProcessCapabilityExample.svg


यदि और का अनुमान क्रमशः 98.94 μm और 1.03 μm है, तो

अनुक्रमणिका

तथ्य यह है कि प्रक्रिया केन्द्र के बाहर (अपने लक्ष्य से लगभग 1σ नीचे) चल रही है, जो Cp, Cpk, Cpm, और Cpkm के लिए स्पष्ट रूप से भिन्न मूल्यों में परिलक्षित होती है।

यह भी देखें

  • प्रक्रिया अभियंता)
  • प्रक्रिया क्षमता
  • प्रक्रिया प्रदर्शन सूचकांक

संदर्भ

  1. ↑ "What is Process Capability?". NIST/Sematech Engineering Statistics Handbook. National Institute of Standards and Technology. Retrieved 2008-06-22. {{cite web}}: External link in |work= (help)
  2. ↑ Boyles, Russell (1991). "The Taguchi Capability Index". Journal of Quality Technology. Vol. 23, no. 1. Milwaukee, Wisconsin: American Society for Quality Control. pp. 17–26. ISSN 0022-4065. OCLC 1800135.
  3. ↑ Montgomery, Douglas (2004). सांख्यिकीय गुणवत्ता नियंत्रण का परिचय. New York, New York: John Wiley & Sons, Inc. p. 776. ISBN 978-0-471-65631-9. OCLC 56729567. Archived from the original on 2008-06-20.
  4. ↑ Booker, J. M.; Raines, M.; Swift, K. G. (2001). सक्षम और विश्वसनीय उत्पाद डिज़ाइन करना. Oxford: Butterworth-Heinemann. ISBN 978-0-7506-5076-2. OCLC 47030836.
  5. ↑ "Sigma Conversion Calculator | BMGI.org". bmgi.org. Archived from the original on 2016-03-16. Retrieved 2016-03-17.
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=प्रक्रिया_क्षमता_सूचकांक&oldid=229132’