आयाम-शिफ्ट कुंजीयन: Difference between revisions
No edit summary |
No edit summary |
||
| (5 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
[[ आयाम |आयाम]]-शिफ्ट कुंजीयन (एएसके) आयाम मॉडुलन का एक ऐसा रूप है जो किसी वाहक तरंग के आयाम में भिन्नता करके डिजिटल डेटा का प्रतिनिधित्व करता है। किसी एएसके प्रणाली में, एक या अधिक [[बिट्स]] का प्रतिनिधित्व करने वाला प्रतीक एक निश्चित समय अवधि के लिए निश्चित [[आवृत्ति]] पर निश्चित-आयाम वाहक तरंग को प्रेषित करके भेजता है। उदाहरण के लिए, यदि प्रत्येक प्रतीक एक बिट का प्रतिनिधित्व करता है, तब वाहक संकेत नाम आयाम पर प्रेषित किया जाता है जब इनपुट मान 1 तब इसे कम आयाम पर संचारित होता है और जब इनपुट मान 0 होता है तब ऐसी स्थिति में इसे बिल्कुल भी संचरित नहीं किया जा सकता है। | [[ आयाम |आयाम]]-शिफ्ट कुंजीयन (एएसके) आयाम मॉडुलन का एक ऐसा रूप है जो किसी वाहक तरंग के आयाम में भिन्नता करके डिजिटल डेटा का प्रतिनिधित्व करता है। किसी एएसके प्रणाली में, एक या अधिक [[बिट्स]] का प्रतिनिधित्व करने वाला प्रतीक एक निश्चित समय अवधि के लिए निश्चित [[आवृत्ति]] पर निश्चित-आयाम वाहक तरंग को प्रेषित करके भेजता है। उदाहरण के लिए, यदि प्रत्येक प्रतीक एक बिट का प्रतिनिधित्व करता है, तब वाहक संकेत नाम आयाम पर प्रेषित किया जाता है जब इनपुट मान 1 तब इसे कम आयाम पर संचारित होता है और जब इनपुट मान 0 होता है तब ऐसी स्थिति में इसे बिल्कुल भी संचरित नहीं किया जा सकता है। | ||
कोई भी डिजिटल मॉडुलन योजना डिजिटल डेटा का प्रतिनिधित्व करने के लिए सीमित संख्या में विशिष्ट संकेतों का उपयोग करती है। एएसके परिमित संख्या में आयामों का उपयोग करता है, सामान्यतः प्रत्येक आयाम समान संख्या में बिट्स को एन्कोड किया जाता है। बिट्स का प्रत्येक | कोई भी डिजिटल मॉडुलन योजना डिजिटल डेटा का प्रतिनिधित्व करने के लिए सीमित संख्या में विशिष्ट संकेतों का उपयोग करती है। एएसके परिमित संख्या में आयामों का उपयोग करता है, सामान्यतः प्रत्येक आयाम समान संख्या में बिट्स को एन्कोड किया जाता है। बिट्स का प्रत्येक [[ प्रतीक (डेटा) ]] विशेष आयाम द्वारा दर्शाया जाता है। [[डिमोडुलेटर]], जिसे विशेष रूप से मॉड्यूलेटर द्वारा उपयोग किए गए प्रतीक सेट के लिए डिज़ाइन किया गया है, प्राप्त सिग्नल के आयाम को निर्धारित करता है और इसे उस प्रतीक पर वापस मैप करता है जो इसे दर्शाता है, इस प्रकार मूल डेटा की पुनर्प्राप्त होती है और वाहक की आवृत्ति और चरण को स्थिर रखा जाता है। | ||
[[ आयाम अधिमिश्रण | आयाम अधिमिश्रण]] की तरह, एएसके भी रैखिक और वायुमंडलीय शोर, विकृतियों, [[ पीएसटीएन | पीएसटीएन]] में विभिन्न मार्गों पर प्रसार की स्थिति आदि के प्रति संवेदनशील है। एएसके मॉडुलन और डिमॉड्यूलेशन दोनों प्रक्रियाएं अपेक्षाकृत सस्ती हैं। एएसके तकनीक का उपयोग सामान्यतः ऑप्टिकल फाइबर पर डिजिटल डेटा संचारित करने के लिए भी किया जाता है। एलईडी ट्रांसमीटरों के लिए, बाइनरी 1 को प्रकाश की एक छोटी पल्स और बाइनरी 0 द्वारा प्रकाश की अनुपस्थिति द्वारा दर्शाया जाता है। लेजर ट्रांसमीटरों में सामान्य रूप से एक निश्चित "पूर्वाग्रह" धारा होती है जो डिवाइस को कम रोशनी के स्तर का उत्सर्जन करने का कारण बनता है। यह निम्न स्तर बाइनरी 0 का प्रतिनिधित्व करता है, जबकि एक उच्च आयाम वाली लाइटवेव बाइनरी 1 का प्रतिनिधित्व करती है। | [[ आयाम अधिमिश्रण | आयाम अधिमिश्रण]] की तरह, एएसके भी रैखिक और वायुमंडलीय शोर, विकृतियों, [[ पीएसटीएन | पीएसटीएन]] में विभिन्न मार्गों पर प्रसार की स्थिति आदि के प्रति संवेदनशील है। एएसके मॉडुलन और डिमॉड्यूलेशन दोनों प्रक्रियाएं अपेक्षाकृत सस्ती हैं। एएसके तकनीक का उपयोग सामान्यतः ऑप्टिकल फाइबर पर डिजिटल डेटा संचारित करने के लिए भी किया जाता है। एलईडी ट्रांसमीटरों के लिए, बाइनरी 1 को प्रकाश की एक छोटी पल्स और बाइनरी 0 द्वारा प्रकाश की अनुपस्थिति द्वारा दर्शाया जाता है। लेजर ट्रांसमीटरों में सामान्य रूप से एक निश्चित "पूर्वाग्रह" धारा होती है जो डिवाइस को कम रोशनी के स्तर का उत्सर्जन करने का कारण बनता है। यह निम्न स्तर बाइनरी 0 का प्रतिनिधित्व करता है, जबकि एक उच्च आयाम वाली लाइटवेव बाइनरी 1 का प्रतिनिधित्व करती है। | ||
| Line 68: | Line 68: | ||
:<math>P_e = 2 \left( 1 - \frac{1}{L} \right) P^+</math> | :<math>P_e = 2 \left( 1 - \frac{1}{L} \right) P^+</math> | ||
अब हमें | अब हमें <math>P^+</math> के मान की गणना करनी है ऐसा करने के लिए हम इसी प्रकार के संदर्भ की उत्पत्ति को स्थानांतरित कर सकते हैं: यहाँ पर फ़ंक्शन के नीचे का क्षेत्र नहीं बदलेगा। हम ऐसी स्थिति में हैं जैसे निम्न चित्र में दिखाया गया है: | ||
[[File:Ask dia calc prob 2.png|center|800px]] | [[File:Ask dia calc prob 2.png|center|800px]] | ||
इससे कोई फर्क नहीं पड़ता कि हम किस गाऊसी फ़ंक्शन पर विचार कर रहे हैं, जिस क्षेत्र की हम गणना करना चाहते हैं वह वही होगा। हम जिस मूल्य | इससे कोई फर्क नहीं पड़ता कि हम किस गाऊसी फ़ंक्शन पर विचार कर रहे हैं, जिस क्षेत्र की हम गणना करना चाहते हैं वह वही होगा। हम जिस मूल्य को ढूंढ रहे है वह निम्नलिखित अभिन्न द्वारा दिया जाएगा: | ||
:<math>P^+ = \int_{\frac{A g(0)}{L-1}}^{\infty} \frac{1}{\sqrt{2 \pi} \sigma_N} e^{-\frac{x^2}{2 \sigma_N^2}} d x = \frac{1}{2} \operatorname{erfc} \left( \frac{A g(0)}{\sqrt{2} (L-1) \sigma_N} \right) </math> | :<math>P^+ = \int_{\frac{A g(0)}{L-1}}^{\infty} \frac{1}{\sqrt{2 \pi} \sigma_N} e^{-\frac{x^2}{2 \sigma_N^2}} d x = \frac{1}{2} \operatorname{erfc} \left( \frac{A g(0)}{\sqrt{2} (L-1) \sigma_N} \right) </math> | ||
| Line 77: | Line 77: | ||
:<math>P_e = \left( 1 - \frac{1}{L} \right) \operatorname{erfc} \left( \frac{A g(0)}{\sqrt{2} (L-1) \sigma_N} \right) </math> | :<math>P_e = \left( 1 - \frac{1}{L} \right) \operatorname{erfc} \left( \frac{A g(0)}{\sqrt{2} (L-1) \sigma_N} \right) </math> | ||
इस सूत्र से हम आसानी से समझ सकते हैं कि यदि प्रेषित सिग्नल का अधिकतम आयाम या सिस्टम का प्रवर्धन अधिक हो जाता है तो त्रुटि होने की संभावना कम हो जाती है; दूसरी ओर | इस सूत्र से हम आसानी से समझ सकते हैं कि यदि प्रेषित सिग्नल का अधिकतम आयाम या सिस्टम का प्रवर्धन अधिक हो जाता है तो त्रुटि होने की संभावना कम हो जाती है; दूसरी ओर स्तरों की संख्या या शोर की शक्ति अधिक होने पर बढ़ जाती है। | ||
यह संबंध उस समय मान्य होता है जब कोई अंतर-प्रतीक हस्तक्षेप नहीं होता है, अर्थात <math>g(t)</math> एक [[ Nyquist ISI मानदंड | न्यक्विस्ट आईएसआई मानदंड]] है। | यह संबंध उस समय मान्य होता है जब कोई अंतर-प्रतीक हस्तक्षेप नहीं होता है, अर्थात <math>g(t)</math> एक [[ Nyquist ISI मानदंड | न्यक्विस्ट आईएसआई मानदंड]] है। | ||
| Line 87: | Line 87: | ||
* [http://www.maxim-ic.com/appnotes.cfm/an_pk/2815/CMP/WP-21 Calculating the Sensitivity of an Amplitude Shift Keying (ASK) Receiver] {{Webarchive|url=https://web.archive.org/web/20090829233902/http://www.maxim-ic.com/appnotes.cfm/an_pk/2815/CMP/WP-21 |date=2009-08-29 }} | * [http://www.maxim-ic.com/appnotes.cfm/an_pk/2815/CMP/WP-21 Calculating the Sensitivity of an Amplitude Shift Keying (ASK) Receiver] {{Webarchive|url=https://web.archive.org/web/20090829233902/http://www.maxim-ic.com/appnotes.cfm/an_pk/2815/CMP/WP-21 |date=2009-08-29 }} | ||
{{DEFAULTSORT:Amplitude-Shift Keying}} | {{DEFAULTSORT:Amplitude-Shift Keying}} | ||
[[Category:Machine Translated Page]] | |||
[[Category: | |||
[[Category:Created On 05/09/2022|Amplitude-Shift Keying]] | |||
[[Category: | [[Category:Webarchive template wayback links|Amplitude-Shift Keying]] | ||
[[Category: | [[Category:अनुप्रयुक्त संभाव्यता|Amplitude-Shift Keying]] | ||
[[Category:दोष सहिष्णुता|Amplitude-Shift Keying]] | |||
[[Category:परिमाणित रेडियो मॉडुलन मोड|Amplitude-Shift Keying]] | |||
Latest revision as of 09:15, 11 November 2022
आयाम-शिफ्ट कुंजीयन (एएसके) आयाम मॉडुलन का एक ऐसा रूप है जो किसी वाहक तरंग के आयाम में भिन्नता करके डिजिटल डेटा का प्रतिनिधित्व करता है। किसी एएसके प्रणाली में, एक या अधिक बिट्स का प्रतिनिधित्व करने वाला प्रतीक एक निश्चित समय अवधि के लिए निश्चित आवृत्ति पर निश्चित-आयाम वाहक तरंग को प्रेषित करके भेजता है। उदाहरण के लिए, यदि प्रत्येक प्रतीक एक बिट का प्रतिनिधित्व करता है, तब वाहक संकेत नाम आयाम पर प्रेषित किया जाता है जब इनपुट मान 1 तब इसे कम आयाम पर संचारित होता है और जब इनपुट मान 0 होता है तब ऐसी स्थिति में इसे बिल्कुल भी संचरित नहीं किया जा सकता है।
कोई भी डिजिटल मॉडुलन योजना डिजिटल डेटा का प्रतिनिधित्व करने के लिए सीमित संख्या में विशिष्ट संकेतों का उपयोग करती है। एएसके परिमित संख्या में आयामों का उपयोग करता है, सामान्यतः प्रत्येक आयाम समान संख्या में बिट्स को एन्कोड किया जाता है। बिट्स का प्रत्येक प्रतीक (डेटा) विशेष आयाम द्वारा दर्शाया जाता है। डिमोडुलेटर, जिसे विशेष रूप से मॉड्यूलेटर द्वारा उपयोग किए गए प्रतीक सेट के लिए डिज़ाइन किया गया है, प्राप्त सिग्नल के आयाम को निर्धारित करता है और इसे उस प्रतीक पर वापस मैप करता है जो इसे दर्शाता है, इस प्रकार मूल डेटा की पुनर्प्राप्त होती है और वाहक की आवृत्ति और चरण को स्थिर रखा जाता है।
आयाम अधिमिश्रण की तरह, एएसके भी रैखिक और वायुमंडलीय शोर, विकृतियों, पीएसटीएन में विभिन्न मार्गों पर प्रसार की स्थिति आदि के प्रति संवेदनशील है। एएसके मॉडुलन और डिमॉड्यूलेशन दोनों प्रक्रियाएं अपेक्षाकृत सस्ती हैं। एएसके तकनीक का उपयोग सामान्यतः ऑप्टिकल फाइबर पर डिजिटल डेटा संचारित करने के लिए भी किया जाता है। एलईडी ट्रांसमीटरों के लिए, बाइनरी 1 को प्रकाश की एक छोटी पल्स और बाइनरी 0 द्वारा प्रकाश की अनुपस्थिति द्वारा दर्शाया जाता है। लेजर ट्रांसमीटरों में सामान्य रूप से एक निश्चित "पूर्वाग्रह" धारा होती है जो डिवाइस को कम रोशनी के स्तर का उत्सर्जन करने का कारण बनता है। यह निम्न स्तर बाइनरी 0 का प्रतिनिधित्व करता है, जबकि एक उच्च आयाम वाली लाइटवेव बाइनरी 1 का प्रतिनिधित्व करती है।
एएसके का सबसे सरल और सबसे सामान्य रूप एक स्विच के रूप में कार्य करता है, जो बाइनरी नंबर को इंगित करने के लिए एक वाहक तरंग की उपस्थिति का उपयोग करते हैं और बाइनरी 0 एवं 1 को इंगित करने के लिए इसकी अनुपस्थिति का उपयोग किया जाता है। इस प्रकार के मॉडुलन को ऑन-ऑफ कुंजीयन (OOK) कहा जाता है, और मोर्स कोड (सतत तरंग संचालन के रूप में संदर्भित) को प्रसारित करने के लिए रेडियो की आवृत्ति पर इसका उपयोग किया जाता है।
अधिक परिष्कृत एन्कोडिंग योजनाएं विकसित की गई हैं जो अतिरिक्त आयाम स्तरों का उपयोग करके समूहों में डेटा का प्रतिनिधित्व करती हैं। उदाहरण के लिए, एक चार-स्तरीय एन्कोडिंग योजना आयाम में प्रत्येक बदलाव के साथ दो बिट्स का प्रतिनिधित्व कर सकती है, आठ-स्तरीय योजना तीन बिट्स का प्रतिनिधित्व करती है। आयाम शिफ्ट कुंजीयन के इन रूपों को उनकी वसूली के लिए शोर अनुपात के लिए एक उच्च संकेत की आवश्यकता होती है, जैसा कि उनके स्वभाव से अधिकांश संकेत कम शक्ति पर प्रेषित होते हैं।
एएसके प्रणाली को तीन ब्लॉकों में विभाजित किया जा सकता है। पहला ट्रांसमीटर का प्रतिनिधित्व करता है, दूसरा एक चैनल के प्रभावों का एक रैखिक मॉडल है, तीसरा एक रिसीवर की संरचना को दर्शाता है। निम्नलिखित संकेतन का उपयोग किया जाता है:
- ht(f) संचरण के लिए वाहक संकेत है
- एचसी (एफ) चैनल की आवेग प्रतिक्रिया है
- n(t) चैनल द्वारा पेश किया गया शोर है
- घंटा (एफ) रिसीवर पर फिल्टर है
- L ट्रांसमिशन के लिए उपयोग किए जाने वाले स्तरों की संख्या है
- T दो प्रतीकों की पीढ़ी के बीच का समय है
अलग-अलग वोल्टेज के साथ अलग-अलग प्रतीकों का प्रतिनिधित्व किया जाता है। यदि वोल्टेज के लिए अधिकतम अनुमत मान A है, तो सभी संभावित मान श्रेणी [−A, A] में हैं और वे इसके द्वारा दिए गए हैं:
एक वोल्टेज और दूसरे के बीच का अंतर है:
चित्र को ध्यान में रखते हुए, प्रतीक v[n] स्रोत S द्वारा यादृच्छिक रूप से उत्पन्न होते हैं, तब आवेग जनरेटर v[n] के क्षेत्र के साथ आवेग उत्पन्न करता है। इन आवेगों को चैनल के माध्यम से भेजे जाने के लिए फिल्टर एचटी को भेजा जाता है। दूसरे शब्दों में, प्रत्येक प्रतीक के लिए सापेक्ष आयाम के साथ एक अलग वाहक तरंग भेजी जाती है।
ट्रांसमीटर में से, संकेत s(t) को रूप में व्यक्त किया जा सकता है:
रिसीवर में, घंटे (टी) के माध्यम से छानने के बाद संकेत है:
जहां हम संकेतन का उपयोग करते हैं:
जहां * दो संकेतों के बीच कनवल्शन को इंगित करता है। A/D रूपांतरण के बाद सिग्नल z[k] को इस रूप में व्यक्त किया जा सकता है:
इस संबंध में, दूसरा पद निकाले जाने वाले प्रतीक का प्रतिनिधित्व करता है। अन्य अवांछित हैं: पहला शोर का प्रभाव है, तीसरा इंटरसिंबल हस्तक्षेप के कारण है।
यदि फिल्टर चुने जाते हैं जिससे g(t) न्यक्विस्ट आईएसआई मानदंड को पूरा करे, तब कोई अंतर-चिह्न हस्तक्षेप नहीं होगा और योग का मान शून्य होगा, इसलिए:
प्रसारण केवल शोर से प्रभावित होगा।
त्रुटि की संभावना
किसी दिए गए आकार की त्रुटि होने की प्रायिकता घनत्व फलन और इसे गाऊसी फलन द्वारा प्रतिरूपित किया जा सकता है; माध्य मान सापेक्ष भेजा गया मान होगा, और इसका विचरण इसके द्वारा दिया जाएगा:
कहाँ पे बैंड के भीतर शोर का वर्णक्रमीय घनत्व है और एचआर (एफ) फिल्टर घंटा (एफ) की आवेग प्रतिक्रिया का निरंतर फूरियर रूपांतरण है।
त्रुटि होने की प्रायिकता निम्न द्वारा दी जाती है:
जहां, उदाहरण के लिए, यह देखते हुए कि एक प्रतीक v0 भेजा गया है, त्रुटि करने की सशर्त संभावना है और प्रतीक v0 भेजने की प्रायिकता है।
यदि किसी प्रतीक को भेजने की प्रायिकता समान है, तो:
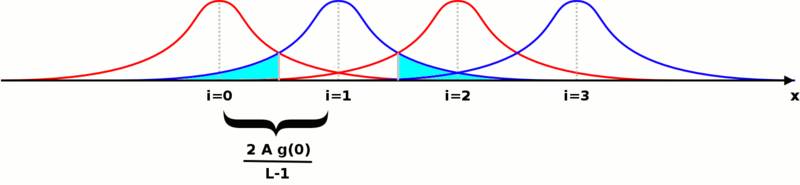
यदि हम प्रेषित होने वाले वोल्टेज के संभावित मूल्य के विरुद्ध एक ही भूखंड पर सभी संभाव्यता घनत्व कार्यों का प्रतिनिधित्व करते हैं, तो हमें इस तरह का एक ग्राफ मिलता है (विशेषतयः दिखाई जा रही है):
एक प्रतीक भेजे जाने के बाद त्रुटि होने की प्रायिकता अन्य प्रतीकों के फलनों के अंतर्गत आने वाले गाऊसी फलन का क्षेत्रफल है। यह उनमें से सिर्फ एक के लिए सियान में दिखाया गया है। अगर हम कॉल करें गाऊसी के एक तरफ का क्षेत्रफल, सभी क्षेत्रों का योग होगा: . त्रुटि होने की कुल संभावना को फॉर्म में व्यक्त किया जा सकता है:
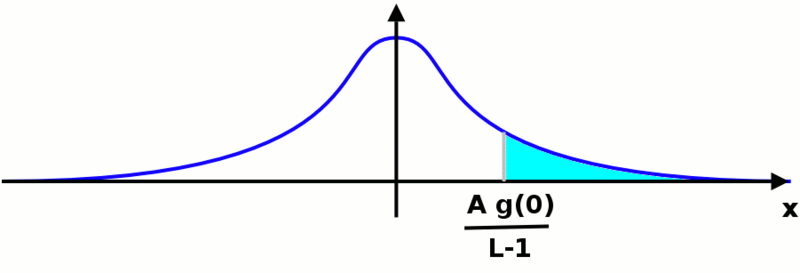
अब हमें के मान की गणना करनी है ऐसा करने के लिए हम इसी प्रकार के संदर्भ की उत्पत्ति को स्थानांतरित कर सकते हैं: यहाँ पर फ़ंक्शन के नीचे का क्षेत्र नहीं बदलेगा। हम ऐसी स्थिति में हैं जैसे निम्न चित्र में दिखाया गया है:
इससे कोई फर्क नहीं पड़ता कि हम किस गाऊसी फ़ंक्शन पर विचार कर रहे हैं, जिस क्षेत्र की हम गणना करना चाहते हैं वह वही होगा। हम जिस मूल्य को ढूंढ रहे है वह निम्नलिखित अभिन्न द्वारा दिया जाएगा:
कहाँ पे पूरक त्रुटि कार्य है। इन सभी परिणामों को एक साथ रखने पर त्रुटि होने की प्रायिकता है:
इस सूत्र से हम आसानी से समझ सकते हैं कि यदि प्रेषित सिग्नल का अधिकतम आयाम या सिस्टम का प्रवर्धन अधिक हो जाता है तो त्रुटि होने की संभावना कम हो जाती है; दूसरी ओर स्तरों की संख्या या शोर की शक्ति अधिक होने पर बढ़ जाती है।
यह संबंध उस समय मान्य होता है जब कोई अंतर-प्रतीक हस्तक्षेप नहीं होता है, अर्थात एक न्यक्विस्ट आईएसआई मानदंड है।
यह भी देखें
- आवृत्ति पारी कुंजीयन (FSK)