चॉम्स्की पदानुक्रम: Difference between revisions
m (added Category:Vigyan Ready using HotCat) |
No edit summary |
||
| (One intermediate revision by one other user not shown) | |||
| Line 87: | Line 87: | ||
| page=[https://archive.org/details/computabilitycom00davi_405/page/n345 327] | | page=[https://archive.org/details/computabilitycom00davi_405/page/n345 327] | ||
}} | }} | ||
[[Category:1956 कंप्यूटिंग में]] | |||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category: | |||
[[Category:Created On 20/07/2023]] | [[Category:Created On 20/07/2023]] | ||
[[Category:Vigyan Ready]] | [[Category:Lua-based templates]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:औपचारिक भाषाएँ]] | |||
[[Category:जनरेटिव भाषाविज्ञान]] | |||
[[Category:नोम चॉम्स्की|पदानुक्रम, चॉम्स्की]] | |||
Latest revision as of 06:53, 1 August 2023
चॉम्स्की पदानुक्रम को अधिकांशतः चॉम्स्की-शूट्ज़ेन बर्गर पदानुक्रम के रूप में जाना जाता है,[1] इस प्रकार औपचारिक भाषा, कंप्यूटर विज्ञान और भाषाविज्ञान के क्षेत्र में, औपचारिक व्याकरण की कक्षाओं का पदानुक्रम कंटेनमेंट पदानुक्रम द्वारा निर्धारित किया जाता है। इस प्रकार औपचारिक व्याकरण यह वर्णन करता है, कि किसी भाषा की शब्दावली या वर्णमाला से प्राप्त होने वाली स्ट्रिंग कैसे बनाई जाती हैं, जिसे उचित भाषा के वाक्यविन्यास के अनुसार मान्य किया जाता हैं। इस प्रकार भाषाविद् नोम चौमस्की ने सिद्धांत दिया हैं कि औपचारिक व्याकरण के चार अलग-अलग वर्ग सम्मिलित हैं, जो तेजी से जटिल भाषाएँ उत्पन्न कर सकते हैं। इस प्रकार प्रत्येक वर्ग को पूर्ण रूप से सभी निम्न वर्गों की भाषा उत्पन्न कर सकता है।
इतिहास
व्याकरण के पदानुक्रम का सामान्य विचार सबसे पहले भाषाविद् नोम चॉम्स्की द्वारा वर्णित किया गया था, चाॅम्स्की 1956 के अनुसार मार्सेल-पॉल शुट्ज़ेनबर्गर ने औपचारिक भाषाओं के सिद्धांत के विकास में भी भूमिका निभाई है; इस प्रकार चाॅम्स्की & शूटज़ेनबर्गर 1963 द्वारा इसके संदर्भ में मुक्त व्याकरण सहित आधुनिक पदानुक्रम का वर्णन करता है।[1]
स्वतंत्र रूप से और भाषाविदों के साथ, गणितज्ञ गणना मॉडल के आधार पर ऑटोमेटा को विकसित कर रहे थे। किसी भाषा में वाक्य को पार्स करना गणना के समान है, और चॉम्स्की द्वारा वर्णित व्याकरण विभिन्न मशीन मॉडलों की कम्प्यूटेशनल शक्ति के समान और समकक्ष प्रमाणित हुए हैं।[2]
पदानुक्रम
निम्नलिखित सूची में चॉम्स्की के चार प्रकार के व्याकरणों में से प्रत्येक का सारांश प्रस्तुत करती है, इस प्रकार इस भाषा का वह वर्ग जो इसे उत्पन्न करता है, इसे ऑटोमेटन का प्रकार माना जाता है, जो इसे पहचानता है, और इसके नियमों का स्वरूप कैसा होना चाहिए।
| व्याकरण | भाषा | ऑटोमेटन को पहचानना | उत्पादन नियम (बाधाएं)* | उदाहरण[3][4] |
|---|---|---|---|---|
| Type-0 | पुनरावर्ती रूप से गणनीय | ट्यूरिंग मशीन | ( non-empty) | एक समाप्ति ट्यूरिंग मशीन का वर्णन करता है |
| Type-1 | संदर्भ के प्रति संवेदनशील | रैखिक-बद्ध गैर-नियतात्मक ट्यूरिंग मशीन | ||
| Type-2 | विषय से मुक्त | गैर-नियतात्मक पुशडाउन ऑटोमेटन | ||
| Type-3 | नियमित | परिमित अवस्था स्वचालन | and |
|
* प्रतीकों का अर्थ:
| ||||
ध्यान दें कि पुनरावर्ती भाषाओं के अनुरूप व्याकरणों का सेट इस पदानुक्रम का सदस्य नहीं है; ये ठीक प्रकार से टाइप-0 और टाइप-1 के बीच होंगे।
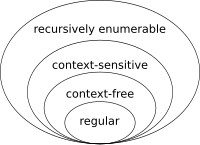
प्रत्येक नियमित भाषा संदर्भ-मुक्त है, प्रत्येक संदर्भ-मुक्त भाषा संदर्भ-संवेदनशील है, प्रत्येक संदर्भ-संवेदनशील भाषा पुनरावर्ती है और प्रत्येक पुनरावर्ती भाषा पुनरावर्ती रूप से गणना योग्य है। ये सभी उचित समावेशन हैं, जिसका अर्थ है कि पुनरावर्ती रूप से गणना योग्य भाषाएं मौजूद हैं जो संदर्भ-संवेदनशील नहीं हैं, संदर्भ-संवेदनशील भाषाएं जो संदर्भ-मुक्त नहीं हैं और संदर्भ-मुक्त भाषाएं जो नियमित नहीं हैं।[5]
टाइप-0 व्याकरण
टाइप-0 व्याकरण में सभी औपचारिक व्याकरण शामिल होते हैं। वे बिल्कुल सभी भाषाएँ उत्पन्न करते हैं जिन्हें ट्यूरिंग मशीन द्वारा पहचाना जा सकता है। इन भाषाओं को पुनरावर्ती गणना योग्य भाषा या ट्यूरिंग-पहचानने योग्य भाषा के रूप में भी जाना जाता है।[6] ध्यान दें कि यह पुनरावर्ती भाषाओं से भिन्न है, जिसे ऐसी मशीन द्वारा तय किया जा सकता है जो ट्यूरिंग मशीन को हमेशा रोकती है।
टाइप-1 व्याकरण
टाइप-1 व्याकरण संदर्भ-संवेदनशील भाषाएँ उत्पन्न करते हैं। इन व्याकरणों में रूप के नियम होते हैं, जिसके लिए के साथ नॉनटर्मिनल और , और टर्मिनलों और/या गैर-टर्मिनलों की स्ट्रिंग्स के रूप में उपयोग होते हैं। स्ट्रि्ंग और रिक्त हो सकते है, अपितु गैररिक्त होना चाहिए, यहाँ पर नियम की अनुमति देता है, इस प्रकार यदि किसी भी नियम के दाईं ओर प्रकट नहीं होता है, जिसके लिए इन व्याकरणों द्वारा वर्णित भाषाएँ वास्तव में सभी भाषाएँ हैं, जिन्हें रैखिक बाउंडेड ऑटोमेटन के आधार पर गैर-नियतात्मक ट्यूरिंग मशीन जिसका टेप इनपुट की लंबाई के निरंतर समय से घिरा होता है, जिसके द्वारा इसे पहचाना जा सकता है।
टाइप-2 व्याकरण
टाइप-2 व्याकरण संदर्भ-मुक्त भाषाएँ उत्पन्न करते हैं। इन्हें प्रपत्र के नियमों द्वारा परिभाषित किया गया है, जिसके आधार पर के साथ नॉनटर्मिनल होने के लिए उपयोग लाये जाते हैं और टर्मिनलों और/या गैर-टर्मिनलों की श्रृंखला में होते हैं। ये भाषाएँ वास्तव में वे सभी भाषाएँ हैं जिन्हें गैर-नियतात्मक पुशडाउन ऑटोमेटन द्वारा पहचाना जा सकता है। इसके लिए संदर्भ-मुक्त भाषाएं - या इसके नियतात्मक संदर्भ-मुक्त भाषा का सबसेट - अधिकांश प्रोग्रामिंग भाषाओं की वाक्यांश संरचना के लिए सैद्धांतिक आधार हैं, चूंकि उनके वाक्यविन्यास में घोषणाओं और स्कोप को कंप्यूटर के कारण संदर्भ-संवेदनशील नाम रिज़ॉल्यूशन प्रोग्रामिंग भाषाएं भी सम्मिलित हैं। इस प्रकार पार्सिंग को सरल बनाने के लिए अधिकांशतः व्याकरणों के उपसमूह का उपयोग किया जाता है, जैसे कि एलएल पार्सर द्वारा इसका उपयोग करते हैं।
टाइप-3 व्याकरण
टाइप-3 व्याकरण नियमित भाषाएँ उत्पन्न करते हैं। ऐसा व्याकरण अपने नियमों को बाईं ओर एकल नॉनटर्मिनल तक सीमित करता है, और दाईं ओर एकल टर्मिनल से युक्त होता है, जिसके पश्चात संभवतः एकल नॉनटर्मिनल दाएं ओर नियमित होते है। इस प्रकार वैकल्पिक रूप से, व्याकरण के दाईं ओर एकल टर्मिनल शामिल हो सकता है, संभवतः एकल नॉनटर्मिनल (बाएं नियमित) से पहले। ये समान भाषाएँ उत्पन्न करते हैं। चूंकि, यदि बाएँ-नियमित नियमों और दाएँ-नियमित नियमों को मिला दिया जाए, तो भाषा को नियमित होने की आवश्यकता नहीं है। इस प्रकार के नियम को द्वारा यदि यहाँ भी अनुमति दी जाती है, इसके लिे किसी भी नियम के दाईं ओर प्रकट नहीं होता है, ये भाषाएँ वास्तव में वे सभी भाषाएँ हैं जिनका निर्णय सीमित राज्य ऑटोमेटन द्वारा किया जा सकता है। इसके अतिरिक्त, औपचारिक भाषाओं के इस परिवार को नियमित अभिव्यक्ति द्वारा प्राप्त किया जा सकता है। इस प्रकार किसी नियमित भाषा का उपयोग सामान्यतः इसे सर्च करने वाले क्रम के लिए और प्रोग्रामिंग भाषाओं की शाब्दिक संरचना को परिभाषित करने के लिए किया जाता है।
यह भी देखें
संदर्भ
- ↑ 1.0 1.1 Allott, Nicholas; Lohndal, Terje; Rey, Georges (27 April 2021). "संक्षिप्त परिचय" (PDF). A Companion to Chomsky: 1–17. doi:10.1002/9781119598732.ch1.
- ↑ Kozen, Dexter C. "Automata and Computability" Springer, 1997. Pages 3-4
- ↑ Geuvers, H.; Rot, J. (2016). "Applications, Chomsky hierarchy, and Recap" (PDF). Regular Languages. Archived (PDF) from the original on 2018-11-19.
- ↑ Sudkamp, Thomas A. "Languages and Machines: An Introduction to the Theory of Computer Science" Second Edition, Addison Wesley Longman, 1997 page 310
- ↑ Chomsky, Noam (1963). "Chapter 12: Formal Properties of Grammars". In Luce, R. Duncan; Bush, Robert R.; Galanter, Eugene (eds.). गणितीय मनोविज्ञान की पुस्तिका. Vol. II. John Wiley and Sons, Inc. pp. 323–418.
- ↑ Sipser, Michael (1997). संगणना के सिद्धांत का परिचय (1st ed.). Cengage Learning. p. 130. ISBN 0-534-94728-X.
The Church-Turing Thesis
- Chomsky, Noam (1956). "Three models for the description of language" (PDF). IRE Transactions on Information Theory. 2 (3): 113–124. doi:10.1109/TIT.1956.1056813. Archived (PDF) from the original on 2016-03-07.
- Chomsky, Noam (1959). "On certain formal properties of grammars" (PDF). Information and Control. 2 (2): 137–167. doi:10.1016/S0019-9958(59)90362-6.
- Chomsky, Noam; Schützenberger, Marcel P. (1963). "The algebraic theory of context free languages". In Braffort, P.; Hirschberg, D. (eds.). Computer Programming and Formal Systems (PDF). Amsterdam: North Holland. pp. 118–161. Archived (PDF) from the original on 2011-06-13.
- Davis, Martin D.; Sigal, Ron; Weyuker, Elaine J. (1994). Computability, Complexity, and Languages: Fundamentals of Theoretical Computer Science (2nd ed.). Boston: Academic Press, Harcourt, Brace. p. 327. ISBN 0-12-206382-1.