वृत्ताकार खंड: Difference between revisions
(Created page with "{{short description|Slice of a circle cut perpendicular to the radius}} Image:Circularsegment.svg|frame|right|एक वृत्ताकार खंड (हरे रं...") |
No edit summary |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Slice of a circle cut perpendicular to the radius}} | {{short description|Slice of a circle cut perpendicular to the radius}} | ||
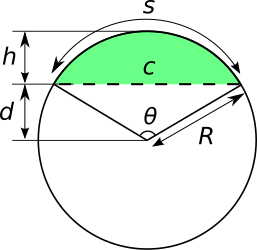
[[Image:Circularsegment.svg|frame|right|एक वृत्ताकार खंड (हरे रंग में) एक सेकेंट/कॉर्ड ( | [[Image:Circularsegment.svg|frame|right|एक वृत्ताकार खंड (हरे रंग में) एक सेकेंट/कॉर्ड (डैश्ड रेखा) और चाप के बीच घिरा हुआ है जिसका समापन बिंदु जीवा (हरे क्षेत्र के ऊपर दिखाया गया चाप) के समान है।]] | ||
ज्यामिति में, एक '''वृत्ताकार खंड''' (प्रतीक: ⌓), जिसे डिस्क खंड के रूप में भी जाना जाता है, एक डिस्क का एक क्षेत्र है जो एक सेकेंट या कॉर्ड द्वारा डिस्क के बाकी भागो से "कट ऑफ़" है। अधिक औपचारिक रूप से, एक वृत्ताकार खंड द्वि-आयामी स्थान का एक क्षेत्र है जो एक वृत्ताकार चाप (परंपरा के अनुसार π रेडियन से कम) और चाप के अंतिम बिंदुओं को जोड़ने वाले वृत्ताकार तार से घिरा होता है। | |||
== सूत्र == | == सूत्र == | ||
मान लीजिए R चाप की त्रिज्या है जो खंड की परिधि | मान लीजिए R चाप की त्रिज्या है जो खंड की परिधि का भाग है, θ चाप को रेडियन में अंतरित करने वाला केंद्रीय कोण है, c तार की लंबाई s चाप की लंबाई है h खंड की धनु (ऊंचाई) d खंड का एपोथेम और खंड का क्षेत्रफल है। | ||
सामान्यतः, तार की लंबाई और ऊंचाई दी जाती है या मापी जाती है, और कभी-कभी चाप की लंबाई परिधि के भाग के रूप में होती है, और अज्ञात क्षेत्र होते हैं और कभी-कभी चाप की लंबाई होती है। इनकी गणना केवल तार की लंबाई और ऊंचाई से नहीं की जा सकती है, इसलिए दो मध्यवर्ती मात्राएं, त्रिज्या और केंद्रीय कोण की गणना सामान्यतः पहले की जाती है। | |||
===त्रिज्या और केंद्रीय कोण === | ===त्रिज्या और केंद्रीय कोण === | ||
त्रिज्या है: | त्रिज्या है: | ||
:<math>R = \tfrac{h}{2}+\tfrac{c^2}{8h}</math><ref>The fundamental relationship between R, c, and h derivable directly from the Pythagorean theorem among R, C/2 and r-h components of a right-angled triangle is: <math>R^2=(\tfrac{c}{2})^2+(R-h)^2</math> which may be solved for R, c, or h as required.</ref> | :<math>R = \tfrac{h}{2}+\tfrac{c^2}{8h} | ||
</math><ref>The fundamental relationship between R, c, and h derivable directly from the Pythagorean theorem among R, C/2 and r-h components of a right-angled triangle is: <math>R^2=(\tfrac{c}{2})^2+(R-h)^2</math> which may be solved for R, c, or h as required.</ref> | |||
=== तार की लंबाई और ऊंचाई === | === तार की लंबाई और ऊंचाई === | ||
तार की लंबाई और ऊंचाई की गणना त्रिज्या और केंद्रीय कोण से की जा सकती है: | तार की लंबाई और ऊंचाई की गणना त्रिज्या और केंद्रीय कोण से की जा सकती है: | ||
| Line 22: | Line 23: | ||
एपोटेम है | एपोटेम है | ||
:<math> d = R - h = \sqrt{R^2-\frac{c^2}{4}} = R\cos\tfrac{\theta}{2} </math> | :<math> d = R - h = \sqrt{R^2-\frac{c^2}{4}} = R\cos\tfrac{\theta}{2} </math> | ||
=== चाप की लंबाई और क्षेत्रफल === | === चाप की लंबाई और क्षेत्रफल === | ||
एक वृत्त की परिचित ज्यामिति से, चाप की लंबाई है | एक वृत्त की परिचित ज्यामिति से, चाप की लंबाई है | ||
:<math>s = {\theta}R</math> वृत्ताकार खंड का क्षेत्रफल a, वृत्ताकार खंड के क्षेत्रफल को घटाकर त्रिकोणीय भाग के क्षेत्रफल के | :<math>s = {\theta}R</math> | ||
:वृत्ताकार खंड का क्षेत्रफल a, वृत्ताकार खंड के क्षेत्रफल को घटाकर त्रिकोणीय भाग के क्षेत्रफल के समान है (<math>\theta</math> के संदर्भ में समीकरण प्राप्त करने के लिए दोहरे कोण सूत्र का उपयोग करें)। | |||
:<math>a = \tfrac{R^2}{2} \left(\theta - \sin \theta\right)</math> | :<math>a = \tfrac{R^2}{2} \left(\theta - \sin \theta\right)</math> | ||
{{math|''R''}} और {{math|''h''}}, के संदर्भ में, | |||
:<math>a = R^2\arccos\left(1-\frac{h}{R}\right) - \left(R-h\right)\sqrt{R^2-\left(R-h\right)^2}</math> | :<math>a = R^2\arccos\left(1-\frac{h}{R}\right) - \left(R-h\right)\sqrt{R^2-\left(R-h\right)^2}</math> | ||
{{math|''c''}} और {{math|''h''}} के अनुसार, | |||
:<math>a = \left(\frac{c^2+4h^2}{8h}\right)^2\arccos\left(\frac{c^2-4h^2}{c^2+4h^2}\right) - \frac{c}{16h}(c^2-4h^2)</math> | :<math>a = \left(\frac{c^2+4h^2}{8h}\right)^2\arccos\left(\frac{c^2-4h^2}{c^2+4h^2}\right) - \frac{c}{16h}(c^2-4h^2)</math> | ||
जो कहा जा सकता है वह यह है कि जैसे-जैसे केंद्रीय कोण छोटा होता जाता है (या वैकल्पिक रूप से त्रिज्या बड़ी होती जाती है), क्षेत्र तेजी से और स्पर्शोन्मुख रूप से | जो कहा जा सकता है वह यह है कि जैसे-जैसे केंद्रीय कोण छोटा होता जाता है (या वैकल्पिक रूप से त्रिज्या बड़ी होती जाती है), क्षेत्र तेजी से और स्पर्शोन्मुख रूप से <math>\tfrac{2}{3}c\cdot h</math>. यदि <math>\theta \ll 1</math>, <math>a = \tfrac{2}{3}c\cdot h</math> तक पहुंचता है, जो अधिक सीमा तक अच्छा अनुमान है। | ||
यदि <math>c</math> स्थिर रखा जाता है, और त्रिज्या को भिन्न होने की अनुमति दी जाती है, तो हमारे पास है<math display="block">\frac{\partial a}{\partial s} = R</math> | |||
जैसे-जैसे केंद्रीय कोण π के करीब पहुंचता है, खंड का क्षेत्रफल अर्धवृत्त के क्षेत्रफल में परिवर्तित हो जाता है, <math>\tfrac{\pi R^2}{2}</math>, इसलिए एक अच्छा सन्निकटन बाद वाले क्षेत्र से डेल्टा ऑफसेट है: | जैसे-जैसे केंद्रीय कोण π के करीब पहुंचता है, खंड का क्षेत्रफल अर्धवृत्त के क्षेत्रफल में परिवर्तित हो जाता है, <math>\tfrac{\pi R^2}{2}</math>, इसलिए एक अच्छा सन्निकटन बाद वाले क्षेत्र से डेल्टा ऑफसेट है: | ||
:<math>a\approx \tfrac{\pi R^2}{2}-(R+\tfrac{c}{2})(R-h)</math> h>.75R के लिए | :<math>a\approx \tfrac{\pi R^2}{2}-(R+\tfrac{c}{2})(R-h)</math> h>.75R के लिए | ||
उदाहरण के | उदाहरण के रूप से, क्षेत्रफल वृत्त का एक चौथाई है जब θ ~ 2.31 रेडियन (132.3°) ~59.6% की ऊंचाई और त्रिज्या के ~183% की जीवा की लंबाई के अनुरूप है। | ||
===आदि === | ===आदि === | ||
परिधि p | परिधि p चाप लंबाई और जीवा लंबाई है, | ||
:<math>p=c+s=c+\theta R</math> | :<math>p=c+s=c+\theta R</math> | ||
डिस्क के संपूर्ण क्षेत्रफल के अनुपात के रूप में, <math>A= \pi R^2</math>, आपके पास | डिस्क के संपूर्ण क्षेत्रफल के अनुपात के रूप में, <math>A= \pi R^2</math>, आपके पास है | ||
:<math> \frac{a}{A}= \frac{\theta - \sin \theta}{2\pi}</math> | :<math> \frac{a}{A}= \frac{\theta - \sin \theta}{2\pi}</math> | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
क्षेत्रफल सूत्र का उपयोग क्षैतिज रूप से बिछाए गए आंशिक रूप से भरे बेलनाकार टैंक की मात्रा की गणना में किया जा सकता है। | क्षेत्रफल सूत्र का उपयोग क्षैतिज रूप से बिछाए गए आंशिक रूप से भरे बेलनाकार टैंक की मात्रा की गणना में किया जा सकता है। | ||
गोल शीर्ष वाली खिड़कियों या दरवाजों के डिज़ाइन में, | गोल शीर्ष वाली खिड़कियों या दरवाजों के डिज़ाइन में, ''c'' और ''h'' ही एकमात्र ज्ञात मान हो सकते हैं और ड्राफ्ट्समैन की कंपास सेटिंग के लिए ''R'' की गणना करने के लिए इसका उपयोग किया जा सकता है। | ||
कोई व्यक्ति चाप की लंबाई और टुकड़े की जीवा की लंबाई को मापकर टुकड़ों से एक पूर्ण | कोई व्यक्ति चाप की लंबाई और टुकड़े की जीवा की लंबाई को मापकर टुकड़ों से एक पूर्ण वृत्ताकार वस्तु के पूर्ण आयामों का पुनर्निर्माण कर सकता है। | ||
वृत्ताकार प्रतिरूप पर छेद की स्थिति की जाँच करने के लिए मशीनी उत्पादों की गुणवत्ता जांच के लिए विशेष रूप से उपयोगी होती है । | |||
किसी समतल आकृति के क्षेत्रफल या केन्द्रक की गणना के लिए जिसमें वृत्ताकार खंड होते हैं। | किसी समतल आकृति के क्षेत्रफल या केन्द्रक की गणना के लिए जिसमें वृत्ताकार खंड होते हैं। | ||
| Line 66: | Line 64: | ||
== यह भी देखें == | == यह भी देखें == | ||
* तार (ज्यामिति) | * तार (ज्यामिति) | ||
* [[गोलाकार टोपी]] | * [[गोलाकार टोपी|वृत्ताकार कैप]] | ||
* वृत्ताकार क्षेत्र | * वृत्ताकार क्षेत्र | ||
| Line 72: | Line 70: | ||
{{reflist}} | {{reflist}} | ||
* {{MathWorld |urlname=CircularSegment |title=Circular segment}} | * {{MathWorld |urlname=CircularSegment |title=Circular segment}} | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
* [http://www.mathopenref.com/segment.html Definition of a circular segment] With interactive animation | * [http://www.mathopenref.com/segment.html Definition of a circular segment] With interactive animation | ||
* [http://www.mathopenref.com/segmentarea.html Formulae for area of a circular segment] With interactive animation | * [http://www.mathopenref.com/segmentarea.html Formulae for area of a circular segment] With interactive animation | ||
[[Category:Created On 13/07/2023]] | [[Category:Created On 13/07/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:मंडलियां]] | |||
Latest revision as of 16:26, 1 August 2023
ज्यामिति में, एक वृत्ताकार खंड (प्रतीक: ⌓), जिसे डिस्क खंड के रूप में भी जाना जाता है, एक डिस्क का एक क्षेत्र है जो एक सेकेंट या कॉर्ड द्वारा डिस्क के बाकी भागो से "कट ऑफ़" है। अधिक औपचारिक रूप से, एक वृत्ताकार खंड द्वि-आयामी स्थान का एक क्षेत्र है जो एक वृत्ताकार चाप (परंपरा के अनुसार π रेडियन से कम) और चाप के अंतिम बिंदुओं को जोड़ने वाले वृत्ताकार तार से घिरा होता है।
सूत्र
मान लीजिए R चाप की त्रिज्या है जो खंड की परिधि का भाग है, θ चाप को रेडियन में अंतरित करने वाला केंद्रीय कोण है, c तार की लंबाई s चाप की लंबाई है h खंड की धनु (ऊंचाई) d खंड का एपोथेम और खंड का क्षेत्रफल है।
सामान्यतः, तार की लंबाई और ऊंचाई दी जाती है या मापी जाती है, और कभी-कभी चाप की लंबाई परिधि के भाग के रूप में होती है, और अज्ञात क्षेत्र होते हैं और कभी-कभी चाप की लंबाई होती है। इनकी गणना केवल तार की लंबाई और ऊंचाई से नहीं की जा सकती है, इसलिए दो मध्यवर्ती मात्राएं, त्रिज्या और केंद्रीय कोण की गणना सामान्यतः पहले की जाती है।
त्रिज्या और केंद्रीय कोण
त्रिज्या है:
तार की लंबाई और ऊंचाई
तार की लंबाई और ऊंचाई की गणना त्रिज्या और केंद्रीय कोण से की जा सकती है:
तार की लंबाई है
धनु_(ज्यामिति) है
एपोटेम है
चाप की लंबाई और क्षेत्रफल
एक वृत्त की परिचित ज्यामिति से, चाप की लंबाई है
- वृत्ताकार खंड का क्षेत्रफल a, वृत्ताकार खंड के क्षेत्रफल को घटाकर त्रिकोणीय भाग के क्षेत्रफल के समान है ( के संदर्भ में समीकरण प्राप्त करने के लिए दोहरे कोण सूत्र का उपयोग करें)।
R और h, के संदर्भ में,
c और h के अनुसार,
जो कहा जा सकता है वह यह है कि जैसे-जैसे केंद्रीय कोण छोटा होता जाता है (या वैकल्पिक रूप से त्रिज्या बड़ी होती जाती है), क्षेत्र तेजी से और स्पर्शोन्मुख रूप से . यदि , तक पहुंचता है, जो अधिक सीमा तक अच्छा अनुमान है।
यदि स्थिर रखा जाता है, और त्रिज्या को भिन्न होने की अनुमति दी जाती है, तो हमारे पास है
- h>.75R के लिए
उदाहरण के रूप से, क्षेत्रफल वृत्त का एक चौथाई है जब θ ~ 2.31 रेडियन (132.3°) ~59.6% की ऊंचाई और त्रिज्या के ~183% की जीवा की लंबाई के अनुरूप है।
आदि
परिधि p चाप लंबाई और जीवा लंबाई है,
डिस्क के संपूर्ण क्षेत्रफल के अनुपात के रूप में, , आपके पास है
अनुप्रयोग
क्षेत्रफल सूत्र का उपयोग क्षैतिज रूप से बिछाए गए आंशिक रूप से भरे बेलनाकार टैंक की मात्रा की गणना में किया जा सकता है।
गोल शीर्ष वाली खिड़कियों या दरवाजों के डिज़ाइन में, c और h ही एकमात्र ज्ञात मान हो सकते हैं और ड्राफ्ट्समैन की कंपास सेटिंग के लिए R की गणना करने के लिए इसका उपयोग किया जा सकता है।
कोई व्यक्ति चाप की लंबाई और टुकड़े की जीवा की लंबाई को मापकर टुकड़ों से एक पूर्ण वृत्ताकार वस्तु के पूर्ण आयामों का पुनर्निर्माण कर सकता है।
वृत्ताकार प्रतिरूप पर छेद की स्थिति की जाँच करने के लिए मशीनी उत्पादों की गुणवत्ता जांच के लिए विशेष रूप से उपयोगी होती है ।
किसी समतल आकृति के क्षेत्रफल या केन्द्रक की गणना के लिए जिसमें वृत्ताकार खंड होते हैं।
यह भी देखें
- तार (ज्यामिति)
- वृत्ताकार कैप
- वृत्ताकार क्षेत्र
संदर्भ
- ↑ The fundamental relationship between R, c, and h derivable directly from the Pythagorean theorem among R, C/2 and r-h components of a right-angled triangle is: which may be solved for R, c, or h as required.
बाहरी संबंध
- Definition of a circular segment With interactive animation
- Formulae for area of a circular segment With interactive animation