स्पर्शरेखा अर्ध-कोण सूत्र: Difference between revisions
No edit summary |
No edit summary |
||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Relates the tangent of half of an angle to trigonometric functions of the entire angle}}{{Trigonometry}} | {{short description|Relates the tangent of half of an angle to trigonometric functions of the entire angle}}{{Trigonometry}} | ||
[[त्रिकोणमिति]] में, '''स्पर्शरेखा अर्ध-कोण सूत्र''' किसी कोण के अर्ध भाग की स्पर्शरेखा को | [[त्रिकोणमिति]] में, '''स्पर्शरेखा अर्ध-कोण सूत्र''' किसी कोण के अर्ध भाग की स्पर्शरेखा को पूर्ण कोण के त्रिकोणमितीय कार्यों से जोड़ते हैं। अर्ध कोण की स्पर्शरेखा किसी रेखा पर वृत्त का [[त्रिविम प्रक्षेपण]] है। इनमें से निम्नलिखित सूत्र हैं: | ||
<math display="block"> | <math display="block"> | ||
| Line 41: | Line 41: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
इनसे अर्ध-कोणों की स्पर्शरेखाओं के कार्यों के रूप में साइन, | इनसे अर्ध-कोणों की स्पर्शरेखाओं के कार्यों के रूप में साइन, कोज्या एवं स्पर्शरेखा को व्यक्त करने वाली पहचान प्राप्त की जा सकती है: | ||
== <math display="block"> | == <math display="block"> | ||
| Line 52: | Line 52: | ||
===बीजगणितीय प्रमाण=== | ===बीजगणितीय प्रमाण=== | ||
दोहरे कोण सूत्रों एवं पायथागॉरियन पहचान <math display="inline">1 + \tan^2 \alpha = 1 \big/ \cos^2 \alpha</math> का उपयोग | दोहरे कोण सूत्रों एवं पायथागॉरियन पहचान <math display="inline">1 + \tan^2 \alpha = 1 \big/ \cos^2 \alpha</math> का उपयोग प्रदान करता है, | ||
<math display="block"> | <math display="block"> | ||
| Line 73: | Line 73: | ||
\quad \text{and} | \quad \text{and} | ||
</math> | </math> | ||
साइन एवं | साइन एवं कोज्या उत्पादक के लिए सूत्रों का भागफल लेना | ||
<math display="block">\tan \alpha = \frac{2\tan \tfrac12 \alpha}{1 - \tan ^2 \tfrac12 \alpha}.</math> | <math display="block">\tan \alpha = \frac{2\tan \tfrac12 \alpha}{1 - \tan ^2 \tfrac12 \alpha}.</math> | ||
कोज्या के लिए पाइथागोरस पहचान को दोहरे कोण सूत्र के साथ जोड़कर, <math display="inline"> \cos 2\alpha = \cos^2 \alpha - \sin^2 \alpha = 1 - 2\sin^2 \alpha = 2\cos^2 \alpha - 1, </math>पुनर्व्यवस्थित करने एवं वर्गमूल लेने से परिणाम प्राप्त होते हैं, | |||
<math display="block"> \left|\sin \alpha\right| = \sqrt {\frac{1-\cos2\alpha}{2}} </math> एवं <math display="block"> \left|\cos \alpha\right| = \sqrt {\frac{1+\cos2\alpha}{2}} </math> | <math display="block"> \left|\sin \alpha\right| = \sqrt {\frac{1-\cos2\alpha}{2}} </math> एवं <math display="block"> \left|\cos \alpha\right| = \sqrt {\frac{1+\cos2\alpha}{2}} </math> | ||
| Line 84: | Line 84: | ||
<math display="block"> \left|\tan \alpha\right| = \frac {\sqrt {1 - \cos 2\alpha}}{\sqrt {1 + \cos 2\alpha}} = \frac {1 - \cos 2\alpha}{ {\sqrt {1 + \cos 2\alpha}}{\sqrt {1 - \cos 2\alpha}} } = \frac{1 - \cos 2\alpha}{{\sqrt {1 - \cos^2 2\alpha}}} = \frac{1 - \cos 2\alpha}{\left|\sin 2\alpha\right|}. </math> | <math display="block"> \left|\tan \alpha\right| = \frac {\sqrt {1 - \cos 2\alpha}}{\sqrt {1 + \cos 2\alpha}} = \frac {1 - \cos 2\alpha}{ {\sqrt {1 + \cos 2\alpha}}{\sqrt {1 - \cos 2\alpha}} } = \frac{1 - \cos 2\alpha}{{\sqrt {1 - \cos^2 2\alpha}}} = \frac{1 - \cos 2\alpha}{\left|\sin 2\alpha\right|}. </math> | ||
इससे ज्ञात होता है कि इन अंतिम दो सूत्रों में निरपेक्ष मान चिह्न हटाये जा सकते हैं, चाहे {{mvar|α}} कोई भी चतुर्थांश में हो। निरपेक्ष मान पट्टियों के साथ या उसके | इससे ज्ञात होता है कि इन अंतिम दो सूत्रों में निरपेक्ष मान चिह्न हटाये जा सकते हैं, चाहे {{mvar|α}} कोई भी चतुर्थांश में हो। निरपेक्ष मान पट्टियों के साथ या उसके अभाव में ये सूत्र तब प्रस्तावित नहीं होते जब दाहिनी ओर अंश एवं हर दोनों शून्य होते हैं। | ||
इसके अतिरिक्त, साइन एवं | इसके अतिरिक्त, साइन एवं कोज्या दोनों के लिए कोण जोड़ एवं घटाव सूत्रों का उपयोग करके कोई प्राप्त करता है: | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
| Line 132: | Line 132: | ||
<math display="block">\frac{t}{\sin \varphi} = \frac{1}{1+ \cos \varphi}.</math> | <math display="block">\frac{t}{\sin \varphi} = \frac{1}{1+ \cos \varphi}.</math> | ||
यह इस प्रकार है | यह इस प्रकार है, | ||
== <math display="block">t = \frac{\sin \varphi}{1+ \cos \varphi} = \frac{\sin \varphi(1- \cos \varphi)}{(1+ \cos \varphi)(1- \cos \varphi)} = \frac{1- \cos \varphi}{\sin \varphi}.</math>अभिन्न कलन में स्पर्शरेखा अर्ध-कोण प्रतिस्थापन == | == <math display="block">t = \frac{\sin \varphi}{1+ \cos \varphi} = \frac{\sin \varphi(1- \cos \varphi)}{(1+ \cos \varphi)(1- \cos \varphi)} = \frac{1- \cos \varphi}{\sin \varphi}.</math>अभिन्न कलन में स्पर्शरेखा अर्ध-कोण प्रतिस्थापन == | ||
| Line 140: | Line 140: | ||
वीयरस्ट्रैस प्रतिस्थापन}} | वीयरस्ट्रैस प्रतिस्थापन}} | ||
[[Image:Weierstrass substitution.svg|right|400px|thumb|वीयरस्ट्रैस प्रतिस्थापन का ज्यामितीय प्रमाण]]त्रिकोणमिति के विभिन्न अनुप्रयोगों में, नए चर <math>t</math> के [[तर्कसंगत कार्य|तर्कसंगत कार्यों]] के संदर्भ में त्रिकोणमितीय कार्यों (जैसे [[ उन लोगों के |साइन]] एवं [[ कोज्या | | [[Image:Weierstrass substitution.svg|right|400px|thumb|वीयरस्ट्रैस प्रतिस्थापन का ज्यामितीय प्रमाण]]त्रिकोणमिति के विभिन्न अनुप्रयोगों में, नए चर <math>t</math> के [[तर्कसंगत कार्य|तर्कसंगत कार्यों]] के संदर्भ में त्रिकोणमितीय कार्यों (जैसे [[ उन लोगों के |साइन]] एवं [[ कोज्या |कोज्या]]) को पुनः लिखना उपयोगी है। <math>t</math> की परिभाषा के कारण इन सर्वसमिकाओं को सामूहिक रूप से स्पर्शरेखा अर्ध-कोण सूत्र के रूप में जाना जाता है। ये पहचानें साइन एवं कोज्या में तर्कसंगत कार्यों को उनके प्रतिअवकलज की शोध के लिए {{math|''t''}} के कार्यों में परिवर्तित करने के लिए [[ गणना |कैलकुलसन]] में उपयोगी हो सकती हैं। | ||
ज्यामितीय रूप से, निर्माण इस प्रकार होता है: [[इकाई चक्र]] पर किसी भी बिंदु के लिए {{math|(cos ''φ'', sin ''φ'')}} के लिए, इससे होकर निकलने वाली रेखा एवं बिंदु के लिए {{math|(−1, 0)}} खींची जाती है। यह बिंदु किसी बिंदु {{math|1=''y'' = ''t''}} पर {{math|''y''}}-अक्ष को पार करता है। कोई सरल ज्यामिति का उपयोग करके यह दिखा सकता है {{math|1=''t'' = tan(φ/2)}} | ज्यामितीय रूप से, निर्माण इस प्रकार होता है: [[इकाई चक्र]] पर किसी भी बिंदु के लिए {{math|(cos ''φ'', sin ''φ'')}} के लिए, इससे होकर निकलने वाली रेखा एवं बिंदु के लिए {{math|(−1, 0)}} खींची जाती है। यह बिंदु किसी बिंदु {{math|1=''y'' = ''t''}} पर {{math|''y''}}-अक्ष को पार करता है। कोई सरल ज्यामिति का उपयोग करके यह दिखा सकता है कि {{math|1=''t'' = tan(φ/2)}} है। खींची गई रेखा का समीकरण {{math|1=''y'' = (1 + ''x'')''t''}} है। रेखा एवं वृत्त के प्रतिच्छेदन का समीकरण तब [[द्विघात समीकरण]] होता है जिसमें {{math|''t''}} सम्मिलित होता है। इस समीकरण के दो समाधान हैं {{math|(−1, 0)}} एवं {{math|(cos ''φ'', sin ''φ'')}} हैं। यह हमें पश्चात वाले को {{math|''t''}} के तर्कसंगत कार्यों के रूप में लिखने की अनुमति देता है (समाधान नीचे दिए गए हैं)। | ||
पैरामीटर {{math|''t''}}, प्रक्षेपण के केंद्र {{math|(−1, 0)}} के साथ {{math|''y''}}-अक्ष | पैरामीटर {{math|''t''}}, प्रक्षेपण के केंद्र {{math|(−1, 0)}} के साथ {{math|''y''}}-अक्ष पर {{math|(cos ''φ'', sin ''φ'')}} के त्रिविम प्रक्षेपण का प्रतिनिधित्व करता है। इस प्रकार, स्पर्शरेखा अर्ध-कोण सूत्र त्रिविम निर्देशांक {{math|''t''}} एवं मानक कोणीय निर्देशांक पर {{math|''φ''}} के मध्य रूपांतरण देते हैं। | ||
तो हमारे पास हैं, | तो हमारे पास हैं, | ||
| Line 163: | Line 163: | ||
e^{-i \varphi} = \frac{1 - i t}{1 + i t}. | e^{-i \varphi} = \frac{1 - i t}{1 + i t}. | ||
</math> | </math> | ||
सीधे ऊपर एवं प्रारंभिक परिभाषा के मध्य फाई को समाप्त करके | सीधे ऊपर एवं <math>t</math> की प्रारंभिक परिभाषा के मध्य फाई को समाप्त करके, कोई [[प्राकृतिक]] लघुगणक के संदर्भ में [[आर्कटिक स्पर्शरेखा]] के लिए निम्नलिखित उपयोगी संबंध पर पहुंचता है, | ||
<math display="block">2 \arctan t = -i \ln\frac{1+it}{1-it}.</math> | <math display="block">2 \arctan t = -i \ln\frac{1+it}{1-it}.</math> | ||
कैलकुलस में, वेयरस्ट्रैस प्रतिस्थापन का उपयोग {{math|sin ''φ''}} एवं {{math|cos ''φ''}} [[तर्कसंगत कार्य|तर्कसंगत कार्यों]] के प्रतिअवकलन की शोध के लिए किया जाता है। समायोजन के पश्चात | कैलकुलस में, वेयरस्ट्रैस प्रतिस्थापन का उपयोग {{math|sin ''φ''}} एवं {{math|cos ''φ''}} [[तर्कसंगत कार्य|तर्कसंगत कार्यों]] के प्रतिअवकलन की शोध के लिए किया जाता है। समायोजन के पश्चात | ||
| Line 193: | Line 193: | ||
<math display="block">e^\psi = \frac{1 + t}{1 - t}, \qquad | <math display="block">e^\psi = \frac{1 + t}{1 - t}, \qquad | ||
e^{-\psi} = \frac{1 - t}{1 + t}.</math> | e^{-\psi} = \frac{1 - t}{1 + t}.</math> | ||
{{math|''t''}} के संदर्भ में {{math|''ψ''}} शोध से [[व्युत्क्रम अतिशयोक्तिपूर्ण कार्य|व्युत्क्रम हाइपरबोलिक स्पर्शरेखा]] <math>\operatorname{artanh}</math> एवं प्राकृतिक लघुगणक के मध्य निम्नलिखित संबंध बनता है: | |||
== <math display="block">2 \operatorname{artanh} t = \ln\frac{1+t}{1-t}.</math>गुडरमैनियन फलन == | == <math display="block">2 \operatorname{artanh} t = \ln\frac{1+t}{1-t}.</math>गुडरमैनियन फलन == | ||
{{Main|गुडर्मनियन फलन}} | {{Main|गुडर्मनियन फलन}} | ||
अतिशयोक्तिपूर्ण पहचानों की अपेक्षा वृत्ताकार पहचानों से करने पर, कोई यह | अतिशयोक्तिपूर्ण पहचानों की अपेक्षा वृत्ताकार पहचानों से करने पर, कोई यह ध्यान देता है कि उनमें {{math|''t''}} के समान कार्य सम्मिलित हैं, अभी क्रमबद्ध किया गया है। यदि हम दोनों ही विषयों में पैरामीटर {{math|''t''}} की पहचान करते हैं तो हम वृत्ताकार फलनों एवं अतिपरवलयिक फलनों के मध्य संबंध पर पहुंचते हैं। अर्थात यदि | ||
<math display="block">t = \tan\tfrac12 \varphi = \tanh\tfrac12 \psi</math> | <math display="block">t = \tan\tfrac12 \varphi = \tanh\tfrac12 \psi</math> | ||
| Line 204: | Line 204: | ||
<math display="block">\varphi = 2\arctan \bigl(\tanh \tfrac12 \psi\,\bigr) \equiv \operatorname{gd} \psi.</math> | <math display="block">\varphi = 2\arctan \bigl(\tanh \tfrac12 \psi\,\bigr) \equiv \operatorname{gd} \psi.</math> | ||
जहाँ {{math|gd(''ψ'')}}[[गुडर्मनियन फ़ंक्शन|गुडर्मनियन फलन]] है। गुडेरमैनियन फलन वृत्ताकार फलन एवं हाइपरबोलिक फलन के मध्य सीधा संबंध देता है जिसमें | जहाँ {{math|gd(''ψ'')}} [[गुडर्मनियन फ़ंक्शन|गुडर्मनियन फलन]] है। गुडेरमैनियन फलन वृत्ताकार फलन एवं हाइपरबोलिक फलन के मध्य सीधा संबंध देता है जिसमें समष्टि संख्याएं सम्मिलित नहीं होती हैं। स्पर्शरेखा अर्ध-कोण सूत्रों के उपरोक्त विवरण (इकाई वृत्त एवं मानक हाइपरबोला को {{math|''y''}}-अक्ष प्रक्षेपित करें)। इस फलन की ज्यामितीय व्याख्या देते हैं। | ||
==तर्कसंगत मान एवं पायथागॉरियन त्रिगुण== | ==तर्कसंगत मान एवं पायथागॉरियन त्रिगुण== | ||
{{main article|पायथागॉरियन त्रिगुण}} | {{main article|पायथागॉरियन त्रिगुण}} | ||
भुजाओं की लंबाई वाले पाइथागोरस त्रिभुज से प्रारंभ करने पर जिसकी भुजाओं की लंबाई {{mvar|a}}, {{mvar|b}}, एवं {{mvar|c}} है, जो धनात्मक पूर्णांक हैं एवं संतुष्ट {{math|''a''{{sup|2}} + ''b''{{sup|2}} {{=}} ''c''{{sup|2}}}} को करते हैं, इससे तुरंत ज्ञात होता है कि त्रिभुज के प्रत्येक [[आंतरिक कोण]] में साइन एवं | भुजाओं की लंबाई वाले पाइथागोरस त्रिभुज से प्रारंभ करने पर जिसकी भुजाओं की लंबाई {{mvar|a}}, {{mvar|b}}, एवं {{mvar|c}} है, जो धनात्मक पूर्णांक हैं एवं संतुष्ट {{math|''a''{{sup|2}} + ''b''{{sup|2}} {{=}} ''c''{{sup|2}}}} को करते हैं, इससे तुरंत ज्ञात होता है कि त्रिभुज के प्रत्येक [[आंतरिक कोण]] में साइन एवं कोज्या के लिए तर्कसंगत मान हैं, क्योंकि ये केवल भुजाओं की लंबाई के अनुपात हैं। इस प्रकार, {{math|tan ''φ''/2 {{=}} sin ''φ'' / (1 + cos ''φ'')}} का उपयोग करते हुए, इनमें से प्रत्येक कोण के अर्ध-कोण स्पर्शरेखा के लिए तर्कसंगत मान होता है। | ||
विपरीत भी सही है। यदि दो धनात्मक कोण हैं जिनका योग 90° है, प्रत्येक परिमेय अर्ध-कोण स्पर्शरेखा के साथ है, एवं तीसरा कोण [[समकोण]] है तो इन आंतरिक कोणों वाला त्रिभुज पाइथागोरस त्रिभुज के [[समान (ज्यामिति)]] हो सकता है। यदि तीसरे कोण का समकोण होना आवश्यक नहीं है, किन्तु वह कोण है जो तीन धनात्मक कोणों का योग 180° बनाता है तो तीसरे कोण के पास आवश्यक रूप से अपने अर्ध-कोण स्पर्शरेखा के लिए तर्कसंगत संख्या होगी जब पूर्व दो ऐसा करते हैं (स्पर्शरेखाओं के लिए कोण जोड़ एवं घटाव सूत्र का उपयोग करके) एवं त्रिभुज को हेरोनियन त्रिभुज में स्केल किया जा सकता है। | विपरीत भी सही है। यदि दो धनात्मक कोण हैं जिनका योग 90° है, प्रत्येक परिमेय अर्ध-कोण स्पर्शरेखा के साथ है, एवं तीसरा कोण [[समकोण]] है तो इन आंतरिक कोणों वाला त्रिभुज पाइथागोरस त्रिभुज के [[समान (ज्यामिति)]] हो सकता है। यदि तीसरे कोण का समकोण होना आवश्यक नहीं है, किन्तु वह कोण है जो तीन धनात्मक कोणों का योग 180° बनाता है तो तीसरे कोण के पास आवश्यक रूप से अपने अर्ध-कोण स्पर्शरेखा के लिए तर्कसंगत संख्या होगी जब पूर्व दो ऐसा करते हैं (स्पर्शरेखाओं के लिए कोण जोड़ एवं घटाव सूत्र का उपयोग करके) एवं त्रिभुज को हेरोनियन त्रिभुज में स्केल किया जा सकता है। | ||
सामान्यतः, | सामान्यतः, यदि {{mvar|K}} सम्मिश्र संख्याओं का [[फ़ील्ड विस्तार|उपक्षेत्र]] है तो {{math|tan ''φ''/2 ∈ ''K'' ∪ {{(}}∞{{)}}}} का तात्पर्य है कि {{math|{sin ''φ'', cos ''φ'', tan ''φ'', sec ''φ'', csc ''φ'', cot ''φ''} ⊆ ''K'' ∪ {{(}}∞{{)}}}} होता है। | ||
==यह भी देखें== | ==यह भी देखें== | ||
| Line 224: | Line 224: | ||
* [http://planetmath.org/encyclopedia/TangentOfHalvedAngle.html ''Tangent Of Halved Angle''] at [[Planetmath]] | * [http://planetmath.org/encyclopedia/TangentOfHalvedAngle.html ''Tangent Of Halved Angle''] at [[Planetmath]] | ||
{{DEFAULTSORT:Tangent Half-Angle Formula}} | {{DEFAULTSORT:Tangent Half-Angle Formula}} | ||
[[Category:Articles with hatnote templates targeting a nonexistent page|Tangent Half-Angle Formula]] | |||
[[Category:Created On 18/07/2023|Tangent Half-Angle Formula]] | |||
[[Category: | [[Category:Lua-based templates|Tangent Half-Angle Formula]] | ||
[[Category:Created On 18/07/2023]] | [[Category:Machine Translated Page|Tangent Half-Angle Formula]] | ||
[[Category:Mathematics sidebar templates|Tangent Half-Angle Formula]] | |||
[[Category:Pages with empty portal template|Tangent Half-Angle Formula]] | |||
[[Category:Pages with script errors|Tangent Half-Angle Formula]] | |||
[[Category:Portal templates with redlinked portals|Tangent Half-Angle Formula]] | |||
[[Category:Short description with empty Wikidata description|Tangent Half-Angle Formula]] | |||
[[Category:Sidebars with styles needing conversion|Tangent Half-Angle Formula]] | |||
[[Category:Templates Vigyan Ready|Tangent Half-Angle Formula]] | |||
[[Category:Templates that add a tracking category|Tangent Half-Angle Formula]] | |||
[[Category:Templates that generate short descriptions|Tangent Half-Angle Formula]] | |||
[[Category:Templates using TemplateData|Tangent Half-Angle Formula]] | |||
[[Category:गणितीय पहचान|Tangent Half-Angle Formula]] | |||
[[Category:त्रिकोणमिति|Tangent Half-Angle Formula]] | |||
[[Category:शंक्वाकार खंड|Tangent Half-Angle Formula]] | |||
Latest revision as of 15:01, 2 August 2023
| त्रिकोणमिति |
|---|
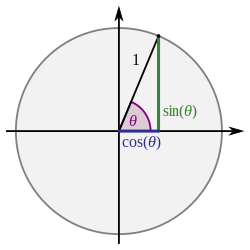 |
| संदर्भ |
| कानून और सिद्धांत |
| पथरी |
त्रिकोणमिति में, स्पर्शरेखा अर्ध-कोण सूत्र किसी कोण के अर्ध भाग की स्पर्शरेखा को पूर्ण कोण के त्रिकोणमितीय कार्यों से जोड़ते हैं। अर्ध कोण की स्पर्शरेखा किसी रेखा पर वृत्त का त्रिविम प्रक्षेपण है। इनमें से निम्नलिखित सूत्र हैं:
प्रमाण
बीजगणितीय प्रमाण
दोहरे कोण सूत्रों एवं पायथागॉरियन पहचान का उपयोग प्रदान करता है,
इससे ज्ञात होता है कि इन अंतिम दो सूत्रों में निरपेक्ष मान चिह्न हटाये जा सकते हैं, चाहे α कोई भी चतुर्थांश में हो। निरपेक्ष मान पट्टियों के साथ या उसके अभाव में ये सूत्र तब प्रस्तावित नहीं होते जब दाहिनी ओर अंश एवं हर दोनों शून्य होते हैं।
इसके अतिरिक्त, साइन एवं कोज्या दोनों के लिए कोण जोड़ एवं घटाव सूत्रों का उपयोग करके कोई प्राप्त करता है:
समायोजन एवं एवं उपज को प्रतिस्थापित करना:
ज्यामितीय प्रमाण

ऊपर दिए गए सूत्रों को दाईं ओर समचतुर्भुज आकृति पर प्रस्तावित करने से यह सरलता से प्रदर्शित किया जा सकता है,
अभिन्न कलन में स्पर्शरेखा अर्ध-कोण प्रतिस्थापन
त्रिकोणमिति के विभिन्न अनुप्रयोगों में, नए चर के तर्कसंगत कार्यों के संदर्भ में त्रिकोणमितीय कार्यों (जैसे साइन एवं कोज्या) को पुनः लिखना उपयोगी है। की परिभाषा के कारण इन सर्वसमिकाओं को सामूहिक रूप से स्पर्शरेखा अर्ध-कोण सूत्र के रूप में जाना जाता है। ये पहचानें साइन एवं कोज्या में तर्कसंगत कार्यों को उनके प्रतिअवकलज की शोध के लिए t के कार्यों में परिवर्तित करने के लिए कैलकुलसन में उपयोगी हो सकती हैं।
ज्यामितीय रूप से, निर्माण इस प्रकार होता है: इकाई चक्र पर किसी भी बिंदु के लिए (cos φ, sin φ) के लिए, इससे होकर निकलने वाली रेखा एवं बिंदु के लिए (−1, 0) खींची जाती है। यह बिंदु किसी बिंदु y = t पर y-अक्ष को पार करता है। कोई सरल ज्यामिति का उपयोग करके यह दिखा सकता है कि t = tan(φ/2) है। खींची गई रेखा का समीकरण y = (1 + x)t है। रेखा एवं वृत्त के प्रतिच्छेदन का समीकरण तब द्विघात समीकरण होता है जिसमें t सम्मिलित होता है। इस समीकरण के दो समाधान हैं (−1, 0) एवं (cos φ, sin φ) हैं। यह हमें पश्चात वाले को t के तर्कसंगत कार्यों के रूप में लिखने की अनुमति देता है (समाधान नीचे दिए गए हैं)।
पैरामीटर t, प्रक्षेपण के केंद्र (−1, 0) के साथ y-अक्ष पर (cos φ, sin φ) के त्रिविम प्रक्षेपण का प्रतिनिधित्व करता है। इस प्रकार, स्पर्शरेखा अर्ध-कोण सूत्र त्रिविम निर्देशांक t एवं मानक कोणीय निर्देशांक पर φ के मध्य रूपांतरण देते हैं।
तो हमारे पास हैं,
गुडरमैनियन फलन
अतिशयोक्तिपूर्ण पहचानों की अपेक्षा वृत्ताकार पहचानों से करने पर, कोई यह ध्यान देता है कि उनमें t के समान कार्य सम्मिलित हैं, अभी क्रमबद्ध किया गया है। यदि हम दोनों ही विषयों में पैरामीटर t की पहचान करते हैं तो हम वृत्ताकार फलनों एवं अतिपरवलयिक फलनों के मध्य संबंध पर पहुंचते हैं। अर्थात यदि
तर्कसंगत मान एवं पायथागॉरियन त्रिगुण
भुजाओं की लंबाई वाले पाइथागोरस त्रिभुज से प्रारंभ करने पर जिसकी भुजाओं की लंबाई a, b, एवं c है, जो धनात्मक पूर्णांक हैं एवं संतुष्ट a2 + b2 = c2 को करते हैं, इससे तुरंत ज्ञात होता है कि त्रिभुज के प्रत्येक आंतरिक कोण में साइन एवं कोज्या के लिए तर्कसंगत मान हैं, क्योंकि ये केवल भुजाओं की लंबाई के अनुपात हैं। इस प्रकार, tan φ/2 = sin φ / (1 + cos φ) का उपयोग करते हुए, इनमें से प्रत्येक कोण के अर्ध-कोण स्पर्शरेखा के लिए तर्कसंगत मान होता है।
विपरीत भी सही है। यदि दो धनात्मक कोण हैं जिनका योग 90° है, प्रत्येक परिमेय अर्ध-कोण स्पर्शरेखा के साथ है, एवं तीसरा कोण समकोण है तो इन आंतरिक कोणों वाला त्रिभुज पाइथागोरस त्रिभुज के समान (ज्यामिति) हो सकता है। यदि तीसरे कोण का समकोण होना आवश्यक नहीं है, किन्तु वह कोण है जो तीन धनात्मक कोणों का योग 180° बनाता है तो तीसरे कोण के पास आवश्यक रूप से अपने अर्ध-कोण स्पर्शरेखा के लिए तर्कसंगत संख्या होगी जब पूर्व दो ऐसा करते हैं (स्पर्शरेखाओं के लिए कोण जोड़ एवं घटाव सूत्र का उपयोग करके) एवं त्रिभुज को हेरोनियन त्रिभुज में स्केल किया जा सकता है।
सामान्यतः, यदि K सम्मिश्र संख्याओं का उपक्षेत्र है तो tan φ/2 ∈ K ∪ {∞} का तात्पर्य है कि {sin φ, cos φ, tan φ, sec φ, csc φ, cot φ} ⊆ K ∪ {∞} होता है।
