रॉडिक्स ट्री: Difference between revisions
No edit summary |
No edit summary |
||
| (25 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Data structure}} | {{Short description|Data structure}} | ||
[[File:Patricia trie.svg|thumb| | [[File:Patricia trie.svg|thumb|रॉडिक्स ट्री का एक उदाहरण|350x350px]][[कंप्यूटर विज्ञान]] में, '''रॉडिक्स ट्री''' एक [[डेटा संरचना]] होती है जो [[मेमोरी अनुकूलन|मेमोरी]] (प्रेफ्फिस ट्री) का प्रतिनिधित्व करती है जिसमें प्रत्येक नोड जो एकमात्र चाइल्ड नोड होते है, जब प्रत्येक नोड चाइल्ड नोड के साथ विलय हो जाता है तब इसका परिणाम प्रत्येक आंतरिक नोड के चाइल्ड नोड की संख्या अधिकतम [[मूलांक|रॉडिक्स]] होता है {{mvar|r}} रॉडिक्स ट्री, जहाँ {{mvar|r}} एक धनात्मक पूर्णांक होता है {{mvar|x}} 2, और {{mvar|x}} ≥ 1. नियमित ट्री के विपरीत, किनारों को आधारों के अनुक्रम के साथ-साथ एकल आधारों के साथ अंकित किया जा सकता है। यह रॉडिक्स ट्री को छोटे सेट के लिए अधिक कुशल बनाता है (विशेषकर यदि स्ट्रिंग लंबी होती है)। | ||
नियमित | नियमित ट्री के विपरीत (जहां संपूर्ण समाधानों की तुलना उनके प्रारंभ से लेकर असमानता के पॉइंट तक की जाती है), प्रत्येक नोड की तुलना बिट्स द्वारा की जाती है, जहां उस बिट्स की मात्रा होती है {{mvar|r}} वह नोड रॉडिक्स होता है। {{mvar|r}} 2, रॉडिक्स बाइनरी होती है (अर्थात, मुख्य नोड के 1-बिट भाग की तुलना करते है), जो अधिकतम करने पर विरलता को कम करते है - अर्थात, बिट-स्ट्रिंग्स के संयोजन को अधिकतम करता है। जब {{mvar|r}} ≥ 4, 2 पूर्णांक होता है, तो रॉडिक्स {{mvar|r}}-एरी ट्री होता है, जो संभावित विरलता के रॉडिक्स ट्री की गहराई को कम करता है। | ||
किनारे के अंकित एक स्ट्रिंग में दो पॉइंट का उपयोग करके स्थिर आकार संग्रहीत किया जा सकता है (पहले और आखिरी आधारों के लिए)।<ref>{{cite web|last=Morin|first=Patrick|title=स्ट्रिंग्स के लिए डेटा संरचनाएँ|url=http://cg.scs.carleton.ca/~morin/teaching/5408/notes/strings.pdf|access-date=15 April 2012}}</ref> | |||
ध्यान दें कि | |||
ध्यान दें कि इस ग्राफ के उदाहरण स्ट्रिंग्स को वर्णों के अनुक्रम के रूप में प्रस्तुत करते है, स्ट्रिंग आधारों के प्रकार को मनमाने रूप से चुना जा सकता है, उदाहरण के लिए, [[ मल्टीबाइट चरित्र |बाइट]] एन्कोडिंग या [[यूनिकोड]] का उपयोग करते समय स्ट्रिंग प्रतिनिधित्व बिट या बाइट के रूप में करता है। | |||
== अनुप्रयोग == | == अनुप्रयोग == | ||
रॉडिक्स ट्री सहयोगी एरे बनाने के लिए उपयोगी होते है जिन्हें स्ट्रिंग के रूप में व्यक्त किया जा सकता है। वह [[इंटरनेट प्रोटोकॉल]] के क्षेत्र में विशेष अनुप्रयोग प्रस्तुत करते है,<ref>{{Cite web|url=https://www.freebsd.org/cgi/man.cgi?query=rtfree&apropos=0&sektion=9&manpath=FreeBSD%2011-current&format=html|title=rtfree(9)|website=www.freebsd.org|access-date=2016-10-23}}</ref><ref>{{cite web |author= The Regents of the University of California |author-link= The Regents of the University of California |date= 1993 |url= http://bxr.su/n/sys/net/radix.c |title= /sys/net/radix.c |website= BSD Cross Reference |publisher= [[NetBSD]] |access-date= 2019-07-25 |quote= "Routines to build and maintain radix trees for routing lookups."}}</ref><ref>{{cite web |url= http://wiki.netbsd.org/projects/project/atomic_radix_patricia_trees/ |title= Lockless, atomic and generic Radix/Patricia trees |publisher= [[NetBSD]] |year= 2011 }}</ref> जहां कुछ मूल्यों की बड़ी श्रृंखला को सम्मलित करने की क्षमता विशेष रूप से आईपी एड्रेस के पदानुक्रमित संगठन के लिए उपयुक्त होती है।<ref>Knizhnik, Konstantin. [http://www.ddj.com/architect/208800854 "Patricia Tries: A Better Index For Prefix Searches"], ''Dr. Dobb's Journal'', June, 2008.</ref> इनका उपयोग सूचना पुनर्प्राप्ति में इंडेक्स के लिए भी किया जाता है। | |||
==संचालन == | ==संचालन == | ||
रॉडिक्स ट्री सम्मिलन, विलोपन का समर्थन करते है। संग्रहीत डेटा की मात्रा को कम करने का प्रयास करते समय यह ट्री में एक नई स्ट्रिंग को जोड़ता है। विलोपन ट्री से एक स्ट्रिंग को हटा देता है। जाँच कार्यों में त्रुटिहीन अवलोकन और प्रेफ्फिस के साथ सभी स्ट्रिंग को प्रस्तुत करना सम्मलित होता है (लेकिन आवश्यक नहीं कि यह इन्हीं तक सीमित हो)। यह सभी संचालन O(k) होते है जहां k सेट में सभी स्ट्रिंग्स की अधिकतम लंबाई होती है, जहां लंबाई रॉडिक्स ट्री के रॉडिक्स के बराबर बिट्स की मात्रा में मापी जाती है। | |||
=== अवलोकन === | |||
[[File:An example of how to find a string in a Patricia trie.png|पेट्रीसिया ट्राइ|थंब|313x313पीएक्स में एक स्ट्रिंग ढूँढना]] | |||
अवलोकन संचालन यह निर्धारित करता है कि किसी ट्री में कोई स्ट्रिंग उपस्थित है या नहीं है। अधिकांश संचालन अपने विशिष्ट कार्यों को संभालने के लिए अवलोकन संचालन का उपयोग करते है। उदाहरण के लिए, वह नोड जहां एक स्ट्रिंग समाप्त होती है। यह संचालन प्रयासों के समान होते है, इसके अतिरिक्त कुछ किनारे कई आधारों का उपभोग करते है। | |||
निम्नलिखित छद्म कोड मानता है कि | निम्नलिखित छद्म कोड मानता है कि इनमें विधियाँ और गुण उपस्थित होते है। | ||
किनारा | किनारा | ||
*नोड लक्ष्यनोड | *नोड लक्ष्यनोड | ||
* स्ट्रिंग | * स्ट्रिंग अंकित | ||
नोड | नोड | ||
* किनारों की | * किनारों की एरे | ||
* फ़ंक्शन लीफ () है | * फ़ंक्शन लीफ () है | ||
| Line 31: | Line 38: | ||
{ | { | ||
// Begin at the root with no elements found | // Begin at the root with no elements found | ||
Node | Node traverseNodeo:= root, | ||
int | int elementsFoundo:= 0, | ||
// Traverse until a leaf is found or it is not possible to continue | // Traverse until a leaf is found or it is not possible to continue | ||
while ( | while (traverseNodes!= null && !traverseNode.isLeaf() && elementsFound < x.length) | ||
{ | { | ||
// Get the next edge to explore based on the elements not yet found in x | // Get the next edge to explore based on the elements not yet found in x | ||
| Line 40: | Line 47: | ||
// x.suffix(elementsFound) returns the last (x.length - elementsFound) elements of x | // x.suffix(elementsFound) returns the last (x.length - elementsFound) elements of x | ||
// Was an edge found? | // Was an edge found? | ||
if ( | if (nextEdgei!= null) | ||
{ | { | ||
// Set the next node to explore | // Set the next node to explore | ||
traverseNode := nextEdge.targetNode | traverseNode := nextEdge.targetNode, | ||
// Increment elements found based on the label stored at the edge | // Increment elements found based on the label stored at the edge | ||
elementsFound += nextEdge.label.length | elementsFound += nextEdge.label.length, | ||
} | } | ||
else | else | ||
{ | { | ||
// Terminate loop | // Terminate loop | ||
traverseNode := null | traverseNode := null, | ||
} | } | ||
} | } | ||
// A match is found if we arrive at a leaf node and have used up exactly x.length elements | // A match is found if we arrive at a leaf node and have used up exactly x.length elements | ||
return (traverseNode != null && traverseNode.isLeaf() && elementsFound == x.length) | return (traverseNode | ||
!= null && traverseNode.isLeaf() && elementsFound == x.length), | |||
} | } | ||
=== निवेशन === | === निवेशन === | ||
इस पॉइंट पर हम इनपुट स्ट्रिंग में अंकित किया गया एक नया बाहरी एज जोड़ते है, या यदि इसमे पहले से ही इनपुट स्ट्रिंग के साथ एक प्रेफ्फिस शेयर करने वाला बाहरी एज होता है, तो हम इसे दो किनारों में विभाजित करते है। यह विभाजन चरण यह सुनिश्चित करता है कि किसी भी नोड में संभावित स्ट्रिंग की तुलना में अधिक चाइल्ड नोड नहीं होते है। | |||
सम्मिलन के कई | सम्मिलन के कई स्थितियां नीचे दिखाई गई है। ध्यान दें कि r केवल मूल का प्रतिनिधित्व करता है। यह माना जाता है कि जहां आवश्यक हो वहां स्ट्रिंग्स को समाप्त करने के लिए किनारों को खाली स्ट्रिंग्स के साथ अंकित किया जा सकता है। (खाली-स्ट्रिंग किनारों का उपयोग करते समय ऊपर वर्णित अवलोकन ऐल्गरिदम काम नहीं करता है।) | ||
<gallery widths="300" heights="200" mode="nolines"> | <gallery widths="300" heights="200" mode="nolines"> | ||
| Line 67: | Line 75: | ||
File:Insert 'slower' with a null node into a Patricia trie.png|'धीमा' रखते हुए 'धीमा' डालें | File:Insert 'slower' with a null node into a Patricia trie.png|'धीमा' रखते हुए 'धीमा' डालें | ||
File:Insert 'test' into a Patricia trie when 'tester' exists.png|'टेस्ट' डालें जो 'टेस्टर' का उपसर्ग है | File:Insert 'test' into a Patricia trie when 'tester' exists.png|'टेस्ट' डालें जो 'टेस्टर' का उपसर्ग है | ||
File:Inserting the word 'team' into a Patricia trie with a split.png|'टेस्ट' को विभाजित करते समय और एक नया एज लेबल ' | File:Inserting the word 'team' into a Patricia trie with a split.png|'टेस्ट' को विभाजित करते समय और एक नया एज लेबल 'समूह' बनाते समय 'समूह' डालें | ||
File:Insert 'toast' into a Patricia trie with a split and a move.png|'ते' को विभाजित करते हुए और पिछले तारों को एक स्तर नीचे ले जाते हुए 'टोस्ट' डालें | File:Insert 'toast' into a Patricia trie with a split and a move.png|'ते' को विभाजित करते हुए और पिछले तारों को एक स्तर नीचे ले जाते हुए 'टोस्ट' डालें | ||
</gallery> | </gallery> | ||
=== विलोपन === | === विलोपन === | ||
किसी | किसी ट्री से एक स्ट्रिंग x को हटाने के लिए, हम पहले x का प्रतिनिधित्व करने वाले लीफ का पता लगाते है। फिर, यह मानते हुए कि x उपस्थित है, हम संबंधित लीफ नोड को हटा देते है। यदि हमारे लीफ नोड के पास केवल एक अन्य चाइल्ड नोड होता है, तो उस चाइल्ड नोड का आने वाले नाम को हटा दिया जाता है। | ||
=== अतिरिक्त संचालन === | === अतिरिक्त संचालन === | ||
* सामान्य | * सामान्य प्रेफ्फिस वाली सभी स्ट्रिंग्स प्राप्त होती है: समान प्रेफ्फिस से प्रारंभ होने वाली स्ट्रिंग्स की एक एरे लौटाता है। | ||
* पूर्ववर्ती | * पूर्ववर्ती जाँचें: लेक्सिको ग्राफ क्रम के अनुसार, किसी दिए गए स्ट्रिंग से सबसे बड़ी स्ट्रिंग का पता लगाता है। | ||
* | * सक्सेसर जाँचें: लेक्सिको ग्राफ क्रम के अनुसार, दी गई स्ट्रिंग से बड़ी सबसे छोटी स्ट्रिंग का पता लगाता है। | ||
== इतिहास == | == इतिहास == | ||
डेटासंरचना का आविष्कार 1968 में डोनाल्ड आर. मॉरिसन द्वारा किया गया था,<ref>Morrison, Donald R. [http://portal.acm.org/citation.cfm?id=321481 PATRICIA -- Practical Algorithm to Retrieve Information Coded in Alphanumeric]</ref> यह मुख्य रूप से गर्नोट ग्वेहेनबर्गर के साथ जुड़ा हुआ है।<ref>G. Gwehenberger, [http://cr.yp.to/bib/1968/gwehenberger.html Anwendung einer binären Verweiskettenmethode beim Aufbau von Listen.] Elektronische Rechenanlagen 10 (1968), pp. 223–226</ref> | |||
[[डोनाल्ड नुथ]], [[कंप्यूटर प्रोग्रामिंग की कला]] के खंड III में पृष्ठ 498-500, इन्हें पेट्रीसिया के | |||
[[डोनाल्ड नुथ]], [[कंप्यूटर प्रोग्रामिंग की कला|कंप्यूटर प्रोग्रामिंग]] के खंड III में पृष्ठ 498-500 में, इन्हें पेट्रीसिया के ट्री कहते थे, संभवतः मॉरिसन के पेपर के शीर्षक में संक्षिप्त नाम के बाद: पेट्रीसिया कोडित सूचना पुनर्प्राप्त करने के लिए व्यावहारिक ऐल्गरिदम का उपयोग किया जाता है। आज, पेट्रीसिया प्रयासों को रॉडिक्स 2 के बराबर रॉडिक्स वाले ट्री के रूप में देखा जाता है, जिसका अर्थ होता है कि प्रत्येक बिट की तुलना व्यक्तिगत रूप से की जाती है और प्रत्येक नोड दो-तरफा (अर्थात, बाएं या दाएं) होते है। | |||
== अन्य डेटा संरचनाओं की तुलना == | == अन्य डेटा संरचनाओं की तुलना == | ||
(निम्नलिखित तुलनाओं में, यह माना जाता है कि | (निम्नलिखित तुलनाओं में, यह माना जाता है कि समाधान k लंबाई है और डेटा संरचना में n गुण है।) | ||
[[संतुलित पेड़]] | [[संतुलित पेड़|संतुलित]] ट्री के विपरीत, रॉडिक्स ट्री ओ (लॉग एन) के अतिरिक्त ओ (के) समय में अवलोकन, सम्मिलन और विलोपन की अनुमति देते है। यह एक लाभ की तरह प्रतीत नहीं होता है, क्योंकि सामान्यतः k ≥ log n होता है, लेकिन एक संतुलित ट्री में हर तुलना एक स्ट्रिंग तुलना होती है जिसके लिए O(k) को सबसे कठिन स्थिति वाले समय की आवश्यकता होती है, जिनमें से कई लंबे सामान्य प्रेफ्फिस के कारण अभ्यास धीमे होते है। एक प्रयास में, सभी तुलनाओं के लिए निरंतर समय की आवश्यकता होती है, लेकिन लंबाई m की एक स्ट्रिंग को देखने के लिए m तुलना की आवश्यकता होती है। रॉडिक्स ट्री इन संचालनों को कम तुलनाओं के साथ कर सकते है, और बहुत कम नोड्स की आवश्यकता होती है। | ||
चूंकि, रॉडिक्स ट्री प्रयासों के नुकसान को भी शेयर करते है: चूंकि उन्हें केवल आधारों की स्ट्रिंग के लिए कुशलतापूर्वक प्रतिवर्ती मैपिंग वाले आधारों पर ही प्रारंभ किया जा सकता है, इसलिए उनमें संतुलित जाँच ट्री की पूर्ण व्यापकता का अभाव होता होता है, जो कुल मिलाकर किसी भी डेटा प्रकार पर प्रारंभ होते है। अनुक्रम संतुलित ट्री के लिए आवश्यक कुल अनुक्रम तैयार करने के लिए स्ट्रिंग्स की प्रतिवर्ती मैपिंग का उपयोग किया जा सकता है। यह भी समस्याग्रस्त हो सकता है यदि डेटा प्रकार केवल इंटरफेस [[इंटरफ़ेस (कंप्यूटर विज्ञान)|(कंप्यूटर विज्ञान)]] एक तुलना संचालन होता है, लेकिन (डी) क्रमांकन संचालन नहीं होता है। | |||
सामान्यतः कहा जाता है कि [[हैश तालिका|हैश तालिकाओं]] में अपेक्षित O(1) सम्मिलन और विलोपन समय होता है, लेकिन यह केवल तभी सच है जब मुख्य के हैश की गणना को एक निरंतर-समय का संचालन माना जाता है। जब मुख्य की हैशिंग को ध्यान में रखा जाता है, तो हैश तालिकाओं में O(k) सम्मिलन और विलोपन समय की अपेक्षा की जाती है, इसके आधार पर इसमें अधिक समय लग सकता है। रॉडिक्स ट्री में सबसे कठिन स्थिति O(k) सम्मिलन और विलोपन की होती है। रॉडिक्स ट्री के सक्सेसर/पूर्ववर्ती संचालन भी हैश तालिकाओं द्वारा कार्यान्वित नहीं किए जाते है। | |||
== | ==प्रकार== | ||
रॉडिक्स ट्री का एक सामान्य विस्तार नोड्स के दो रंगों, 'काले' और 'सफ़ेद' का उपयोग करता है। यह जांचने के लिए कि क्या दिया गया स्ट्रिंग ट्री में संग्रहीत है या नहीं है, जाँच ऊपर से प्रारंभ होती है और इनपुट स्ट्रिंग के किनारों का अनुसरण करती है। यदि जाँच स्ट्रिंग समाप्त हो जाती है और अंतिम नोड एक काला नोड होता है, तो यह जाँच विफल होने का संकेत देता है, यदि यह सफेद होता है, तो यह जाँच सफल होने का संकेत देता है। यह हमें सफेद नोड्स का उपयोग करके ट्री में एक सामान्य प्रेफ्फिस के साथ स्ट्रिंग की एक बड़ी श्रृंखला जोड़ने में सक्षम बनाता है, फिर काले नोड्स का उपयोग करके उन्हें कुशल विधि से एक छोटे सेट को हटा देता है। | |||
'[[HAT-trie]]' | '[[HAT-trie|हैट ट्री]]' रॉडिक्स ट्री पर आधारित एक कैश-सचेत डेटा संरचना होती है जो कुशल स्ट्रिंग स्टॉरेज और पुनर्प्राप्ति और अनुक्रमित पुनरावृत्तियों को प्रस्तुत करता है। समय और स्थान दोनों के संबंध में [[ हैश तालिका |हैश तालिका]] का तुलनीय प्रदर्शन होता है।<ref>{{Cite book | title=HAT-trie: A Cache-conscious Trie-based Data Structure for Strings | first1=Nikolas | last1=Askitis | first2=Ranjan | last2=Sinha | year=2007 | url=http://portal.acm.org/citation.cfm?id=1273749.1273761&coll=GUIDE&dl= | isbn=1-920682-43-0 | pages=97–105 | volume=62 | journal=Proceedings of the 30th Australasian Conference on Computer science }}</ref><ref> | ||
{{Cite journal | {{Cite journal | ||
| title=Engineering scalable, cache and space efficient tries for strings | | title=Engineering scalable, cache and space efficient tries for strings | ||
| Line 117: | Line 135: | ||
</ref> | </ref> | ||
पेट्रीसिया | पेट्रीसिया ट्री रॉडिक्स 2 (बाइनरी) ट्री का एक विशेष प्रकार होता है, जिसमें प्रत्येक मुख्य बिट को स्पष्ट रूप से संग्रहीत करने के अतिरिक्त, नोड्स केवल पहले बिट की स्थिति को संग्रहीत करते है जो दो ट्री को अलग करते है। ट्रैवर्सल के समय ऐल्गरिदम जाँच अनुक्रमित बिट की जांच करता है और उपयुक्त बाएं या दाएं ट्री को चुनता है। पेट्रीसिया ट्री की उल्लेखनीय विशेषताओं में यह सम्मलित है कि ट्री को संग्रहीत प्रत्येक अद्वितीय मुख्य नोड के लिए केवल एक नोड की आवश्यकता होती है, जो पेट्रीसिया को मानक बाइनरी ट्री की तुलना में अधिक सघन बनाता है। इसके अतिरिक्त, चूंकि वास्तविक समाधान स्पष्ट रूप से संग्रहीत नहीं होते है, तो मिलान की पुष्टि करने के लिए अनुक्रमित रिकॉर्ड पर एक पूर्ण मुख्य तुलना करना आवश्यक होता है। इस संबंध में पेट्रीसिया हैश तालिका का उपयोग करके अनुक्रमण के साथ एक निश्चित समानता होती है।<ref>Morrison, Donald R. [http://portal.acm.org/citation.cfm?id=321481 PATRICIA -- Practical Algorithm to Retrieve Information Coded in Alphanumeric]</ref> | ||
रॉडिक्स ट्री नोड के आकार को एकीकृत करता है। सामान्य रॉडिक्स ट्री में एक बड़े स्थान का उपयोग होता है, क्योंकि यह हर स्तर पर एक स्थिर नोड आकार का उपयोग करता है। रॉडिक्स ट्री के अंतर्गत चाइल्ड आधारों की संख्या के आधार पर प्रत्येक नोड के लिए अंतर होता है। इसलिए, यह रॉडिक्स ट्री की गति को कम किए बिना उसका बेहतर उपयोग करता है।<ref> | |||
{{Cite book | {{Cite book | ||
| title=Datenbanksysteme, Eine Einführung | | title=Datenbanksysteme, Eine Einführung | ||
| Line 131: | Line 150: | ||
}} | }} | ||
</ref><ref>{{cite web|url=https://github.com/armon/libart|title=armon/libart: Adaptive Radix Trees implemented in C|work=GitHub|access-date=17 September 2014}}</ref><ref>{{cite journal|author=Viktor Leis|display-authors=et. al.|title=The adaptive radix tree: ARTful indexing for main-memory databases|journal=IEEE 29th International Conference on Data Engineering (ICDE)|year=2013|pages=38-49|doi=10.1109/ICDE.2013.6544812}}</ref> | </ref><ref>{{cite web|url=https://github.com/armon/libart|title=armon/libart: Adaptive Radix Trees implemented in C|work=GitHub|access-date=17 September 2014}}</ref><ref>{{cite journal|author=Viktor Leis|display-authors=et. al.|title=The adaptive radix tree: ARTful indexing for main-memory databases|journal=IEEE 29th International Conference on Data Engineering (ICDE)|year=2013|pages=38-49|doi=10.1109/ICDE.2013.6544812}}</ref> | ||
ऐसी स्थितियों में जहां | |||
ऐसी स्थितियों में जहां डेटा सेट में एक मुख्य ट्री का प्रतिनिधित्व करते है। रॉडिक्स ट्री का यह संस्करण उस संस्करण की तुलना में उच्च स्थान दक्षता प्राप्त करता है जो केवल कम से कम दो चाइल्ड नोड के साथ आंतरिक नोड्स की अनुमति देता है।<ref>[https://cs.stackexchange.com/q/98459 Can a node of Radix tree which represents a valid key have one child?]</ref> | |||
== यह भी देखें == | == यह भी देखें == | ||
{{Portal|Computer programming}} | {{Portal|Computer programming}} | ||
| Line 151: | Line 171: | ||
{{div col end}} | {{div col end}} | ||
| Line 169: | Line 198: | ||
===कार्यान्वयन=== | ===कार्यान्वयन=== | ||
*[http://bxr.su/f/sys/net/radix.h FreeBSD कार्यान्वयन], पेजिंग, अग्रेषण और अन्य चीजों के लिए उपयोग किया जाता है। | *[http://bxr.su/f/sys/net/radix.h FreeBSD कार्यान्वयन], पेजिंग, अग्रेषण और अन्य चीजों के लिए उपयोग किया जाता है। | ||
*[https://git.kernel.org/cgit/linux/kernel/git/torvalds/linux.git/tree/lib/radix-tree.c लिनक्स कर्नेल कार्यान्वयन], अन्य चीजों के | *[https://git.kernel.org/cgit/linux/kernel/git/torvalds/linux.git/tree/lib/radix-tree.c लिनक्स कर्नेल कार्यान्वयन], अन्य चीजों के अतिरिक्त पेज कैश के लिए उपयोग किया जाता है। | ||
*[https://gcc.gnu.org/onlinedocs/libstdc++/ext/pb_ds/trie_आधारित_containers.html GNU C++ मानक लाइब्रेरी में एक त्रि कार्यान्वयन है] | *[https://gcc.gnu.org/onlinedocs/libstdc++/ext/pb_ds/trie_आधारित_containers.html GNU C++ मानक लाइब्रेरी में एक त्रि कार्यान्वयन है] | ||
*[https://code.google.com/p/concurrent-trees/ समवर्ती | *[https://code.google.com/p/concurrent-trees/ समवर्ती रॉडिक्स ट्री का जावा कार्यान्वयन], नियाल गैलाघेर द्वारा | ||
*[http://paratechnical.blogspot.com/2011/03/radix-tree-implementation-in-c.html C# | *[http://paratechnical.blogspot.com/2011/03/radix-tree-implementation-in-c.html C# रॉडिक्स ट्री का कार्यान्वयन] | ||
*[https://code.google.com/p/patl/ प्रैक्टिकल एल्गोरिथम टेम्प्लेट लाइब्रेरी], PATRICIA पर एक C++ लाइब्रेरी (VC++ >=2003, GCC G++ 3.x), रोमन एस. क्लुजकोव द्वारा | *[https://code.google.com/p/patl/ प्रैक्टिकल एल्गोरिथम टेम्प्लेट लाइब्रेरी], PATRICIA पर एक C++ लाइब्रेरी (VC++ >=2003, GCC G++ 3.x), रोमन एस. क्लुजकोव द्वारा | ||
*[http://www.codeproject.com/KB/string/PatriciaTreeTemplateClass.aspx पेट्रीसिया | *[http://www.codeproject.com/KB/string/PatriciaTreeTemplateClass.aspx पेट्रीसिया ट्री C++ टेम्पलेट क्लास कार्यान्वयन], राडू ग्रुइयन द्वारा | ||
*[https://hackage.haskell.org/package/containers/docs/Data-IntMap-Internal.html हास्केल मानक पुस्तकालय कार्यान्वयन] बड़े-एंडियन पेट्रीसिया | *[https://hackage.haskell.org/package/containers/docs/Data-IntMap-Internal.html हास्केल मानक पुस्तकालय कार्यान्वयन] बड़े-एंडियन पेट्रीसिया ट्री पर आधारित। वेब-ब्राउज़ करने योग्य [https://hackage.haskell.org/package/containers/docs/src/Data.IntMap.Internal.html स्रोत कोड]। | ||
*[https://github.com/rkapsi/patricia-trie जावा में पेट्रीसिया | *[https://github.com/rkapsi/patricia-trie जावा में पेट्रीसिया ट्री कार्यान्वयन], रोजर काप्सी और सैम बर्लिन द्वारा | ||
*[https://github.com/agl/critbit क्रिट-बिट | *[https://github.com/agl/critbit क्रिट-बिट ट्री] डैनियल जे. बर्नस्टीन द्वारा सी कोड से लिया गया | ||
*[http://cprops.sourceforge.net/gen/docs/trie_8c-source.html सी में पेट्रीसिया | *[http://cprops.sourceforge.net/gen/docs/trie_8c-source.html सी में पेट्रीसिया ट्री कार्यान्वयन], [http://cprops.sourceforge.net libcprops] में | ||
*[http://www.lri.fr/~filliatr/ftp/ocaml/ds पेट्रीसिया ट्रीज़: पूर्णांकों पर कुशल सेट और मानचित्र] :fr:ऑब्जेक्टिव कैमल, जीन-क्रिस्टोफ़ फ़िलियाट्रे द्वारा | *[http://www.lri.fr/~filliatr/ftp/ocaml/ds पेट्रीसिया ट्रीज़: पूर्णांकों पर कुशल सेट और मानचित्र] :fr:ऑब्जेक्टिव कैमल, जीन-क्रिस्टोफ़ फ़िलियाट्रे द्वारा | ||
*[https://github.com/balena/radixdb | *[https://github.com/balena/radixdb रॉडिक्स डीबी (पेट्रीसिया ट्री) सी में कार्यान्वयन], जी. बी. वर्सियानी द्वारा | ||
*[https://github.com/armon/libart लिबार्ट - सी में | *[https://github.com/armon/libart लिबार्ट - सी में प्रारंभ अनुकूली रॉडिक्स ट्री], अन्य योगदानकर्ताओं के साथ आर्मोन डैडगर द्वारा (ओपन सोर्स, बीएसडी 3-क्लॉज लाइसेंस) | ||
*[https://nim-lang.org/docs/critbits.html क्रिट-बिट ट्री का निम कार्यान्वयन] | *[https://nim-lang.org/docs/critbits.html क्रिट-बिट ट्री का निम कार्यान्वयन] | ||
*[https://github.com/antirez/rax rax], [[साल्वाटोर सैनफिलिपो]] ([https://redis.io/ REDIS] के निर्माता) द्वारा ANSI C में एक | *[https://github.com/antirez/rax rax], [[साल्वाटोर सैनफिलिपो]] ([https://redis.io/ REDIS] के निर्माता) द्वारा ANSI C में एक रॉडिक्स ट्री कार्यान्वयन | ||
{{CS-Trees}} | {{CS-Trees}} | ||
[[Category:Collapse templates]] | |||
[[Category:Commons category link is the pagename]] | |||
[[Category: | |||
[[Category:Created On 10/07/2023]] | [[Category:Created On 10/07/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Multi-column templates]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages using div col with small parameter]] | |||
[[Category:Pages with broken file links]] | |||
[[Category:Pages with empty portal template]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Portal templates with redlinked portals]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Templates using under-protected Lua modules]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:Wikipedia metatemplates]] | |||
Latest revision as of 11:52, 12 August 2023
कंप्यूटर विज्ञान में, रॉडिक्स ट्री एक डेटा संरचना होती है जो मेमोरी (प्रेफ्फिस ट्री) का प्रतिनिधित्व करती है जिसमें प्रत्येक नोड जो एकमात्र चाइल्ड नोड होते है, जब प्रत्येक नोड चाइल्ड नोड के साथ विलय हो जाता है तब इसका परिणाम प्रत्येक आंतरिक नोड के चाइल्ड नोड की संख्या अधिकतम रॉडिक्स होता है r रॉडिक्स ट्री, जहाँ r एक धनात्मक पूर्णांक होता है x 2, और x ≥ 1. नियमित ट्री के विपरीत, किनारों को आधारों के अनुक्रम के साथ-साथ एकल आधारों के साथ अंकित किया जा सकता है। यह रॉडिक्स ट्री को छोटे सेट के लिए अधिक कुशल बनाता है (विशेषकर यदि स्ट्रिंग लंबी होती है)।
नियमित ट्री के विपरीत (जहां संपूर्ण समाधानों की तुलना उनके प्रारंभ से लेकर असमानता के पॉइंट तक की जाती है), प्रत्येक नोड की तुलना बिट्स द्वारा की जाती है, जहां उस बिट्स की मात्रा होती है r वह नोड रॉडिक्स होता है। r 2, रॉडिक्स बाइनरी होती है (अर्थात, मुख्य नोड के 1-बिट भाग की तुलना करते है), जो अधिकतम करने पर विरलता को कम करते है - अर्थात, बिट-स्ट्रिंग्स के संयोजन को अधिकतम करता है। जब r ≥ 4, 2 पूर्णांक होता है, तो रॉडिक्स r-एरी ट्री होता है, जो संभावित विरलता के रॉडिक्स ट्री की गहराई को कम करता है।
किनारे के अंकित एक स्ट्रिंग में दो पॉइंट का उपयोग करके स्थिर आकार संग्रहीत किया जा सकता है (पहले और आखिरी आधारों के लिए)।[1]
ध्यान दें कि इस ग्राफ के उदाहरण स्ट्रिंग्स को वर्णों के अनुक्रम के रूप में प्रस्तुत करते है, स्ट्रिंग आधारों के प्रकार को मनमाने रूप से चुना जा सकता है, उदाहरण के लिए, बाइट एन्कोडिंग या यूनिकोड का उपयोग करते समय स्ट्रिंग प्रतिनिधित्व बिट या बाइट के रूप में करता है।
अनुप्रयोग
रॉडिक्स ट्री सहयोगी एरे बनाने के लिए उपयोगी होते है जिन्हें स्ट्रिंग के रूप में व्यक्त किया जा सकता है। वह इंटरनेट प्रोटोकॉल के क्षेत्र में विशेष अनुप्रयोग प्रस्तुत करते है,[2][3][4] जहां कुछ मूल्यों की बड़ी श्रृंखला को सम्मलित करने की क्षमता विशेष रूप से आईपी एड्रेस के पदानुक्रमित संगठन के लिए उपयुक्त होती है।[5] इनका उपयोग सूचना पुनर्प्राप्ति में इंडेक्स के लिए भी किया जाता है।
संचालन
रॉडिक्स ट्री सम्मिलन, विलोपन का समर्थन करते है। संग्रहीत डेटा की मात्रा को कम करने का प्रयास करते समय यह ट्री में एक नई स्ट्रिंग को जोड़ता है। विलोपन ट्री से एक स्ट्रिंग को हटा देता है। जाँच कार्यों में त्रुटिहीन अवलोकन और प्रेफ्फिस के साथ सभी स्ट्रिंग को प्रस्तुत करना सम्मलित होता है (लेकिन आवश्यक नहीं कि यह इन्हीं तक सीमित हो)। यह सभी संचालन O(k) होते है जहां k सेट में सभी स्ट्रिंग्स की अधिकतम लंबाई होती है, जहां लंबाई रॉडिक्स ट्री के रॉडिक्स के बराबर बिट्स की मात्रा में मापी जाती है।
अवलोकन
अवलोकन संचालन यह निर्धारित करता है कि किसी ट्री में कोई स्ट्रिंग उपस्थित है या नहीं है। अधिकांश संचालन अपने विशिष्ट कार्यों को संभालने के लिए अवलोकन संचालन का उपयोग करते है। उदाहरण के लिए, वह नोड जहां एक स्ट्रिंग समाप्त होती है। यह संचालन प्रयासों के समान होते है, इसके अतिरिक्त कुछ किनारे कई आधारों का उपभोग करते है।
निम्नलिखित छद्म कोड मानता है कि इनमें विधियाँ और गुण उपस्थित होते है।
किनारा
- नोड लक्ष्यनोड
- स्ट्रिंग अंकित
नोड
- किनारों की एरे
- फ़ंक्शन लीफ () है
function lookup(string x)
{
// Begin at the root with no elements found
Node traverseNodeo:= root,
int elementsFoundo:= 0,
// Traverse until a leaf is found or it is not possible to continue
while (traverseNodes!= null && !traverseNode.isLeaf() && elementsFound < x.length)
{
// Get the next edge to explore based on the elements not yet found in x
Edge nextEdge := select edge from traverseNode.edges where edge.label is a prefix of x.suffix(elementsFound)
// x.suffix(elementsFound) returns the last (x.length - elementsFound) elements of x
// Was an edge found?
if (nextEdgei!= null)
{
// Set the next node to explore
traverseNode := nextEdge.targetNode,
// Increment elements found based on the label stored at the edge
elementsFound += nextEdge.label.length,
}
else
{
// Terminate loop
traverseNode := null,
}
}
// A match is found if we arrive at a leaf node and have used up exactly x.length elements
return (traverseNode
!= null && traverseNode.isLeaf() && elementsFound == x.length),
}
निवेशन
इस पॉइंट पर हम इनपुट स्ट्रिंग में अंकित किया गया एक नया बाहरी एज जोड़ते है, या यदि इसमे पहले से ही इनपुट स्ट्रिंग के साथ एक प्रेफ्फिस शेयर करने वाला बाहरी एज होता है, तो हम इसे दो किनारों में विभाजित करते है। यह विभाजन चरण यह सुनिश्चित करता है कि किसी भी नोड में संभावित स्ट्रिंग की तुलना में अधिक चाइल्ड नोड नहीं होते है।
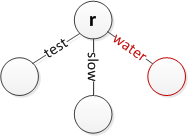
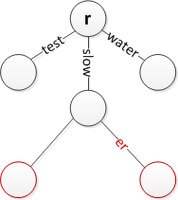
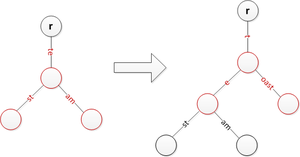
सम्मिलन के कई स्थितियां नीचे दिखाई गई है। ध्यान दें कि r केवल मूल का प्रतिनिधित्व करता है। यह माना जाता है कि जहां आवश्यक हो वहां स्ट्रिंग्स को समाप्त करने के लिए किनारों को खाली स्ट्रिंग्स के साथ अंकित किया जा सकता है। (खाली-स्ट्रिंग किनारों का उपयोग करते समय ऊपर वर्णित अवलोकन ऐल्गरिदम काम नहीं करता है।)
विलोपन
किसी ट्री से एक स्ट्रिंग x को हटाने के लिए, हम पहले x का प्रतिनिधित्व करने वाले लीफ का पता लगाते है। फिर, यह मानते हुए कि x उपस्थित है, हम संबंधित लीफ नोड को हटा देते है। यदि हमारे लीफ नोड के पास केवल एक अन्य चाइल्ड नोड होता है, तो उस चाइल्ड नोड का आने वाले नाम को हटा दिया जाता है।
अतिरिक्त संचालन
- सामान्य प्रेफ्फिस वाली सभी स्ट्रिंग्स प्राप्त होती है: समान प्रेफ्फिस से प्रारंभ होने वाली स्ट्रिंग्स की एक एरे लौटाता है।
- पूर्ववर्ती जाँचें: लेक्सिको ग्राफ क्रम के अनुसार, किसी दिए गए स्ट्रिंग से सबसे बड़ी स्ट्रिंग का पता लगाता है।
- सक्सेसर जाँचें: लेक्सिको ग्राफ क्रम के अनुसार, दी गई स्ट्रिंग से बड़ी सबसे छोटी स्ट्रिंग का पता लगाता है।
इतिहास
डेटासंरचना का आविष्कार 1968 में डोनाल्ड आर. मॉरिसन द्वारा किया गया था,[6] यह मुख्य रूप से गर्नोट ग्वेहेनबर्गर के साथ जुड़ा हुआ है।[7]
डोनाल्ड नुथ, कंप्यूटर प्रोग्रामिंग के खंड III में पृष्ठ 498-500 में, इन्हें पेट्रीसिया के ट्री कहते थे, संभवतः मॉरिसन के पेपर के शीर्षक में संक्षिप्त नाम के बाद: पेट्रीसिया कोडित सूचना पुनर्प्राप्त करने के लिए व्यावहारिक ऐल्गरिदम का उपयोग किया जाता है। आज, पेट्रीसिया प्रयासों को रॉडिक्स 2 के बराबर रॉडिक्स वाले ट्री के रूप में देखा जाता है, जिसका अर्थ होता है कि प्रत्येक बिट की तुलना व्यक्तिगत रूप से की जाती है और प्रत्येक नोड दो-तरफा (अर्थात, बाएं या दाएं) होते है।
अन्य डेटा संरचनाओं की तुलना
(निम्नलिखित तुलनाओं में, यह माना जाता है कि समाधान k लंबाई है और डेटा संरचना में n गुण है।)
संतुलित ट्री के विपरीत, रॉडिक्स ट्री ओ (लॉग एन) के अतिरिक्त ओ (के) समय में अवलोकन, सम्मिलन और विलोपन की अनुमति देते है। यह एक लाभ की तरह प्रतीत नहीं होता है, क्योंकि सामान्यतः k ≥ log n होता है, लेकिन एक संतुलित ट्री में हर तुलना एक स्ट्रिंग तुलना होती है जिसके लिए O(k) को सबसे कठिन स्थिति वाले समय की आवश्यकता होती है, जिनमें से कई लंबे सामान्य प्रेफ्फिस के कारण अभ्यास धीमे होते है। एक प्रयास में, सभी तुलनाओं के लिए निरंतर समय की आवश्यकता होती है, लेकिन लंबाई m की एक स्ट्रिंग को देखने के लिए m तुलना की आवश्यकता होती है। रॉडिक्स ट्री इन संचालनों को कम तुलनाओं के साथ कर सकते है, और बहुत कम नोड्स की आवश्यकता होती है।
चूंकि, रॉडिक्स ट्री प्रयासों के नुकसान को भी शेयर करते है: चूंकि उन्हें केवल आधारों की स्ट्रिंग के लिए कुशलतापूर्वक प्रतिवर्ती मैपिंग वाले आधारों पर ही प्रारंभ किया जा सकता है, इसलिए उनमें संतुलित जाँच ट्री की पूर्ण व्यापकता का अभाव होता होता है, जो कुल मिलाकर किसी भी डेटा प्रकार पर प्रारंभ होते है। अनुक्रम संतुलित ट्री के लिए आवश्यक कुल अनुक्रम तैयार करने के लिए स्ट्रिंग्स की प्रतिवर्ती मैपिंग का उपयोग किया जा सकता है। यह भी समस्याग्रस्त हो सकता है यदि डेटा प्रकार केवल इंटरफेस (कंप्यूटर विज्ञान) एक तुलना संचालन होता है, लेकिन (डी) क्रमांकन संचालन नहीं होता है।
सामान्यतः कहा जाता है कि हैश तालिकाओं में अपेक्षित O(1) सम्मिलन और विलोपन समय होता है, लेकिन यह केवल तभी सच है जब मुख्य के हैश की गणना को एक निरंतर-समय का संचालन माना जाता है। जब मुख्य की हैशिंग को ध्यान में रखा जाता है, तो हैश तालिकाओं में O(k) सम्मिलन और विलोपन समय की अपेक्षा की जाती है, इसके आधार पर इसमें अधिक समय लग सकता है। रॉडिक्स ट्री में सबसे कठिन स्थिति O(k) सम्मिलन और विलोपन की होती है। रॉडिक्स ट्री के सक्सेसर/पूर्ववर्ती संचालन भी हैश तालिकाओं द्वारा कार्यान्वित नहीं किए जाते है।
प्रकार
रॉडिक्स ट्री का एक सामान्य विस्तार नोड्स के दो रंगों, 'काले' और 'सफ़ेद' का उपयोग करता है। यह जांचने के लिए कि क्या दिया गया स्ट्रिंग ट्री में संग्रहीत है या नहीं है, जाँच ऊपर से प्रारंभ होती है और इनपुट स्ट्रिंग के किनारों का अनुसरण करती है। यदि जाँच स्ट्रिंग समाप्त हो जाती है और अंतिम नोड एक काला नोड होता है, तो यह जाँच विफल होने का संकेत देता है, यदि यह सफेद होता है, तो यह जाँच सफल होने का संकेत देता है। यह हमें सफेद नोड्स का उपयोग करके ट्री में एक सामान्य प्रेफ्फिस के साथ स्ट्रिंग की एक बड़ी श्रृंखला जोड़ने में सक्षम बनाता है, फिर काले नोड्स का उपयोग करके उन्हें कुशल विधि से एक छोटे सेट को हटा देता है।
'हैट ट्री' रॉडिक्स ट्री पर आधारित एक कैश-सचेत डेटा संरचना होती है जो कुशल स्ट्रिंग स्टॉरेज और पुनर्प्राप्ति और अनुक्रमित पुनरावृत्तियों को प्रस्तुत करता है। समय और स्थान दोनों के संबंध में हैश तालिका का तुलनीय प्रदर्शन होता है।[8][9]
पेट्रीसिया ट्री रॉडिक्स 2 (बाइनरी) ट्री का एक विशेष प्रकार होता है, जिसमें प्रत्येक मुख्य बिट को स्पष्ट रूप से संग्रहीत करने के अतिरिक्त, नोड्स केवल पहले बिट की स्थिति को संग्रहीत करते है जो दो ट्री को अलग करते है। ट्रैवर्सल के समय ऐल्गरिदम जाँच अनुक्रमित बिट की जांच करता है और उपयुक्त बाएं या दाएं ट्री को चुनता है। पेट्रीसिया ट्री की उल्लेखनीय विशेषताओं में यह सम्मलित है कि ट्री को संग्रहीत प्रत्येक अद्वितीय मुख्य नोड के लिए केवल एक नोड की आवश्यकता होती है, जो पेट्रीसिया को मानक बाइनरी ट्री की तुलना में अधिक सघन बनाता है। इसके अतिरिक्त, चूंकि वास्तविक समाधान स्पष्ट रूप से संग्रहीत नहीं होते है, तो मिलान की पुष्टि करने के लिए अनुक्रमित रिकॉर्ड पर एक पूर्ण मुख्य तुलना करना आवश्यक होता है। इस संबंध में पेट्रीसिया हैश तालिका का उपयोग करके अनुक्रमण के साथ एक निश्चित समानता होती है।[10]
रॉडिक्स ट्री नोड के आकार को एकीकृत करता है। सामान्य रॉडिक्स ट्री में एक बड़े स्थान का उपयोग होता है, क्योंकि यह हर स्तर पर एक स्थिर नोड आकार का उपयोग करता है। रॉडिक्स ट्री के अंतर्गत चाइल्ड आधारों की संख्या के आधार पर प्रत्येक नोड के लिए अंतर होता है। इसलिए, यह रॉडिक्स ट्री की गति को कम किए बिना उसका बेहतर उपयोग करता है।[11][12][13]
ऐसी स्थितियों में जहां डेटा सेट में एक मुख्य ट्री का प्रतिनिधित्व करते है। रॉडिक्स ट्री का यह संस्करण उस संस्करण की तुलना में उच्च स्थान दक्षता प्राप्त करता है जो केवल कम से कम दो चाइल्ड नोड के साथ आंतरिक नोड्स की अनुमति देता है।[14]
यह भी देखें
- उपसर्ग वृक्ष (जिसे ट्राइ के नाम से भी जाना जाता है)
- नियतात्मक चक्रीय परिमित अवस्था ऑटोमेटन (डीएएफएसए)
- टर्नरी खोज प्रयास करता है
- हैश ट्राई
- नियतात्मक परिमित ऑटोमेटा
- जूडी सरणी
- खोज एल्गोरिथ्म
- विस्तार योग्य हैशिंग
- हैश ऐरे मैप किया गया ट्राई
- उपसर्ग हैश ट्री
- बर्स्टसॉर्ट
- लुलेआ एल्गोरिथ्म
- हफ़मैन कोडिंग
बाहरी संबंध
- Algorithms and Data Structures Research & Reference Material: PATRICIA, by Lloyd Allison, Monash University
- Patricia Tree, NIST Dictionary of Algorithms and Data Structures
- Crit-bit trees, by Daniel J. Bernstein
- Radix Tree API in the Linux Kernel, by Jonathan Corbet
- Kart (key alteration radix tree), by Paul Jarc
- The Adaptive Radix Tree: ARTful Indexing for Main-Memory Databases, by Viktor Leis, Alfons Kemper, Thomas Neumann, Technical University of Munich
कार्यान्वयन
- FreeBSD कार्यान्वयन, पेजिंग, अग्रेषण और अन्य चीजों के लिए उपयोग किया जाता है।
- लिनक्स कर्नेल कार्यान्वयन, अन्य चीजों के अतिरिक्त पेज कैश के लिए उपयोग किया जाता है।
- GNU C++ मानक लाइब्रेरी में एक त्रि कार्यान्वयन है
- समवर्ती रॉडिक्स ट्री का जावा कार्यान्वयन, नियाल गैलाघेर द्वारा
- C# रॉडिक्स ट्री का कार्यान्वयन
- प्रैक्टिकल एल्गोरिथम टेम्प्लेट लाइब्रेरी, PATRICIA पर एक C++ लाइब्रेरी (VC++ >=2003, GCC G++ 3.x), रोमन एस. क्लुजकोव द्वारा
- पेट्रीसिया ट्री C++ टेम्पलेट क्लास कार्यान्वयन, राडू ग्रुइयन द्वारा
- हास्केल मानक पुस्तकालय कार्यान्वयन बड़े-एंडियन पेट्रीसिया ट्री पर आधारित। वेब-ब्राउज़ करने योग्य स्रोत कोड।
- जावा में पेट्रीसिया ट्री कार्यान्वयन, रोजर काप्सी और सैम बर्लिन द्वारा
- क्रिट-बिट ट्री डैनियल जे. बर्नस्टीन द्वारा सी कोड से लिया गया
- सी में पेट्रीसिया ट्री कार्यान्वयन, libcprops में
- पेट्रीसिया ट्रीज़: पूर्णांकों पर कुशल सेट और मानचित्र :fr:ऑब्जेक्टिव कैमल, जीन-क्रिस्टोफ़ फ़िलियाट्रे द्वारा
- रॉडिक्स डीबी (पेट्रीसिया ट्री) सी में कार्यान्वयन, जी. बी. वर्सियानी द्वारा
- लिबार्ट - सी में प्रारंभ अनुकूली रॉडिक्स ट्री, अन्य योगदानकर्ताओं के साथ आर्मोन डैडगर द्वारा (ओपन सोर्स, बीएसडी 3-क्लॉज लाइसेंस)
- क्रिट-बिट ट्री का निम कार्यान्वयन
- rax, साल्वाटोर सैनफिलिपो (REDIS के निर्माता) द्वारा ANSI C में एक रॉडिक्स ट्री कार्यान्वयन
- ↑ Morin, Patrick. "स्ट्रिंग्स के लिए डेटा संरचनाएँ" (PDF). Retrieved 15 April 2012.
- ↑ "rtfree(9)". www.freebsd.org. Retrieved 2016-10-23.
- ↑ The Regents of the University of California (1993). "/sys/net/radix.c". BSD Cross Reference. NetBSD. Retrieved 2019-07-25.
Routines to build and maintain radix trees for routing lookups.
- ↑ "Lockless, atomic and generic Radix/Patricia trees". NetBSD. 2011.
- ↑ Knizhnik, Konstantin. "Patricia Tries: A Better Index For Prefix Searches", Dr. Dobb's Journal, June, 2008.
- ↑ Morrison, Donald R. PATRICIA -- Practical Algorithm to Retrieve Information Coded in Alphanumeric
- ↑ G. Gwehenberger, Anwendung einer binären Verweiskettenmethode beim Aufbau von Listen. Elektronische Rechenanlagen 10 (1968), pp. 223–226
- ↑ Askitis, Nikolas; Sinha, Ranjan (2007). HAT-trie: A Cache-conscious Trie-based Data Structure for Strings. pp. 97–105. ISBN 1-920682-43-0.
{{cite book}}:|journal=ignored (help) - ↑ Askitis, Nikolas; Sinha, Ranjan (October 2010). "Engineering scalable, cache and space efficient tries for strings". The VLDB Journal. 19 (5): 633–660. doi:10.1007/s00778-010-0183-9.
- ↑ Morrison, Donald R. PATRICIA -- Practical Algorithm to Retrieve Information Coded in Alphanumeric
- ↑ Kemper, Alfons; Eickler, André (2013). Datenbanksysteme, Eine Einführung. Vol. 9. pp. 604–605. ISBN 978-3-486-72139-3.
- ↑ "armon/libart: Adaptive Radix Trees implemented in C". GitHub. Retrieved 17 September 2014.
- ↑ Viktor Leis; et al. (2013). "The adaptive radix tree: ARTful indexing for main-memory databases". IEEE 29th International Conference on Data Engineering (ICDE): 38–49. doi:10.1109/ICDE.2013.6544812.
- ↑ Can a node of Radix tree which represents a valid key have one child?