कम-घनत्व समता-जाँच कोड: Difference between revisions

Latest revision as of 12:04, 18 August 2023

सूचना सिद्धांत में, कम-घनत्व समता-जांच (एलडीपीसी) कोड एक रैखिक त्रुटि सुधार कोड है, जो एक ध्वनि संचरण चैनल पर एक संदेश प्रसारित करने की एक विधि है ^[1]^[2] एक एलडीपीसी कोड एक विरल टान्नर ग्राफ (द्विपक्षीय ग्राफ का उपवर्ग) का उपयोग करके बनाया गया है।^[3] एलडीपीसी कोड हैं:श्रेणी:क्षमता-अनुमोदन कोड|क्षमता-अनुमोदन कोड, जिसका अर्थ है कि व्यावहारिक निर्माण उपस्थित हैं जो एक सममित मेमोरी लेस चैनल के लिए ध्वनि सीमा को सैद्धांतिक अधिकतम (शैनन-हार्टले प्रमेय) के बहुत समीप सेट करने की अनुमति देते हैं। ध्वनि सीमा चैनल ध्वनि के लिए ऊपरी सीमा को परिभाषित करती है, जहां तक खोई हुई जानकारी की संभावना को इच्छानुसार छोटा किया जा सकता है। पुनरावृत्तीय विश्वास प्रसार तकनीकों का उपयोग करके, एलडीपीसी कोड को उनकी ब्लॉक लंबाई के रैखिक समय में डिकोड किया जा सकता है।

व्यर्थ ध्वनि की उपस्थिति में बैंडविड्थ-बाधित या रिटर्न-चैनल-बाधित लिंक पर विश्वसनीय और अत्यधिक कुशल सूचना हस्तांतरण की आवश्यकता वाले एप्लीकेशन में एलडीपीसी कोड का उपयोग बढ़ रहा है। एलडीपीसी कोड का कार्यान्वयन अन्य कोड, विशेषकर टर्बो कोड से पिछड़ गया है। टर्बो कोड के लिए मौलिक पेटेंट 29 अगस्त 2013 को समाप्त हो गया।^[4]^[5]

एलडीपीसी कोड को रॉबर्ट जी गैलगर के सम्मान में गैलगर कोड के रूप में भी जाना जाता है, जिन्होंने 1960 में मैसाचुसेट्स की तकनीकी संस्था में अपने डॉक्टरेट शोध प्रबंध में एलडीपीसी अवधारणा विकसित की थी।^[6]^[7] एलडीपीसी कोड में आदर्श संयोजन गुण भी दिखाए गए हैं। अपने शोध प्रबंध में, गैलागर ने दिखाया कि एलडीपीसी कोड उच्च संभावना वाले बाइनरी क्षेत्रों पर रैखिक कोड के लिए बाध्य गिल्बर्ट-वार्शमोव को प्राप्त करते हैं। 2020 में यह दिखाया गया कि गैलेजर के एलडीपीसी कोड सूची डिकोडिंग क्षमता प्राप्त करते हैं और सामान्य क्षेत्रों पर रैखिक कोड के लिए बाध्य गिल्बर्ट-वार्शमोव भी प्राप्त करते हैं। ^[8]

इतिहास

1963 में रॉबर्ट जी. गैलागर द्वारा पहली बार विकसित होने पर इसे प्रयुक्त करना अव्यावहारिक था।^[9] 1996 में उनका काम दोबारा खोजे जाने तक एलडीपीसी कोड भुला दिए गए थे।^[10] टर्बो कोड, 1993 में खोजे गए क्षमता-अनुरूप कोड का एक और वर्ग, 1990 के दशक के अंत में पसंद की कोडिंग योजना बन गया, जिसका उपयोग डीप स्पेस नेटवर्क और उपग्रह संचार जैसे एप्लीकेशन के लिए किया जाता था। चूँकि, कम-घनत्व समता-जाँच कोड में प्रगति ने उन्हें त्रुटि स्तर और उच्च कोड दर सीमा में प्रदर्शन के स्थिति में टर्बो कोड से आगे निकलते देखा है, जिससे टर्बो कोड केवल कम कोड दरों के लिए उत्तम अनुकूल हो गए हैं।^[11]

एप्लीकेशन

2003 में, एक रिपीट-एक्युमुलेट कोड या इररेगुलर रिपीट एक्युमुलेट कोड्स (आईआरए) स्टाइल एलडीपीसी कोड छह टर्बो कोड को पराजित करके डिजिटल टेलीविजन के लिए नए डीवीबी-एस 2 मानक में त्रुटि-सुधार करने वाला कोड बन गया।^[12] डीवीबी-S2 चयन समिति ने समानांतर डिकोडर आर्किटेक्चर के अतिरिक्त बहुत कम कुशल सीरियल डिकोडर आर्किटेक्चर का उपयोग करके टर्बो कोड प्रस्तावों के लिए डिकोडर कॉम्प्लेक्सिटी अनुमान लगाया। इसने टर्बो कोड प्रस्तावों को एलडीपीसी प्रस्तावों के आधे फ्रेम आकार के क्रम पर फ्रेम आकार का उपयोग करने के लिए विविश किया था।

2008 में, एलडीपीसी ने ITU-T G.hn मानक के लिए फॉरवर्ड त्रुटि सुधार (एफईसी) प्रणाली के रूप में कन्वेन्शनल टर्बो कोड को पराजित करते है।^[13] G.hn ने टर्बो कोड की तुलना में एलडीपीसी कोड को उनकी कम डिकोडिंग कॉम्प्लेक्सिटी के कारण चुना (विशेषकर जब 1.0 Gbit/s के समीप डेटा दरों पर काम कर रहा हो) और क्योंकि प्रस्तावित टर्बो कोड ने ऑपरेशन की वांछित सीमा पर एक महत्वपूर्ण त्रुटि स्तर प्रदर्शित किया था।^[14]

एलडीपीसी कोड का उपयोग 10GBASE-T ईथरनेट के लिए भी किया जाता है, जो ट्विस्टेड-पेयर केबल पर 10 गीगाबिट प्रति सेकंड पर डेटा भेजता है। 2009 तक, हाई थ्रूपुट (HT) पीएचवाई विनिर्देश में, एलडीपीसी कोड 802.11n और 802.11ac के वैकल्पिक भाग के रूप में वाई-फाई 802.11 मानक का भी भाग हैं।^[15] एलडीपीसी 802.11ax (वाई-फाई 6) का एक अनिवार्य भाग है।^[16]

कुछ ओएफडीएम प्रणाली एक अतिरिक्त बाहरी त्रुटि सुधार जोड़ते हैं जो कभी-कभी होने वाली त्रुटियों (त्रुटि स्तर) को ठीक करता है जो कम बिट त्रुटि दर पर भी एलडीपीसी सुधार आंतरिक कोड से आगे निकल जाता है।

उदाहरण के लिए: एलडीपीसी कोडेड मॉड्यूलेशन (आरएस-एलसीएम) के साथ रीड-सोलोमन कोड रीड-सोलोमन बाहरी कोड का उपयोग करता है।^[17] डीवीबी-S2, डीवीबी-T2 और डीवीबी-C2 मानक सभी एलडीपीसी डिकोडिंग के बाद अवशिष्ट त्रुटियों को मिटाने के लिए BCH कोड बीसीएच कोड का उपयोग करते हैं।^[18]

5जी नं नियंत्रण चैनलों के लिए पोलर कोड (कोडिंग सिद्धांत) और डेटा चैनलों के लिए एलडीपीसी का उपयोग करता है।^[19]^[20]

यद्यपि एलडीपीसी कोड को वाणिज्यिक हार्ड डिस्क ड्राइव में सफलता मिली है, एसएसडी में इसकी त्रुटि सुधार क्षमता का पूरी तरह से लाभ उठाने के लिए अपरंपरागत समीप फ्लैश मेमोरी सेंसिंग की आवश्यकता होती है, जिससे मेमोरी रीड विलंबता में वृद्धि होती है। एलडीपीसी-इन-एसएसडी^[21] बहुत कम विलंबता वृद्धि के साथ एसएसडी में एलडीपीसी को तैनात करने का एक प्रभावी विधि है, जो एसएसडी में एलडीपीसी को वास्तविकता में बदल देता है। तब से, एलडीपीसी को प्रमुख संचयन विक्रेताओं द्वारा ग्राहक-ग्रेड और एंटरप्राइज़-ग्रेड दोनों में वाणिज्यिक एसएसडी में व्यापक रूप से अपनाया गया है। कई टीएलसी (और बाद के) एसएसडी एलडीपीसी कोड का उपयोग कर रहे हैं। सबसे पहले एक तेज़ हार्ड-डिकोड (बाइनरी इरेज़र) का प्रयास किया जाता है, जो धीमी किंतु अधिक शक्तिशाली सॉफ्ट डिकोडिंग में वापस आ सकता है।^[22]

परिचालन उपयोग

एलडीपीसी कोड कार्यात्मक रूप से विरल समता-जांच आव्यूह द्वारा परिभाषित किए जाते हैं। यह विरल आव्यूह अधिकांशतः यादृच्छिक रूप से उत्पन्न होता है, विरलता बाधाओं के अधीन - एलडीपीसी कोड निर्माण पर बाद में चर्चा की जाती है। ये कोड पहली बार 1960 में रॉबर्ट गैलागर द्वारा डिज़ाइन किए गए थे।^[7]

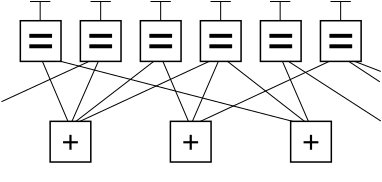
नीचे फ़ॉर्नी के फ़ैक्टर ग्राफ़ नोटेशन का उपयोग करते हुए एक उदाहरण एलडीपीसी कोड का ग्राफ़ टुकड़ा दिया गया है। इस ग्राफ़ में, ग्राफ़ के शीर्ष में n वैरिएबल नोड्स ग्राफ़ के निचले भाग में (n−k) बाधा नोड्स से जुड़े हुए हैं।

यह (n , k) एलडीपीसी कोड को ग्राफ़िक रूप से प्रस्तुत करने का एक लोकप्रिय विधि है। एक वैध संदेश के बिट्स, जब ग्राफ़ के शीर्ष पर 'T's' पर रखे जाते हैं, तो ग्राफिकल बाधाओं को पूरा करते हैं। विशेष रूप से, एक वेरिएबल नोड ('=' चिन्ह वाला बॉक्स) से जुड़ने वाली सभी पंक्तियों का मान समान होता है, और कारक नोड ('+' चिन्ह वाला बॉक्स) से जुड़ने वाले सभी मानों का योग, मॉड्यूलर अंकगणित दो, शून्य तक होना चाहिए (दूसरे शब्दों में, उन्हें एक सम संख्या में योग करना चाहिए; या विषम मानों की एक सम संख्या होनी चाहिए)।

छवि से बाहर जाने वाली किसी भी लाइन को अनदेखा करते हुए, वैध कोडवर्ड के अनुरूप आठ संभावित छह-बिट स्ट्रिंग हैं: (अथार्थ , 000000, 011001, 110010, 101011, 111100, 100101, 001110, 010111)। यह एलडीपीसी कोड खंड छह बिट्स के रूप में एन्कोडेड तीन-बिट संदेश का प्रतिनिधित्व करता है। चैनल त्रुटियों से उबरने की संभावना बढ़ाने के लिए, यहां अतिरेक का उपयोग किया जाता है। यह एक (6, 3) रैखिक कोड है, जिसमें n = 6 और k = 3 है।

चित्र से बाहर जाने वाली रेखाओं को फिर से अनदेखा करते हुए, समता-जाँच आव्यूह इस ग्राफ़ खंड का प्रतिनिधित्व करता है

\mathbf {H} ={\begin{pmatrix}1&1&1&1&0&0\\0&0&1&1&0&1\\1&0&0&1&1&0\\\end{pmatrix}}.

इस आव्यूह में, प्रत्येक पंक्ति तीन समता-जांच बाधाओं में से एक का प्रतिनिधित्व करती है, जबकि प्रत्येक स्तम्भ प्राप्त कोडवर्ड में छह बिट्स में से एक का प्रतिनिधित्व करता है।

इस उदाहरण में, जीएफ(2) में मूलभूत पंक्ति संचालन के माध्यम से समता-जांच आव्यूह H को इस फॉर्म ${\begin{bmatrix}-P^{T}|I_{n-k}\end{bmatrix}}$ में डालकर आठ कोडवर्ड प्राप्त किए जा सकते हैं:

\mathbf {H} ={\begin{pmatrix}1&1&1&1&0&0\\0&0&1&1&0&1\\1&0&0&1&1&0\\\end{pmatrix}}_{1}\sim {\begin{pmatrix}1&1&1&1&0&0\\0&0&1&1&0&1\\0&1&1&0&1&0\\\end{pmatrix}}_{2}\sim {\begin{pmatrix}1&1&1&1&0&0\\0&1&1&0&1&0\\0&0&1&1&0&1\\\end{pmatrix}}_{3}\sim {\begin{pmatrix}1&1&1&1&0&0\\0&1&1&0&1&0\\1&1&0&0&0&1\\\end{pmatrix}}_{4}.

चरण 1: एच.

चरण 2: पंक्ति 1 को पंक्ति 3 में जोड़ा जाता है।

चरण 3: पंक्ति 2 और 3 की अदला-बदली की जाती है।

चरण 4: पंक्ति 1 को पंक्ति 3 में जोड़ा जाता है।

इससे, जनरेटर आव्यूह G को ${\begin{bmatrix}I_{k}|P\end{bmatrix}}$ के रूप में प्राप्त किया जा सकता है (ध्यान दें कि विशेष स्थिति में यह एक बाइनरी कोड $P=-P$ है), या विशेष रूप से:

\mathbf {G} ={\begin{pmatrix}1&0&0&1&0&1\\0&1&0&1&1&1\\0&0&1&1&1&0\\\end{pmatrix}}.

अंत में, सभी आठ संभावित 3-बिट स्ट्रिंग्स को G से गुणा करने पर, सभी आठ वैध कोडवर्ड प्राप्त होते हैं। उदाहरण के लिए, बिट-स्ट्रिंग '101' के लिए कोडवर्ड इसके द्वारा प्राप्त किया जाता है:

{\begin{pmatrix}1&0&1\\\end{pmatrix}}\odot {\begin{pmatrix}1&0&0&1&0&1\\0&1&0&1&1&1\\0&0&1&1&1&0\\\end{pmatrix}}={\begin{pmatrix}1&0&1&0&1&1\\\end{pmatrix}}

,

जहाँ $\odot$ मॉड 2 गुणन का प्रतीक है।

जाँच के रूप में, G की पंक्ति का स्थान H के लिए ओर्थोगोनल है जैसे कि $G\odot H^{T}=0$

बिट-स्ट्रिंग '101' कोडवर्ड '101011' के पहले 3 बिट्स के रूप में पाई जाती है।

उदाहरण एन्कोडर

एलडीपीसी एनकोडर

एक फ्रेम के एन्कोडिंग के समय , इनपुट डेटा बिट्स (डी) को दोहराया जाता है और कांस्टीटुएंट एन्कोडर्स के एक सेट में वितरित किया जाता है। कांस्टीटुएंट एनकोडर समान्यत: संचायक होते हैं और प्रत्येक संचायक का उपयोग समता प्रतीक उत्पन्न करने के लिए किया जाता है। मूल डेटा की एक प्रति (S_0,K-1) कोड प्रतीकों को बनाने के लिए समता बिट्स (पी) के साथ प्रेषित होता है। प्रत्येक कांस्टीटुएंट एनकोडर से एस बिट्स को हटा दिया जाता है।

समता बिट का उपयोग किसी अन्य कांस्टीटुएंट कोड के अंदर किया जा सकता है।

डीवीबी-S2 रेट 2/3 कोड का उपयोग करते हुए एक उदाहरण में एन्कोडेड ब्लॉक का आकार 64800 प्रतीक (N=64800) है जिसमें 43200 डेटा बिट्स (K=43200) और 21600 पैरिटी बिट्स (M=21600) हैं। प्रत्येक कांस्टीटुएंट कोड (चेक नोड) पहले समता बिट को छोड़कर 16 डेटा बिट्स को एनकोड करता है जो 8 डेटा बिट्स को एनकोड करता है। पहले 4680 डेटा बिट्स को 13 बार दोहराया जाता है (13 समता कोड में उपयोग किया जाता है), जबकि शेष डेटा बिट्स 3 समता कोड (अनियमित एलडीपीसी कोड) में उपयोग किया जाता है।

तुलना के लिए, क्लासिक टर्बो कोड समान्यत: समानांतर में कॉन्फ़िगर किए गए दो कांस्टीटुएंट कोड का उपयोग करते हैं, जिनमें से प्रत्येक डेटा बिट्स के संपूर्ण इनपुट ब्लॉक (K) को एन्कोड करता है। ये कांस्टीटुएंट एनकोडर मध्यम गहराई (8 या 16 स्थिति) के पुनरावर्ती कन्वेन्शनल कोड (आरएससी) हैं जो एक कोड इंटरलीवर द्वारा अलग किए जाते हैं जो फ्रेम की एक प्रति को इंटरलीव करता है।

इसके विपरीत, एलडीपीसी कोड, समानांतर में कई कम गहराई वाले कांस्टीटुएंट कोड (संचायक) का उपयोग करता है, जिनमें से प्रत्येक इनपुट फ्रेम के केवल एक छोटे भाग को एन्कोड करता है। कई कांस्टीटुएंट कोडों को कई कम गहराई (2 स्थिति ) कन्वेन्शनल कोड के रूप में देखा जा सकता है जो दोहराव और वितरण संचालन के माध्यम से जुड़े हुए हैं। दोहराव और वितरण ऑपरेशन टर्बो कोड में इंटरलीवर का कार्य करते हैं।

विभिन्न कांस्टीटुएंट कोडों के कनेक्शन को अधिक स्पष्ट रूप से प्रबंधित करने की क्षमता और प्रत्येक इनपुट बिट के लिए अतिरेक का स्तर एलडीपीसी कोड के डिजाइन में अधिक लचीलापन देता है, जिससे कुछ स्थिति में टर्बो कोड की तुलना में उत्तम प्रदर्शन हो सकता है। टर्बो कोड अभी भी कम कोड दरों पर एलडीपीसी से उत्तम प्रदर्शन करते प्रतीत होते हैं, या कम से कम अच्छा प्रदर्शन करने वाले कम दर कोड का डिज़ाइन टर्बो कोड के लिए आसान है।

व्यावहारिक रूप में, संचायक बनाने वाले हार्डवेयर को एन्कोडिंग प्रक्रिया के समय पुन: उपयोग किया जाता है। अर्थात्, एक बार समता बिट्स का पहला सेट उत्पन्न हो जाता है और समता बिट्स संग्रहीत हो जाते हैं, उसी संचायक हार्डवेयर का उपयोग समता बिट्स का अगला सेट उत्पन्न करने के लिए किया जाता है।

डिकोडिंग

अन्य कोडों की तरह, बाइनरी सममित चैनल पर एलडीपीसी कोड की अधिकतम संभावना डिकोडिंग एक एनपी-पूर्ण समस्या है। किसी भी उपयोगी आकार के एनपी-पूर्ण कोड के लिए इष्टतम डिकोडिंग करना व्यावहारिक नहीं है।

चूँकि , पुनरावृत्तीय विश्वास प्रसार डिकोडिंग पर आधारित उप-इष्टतम तकनीकें उत्कृष्ट परिणाम देती हैं और इन्हें व्यावहारिक रूप से प्रयुक्त किया जा सकता है। उप-इष्टतम डिकोडिंग तकनीक प्रत्येक समता जांच को देखती है जो एलडीपीसी को एक स्वतंत्र एकल समता जांच (एसपीसी) कोड के रूप में बनाती है। प्रत्येक एसपीसी कोड को सॉफ्ट-इन सॉफ्ट-आउट डिकोडर या सॉफ्ट-इन-सॉफ्ट-आउट (एसआईएसओ) तकनीकों जैसे सॉफ्ट आउटपुट विटर्बी एल्गोरिदम, बीसीजेआर एल्गोरिदम, मैक्सिमम ए पोस्टीरियरी अनुमान और उसके अन्य व्युत्पन्न का उपयोग करके अलग से डिकोड किया जाता है। प्रत्येक एसआईएसओ डिकोडिंग से सरल निर्णय जानकारी को क्रॉस-चेक किया जाता है और उसी सूचना बिट के अन्य अनावश्यक एसपीसी डिकोडिंग के साथ अपडेट किया जाता है। प्रत्येक एसपीसी कोड को अपडेट सॉफ्ट निर्णय जानकारी का उपयोग करके फिर से डिकोड किया जाता है। यह प्रक्रिया तब तक दोहराई जाती है जब तक कि एक वैध कोडवर्ड प्राप्त न हो जाए या डिकोडिंग समाप्त न हो जाए। इस प्रकार की डिकोडिंग को अधिकांशतः सम-प्रोडक्ट डिकोडिंग के रूप में जाना जाता है।

एसपीसी कोड की डिकोडिंग को अधिकांशतः चेक नोड प्रोसेसिंग के रूप में जाना जाता है, और वेरिएबल्स की क्रॉस-चेकिंग को अधिकांशतः वेरिएबल-नोड प्रोसेसिंग के रूप में जाना जाता है।

व्यावहारिक एलडीपीसी डिकोडर कार्यान्वयन में, थ्रूपुट बढ़ाने के लिए एसपीसी कोड के सेट को समानांतर में डिकोड किया जाता है।

इसके विपरीत, बाइनरी इरेज़र चैनल पर विश्वास का प्रसार विशेष रूप से सरल है जहां इसमें पुनरावृत्त बाधा संतुष्टि सम्मिलित है।

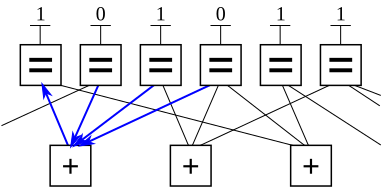
उदाहरण के लिए, मान लें कि उपरोक्त उदाहरण से मान्य कोडवर्ड, 101011, एक बाइनरी इरेज़र चैनल में प्रसारित होता है और ?01?11 प्राप्त करने के लिए पहले और चौथे बिट को मिटाकर प्राप्त किया जाता है। चूंकि प्रेषित संदेश को कोड की बाधाओं को पूरा करना होगा, इसलिए संदेश को कारक ग्राफ़ के शीर्ष पर प्राप्त संदेश लिखकर दर्शाया जा सकता है।

इस उदाहरण में, पहला बिट अभी भी पुनर्प्राप्त नहीं किया जा सकता है, क्योंकि इससे जुड़े सभी अवरोधों में एक से अधिक अज्ञात बिट हैं। संदेश को डिकोड करने के लिए आगे बढ़ने के लिए, मिटाए गए बिट्स में से केवल एक से कनेक्ट होने वाली बाधाओं की पहचान की जानी चाहिए। इस उदाहरण में, केवल दूसरा अवरोध ही पर्याप्त है। दूसरे अवरोध की जांच करने पर, चौथा बिट शून्य रहा होगा, क्योंकि उस स्थिति में केवल एक शून्य ही अवरोध को संतुष्ट करेगा।

फिर यह प्रक्रिया दोहराई जाती है चौथे बिट के लिए नया मान अब पहले बिट को पुनर्प्राप्त करने के लिए पहले बाधा के साथ संयोजन में उपयोग किया जा सकता है जैसा कि नीचे देखा गया है। इसका अर्थ यह है कि पहला बिट सबसे बाईं ओर की बाधा को पूरा करने वाला होना चाहिए।

इस प्रकार, संदेश को पुनरावृत्त रूप से डिकोड किया जा सकता है। अन्य चैनल मॉडल के लिए, वेरिएबल नोड्स और चेक नोड्स के बीच पारित संदेश वास्तविक संख्याएं हैं, जो विश्वास की संभावनाओं और संभावनाओं को व्यक्त करते हैं।

इस परिणाम को समता-जांच आव्यूह H द्वारा सही कोडवर्ड r को गुणा करके मान्य किया जा सकता है:

\mathbf {z} =\mathbf {H\odot r} ={\begin{pmatrix}1&1&1&1&0&0\\0&0&1&1&0&1\\1&0&0&1&1&0\\\end{pmatrix}}\odot {\begin{pmatrix}1\\0\\1\\0\\1\\1\\\end{pmatrix}}={\begin{pmatrix}0\\0\\0\\\end{pmatrix}}.

चूँकि इस ऑपरेशन का परिणाम z (डिकोडिंग विधियाँ या सिंड्रोम डिकोडिंग) तीन × एक शून्य वेक्टर है, परिणामी कोडवर्ड r सफलतापूर्वक मान्य है।

डिकोडिंग पूरी होने के बाद, कोडवर्ड के पहले 3 बिट्स को देखकर मूल संदेश बिट्स '101' निकाला जा सकता है।

उदाहरणात्मक होते हुए भी, यह इरेज़र उदाहरण सॉफ्ट-डिसीजन डिकोडिंग या सॉफ्ट-डिसीजन संदेश पासिंग का उपयोग नहीं दिखाता है, जिसका उपयोग लगभग सभी वाणिज्यिक एलडीपीसी डिकोडर्स में किया जाता है।

नोड जानकारी अपडेट करना

वर्तमान के वर्षों में, वैरिएबल-नोड और बाधा-नोड अपडेट के लिए वैकल्पिक शेड्यूल के प्रभावों का अध्ययन करने में भी अधिक काम किया गया है। एलडीपीसी कोड को डिकोड करने के लिए जिस मूल तकनीक का उपयोग किया गया था उसे बाढ़ के रूप में जाना जाता था। इस प्रकार के अपडेट के लिए आवश्यक है कि, एक चर नोड को अपडेट करने से पहले, सभी बाधा नोड्स को अपडेट करने की आवश्यकता हो और इसके विपरीत विला कैसाडो एट अल द्वारा बाद के काम में,^[23] वैकल्पिक अपडेट तकनीकों का अध्ययन किया गया, जिसमें परिवर्तनीय नोड्स को नवीनतम उपलब्ध चेक-नोड जानकारी के साथ अपडेट किया जाता है।

इन एल्गोरिदम के पीछे अंतर्ज्ञान यह है कि वेरिएबल नोड्स जिनके मान सबसे अधिक भिन्न होते हैं, उन्हें पहले अपडेट करने की आवश्यकता होती है। अत्यधिक विश्वसनीय नोड्स, जिनका लॉग-संभावना अनुपात (एलएलआर) परिमाण बड़ा है और एक अपडेट से दूसरे अपडेट में महत्वपूर्ण रूप से नहीं बदलता है, उन्हें अन्य नोड्स के समान आवृत्ति के साथ अपडेट की आवश्यकता नहीं होती है, जिनके संकेत और परिमाण में अधिक व्यापक रूप से उतार-चढ़ाव होता है।

ये शेड्यूलिंग एल्गोरिदम बाढ़ का उपयोग करने वाले एल्गोरिदम की तुलना में अभिसरण की अधिक गति और कम त्रुटि वाले फर्श दिखाते हैं। ये निचली त्रुटि मंजिलें सूचित गतिशील शेड्यूलिंग (आईडीएस) की क्षमता से हासिल की जाती हैं^[23] निकट कोडवर्ड के अधिकृत करने वाले सेटों पर नियंत्रण पाने के लिए एल्गोरिदम है ।^[24]

जब गैर-फ्शेलूडिंग ड्यूलिंग एल्गोरिदम का उपयोग किया जाता है, तो पुनरावृत्ति की एक वैकल्पिक परिभाषा का उपयोग किया जाता है। दर k/n के (n,k) एलडीपीसी कोड के लिए, एक पूर्ण पुनरावृत्ति तब होती है जब n चर और n − k बाधा नोड्स को अपडेट किया गया है, इससे कोई अंतर नहीं पड़ता कि वे किस क्रम में अपडेट किए गए थे।

कोड निर्माण

बड़े ब्लॉक आकारों के लिए, एलडीपीसी कोड समान्यत: पहले डिकोडर्स के व्यवहार का अध्ययन करके बनाए जाते हैं। चूंकि ब्लॉक का आकार अनंत तक जाता है, एलडीपीसी डिकोडर्स को एक ध्वनि सीमा दिखाई जा सकती है जिसके नीचे डिकोडिंग विश्वसनीय रूप से प्राप्त की जाती है, और जिसके ऊपर डिकोडिंग प्राप्त नहीं की जाती है,^[25] बोलचाल की भाषा में इसे क्लिफ इफ़ेक्ट कहा जाता है। इस सीमा को चेक नोड्स से आर्क और वेरिएबल नोड्स से आर्क का सर्वोत्तम अनुपात खोजकर अनुकूलित किया जा सकता है। इस सीमा को देखने के लिए एक अनुमानित ग्राफिकल दृष्टिकोण एक EXIT चार्ट है।

इस अनुकूलन के बाद एक विशिष्ट एलडीपीसी कोड का निर्माण दो मुख्य प्रकार की तकनीकों में आता है:

छद्म यादृच्छिक दृष्टिकोण
संयुक्त दृष्टिकोण

छद्म-यादृच्छिक दृष्टिकोण द्वारा निर्माण सैद्धांतिक परिणामों पर आधारित होता है, जो बड़े ब्लॉक आकार के लिए, एक यादृच्छिक निर्माण अच्छा डिकोडिंग प्रदर्शन देता है।^[10] सामान्य रूप से, छद्म यादृच्छिक कोड में काम्प्लेक्स एनकोडर होते हैं, किंतु सर्वोत्तम डिकोडर वाले छद्म यादृच्छिक कोड में सरल एनकोडर हो सकते हैं।^[26] यह सुनिश्चित करने में सहायता के लिए अधिकांशतः विभिन्न बाधाएं प्रयुक्त की जाती हैं कि अनंत ब्लॉक आकार की सैद्धांतिक सीमा पर अपेक्षित वांछित गुण एक सीमित ब्लॉक आकार पर होते हैं।

कॉम्बिनेटोरियल दृष्टिकोण का उपयोग छोटे ब्लॉक-आकार के एलडीपीसी कोड के गुणों को अनुकूलित करने या सरल एनकोडर के साथ कोड बनाने के लिए किया जा सकता है।

कुछ एलडीपीसी कोड रीड-सोलोमन कोड पर आधारित होते हैं, जैसे 10 गीगाबिट ईथरनेट मानक में उपयोग किया जाने वाला आरएस-एलडीपीसी कोड^[27] व्यवस्थित रूप से उत्पन्न एलडीपीसी कोड की तुलना में, संरचित एलडीपीसी कोड - जैसे कि डीवीबी-एस 2 मानक में प्रयुक्त एलडीपीसी कोड - में सरल और इसलिए कम निवेश वाले हार्डवेयर हो सकते हैं - विशेष रूप से, कोड ऐसे निर्मित होते हैं कि एच आव्यूह एक आव्यूह सर्कुलर आव्यूह है।^[28]

एलडीपीसी कोड बनाने का एक अन्य विधि परिमित ज्यामिति का उपयोग करना है। यह विधि 2001 में वाई. कोउ एट अल द्वारा प्रस्तावित की गई थी।^[29]

एलडीपीसी कोड बनाम टर्बो कोड

एलडीपीसी कोड की तुलना अन्य शक्तिशाली कोडिंग योजनाओं से की जा सकती है, जैसे टर्बो कोड.^[30] एक ओर, टर्बो कोड की बिट त्रुटि दर प्रदर्शन कम कोड सीमाओं से प्रभावित होती है।^[31] एलडीपीसी कोड में न्यूनतम दूरी की कोई सीमा नहीं है,^[32] इसका अप्रत्यक्ष अर्थ यह है कि एलडीपीसी कोड टर्बो कोड की तुलना में अपेक्षाकृत बड़ी कोड दरों (जैसे 3/4, 5/6, 7/8) पर अधिक कुशल हो सकते हैं। चूँकि एलडीपीसी कोड पूर्ण प्रतिस्थापन नहीं हैं: टर्बो कोड कम कोड दरों (जैसे 1/6, 1/3, 1/2) पर सबसे अच्छा समाधान हैं।^[33]^[34]

यह भी देखें

लोग

रिचर्ड हैमिंग
क्लाउड शैनन
डेविड जे.सी. मैके
इरविंग एस रीड
माइकल लुबी

सिद्धांत

अनुप्रयोग

जी.एचएन या जी.एचएन/जी.9960 (बिजली लाइनों, फोन लाइनों और समाक्षीय केबल पर नेटवर्किंग के लिए आईटीयू-टी मानक)
802.3an या 10GBASE-T (ट्विस्टेड पेयर पर 10 गीगाबिट/सेकेंड ईथरनेट)
सीएमएमबी (चीन मल्टीमीडिया मोबाइल ब्रॉडकास्टिंग)
डीवीबी-S2 / डीवीबी-T2 / डीवीबी-C2 (डिजिटल वीडियो प्रसारण, दूसरी पीढ़ी)
डीएमबी-टी/एच (डिजिटल वीडियो प्रसारण)^[35]
वाइमैक्स (माइक्रोवेव संचार के लिए आईईईई 802.16e मानक)
आईईईई 802.11n-2009 (वाई-फ़ाई मानक)
डॉक्सिस 3.1
एटीएससी 3.0 (अगली पीढ़ी उत्तरी अमेरिका डिजिटल स्थलीय प्रसारण)
3जीपीपी (5जी-एनआर डेटा चैनल)

अन्य क्षमता-अनुरूप कोड

टर्बो कोड
क्रमिक संयोजित कन्वेन्शनल कोड
ऑनलाइन कोड
फव्वारा कोड
एलटी कोड
रैप्टर कोड
दोहराएँ-संचित कोड (सरल टर्बो कोड का एक वर्ग)
बवंडर कोड (बाइनरी इरेज़र चैनल के लिए डिज़ाइन किए गए एलडीपीसी कोड)
ध्रुवीय कोड (कोडिंग सिद्धांत)

संदर्भ

↑ David J.C. MacKay (2003) Information theory, Inference and Learning Algorithms, CUP, ISBN 0-521-64298-1, (also available online)
↑ Todd K. Moon (2005) Error Correction Coding, Mathematical Methods and Algorithms. Wiley, ISBN 0-471-64800-0 (Includes code)
↑ Amin Shokrollahi (2003) LDPC Codes: An Introduction
↑ US 5446747
↑ NewScientist, Communication speed nears terminal velocity, by Dana Mackenzie, 9 July 2005
↑ Larry Hardesty (January 21, 2010). "Explained: Gallager codes". MIT News. Retrieved August 7, 2013.
↑ ^7.0 ^7.1 [1] R. G. Gallager, "Low density parity check codes," IRE Trans. Inf. Theory, vol. IT-8, no. 1, pp. 21- 28, Jan. 1962.
↑ [2] J. Moshieff, N. Resch, N. Ron-Zewi, S. Silas, M. Wootters, "Low-density parity-check codes achieve list-decoding capacity," SIAM Journal on Computing, FOCS20-38-FOCS20-73.
↑ Robert G. Gallager (1963). कम घनत्व समता जाँच कोड (PDF). Monograph, M.I.T. Press. Retrieved August 7, 2013.
↑ ^10.0 ^10.1 David J.C. MacKay and Radford M. Neal, "Near Shannon Limit Performance of Low Density Parity Check Codes," Electronics Letters, July 1996
↑ Telemetry Data Decoding, Design Handbook
↑ Presentation by Hughes Systems Archived 2006-10-08 at the Wayback Machine
↑ HomePNA Blog: G.hn, a PHY For All Seasons
↑ IEEE Communications Magazine paper on G.hn Archived 2009-12-13 at the Wayback Machine
↑ IEEE Standard, section 20.3.11.6 "802.11n-2009", IEEE, October 29, 2009, accessed March 21, 2011.
↑ "IEEE SA - IEEE 802.11ax-2021". IEEE Standards Association (in English). Retrieved 22 May 2022.
↑ Chih-Yuan Yang, Mong-Kai Ku. http://123seminarsonly.com/Seminar-Reports/029/26540350-Ldpc-Coded-Ofdm-Modulation.pdf "LDPC coded OFDM modulation for high spectral efficiency transmission"
↑ Nick Wells. "DVB-T2 in relation to the DVB-x2 Family of Standards" Archived 2013-05-26 at the Wayback Machine
↑ "5G Channel Coding" (PDF). Archived from the original (PDF) on December 6, 2018. Retrieved January 6, 2019.
↑ Maunder, Robert (September 2016). "A Vision for 5G Channel Coding" (PDF). Archived from the original (PDF) on December 6, 2018. Retrieved January 6, 2019.
↑ Kai Zhao, Wenzhe Zhao, Hongbin Sun, Tong Zhang, Xiaodong Zhang, and Nanning Zheng (2013). " LDPC-in-SSD: Making Advanced Error Correction Codes Work Effectively in Solid State Drives" (PDF). FAST' 13. pp. 243–256.{{cite conference}}: CS1 maint: multiple names: authors list (link)
↑ "Soft-Decoding in LDPC based SSD Controllers". EE Times. 2015.
↑ ^23.0 ^23.1 A.I. Vila Casado, M. Griot, and R.Wesel, "Informed dynamic scheduling for belief propagation decoding of LDPC codes," Proc. IEEE Int. Conf. on Comm. (ICC), June 2007.
↑ T. Richardson, "Error floors of LDPC codes," in Proc. 41st Allerton Conf. Comm., Control, and Comput., Monticello, IL, 2003.
↑ Thomas J. Richardson and M. Amin Shokrollahi and Rüdiger L. Urbanke, "Design of Capacity-Approaching Irregular Low-Density Parity-Check Codes," IEEE Transactions on Information Theory, 47(2), February 2001
↑ Thomas J. Richardson and Rüdiger L. Urbanke, "Efficient Encoding of Low-Density Parity-Check Codes," IEEE Transactions on Information Theory, 47(2), February 2001
↑ Ahmad Darabiha, Anthony Chan Carusone, Frank R. Kschischang. "Power Reduction Techniques for LDPC Decoders"
↑ Zhengya Zhang, Venkat Anantharam, Martin J. Wainwright, and Borivoje Nikolic. "An Efficient 10GBASE-T Ethernet LDPC Decoder Design With Low Error Floors".
↑ Y. Kou, S. Lin and M. Fossorier, "Low-Density Parity-Check Codes Based on Finite Geometries: A Rediscovery and New Results," IEEE Transactions on Information Theory, vol. 47, no. 7, November 2001, pp. 2711- 2736.
↑ Tahir, B., Schwarz, S., & Rupp, M. (2017, May). BER comparison between Convolutional, Turbo, LDPC, and Polar codes. In 2017 24th International Conference on Telecommunications (ICT) (pp. 1-7). IEEE.
↑ Moon Todd, K. Error correction coding: mathematical methods and algorithms. 2005 by John Wiley & Sons. ISBN 0-471-64800-0. - p.614
↑ Moon Todd, K. Error correction coding: mathematical methods and algorithms. 2005 by John Wiley & Sons. ISBN 0-471-64800-0. - p.653
↑ Andrews, Kenneth S., et al. "The development of turbo and LDPC codes for deep-space applications." Proceedings of the IEEE 95.11 (2007): 2142-2156.
↑ Hassan, A.E.S., Dessouky, M., Abou Elazm, A. and Shokair, M., 2012. Evaluation of complexity versus performance for turbo code and LDPC under different code rates. Proc. SPACOMM, pp.93-98.
↑ "IEEE Spectrum: Does China Have the Best Digital Television Standard on the Planet?". spectrum.ieee.org. Archived from the original on 2009-12-12.

बाहरी संबंध

Introducing Low-Density Parity-Check Codes (by Sarah J Johnson, 2010)
एलडीपीसी Codes – a brief Tutorial (by Bernhard Leiner, 2005)
एलडीपीसी Codes (TU Wien) Archived February 28, 2019, at the Wayback Machine
The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay, discusses एलडीपीसी codes in Chapter 47.
Iterative Decoding of Low-Density Parity Check Codes (by Venkatesan Guruswami, 2006)
एलडीपीसी Codes: An Introduction (by Amin Shokrollahi, 2003)
Belief-Propagation Decoding of एलडीपीसी Codes (by Amir Bennatan, Princeton University)
Turbo and एलडीपीसी Codes: Implementation, Simulation, and Standardization (West Virginia University)
Information theory and coding (Marko Hennhöfer, 2011, TU Ilmenau) - discusses एलडीपीसी codes at pages 74–78.
एलडीपीसी codes and performance results
डीवीबी-S.2 Link, Including एलडीपीसी Coding (MatLab)
Source code for encoding, decoding, and simulating एलडीपीसी codes is available from a variety of locations:
- Binary एलडीपीसी codes in C
- Binary एलडीपीसी codes for Python (core algorithm in C)
- एलडीपीसी encoder and एलडीपीसी decoder in MATLAB
- A Fast Forward Error Correction Toolbox (AFF3CT) in C++11 for fast एलडीपीसी simulations

[1] David J.C. MacKay (2003) Information theory, Inference and Learning Algorithms, CUP, ISBN 0-521-64298-1, (also available online)

[2] Todd K. Moon (2005) Error Correction Coding, Mathematical Methods and Algorithms. Wiley, ISBN 0-471-64800-0 (Includes code)

[3] Amin Shokrollahi (2003) LDPC Codes: An Introduction

[4] US 5446747

[5] NewScientist, Communication speed nears terminal velocity, by Dana Mackenzie, 9 July 2005

[6] Larry Hardesty (January 21, 2010). "Explained: Gallager codes". MIT News. Retrieved August 7, 2013.

[G1962-7] 7.0 ^7.1 [1] R. G. Gallager, "Low density parity check codes," IRE Trans. Inf. Theory, vol. IT-8, no. 1, pp. 21- 28, Jan. 1962.

[MRRSW20-8] [2] J. Moshieff, N. Resch, N. Ron-Zewi, S. Silas, M. Wootters, "Low-density parity-check codes achieve list-decoding capacity," SIAM Journal on Computing, FOCS20-38-FOCS20-73.

[9] Robert G. Gallager (1963). कम घनत्व समता जाँच कोड (PDF). Monograph, M.I.T. Press. Retrieved August 7, 2013.

[MacKay96-10] 10.0 ^10.1 David J.C. MacKay and Radford M. Neal, "Near Shannon Limit Performance of Low Density Parity Check Codes," Electronics Letters, July 1996

[11] Telemetry Data Decoding, Design Handbook

[hughesdvb-12] Presentation by Hughes Systems Archived 2006-10-08 at the Wayback Machine

[13] HomePNA Blog: G.hn, a PHY For All Seasons

[14] IEEE Communications Magazine paper on G.hn Archived 2009-12-13 at the Wayback Machine

[15] IEEE Standard, section 20.3.11.6 "802.11n-2009", IEEE, October 29, 2009, accessed March 21, 2011.

[16] "IEEE SA - IEEE 802.11ax-2021". IEEE Standards Association (in English). Retrieved 22 May 2022.

[17] Chih-Yuan Yang, Mong-Kai Ku. http://123seminarsonly.com/Seminar-Reports/029/26540350-Ldpc-Coded-Ofdm-Modulation.pdf "LDPC coded OFDM modulation for high spectral efficiency transmission"

[18] Nick Wells. "DVB-T2 in relation to the DVB-x2 Family of Standards" Archived 2013-05-26 at the Wayback Machine

[19] "5G Channel Coding" (PDF). Archived from the original (PDF) on December 6, 2018. Retrieved January 6, 2019.

[20] Maunder, Robert (September 2016). "A Vision for 5G Channel Coding" (PDF). Archived from the original (PDF) on December 6, 2018. Retrieved January 6, 2019.

[21] Kai Zhao, Wenzhe Zhao, Hongbin Sun, Tong Zhang, Xiaodong Zhang, and Nanning Zheng (2013). " LDPC-in-SSD: Making Advanced Error Correction Codes Work Effectively in Solid State Drives" (PDF). FAST' 13. pp. 243–256.{{cite conference}}: CS1 maint: multiple names: authors list (link)

[22] "Soft-Decoding in LDPC based SSD Controllers". EE Times. 2015.

[Vila07-23] 23.0 ^23.1 A.I. Vila Casado, M. Griot, and R.Wesel, "Informed dynamic scheduling for belief propagation decoding of LDPC codes," Proc. IEEE Int. Conf. on Comm. (ICC), June 2007.

[Richardson03-24] T. Richardson, "Error floors of LDPC codes," in Proc. 41st Allerton Conf. Comm., Control, and Comput., Monticello, IL, 2003.

[richardson01-25] Thomas J. Richardson and M. Amin Shokrollahi and Rüdiger L. Urbanke, "Design of Capacity-Approaching Irregular Low-Density Parity-Check Codes," IEEE Transactions on Information Theory, 47(2), February 2001

[richardson01b-26] Thomas J. Richardson and Rüdiger L. Urbanke, "Efficient Encoding of Low-Density Parity-Check Codes," IEEE Transactions on Information Theory, 47(2), February 2001

[27] Ahmad Darabiha, Anthony Chan Carusone, Frank R. Kschischang. "Power Reduction Techniques for LDPC Decoders"

[28] Zhengya Zhang, Venkat Anantharam, Martin J. Wainwright, and Borivoje Nikolic. "An Efficient 10GBASE-T Ethernet LDPC Decoder Design With Low Error Floors".

[Kou1-29] Y. Kou, S. Lin and M. Fossorier, "Low-Density Parity-Check Codes Based on Finite Geometries: A Rediscovery and New Results," IEEE Transactions on Information Theory, vol. 47, no. 7, November 2001, pp. 2711- 2736.

[30] Tahir, B., Schwarz, S., & Rupp, M. (2017, May). BER comparison between Convolutional, Turbo, LDPC, and Polar codes. In 2017 24th International Conference on Telecommunications (ICT) (pp. 1-7). IEEE.

[31] Moon Todd, K. Error correction coding: mathematical methods and algorithms. 2005 by John Wiley & Sons. ISBN 0-471-64800-0. - p.614

[32] Moon Todd, K. Error correction coding: mathematical methods and algorithms. 2005 by John Wiley & Sons. ISBN 0-471-64800-0. - p.653

[33] Andrews, Kenneth S., et al. "The development of turbo and LDPC codes for deep-space applications." Proceedings of the IEEE 95.11 (2007): 2142-2156.

[34] Hassan, A.E.S., Dessouky, M., Abou Elazm, A. and Shokair, M., 2012. Evaluation of complexity versus performance for turbo code and LDPC under different code rates. Proc. SPACOMM, pp.93-98.

[35] "IEEE Spectrum: Does China Have the Best Digital Television Standard on the Planet?". spectrum.ieee.org. Archived from the original on 2009-12-12.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

@@ Line 60: / Line 60: @@
 इस आव्यूह में, प्रत्येक पंक्ति तीन समता-जांच बाधाओं में से एक का प्रतिनिधित्व करती है, जबकि प्रत्येक स्तम्भ प्राप्त कोडवर्ड में छह बिट्स में से एक का प्रतिनिधित्व करता है।
-इस उदाहरण में, जीएफ(2) में मूलभूत पंक्ति संचालन के माध्यम से समता-जांच आव्यूह '''H''' को इस फॉर्म <math>\begin{bmatrix} -P^T | I_{n-k} \end{bmatrix}</math> में डालकर आठ कोडवर्ड प्राप्त किए जा सकते हैं:
+इस उदाहरण में, जीएफ(2) में मूलभूत पंक्ति संचालन के माध्यम से समता-जांच आव्यूह '''H''' को इस फॉर्म <math>\begin{bmatrix} -P^T | I_{n-k} \end{bmatrix}
+                           </math> में डालकर आठ कोडवर्ड प्राप्त किए जा सकते हैं:
 :<math>\mathbf{H}
 =
@@ Line 289: / Line 291: @@
 ** [https://aff3ct.github.io A Fast Forward Error Correction Toolbox] (AFF3CT) in [[C++11]] for fast एलडीपीसी simulations
-{{DEFAULTSORT:Low-Density Parity-Check Code}}[[Category: त्रुटि का पता लगाना और सुधार करना]] [[Category: कोडिंग सिद्धांत]] [[Category: क्षमता-अनुरूप कोड]]
+{{DEFAULTSORT:Low-Density Parity-Check Code}}
+[[Category:CS1 English-language sources (en)]]
+[[Category:CS1 maint]]
-[[Category: Machine Translated Page]]
+[[Category:Created On 25/07/2023|Low-Density Parity-Check Code]]
-[[Category:Created On 25/07/2023]]
+[[Category:Lua-based templates|Low-Density Parity-Check Code]]
+[[Category:Machine Translated Page|Low-Density Parity-Check Code]]
+[[Category:Pages with script errors|Low-Density Parity-Check Code]]
+[[Category:Short description with empty Wikidata description|Low-Density Parity-Check Code]]
+[[Category:Templates Vigyan Ready|Low-Density Parity-Check Code]]
+[[Category:Templates that add a tracking category|Low-Density Parity-Check Code]]
+[[Category:Templates that generate short descriptions|Low-Density Parity-Check Code]]
+[[Category:Templates using TemplateData|Low-Density Parity-Check Code]]
+[[Category:Webarchive template wayback links|Low-Density Parity-Check Code]]
+[[Category:कोडिंग सिद्धांत|Low-Density Parity-Check Code]]
+[[Category:क्षमता-अनुरूप कोड|Low-Density Parity-Check Code]]
+[[Category:त्रुटि का पता लगाना और सुधार करना|Low-Density Parity-Check Code]]

Anonymous

Search

कम-घनत्व समता-जाँच कोड: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 12:04, 18 August 2023

Contents

इतिहास

एप्लीकेशन

परिचालन उपयोग

उदाहरण एन्कोडर

डिकोडिंग

नोड जानकारी अपडेट करना

कोड निर्माण

एलडीपीसी कोड बनाम टर्बो कोड

यह भी देखें

लोग

सिद्धांत

अनुप्रयोग

अन्य क्षमता-अनुरूप कोड

संदर्भ

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

कम-घनत्व समता-जाँच कोड: Difference between revisions

Latest revision as of 12:04, 18 August 2023

इतिहास

एप्लीकेशन

परिचालन उपयोग

उदाहरण एन्कोडर

डिकोडिंग

नोड जानकारी अपडेट करना

कोड निर्माण

एलडीपीसी कोड बनाम टर्बो कोड

यह भी देखें

लोग

सिद्धांत

अनुप्रयोग

अन्य क्षमता-अनुरूप कोड

संदर्भ

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Categories