चक्रीय अतिरेक जांच की गणना: Difference between revisions

Latest revision as of 12:08, 18 August 2023

साइक्लिक रिडंडेंसी जांच की कंप्यूटिंग पॉलीनोमियल डिवीज़न, मोडुलो टू के गणित से ली गई है। व्यवहार में, यह बाइनरी कोड मेसेज स्ट्रिंग के लॉन्ग डिवीज़न जैसा दिखता है, जिसमें जेनरेटर पॉलीनोमियल स्ट्रिंग द्वारा निश्चित संख्या में शून्य जोड़े जाते हैं, अतिरिक्त इसके कि एकमात्र ऑपरेशन रिप्लेस का स्थान लेते हैं। इस प्रकार का डिवीज़न एक संशोधित शिफ्ट का रजिस्टर द्वारा हार्डवेयर में कुशलतापूर्वक किया जाता है,^[1] और सॉफ्टवेयर में समतुल्य एल्गोरिदम की एक श्रृंखला द्वारा, बाइट-वाइज पॅरेललिज्म और स्पेस-टाइम ट्रेडऑफ़ के माध्यम से गणित के समीप सरल कोड से प्रारम्भ होता है और बाइट के माध्यम से शीघ्र (और निश्चित रूप से अधिक अस्पष्ट कोड) होता जाता है।^[2]

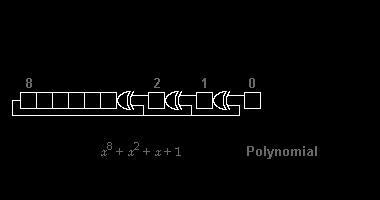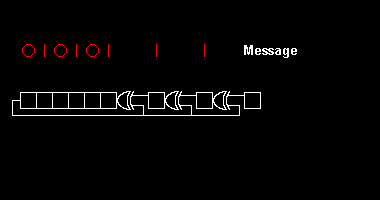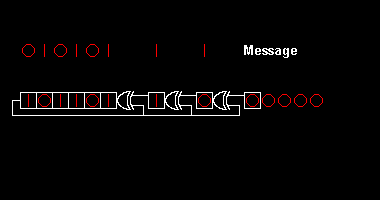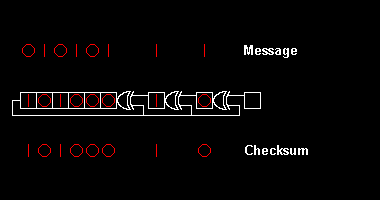
8-बिट साइक्लिक रिडंडेंसी जांच उत्पन्न करने का उदाहरण। जनरेटर एक गैलोइस-प्रकार का लीनियर-फीडबैक शिफ्ट रजिस्टर है जिसमें जनरेटर पॉलीनोमियल में x की पॉवरों (सफेद संख्या) के अनुसार एक्सओआर गेट लगाए गए हैं। मेसेज स्ट्रीम किसी भी लम्बा की हो सकती है। इसे रजिस्टर के माध्यम से स्थानांतरित करने के पश्चात्, 8 शून्य के पश्चात्, रजिस्टर में परिणाम चेकसम होता है।

चेकसम के साथ प्राप्त डेटा की जाँच करना। प्राप्त मेसेज को उसी रजिस्टर के माध्यम से स्थानांतरित किया जाता है जैसा कि जनरेटर में उपयोग किया जाता है, लेकिन प्राप्त चेकसम शून्य के अतिरिक्त इसके साथ जुड़ा होता है। करेक्ट डेटा से आल-जीरो परिणाम प्राप्त होता है; मेसेज या चेकसम में एक करेप्टेड बिट एक अलग परिणाम देगा, वार्निंग देगा कि कोई एरर हुई है।

विभिन्न सीआरसी मानक एक प्रारंभिक शिफ्ट रजिस्टर मान, एक अंतिम एक्सक्लूसिव-या स्टेप और, सबसे गंभीर रूप से, बिट ऑर्डरिंग (एन्डिननेस) निर्दिष्ट करके पॉलीनोमियल डिवीज़न एल्गोरिदम का विस्तार करते हैं। परिणामस्वरूप, व्यवहार में देखा जाने वाला कोड प्योर डिवीज़न से कंफ्यूज होकर डैविएट्स हो जाता है,^[2]और रजिस्टर बाएँ या दाएँ शिफ्ट हो सकता है।

उदाहरण

हार्डवेयर में पॉलीनोमियल डिवीज़न को प्रयुक्त करने के एक उदाहरण के रूप में, मान लीजिए कि हम ASCII वर्ण W से बने 8-बिट मेसेज के 8-बिट सीआरसी की कंप्यूटिंग करने का प्रयास कर रहे हैं, जो बाइनरी 01010111 है, डेसिमल 87₁₀, या हेक्साडेसिमल 57₁₆ होता है। उदाहरण के लिए, हम सीआरसी-8-ATM (HEC) पोल्य्नोमिअल $x^{8}+x^{2}+x+1$ का उपयोग करेंगे। ट्रांसमिटेड पहली बिट ट्रांसमिट(उच्चतम पॉवर का गुणांक $x$ ) बाईं ओर, यह 9-बिट स्ट्रिंग 100000111 के समरूप होता है।

बाइट मान 57₁₆ उपयोग किए गए बिट ऑर्डरिंग कन्वेंशन के आधार पर, दो अलग-अलग ऑर्डर में ट्रांसमिट किया जा सकता है। प्रत्येक एक अलग मेसेज पॉलीनोमियल $M(x)$ उत्पन्न करता है। एमएसबिट-फर्स्ट, यह $x^{6}+x^{4}+x^{2}+x+1$ = 01010111 होता है, जबकि एलएसबिट-फर्स्ट, यह $x^{7}+x^{6}+x^{5}+x^{3}+x$ = 11101010 होता है। दो 16-बिट मेसेज पॉलीनोमियल $x^{8}M(x)$ बनाने के लिए इन्हे $x^{8}$ से गुणा किया जा सकता है।

फिर रेमैंडर की कंप्यूटिंग में जेनरेटर पॉलीनोमियल $G(x)$ के गुणजों को सब्सट्रैक्ट करना सम्मिलित होता है। यह सम्पूर्ण रूप में दशमलव लॉन्ग डिवीज़न के अनुरूप होता है, परन्तु इससे सरल होता है क्योंकि प्रत्येक स्टेप में एकमात्र संभावित गुणज 0 और 1 होते हैं, और ऊपरी अंकों को कम करने के अतिरिक्त सबस्ट्रक्शन इनफिनिटी से बोर्रो किया जाता है। चूँकि हमें भागफल की केयर नहीं है, इसलिए इसे रिकॉर्ड करने की कोई आवश्यकता नहीं होती है।

मोस्ट- सिग्निफिकेंट बिट फर्स्ट

लीस्ट-सिग्निफिकेंट बिट फर्स्ट

	0	1	0	1	0	1	1	1	0	0	0	0	0	0	0	0
−	0	0	0	0	0	0	0	0	0
=	0	1	0	1	0	1	1	1	0	0	0	0	0	0	0	0
	−	1	0	0	0	0	0	1	1	1
=	0	0	0	1	0	1	1	0	1	1	0	0	0	0	0	0
		−	0	0	0	0	0	0	0	0	0
=	0	0	0	1	0	1	1	0	1	1	0	0	0	0	0	0
			−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	1	1	0	1	0	1	1	0	0	0	0
				−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	1	1	0	1	0	1	1	0	0	0	0
					−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	0	1	0	1	0	1	0	1	1	0	0
						−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	0	0	0	1	0	1	0	0	0	1	0
							−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	1	0	0	0	1	0

	1	1	1	0	1	0	1	0	0	0	0	0	0	0	0	0
−	1	0	0	0	0	0	1	1	1
=	0	1	1	0	1	0	0	1	1	0	0	0	0	0	0	0
	−	1	0	0	0	0	0	1	1	1
=	0	0	1	0	1	0	0	0	0	1	0	0	0	0	0	0
		−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	1	0	0	0	1	0	1	0	0	0	0	0
			−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	1	0	0	0	1	0	1	0	0	0	0	0
				−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0
					−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0
						−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0
							−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0

ध्यान दें कि प्रत्येक सबस्ट्रक्शन के पश्चात्, बिट्स को तीन समूहों में विभाजित किया जाता है: प्रारम्भ में, एक समूह जो सभी शून्य होता है; अंत में, एक समूह जो मूल से अपरिवर्तित होता है; और मध्य में एक नीला शेडेड समूह होता जो इंटररेस्टिंग होता है। इंटररेस्टिंग समूह 8 बिट लॉन्ग होता है, जो पॉलीनोमियल की डिग्री के समरूप होता है। प्रत्येक स्टेप में, शून्य समूह को एक बिट लॉन्ग बनाने के लिए पॉलीनोमियल के उपयुक्त गुणज को सब्सट्रैक्ट किया जाता है, और अपरिवर्तित समूह एक बिट छोटा हो जाता है, जब तक कि मात्र अंतिम रेमैंडर न बचा हो।

एमएसबिट-फर्स्ट उदाहरण में, रेमैंडर पॉलीनोमियल $x^{7}+x^{5}+x$ होता है। हेक्साडेसिमल संख्या को कनवर्ट करने के लिए कन्वेंशन का उपयोग किया जाता है जो x की उच्चतम पॉवर एमएसबिट होता है; यह A2₁₆ होता है। एलएसबिट-फर्स्ट में रेमैंडरफल $x^{7}+x^{4}+x^{3}$ होता है। हेक्साडेसिमल संख्या को कनवर्ट करने के लिए कन्वेंशन का उपयोग किया जाता है जो x की उच्चतम पॉवर एलएसबिट होता है; यह 19₁₆ होता है।

इम्प्लीमेंटेशन

प्रत्येक स्टेप पर पूरा मेसेज लिखना, जैसा कि ऊपर दिए गए उदाहरण में किया गया है, बहुत कठिन होता है। मात्र इंटररेस्टिंग बिट्स को रखने के लिए कुशल इम्प्लीमेंटेशन $n$ -बिट शिफ्ट रजिस्टर का उपयोग करता है। पॉलीनोमियल का $x$ से गुणा किया जाता है जो रजिस्टर को एक स्थान से स्थानांतरित करने के समान होता है, क्योंकि गुणांक मूल्य में नहीं बदलते हैं बल्कि मात्र पॉलीनोमियल के अगले पद तक बढ़ते हैं।

यहां एन-बिट सीआरसी की कंप्यूटिंग के लिए कुछ स्यूडोकोड का फर्स्ट ड्राफ्ट होता है। यह पॉलीनोमियलों के लिए एक काल्पनिक वस्तु संरचना का उपयोग करता है, जहाँ x एक पूर्णांक चर नहीं होता है, तथापि एक कंस्ट्रक्टर एक पॉलीनोमियल ऑब्जेक्ट उत्पन्न करता है जिसे जोड़ा, गुणा और घातांकित किया जा सकता है। एक्सओआर के लिए दो पॉलीनोमियलों को जोड़ा जाता है, मॉड्यूलो दो; अर्थात्, दोनों पॉलीनोमियलों से प्रत्येक मिलान पद के गुणांकों को अलग किया जाता है।

function crc(bit array bitString[1..len], int len) {
    remainderPolynomial := polynomialForm(bitString[1..n])   // First n bits of the message
    // A popular variant complements remainderPolynomial here; see § Preset to −1
    for i from 1 to len {
        remainderPolynomial := remainderPolynomial * x + bitString[i+n] * x⁰   // Define bitString[k]=0 for k>len
        if coefficient of xⁿ of remainderPolynomial = 1 {
            remainderPolynomial := remainderPolynomial xor generatorPolynomial
        }
    }
    // A popular variant complements remainderPolynomial here; see § Post-invert below
    return remainderPolynomial

}

कोड फ्रेगमेंट 1: सरल पॉलीनोमियल डिवीज़न

ध्यान दें कि यह उदाहरण कोड बाइट्स का उपयोग न करके बिट-ऑर्डरिंग कन्वेंशन को निर्दिष्ट करने की आवश्यकता से बचाता है; इनपुट बिटस्ट्रिंग फर्स्ट से ही एक बिट ऐरे के रूप में होता है, और रेमैंडरपॉलीनोमियल संक्रियाओं के संदर्भ में मैनिपुलेट किया जाता है; $x$ से गुणा बाएँ या दाएँ शिफ्ट में हो सकता है, और बिटस्ट्रिंग[i+n] का ऐड $x^{0}$ गुणांक में किया जाता है, जो रजिस्टर का दायां या बायां अंत हो सकता है।

इस कोड की दो हानि होती हैं. सर्व प्रथम, इसे रेमैंडरपॉलीनोमियलको रखने के लिए वास्तव में n+1-बिट रजिस्टर की आवश्यकता होती है इस प्रकार $x^{n}$ गुणांक का परीक्षण किया जा सकता है। इससे भी महत्वपूर्ण बात यह है n शून्य बिट्स के साथ पैडेड होने के लिए बिटस्ट्रिंग की आवश्यकता होती है।

पहली समस्या को $x$ से गुणा करने से फर्स्ट रेमैंडरपॉलीनोमियल के $x^{n-1}$ गुणांक का परीक्षण करके हल किया जा सकता है।

दूसरी समस्या को अंतिम n पुनरावृत्तियों को अलग विधि से करके हल किया जा सकता है, परन्तु एक अधिक सूक्ष्म अनुकूलन होता है जिसका उपयोग हार्डवेयर और सॉफ्टवेयर दोनों इम्प्लीमेंटेशनों में सार्वभौमिक रूप से किया जाता है।

क्योंकि मेसेज से जनरेटर पॉलीनोमियल को घटाने के लिए उपयोग किया जाने वाला एक्सओआर ऑपरेशन कम्युएटीव और अस्सोसिएटिव होता है, इससे कोई अंतर नहीं पड़ता कि विभिन्न इनपुट रेमैंडरपॉलीनोमियल से किस क्रम में संयुक्त होते हैं। और विरेमैंडर रूप से, बिटस्ट्रिंग के दिए गए बिट को अंतिम क्षण तक रेमैंडरपॉलीनोमियल में जोड़ने की आवश्यकता नहीं होती है जब यह निर्धारित करने के लिए परीक्षण किया जाता है कि जनरेटरपॉलीनोमियलके साथ एक्सओआर करना है या नहीं।

इससे मेसेज के फर्स्ट n बिट्स के साथ रेमैंडरपॉलीनोमियल को प्रीलोड करने की आवश्यकता समाप्त हो जाती है:

function crc(bit array bitString[1..len], int len) {
    remainderPolynomial := 0
    // A popular variant complements remainderPolynomial here; see § Preset to −1 below
    for i from 1 to len {
        remainderPolynomial := remainderPolynomial xor (bitstring[i] * xⁿ⁻¹)
        if (coefficient of xⁿ⁻¹ of remainderPolynomial) = 1 {
            remainderPolynomial := (remainderPolynomial * x) xor generatorPolynomial
        } else {
            remainderPolynomial := (remainderPolynomial * x)
        }
    }
    // A popular variant complements remainderPolynomial here; see § Post-invert below
    return remainderPolynomial
}

कोड फ्रेगमेंट 2: डिफर्ड एक्सओआरआईएनजी के साथ पॉलीनोमियल डिवीज़न

यह मानक बिट-ए-टाइम हार्डवेयर सीआरसी इम्प्लीमेंटेशन होता है, और अध्ययन के योग्य होता है; एक बार जब आप समझ जाते हैं कि यह फर्स्ट संस्करण के समान परिणाम की कंप्यूटिंग क्यों करता है, तो रेमैंडर अनुकूलन अत्यधिक सरल हो जाता हैं। यदि रेमैंडरपॉलीनोमियल मात्र n बिट लॉन्ग होता है, तो इसके और जनरेटरपॉलीनोमियल के $x^{n}$ गुणांक को सरलता से त्याग दिया जाता है। यही कारण है कि आप सामान्यतः सीआरसी पॉलीनोमियलों को बाइनरी में लिखे हुए देखेंगे, जिसमें प्रमुख गुणांक हटा दिया जाएगा।

सॉफ्टवेयर में, यह नोट करना सुविधाजनक है कि जहां कोई प्रत्येक बिट के एक्सओआर को अंतिम क्षण तक विलंबित कर सकता है, वहीं इसे फर्स्ट करना भी संभव है। एक्सओआर को एक समय में एक बाइट निष्पादित करना आमतौर पर सुविधाजनक होता है, यहां तक कि इस तरह से एक बिट-ए-टाइम इम्प्लीमेंटेशन में भी:

function crc(byte array string[1..len], int len) {
    remainderPolynomial := 0
    // A popular variant complements remainderPolynomial here; see § Preset to −1 below
    for i from 1 to len {
        remainderPolynomial := remainderPolynomial xor polynomialForm(string[i]) * xⁿ⁻⁸
        for j from 1 to 8 {    // Assuming 8 bits per byte
            if coefficient of xⁿ⁻¹ of remainderPolynomial = 1 {
                remainderPolynomial := (remainderPolynomial * x) xor generatorPolynomial
            } else {
                remainderPolynomial := (remainderPolynomial * x)
            }
        }
    }
    // A popular variant complements remainderPolynomial here; see § Post-invert below
    return remainderPolynomial
}

कोड फ्रेगमेंट 3: बाइटवाइज मेसेज एक्सओआरआईएनजी के साथ पॉलीनोमियल डिवीज़न

यह सामान्यतः सबसे कॉम्पैक्ट सॉफ़्टवेयर इम्प्लीमेंटेशन होता है, जिसका उपयोग माइक्रोकंट्रोलर्स में तब किया जाता है जब स्पेस प्रीमियम ओवर स्पीड पर होता है।

बिट ऑर्डरिंग (एंडियननेस)

जब बिट-सीरियल आर्किटेक्चर हार्डवेयर में प्रयुक्त किया जाता है, तो जनरेटर पॉलीनोमियल विशिष्ट रूप से बिट असाइनमेंट का वर्णन करता है; ट्रांसमिटेड प्रथम बिट सदैव उच्चतम पॉवर का गुणांक $x$ होता है, और लास्ट बात $n$ ट्रांसमिटेड बिट्स सीआरसी रेमैंडर $R(x)$ हैं , $x^{n-1}$ के गुणांक से प्रारंभ करते हुए और के $x^{0}$ गुणांक के साथ समाप्त होता है, अर्थात् 1 का गुणांक होता है।

यघपि, जब बिट्स को एक समय में एक बाइट संसाधित किया जाता है, जैसे कि समानांतर ट्रांसमिशन का उपयोग करते समय, 8बी/10बी एन्कोडिंग या आरएस-232-शैली एसिंक्रोनस सीरियल संचार के रूप में बाइट फ़्रेमिंग, या सॉफ़्टवेयर में सीआरसी प्रयुक्त करते समय, डेटा के बिट ऑर्डरिंग (एंडियननेस) को निर्दिष्ट करना आवश्यक होता है; प्रत्येक बाइट में कौन सा बिट "फर्स्ट" माना जाता है और उच्च पॉवर का गुणांक $x$ होता है।

यदि डेटा सीरियल कम्युनिकेशनर के लिए नियत है, तो बिट ऑर्डर का उपयोग करना सबसे अच्छा है जिससे डेटा अंततः भेजा जाएगा। ऐसा इसलिए है क्योंकि सीआरसी की बर्स्ट एरर का पता लगाने की एबिलिटी मेसेज पॉलीनोमियल $M(x)$ में निकटता पर आधारित होती है ; यदि आसन्न पॉलीनोमियल शब्दों को क्रमिक रूप सेट्रांसमिट नहीं किया जाता है, तो बिट्स के पुनर्व्यवस्था के कारण एक भौतिक एरर बर्स्ट को लॉन्ग बर्स्ट के रूप में देखा जा सकता है।

उदाहरण के लिए, आईईईई 802 (ईथरनेट) और आरएस-232 (सीरियल पोर्ट ) दोनों मानक कम से कम महत्वपूर्ण बिट फर्स्ट (लिटिल-एंडियन) ट्रांसमिशन को निर्दिष्ट करते हैं, इसलिए ऐसे लिंक पर भेजे गए डेटा की सुरक्षा के लिए एक सॉफ्टवेयर सीआरसी इम्प्लीमेंटेशन को प्रत्येक बाइट में कम से कम महत्वपूर्ण बिट्स को उच्चतम पॉवरों के गुणांक $x$ में मैप करना चाहिए। दूसरी ओर, फ्लॉपी डिस्क और अधिकांश हार्ड ड्राइव फर्स्ट प्रत्येक बाइट का सबसे महत्वपूर्ण बिट लिखते हैं।

एलएसबिट-फर्स्ट सीआरसी को सॉफ़्टवेयर में प्रयुक्त करना थोड़ा आसान होता है, इसलिए इसे कुछ हद तक सामान्य रूप से देखा जाता है, लेकिन कई प्रोग्रामर एमएसबिट-फर्स्ट बिट ऑर्डर का पालन करना आसान पाते हैं। इस प्रकार, उदाहरण के लिए, एक्सएमओडीईएम-सीआरसी एक्सटेंशन, सॉफ्टवेयर में सीआरसी का प्रारंभिक उपयोग, एमएसबिट-फर्स्ट सीआरसी का उपयोग करता है।

अब तक, स्यूडोकोड ने स्यूडोकोड में बदलावों को गुणन के रूप में वर्णित करके बाइट्स के भीतर बिट्स के क्रम को निर्दिष्ट करने से बचता है। $x$ और द्विआधारी से पॉलीनोमियल रूप में स्पष्ट रूपांतरण लिखना। व्यवहार में, सीआरसी को एक विरेमैंडर बिट-ऑर्डरिंग कन्वेंशन का उपयोग करके एक मानक बाइनरी रजिस्टर में रखा जाता है। एमएसबिट-फर्स्ट रूप में, सबसे महत्वपूर्ण बाइनरी बिट्स फर्स्ट भेजे जाएंगे और इसलिए इसमें उच्च-क्रम पॉलीनोमियल गुणांक होंगे, जबकि एलएसबिट-फर्स्ट रूप में, कम से कम महत्वपूर्ण बाइनरी बिट्स में उच्च-क्रम गुणांक होंगे। उपरोक्त स्यूडोकोड दोनों रूपों में लिखा जा सकता है। कंसर्टर्नर्स के लिए, यह 16-बिट सीआरसी-16-सीसीआईटीटी पॉलीनोमियल $x^{16}+x^{12}+x^{5}+1$ का उपयोग करता है।

/// Most significant bit first (big-endian)

// x^16+x^12+x^5+1 = (1) 0001 0000 0010 0001 = 0x1021
function crc(byte array string[1..len], int len) {
    rem := 0
    // A popular variant complements rem here
    for i from 1 to len {
        rem  := rem xor (string[i] leftShift (n-8))   // n = 16 in this example
        for j from 1 to 8 {   // Assuming 8 bits per byte
            if rem and 0x8000 {   // if leftmost (most significant) bit is set
                rem  := (rem leftShift 1) xor 0x1021
            } else {
                rem  := rem leftShift 1
            }
            rem  := rem and 0xffff      // Trim remainder to 16 bits
        }
    }
    // A popular variant complements rem here
    return rem
}

'कोड फ्रेगमेंट 4: शिफ्ट रजिस्टर बेस्ड डिवीज़न, एमएसबी फर्स्ट

// Least significant bit first (little-endian)
// x^16+x^12+x^5+1 = 1000 0100 0000 1000 (1) = 0x8408
function crc(byte array string[1..len], int len) {
    rem  := 0
    // A popular variant complements rem here
    for i from 1 to len {
        rem  := rem xor string[i]
        for j from 1 to 8 {   // Assuming 8 bits per byte
            if rem and 0x0001 {   // if rightmost (most significant) bit is set
                rem  := (rem rightShift 1) xor 0x8408
            } else {
                rem  := rem rightShift 1
            }
        }
    }
    // A popular variant complements rem here
    return rem
}

कोड फ्रेगमेंट 5: शिफ्ट रजिस्टर बेस्ड डिवीज़न, एलएसबी फर्स्ट

ध्यान दें कि एलएसबिट-फर्स्ट फॉर्म शिफ्ट करने की आवश्यकता से बचाता है स्ट्रिंग[i] से फर्स्ट एक्सओआर. किसी भी स्थिति में, सीआरसी के बाइट्स को उस क्रम में ट्रांसमिट करना सुनिश्चित करें जो आपके चुने हुए बिट-ऑर्डरिंग कन्वेंशन के समरूप होता है।

ध्यान दें कि एलएसबिट-फर्स्ट फॉर्म से एक्सओआरहले स्ट्रिंग [i] को स्थानांतरित करने की आवश्यकता से बचाता है। किसी भी स्थिति में, सीआरसी के बाइट्स को उस क्रम में ट्रांसमिट करना सुनिश्चित करें जो आपके चुने हुए बिट-ऑर्डरिंग कन्वेंशन के समरूप होता है।

मल्टी-बिट कंप्यूटिंग

सरवटे एल्गोरिदम (एकल लुकअप टेबल)

एक अन्य सामान्य अनुकूलन प्रति पुनरावृत्ति एक से अधिक बिट लाभांश को संसाधित करने के लिएरेम के उच्चतम क्रम गुणांक द्वारा अनुक्रमित लुकअप टेबल का उपयोग करता है।^[3] सामान्यतः, 256-एंट्री लुकअप टेबल का उपयोग किया जाता है, जो बाहरी लूप (iऊपर) की बॉडी को प्रतिस्थापित करता है।

// Msbit-first
rem = (rem leftShift 8) xor big_endian_table[string[i] xor ((leftmost 8 bits of rem) rightShift (n-8))]
// Lsbit-first
rem = (rem rightShift 8) xor little_endian_table[string[i] xor (rightmost 8 bits of rem)]

कोड फ्रेगमेंट 6: टेबल आधारित डिवीज़न के कोर

सबसे सामान्यतः सामने आने वाले सीआरसी एल्गोरिदम में से एक को सीआरसी-32 के रूप में जाना जाता है, जिसका उपयोग (अन्य के अलावा) ईथरनेट, एफडीडीआई, ज़िप (फ़ाइल फॉर्मेट) और अन्य आर्काइव फॉर्मेट, और पोर्टेबल नेटवर्क ग्राफिक्स इमेज फॉर्मेट द्वारा किया जाता है। इसके पॉलीनोमियल को एमएसबिट-फर्स्ट को 0x04C11DB7, या एलएसबिट-फर्स्ट को 0xEDB88320 के रूप में लिखा जा सकता है। पोर्टेबल नेटवर्क ग्राफ़िक्स पर W3C वेबपेज में सीआरसी-32 के C में एक संक्षिप्त और सरल टेबल-संचालित इम्प्लीमेंटेशन के साथ एक अपेंडिक्स सम्मलित होता है।^[4] आप देखेंगे कि कोड यहां प्रस्तुत एलएसबिट-फर्स्ट बिट-एट-ए-टाइम स्यूडोकोड के समरूप होता है, और टेबल बिट-एट-ए-टाइम कोड का उपयोग करके बनाई गई है।

256-प्रविष्टि टेबल का उपयोग करना सामान्यतः सबसे सुविधाजनक होता है, लेकिन अन्य आकारों का उपयोग किया जा सकता है। छोटे माइक्रोकंट्रोलर में, एक समय में चार बिट्स को प्रोसेस करने के लिए 16-एंट्री टेबल का उपयोग करने से टेबल को छोटा रखते हुए उपयोगी गति में सुधार होता है। पर्याप्त स्टोरेज वाले कंप्यूटरों पर, a 65536-एंट्री टेबल का उपयोग एक समय में 16 बिट्स को प्रोसेस करने के लिए किया जा सकता है।

टेबल जनरेट करना

टेबल उत्पन्न करने वाला सॉफ़्टवेयर इतना छोटा और उच्चतम होता है कि स्टोरेज से पूर्व-कंप्यूटिंग की गई टेबलओं को लोड करने की तुलना में प्रोग्राम स्टार्टअप पर उनकी कंप्यूटिंग करना सामान्यतः उच्चतम होता है। एक लोकप्रिय तकनीक 256 संभावित 8-बिट बाइट्स के सीआरसी उत्पन्न करने के लिए 256 बार बिट-ए-टाइम कोड का उपयोग करता है। यघपि, टेबल[i एक्सओआर j] == टेबल[i] एक्सओआर टेबल[j] की प्रॉपर्टी का लाभ उठाकर इसे महत्वपूर्ण रूप से अनुकूलित किया जा सकता है। मात्र दो की पॉवरों के अनुरूप टेबल एंटरी की सीधे कंप्यूटिंग करने की आवश्यकता होती है।

निम्नलिखित उदाहरण कोड में, सीआरसी टेबल[i]का मान रखता है :

big_endian_table[0] := 0
crc := 0x8000 // Assuming a 16-bit polynomial
i := 1
do {
    if crc and 0x8000 {
        crc := (crc leftShift 1) xor 0x1021 // The CRC polynomial
    } else {
        crc := crc leftShift 1
    }
    // crc is the value of big_endian_table[i]; let j iterate over the already-initialized entries
    for j from 0 to i−1 {
        big_endian_table[i + j] := crc xor big_endian_table[j];
    }
    i := i leftshift 1
} while i < 256

'कोड फ्रेगमेंट 7: बाइट-एट-ए-टाइम सीआरसी टेबल जनरेशन, एमएसबी फर्स्ट'

little_endian_table[0] := 0
crc := 1;
i := 128
do {
    if crc and 1 {
        crc := (crc rightShift 1) xor 0x8408 // The CRC polynomial
    } else {
        crc := crc rightShift 1
    }
    // crc is the value of little_endian_table[i]; let j iterate over the already-initialized entries
    for j from 0 to 255 by 2 × i {
        little_endian_table[i + j] := crc xor little_endian_table[j];
    }
    i := i rightshift 1
} while i > 0

'कोड फ्रेगमेंट 8: बाइट-एट-ए-टाइम सीआरसी टेबल जनरेशन, एलएसबी फर्स्ट'

इन कोड नमूनों में, टेबल अनुक्रमणिका i + j के समान होती है i एक्सओआर j; आप जो भी फॉर्म अधिक सुविधाजनक हो उसका उपयोग कर सकते हैं।

सीआरसी-32 एल्गोरिथ्म

यह सीआरसी के सीआरसी-32 संस्करण के लिए एक व्यावहारिक एल्गोरिदम है।^[5] सीआरसीटेबल एक कंप्यूटिंग का संस्मरण है जिसे मेसेज के प्रत्येक बाइट के लिए दोहराया जाना होगा (कम्प्यूटेशन ऑफ़ साइक्लिक रीडेंडेन्सी चेक्स § मल्टी-बिट कम्प्यूटेशन)।

Function CRC32
   Input:
      data:  Bytes     // Array of bytes
   Output:
      crc32: UInt32    // 32-bit unsigned CRC-32 value

// Initialize CRC-32 to starting value
crc32 ← 0xFFFFFFFF

for each byte in data do
   nLookupIndex ← (crc32 xor byte) and 0xFF
   crc32 ← (crc32 shr 8) xor CRCTable[nLookupIndex]  // CRCTable is an array of 256 32-bit constants

// Finalize the CRC-32 value by inverting all the bits
crc32 ← crc32 xor 0xFFFFFFFF
return crc32

C में, एल्गोरिथ्म इस प्रकार दिखता है:

#include <inttypes.h> // uint32_t, uint8_t

uint32_t CRC32(const uint8_t data[], size_t data_length) {
	uint32_t crc32 = 0xFFFFFFFFu;
	
	for (size_t i = 0; i < data_length; i++) {
		const uint32_t lookupIndex = (crc32 ^ data[i]) & 0xff;
		crc32 = (crc32 >> 8) ^ CRCTable[lookupIndex];  // CRCTable is an array of 256 32-bit constants
	}
	
	// Finalize the CRC-32 value by inverting all the bits
	crc32 ^= 0xFFFFFFFFu;
	return crc32;
}

बाइट-स्लाइसिंग यूजिंग मल्टीप्ल टेबल

एक स्लाइस-बाय-एन (सामान्यतः सीआरसी32 के लिए स्लाइस-बाय-8; एन ≤ 64) एल्गोरिदम उपस्थित होता है जो सामान्यतः पर सरवटे एल्गोरिदम की तुलना में प्रदर्शन को दोगुना या तिगुना कर देता है। एक समय में 8 बिट्स पढ़ने के अतिरिक्त, एल्गोरिदम एक समय में 8N बिट्स पढ़ता है। ऐसा करने से सुपरस्केलर प्रोसेसर पर प्रदर्शन अधिकतम हो जाता है।^[6]^[7]^[8]^[9]यह स्पष्ट नहीं है कि वास्तव में एल्गोरिदम का आविष्कार किसने किया था।^[10]

पैरेलल कम्प्यूटेशन विदाउट टेबल

एक समय में किसी बाइट या शब्द का समानांतर अपडेट विदाउट टेबल को भी एक्स्प्लिसिटी किया जा सकता है।^[11] इसका उपयोग सामान्यतः हाई-स्पीड हार्डवेयर इम्प्लीमेंटेशन में किया जाता है। प्रत्येक बिट के लिए 8 बिट्स को स्थानांतरित करने के बाद एक समीकरण हल किया जाता है। निम्नलिखित टेबल निम्नलिखित सिग्नलों का उपयोग करके कुछ सामान्य रूप से उपयोग किए जाने वाले पॉलीनोमियलों के समीकरणों को सूचीबद्ध करती हैं:

c_i	सीआरसी बिट 7…0 (or 15…0) बिफोर अपडेट
r_i	सीआरसी बिट 7…0 (or 15…0) आफ्टर अपडेट
d_i	इनपुट डाटा बिट 7…0
e_i = d_i + c_i	e_p = e₇ + e₆ + … + e₁ + e₀ (पैरिटी बिट )
s_i = d_i + c_i+8	s_p = s₇ + s₆ + … + s₁ + s₀ (पैरिटी बिट )

8 बिट्स को शिफ्ट करने के बाद कुछ सीआरसी-8 पॉलीनोमियलों के लिए बिट-वार अपडेट समीकरण
पॉलीनोमियल:	(x⁷ + x³ + 1) × x (लेफ्ट-शिफ्टेड सीआरसी-7-सीसीआईटीटी)	x⁸ + x⁵ + x⁴ + 1 (सीआरसी-8-डलास /मैक्सिम )
कोएफिशिएंट:	0x12 = (0x09 << 1) (एमएसबीएफ/नार्मल)	0x8c (एलएसबीएफ/रिवर्स )
r₀ ← r₁ ← r₂ ← r₃ ← r₄ ← r₅ ← r₆ ← r₇ ←	0 e₀ + e₄ + e₇ e₁ + e₅ e₂ + e₆ e₃ + e₇ + e₀ + e₄ + e₇ e₄ + e₁ + e₅ e₅ + e₂ + e₆ e₆ + e₃ + e₇	e₀ + e₄ + e₁ + e₀ + e₅ + e₂ + e₁ e₁ + e₅ + e₂ + e₁ + e₆ + e₃ + e₂ + e₀ e₂ + e₆ + e₃ + e₂ + e₀ + e₇ + e₄ + e₃ + e₁ e₃ + e₀ + e₇ + e₄ + e₃ + e₁ e₄ + e₁ + e₀ e₅ + e₂ + e₁ e₆ + e₃ + e₂ + e₀ e₇ + e₄ + e₃ + e₁
C कोड फ़्रैगमेन्ट्स:	uint8_t c, d, e, f, r; … e = c ^ d; f = e ^ (e >> 4) ^ (e >> 7); r = (f << 1) ^ (f << 4);	uint8_t c, d, e, f, r; … e = c ^ d; f = e ^ (e << 3) ^ (e << 4) ^ (e << 6); r = f ^ (f >> 4) ^ (f >> 5);

8 बिट्स को स्थानांतरित करने के बाद कुछ सीआरसी-16 पॉलीनोमियलों के लिए बिट-वार अपडेट समीकरण
पॉलीनोमियल:	x¹⁶ + x¹² + x⁵ + 1 (सीआरसी-16-सीसीआईटीटी)		x¹⁶ + x¹⁵ + x² + 1 (सीआरसी-16-एएनएसआई)
कोएफिशिएंट:	0x1021 (एमएसबीएफ/नार्मल)	0x8408 (एलएसबीएफ/रिवर्स)	0x8005 (एमएसबीएफ/नार्मल)	0xa001 (एलएसबीएफ/रिवर्स)
r₀ ← r₁ ← r₂ ← r₃ ← r₄ ← r₅ ← r₆ ← r₇ ← r₈ ← r₉ ← r₁₀ ← r₁₁ ← r₁₂ ← r₁₃ ← r₁₄ ← r₁₅ ←	s₄ + s₀ s₅ + s₁ s₆ + s₂ s₇ + s₃ s₄ s₅ + s₄ + s₀ s₆ + s₅ + s₁ s₇ + s₆ + s₂ c₀ + s₇ + s₃ c₁ + s₄ c₂ + s₅ c₃ + s₆ c₄ + s₇ + s₄ + s₀ c₅ + s₅ + s₁ c₆ + s₆ + s₂ c₇ + s₇ + s₃	c₈ + e₄ + e₀ c₉ + e₅ + e₁ c₁₀ + e₆ + e₂ c₁₁ + e₀ + e₇ + e₃ c₁₂ + e₁ c₁₃ + e₂ c₁₄ + e₃ c₁₅ + e₄ + e₀ e₀ + e₅ + e₁ e₁ + e₆ + e₂ e₂ + e₇ + e₃ e₃ e₄ + e₀ e₅ + e₁ e₆ + e₂ e₇ + e₃	s_p s₀ + s_p s₁ + s₀ s₂ + s₁ s₃ + s₂ s₄ + s₃ s₅ + s₄ s₆ + s₅ c₀ + s₇ + s₆ c₁ + s₇ c₂ c₃ c₄ c₅ c₆ c₇ + s_p	c₈ + e_p c₉ c₁₀ c₁₁ c₁₂ c₁₃ c₁₄ + e₀ c₁₅ + e₁ + e₀ e₂ + e₁ e₃ + e₂ e₄ + e₃ e₅ + e₄ e₆ + e₅ e₇ + e₆ e_p + e₇ e_p
C कोड फ़्रैगमेन्ट्स:	uint8_t d, s, t; uint16_t c, r; … s = d ^ (c >> 8); t = s ^ (s >> 4); r = (c << 8) ^ t ^ (t << 5) ^ (t << 12);	uint8_t d, e, f; uint16_t c, r; … e = c ^ d; f = e ^ (e << 4); r = (c >> 8) ^ (f << 8) ^ (f << 3) ^ (f >> 4);	uint8_t d, s, p; uint16_t c, r, t; … s = d ^ (c >> 8); p = s ^ (s >> 4); p = p ^ (p >> 2); p = p ^ (p >> 1); p = p & 1; t = p \| (s << 1); r = (c << 8) ^ (t << 15) ^ t ^ (t << 1);	uint8_t d, e, p; uint16_t c, r, f; … e = c ^ d; p = e ^ (e >> 4); p = p ^ (p >> 2); p = p ^ (p >> 1); p = p & 1; f = e \| (p << 8); r = (c >> 8) ^ (f << 6) ^ (f << 7) ^ (f >> 8);

टू-स्टेपीय कंप्यूटिंग

चूँकि सीआरसी-32 पॉलीनोमियल में बड़ी संख्या में पद होते हैं, एक समय में रेमैंडर बाइट की कंप्यूटिंग करते समय प्रत्येक बिट पिछले पुनरावृत्ति के कई बिट्स पर निर्भर करता है। बाइट-समानांतर हार्डवेयर इम्प्लीमेंटेशन में इसके लिए मल्टीपल-इनपुट या कैस्केड एक्सओआर गेट्स की आवश्यकता होती है जो प्रोपागेशन डिले को बढ़ाता है।

कंप्यूटिंग गति को अधिकतम करने के लिए, 123-बिट शिफ्ट रजिस्टर के माध्यम से मेसेज को पारित करके एक मध्यवर्ती रेमैंडर की कंप्यूटिंग की जा सकती है। पॉलीनोमियल मानक पॉलीनोमियल का सावधानीपूर्वक चयनित गुणज होता है, जैसे कि पद (फीडबैक टैप) व्यापक रूप से दूरी पर होता हैं, और रेमैंडर का कोई भी बिट प्रति बाइट पुनरावृत्ति में एक बार से अधिक एक्सओआरed नहीं होता है। इस प्रकार मात्र दो-इनपुट एक्सओआर गेट, सबसे तेज़ संभव, की आवश्यकता होती है। अंत में सीआरसी-32 रेमैंडर प्राप्त करने के लिए मध्यवर्ती रेमैंडर को दूसरी शिफ्ट रजिस्टर में मानक पॉलीनोमियल द्वारा विभाजित किया जाता है।^[12]

ब्लॉकवार कंप्यूटिंग

रेमैंडर की ब्लॉक-वार कंप्यूटिंग किसी भी सीआरसी पॉलीनोमियल के लिए हार्डवेयर में स्टेट स्पेस ट्रांसफॉर्मेशन मैट्रिक्स को फैक्टर करके की जा सकती है, जो रेमैंडर को दो सरल टोप्लिट्ज मैट्रिक्स में कंप्यूटिंग करने के लिए आवश्यक होता है।^[13]

एक-पास चेकिंग

किसी मेसेज में सीआरसी जोड़ते समय, ट्रांसमिटेड सीआरसी को अलग करना, उसकी पुन: कंप्यूटिंग करना और ट्रांसमिटेड सीआरसी के विरुद्ध पुन: संगणित मूल्य को सत्यापित करना संभव होता है। याग्पी, सामान्यतः एक सरल तकनीक होती है जिसे हार्डवेयर में उपयोग किया जाता है।

जब सीआरसी करेक्ट बाइट ऑर्डर (चयनित बिट-ऑर्डरिंग कन्वेंशन के समरूप होते हुए) के साथ ट्रांसमिट होता है, तो एक रिसीवर मेसेज और सीआरसी पर समग्र सीआरसी की कंप्यूटिंग कर सकता है, और यदि वे करेक्ट होता हैं, तो परिणाम शून्य होगा।^[14]यह पोस्सिबिलिटी का यही कारण है कि अधिकांश नेटवर्क प्रोटोकॉल जिनमें सीआरसी सम्मलित होता है, एंडिंग डिलिमिटर से फर्स्ट ऐसा करते हैं; सीआरसी के चेक के लिए यह जानना जरूरी नहीं है कि पैकेट का एंड निकट है या नहीं।वास्तव में, कुछ प्रोटोकॉल सीआरसी का उपयोग एंडिंग डिलिमिटर- सीआरसी-आधारित फ़्रेमिंग के रूप में करते हैं।

सीआरसी वेरिएंट

व्यवहार में, अधिकांश मानक रजिस्टर को ऑल-वन पर प्रीसेट करने और ट्रांसमिशन से फर्स्ट सीआरसी को इन्वर्ट करने को निर्दिष्ट करते हैं। इससे सीआरसी की परिवर्तित बिट्स का पता लगाने की एबिलिटी पर कोई प्रभाव नहीं पड़ता है, लेकिन यह मेसेज में जोड़े गए बिट्स को नोटिस करने की एबिलिटी देता है।

प्रीसेट टू−1

सीआरसी का बेसिक गणित उन मेसेजों को स्वीकार करता है (सही विधि से ट्रांसमिट माना जाता है) जिन्हें पॉलीनोमियल के रूप में व्याख्या किए जाने पर, सीआरसी पॉलीनोमियल का एक गुणक होता है। यदि कुछ लीडिंग 0 बिट्स को ऐसे मेसेज से जोड़ा जाता है, तो वे पॉलीनोमियल के रूप में इसकी व्याख्या को नहीं बदलेंगे। यह इस तथ्य के समतुल्य है कि 0001 और 1 एक ही संख्या होती हैं।

परन्तु यदि ट्रांसमिटेड किया जा रहा मेसेज लीडिंग 0 बिट्स की केयर करता है, तो ऐसे परिवर्तन का पता लगाने के लिए बेसिक सीआरसी एल्गोरिदम की अएबिलिटी अवांछनीय होती है। यदि यह संभव है कि एक ट्रांसमिशन एरर ऐसे बिट्स को जोड़ सकती है, तो एक सरल समाधान यह है कि रेम शिफ्ट रजिस्टर को कुछ नॉन-जीरो वैल्यू पर सेट करके प्रारम्भ किया जाए; सुविधा के लिए, सामान्यतः पर ऑल-वन्स मान का उपयोग किया जाता है।। यह गणितीय रूप से मेसेज के फर्स्ट एन बिट्स को पूरक करने (बाइनरी नोट) के समान होता है, जहां एन सीआरसी रजिस्टर में बिट्स की संख्या होती है।

यह सीआरसी निर्माण और जांच को किसी भी तरह से प्रभावित नहीं करता है, जब तक जनरेटर और चेकर दोनों समान प्रारंभिक मूल्य का उपयोग करते हैं। कोई भी नॉन-जीरो प्रारंभिक वैल्यू काम करेगी, और कुछ मानक असामान्य मान निर्दिष्ट करते हैं,^[15] लेकिन सभी का मान (दो में −1 पूरक बाइनरी) अब तक का सबसे कॉमन होता है। ध्यान दें कि एक-पास सीआरसी जनरेट/चेक प्रीसेट मूल्य की केयर किए बिना, मेसेज सही होने पर भी शून्य का परिणाम देगा।

पोस्ट-इन्वर्ट

उसी प्रकार की एरर मेसेज के एंड में हो सकती है, तथापि मेसेजों के अधिक लिमटेड सेट के साथ। किसी मेसेज में 0 बिट जोड़ना उसके पॉलीनोमियल को x से गुणा करने के समान होता है, और यदि यह फर्स्ट सीआरसी पॉलीनोमियल का गुणज था, तो उस गुणन का परिणाम भी होगा। यह इस तथ्य के समतुल्य है कि, चूँकि 726, 11 का गुणज है, इसलिए 7260 भी है।

एक समान सलूशन मेसेज के अंत में प्रयुक्त किया जा सकता है, मेसेज में जोड़ने से फर्स्ट सीआरसी रजिस्टर को इन्वर्ट कर दिया जा सकता है। फिर, कोई भी नॉन-जीरो परिवर्तन करेगा; सभी बिट्स को इन्वर्ट करना (ऑल-वन्स पैटर्न के साथ एक्सओआरआईएनजी) सबसे कॉमन होता है।

इसका एक-पास सीआरसी जाँच पर प्रभाव पड़ता है: मेसेज सही होने पर शून्य का परिणाम उत्पन्न करने के अतिरिक्त, यह एक निश्चित नॉन -शून्य परिणाम उत्पन्न करता है। (स्पष्ट होने के लिए, परिणाम इन्वर्ट पैटर्न का सीआरसी (नॉन-जीरो प्रीसेट के बिना, लेकिन पोस्ट-इनवर्ट के साथ) है।) एक बार जब यह कांस्टेंट प्राप्त हो जाता है (एक आरबिटरेरी मेसेज पर एक-पास सीआरसी उत्पन्न/चेक करके सबसे आसानी से), इसका उपयोग उसी सीआरसी एल्गोरिथ्म का उपयोग करके चेक किये गए किसी भी अन्य मेसेज की प्योरता को सत्यापित करने के लिए सीधे किया जा सकता है।

यह भी देखें

सामान्य वर्ग

कोड कोर्रेक्टिंग एरर
हैश फ़ंक्शंस की टेबल
पैरिटी पॉलीनोमियल $x +1$ के साथ 1-बिट सीआरसी के समान है।

नॉन-सीआरसी चेकसम

एडलर-32
फ्लेचर का चेकसम

संदर्भ

↑ Dubrova, Elena; Mansouri, Shohreh Sharif (May 2012). "A BDD-Based Approach to Constructing LFSRS for Parallel CRC Encoding". 2012 IEEE 42nd International Symposium on Multiple-Valued Logic. pp. 128–133. doi:10.1109/ISMVL.2012.20. ISBN 978-0-7695-4673-5. S2CID 27306826.
↑ ^2.0 ^2.1 Williams, Ross N. (1996-09-24). "A Painless Guide to CRC Error Detection Algorithms V3.00". Archived from the original on 2006-09-27. Retrieved 2016-02-16.
↑ Sarwate, Dilip V. (August 1998). "टेबल लुक-अप के माध्यम से चक्रीय अतिरेक जांच की गणना". Communications of the ACM. 31 (8): 1008–1013. doi:10.1145/63030.63037. S2CID 5363350.
↑ "Portable Network Graphics (PNG) Specification (Second Edition): Annex D, Sample Cyclic Redundancy Code implementation". W3C. 2003-11-10. Retrieved 2016-02-16.
↑ "[MS-ABS]: 32-Bit CRC Algorithm". msdn.microsoft.com. Archived from the original on 7 November 2017. Retrieved 4 November 2017.
↑ Kounavis, M.E.; Berry, F.L. (2005). "A Systematic Approach to Building High Performance Software-Based CRC Generators". 10th IEEE Symposium on Computers and Communications (ISCC'05) (PDF). pp. 855–862. doi:10.1109/ISCC.2005.18. ISBN 0-7695-2373-0. S2CID 10308354.
↑ Berry, Frank L.; Kounavis, Michael E. (November 2008). "उच्च-प्रदर्शन सीआरसी पीढ़ी के लिए नवीन तालिका लुकअप-आधारित एल्गोरिदम". IEEE Transactions on Computers. 57 (11): 1550–1560. doi:10.1109/TC.2008.85. S2CID 206624854.
↑ High Octane CRC Generation with the Intel Slicing-by-8 Algorithm (PDF) (Technical report). Intel. Archived from the original (PDF) on 2012-07-22.
↑ "सीआरसी गणना पर संक्षिप्त ट्यूटोरियल". The Linux Kernel Archives.
↑ Menon-Sen, Abhijit (2017-01-20). "Who invented the slicing-by-N CRC32 algorithm?".
↑ Jon Buller (1996-03-15). "Re: 8051 and CRC-CCITT". Newsgroup: comp.arch.embedded. Usenet: 31498ED0.7C0A@nortel.com. Retrieved 2016-02-16.
↑ Glaise, René J. (1997-01-20). "A two-step computation of cyclic redundancy code CRC-32 for ATM networks". IBM Journal of Research and Development. Armonk, NY: IBM. 41 (6): 705. doi:10.1147/rd.416.0705. Archived from the original on 2009-01-30. Retrieved 2016-02-16.
↑ Das, Arindam (2022). "लुक-अप टेबल के स्थान पर फैक्टर्ड टोप्लिट्ज़ मैट्रिसेस का उपयोग करके चक्रीय रिडंडेंसी कोड की ब्लॉक-वार गणना". IEEE Transactions on Computers. 72 (4): 1110–1121. doi:10.1109/TC.2022.3189574. ISSN 0018-9340. S2CID 250472783.
↑ Andrew Kadatch, Bob Jenkins. "Everything we know about CRC but afraid to forget". 2007. quote: "The fact that the CRC of a message followed by its CRC is a constant value which does not depend on the message... is well known and has been widely used in the telecommunication industry for long time."
↑ E.g. low-frequency RFID TMS37157 data sheet - Passive Low Frequency Interface Device With EEPROM and 134.2 kHz Transponder Interface (PDF), Texas Instruments, November 2009, p. 39, retrieved 2016-02-16, The CRC Generator is initialized with the value 0x3791 as shown in Figure 50.

बाहरी संबंध

JohnPaul Adamovsky. "64 Bit Cyclic Redundant Code – XOR Long Division To Bytewise Table Lookup".

Andrew Kadarch, Bob Jenkins. "Efficient (~1 CPU cycle per byte) CRC implementation". GitHub.

[1] Dubrova, Elena; Mansouri, Shohreh Sharif (May 2012). "A BDD-Based Approach to Constructing LFSRS for Parallel CRC Encoding". 2012 IEEE 42nd International Symposium on Multiple-Valued Logic. pp. 128–133. doi:10.1109/ISMVL.2012.20. ISBN 978-0-7695-4673-5. S2CID 27306826.

[williams96-2] 2.0 ^2.1 Williams, Ross N. (1996-09-24). "A Painless Guide to CRC Error Detection Algorithms V3.00". Archived from the original on 2006-09-27. Retrieved 2016-02-16.

[3] Sarwate, Dilip V. (August 1998). "टेबल लुक-अप के माध्यम से चक्रीय अतिरेक जांच की गणना". Communications of the ACM. 31 (8): 1008–1013. doi:10.1145/63030.63037. S2CID 5363350.

[4] "Portable Network Graphics (PNG) Specification (Second Edition): Annex D, Sample Cyclic Redundancy Code implementation". W3C. 2003-11-10. Retrieved 2016-02-16.

[5] "[MS-ABS]: 32-Bit CRC Algorithm". msdn.microsoft.com. Archived from the original on 7 November 2017. Retrieved 4 November 2017.

[6] Kounavis, M.E.; Berry, F.L. (2005). "A Systematic Approach to Building High Performance Software-Based CRC Generators". 10th IEEE Symposium on Computers and Communications (ISCC'05) (PDF). pp. 855–862. doi:10.1109/ISCC.2005.18. ISBN 0-7695-2373-0. S2CID 10308354.

[7] Berry, Frank L.; Kounavis, Michael E. (November 2008). "उच्च-प्रदर्शन सीआरसी पीढ़ी के लिए नवीन तालिका लुकअप-आधारित एल्गोरिदम". IEEE Transactions on Computers. 57 (11): 1550–1560. doi:10.1109/TC.2008.85. S2CID 206624854.

[8] High Octane CRC Generation with the Intel Slicing-by-8 Algorithm (PDF) (Technical report). Intel. Archived from the original (PDF) on 2012-07-22.

[9] "सीआरसी गणना पर संक्षिप्त ट्यूटोरियल". The Linux Kernel Archives.

[10] Menon-Sen, Abhijit (2017-01-20). "Who invented the slicing-by-N CRC32 algorithm?".

[11] Jon Buller (1996-03-15). "Re: 8051 and CRC-CCITT". Newsgroup: comp.arch.embedded. Usenet: 31498ED0.7C0A@nortel.com. Retrieved 2016-02-16.

[glaise-12] Glaise, René J. (1997-01-20). "A two-step computation of cyclic redundancy code CRC-32 for ATM networks". IBM Journal of Research and Development. Armonk, NY: IBM. 41 (6): 705. doi:10.1147/rd.416.0705. Archived from the original on 2009-01-30. Retrieved 2016-02-16.

[13] Das, Arindam (2022). "लुक-अप टेबल के स्थान पर फैक्टर्ड टोप्लिट्ज़ मैट्रिसेस का उपयोग करके चक्रीय रिडंडेंसी कोड की ब्लॉक-वार गणना". IEEE Transactions on Computers. 72 (4): 1110–1121. doi:10.1109/TC.2022.3189574. ISSN 0018-9340. S2CID 250472783.

[14] Andrew Kadatch, Bob Jenkins. "Everything we know about CRC but afraid to forget". 2007. quote: "The fact that the CRC of a message followed by its CRC is a constant value which does not depend on the message... is well known and has been widely used in the telecommunication industry for long time."

[15] E.g. low-frequency RFID TMS37157 data sheet - Passive Low Frequency Interface Device With EEPROM and 134.2 kHz Transponder Interface (PDF), Texas Instruments, November 2009, p. 39, retrieved 2016-02-16, The CRC Generator is initialized with the value 0x3791 as shown in Figure 50.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

Anonymous

Search

चक्रीय अतिरेक जांच की गणना: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 12:08, 18 August 2023

Contents

उदाहरण

इम्प्लीमेंटेशन

बिट ऑर्डरिंग (एंडियननेस)

मल्टी-बिट कंप्यूटिंग

सरवटे एल्गोरिदम (एकल लुकअप टेबल)

टेबल जनरेट करना

सीआरसी-32 एल्गोरिथ्म

बाइट-स्लाइसिंग यूजिंग मल्टीप्ल टेबल

पैरेलल कम्प्यूटेशन विदाउट टेबल

टू-स्टेपीय कंप्यूटिंग

ब्लॉकवार कंप्यूटिंग

एक-पास चेकिंग

सीआरसी वेरिएंट

प्रीसेट टू−1

पोस्ट-इन्वर्ट

यह भी देखें

संदर्भ

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

@@ Line 1: / Line 1: @@
-{{short description|Overview of the computation of cyclic redundancy checks}}'''साइक्लिक रिडंडेंसी जांच की कंप्यूटिंग''' पॉलीनोमियल डिवीज़न , मोडुलो टू के गणित से ली गई है। व्यवहार में, यह [[बाइनरी कोड]] मेसेज स्ट्रिंग के लॉन्ग डिवीज़न  जैसा दिखता है, जिसमें जेनरेटर पॉलीनोमियल स्ट्रिंग द्वारा निश्चित संख्या में शून्य जोड़े जाते हैं, अतिरिक्त इसके कि [[एकमात्र]] ऑपरेशन रिप्लेस का स्थान लेते हैं। इस प्रकार का डिवीज़न  एक संशोधित [[ शिफ्ट का रजिस्टर ]] द्वारा हार्डवेयर में कुशलतापूर्वक किया जाता है,<ref>{{cite book
+{{short description|Overview of the computation of cyclic redundancy checks}}'''साइक्लिक रिडंडेंसी जांच की कंप्यूटिंग''' पॉलीनोमियल डिवीज़न, मोडुलो टू के गणित से ली गई है। व्यवहार में, यह [[बाइनरी कोड]] मेसेज स्ट्रिंग के लॉन्ग डिवीज़न जैसा दिखता है, जिसमें जेनरेटर पॉलीनोमियल स्ट्रिंग द्वारा निश्चित संख्या में शून्य जोड़े जाते हैं, अतिरिक्त इसके कि [[एकमात्र]] ऑपरेशन रिप्लेस का स्थान लेते हैं। इस प्रकार का डिवीज़न एक संशोधित [[ शिफ्ट का रजिस्टर |शिफ्ट का रजिस्टर]] द्वारा हार्डवेयर में कुशलतापूर्वक किया जाता है,<ref>{{cite book
 | first1=Elena
 | last1=Dubrova
@@ Line 23: / Line 23: @@
 }}</ref>
-[[Image:CRC8-gen.gif|thumb|right|380 px|8-बिट साइक्लिक रिडंडेंसी जांच उत्पन्न करने का उदाहरण। जनरेटर एक गैलोइस-प्रकार का [[लीनियर-फीडबैक शिफ्ट रजिस्टर]] है जिसमें जनरेटर पॉलीनोमियल में x की पॉवरयों (सफेद संख्या) के अनुसार XOR गेट लगाए गए हैं। मेसेज स्ट्रीम किसी भी लॉन्गई की हो सकती है. इसे रजिस्टर के माध्यम से स्थानांतरित करने के बाद, 8 शून्य के बाद, रजिस्टर में परिणाम चेकसम है।]]
+[[Image:CRC8-gen.gif|thumb|right|380 px|8-बिट साइक्लिक रिडंडेंसी जांच उत्पन्न करने का उदाहरण। जनरेटर एक गैलोइस-प्रकार का [[लीनियर-फीडबैक शिफ्ट रजिस्टर]] है जिसमें जनरेटर पॉलीनोमियल में x की पॉवरों (सफेद संख्या) के अनुसार एक्सओआर गेट लगाए गए हैं। मेसेज स्ट्रीम किसी भी लम्बा की हो सकती है। इसे रजिस्टर के माध्यम से स्थानांतरित करने के पश्चात्, 8 शून्य के पश्चात्, रजिस्टर में परिणाम चेकसम होता है।]]
-[[Image:CRC8-rx.gif|thumb|380 px|चेकसम के साथ प्राप्त डेटा की जाँच करना। प्राप्त मेसेज को उसी रजिस्टर के माध्यम से स्थानांतरित किया जाता है जैसा कि जनरेटर में उपयोग किया जाता है, लेकिन प्राप्त चेकसम शून्य के बजाय इसके साथ जुड़ा होता है। सही डेटा से सर्व-शून्य परिणाम प्राप्त होता है; मेसेज या चेकसम में एक दूषित बिट एक अलग परिणाम देगा, चेतावनी देगा कि कोई त्रुटि हुई है।]]विभिन्न सीआरसी मानक एक प्रारंभिक शिफ्ट रजिस्टर मान, एक अंतिम एक्सक्लूसिव-या स्टेप और, सबसे गंभीर रूप से, थोड़ा ऑर्डरिंग ([[endianness|अंतहीनता]]) निर्दिष्ट करके पॉलीनोमियल डिवीज़न  एल्गोरिदम का विस्तार करते हैं। परिणामस्वरूप, व्यवहार में देखा जाने वाला कोड प्योर डिवीज़न से कंफ्यूज  रूप से भटक जाता है,<ref name="williams96"/>और रजिस्टर बाएँ या दाएँ शिफ्ट हो सकता है।
+[[Image:CRC8-rx.gif|thumb|380 px|चेकसम के साथ प्राप्त डेटा की जाँच करना। प्राप्त मेसेज को उसी रजिस्टर के माध्यम से स्थानांतरित किया जाता है जैसा कि जनरेटर में उपयोग किया जाता है, लेकिन प्राप्त चेकसम शून्य के अतिरिक्त इसके साथ जुड़ा होता है। करेक्ट डेटा से आल-जीरो परिणाम प्राप्त होता है; मेसेज या चेकसम में एक करेप्टेड बिट एक अलग परिणाम देगा, वार्निंग देगा कि कोई एरर हुई है।]]विभिन्न सीआरसी मानक एक प्रारंभिक शिफ्ट रजिस्टर मान, एक अंतिम एक्सक्लूसिव-या स्टेप और, सबसे गंभीर रूप से, बिट ऑर्डरिंग ([[endianness|एन्डिननेस]]) निर्दिष्ट करके पॉलीनोमियल डिवीज़न एल्गोरिदम का विस्तार करते हैं। परिणामस्वरूप, व्यवहार में देखा जाने वाला कोड प्योर डिवीज़न से कंफ्यूज होकर डैविएट्स हो जाता है,<ref name="williams96"/>और रजिस्टर बाएँ या दाएँ शिफ्ट हो सकता है।
 == उदाहरण ==
-हार्डवेयर में पॉलीनोमियल डिवीज़न को प्रयुक्त करने के एक उदाहरण के रूप में, मान लीजिए कि हम [[ASCII]] वर्ण W से बने 8-बिट मेसेज के 8-बिट सीआरसी की कंप्यूटिंग करने का प्रयास कर रहे हैं, जो बाइनरी 01010111 है, डेसिमल 87<sub>10</sub>, या [[हेक्साडेसिमल]] 57<sub>16</sub> होता है। उदाहरण के लिए, हम सीआरसी-8-ATM (HEC) पोल्य्नोमिअल  <math>x^8+x^2+x+1</math> का उपयोग करेंगे। ट्रांसमिटेड पहली बिट ट्रांसमिट(उच्चतम पॉवर का गुणांक <math>x</math>) बाईं ओर, यह 9-बिट स्ट्रिंग 100000111 के समरूप होता है।
+हार्डवेयर में पॉलीनोमियल डिवीज़न को प्रयुक्त करने के एक उदाहरण के रूप में, मान लीजिए कि हम [[ASCII]] वर्ण W से बने 8-बिट मेसेज के 8-बिट सीआरसी की कंप्यूटिंग करने का प्रयास कर रहे हैं, जो बाइनरी 01010111 है, डेसिमल 87<sub>10</sub>, या [[हेक्साडेसिमल]] 57<sub>16</sub> होता है। उदाहरण के लिए, हम सीआरसी-8-ATM (HEC) पोल्य्नोमिअल <math>x^8+x^2+x+1</math> का उपयोग करेंगे। ट्रांसमिटेड पहली बिट ट्रांसमिट(उच्चतम पॉवर का गुणांक <math>x</math>) बाईं ओर, यह 9-बिट स्ट्रिंग 100000111 के समरूप होता है।
-बाइट मान 57<sub>16</sub> उपयोग किए गए बिट ऑर्डरिंग कन्वेंशन के आधार पर, दो अलग-अलग ऑर्डर में प्रसारित किया जा सकता है। प्रत्येक एक अलग मेसेज पॉलीनोमियल <math>M(x)</math> उत्पन्न करता है। एमएसबिट-फर्स्ट, यह<math>x^6+x^4+x^2+x+1</math> = 01010111 होता है, जबकि एलएसबिट-फर्स्ट, यह <math>x^7+x^6+x^5+x^3+x</math> = 11101010 होता है। दो 16-बिट मेसेज पॉलीनोमियल <math>x^8 M(x)</math>बनाने के लिए इन्हे <math>x^8</math> से गुणा किया जा सकता है।
+बाइट मान 57<sub>16</sub> उपयोग किए गए बिट ऑर्डरिंग कन्वेंशन के आधार पर, दो अलग-अलग ऑर्डर में ट्रांसमिट किया जा सकता है। प्रत्येक एक अलग मेसेज पॉलीनोमियल <math>M(x)</math> उत्पन्न करता है। एमएसबिट-फर्स्ट, यह<math>x^6+x^4+x^2+x+1</math> = 01010111 होता है, जबकि एलएसबिट-फर्स्ट, यह <math>x^7+x^6+x^5+x^3+x</math> = 11101010 होता है। दो 16-बिट मेसेज पॉलीनोमियल <math>x^8 M(x)</math>बनाने के लिए इन्हे <math>x^8</math> से गुणा किया जा सकता है।
-फिर रेमैंडरफल की कंप्यूटिंग में जेनरेटर पॉलीनोमियल <math>G(x)</math>के गुणजों को सब्सट्रैक्ट करना सम्मिलित होता है। यह सम्पूर्ण रूप में दशमलव लॉन्ग डिवीज़न के अनुरूप होता है, परन्तु इससे सरल होता है क्योंकि प्रत्येक स्टेप में एकमात्र संभावित गुणज 0 और 1 होते हैं, और ऊपरी अंकों को कम करने के अतिरिक्त सबस्ट्रक्शन इनफिनिटी से बोर्रो किया जाता है। चूँकि हमें भागफल की केयर नहीं है, इसलिए इसे रिकॉर्ड करने की कोई आवश्यकता नहीं होती है।
+फिर रेमैंडर की कंप्यूटिंग में जेनरेटर पॉलीनोमियल <math>G(x)</math>के गुणजों को सब्सट्रैक्ट करना सम्मिलित होता है। यह सम्पूर्ण रूप में दशमलव लॉन्ग डिवीज़न के अनुरूप होता है, परन्तु इससे सरल होता है क्योंकि प्रत्येक स्टेप में एकमात्र संभावित गुणज 0 और 1 होते हैं, और ऊपरी अंकों को कम करने के अतिरिक्त सबस्ट्रक्शन इनफिनिटी से बोर्रो किया जाता है। चूँकि हमें भागफल की केयर नहीं है, इसलिए इसे रिकॉर्ड करने की कोई आवश्यकता नहीं होती है।
 {| border="1" style="margin:auto;"
-! Most-significant bit फर्स्ट !! Least-significant bit फर्स्ट
+! मोस्ट- सिग्निफिकेंट बिट फर्स्ट !! लीस्ट-सिग्निफिकेंट बिट फर्स्ट
 |-
 |
@@ Line 111: / Line 111: @@
 |}
 |}
-ध्यान दें कि प्रत्येक सबस्ट्रक्शन के पश्चात्, बिट्स को तीन समूहों में विभाजित किया जाता है: प्रारम्भ में, एक समूह जो सभी शून्य होता है; अंत में, एक समूह जो मूल से अपरिवर्तित होता  है; और मध्य में एक नीला शेडेड समूह होता जो इंटररेस्टिंग होता है। इंटररेस्टिंग समूह 8 बिट लॉन्ग होता है, जो पॉलीनोमियल की डिग्री के समरूप होता है। प्रत्येक स्टेप में, शून्य समूह को एक बिट लॉन्ग बनाने के लिए पॉलीनोमियल के उपयुक्त गुणज को सब्सट्रैक्ट किया जाता है, और अपरिवर्तित समूह एक बिट छोटा हो जाता है, जब तक कि मात्र अंतिम रेमैंडर न बचा हो।
+ध्यान दें कि प्रत्येक सबस्ट्रक्शन के पश्चात्, बिट्स को तीन समूहों में विभाजित किया जाता है: प्रारम्भ में, एक समूह जो सभी शून्य होता है; अंत में, एक समूह जो मूल से अपरिवर्तित होता है; और मध्य में एक नीला शेडेड समूह होता जो इंटररेस्टिंग होता है। इंटररेस्टिंग समूह 8 बिट लॉन्ग होता है, जो पॉलीनोमियल की डिग्री के समरूप होता है। प्रत्येक स्टेप में, शून्य समूह को एक बिट लॉन्ग बनाने के लिए पॉलीनोमियल के उपयुक्त गुणज को सब्सट्रैक्ट किया जाता है, और अपरिवर्तित समूह एक बिट छोटा हो जाता है, जब तक कि मात्र अंतिम रेमैंडर न बचा हो।
-एमएसबिट-फर्स्ट उदाहरण में, रेमैंडर पॉलीनोमियल <math>x^7+x^5+x</math> होता है। हेक्साडेसिमल संख्या को कनवर्ट करने के लिए  कन्वेंशन का उपयोग किया जाता है जो  x की उच्चतम पॉवर एमएसबिट होता  है; यह A2<sub>16</sub> होता है। एलएसबिट-फर्स्ट में रेमैंडरफल  <math>x^7+x^4+x^3</math> होता है। हेक्साडेसिमल संख्या को कनवर्ट करने के लिए  कन्वेंशन का उपयोग किया जाता है जो  x की उच्चतम पॉवर एलएसबिट होता  है; यह 19<sub>16</sub> होता है।
+एमएसबिट-फर्स्ट उदाहरण में, रेमैंडर पॉलीनोमियल <math>x^7+x^5+x</math> होता है। हेक्साडेसिमल संख्या को कनवर्ट करने के लिए कन्वेंशन का उपयोग किया जाता है जो x की उच्चतम पॉवर एमएसबिट होता है; यह A2<sub>16</sub> होता है। एलएसबिट-फर्स्ट में रेमैंडरफल <math>x^7+x^4+x^3</math> होता है। हेक्साडेसिमल संख्या को कनवर्ट करने के लिए कन्वेंशन का उपयोग किया जाता है जो x की उच्चतम पॉवर एलएसबिट होता है; यह 19<sub>16</sub> होता है।
 == इम्प्लीमेंटेशन ==
-प्रत्येक स्टेप पर पूरा मेसेज लिखना, जैसा कि ऊपर दिए गए उदाहरण में किया गया है, बहुत कठिन होता है। मात्र  इंटररेस्टिंग बिट्स को रखने के लिए कुशल इम्प्लीमेंटेशन <math>n</math>-बिट शिफ्ट रजिस्टर का उपयोग करता है। पॉलीनोमियल का  <math>x</math> से गुणा किया जाता है जो रजिस्टर को एक स्थान से स्थानांतरित करने के समान होता है, क्योंकि गुणांक मूल्य में नहीं बदलते हैं बल्कि मात्र  पॉलीनोमियल के अगले पद तक बढ़ते हैं।
+प्रत्येक स्टेप पर पूरा मेसेज लिखना, जैसा कि ऊपर दिए गए उदाहरण में किया गया है, बहुत कठिन होता है। मात्र इंटररेस्टिंग बिट्स को रखने के लिए कुशल इम्प्लीमेंटेशन <math>n</math>-बिट शिफ्ट रजिस्टर का उपयोग करता है। पॉलीनोमियल का <math>x</math> से गुणा किया जाता है जो रजिस्टर को एक स्थान से स्थानांतरित करने के समान होता है, क्योंकि गुणांक मूल्य में नहीं बदलते हैं बल्कि मात्र पॉलीनोमियल के अगले पद तक बढ़ते हैं।
-यहां एन-बिट सीआरसी की कंप्यूटिंग के लिए कुछ स्यूडोकोड का फर्स्ट ड्राफ्ट होता है। यह पॉलीनोमियलों के लिए एक काल्पनिक वस्तु संरचना का उपयोग करता है, जहाँ <code>''x''</code> एक पूर्णांक चर नहीं होता है, तथापि  एक [[कंस्ट्रक्टर (कंप्यूटर विज्ञान)|कंस्ट्रक्टर]] एक पॉलीनोमियल [[वस्तु (कंप्यूटर विज्ञान)|ऑब्जेक्ट]]  उत्पन्न करता है जिसे जोड़ा, गुणा और घातांकित किया जा सकता है। <code>'''xor'''</code> के लिए दो पॉलीनोमियलों को जोड़ा जाता है, मॉड्यूलो दो; अर्थात्, दोनों पॉलीनोमियलों से प्रत्येक मिलान पद के गुणांकों को अलग किया जाता है।
+यहां एन-बिट सीआरसी की कंप्यूटिंग के लिए कुछ स्यूडोकोड का फर्स्ट ड्राफ्ट होता है। यह पॉलीनोमियलों के लिए एक काल्पनिक वस्तु संरचना का उपयोग करता है, जहाँ <code>''x''</code> एक पूर्णांक चर नहीं होता है, तथापि एक [[कंस्ट्रक्टर (कंप्यूटर विज्ञान)|कंस्ट्रक्टर]] एक पॉलीनोमियल [[वस्तु (कंप्यूटर विज्ञान)|ऑब्जेक्ट]] उत्पन्न करता है जिसे जोड़ा, गुणा और घातांकित किया जा सकता है। <code>'''एक्सओआर'''</code> के लिए दो पॉलीनोमियलों को जोड़ा जाता है, मॉड्यूलो दो; अर्थात्, दोनों पॉलीनोमियलों से प्रत्येक मिलान पद के गुणांकों को अलग किया जाता है।
   '''function''' crc(''bit array'' bitString[1..len], ''int'' len) {
-      remainderPolynomial := 0
+      remainderPolynomial := '''polynomialForm'''(bitString[1..n])   ''// First n bits of the message''
-      ''// A popular variant complements remainderPolynomial here; see {{slink||Preset to −1}} below''
+      ''// A popular variant complements remainderPolynomial here; see {{slink|| Preset to −1 }}''
       '''for''' i '''from''' 1 '''to''' len {
-          remainderPolynomial := remainderPolynomial '''xor''' (bitstring[i] * ''x''<sup>n−1</sup>)
+          remainderPolynomial := remainderPolynomial * ''x'' + bitString[i+n] * ''x''<sup>0</sup>   ''// Define bitString[k]=0 for k>len''
-          '''if''' (coefficient of ''x''<sup>n−1</sup> of remainderPolynomial) = 1 {
+          '''if''' coefficient of ''x''<sup>n</sup> of remainderPolynomial = 1 {
-              remainderPolynomial := (remainderPolynomial * ''x'') '''xor''' generatorPolynomial
+              remainderPolynomial := remainderPolynomial '''xor''' generatorPolynomial
-         } '''else''' {
-             remainderPolynomial := (remainderPolynomial * ''x'')
           }
       }
-      ''// A popular variant complements remainderPolynomial here; see {{slink||Post-invert}} below''
+      ''// A popular variant complements remainderPolynomial here; see {{slink||Post-invert }} below''
       '''return''' remainderPolynomial
   }
 :कोड फ्रेगमेंट 1: सरल पॉलीनोमियल डिवीज़न
-ध्यान दें कि यह उदाहरण कोड बाइट्स का उपयोग न करके बिट-ऑर्डरिंग कन्वेंशन को निर्दिष्ट करने की आवश्यकता से बचाता है; इनपुट <code>बिटस्ट्रिंग</code> फर्स्ट से ही एक बिट ऐरे के रूप में होता है, और <code>रेमैंडरपॉलीनोमियल</code>  संक्रियाओं के संदर्भ में मैनिपुलेट किया जाता है; <math>x</math> से गुणा  बाएँ या दाएँ शिफ्ट में हो सकता है, और  <code>बिटस्ट्रिंग[i+n]</code> का ऐड  <math>x^0</math> गुणांक में किया जाता है, जो रजिस्टर का दायां या बायां अंत हो सकता है।
+ध्यान दें कि यह उदाहरण कोड बाइट्स का उपयोग न करके बिट-ऑर्डरिंग कन्वेंशन को निर्दिष्ट करने की आवश्यकता से बचाता है; इनपुट <code>बिटस्ट्रिंग</code> फर्स्ट से ही एक बिट ऐरे के रूप में होता है, और <code>रेमैंडरपॉलीनोमियल</code> संक्रियाओं के संदर्भ में मैनिपुलेट किया जाता है; <math>x</math> से गुणा बाएँ या दाएँ शिफ्ट में हो सकता है, और <code>बिटस्ट्रिंग[i+n]</code> का ऐड <math>x^0</math> गुणांक में किया जाता है, जो रजिस्टर का दायां या बायां अंत हो सकता है।
-इस कोड की दो हानि होती हैं. सर्व प्रथम, इसे <code>रेमैंडरपॉलीनोमियल</code>को रखने के लिए वास्तव में n+1-बिट रजिस्टर की आवश्यकता होती है  इस प्रकार  <math>x^n</math> गुणांक का परीक्षण किया जा सकता है। इससे भी महत्वपूर्ण बात यह है n शून्य बिट्स के साथ पैडेड होने के लिए <code>बिटस्ट्रिंग</code> की आवश्यकता होती  है।
+इस कोड की दो हानि होती हैं. सर्व प्रथम, इसे <code>रेमैंडरपॉलीनोमियल</code>को रखने के लिए वास्तव में n+1-बिट रजिस्टर की आवश्यकता होती है इस प्रकार <math>x^n</math> गुणांक का परीक्षण किया जा सकता है। इससे भी महत्वपूर्ण बात यह है n शून्य बिट्स के साथ पैडेड होने के लिए <code>बिटस्ट्रिंग</code> की आवश्यकता होती है।
 पहली समस्या को <math>x</math> से गुणा करने से फर्स्ट <code>रेमैंडरपॉलीनोमियल</code> के <math>x^{n-1}</math> गुणांक का परीक्षण करके हल किया जा सकता है।
@@ Line 145: / Line 143: @@
 दूसरी समस्या को अंतिम n पुनरावृत्तियों को अलग विधि से करके हल किया जा सकता है, परन्तु एक अधिक सूक्ष्म अनुकूलन होता है जिसका उपयोग हार्डवेयर और सॉफ्टवेयर दोनों इम्प्लीमेंटेशनों में सार्वभौमिक रूप से किया जाता है।
-क्योंकि मेसेज से जनरेटर पॉलीनोमियल को घटाने के लिए उपयोग किया जाने वाला XOR ऑपरेशन कम्युएटीव और अस्सोसिएटिव होता है, इससे कोई अंतर  नहीं पड़ता कि विभिन्न इनपुट <code>रेमैंडरपॉलीनोमियल</code> से किस क्रम में संयुक्त होते हैं।  और विरेमैंडर रूप से, <code>बिटस्ट्रिंग</code> के दिए गए बिट को अंतिम क्षण तक <code>रेमैंडरपॉलीनोमियल</code> में जोड़ने की आवश्यकता नहीं होती है  जब यह निर्धारित करने के लिए परीक्षण किया जाता है कि <code>जनरेटरपॉलीनोमियल</code>के साथ <code>xor</code> करना है या नहीं।
+क्योंकि मेसेज से जनरेटर पॉलीनोमियल को घटाने के लिए उपयोग किया जाने वाला एक्सओआर ऑपरेशन कम्युएटीव और अस्सोसिएटिव होता है, इससे कोई अंतर नहीं पड़ता कि विभिन्न इनपुट <code>रेमैंडरपॉलीनोमियल</code> से किस क्रम में संयुक्त होते हैं। और विरेमैंडर रूप से, <code>बिटस्ट्रिंग</code> के दिए गए बिट को अंतिम क्षण तक <code>रेमैंडरपॉलीनोमियल</code> में जोड़ने की आवश्यकता नहीं होती है जब यह निर्धारित करने के लिए परीक्षण किया जाता है कि <code>जनरेटरपॉलीनोमियल</code>के साथ <code>एक्सओआर</code> करना है या नहीं।
 इससे मेसेज के फर्स्ट n बिट्स के साथ <code>रेमैंडरपॉलीनोमियल</code> को प्रीलोड करने की आवश्यकता समाप्त हो जाती है:
-  '''function''' crc(''byte array'' string[1..len], ''int'' len) {
+  '''function''' crc(''bit array'' bitString[1..len], ''int'' len) {
       remainderPolynomial := 0
-      ''// A popular variant complements remainderPolynomial here; see {{slink||Preset to −1}} below''
+      ''// A popular variant complements remainderPolynomial here; see {{slink|| Preset to −1 }} below''
       '''for''' i '''from''' 1 '''to''' len {
-          remainderPolynomial := remainderPolynomial '''xor''' '''polynomialForm'''(string[i]) * x<sup>n−8</sup>
+          remainderPolynomial := remainderPolynomial '''xor''' (bitstring[i] * ''x''<sup>n−1</sup>)
-          '''for''' j '''from''' 1 '''to''' 8 {    ''// Assuming 8 bits per byte''
+          '''if''' (coefficient of ''x''<sup>n−1</sup> of remainderPolynomial) = 1 {
-             '''if''' coefficient of ''x''<sup>n−1</sup> of remainderPolynomial = 1 {
+             remainderPolynomial := (remainderPolynomial * ''x'') '''xor''' generatorPolynomial
-                 remainderPolynomial := (remainderPolynomial * ''x'') '''xor''' generatorPolynomial
+         } '''else''' {
-             } '''else''' {
+             remainderPolynomial := (remainderPolynomial * ''x'')
-                 remainderPolynomial := (remainderPolynomial * ''x'')
-             }
           }
       }
-      ''// A popular variant complements remainderPolynomial here; see {{slink||Post-invert}} below''
+      ''// A popular variant complements remainderPolynomial here; see {{slink||Post-invert }} below''
       '''return''' remainderPolynomial
   }
-:कोड फ्रेगमेंट 2: डिफर्ड XORing के साथ पॉलीनोमियल डिवीज़न
+:कोड फ्रेगमेंट 2: डिफर्ड एक्सओआरआईएनजी के साथ पॉलीनोमियल डिवीज़न
-यह मानक बिट-ए-टाइम हार्डवेयर सीआरसी इम्प्लीमेंटेशन होता है, और अध्ययन के योग्य होता है; एक बार जब आप समझ जाते हैं कि यह फर्स्ट संस्करण के समान परिणाम की कंप्यूटिंग क्यों करता है, तो रेमैंडर अनुकूलन अत्यधिक सरल हो जाता हैं। यदि <code>रेमैंडरपॉलीनोमियल</code> मात्र n बिट लॉन्ग होता है, तो  इसके और <code>जनरेटरपॉलीनोमियल</code> के <math>x^n</math> गुणांक को सरलता से त्याग दिया जाता है। यही कारण है कि आप सामान्यतः सीआरसी पॉलीनोमियलों को बाइनरी में लिखे हुए देखेंगे, जिसमें प्रमुख गुणांक हटा दिया जाएगा।
+यह मानक बिट-ए-टाइम हार्डवेयर सीआरसी इम्प्लीमेंटेशन होता है, और अध्ययन के योग्य होता है; एक बार जब आप समझ जाते हैं कि यह फर्स्ट संस्करण के समान परिणाम की कंप्यूटिंग क्यों करता है, तो रेमैंडर अनुकूलन अत्यधिक सरल हो जाता हैं। यदि <code>रेमैंडरपॉलीनोमियल</code> मात्र n बिट लॉन्ग होता है, तो इसके और <code>जनरेटरपॉलीनोमियल</code> के <math>x^n</math> गुणांक को सरलता से त्याग दिया जाता है। यही कारण है कि आप सामान्यतः सीआरसी पॉलीनोमियलों को बाइनरी में लिखे हुए देखेंगे, जिसमें प्रमुख गुणांक हटा दिया जाएगा।
-सॉफ्टवेयर में, यह नोट करना सुविधाजनक है कि जहां कोई प्रत्येक बिट के <code>xor</code> को अंतिम क्षण तक विलंबित कर सकता है, वहीं इसे फर्स्ट करना भी संभव है। <code>xor</code> को एक समय में एक बाइट निष्पादित करना आमतौर पर सुविधाजनक होता है, यहां तक कि इस तरह से एक बिट-ए-टाइम इम्प्लीमेंटेशन में भी:
+सॉफ्टवेयर में, यह नोट करना सुविधाजनक है कि जहां कोई प्रत्येक बिट के <code>एक्सओआर</code> को अंतिम क्षण तक विलंबित कर सकता है, वहीं इसे फर्स्ट करना भी संभव है। <code>एक्सओआर</code> को एक समय में एक बाइट निष्पादित करना आमतौर पर सुविधाजनक होता है, यहां तक कि इस तरह से एक बिट-ए-टाइम इम्प्लीमेंटेशन में भी:
   '''function''' crc(''byte array'' string[1..len], ''int'' len) {
       remainderPolynomial := 0
-      ''// A popular variant complements remainderPolynomial here; see {{slink||Preset to −1}} below''
+      ''// A popular variant complements remainderPolynomial here; see {{slink|| Preset to −1 }} below''
       '''for''' i '''from''' 1 '''to''' len {
           remainderPolynomial := remainderPolynomial '''xor''' '''polynomialForm'''(string[i]) * x<sup>n−8</sup>
@@ Line 185: / Line 180: @@
           }
       }
-      ''// A popular variant complements remainderPolynomial here; see {{slink||Post-invert}} below''
+      ''// A popular variant complements remainderPolynomial here; see {{slink||Post-invert }} below''
       '''return''' remainderPolynomial
   }
-:कोड फ्रेगमेंट 3: बाइटवाइज मेसेज XORing के साथ पॉलीनोमियल डिवीज़न
+:कोड फ्रेगमेंट 3: बाइटवाइज मेसेज एक्सओआरआईएनजी के साथ पॉलीनोमियल डिवीज़न
 यह सामान्यतः सबसे कॉम्पैक्ट सॉफ़्टवेयर इम्प्लीमेंटेशन होता है, जिसका उपयोग [[माइक्रोकंट्रोलर्स]] में तब किया जाता है जब स्पेस प्रीमियम ओवर स्पीड पर होता है।
 == बिट ऑर्डरिंग (एंडियननेस) ==
-जब [[बिट-सीरियल आर्किटेक्चर]] [[हार्डवेयर (कंप्यूटर)|हार्डवेयर]] में प्रयुक्त किया जाता है, तो जनरेटर पॉलीनोमियल विशिष्ट रूप से बिट असाइनमेंट का वर्णन करता है; ट्रांसमिटेड प्रथम बिट सदैव उच्चतम पॉवर का गुणांक <math>x</math> होता है, और लास्ट बात <math>n</math> ट्रांसमिटेड बिट्स सीआरसी रेमैंडर <math>R(x)</math> हैं , <math>x^{n-1}</math> के गुणांक से प्रारंभ करते हुए  और के <math>x^0</math> गुणांक के साथ समाप्त होता है, अर्थात् 1 का गुणांक होता है।
+जब [[बिट-सीरियल आर्किटेक्चर]] [[हार्डवेयर (कंप्यूटर)|हार्डवेयर]] में प्रयुक्त किया जाता है, तो जनरेटर पॉलीनोमियल विशिष्ट रूप से बिट असाइनमेंट का वर्णन करता है; ट्रांसमिटेड प्रथम बिट सदैव उच्चतम पॉवर का गुणांक <math>x</math> होता है, और लास्ट बात <math>n</math> ट्रांसमिटेड बिट्स सीआरसी रेमैंडर <math>R(x)</math> हैं , <math>x^{n-1}</math> के गुणांक से प्रारंभ करते हुए और के <math>x^0</math> गुणांक के साथ समाप्त होता है, अर्थात् 1 का गुणांक होता है।
 यघपि, जब बिट्स को एक समय में एक बाइट संसाधित किया जाता है, जैसे कि समानांतर ट्रांसमिशन का उपयोग करते समय, 8बी/10बी एन्कोडिंग या आरएस-232-शैली एसिंक्रोनस सीरियल संचार के रूप में बाइट फ़्रेमिंग, या [[सॉफ़्टवेयर]] में सीआरसी प्रयुक्त करते समय, डेटा के बिट ऑर्डरिंग (एंडियननेस) को निर्दिष्ट करना आवश्यक होता है; प्रत्येक बाइट में कौन सा बिट "फर्स्ट" माना जाता है और उच्च पॉवर का गुणांक <math>x</math> होता है।
-यदि डेटा [[धारावाहिक संचार|सीरियल कम्युनिकेशनर]] के लिए नियत है, तो बिट ऑर्डर का उपयोग करना सबसे अच्छा है जिससे डेटा अंततः भेजा जाएगा। ऐसा इसलिए है क्योंकि सीआरसी की [[विस्फोट त्रुटि|बर्स्ट एरर]] का पता लगाने की क्षमता मेसेज पॉलीनोमियल <math>M(x)</math> में निकटता पर आधारित होती है ; यदि आसन्न पॉलीनोमियल शब्दों को क्रमिक रूप सेट्रांसमिट नहीं किया जाता है, तो बिट्स के पुनर्व्यवस्था के कारण एक भौतिक एरर बर्स्ट को लॉन्ग बर्स्ट के रूप में देखा जा सकता है।
+यदि डेटा [[धारावाहिक संचार|सीरियल कम्युनिकेशनर]] के लिए नियत है, तो बिट ऑर्डर का उपयोग करना सबसे अच्छा है जिससे डेटा अंततः भेजा जाएगा। ऐसा इसलिए है क्योंकि सीआरसी की [[विस्फोट त्रुटि|बर्स्ट एरर]] का पता लगाने की एबिलिटी मेसेज पॉलीनोमियल <math>M(x)</math> में निकटता पर आधारित होती है ; यदि आसन्न पॉलीनोमियल शब्दों को क्रमिक रूप सेट्रांसमिट नहीं किया जाता है, तो बिट्स के पुनर्व्यवस्था के कारण एक भौतिक एरर बर्स्ट को लॉन्ग बर्स्ट के रूप में देखा जा सकता है।
 उदाहरण के लिए, [[आईईईई 802]] ([[ईथरनेट]]) और आरएस-232 ([[ आनुक्रमिक द्वार |सीरियल पोर्ट]] ) दोनों मानक कम से कम महत्वपूर्ण बिट फर्स्ट (लिटिल-एंडियन) ट्रांसमिशन को निर्दिष्ट करते हैं, इसलिए ऐसे लिंक पर भेजे गए डेटा की सुरक्षा के लिए एक सॉफ्टवेयर सीआरसी इम्प्लीमेंटेशन को प्रत्येक बाइट में कम से कम महत्वपूर्ण बिट्स को उच्चतम पॉवरों के गुणांक <math>x</math> में मैप करना चाहिए। दूसरी ओर, [[फ्लॉपी डिस्क]] और अधिकांश [[हार्ड ड्राइव]] फर्स्ट प्रत्येक बाइट का सबसे महत्वपूर्ण बिट लिखते हैं।
@@ Line 204: / Line 198: @@
 एलएसबिट-फर्स्ट सीआरसी को सॉफ़्टवेयर में प्रयुक्त करना थोड़ा आसान होता है, इसलिए इसे कुछ हद तक सामान्य रूप से देखा जाता है, लेकिन कई प्रोग्रामर एमएसबिट-फर्स्ट बिट ऑर्डर का पालन करना आसान पाते हैं। इस प्रकार, उदाहरण के लिए, एक्सएमओडीईएम-सीआरसी एक्सटेंशन, सॉफ्टवेयर में सीआरसी का प्रारंभिक उपयोग, एमएसबिट-फर्स्ट सीआरसी का उपयोग करता है।
-अब तक, स्यूडोकोड ने स्यूडोकोड में बदलावों को गुणन के रूप में वर्णित करके बाइट्स के भीतर बिट्स के क्रम को निर्दिष्ट करने से बचता  है। <math>x</math> और द्विआधारी से पॉलीनोमियल रूप में स्पष्ट रूपांतरण लिखना। व्यवहार में, सीआरसी को एक विरेमैंडर बिट-ऑर्डरिंग कन्वेंशन का उपयोग करके एक मानक बाइनरी रजिस्टर में रखा जाता है। एमएसबिट-फर्स्ट रूप में, सबसे महत्वपूर्ण बाइनरी बिट्स फर्स्ट भेजे जाएंगे और इसलिए इसमें उच्च-क्रम पॉलीनोमियल गुणांक होंगे, जबकि एलएसबिट-फर्स्ट रूप में, कम से कम महत्वपूर्ण बाइनरी बिट्स में उच्च-क्रम गुणांक होंगे। उपरोक्त स्यूडोकोड दोनों रूपों में लिखा जा सकता है। कंसर्टर्नर्स के लिए, यह 16-बिट सीआरसी-16-[[CCITT]] पॉलीनोमियल <math>x^{16} + x^{12} + x^5 + 1</math> का उपयोग करता है।
+अब तक, स्यूडोकोड ने स्यूडोकोड में बदलावों को गुणन के रूप में वर्णित करके बाइट्स के भीतर बिट्स के क्रम को निर्दिष्ट करने से बचता है। <math>x</math> और द्विआधारी से पॉलीनोमियल रूप में स्पष्ट रूपांतरण लिखना। व्यवहार में, सीआरसी को एक विरेमैंडर बिट-ऑर्डरिंग कन्वेंशन का उपयोग करके एक मानक बाइनरी रजिस्टर में रखा जाता है। एमएसबिट-फर्स्ट रूप में, सबसे महत्वपूर्ण बाइनरी बिट्स फर्स्ट भेजे जाएंगे और इसलिए इसमें उच्च-क्रम पॉलीनोमियल गुणांक होंगे, जबकि एलएसबिट-फर्स्ट रूप में, कम से कम महत्वपूर्ण बाइनरी बिट्स में उच्च-क्रम गुणांक होंगे। उपरोक्त स्यूडोकोड दोनों रूपों में लिखा जा सकता है। कंसर्टर्नर्स के लिए, यह 16-बिट सीआरसी-16-[[CCITT|सीसीआईटीटी]] पॉलीनोमियल <math>x^{16} + x^{12} + x^5 + 1</math> का उपयोग करता है।
+ ''/// Most significant bit first (big-endian)''
- ''// Most significant bit first (big-endian)''
   ''// x^16+x^12+x^5+1 = (1) 0001 0000 0010 0001 = 0x1021''
   '''function''' crc(''byte array'' string[1..len], ''int'' len) {
@@ Line 223: / Line 218: @@
       }
       ''// A popular variant complements rem here''
       '''return''' rem
   }
@@ Line 244: / Line 238: @@
       }
       ''// A popular variant complements rem here''
       '''return''' rem
   }
 :कोड फ्रेगमेंट 5: शिफ्ट रजिस्टर बेस्ड डिवीज़न, एलएसबी फर्स्ट
-ध्यान दें कि एलएसबिट-फर्स्ट  फॉर्म शिफ्ट करने की आवश्यकता से बचाता है <code>string[i]</code> से फर्स्ट <code>xor</code>. किसी भी स्थिति में, सीआरसी के बाइट्स को उस क्रम में प्रसारित करना सुनिश्चित करें जो आपके चुने हुए बिट-ऑर्डरिंग कन्वेंशन के समरूप होता है।
+ध्यान दें कि एलएसबिट-फर्स्ट फॉर्म शिफ्ट करने की आवश्यकता से बचाता है <code>स्ट्रिंग[i]</code> से फर्स्ट <code>एक्सओआर</code>. किसी भी स्थिति में, सीआरसी के बाइट्स को उस क्रम में ट्रांसमिट करना सुनिश्चित करें जो आपके चुने हुए बिट-ऑर्डरिंग कन्वेंशन के समरूप होता है।
-ध्यान दें कि एलएसबिट-फर्स्ट फॉर्म से <code>xor</code>हले स्ट्रिंग [i] को स्थानांतरित करने की आवश्यकता से बचाता है। किसी भी स्थिति में, सीआरसी के बाइट्स को उस क्रम में प्रसारित करना सुनिश्चित करें जो आपके चुने हुए बिट-ऑर्डरिंग कन्वेंशन के समरूप होता है।
+ध्यान दें कि एलएसबिट-फर्स्ट फॉर्म से <code>एक्सओआर</code>हले स्ट्रिंग [i] को स्थानांतरित करने की आवश्यकता से बचाता है। किसी भी स्थिति में, सीआरसी के बाइट्स को उस क्रम में ट्रांसमिट करना सुनिश्चित करें जो आपके चुने हुए बिट-ऑर्डरिंग कन्वेंशन के समरूप होता है।
 == मल्टी-बिट कंप्यूटिंग ==
@@ Line 261: / Line 254: @@
   rem = (rem '''leftShift''' 8) '''xor''' big_endian_table[string[i] '''xor''' ((leftmost 8 bits of rem) '''rightShift''' (n-8))]
   // Lsbit-first
   rem = (rem '''rightShift''' 8) '''xor''' little_endian_table[string[i] '''xor''' (rightmost 8 bits of rem)]
-:कोड फ्रेगमेंट 6: टेबल आधारित डिवीज़न  के कोर
+:कोड फ्रेगमेंट 6: टेबल आधारित डिवीज़न के कोर
-सबसे सामान्यतः सामने आने वाले सीआरसी एल्गोरिदम में से एक को सीआरसी-32 के रूप में जाना जाता है, जिसका उपयोग (अन्य के अलावा) ईथरनेट, [[एफडीडीआई]], ज़िप (फ़ाइल फॉर्मेट) और अन्य आर्काइव  फॉर्मेट, और पोर्टेबल नेटवर्क ग्राफिक्स [[छवि प्रारूप|इमेज फॉर्मेट]] द्वारा किया जाता है। इसके पॉलीनोमियल को एमएसबिट-फर्स्ट को 0x04C11DB7, या एलएसबिट-फर्स्ट को 0xEDB88320 के रूप में लिखा जा सकता है। [[पोर्टेबल नेटवर्क ग्राफ़िक्स]] पर W3C वेबपेज में सीआरसी-32 के C में एक संक्षिप्त और सरल टेबल-संचालित इम्प्लीमेंटेशन के साथ एक अपेंडिक्स सम्मलित होता है।<ref>{{cite web
+सबसे सामान्यतः सामने आने वाले सीआरसी एल्गोरिदम में से एक को सीआरसी-32 के रूप में जाना जाता है, जिसका उपयोग (अन्य के अलावा) ईथरनेट, [[एफडीडीआई]], ज़िप (फ़ाइल फॉर्मेट) और अन्य आर्काइव फॉर्मेट, और पोर्टेबल नेटवर्क ग्राफिक्स [[छवि प्रारूप|इमेज फॉर्मेट]] द्वारा किया जाता है। इसके पॉलीनोमियल को एमएसबिट-फर्स्ट को 0x04C11DB7, या एलएसबिट-फर्स्ट को 0xEDB88320 के रूप में लिखा जा सकता है। [[पोर्टेबल नेटवर्क ग्राफ़िक्स]] पर W3C वेबपेज में सीआरसी-32 के C में एक संक्षिप्त और सरल टेबल-संचालित इम्प्लीमेंटेशन के साथ एक अपेंडिक्स सम्मलित होता है।<ref>{{cite web
 | url=https://www.w3.org/TR/PNG/#D-CRCAppendix
 | title=Portable Network Graphics (PNG) Specification (Second Edition): Annex D, Sample Cyclic Redundancy Code implementation
@@ Line 272: / Line 264: @@
 | access-date = 2016-02-16}}</ref> आप देखेंगे कि कोड यहां प्रस्तुत एलएसबिट-फर्स्ट बिट-एट-ए-टाइम स्यूडोकोड के समरूप होता है, और टेबल बिट-एट-ए-टाइम कोड का उपयोग करके बनाई गई है।
--प्रविष्टि टेबल का उपयोग करना सामान्यतः सबसे सुविधाजनक होता है, लेकिन अन्य आकारों का उपयोग किया जा सकता है। छोटे माइक्रोकंट्रोलर में, एक समय में चार बिट्स को प्रोसेस करने के लिए 16-एंट्री टेबल का उपयोग करने से टेबल को छोटा रखते हुए उपयोगी गति में सुधार होता है। पर्याप्त स्टोरेज  वाले कंप्यूटरों पर, a {{val|65536}}-एंट्री टेबल का उपयोग एक समय में 16 बिट्स को प्रोसेस करने के लिए किया जा सकता है।
+-प्रविष्टि टेबल का उपयोग करना सामान्यतः सबसे सुविधाजनक होता है, लेकिन अन्य आकारों का उपयोग किया जा सकता है। छोटे माइक्रोकंट्रोलर में, एक समय में चार बिट्स को प्रोसेस करने के लिए 16-एंट्री टेबल का उपयोग करने से टेबल को छोटा रखते हुए उपयोगी गति में सुधार होता है। पर्याप्त स्टोरेज वाले कंप्यूटरों पर, a {{val|65536}}-एंट्री टेबल का उपयोग एक समय में 16 बिट्स को प्रोसेस करने के लिए किया जा सकता है।
 ==== टेबल जनरेट करना ====
-टेबल उत्पन्न करने वाला सॉफ़्टवेयर इतना छोटा और तेज़ है कि स्टोरेज से पूर्व-कंप्यूटिंग की गई टेबलओं को लोड करने की तुलना में प्रोग्राम स्टार्टअप पर उनकी कंप्यूटिंग करना आमतौर पर तेज़ होता है। एक लोकप्रिय तकनीक 256 संभावित 8-बिट बाइट्स के सीआरसी उत्पन्न करने के लिए 256 बार बिट-ए-टाइम कोड का उपयोग करना है। हालाँकि, उस संपत्ति का लाभ उठाकर इसे महत्वपूर्ण रूप से अनुकूलित किया जा सकता है <code>table[i '''xor''' j] == table[i] '''xor''' table[j]</code>. मात्र दो की पॉवरयों के अनुरूप टेबल प्रविष्टियों की सीधे कंप्यूटिंग करने की आवश्यकता है।
+टेबल उत्पन्न करने वाला सॉफ़्टवेयर इतना छोटा और उच्चतम होता है कि स्टोरेज से पूर्व-कंप्यूटिंग की गई टेबलओं को लोड करने की तुलना में प्रोग्राम स्टार्टअप पर उनकी कंप्यूटिंग करना सामान्यतः उच्चतम होता है। एक लोकप्रिय तकनीक 256 संभावित 8-बिट बाइट्स के सीआरसी उत्पन्न करने के लिए 256 बार बिट-ए-टाइम कोड का उपयोग करता है। यघपि, <code>टेबल[i '''एक्सओआर''' j] == टेबल[i] '''एक्सओआर''' टेबल[j]</code> की प्रॉपर्टी का लाभ उठाकर इसे महत्वपूर्ण रूप से अनुकूलित किया जा सकता है। मात्र दो की पॉवरों के अनुरूप टेबल एंटरी की सीधे कंप्यूटिंग करने की आवश्यकता होती है।
-निम्नलिखित उदाहरण कोड में, <code>सीआरसी</code> का मान रखता है <code>table[i]</code>:
+निम्नलिखित उदाहरण कोड में, <code>सीआरसी</code> <code>टेबल[i]</code>का मान रखता है :
   big_endian_table[0] := 0
@@ Line 294: / Line 286: @@
       }
       i := i '''leftshift''' 1
   } '''while''' i < 256
 :'कोड फ्रेगमेंट 7: बाइट-एट-ए-टाइम सीआरसी टेबल जनरेशन, एमएसबी फर्स्ट'
@@ Line 312: / Line 303: @@
       }
       i := i '''rightshift''' 1
   } '''while''' i > 0
 :'कोड फ्रेगमेंट 8: बाइट-एट-ए-टाइम सीआरसी टेबल जनरेशन, एलएसबी फर्स्ट'
-इन कोड नमूनों में, टेबल अनुक्रमणिका <code>i + j</code> के बराबर है <code>i '''xor''' j</code>; आप जो भी फॉर्म अधिक सुविधाजनक हो उसका उपयोग कर सकते हैं।
+इन कोड नमूनों में, टेबल अनुक्रमणिका <code>i + j</code> के समान होती है <code>i '''एक्सओआर''' j</code>; आप जो भी फॉर्म अधिक सुविधाजनक हो उसका उपयोग कर सकते हैं।
 ==== सीआरसी-32 एल्गोरिथ्म ====
-यह सीआरसी के सीआरसी-32 संस्करण के लिए एक व्यावहारिक एल्गोरिदम है।<ref>{{cite web|url=https://msdn.microsoft.com/en-us/library/dd905031.aspx|title=[MS-ABS]: 32-Bit CRC Algorithm|website=msdn.microsoft.com|access-date=4 November 2017|archive-date=7 November 2017|archive-url=https://web.archive.org/web/20171107004846/https://msdn.microsoft.com/en-us/library/dd905031.aspx|url-status=live}}</ref> सीआरसीटेबल एक कंप्यूटिंग का [[संस्मरण]] है जिसे मेसेज के प्रत्येक बाइट के लिए दोहराया जाना होगा ({{section link|Computation of cyclic redundancy checks|Multi-bit computation}}). <syntaxhighlight>
+यह सीआरसी के सीआरसी-32 संस्करण के लिए एक व्यावहारिक एल्गोरिदम है।<ref>{{cite web|url=https://msdn.microsoft.com/en-us/library/dd905031.aspx|title=[MS-ABS]: 32-Bit CRC Algorithm|website=msdn.microsoft.com|access-date=4 November 2017|archive-date=7 November 2017|archive-url=https://web.archive.org/web/20171107004846/https://msdn.microsoft.com/en-us/library/dd905031.aspx|url-status=live}}</ref> सीआरसीटेबल एक कंप्यूटिंग का [[संस्मरण]] है जिसे मेसेज के प्रत्येक बाइट के लिए दोहराया जाना होगा ({{section link|कम्प्यूटेशन ऑफ़ साइक्लिक रीडेंडेन्सी चेक्स |मल्टी-बिट कम्प्यूटेशन}})।  <syntaxhighlight>
 Function CRC32
     Input:
@@ Line 337: / Line 327: @@
 return crc32
 </syntaxhighlight>
 C में, एल्गोरिथ्म इस प्रकार दिखता है:
@@ Line 357: / Line 346: @@
 </syntaxhighlight>
+=== बाइट-स्लाइसिंग यूजिंग मल्टीप्ल टेबल ===
+एक स्लाइस-बाय-एन (सामान्यतः सीआरसी32 के लिए स्लाइस-बाय-8; एन ≤ 64) एल्गोरिदम उपस्थित होता है जो सामान्यतः पर सरवटे एल्गोरिदम की तुलना में प्रदर्शन को दोगुना या तिगुना कर देता है। एक समय में 8 बिट्स पढ़ने के अतिरिक्त, एल्गोरिदम एक समय में 8N बिट्स पढ़ता है। ऐसा करने से [[सुपरस्केलर]] प्रोसेसर पर प्रदर्शन अधिकतम हो जाता है।<ref>{{cite book |doi=10.1109/ISCC.2005.18 |url=https://static.aminer.org/pdf/PDF/000/432/446/a_systematic_approach_to_building_high_performance_software_based_crc.pdf |chapter=A Systematic Approach to Building High Performance Software-Based CRC Generators |title=10th IEEE Symposium on Computers and Communications (ISCC'05) |year=2005 |last1=Kounavis |first1=M.E. |last2=Berry |first2=F.L. |pages=855–862 |isbn=0-7695-2373-0 |s2cid=10308354 }}</ref><ref>{{cite journal |title=उच्च-प्रदर्शन सीआरसी पीढ़ी के लिए नवीन तालिका लुकअप-आधारित एल्गोरिदम|journal=IEEE Transactions on Computers |date=November 2008 |volume=57 |issue=11 |pages=1550–1560 |doi=10.1109/TC.2008.85 |first1=Frank L. |last1=Berry |first2=Michael E. |last2=Kounavis|s2cid=206624854 }}</ref><ref>{{cite tech report |title=High Octane CRC Generation with the Intel Slicing-by-8 Algorithm |publisher=[[Intel]] |url=http://download.intel.com:80/technology/comms/perfnet/download/slicing-by-8.pdf |archive-url=https://web.archive.org/web/20120722193753/http://download.intel.com/technology/comms/perfnet/download/slicing-by-8.pdf |archive-date=2012-07-22 |url-status=dead }}</ref><ref>{{Cite web|url=https://www.kernel.org/doc/Documentation/crc32.txt|title=सीआरसी गणना पर संक्षिप्त ट्यूटोरियल|work=The Linux Kernel Archives}}</ref>यह स्पष्ट नहीं है कि वास्तव में एल्गोरिदम का आविष्कार किसने किया था।<ref>{{cite web |title=Who invented the slicing-by-N CRC32 algorithm? |first=Abhijit |last=Menon-Sen |date=2017-01-20 |url=http://toroid.org/crc32-slicing-by-N-paper}}</ref>
-=== एकाधिक टेबलओं का उपयोग करके बाइट-स्लाइसिंग ===
+=== पैरेलल कम्प्यूटेशन विदाउट टेबल ===
-एक स्लाइस-बाय-एन (आमतौर पर सीआरसी32 के लिए स्लाइस-बाय-8; एन ≤ 64) एल्गोरिदम मौजूद है जो आमतौर पर सरवटे एल्गोरिदम की तुलना में प्रदर्शन को दोगुना या तिगुना कर देता है। एक समय में 8 बिट्स पढ़ने के बजाय, एल्गोरिदम एक समय में 8N बिट्स पढ़ता है। ऐसा करने से [[सुपरस्केलर]] प्रोसेसर पर प्रदर्शन अधिकतम हो जाता है।<ref>{{cite book |doi=10.1109/ISCC.2005.18 |url=https://static.aminer.org/pdf/PDF/000/432/446/a_systematic_approach_to_building_high_performance_software_based_crc.pdf |chapter=A Systematic Approach to Building High Performance Software-Based CRC Generators |title=10th IEEE Symposium on Computers and Communications (ISCC'05) |year=2005 |last1=Kounavis |first1=M.E. |last2=Berry |first2=F.L. |pages=855–862 |isbn=0-7695-2373-0 |s2cid=10308354 }}</ref><ref>{{cite journal |title=उच्च-प्रदर्शन सीआरसी पीढ़ी के लिए नवीन तालिका लुकअप-आधारित एल्गोरिदम|journal=IEEE Transactions on Computers |date=November 2008 |volume=57 |issue=11 |pages=1550–1560 |doi=10.1109/TC.2008.85 |first1=Frank L. |last1=Berry |first2=Michael E. |last2=Kounavis|s2cid=206624854 }}</ref><ref>{{cite tech report |title=High Octane CRC Generation with the Intel Slicing-by-8 Algorithm |publisher=[[Intel]] |url=http://download.intel.com:80/technology/comms/perfnet/download/slicing-by-8.pdf |archive-url=https://web.archive.org/web/20120722193753/http://download.intel.com/technology/comms/perfnet/download/slicing-by-8.pdf |archive-date=2012-07-22 |url-status=dead }}</ref><ref>{{Cite web|url=https://www.kernel.org/doc/Documentation/crc32.txt|title=सीआरसी गणना पर संक्षिप्त ट्यूटोरियल|work=The Linux Kernel Archives}}</ref>
+एक समय में किसी बाइट या शब्द का समानांतर अपडेट विदाउट टेबल को भी एक्स्प्लिसिटी किया जा सकता है।<ref>{{cite newsgroup
-यह स्पष्ट नहीं है कि वास्तव में एल्गोरिदम का आविष्कार किसने किया था।<ref>{{cite web |title=Who invented the slicing-by-N CRC32 algorithm? |first=Abhijit |last=Menon-Sen |date=2017-01-20 |url=http://toroid.org/crc32-slicing-by-N-paper}}</ref>
-=== टेबल के बिना समानांतर कंप्यूटिंग ===
-एक समय में किसी बाइट या शब्द का समानांतर अद्यतन बिना टेबल के भी स्पष्ट रूप से किया जा सकता है।<ref>{{cite newsgroup
    | title = Re: 8051 and CRC-CCITT
    | author = Jon Buller
@@ Line 371: / Line 358: @@
    | url = https://groups.google.com/d/msg/comp.arch.embedded/fvQ7yM5F6ys/3xcgqF3Kqc4J
    | access-date = 2016-02-16
-}}</ref> इसका उपयोग आमतौर पर हाई-स्पीड हार्डवेयर इम्प्लीमेंटेशन में किया जाता है। प्रत्येक बिट के लिए 8 बिट्स को स्थानांतरित करने के बाद एक समीकरण हल किया जाता है। निम्नलिखित टेबल निम्नलिखित प्रतीकों का उपयोग करके कुछ सामान्य रूप से उपयोग किए जाने वाले पॉलीनोमियलों के समीकरणों को सूचीबद्ध करती हैं:
+}}</ref> इसका उपयोग सामान्यतः हाई-स्पीड हार्डवेयर इम्प्लीमेंटेशन में किया जाता है। प्रत्येक बिट के लिए 8 बिट्स को स्थानांतरित करने के बाद एक समीकरण हल किया जाता है। निम्नलिखित टेबल निम्नलिखित सिग्नलों का उपयोग करके कुछ सामान्य रूप से उपयोग किए जाने वाले पॉलीनोमियलों के समीकरणों को सूचीबद्ध करती हैं:
 {| class="wikitable"
 |-
-| c<sub>i</sub> || सीआरसी bit 7…0 (or 15…0) before update
+| c<sub>i</sub> || सीआरसी बिट 7…0 (or 15…0) बिफोर अपडेट
 |-
-| r<sub>i</sub> || सीआरसी bit 7…0 (or 15…0) after update
+| r<sub>i</sub> || सीआरसी बिट 7…0 (or 15…0) आफ्टर अपडेट
 |-
-| d<sub>i</sub> || input data bit 7…0
+| d<sub>i</sub> || इनपुट डाटा बिट 7…0
 |-
 | e<sub>i</sub> = d<sub>i</sub> + c<sub>i</sub>
-| e<sub>p</sub> = e<sub>7</sub> + e<sub>6</sub> + … + e<sub>1</sub> + e<sub>0</sub> ''(parity bit)''
+| e<sub>p</sub> = e<sub>7</sub> + e<sub>6</sub> + … + e<sub>1</sub> + e<sub>0</sub> ''(पैरिटी बिट )''
 |-
 | s<sub>i</sub> = d<sub>i</sub> + c<sub>i+8</sub>
-| s<sub>p</sub> = s<sub>7</sub> + s<sub>6</sub> + … + s<sub>1</sub> + s<sub>0</sub> ''(parity bit)''
+| s<sub>p</sub> = s<sub>7</sub> + s<sub>6</sub> + … + s<sub>1</sub> + s<sub>0</sub> ''(पैरिटी बिट )''
 |}
 {| class="wikitable"
-|+ Bit-wise update equations for some सीआरसी-8 पॉलीनोमियलs after 8 bits have been shifted in
+|+ 8 बिट्स को शिफ्ट करने के बाद कुछ सीआरसी-8 पॉलीनोमियलों के लिए बिट-वार अपडेट समीकरण
 ! पॉलीनोमियल:
-| (''x''<sup>7</sup> + ''x''<sup>3</sup> + 1) &times; ''x'' ''(left-shifted सीआरसी-7-CCITT)''
+| (''x''<sup>7</sup> + ''x''<sup>3</sup> + 1) &times; ''x'' ''(लेफ्ट-शिफ्टेड सीआरसी-7-सीसीआईटीटी)''
-| ''x''<sup>8</sup> + ''x''<sup>5</sup> + ''x''<sup>4</sup> + 1 ''(सीआरसी-8-Dallas/Maxim)''
+| ''x''<sup>8</sup> + ''x''<sup>5</sup> + ''x''<sup>4</sup> + 1 ''(सीआरसी-8-डलास /मैक्सिम )''
 |-
-! Coefficients:
+! कोएफिशिएंट:
-| 0x12 = (0x09 << 1) ''([[Most significant bit|MSBF]]/normal)''
+| 0x12 = (0x09 << 1) ''([[Most significant bit|एमएसबीएफ]]/नार्मल)''
-| 0x8c ''([[Least significant bit|LSBF]]/reverse)''
+| 0x8c ''([[Least significant bit|एलएसबीएफ]]/रिवर्स )''
 |-
 |
-  r<sub>0 </sub> &larr;
+  r<sub>0</sub> &larr;
-  r<sub>1 </sub> &larr;
+  r<sub>1</sub> &larr;
-  r<sub>2 </sub> &larr;
+  r<sub>2</sub> &larr;
-  r<sub>3 </sub> &larr;
+  r<sub>3</sub> &larr;
-  r<sub>4 </sub> &larr;
+  r<sub>4</sub> &larr;
-  r<sub>5 </sub> &larr;
+  r<sub>5</sub> &larr;
-  r<sub>6 </sub> &larr;
+  r<sub>6</sub> &larr;
-  r<sub>7 </sub> &larr;
+  r<sub>7</sub> &larr;
 |
@@ Line 412: / Line 399: @@
   e<sub>1</sub> + e<sub>5</sub>
   e<sub>2</sub> + e<sub>6</sub>
-  e<sub>3</sub> + e<sub>7</sub>    <sub> </sub> + e<sub>0</sub> + e<sub>4</sub> + e<sub>7</sub>
+  e<sub>3</sub> + e<sub>7</sub>  + e<sub>0</sub> + e<sub>4</sub> + e<sub>7</sub>
-  e<sub>4</sub>    <sub> </sub>    <sub> </sub> + e<sub>1</sub> + e<sub>5</sub>
+  e<sub>4</sub>   + e<sub>1</sub> + e<sub>5</sub>
-  e<sub>5</sub>    <sub> </sub>    <sub> </sub> + e<sub>2</sub> + e<sub>6</sub>
+  e<sub>5</sub>   + e<sub>2</sub> + e<sub>6</sub>
-  e<sub>6</sub>    <sub> </sub>    <sub> </sub> + e<sub>3</sub> + e<sub>7</sub>
+  e<sub>6</sub>   + e<sub>3</sub> + e<sub>7</sub>
 |
-  e<sub>0</sub>    <sub> </sub>    <sub> </sub> + e<sub>4</sub> + e<sub>1</sub> + e<sub>0</sub>    <sub> </sub>   + e<sub>5</sub> + e<sub>2</sub> + e<sub>1</sub>
+  e<sub>0</sub>   + e<sub>4</sub> + e<sub>1</sub> + e<sub>0</sub>  + e<sub>5</sub> + e<sub>2</sub> + e<sub>1</sub>
-  e<sub>1</sub>    <sub> </sub>    <sub> </sub> + e<sub>5</sub> + e<sub>2</sub> + e<sub>1</sub>    <sub> </sub>   + e<sub>6</sub> + e<sub>3</sub> + e<sub>2</sub> + e<sub>0</sub>
+  e<sub>1</sub>   + e<sub>5</sub> + e<sub>2</sub> + e<sub>1</sub>  + e<sub>6</sub> + e<sub>3</sub> + e<sub>2</sub> + e<sub>0</sub>
-  e<sub>2</sub>    <sub> </sub>    <sub> </sub> + e<sub>6</sub> + e<sub>3</sub> + e<sub>2</sub> + e<sub>0</sub>   + e<sub>7</sub> + e<sub>4</sub> + e<sub>3</sub> + e<sub>1</sub>
+  e<sub>2</sub>   + e<sub>6</sub> + e<sub>3</sub> + e<sub>2</sub> + e<sub>0</sub> + e<sub>7</sub> + e<sub>4</sub> + e<sub>3</sub> + e<sub>1</sub>
-  e<sub>3</sub> + e<sub>0</sub>    <sub> </sub> + e<sub>7</sub> + e<sub>4</sub> + e<sub>3</sub> + e<sub>1</sub>
+  e<sub>3</sub> + e<sub>0</sub>  + e<sub>7</sub> + e<sub>4</sub> + e<sub>3</sub> + e<sub>1</sub>
   e<sub>4</sub> + e<sub>1</sub> + e<sub>0</sub>
   e<sub>5</sub> + e<sub>2</sub> + e<sub>1</sub>
@@ Line 426: / Line 413: @@
   e<sub>7</sub> + e<sub>4</sub> + e<sub>3</sub> + e<sub>1</sub>
 |-valign="top"
-! C code<br />fragments:
+! C कोड <br />फ़्रैगमेन्ट्स:
 |<syntaxhighlight lang="c">
   uint8_t c, d, e, f, r;
@@ Line 442: / Line 429: @@
 {| class="wikitable"
-|+ Bit-wise update equations for some सीआरसी-16 पॉलीनोमियलs after 8 bits have been shifted in
+|+ 8 बिट्स को स्थानांतरित करने के बाद कुछ सीआरसी-16 पॉलीनोमियलों के लिए बिट-वार अपडेट समीकरण
 ! पॉलीनोमियल:
-| colspan="2" | ''x''<sup>16</sup> + ''x''<sup>12</sup> + ''x''<sup>5</sup> + 1 ''(सीआरसी-16-CCITT)''
+| colspan="2" | ''x''<sup>16</sup> + ''x''<sup>12</sup> + ''x''<sup>5</sup> + 1 ''(सीआरसी-16-सीसीआईटीटी)''
-| colspan="2" | ''x''<sup>16</sup> + ''x''<sup>15</sup> + ''x''<sup>2</sup> + 1 ''(सीआरसी-16-ANSI)''
+| colspan="2" | ''x''<sup>16</sup> + ''x''<sup>15</sup> + ''x''<sup>2</sup> + 1 ''(सीआरसी-16-एएनएसआई)''
 |-
-! Coefficients:
+! कोएफिशिएंट:
-| 0x1021 ''(MSBF/normal)''
+| 0x1021 ''(एमएसबीएफ/नार्मल)''
-| 0x8408 ''(LSBF/reverse)''
+| 0x8408 ''(एलएसबीएफ/रिवर्स)''
-| 0x8005 ''(MSBF/normal)''
+| 0x8005 ''(एमएसबीएफ/नार्मल)''
-| 0xa001 ''(LSBF/reverse)''
+| 0xa001 ''(एलएसबीएफ/रिवर्स)''
 |-
 |
-  r<sub>0 </sub> &larr;
+  r<sub>0</sub> &larr;
-  r<sub>1 </sub> &larr;
+  r<sub>1</sub> &larr;
-  r<sub>2 </sub> &larr;
+  r<sub>2</sub> &larr;
-  r<sub>3 </sub> &larr;
+  r<sub>3</sub> &larr;
-  r<sub>4 </sub> &larr;
+  r<sub>4</sub> &larr;
-  r<sub>5 </sub> &larr;
+  r<sub>5</sub> &larr;
-  r<sub>6 </sub> &larr;
+  r<sub>6</sub> &larr;
-  r<sub>7 </sub> &larr;
+  r<sub>7</sub> &larr;
-  r<sub>8 </sub> &larr;
+  r<sub>8</sub> &larr;
-  r<sub>9 </sub> &larr;
+  r<sub>9</sub> &larr;
   r<sub>10</sub> &larr;
   r<sub>11</sub> &larr;
@@ Line 475: / Line 462: @@
   s<sub>6</sub> + s<sub>2</sub>
   s<sub>7</sub> + s<sub>3</sub>
-  <sub> </sub>   s<sub>4</sub>
+   s<sub>4</sub>
-  <sub> </sub>   s<sub>5</sub>  + s<sub>4</sub> + s<sub>0</sub>
+   s<sub>5</sub> + s<sub>4</sub> + s<sub>0</sub>
-  <sub> </sub>   s<sub>6</sub>  + s<sub>5</sub> + s<sub>1</sub>
+   s<sub>6</sub> + s<sub>5</sub> + s<sub>1</sub>
-  <sub> </sub>   s<sub>7</sub>  + s<sub>6</sub> + s<sub>2</sub>
+   s<sub>7</sub> + s<sub>6</sub> + s<sub>2</sub>
-  c<sub>0</sub>    <sub> </sub>  + s<sub>7</sub> + s<sub>3</sub>
+  c<sub>0</sub>  + s<sub>7</sub> + s<sub>3</sub>
-  c<sub>1</sub>    <sub> </sub>     <sub> </sub> + s<sub>4</sub>
+  c<sub>1</sub>   + s<sub>4</sub>
-  c<sub>2</sub>    <sub> </sub>     <sub> </sub> + s<sub>5</sub>
+  c<sub>2</sub>   + s<sub>5</sub>
-  c<sub>3</sub>    <sub> </sub>     <sub> </sub> + s<sub>6</sub>
+  c<sub>3</sub>   + s<sub>6</sub>
-  c<sub>4</sub>    <sub> </sub>     <sub> </sub> + s<sub>7</sub>  + s<sub>4</sub> + s<sub>0</sub>
+  c<sub>4</sub>   + s<sub>7</sub> + s<sub>4</sub> + s<sub>0</sub>
-  c<sub>5</sub>    <sub> </sub>     <sub> </sub>    <sub> </sub>  + s<sub>5</sub> + s<sub>1</sub>
+  c<sub>5</sub>     + s<sub>5</sub> + s<sub>1</sub>
-  c<sub>6</sub>    <sub> </sub>     <sub> </sub>    <sub> </sub>  + s<sub>6</sub> + s<sub>2</sub>
+  c<sub>6</sub>     + s<sub>6</sub> + s<sub>2</sub>
-  c<sub>7</sub>    <sub> </sub>     <sub> </sub>    <sub> </sub>  + s<sub>7</sub> + s<sub>3</sub>
+  c<sub>7</sub>     + s<sub>7</sub> + s<sub>3</sub>
 |
-  c<sub>8 </sub>   <sub> </sub>     <sub> </sub>  + e<sub>4</sub> + e<sub>0</sub>
+  c<sub>8</sub>    + e<sub>4</sub> + e<sub>0</sub>
-  c<sub>9 </sub>   <sub> </sub>     <sub> </sub>  + e<sub>5</sub> + e<sub>1</sub>
+  c<sub>9</sub>    + e<sub>5</sub> + e<sub>1</sub>
-  c<sub>10</sub>   <sub> </sub>     <sub> </sub>  + e<sub>6</sub> + e<sub>2</sub>
+  c<sub>10</sub>   + e<sub>6</sub> + e<sub>2</sub>
-  c<sub>11</sub>   <sub> </sub>  + e<sub>0</sub>  + e<sub>7</sub> + e<sub>3</sub>
+  c<sub>11</sub>  + e<sub>0</sub> + e<sub>7</sub> + e<sub>3</sub>
-  c<sub>12</sub>   <sub> </sub>  + e<sub>1</sub>
+  c<sub>12</sub>  + e<sub>1</sub>
-  c<sub>13</sub>   <sub> </sub>  + e<sub>2</sub>
+  c<sub>13</sub>  + e<sub>2</sub>
-  c<sub>14</sub>   <sub> </sub>  + e<sub>3</sub>
+  c<sub>14</sub>  + e<sub>3</sub>
-  c<sub>15</sub>   <sub> </sub>  + e<sub>4</sub> + e<sub>0</sub>
+  c<sub>15</sub>  + e<sub>4</sub> + e<sub>0</sub>
-  <sub>  </sub>  e<sub>0</sub>  + e<sub>5</sub> + e<sub>1</sub>
+   e<sub>0</sub> + e<sub>5</sub> + e<sub>1</sub>
-  <sub>  </sub>  e<sub>1</sub>  + e<sub>6</sub> + e<sub>2</sub>
+   e<sub>1</sub> + e<sub>6</sub> + e<sub>2</sub>
-  <sub>  </sub>  e<sub>2</sub>  + e<sub>7</sub> + e<sub>3</sub>
+   e<sub>2</sub> + e<sub>7</sub> + e<sub>3</sub>
-  <sub>  </sub>  e<sub>3</sub>
+   e<sub>3</sub>
-  <sub>  </sub>  e<sub>4</sub> + e<sub>0</sub>
+   e<sub>4</sub> + e<sub>0</sub>
-  <sub>  </sub>  e<sub>5</sub> + e<sub>1</sub>
+   e<sub>5</sub> + e<sub>1</sub>
-  <sub>  </sub>  e<sub>6</sub> + e<sub>2</sub>
+   e<sub>6</sub> + e<sub>2</sub>
-  <sub>  </sub>  e<sub>7</sub> + e<sub>3</sub>
+   e<sub>7</sub> + e<sub>3</sub>
 |
-  <sub> </sub>    <sub> </sub>   s<sub>p</sub>
+    s<sub>p</sub>
-  <sub> </sub>    <sub> </sub>   s<sub>0</sub> + s<sub>p</sub>
+    s<sub>0</sub> + s<sub>p</sub>
-  <sub> </sub>    <sub> </sub>   s<sub>1</sub> + s<sub>0</sub>
+    s<sub>1</sub> + s<sub>0</sub>
-  <sub> </sub>    <sub> </sub>   s<sub>2</sub> + s<sub>1</sub>
+    s<sub>2</sub> + s<sub>1</sub>
-  <sub> </sub>    <sub> </sub>   s<sub>3</sub> + s<sub>2</sub>
+    s<sub>3</sub> + s<sub>2</sub>
-  <sub> </sub>    <sub> </sub>   s<sub>4</sub> + s<sub>3</sub>
+    s<sub>4</sub> + s<sub>3</sub>
-  <sub> </sub>    <sub> </sub>   s<sub>5</sub> + s<sub>4</sub>
+    s<sub>5</sub> + s<sub>4</sub>
-  <sub> </sub>    <sub> </sub>   s<sub>6</sub> + s<sub>5</sub>
+    s<sub>6</sub> + s<sub>5</sub>
-  c<sub>0</sub>    <sub> </sub> + s<sub>7</sub> + s<sub>6</sub>
+  c<sub>0</sub>  + s<sub>7</sub> + s<sub>6</sub>
-  c<sub>1</sub>    <sub> </sub>    <sub> </sub> + s<sub>7</sub>
+  c<sub>1</sub>   + s<sub>7</sub>
   c<sub>2</sub>
   c<sub>3</sub>
@@ Line 522: / Line 509: @@
   c<sub>7</sub> + s<sub>p</sub>
 |
-  c<sub>8 </sub>    <sub> </sub>    <sub> </sub> + e<sub>p</sub>
+  c<sub>8</sub>   + e<sub>p</sub>
   c<sub>9 </sub>
   c<sub>10</sub>
@@ Line 530: / Line 517: @@
   c<sub>14</sub> + e<sub>0</sub>
   c<sub>15</sub> + e<sub>1</sub> + e<sub>0</sub>
-  <sub>  </sub>   e<sub>2</sub> + e<sub>1</sub>
+   e<sub>2</sub> + e<sub>1</sub>
-  <sub>  </sub>   e<sub>3</sub> + e<sub>2</sub>
+   e<sub>3</sub> + e<sub>2</sub>
-  <sub>  </sub>   e<sub>4</sub> + e<sub>3</sub>
+   e<sub>4</sub> + e<sub>3</sub>
-  <sub>  </sub>   e<sub>5</sub> + e<sub>4</sub>
+   e<sub>5</sub> + e<sub>4</sub>
-  <sub>  </sub>   e<sub>6</sub> + e<sub>5</sub>
+   e<sub>6</sub> + e<sub>5</sub>
-  <sub>  </sub>   e<sub>7</sub> + e<sub>6</sub>
+   e<sub>7</sub> + e<sub>6</sub>
-  <sub>  </sub>   e<sub>p</sub> + e<sub>7</sub>
+   e<sub>p</sub> + e<sub>7</sub>
-  <sub>  </sub>    <sub> </sub>   e<sub>p</sub>
+    e<sub>p</sub>
 |-valign="top"
-! C code<br />fragments:
+! C कोड <br />फ़्रैगमेन्ट्स:
 |<syntaxhighlight lang="c">
   uint8_t  d, s, t;
@@ Line 591: / Line 578: @@
 === टू-स्टेपीय कंप्यूटिंग ===
-चूँकि सीआरसी-32 पॉलीनोमियल में बड़ी संख्या में पद होते हैं, एक समय में रेमैंडर बाइट की कंप्यूटिंग करते समय प्रत्येक बिट पिछले पुनरावृत्ति के कई बिट्स पर निर्भर करता है। बाइट-समानांतर हार्डवेयर इम्प्लीमेंटेशन में इसके लिए मल्टीपल-इनपुट या कैस्केड XOR गेट्स की आवश्यकता होती है जो प्रसार विलंब को बढ़ाता है।
+चूँकि सीआरसी-32 पॉलीनोमियल में बड़ी संख्या में पद होते हैं, एक समय में रेमैंडर बाइट की कंप्यूटिंग करते समय प्रत्येक बिट पिछले पुनरावृत्ति के कई बिट्स पर निर्भर करता है। बाइट-समानांतर हार्डवेयर इम्प्लीमेंटेशन में इसके लिए मल्टीपल-इनपुट या कैस्केड एक्सओआर गेट्स की आवश्यकता होती है जो प्रोपागेशन डिले को बढ़ाता है।
-कंप्यूटिंग गति को अधिकतम करने के लिए, 123-बिट शिफ्ट रजिस्टर के माध्यम से मेसेज को पारित करके एक मध्यवर्ती रेमैंडर की कंप्यूटिंग की जा सकती है। पॉलीनोमियल मानक पॉलीनोमियल का सावधानीपूर्वक चयनित गुणज होता है, जैसे कि पद (फीडबैक टैप) व्यापक रूप से दूरी पर हैं, और रेमैंडर का कोई भी बिट प्रति बाइट पुनरावृत्ति में एक बार से अधिक XORed नहीं होता है। इस प्रकार मात्र दो-इनपुट XOR गेट, सबसे तेज़ संभव, की आवश्यकता होती है। अंत में सीआरसी-32 रेमैंडर प्राप्त करने के लिए मध्यवर्ती रेमैंडर को दूसरी शिफ्ट रजिस्टर में मानक पॉलीनोमियल द्वारा विभाजित किया जाता है।<ref name="glaise">{{cite journal
+कंप्यूटिंग गति को अधिकतम करने के लिए, 123-बिट शिफ्ट रजिस्टर के माध्यम से मेसेज को पारित करके एक मध्यवर्ती रेमैंडर की कंप्यूटिंग की जा सकती है। पॉलीनोमियल मानक पॉलीनोमियल का सावधानीपूर्वक चयनित गुणज होता है, जैसे कि पद (फीडबैक टैप) व्यापक रूप से दूरी पर होता हैं, और रेमैंडर का कोई भी बिट प्रति बाइट पुनरावृत्ति में एक बार से अधिक एक्सओआरed नहीं होता है। इस प्रकार मात्र दो-इनपुट एक्सओआर गेट, सबसे तेज़ संभव, की आवश्यकता होती है। अंत में सीआरसी-32 रेमैंडर प्राप्त करने के लिए मध्यवर्ती रेमैंडर को दूसरी शिफ्ट रजिस्टर में मानक पॉलीनोमियल द्वारा विभाजित किया जाता है।<ref name="glaise">{{cite journal
 | last=Glaise
 | first=René J.
@@ Line 611: / Line 598: @@
 === ब्लॉकवार कंप्यूटिंग ===
-रेमैंडर की ब्लॉक-वार कंप्यूटिंग किसी भी सीआरसी पॉलीनोमियल के लिए हार्डवेयर में राज्य अंतरिक्ष परिवर्तन मैट्रिक्स को गुणनफ्रेगमेंटित करके की जा सकती है, जो रेमैंडर को दो सरल टोप्लिट्ज मैट्रिक्स में कंप्यूटिंग करने के लिए आवश्यक है।<ref>{{Cite journal |last=Das |first=Arindam |date=2022 |title=लुक-अप टेबल के स्थान पर फैक्टर्ड टोप्लिट्ज़ मैट्रिसेस का उपयोग करके चक्रीय रिडंडेंसी कोड की ब्लॉक-वार गणना|url=https://ieeexplore.ieee.org/document/9826414 |journal=IEEE Transactions on Computers |volume=72 |issue=4 |pages=1110–1121 |doi=10.1109/TC.2022.3189574 |s2cid=250472783 |issn=0018-9340}}</ref>
+रेमैंडर की ब्लॉक-वार कंप्यूटिंग किसी भी सीआरसी पॉलीनोमियल के लिए हार्डवेयर में स्टेट स्पेस ट्रांसफॉर्मेशन मैट्रिक्स को फैक्टर करके की जा सकती है, जो रेमैंडर को दो सरल टोप्लिट्ज मैट्रिक्स में कंप्यूटिंग करने के लिए आवश्यक होता है।<ref>{{Cite journal |last=Das |first=Arindam |date=2022 |title=लुक-अप टेबल के स्थान पर फैक्टर्ड टोप्लिट्ज़ मैट्रिसेस का उपयोग करके चक्रीय रिडंडेंसी कोड की ब्लॉक-वार गणना|url=https://ieeexplore.ieee.org/document/9826414 |journal=IEEE Transactions on Computers |volume=72 |issue=4 |pages=1110–1121 |doi=10.1109/TC.2022.3189574 |s2cid=250472783 |issn=0018-9340}}</ref>
-एक-पास चेकिंग
-किसी मेसेज में सीआरसी जोड़ते समय, ट्रांसमिटेड सीआरसी को अलग करना, उसकी पुन: कंप्यूटिंग करना और ट्रांसमिटेड सीआरसी के विरुद्ध पुन: संगणित मूल्य को सत्यापित करना संभव है। हालाँकि, आमतौर पर एक सरल तकनीक होती है
+== एक-पास चेकिंग ==
-हार्डवेयर में उपयोग किया जाता है।
+किसी मेसेज में सीआरसी जोड़ते समय, ट्रांसमिटेड सीआरसी को अलग करना, उसकी पुन: कंप्यूटिंग करना और ट्रांसमिटेड सीआरसी के विरुद्ध पुन: संगणित मूल्य को सत्यापित करना संभव होता है। याग्पी, सामान्यतः एक सरल तकनीक होती है जिसे हार्डवेयर में उपयोग किया जाता है।
-जब सीआरसी सही बाइट ऑर्डर (चयनित बिट-ऑर्डरिंग कन्वेंशन से मेल खाते हुए) के साथ प्रसारित होता है, तो एक रिसीवर मेसेज और सीआरसी पर समग्र सीआरसी की कंप्यूटिंग कर सकता है, और यदि वे सही हैं, तो परिणाम शून्य होगा।<ref>
+जब सीआरसी करेक्ट बाइट ऑर्डर (चयनित बिट-ऑर्डरिंग कन्वेंशन के समरूप होते हुए) के साथ ट्रांसमिट होता है, तो एक रिसीवर मेसेज और सीआरसी पर समग्र सीआरसी की कंप्यूटिंग कर सकता है, और यदि वे करेक्ट होता हैं, तो परिणाम शून्य होगा।<ref>
 Andrew Kadatch, Bob Jenkins.
 [https://github.com/rurban/crcutil/raw/master/doc/crc.pdf "Everything we know about CRC but afraid to forget"].
@@ Line 625: / Line 610: @@
 which does not depend on the message... is well known
 and has been widely used in the telecommunication industry for long time."
-</ref>
+</ref>यह पोस्सिबिलिटी का यही कारण है कि अधिकांश नेटवर्क प्रोटोकॉल जिनमें सीआरसी सम्मलित होता है, एंडिंग डिलिमिटर से फर्स्ट ऐसा करते हैं; सीआरसी के चेक के लिए यह जानना जरूरी नहीं है कि पैकेट का एंड निकट है या नहीं।वास्तव में, कुछ प्रोटोकॉल सीआरसी का उपयोग एंडिंग डिलिमिटर- सीआरसी-आधारित फ़्रेमिंग के रूप में करते हैं।
-यह संभावना यही कारण है कि अधिकांश नेटवर्क प्रोटोकॉल जिनमें सीआरसी शामिल है, अंतिम सीमांकक से फर्स्ट ऐसा करते हैं; सीआरसी की जांच के लिए यह जानना जरूरी नहीं है कि पैकेट का अंत निकट है या नहीं।
-वास्तव में, कुछ प्रोटोकॉल सीआरसी का उपयोग अंतिम सीमांकक - सीआरसी-आधारित फ़्रेमिंग के रूप में करते हैं।
 == सीआरसी वेरिएंट ==
-व्यवहार में, अधिकांश मानक रजिस्टर को ऑल-वन पर प्रीसेट करने और ट्रांसमिशन से फर्स्ट सीआरसी को उल्टा करने को निर्दिष्ट करते हैं। इससे सीआरसी की परिवर्तित बिट्स का पता लगाने की क्षमता पर कोई प्रभाव नहीं पड़ता है, लेकिन यह मेसेज में जोड़े गए बिट्स को नोटिस करने की क्षमता देता है।
+व्यवहार में, अधिकांश मानक रजिस्टर को ऑल-वन पर प्रीसेट करने और ट्रांसमिशन से फर्स्ट सीआरसी को इन्वर्ट करने को निर्दिष्ट करते हैं। इससे सीआरसी की परिवर्तित बिट्स का पता लगाने की एबिलिटी पर कोई प्रभाव नहीं पड़ता है, लेकिन यह मेसेज में जोड़े गए बिट्स को नोटिस करने की एबिलिटी देता है।
-=== −1 === पर प्रीसेट
+=== प्रीसेट टू−1 ===
-सीआरसी का बुनियादी गणित उन मेसेजों को स्वीकार करता है (सही ढंग से प्रसारित माना जाता है) जिन्हें पॉलीनोमियल के रूप में व्याख्या किए जाने पर, सीआरसी पॉलीनोमियल का एक गुणक होता है। यदि कुछ अग्रणी 0 बिट्स को ऐसे मेसेज से जोड़ा जाता है, तो वे पॉलीनोमियल के रूप में इसकी व्याख्या को नहीं बदलेंगे। यह इस तथ्य के समतुल्य है कि 0001 और 1 एक ही संख्या हैं।
+सीआरसी का बेसिक गणित उन मेसेजों को स्वीकार करता है (सही विधि से ट्रांसमिट माना जाता है) जिन्हें पॉलीनोमियल के रूप में व्याख्या किए जाने पर, सीआरसी पॉलीनोमियल का एक गुणक होता है। यदि कुछ लीडिंग 0 बिट्स को ऐसे मेसेज से जोड़ा जाता है, तो वे पॉलीनोमियल के रूप में इसकी व्याख्या को नहीं बदलेंगे। यह इस तथ्य के समतुल्य है कि 0001 और 1 एक ही संख्या होती हैं।
-लेकिन यदि ट्रांसमिटेड किया जा रहा मेसेज अग्रणी 0 बिट्स की परवाह करता है, तो ऐसे परिवर्तन का पता लगाने के लिए बुनियादी सीआरसी एल्गोरिदम की अक्षमता अवांछनीय है। यदि यह संभव है कि एक ट्रांसमिशन त्रुटि ऐसे बिट्स को जोड़ सकती है, तो एक सरल समाधान यह है कि प्रारम्भ करें <code>rem</code> शिफ्ट रजिस्टर को कुछ गैर-शून्य मान पर सेट किया गया; सुविधा के लिए, आमतौर पर ऑल-वन्स मान का उपयोग किया जाता है। यह गणितीय रूप से मेसेज के फर्स्ट एन बिट्स को पूरक करने (बाइनरी नोट) के बराबर है, जहां एन सीआरसी रजिस्टर में बिट्स की संख्या है।
+परन्तु यदि ट्रांसमिटेड किया जा रहा मेसेज लीडिंग 0 बिट्स की केयर करता है, तो ऐसे परिवर्तन का पता लगाने के लिए बेसिक सीआरसी एल्गोरिदम की अएबिलिटी अवांछनीय होती है। यदि यह संभव है कि एक ट्रांसमिशन एरर ऐसे बिट्स को जोड़ सकती है, तो एक सरल समाधान यह है कि रेम शिफ्ट रजिस्टर को कुछ नॉन-जीरो वैल्यू पर सेट करके प्रारम्भ किया जाए; सुविधा के लिए, सामान्यतः पर ऑल-वन्स मान का उपयोग किया जाता है।। यह गणितीय रूप से मेसेज के फर्स्ट एन बिट्स को पूरक करने (बाइनरी नोट) के समान होता है, जहां एन सीआरसी रजिस्टर में बिट्स की संख्या होती है।
-यह सीआरसी निर्माण और जांच को किसी भी तरह से प्रभावित नहीं करता है, जब तक जनरेटर और चेकर दोनों समान प्रारंभिक मूल्य का उपयोग करते हैं। कोई भी गैर-शून्य प्रारंभिक मान काम करेगा, और कुछ मानक असामान्य मान निर्दिष्ट करते हैं,<ref>E.g. low-frequency RFID {{Citation
+यह सीआरसी निर्माण और जांच को किसी भी तरह से प्रभावित नहीं करता है, जब तक जनरेटर और चेकर दोनों समान प्रारंभिक मूल्य का उपयोग करते हैं। कोई भी नॉन-जीरो प्रारंभिक वैल्यू काम करेगी, और कुछ मानक असामान्य मान निर्दिष्ट करते हैं,<ref>E.g. low-frequency RFID {{Citation
 | url=http://www.ti.com/lit/ds/symlink/tms37157.pdf
 | title=TMS37157 data sheet - Passive Low Frequency Interface Device With EEPROM and 134.2 kHz Transponder Interface
@@ Line 644: / Line 627: @@
 | page=39
 | quote=The CRC Generator is initialized with the value 0x3791 as shown in Figure 50.
-| access-date=2016-02-16}}</ref> लेकिन सभी का मान (दो में −1 पूरक बाइनरी) अब तक का सबसे आम है। ध्यान दें कि एक-पास सीआरसी जनरेट/चेक पूर्व निर्धारित मूल्य की परवाह किए बिना, मेसेज सही होने पर भी शून्य का परिणाम देगा।
+| access-date=2016-02-16}}</ref> लेकिन सभी का मान (दो में −1 पूरक बाइनरी) अब तक का सबसे कॉमन होता है। ध्यान दें कि एक-पास सीआरसी जनरेट/चेक प्रीसेट मूल्य की केयर किए बिना, मेसेज सही होने पर भी शून्य का परिणाम देगा।
-=== पोस्ट-उलटा ===
+=== पोस्ट-इन्वर्ट ===
-उसी प्रकार की त्रुटि मेसेज के अंत में हो सकती है, भले ही मेसेजों के अधिक सीमित सेट के साथ। किसी मेसेज में 0 बिट जोड़ना उसके पॉलीनोमियल को x से गुणा करने के बराबर है, और यदि यह फर्स्ट सीआरसी पॉलीनोमियल का गुणज था, तो उस गुणन का परिणाम भी होगा। यह इस तथ्य के समतुल्य है कि, चूँकि 726, 11 का गुणज है, इसलिए 7260 भी है।
+उसी प्रकार की एरर मेसेज के एंड में हो सकती है, तथापि मेसेजों के अधिक लिमटेड सेट के साथ। किसी मेसेज में 0 बिट जोड़ना उसके पॉलीनोमियल को x से गुणा करने के समान होता है, और यदि यह फर्स्ट सीआरसी पॉलीनोमियल का गुणज था, तो उस गुणन का परिणाम भी होगा। यह इस तथ्य के समतुल्य है कि, चूँकि 726, 11 का गुणज है, इसलिए 7260 भी है।
-एक समान समाधान मेसेज के अंत में प्रयुक्त किया जा सकता है, मेसेज में जोड़ने से फर्स्ट सीआरसी रजिस्टर को उल्टा कर दिया जा सकता है। फिर, कोई भी गैर-शून्य परिवर्तन करेगा; सभी बिट्स को उलटना (ऑल-वन्स पैटर्न के साथ XORing) सबसे आम है।
+एक समान सलूशन मेसेज के अंत में प्रयुक्त किया जा सकता है, मेसेज में जोड़ने से फर्स्ट सीआरसी रजिस्टर को इन्वर्ट कर दिया जा सकता है। फिर, कोई भी नॉन-जीरो परिवर्तन करेगा; सभी बिट्स को इन्वर्ट करना (ऑल-वन्स पैटर्न के साथ एक्सओआरआईएनजी) सबसे कॉमन होता है।
-इसका एक-पास सीआरसी जाँच पर प्रभाव पड़ता है: मेसेज सही होने पर शून्य का परिणाम उत्पन्न करने के बजाय, यह एक निश्चित गैर-शून्य परिणाम उत्पन्न करता है। (सटीक होने के लिए, परिणाम व्युत्क्रम पैटर्न का सीआरसी (गैर-शून्य प्रीसेट के बिना, लेकिन पोस्ट-इनवर्ट के साथ) है।) एक बार जब यह स्थिरांक प्राप्त हो जाता है (एक मनमाना मेसेज पर एक-पास सीआरसी उत्पन्न/चेक करके सबसे आसानी से), इसका उपयोग उसी सीआरसी एल्गोरिथ्म का उपयोग करके जांचे गए किसी भी अन्य मेसेज की प्योरता को सत्यापित करने के लिए सीधे किया जा सकता है।
+इसका एक-पास सीआरसी जाँच पर प्रभाव पड़ता है: मेसेज सही होने पर शून्य का परिणाम उत्पन्न करने के अतिरिक्त, यह एक निश्चित नॉन -शून्य परिणाम उत्पन्न करता है। (स्पष्ट होने के लिए, परिणाम इन्वर्ट पैटर्न का सीआरसी (नॉन-जीरो प्रीसेट के बिना, लेकिन पोस्ट-इनवर्ट के साथ) है।) एक बार जब यह कांस्टेंट प्राप्त हो जाता है (एक आरबिटरेरी मेसेज पर एक-पास सीआरसी उत्पन्न/चेक करके सबसे आसानी से), इसका उपयोग उसी सीआरसी एल्गोरिथ्म का उपयोग करके चेक किये गए किसी भी अन्य मेसेज की प्योरता को सत्यापित करने के लिए सीधे किया जा सकता है।
 == यह भी देखें ==
 सामान्य वर्ग
-* [[कोड सुधारने में त्रुटि]]
+* [[कोड सुधारने में त्रुटि|कोड कोर्रेक्टिंग एरर]]
-* [[हैश फ़ंक्शंस की सूची]]
+* [[हैश फ़ंक्शंस की सूची|हैश फ़ंक्शंस की टेबल]]
-* [[समता (दूरसंचार)]] पॉलीनोमियल के साथ 1-बिट सीआरसी के बराबर है {{math|''x''+1}}.
+* [[समता (दूरसंचार)|पैरिटी]] पॉलीनोमियल {{math|''x''+1}}के साथ 1-बिट सीआरसी के समान है।
-गैर-सीआरसी चेकसम
+नॉन-सीआरसी चेकसम
 * [[एडलर-32]]
 * फ्लेचर का चेकसम
@@ Line 678: / Line 661: @@
 | author=Andrew Kadarch, Bob Jenkins| website=[[GitHub]]
 }}
-[[Category: चक्रीय अतिरेक जाँच]] [[Category: परिमित क्षेत्र]] [[Category: स्यूडोकोड उदाहरण सहित लेख]]
-[[Category: Machine Translated Page]]
 [[Category:Created On 25/07/2023]]
+[[Category:Lua-based templates]]
+[[Category:Machine Translated Page]]
+[[Category:Pages with script errors]]
+[[Category:Pages with syntax highlighting errors]]
+[[Category:Short description with empty Wikidata description]]
+[[Category:Templates Vigyan Ready]]
+[[Category:Templates that add a tracking category]]
+[[Category:Templates that generate short descriptions]]
+[[Category:Templates using TemplateData]]
+[[Category:चक्रीय अतिरेक जाँच]]
+[[Category:परिमित क्षेत्र]]
+[[Category:स्यूडोकोड उदाहरण सहित लेख]]

Anonymous

Search

चक्रीय अतिरेक जांच की गणना: Difference between revisions

Latest revision as of 12:08, 18 August 2023

उदाहरण

इम्प्लीमेंटेशन

बिट ऑर्डरिंग (एंडियननेस)

मल्टी-बिट कंप्यूटिंग

सरवटे एल्गोरिदम (एकल लुकअप टेबल)

टेबल जनरेट करना

सीआरसी-32 एल्गोरिथ्म

बाइट-स्लाइसिंग यूजिंग मल्टीप्ल टेबल

पैरेलल कम्प्यूटेशन विदाउट टेबल

टू-स्टेपीय कंप्यूटिंग

ब्लॉकवार कंप्यूटिंग

एक-पास चेकिंग

सीआरसी वेरिएंट

प्रीसेट टू−1

पोस्ट-इन्वर्ट

यह भी देखें

संदर्भ

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Categories