तंत्र डिज़ाइन: Difference between revisions
No edit summary |
No edit summary |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Field in game theory}} | {{Short description|Field in game theory}} | ||
[[Image:Stanley Reiter MDdiagram.png|thumb|345px| ऊपर दिया गया स्टैनली रेइटर आरेख तंत्र डिज़ाइन के खेल को दर्शाता है। ऊपरी बाएँ स्थान <math>\Theta</math> प्रकार स्थान और ऊपरी-दाएँ स्थान X परिणामों के स्थान को दर्शाता है। सामाजिक चयन फलन <math>f(\theta)</math> किसी परिणाम के लिए प्रकार की प्रोफ़ाइल मैप करता है। तंत्र डिज़ाइन के खेलों में, एजेंट संदेश भेजते हैं <math>M</math> खेल के माहौल में <math>g</math>. खेल में संतुलन <math>\xi(M,g,\theta)</math> कुछ सामाजिक चयन फलन को कार्यान्वित करने के लिए डिज़ाइन किया जा सकता है <math>f(\theta)</math>.]]तंत्र डिजाइन अर्थशास्त्र और खेल सिद्धांत में क्षेत्र है जो रणनीतिक सेटिंग्स में, वांछित उद्देश्यों की ओर, आर्थिक तंत्र या प्रोत्साहन को डिजाइन करने के लिए उद्देश्य-प्रथम दृष्टिकोण लेता है, जहां खिलाड़ी तर्कसंगत रूप से कार्य करते हैं। | [[Image:Stanley Reiter MDdiagram.png|thumb|345px| ऊपर दिया गया स्टैनली रेइटर आरेख तंत्र डिज़ाइन के खेल को दर्शाता है। ऊपरी बाएँ स्थान <math>\Theta</math> प्रकार स्थान और ऊपरी-दाएँ स्थान X परिणामों के स्थान को दर्शाता है। सामाजिक चयन फलन <math>f(\theta)</math> किसी परिणाम के लिए प्रकार की प्रोफ़ाइल मैप करता है। तंत्र डिज़ाइन के खेलों में, एजेंट संदेश भेजते हैं <math>M</math> खेल के माहौल में <math>g</math>. खेल में संतुलन <math>\xi(M,g,\theta)</math> कुछ सामाजिक चयन फलन को कार्यान्वित करने के लिए डिज़ाइन किया जा सकता है <math>f(\theta)</math>.]]'''तंत्र डिजाइन''' अर्थशास्त्र और खेल सिद्धांत में एक क्षेत्र होता है जो रणनीतिक सेटिंग्स में, वांछित उद्देश्यों की ओर, आर्थिक तंत्र या प्रोत्साहन को डिजाइन करने के लिए उद्देश्य-प्रथम दृष्टिकोण लेता है, जहां खिलाड़ी तर्कसंगत रूप से कार्य करते हैं। जिससे कि यह खेल के अंत में प्रारंभ होता है, और फिर पीछे की ओर जाता है, इसे '''उल्टा खेल सिद्धांत''' भी कहा जाता है। इस प्रकार इसमें अर्थशास्त्र और राजनीति से लेकर बाजार डिजाइन, [[नीलामी सिद्धांत]] और सामाजिक विकल्प सिद्धांत से लेकर नेटवर्क-सिस्टम (इंटरनेट इंटरडोमेन रूटिंग, प्रायोजित खोज नीलामी) जैसे क्षेत्रों में व्यापक अनुप्रयोग होता हैं। | ||
मैकेनिज्म डिज़ाइन निजी-सूचना खेलों के वर्ग के लिए समाधान अवधारणाओं का अध्ययन करता है। [[लियोनिद हर्विक्ज़]] बताते हैं कि ' | मैकेनिज्म डिज़ाइन निजी-सूचना खेलों के वर्ग के लिए समाधान अवधारणाओं का अध्ययन करता है। इस प्रकार [[लियोनिद हर्विक्ज़]] बताते हैं कि '''<nowiki/>'डिज़ाइन समस्या में, लक्ष्य फलन मुख्य "दिया" होता है, जबकि तंत्र अज्ञात होता है। इसलिए, डिज़ाइन समस्या पारंपरिक आर्थिक सिद्धांत का "उलटा" देती है, अतः जो सामान्यतः किसी दिए गए तंत्र के प्रदर्शन के विश्लेषण के लिए समर्पित होते है।''''<ref>L. Hurwicz & S. Reiter (2006) [[Designing Economic Mechanisms]], p. 30</ref> तब, इन खेलों की दो विशिष्ट विशेषताएं होती हैं। | ||
तंत्र अज्ञात | |||
* कि | * कि खेल '''"डिज़ाइनर"''' किसी खेल को विरासत में लेने के अतिरिक्त खेल संरचना को चुनता है | ||
* कि डिज़ाइनर को खेल के परिणाम में रुचि है | * कि डिज़ाइनर को खेल के परिणाम में रुचि होती है | ||
2007 में [[आर्थिक विज्ञान में नोबेल मेमोरियल पुरस्कार]] लियोनिद हरविक्ज़, [[एरिक मास्किन]] और रोजर मायर्सन को | सन्न 2007 में [[आर्थिक विज्ञान में नोबेल मेमोरियल पुरस्कार]] लियोनिद हरविक्ज़, [[एरिक मास्किन]] और रोजर मायर्सन को '''"मैकेनिज्म डिज़ाइन सिद्धांत की नींव रखने के लिए"''' प्रदान किया गया था।<ref>{{cite press release |url=http://nobelprize.org/nobel_prizes/economics/laureates/2007/press.html |title=The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 2007 |date=October 15, 2007 |access-date=2008-08-15 |publisher=[[Nobel Foundation]]}}</ref> | ||
==अंतर्ज्ञान== | =='''अंतर्ज्ञान'''== | ||
[[बायेसियन खेल]] की रोचक कक्षा में, खिलाड़ी, जिसे प्रिंसिपल कहा जाता है, अन्य खिलाड़ियों को निजी | [[बायेसियन खेल]] की रोचक कक्षा में, खिलाड़ी, जिसे '''"प्रिंसिपल"''' कहा जाता है, जिससे कि अन्य खिलाड़ियों को निजी रूप पर ज्ञात जानकारी के आधार पर अपने व्यवहार को नियंत्रित किया जाता है। उदाहरण के लिए, प्रिंसिपल यह जानना चाहेंगे कि सेल्समैन जिस पुरानी कार के बारे में बता रहा है, उसकी वास्तविक गुणवत्ता क्या है। वह सिर्फ सेल्समैन से पूछकर कुछ नहीं सीख सकता, जिससे कि सच्चाई को तोड़-मरोड़कर प्रस्तुत करना सेल्समैन के हित में है। यद्यपि, तंत्र डिज़ाइन में प्रिंसिपल को लाभ होता है: वह खेल डिज़ाइन कर सकता है जिसके नियम दूसरों को उस तरह से कार्य करने के लिए प्रभावित कर सकते हैं जैसा वह चाहता है। | ||
तंत्र डिज़ाइन सिद्धांत के बिना, प्रिंसिपल की समस्या को हल करना कठिनाई होगा। उसे सभी संभावित खेलों पर विचार करना होगा और उसे चुनना होगा जो अन्य खिलाड़ियों की रणनीति पर सबसे अच्छा प्रभाव डालता है। इसके अतिरिक्त, प्रिंसिपल को उन एजेंटों से निष्कर्ष निकालना होगा जो उससे झूठ बोल सकते हैं। तंत्र डिज़ाइन और विशेष रूप से रहस्योद्घाटन सिद्धांत के लिए धन्यवाद, प्रिंसिपल को केवल उन खेलों पर विचार करने की आवश्यकता है जिनमें एजेंट अपनी निजी जानकारी को सच्चाई से रिपोर्ट करते हैं। | तंत्र डिज़ाइन सिद्धांत के बिना, प्रिंसिपल की समस्या को हल करना कठिनाई होगा। उसे सभी संभावित खेलों पर विचार करना होगा और उसे चुनना होगा जो अन्य खिलाड़ियों की रणनीति पर सबसे अच्छा प्रभाव डालता है। इसके अतिरिक्त, प्रिंसिपल को उन एजेंटों से निष्कर्ष निकालना होगा जो उससे झूठ बोल सकते हैं। तंत्र डिज़ाइन और विशेष रूप से रहस्योद्घाटन सिद्धांत के लिए धन्यवाद, प्रिंसिपल को केवल उन खेलों पर विचार करने की आवश्यकता है जिनमें एजेंट अपनी निजी जानकारी को सच्चाई से रिपोर्ट करते हैं। | ||
| Line 20: | Line 19: | ||
===तंत्र=== | ===तंत्र=== | ||
तंत्र डिज़ाइन का खेल निजी जानकारी का खेल है जिसमें एजेंटों में से एक, जिसे प्रिंसिपल कहा जाता है, भुगतान संरचना चुनता है। अगले {{harvs|txt|last= | तंत्र डिज़ाइन का खेल निजी जानकारी का खेल है जिसमें एजेंटों में से एक, जिसे प्रिंसिपल कहा जाता है, भुगतान संरचना चुनता है। अगले {{harvs|txt|last=हर्सेन्यि|year=1967|author-link=जॉन हरसैनी}}, एजेंटों को प्रकृति से गुप्त संदेश प्राप्त होते हैं जिनमें भुगतान से संबंधित जानकारी होती है। उदाहरण के लिए, किसी संदेश में उनकी प्राथमिकताओं या बिक्री के लिए किसी वस्तु की गुणवत्ता के बारे में जानकारी हो सकती है। हम इस जानकारी को एजेंट का प्रकार कहते हैं (सामान्यतः नोट किया जाता है)। <math>\theta</math> और तदनुसार प्रकारों का स्थान <math>\Theta</math>). फिर एजेंट प्रिंसिपल को प्रकार की रिपोर्ट करते हैं (सामान्यतः टोपी के साथ नोट किया जाता है)। <math>\hat\theta</math>) यह रणनीतिक झूठ हो सकता है। रिपोर्ट के पश्चात्, प्रिंसिपल और एजेंटों को प्रिंसिपल द्वारा चुनी गई भुगतान संरचना के अनुसार भुगतान किया जाता है। | ||
खेल का समय है: | खेल का समय है: | ||
| Line 36: | Line 35: | ||
:<math>y(\hat\theta): \Theta \rightarrow Y</math> | :<math>y(\hat\theta): \Theta \rightarrow Y</math> | ||
===रहस्योद्घाटन सिद्धांत=== | ===रहस्योद्घाटन सिद्धांत=== | ||
{{main| | {{main|रहस्योद्घाटन सिद्धांत}} | ||
एक प्रस्तावित तंत्र बायेसियन | एक प्रस्तावित तंत्र बायेसियन खेल (निजी जानकारी का खेल) का गठन करता है, और यदि यह अच्छी तरह से व्यवहार किया जाता है तब खेल में [[बायेसियन नैश संतुलन]] होता है। संतुलन पर एजेंट प्रकार के कार्य के रूप में रणनीतिक रूप से अपनी रिपोर्ट चुनते हैं | ||
:<math>\hat\theta(\theta)</math> | :<math>\hat\theta(\theta)</math> | ||
ऐसी सेटिंग में बायेसियन संतुलन को हल करना कठिनाई है | ऐसी सेटिंग में बायेसियन संतुलन को हल करना कठिनाई है जिससे कि इसमें एजेंटों की सर्वोत्तम-प्रतिक्रिया रणनीतियों और संभावित रणनीतिक झूठ से सर्वोत्तम अनुमान को हल करना सम्मिलित है। व्यापक परिणाम के लिए धन्यवाद, जिसे रहस्योद्घाटन सिद्धांत कहा जाता है, इससे कोई फर्क नहीं पड़ता कि डिजाइनर कोई भी तंत्र बना सकता है<ref>In unusual circumstances some truth-telling games have more equilibria than the Bayesian game they mapped from. See Fudenburg-Tirole Ch. 7.2 for some references.</ref> संतुलन पर ध्यान केंद्रित करें जिसमें एजेंट सच्चाई से प्रकार की रिपोर्ट करते हैं। रहस्योद्घाटन सिद्धांत कहता है: प्रत्येक बायेसियन नैश संतुलन के लिए बायेसियन खेल समान संतुलन परिणाम के साथ मेल खाता है किन्तु जिसमें खिलाड़ी सच्चाई से रिपोर्ट प्रकार करते हैं। | ||
यह अत्यंत उपयोगी है. सिद्धांत सभी खिलाड़ियों को सच्चाई से रिपोर्ट प्रकार (एक [[प्रोत्साहन अनुकूलता]] बाधा के अधीन) मानकर बायेसियन संतुलन को हल करने की अनुमति देता है। झटके में यह रणनीतिक व्यवहार या झूठ पर विचार करने की आवश्यकता को समाप्त कर देता है। | यह अत्यंत उपयोगी है. सिद्धांत सभी खिलाड़ियों को सच्चाई से रिपोर्ट प्रकार (एक [[प्रोत्साहन अनुकूलता]] बाधा के अधीन) मानकर बायेसियन संतुलन को हल करने की अनुमति देता है। झटके में यह रणनीतिक व्यवहार या झूठ पर विचार करने की आवश्यकता को समाप्त कर देता है। | ||
इसका प्रमाण बिल्कुल प्रत्यक्ष है. बायेसियन | इसका प्रमाण बिल्कुल प्रत्यक्ष है. बायेसियन खेल मान लें जिसमें एजेंट की रणनीति और भुगतान उसके प्रकार के कार्य हैं और अन्य क्या करते हैं, <math>u_i\left(s_i(\theta_i),s_{-i}(\theta_{-i}), \theta_{i} \right)</math>. परिभाषा के अनुसार एजेंट I की संतुलन रणनीति <math>s(\theta_i)</math> क्या नैश अपेक्षित उपयोगिता में है: | ||
:<math>s_i(\theta_i) \in \arg\max_{s'_i \in S_i} \sum_{\theta_{-i}} \ p(\theta_{-i} \mid \theta_i) \ u_i\left(s'_i, s_{-i}(\theta_{-i}),\theta_i \right)</math> | :<math>s_i(\theta_i) \in \arg\max_{s'_i \in S_i} \sum_{\theta_{-i}} \ p(\theta_{-i} \mid \theta_i) \ u_i\left(s'_i, s_{-i}(\theta_{-i}),\theta_i \right)</math> | ||
बस तंत्र को परिभाषित करें जो एजेंटों को समान संतुलन चुनने के लिए प्रेरित करेगा। परिभाषित करने के लिए सबसे आसान प्रणाली यह है कि तंत्र उनके लिए एजेंटों की संतुलन रणनीतियों को निभाने के लिए प्रतिबद्ध हो। | बस तंत्र को परिभाषित करें जो एजेंटों को समान संतुलन चुनने के लिए प्रेरित करेगा। परिभाषित करने के लिए सबसे आसान प्रणाली यह है कि तंत्र उनके लिए एजेंटों की संतुलन रणनीतियों को निभाने के लिए प्रतिबद्ध हो। | ||
:<math>y(\hat\theta) : \Theta \rightarrow S(\Theta) \rightarrow Y </math> | :<math>y(\hat\theta) : \Theta \rightarrow S(\Theta) \rightarrow Y </math> | ||
ऐसे तंत्र के अनुसार एजेंटों को निश्चित रूप से प्रकार प्रकट करना इष्टतम लगता है | ऐसे तंत्र के अनुसार एजेंटों को निश्चित रूप से प्रकार प्रकट करना इष्टतम लगता है जिससे कि तंत्र उन रणनीतियों को खेलता है जिन्हें यह वैसे भी इष्टतम पाते हैं। औपचारिक रूप से, चुनें <math>y(\theta)</math> ऐसा है कि | ||
: <math> | : <math> | ||
\begin{align} | \begin{align} | ||
| Line 67: | Line 66: | ||
रहस्योद्घाटन सिद्धांत के लिए धन्यवाद, डिजाइनर सामान्यतः स्थानांतरण फलन ढूंढ सकता है <math>t(\theta)</math> संबंधित सत्य कथन खेल को हल करके सामाजिक विकल्प को क्रियान्वित करना। यदि एजेंटों को सत्यतापूर्वक रिपोर्ट प्रकार देना सर्वोत्तम लगता है, | रहस्योद्घाटन सिद्धांत के लिए धन्यवाद, डिजाइनर सामान्यतः स्थानांतरण फलन ढूंढ सकता है <math>t(\theta)</math> संबंधित सत्य कथन खेल को हल करके सामाजिक विकल्प को क्रियान्वित करना। यदि एजेंटों को सत्यतापूर्वक रिपोर्ट प्रकार देना सर्वोत्तम लगता है, | ||
:<math>\hat\theta(\theta) = \theta</math> | :<math>\hat\theta(\theta) = \theta</math> | ||
हम कहते हैं कि ऐसा तंत्र सचमुच कार्यान्वयन योग्य है (या बस कार्यान्वयन योग्य है)। फिर कार्य को सत्यतापूर्वक कार्यान्वयन के लिए हल करना है <math>t(\theta)</math> और इस स्थानांतरण फलन को मूल | हम कहते हैं कि ऐसा तंत्र सचमुच कार्यान्वयन योग्य है (या बस कार्यान्वयन योग्य है)। फिर कार्य को सत्यतापूर्वक कार्यान्वयन के लिए हल करना है <math>t(\theta)</math> और इस स्थानांतरण फलन को मूल खेल में क्रियान्वित करें। आवंटन <math>x(\theta)</math> यदि कोई स्थानांतरण फलन उपस्तिथ है तब यह वास्तव में कार्यान्वयन योग्य है <math>t(\theta)</math> ऐसा है कि | ||
: <math>u(x(\theta),t(\theta),\theta) \geq u(x(\hat\theta),t(\hat\theta),\theta) \ \forall \theta,\hat\theta \in \Theta</math> | : <math>u(x(\theta),t(\theta),\theta) \geq u(x(\hat\theta),t(\hat\theta),\theta) \ \forall \theta,\hat\theta \in \Theta</math> | ||
जिसे प्रोत्साहन अनुकूलता (आईसी) बाधा भी कहा जाता है। | जिसे प्रोत्साहन अनुकूलता (आईसी) बाधा भी कहा जाता है। | ||
| Line 87: | Line 86: | ||
जिसका, धनात्मक होने का कारण है कि उच्च प्रकारों को अधिक अच्छाई दी जानी चाहिए। | जिसका, धनात्मक होने का कारण है कि उच्च प्रकारों को अधिक अच्छाई दी जानी चाहिए। | ||
दोनों टुकड़ों के मध्य बातचीत की संभावना है। यदि किसी प्रकार की श्रेणी के लिए अनुबंध में उच्च प्रकार की तुलना में कम मात्रा की पेशकश की जाती है <math>\partial x / \partial \theta < 0</math>, यह संभव है कि तंत्र उच्च प्रकार की छूट देकर क्षतिपूर्ति कर सके। किन्तु निम्न-प्रकार के एजेंटों के लिए ऐसा अनुबंध पहले से उपस्तिथ है, इसलिए यह समाधान रोगविज्ञानी है। ऐसा समाधान कभी-कभी किसी तंत्र के समाधान की प्रक्रिया में होता है। इन स्थितियोंमें यह | दोनों टुकड़ों के मध्य बातचीत की संभावना है। यदि किसी प्रकार की श्रेणी के लिए अनुबंध में उच्च प्रकार की तुलना में कम मात्रा की पेशकश की जाती है <math>\partial x / \partial \theta < 0</math>, यह संभव है कि तंत्र उच्च प्रकार की छूट देकर क्षतिपूर्ति कर सके। किन्तु निम्न-प्रकार के एजेंटों के लिए ऐसा अनुबंध पहले से उपस्तिथ है, इसलिए यह समाधान रोगविज्ञानी है। ऐसा समाधान कभी-कभी किसी तंत्र के समाधान की प्रक्रिया में होता है। इन स्थितियोंमें यह तंत्र डिजाइन मायर्सन इस्त्री होना चाहिए। बहु-अच्छे वातावरण में डिज़ाइनर के लिए यह भी संभव है कि वह एजेंट को किसी अन्य वस्तु के कम के स्थान पर अधिक वस्तु देकर पुरस्कृत करे (जैसे [[नकली [[मक्खन]]]] के लिए मक्खन)। तंत्र डिजाइन सिद्धांत में बहु-अच्छे तंत्र सतत समस्या हैं। | ||
====पर्याप्तता==== | ====पर्याप्तता==== | ||
| Line 102: | Line 101: | ||
===राजस्व तुल्यता प्रमेय=== | ===राजस्व तुल्यता प्रमेय=== | ||
{{main| | {{main|राजस्व तुल्यता}} | ||
{{harvs|txt|last=Vickrey|year=1961|author-link=William Vickrey}} प्रतिष्ठित परिणाम देता है कि नीलामी के बड़े वर्ग का कोई भी सदस्य विक्रेता को समान अपेक्षित राजस्व का आश्वासन देता है और यह कि अपेक्षित राजस्व विक्रेता के लिए सबसे अच्छा है। यही स्थिति है यदि | {{harvs|txt|last=Vickrey|year=1961|author-link=William Vickrey}} प्रतिष्ठित परिणाम देता है कि नीलामी के बड़े वर्ग का कोई भी सदस्य विक्रेता को समान अपेक्षित राजस्व का आश्वासन देता है और यह कि अपेक्षित राजस्व विक्रेता के लिए सबसे अच्छा है। यही स्थिति है यदि | ||
| Line 114: | Line 113: | ||
===विक्रे-क्लार्क-ग्रोव्स तंत्र=== | ===विक्रे-क्लार्क-ग्रोव्स तंत्र=== | ||
{{main| | {{main|विक्रे-क्लार्क-ग्रोव्स तंत्र}} | ||
विक्की (1961) नीलामी मॉडल का पश्चात् में विस्तार किया गया {{harvs|txt|last= | विक्की (1961) नीलामी मॉडल का पश्चात् में विस्तार किया गया {{harvs|txt|last=क्लार्क|year=1971|author-link=एडवर्ड एच. क्लार्क}} और ग्रूव्स सार्वजनिक पसंद की समस्या का इलाज करते हैं जिसमें सार्वजनिक परियोजना की निवेश सभी एजेंटों द्वारा वहन की जाती है, उदाहरण के लिए। क्या नगरपालिका पुल बनाना है। परिणामी विकी-क्लार्क-ग्रोव्स तंत्र एजेंटों को जनता की भलाई के सामाजिक रूप से कुशल आवंटन को चुनने के लिए प्रेरित कर सकता है, यदि एजेंटों के पास निजी तौर पर ज्ञात मूल्यांकन हो। दूसरे शब्दों में, यह आम लोगों की त्रासदी को हल कर सकता है - कुछ शर्तों के अनुसार , विशेष रूप से क्वासिलिनियर उपयोगिता में या यदि बजट संतुलन की आवश्यकता नहीं है। | ||
जिसमें सेटिंग पर विचार करें <math>I</math> अनेक एजेंटों के पास निजी मूल्यांकन के साथ चतुर्रेखीय उपयोगिता है <math>v(x,t,\theta)</math> मुद्रा कहां है <math>t</math> रैखिक रूप से मूल्यांकित किया जाता है। वीसीजी डिज़ाइनर वास्तविक प्रकार की प्रोफ़ाइल प्राप्त करने के लिए प्रोत्साहन संगत (इसलिए सच्चाई से कार्यान्वयन योग्य) तंत्र डिज़ाइन करता है, जिससे डिज़ाइनर सामाजिक रूप से इष्टतम आवंटन क्रियान्वित करता है | जिसमें सेटिंग पर विचार करें <math>I</math> अनेक एजेंटों के पास निजी मूल्यांकन के साथ चतुर्रेखीय उपयोगिता है <math>v(x,t,\theta)</math> मुद्रा कहां है <math>t</math> रैखिक रूप से मूल्यांकित किया जाता है। वीसीजी डिज़ाइनर वास्तविक प्रकार की प्रोफ़ाइल प्राप्त करने के लिए प्रोत्साहन संगत (इसलिए सच्चाई से कार्यान्वयन योग्य) तंत्र डिज़ाइन करता है, जिससे डिज़ाइनर सामाजिक रूप से इष्टतम आवंटन क्रियान्वित करता है | ||
| Line 126: | Line 125: | ||
===गिब्बार्ड-सैटरथवेट प्रमेय=== | ===गिब्बार्ड-सैटरथवेट प्रमेय=== | ||
{{main| | {{main|गिबार्ड-सैटरथवेट प्रमेय}} | ||
{{harvs|txt|last= | {{harvs|txt|last=गिब्बार्ड|year=1973|author-link=एलन गिब्बार्ड}} और {{harvs|txt|last=सैटरथवेट|year=1975|author-link=मार्क सैटरथवेट}} एरो की असंभवता प्रमेय की भावना के समान असंभवता परिणाम दें। खेलों के बहुत ही सामान्य वर्ग के लिए, केवल तानाशाही सामाजिक चयन कार्यों को क्रियान्वित किया जा सकता है। | ||
एक सामाजिक चयन फलन f() 'तानाशाहीपूर्ण' है यदि एजेंट को हमेशा अपना सबसे पसंदीदा सामान आवंटन प्राप्त होता है, | एक सामाजिक चयन फलन f() '''<nowiki/>'तानाशाहीपूर्ण'''' है यदि एजेंट को हमेशा अपना सबसे पसंदीदा सामान आवंटन प्राप्त होता है, | ||
:<math>\text{for } f(\Theta)\text{, } \exists i \in I \text{ such that } u_i(x,\theta_i) \geq u_i(x',\theta_i) \ \forall x' \in X</math> | :<math>\text{for } f(\Theta)\text{, } \exists i \in I \text{ such that } u_i(x,\theta_i) \geq u_i(x',\theta_i) \ \forall x' \in X</math> | ||
प्रमेय में कहा गया है कि सामान्य परिस्थितियों में कोई भी सत्यतापूर्वक कार्यान्वयन योग्य सामाजिक चयन कार्य तानाशाही होना चाहिए यदि, | प्रमेय में कहा गया है कि सामान्य परिस्थितियों में कोई भी सत्यतापूर्वक कार्यान्वयन योग्य सामाजिक चयन कार्य तानाशाही होना चाहिए यदि, | ||
| Line 137: | Line 136: | ||
# <math>f(\Theta) = X</math> | # <math>f(\Theta) = X</math> | ||
===मायर्सन-सैटरथवेट प्रमेय=== | ===मायर्सन-सैटरथवेट प्रमेय=== | ||
{{main| | {{main|मायर्सन-सैटरथवेट प्रमेय}} | ||
{{harvs|txt|last=Myerson|last2=Satterthwaite|year=1983|author-link=Roger Myerson}}दिखाता है कि दो पार्टियों के लिए किसी वस्तु का व्यापार करने का कोई प्रभावी प्रणाली नहीं है, जब उनमें से प्रत्येक के पास इसके लिए गुप्त और संभावित रूप से भिन्न-भिन्न मूल्यांकन हों, बिना किसी पार्टी को घाटे में व्यापार करने के लिए मजबूर करने के कठिन परिस्थिति के बिना। यह अर्थशास्त्र में सबसे उल्लेखनीय ऋणात्मक परिणामों में से है - कल्याणकारी अर्थशास्त्र के मूलभूत प्रमेयों का प्रकार का ऋणात्मक दर्पण। | {{harvs|txt|last=Myerson|last2=Satterthwaite|year=1983|author-link=Roger Myerson}}दिखाता है कि दो पार्टियों के लिए किसी वस्तु का व्यापार करने का कोई प्रभावी प्रणाली नहीं है, जब उनमें से प्रत्येक के पास इसके लिए गुप्त और संभावित रूप से भिन्न-भिन्न मूल्यांकन हों, बिना किसी पार्टी को घाटे में व्यापार करने के लिए मजबूर करने के कठिन परिस्थिति के बिना। यह अर्थशास्त्र में सबसे उल्लेखनीय ऋणात्मक परिणामों में से है - कल्याणकारी अर्थशास्त्र के मूलभूत प्रमेयों का प्रकार का ऋणात्मक दर्पण। | ||
=== शेपली मान === | === शेपली मान === | ||
{{main| | {{main|शेपली मूल्य}} | ||
फिलिप्स और मार्डेन (2018) ने सिद्ध करना किया कि अवतल निवेश कार्यों के साथ निवेश-साझाकरण | फिलिप्स और मार्डेन (2018) ने सिद्ध करना किया कि अवतल निवेश कार्यों के साथ निवेश-साझाकरण खेल के लिए, इष्टतम निवेश-साझाकरण नियम जो सबसे पहले खेल में सबसे खराब स्थिति की अक्षमताओं (अराजकता की कीमत) को अनुकूलित करता है, और फिर दूसरे सबसे अच्छे स्थितियोंको अनुकूलित करता है। परिणाम (स्थिरता की कीमत), बिल्कुल शेपली मूल्य निवेश-साझाकरण नियम है।<ref>{{Cite journal|last1=Phillips|first1=Matthew|last2=Marden|first2=Jason R.|date=July 2018|title=अवतल लागत-साझाकरण खेलों में डिज़ाइन ट्रेडऑफ़|journal=IEEE Transactions on Automatic Control|language=en-US|volume=63|issue=7|pages=2242–2247|doi=10.1109/tac.2017.2765299|issn=0018-9286|s2cid=45923961}}</ref> सममित कथन उत्तल उपयोगिता कार्यों के साथ उपयोगिता-साझाकरण खेल के लिए समान रूप से मान्य है। | ||
==उदाहरण== | ==उदाहरण== | ||
| Line 150: | Line 149: | ||
===मूल्य भेदभाव=== | ===मूल्य भेदभाव=== | ||
{{harvs|txt|last= | {{harvs|txt|last=मिर्र्लीस|year=1971|author-link=जेम्स मिरलिस}} ऐसी सेटिंग प्रस्तुत करता है जिसमें ट्रांसफर फलन t() को हल करना आसान है। अपनी प्रासंगिकता और सुगमता के कारण यह साहित्य में सामान्य सेटिंग है। एकल-अच्छी, एकल-एजेंट सेटिंग पर विचार करें जिसमें एजेंट के पास अज्ञात प्रकार के पैरामीटर के साथ क्वासिलिनियर उपयोगिता है <math>\theta</math> | ||
:<math>u(x,t,\theta) = V(x,\theta) - t</math> | :<math>u(x,t,\theta) = V(x,\theta) - t</math> | ||
और जिसमें प्रिंसिपल के पास एजेंट के प्रकार पर पूर्व संचयी वितरण फलन होता है <math>P(\theta)</math>. प्रिंसिपल उत्तल सीमांत निवेश c(x) पर माल का उत्पादन कर सकता है और लेनदेन से अपेक्षित लाभ को अधिकतम करना चाहता है | और जिसमें प्रिंसिपल के पास एजेंट के प्रकार पर पूर्व संचयी वितरण फलन होता है <math>P(\theta)</math>. प्रिंसिपल उत्तल सीमांत निवेश c(x) पर माल का उत्पादन कर सकता है और लेनदेन से अपेक्षित लाभ को अधिकतम करना चाहता है | ||
| Line 169: | Line 168: | ||
भागों द्वारा एकीकरण के पश्चात्. इस फलन को बिंदुवार अधिकतम किया जा सकता है. | भागों द्वारा एकीकरण के पश्चात्. इस फलन को बिंदुवार अधिकतम किया जा सकता है. | ||
जिससे कि <math>U(\theta)</math> प्रोत्साहन-संगत है पहले से ही डिजाइनर आईसी बाधा को हटा सकता है। यदि उपयोगिता फलन स्पेंस-मिर्लीज़ स्थिति को संतुष्ट करता है तब मोनोटोनिक <math>x(\theta)</math> फलन उपस्तिथ है. आईआर बाधा को संतुलन पर जांचा जा सकता है और शुल्क अनुसूची को तदनुसार बढ़ाया या घटाया जा सकता है। इसके अतिरिक्त, अभिव्यक्ति में खतरे की दर की उपस्थिति पर ध्यान दें। यदि प्रकार वितरण में मोनोटोन खतरा अनुपात गुण होता है, तब FOC t() को हल करने के लिए पर्याप्त है। यदि नहीं, तब यह जांचना आवश्यक है कि आवंटन और शुल्क अनुसूचियों के समय एकरसता बाधा (ऊपर तंत्र डिजाइन#पर्याप्तता देखें) हर जगह संतुष्ट है या नहीं। यदि नहीं, तब डिज़ाइनर को मायर्सन इस्त्री का उपयोग करना चाहिए। | |||
===मायर्सन इस्त्री=== | ===मायर्सन इस्त्री=== | ||
| Line 187: | Line 186: | ||
# जो एकरसता को संतुष्ट करता है | # जो एकरसता को संतुष्ट करता है | ||
# जिसके लिए एकरसता बाधा अंतराल की सीमाओं पर बाध्यकारी नहीं है | # जिसके लिए एकरसता बाधा अंतराल की सीमाओं पर बाध्यकारी नहीं है | ||
शर्त दो यह सुनिश्चित करती है कि <math>x(\theta)</math> इष्टतम नियंत्रण समस्या को संतुष्ट करने से अंतराल सीमाओं पर मूल समस्या में शेड्यूल फिर से जुड़ जाता है (कोई छलांग नहीं)। कोई <math>x(\theta)</math> आवश्यक शर्तों को पूरा करना समतल होना चाहिए | शर्त दो यह सुनिश्चित करती है कि <math>x(\theta)</math> इष्टतम नियंत्रण समस्या को संतुष्ट करने से अंतराल सीमाओं पर मूल समस्या में शेड्यूल फिर से जुड़ जाता है (कोई छलांग नहीं)। कोई <math>x(\theta)</math> आवश्यक शर्तों को पूरा करना समतल होना चाहिए जिससे कि यह एकरस होना चाहिए और फिर भी सीमाओं पर पुनः जुड़ना चाहिए। | ||
पहले की तरह, मूलधन की अपेक्षित अदायगी को अधिकतम करें, किन्तु इस बार एकरसता की बाधा के अधीन | पहले की तरह, मूलधन की अपेक्षित अदायगी को अधिकतम करें, किन्तु इस बार एकरसता की बाधा के अधीन | ||
| Line 201: | Line 200: | ||
मूलधन के अधिशेष का औसत विरूपण 0 होना चाहिए। शेड्यूल को समतल करने के लिए, खोजें <math>x</math> इस तरह कि इसकी उलटी छवि पर मैप होती है <math>\theta</math> उपरोक्त शर्त को संतुष्ट करने वाला अंतराल। | मूलधन के अधिशेष का औसत विरूपण 0 होना चाहिए। शेड्यूल को समतल करने के लिए, खोजें <math>x</math> इस तरह कि इसकी उलटी छवि पर मैप होती है <math>\theta</math> उपरोक्त शर्त को संतुष्ट करने वाला अंतराल। | ||
== यह भी देखें == | == '''यह भी देखें''' == | ||
{{div col|colwidth=22em}} | {{div col|colwidth=22em}} | ||
*एल्गोरिदमिक तंत्र डिजाइन | *एल्गोरिदमिक तंत्र डिजाइन | ||
| Line 231: | Line 230: | ||
* [[Noam Nisan|नोआम निसान]]. एक [https://www.youtube.com/watch?v=Ps5aYsG8jY0 गूगल तकनीक वार्ता] तंत्र डिजाइन पर. | * [[Noam Nisan|नोआम निसान]]. एक [https://www.youtube.com/watch?v=Ps5aYsG8jY0 गूगल तकनीक वार्ता] तंत्र डिजाइन पर. | ||
* {{cite web | url = https://voxeu.org/article/nobel-prize-what-mechanism-design-and-why-does-it-matter | title = तंत्र डिज़ाइन क्या है और यह नीति-निर्माण के लिए क्यों मायने रखता है? | last1 = लेग्रोस | first1 = पैट्रिक | last2 = कैंटिलोन | first2 = एस्टेले |author-link2=एस्टेले केंटिलोन | year = 2007 | publisher = [[आर्थिक नीति अनुसंधान केंद्र]] }} | * {{cite web | url = https://voxeu.org/article/nobel-prize-what-mechanism-design-and-why-does-it-matter | title = तंत्र डिज़ाइन क्या है और यह नीति-निर्माण के लिए क्यों मायने रखता है? | last1 = लेग्रोस | first1 = पैट्रिक | last2 = कैंटिलोन | first2 = एस्टेले |author-link2=एस्टेले केंटिलोन | year = 2007 | publisher = [[आर्थिक नीति अनुसंधान केंद्र]] }} | ||
* [[Roger B. Myerson|रोजर बी मायर्सन]] (2008). " | * [[Roger B. Myerson|रोजर बी मायर्सन]] (2008). "तंत्र डिज़ाइन," द न्यू पालग्रेव डिक्शनरी ऑफ़ इकोनॉमिक्स ऑनलाइन, ''[https://link.springer.com/referenceworkentry/10.1057/978-1-349-95121-5_2675-1 अमूर्त.]'' | ||
* {{Citation | last1=डायमंटारस | first1=डिमिट्रायस | title=आर्थिक डिज़ाइन के लिए एक टूलबॉक्स | publisher=[[पालग्रेव मैकमिलन]] | isbn=978-0-230-61060-6 | year=2009| location=न्यूयॉर्क}}. एक स्नातक पाठ विशेष रूप से तंत्र डिजाइन पर केंद्रित है। | * {{Citation | last1=डायमंटारस | first1=डिमिट्रायस | title=आर्थिक डिज़ाइन के लिए एक टूलबॉक्स | publisher=[[पालग्रेव मैकमिलन]] | isbn=978-0-230-61060-6 | year=2009| location=न्यूयॉर्क}}. एक स्नातक पाठ विशेष रूप से तंत्र डिजाइन पर केंद्रित है। | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
* [[Eric Maskin|एरिक मास्किन]] "[https://www.nobelprize.org/mediaplayer/index.php?id=789 नोबेल पुरस्कार व्याख्यान]" 8 दिसंबर 2007 को [[Aula Magna (Stockholm University)|औला मैग्ना]], स्टॉकहोम विश्वविद्यालय में वितरित किया गया। | * [[Eric Maskin|एरिक मास्किन]] "[https://www.nobelprize.org/mediaplayer/index.php?id=789 नोबेल पुरस्कार व्याख्यान]" 8 दिसंबर 2007 को [[Aula Magna (Stockholm University)|औला मैग्ना]], स्टॉकहोम विश्वविद्यालय में वितरित किया गया। | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:CS1 errors]] | |||
[[Category: | |||
[[Category:Created On 27/07/2023]] | [[Category:Created On 27/07/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Multi-column templates]] | |||
[[Category:Pages using div col with small parameter]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Templates using under-protected Lua modules]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:तंत्र डिज़ाइन| तंत्र डिज़ाइन]] | |||
[[Category:सामाजिक चयन सिद्धांत]] | |||
Latest revision as of 10:18, 22 August 2023
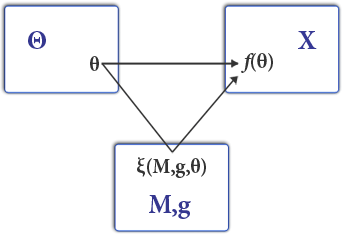
तंत्र डिजाइन अर्थशास्त्र और खेल सिद्धांत में एक क्षेत्र होता है जो रणनीतिक सेटिंग्स में, वांछित उद्देश्यों की ओर, आर्थिक तंत्र या प्रोत्साहन को डिजाइन करने के लिए उद्देश्य-प्रथम दृष्टिकोण लेता है, जहां खिलाड़ी तर्कसंगत रूप से कार्य करते हैं। जिससे कि यह खेल के अंत में प्रारंभ होता है, और फिर पीछे की ओर जाता है, इसे उल्टा खेल सिद्धांत भी कहा जाता है। इस प्रकार इसमें अर्थशास्त्र और राजनीति से लेकर बाजार डिजाइन, नीलामी सिद्धांत और सामाजिक विकल्प सिद्धांत से लेकर नेटवर्क-सिस्टम (इंटरनेट इंटरडोमेन रूटिंग, प्रायोजित खोज नीलामी) जैसे क्षेत्रों में व्यापक अनुप्रयोग होता हैं।
मैकेनिज्म डिज़ाइन निजी-सूचना खेलों के वर्ग के लिए समाधान अवधारणाओं का अध्ययन करता है। इस प्रकार लियोनिद हर्विक्ज़ बताते हैं कि 'डिज़ाइन समस्या में, लक्ष्य फलन मुख्य "दिया" होता है, जबकि तंत्र अज्ञात होता है। इसलिए, डिज़ाइन समस्या पारंपरिक आर्थिक सिद्धांत का "उलटा" देती है, अतः जो सामान्यतः किसी दिए गए तंत्र के प्रदर्शन के विश्लेषण के लिए समर्पित होते है।'[1] तब, इन खेलों की दो विशिष्ट विशेषताएं होती हैं।
- कि खेल "डिज़ाइनर" किसी खेल को विरासत में लेने के अतिरिक्त खेल संरचना को चुनता है
- कि डिज़ाइनर को खेल के परिणाम में रुचि होती है
सन्न 2007 में आर्थिक विज्ञान में नोबेल मेमोरियल पुरस्कार लियोनिद हरविक्ज़, एरिक मास्किन और रोजर मायर्सन को "मैकेनिज्म डिज़ाइन सिद्धांत की नींव रखने के लिए" प्रदान किया गया था।[2]
अंतर्ज्ञान
बायेसियन खेल की रोचक कक्षा में, खिलाड़ी, जिसे "प्रिंसिपल" कहा जाता है, जिससे कि अन्य खिलाड़ियों को निजी रूप पर ज्ञात जानकारी के आधार पर अपने व्यवहार को नियंत्रित किया जाता है। उदाहरण के लिए, प्रिंसिपल यह जानना चाहेंगे कि सेल्समैन जिस पुरानी कार के बारे में बता रहा है, उसकी वास्तविक गुणवत्ता क्या है। वह सिर्फ सेल्समैन से पूछकर कुछ नहीं सीख सकता, जिससे कि सच्चाई को तोड़-मरोड़कर प्रस्तुत करना सेल्समैन के हित में है। यद्यपि, तंत्र डिज़ाइन में प्रिंसिपल को लाभ होता है: वह खेल डिज़ाइन कर सकता है जिसके नियम दूसरों को उस तरह से कार्य करने के लिए प्रभावित कर सकते हैं जैसा वह चाहता है।
तंत्र डिज़ाइन सिद्धांत के बिना, प्रिंसिपल की समस्या को हल करना कठिनाई होगा। उसे सभी संभावित खेलों पर विचार करना होगा और उसे चुनना होगा जो अन्य खिलाड़ियों की रणनीति पर सबसे अच्छा प्रभाव डालता है। इसके अतिरिक्त, प्रिंसिपल को उन एजेंटों से निष्कर्ष निकालना होगा जो उससे झूठ बोल सकते हैं। तंत्र डिज़ाइन और विशेष रूप से रहस्योद्घाटन सिद्धांत के लिए धन्यवाद, प्रिंसिपल को केवल उन खेलों पर विचार करने की आवश्यकता है जिनमें एजेंट अपनी निजी जानकारी को सच्चाई से रिपोर्ट करते हैं।
नींव
तंत्र
तंत्र डिज़ाइन का खेल निजी जानकारी का खेल है जिसमें एजेंटों में से एक, जिसे प्रिंसिपल कहा जाता है, भुगतान संरचना चुनता है। अगले हर्सेन्यि (1967), एजेंटों को प्रकृति से गुप्त संदेश प्राप्त होते हैं जिनमें भुगतान से संबंधित जानकारी होती है। उदाहरण के लिए, किसी संदेश में उनकी प्राथमिकताओं या बिक्री के लिए किसी वस्तु की गुणवत्ता के बारे में जानकारी हो सकती है। हम इस जानकारी को एजेंट का प्रकार कहते हैं (सामान्यतः नोट किया जाता है)। और तदनुसार प्रकारों का स्थान ). फिर एजेंट प्रिंसिपल को प्रकार की रिपोर्ट करते हैं (सामान्यतः टोपी के साथ नोट किया जाता है)। ) यह रणनीतिक झूठ हो सकता है। रिपोर्ट के पश्चात्, प्रिंसिपल और एजेंटों को प्रिंसिपल द्वारा चुनी गई भुगतान संरचना के अनुसार भुगतान किया जाता है।
खेल का समय है:
- प्रिंसिपल तंत्र के लिए प्रतिबद्ध है जो परिणाम देता है रिपोर्ट किए गए प्रकार के फलन के रूप में
- एजेंट, संभवतः बेईमानी से, प्रकार की प्रोफ़ाइल की रिपोर्ट करते हैं
- तंत्र निष्पादित होता है (एजेंट परिणाम प्राप्त करते हैं )
यह समझने के लिए कि किसे क्या मिलता है, परिणाम को विभाजित करना आम बात है माल आवंटन और धन हस्तांतरण में, कहाँ प्रकार के कार्य के रूप में प्रदान की गई या प्राप्त की गई वस्तुओं के आवंटन के लिए खड़ा है, और प्रकार के कार्य के रूप में मौद्रिक हस्तांतरण को दर्शाता है।
एक बेंचमार्क के रूप में डिजाइनर अधिकांशतः यह परिभाषित करते हैं कि पूरी जानकारी के अनुसार क्या होगा। ए को परिभाषित करेंsocial choice function प्राप्त या प्रदान किए गए माल के आवंटन के लिए (सही) प्रकार की प्रोफ़ाइल को सीधे मैप करना,
इसके विपरीत तंत्र रिपोर्ट प्रकार की प्रोफ़ाइल को परिणाम (फिर से, माल आवंटन दोनों) में मैप करता है और धन हस्तांतरण )
रहस्योद्घाटन सिद्धांत
एक प्रस्तावित तंत्र बायेसियन खेल (निजी जानकारी का खेल) का गठन करता है, और यदि यह अच्छी तरह से व्यवहार किया जाता है तब खेल में बायेसियन नैश संतुलन होता है। संतुलन पर एजेंट प्रकार के कार्य के रूप में रणनीतिक रूप से अपनी रिपोर्ट चुनते हैं
ऐसी सेटिंग में बायेसियन संतुलन को हल करना कठिनाई है जिससे कि इसमें एजेंटों की सर्वोत्तम-प्रतिक्रिया रणनीतियों और संभावित रणनीतिक झूठ से सर्वोत्तम अनुमान को हल करना सम्मिलित है। व्यापक परिणाम के लिए धन्यवाद, जिसे रहस्योद्घाटन सिद्धांत कहा जाता है, इससे कोई फर्क नहीं पड़ता कि डिजाइनर कोई भी तंत्र बना सकता है[3] संतुलन पर ध्यान केंद्रित करें जिसमें एजेंट सच्चाई से प्रकार की रिपोर्ट करते हैं। रहस्योद्घाटन सिद्धांत कहता है: प्रत्येक बायेसियन नैश संतुलन के लिए बायेसियन खेल समान संतुलन परिणाम के साथ मेल खाता है किन्तु जिसमें खिलाड़ी सच्चाई से रिपोर्ट प्रकार करते हैं।
यह अत्यंत उपयोगी है. सिद्धांत सभी खिलाड़ियों को सच्चाई से रिपोर्ट प्रकार (एक प्रोत्साहन अनुकूलता बाधा के अधीन) मानकर बायेसियन संतुलन को हल करने की अनुमति देता है। झटके में यह रणनीतिक व्यवहार या झूठ पर विचार करने की आवश्यकता को समाप्त कर देता है।
इसका प्रमाण बिल्कुल प्रत्यक्ष है. बायेसियन खेल मान लें जिसमें एजेंट की रणनीति और भुगतान उसके प्रकार के कार्य हैं और अन्य क्या करते हैं, . परिभाषा के अनुसार एजेंट I की संतुलन रणनीति क्या नैश अपेक्षित उपयोगिता में है:
बस तंत्र को परिभाषित करें जो एजेंटों को समान संतुलन चुनने के लिए प्रेरित करेगा। परिभाषित करने के लिए सबसे आसान प्रणाली यह है कि तंत्र उनके लिए एजेंटों की संतुलन रणनीतियों को निभाने के लिए प्रतिबद्ध हो।
ऐसे तंत्र के अनुसार एजेंटों को निश्चित रूप से प्रकार प्रकट करना इष्टतम लगता है जिससे कि तंत्र उन रणनीतियों को खेलता है जिन्हें यह वैसे भी इष्टतम पाते हैं। औपचारिक रूप से, चुनें ऐसा है कि
कार्यान्वयनशीलता
किसी तंत्र का डिज़ाइनर सामान्यतः या तब आशा करता है
- एक तंत्र डिज़ाइन करना जो सामाजिक चयन फलन को कार्यान्वित करता है
- तंत्र खोजने के लिए जो कुछ मूल्य मानदंड को अधिकतम करता है (जैसे लाभ)
सामाजिक चयन फलन को कार्यान्वित करना कुछ ढूंढना है स्थानांतरण फलन जो एजेंटों को चुनने के लिए प्रेरित करता है . औपचारिक रूप से, यदि तंत्र के अनुसार संतुलन रणनीति प्रोफ़ाइल सामाजिक चयन फलन के समान सामान आवंटन पर मैप करती है,
हम कहते हैं कि तंत्र सामाजिक चयन फलन को कार्यान्वित करता है।
रहस्योद्घाटन सिद्धांत के लिए धन्यवाद, डिजाइनर सामान्यतः स्थानांतरण फलन ढूंढ सकता है संबंधित सत्य कथन खेल को हल करके सामाजिक विकल्प को क्रियान्वित करना। यदि एजेंटों को सत्यतापूर्वक रिपोर्ट प्रकार देना सर्वोत्तम लगता है,
हम कहते हैं कि ऐसा तंत्र सचमुच कार्यान्वयन योग्य है (या बस कार्यान्वयन योग्य है)। फिर कार्य को सत्यतापूर्वक कार्यान्वयन के लिए हल करना है और इस स्थानांतरण फलन को मूल खेल में क्रियान्वित करें। आवंटन यदि कोई स्थानांतरण फलन उपस्तिथ है तब यह वास्तव में कार्यान्वयन योग्य है ऐसा है कि
जिसे प्रोत्साहन अनुकूलता (आईसी) बाधा भी कहा जाता है।
अनुप्रयोगों में, आईसी स्थिति आकार का वर्णन करने की कुंजी है किसी भी उपयोगी तरीके से. कुछ शर्तों के अनुसार यह स्थानांतरण फलन को विश्लेषणात्मक रूप से भिन्न भी कर सकता है। इसके अतिरिक्त, यदि एजेंटों के पास नहीं खेलने का विकल्प होता है तब कभी-कभी भागीदारी (व्यक्तिगत तर्कसंगतता) बाधा भी जोड़ी जाती है।
आवश्यकता
एक ऐसी सेटिंग पर विचार करें जिसमें सभी एजेंटों के पास प्रकार-आकस्मिक उपयोगिता फलन हो . माल आवंटन पर भी विचार करें वह सदिश-मूल्यवान और आकार है (जो अनुमति देता है वस्तुओं की संख्या) और मान लें कि यह अपने तर्कों के संबंध में टुकड़ों में निरंतर है।
कार्यक्रम कार्यान्वयन तभी संभव है जब
जब कभी भी और और x निरंतर है . यह आवश्यक शर्त है और सत्य-कथन को मानते हुए एजेंट की अनुकूलन समस्या के पहले और दूसरे क्रम की स्थितियों से ली गई है।
इसका अर्थ दो टुकड़ों में समझा जा सकता है. पहला भाग कहता है कि एजेंट की प्रतिस्थापन की सीमांत दर (एमआरएस) प्रकार के फलन के रूप में बढ़ती है,
संक्षेप में, यदि तंत्र उच्च प्रकार के एजेंट को उत्तम सौदा प्रदान नहीं करता है तब एजेंट सच नहीं बताएंगे। अन्यथा, किसी भी तंत्र का सामना करने वाले उच्च प्रकार, जो रिपोर्टिंग के लिए उच्च प्रकार को दंडित करते हैं, झूठ बोलेंगे और घोषणा करेंगे कि वे निम्न प्रकार के हैं, सत्य बताने वाली आईसी बाधा का उल्लंघन करेंगे। दूसरा भाग एकरसता की स्थिति है जो घटित होने की प्रतीक्षा कर रही है,
जिसका, धनात्मक होने का कारण है कि उच्च प्रकारों को अधिक अच्छाई दी जानी चाहिए।
दोनों टुकड़ों के मध्य बातचीत की संभावना है। यदि किसी प्रकार की श्रेणी के लिए अनुबंध में उच्च प्रकार की तुलना में कम मात्रा की पेशकश की जाती है , यह संभव है कि तंत्र उच्च प्रकार की छूट देकर क्षतिपूर्ति कर सके। किन्तु निम्न-प्रकार के एजेंटों के लिए ऐसा अनुबंध पहले से उपस्तिथ है, इसलिए यह समाधान रोगविज्ञानी है। ऐसा समाधान कभी-कभी किसी तंत्र के समाधान की प्रक्रिया में होता है। इन स्थितियोंमें यह तंत्र डिजाइन मायर्सन इस्त्री होना चाहिए। बहु-अच्छे वातावरण में डिज़ाइनर के लिए यह भी संभव है कि वह एजेंट को किसी अन्य वस्तु के कम के स्थान पर अधिक वस्तु देकर पुरस्कृत करे (जैसे [[नकली मक्खन]] के लिए मक्खन)। तंत्र डिजाइन सिद्धांत में बहु-अच्छे तंत्र सतत समस्या हैं।
पर्याप्तता
कार्यान्वयन सुनिश्चित करने के लिए तंत्र डिज़ाइन पेपर सामान्यतः दो धारणाएँ बनाते हैं:
इसे अनेक नामों से जाना जाता है: सिंगल-क्रॉसिंग स्थिति, सॉर्टिंग स्थिति और स्पेंस-मिर्लीज़ स्थिति। इसका कारण है कि उपयोगिता फलन इस प्रकार का है कि एजेंट की एमआरएस प्रकार में वृद्धि हो रही है।
- <ली मान= 2 >
यह एमआरएस की वृद्धि दर को सीमित करने वाली विधि स्थिति है।
यह धारणाएँ किसी भी एकरसता प्रदान करने के लिए पर्याप्त हैं कार्यान्वयन योग्य है (ए उपस्तिथ है जो इसे कार्यान्वित कर सकता है)। इसके अतिरिक्त, एकल-अच्छी सेटिंग में एकल-क्रॉसिंग स्थिति केवल मोनोटोनिक प्रदान करने के लिए पर्याप्त है कार्यान्वयन योग्य है, इसलिए डिज़ाइनर अपनी खोज को मोनोटोनिक तक सीमित कर सकता है .
हाइलाइट किए गए परिणाम
राजस्व तुल्यता प्रमेय
Vickrey (1961) प्रतिष्ठित परिणाम देता है कि नीलामी के बड़े वर्ग का कोई भी सदस्य विक्रेता को समान अपेक्षित राजस्व का आश्वासन देता है और यह कि अपेक्षित राजस्व विक्रेता के लिए सबसे अच्छा है। यही स्थिति है यदि
- खरीदारों के पास समान मूल्यांकन कार्य हैं (जो प्रकार का कार्य हो सकता है)
- खरीदारों के प्रकार स्वतंत्र रूप से वितरित किए जाते हैं
- खरीदार प्रकार सतत वितरण # सतत संभाव्यता वितरण से लिए गए हैं
- प्रकार वितरण में मोनोटोन कठिन परिस्थिति दर गुण होता है
- तंत्र उच्चतम मूल्यांकन वाले खरीदार को सामान बेचता है
अंतिम शर्त प्रमेय के लिए महत्वपूर्ण है। निहितार्थ यह है कि विक्रेता को अधिक राजस्व प्राप्त करने के लिए कम मूल्यांकन वाले एजेंट को वस्तु देने का मौका लेना चाहिए। सामान्यतः इसका कारण यह है कि उसे वस्तु बिल्कुल भी न बेचने का कठिन परिस्थिति उठाना होगा।
विक्रे-क्लार्क-ग्रोव्स तंत्र
विक्की (1961) नीलामी मॉडल का पश्चात् में विस्तार किया गया क्लार्क (1971) और ग्रूव्स सार्वजनिक पसंद की समस्या का इलाज करते हैं जिसमें सार्वजनिक परियोजना की निवेश सभी एजेंटों द्वारा वहन की जाती है, उदाहरण के लिए। क्या नगरपालिका पुल बनाना है। परिणामी विकी-क्लार्क-ग्रोव्स तंत्र एजेंटों को जनता की भलाई के सामाजिक रूप से कुशल आवंटन को चुनने के लिए प्रेरित कर सकता है, यदि एजेंटों के पास निजी तौर पर ज्ञात मूल्यांकन हो। दूसरे शब्दों में, यह आम लोगों की त्रासदी को हल कर सकता है - कुछ शर्तों के अनुसार , विशेष रूप से क्वासिलिनियर उपयोगिता में या यदि बजट संतुलन की आवश्यकता नहीं है।
जिसमें सेटिंग पर विचार करें अनेक एजेंटों के पास निजी मूल्यांकन के साथ चतुर्रेखीय उपयोगिता है मुद्रा कहां है रैखिक रूप से मूल्यांकित किया जाता है। वीसीजी डिज़ाइनर वास्तविक प्रकार की प्रोफ़ाइल प्राप्त करने के लिए प्रोत्साहन संगत (इसलिए सच्चाई से कार्यान्वयन योग्य) तंत्र डिज़ाइन करता है, जिससे डिज़ाइनर सामाजिक रूप से इष्टतम आवंटन क्रियान्वित करता है
वीसीजी तंत्र की चतुराई वह प्रणाली है जिससे यह सत्य रहस्योद्घाटन को प्रेरित करता है। यह किसी भी एजेंट को उसके कारण होने वाली विकृति की कीमत पर दंडित करके गलत रिपोर्ट करने के प्रोत्साहन को समाप्त करता है। एजेंट जो रिपोर्ट बना सकता है, उनमें से वीसीजी तंत्र अशक्त रिपोर्ट की अनुमति देता है जिसमें कहा गया है कि वह जनता की भलाई के प्रति उदासीन है और केवल धन हस्तांतरण की परवाह करता है। यह प्रभावी रूप से एजेंट को खेल से हटा देता है। यदि कोई एजेंट किसी प्रकार की रिपोर्ट करना चुनता है, तब वीसीजी तंत्र एजेंट से शुल्क लेता है यदि उसकी रिपोर्ट महत्वपूर्ण है, अर्थात यदि उसकी रिपोर्ट अन्य एजेंटों को हानि पहुंचाने के लिए इष्टतम आवंटन x को बदल देती है। भुगतान की गणना की जाती है
जो एजेंट की रिपोर्टिंग के कारण अन्य एजेंटों (और उसके अपने नहीं) की उपयोगिताओं में आई विकृति का सारांश देता है।
गिब्बार्ड-सैटरथवेट प्रमेय
गिब्बार्ड (1973) और सैटरथवेट (1975) एरो की असंभवता प्रमेय की भावना के समान असंभवता परिणाम दें। खेलों के बहुत ही सामान्य वर्ग के लिए, केवल तानाशाही सामाजिक चयन कार्यों को क्रियान्वित किया जा सकता है।
एक सामाजिक चयन फलन f() 'तानाशाहीपूर्ण' है यदि एजेंट को हमेशा अपना सबसे पसंदीदा सामान आवंटन प्राप्त होता है,
प्रमेय में कहा गया है कि सामान्य परिस्थितियों में कोई भी सत्यतापूर्वक कार्यान्वयन योग्य सामाजिक चयन कार्य तानाशाही होना चाहिए यदि,
- X परिमित है और इसमें कम से कम तीन तत्व हैं
- प्राथमिकताएँ तर्कसंगत हैं
मायर्सन-सैटरथवेट प्रमेय
Myerson and Satterthwaite (1983)दिखाता है कि दो पार्टियों के लिए किसी वस्तु का व्यापार करने का कोई प्रभावी प्रणाली नहीं है, जब उनमें से प्रत्येक के पास इसके लिए गुप्त और संभावित रूप से भिन्न-भिन्न मूल्यांकन हों, बिना किसी पार्टी को घाटे में व्यापार करने के लिए मजबूर करने के कठिन परिस्थिति के बिना। यह अर्थशास्त्र में सबसे उल्लेखनीय ऋणात्मक परिणामों में से है - कल्याणकारी अर्थशास्त्र के मूलभूत प्रमेयों का प्रकार का ऋणात्मक दर्पण।
शेपली मान
फिलिप्स और मार्डेन (2018) ने सिद्ध करना किया कि अवतल निवेश कार्यों के साथ निवेश-साझाकरण खेल के लिए, इष्टतम निवेश-साझाकरण नियम जो सबसे पहले खेल में सबसे खराब स्थिति की अक्षमताओं (अराजकता की कीमत) को अनुकूलित करता है, और फिर दूसरे सबसे अच्छे स्थितियोंको अनुकूलित करता है। परिणाम (स्थिरता की कीमत), बिल्कुल शेपली मूल्य निवेश-साझाकरण नियम है।[4] सममित कथन उत्तल उपयोगिता कार्यों के साथ उपयोगिता-साझाकरण खेल के लिए समान रूप से मान्य है।
उदाहरण
मूल्य भेदभाव
मिर्र्लीस (1971) ऐसी सेटिंग प्रस्तुत करता है जिसमें ट्रांसफर फलन t() को हल करना आसान है। अपनी प्रासंगिकता और सुगमता के कारण यह साहित्य में सामान्य सेटिंग है। एकल-अच्छी, एकल-एजेंट सेटिंग पर विचार करें जिसमें एजेंट के पास अज्ञात प्रकार के पैरामीटर के साथ क्वासिलिनियर उपयोगिता है
और जिसमें प्रिंसिपल के पास एजेंट के प्रकार पर पूर्व संचयी वितरण फलन होता है . प्रिंसिपल उत्तल सीमांत निवेश c(x) पर माल का उत्पादन कर सकता है और लेनदेन से अपेक्षित लाभ को अधिकतम करना चाहता है
आईसी और आईआर शर्तों के अधीन
यहां प्रिंसिपल एकाधिकारवादी है जो लाभ-अधिकतम मूल्य योजना निर्धारित करने की कोशिश कर रहा है जिसमें वह ग्राहक के प्रकार की पहचान नहीं कर सकता है। सामान्य उदाहरण व्यवसाय, अवकाश और छात्र यात्रियों के लिए किराया निर्धारित करने वाली एयरलाइन है। आईआर शर्त के कारण इसे भागीदारी को प्रेरित करने के लिए हर प्रकार को पर्याप्त अच्छा सौदा देना पड़ता है। आईसी शर्त के कारण इसे प्रत्येक प्रकार को इतना अच्छा सौदा देना होता है कि वह प्रकार किसी अन्य प्रकार के सौदे को प्राथमिकता दे।
मिर्लीज़ (1971) द्वारा दी गई तरकीब यह है कि ट्रांसफर फलन को अधिकतम होने की उम्मीद से खत्म करने के लिए लिफ़ाफ़ा प्रमेय का उपयोग किया जाए,
एकीकरण,
कहाँ कुछ सूचकांक प्रकार है. प्रोत्साहन-संगत की जगह अधिकतम में,
भागों द्वारा एकीकरण के पश्चात्. इस फलन को बिंदुवार अधिकतम किया जा सकता है.
जिससे कि प्रोत्साहन-संगत है पहले से ही डिजाइनर आईसी बाधा को हटा सकता है। यदि उपयोगिता फलन स्पेंस-मिर्लीज़ स्थिति को संतुष्ट करता है तब मोनोटोनिक फलन उपस्तिथ है. आईआर बाधा को संतुलन पर जांचा जा सकता है और शुल्क अनुसूची को तदनुसार बढ़ाया या घटाया जा सकता है। इसके अतिरिक्त, अभिव्यक्ति में खतरे की दर की उपस्थिति पर ध्यान दें। यदि प्रकार वितरण में मोनोटोन खतरा अनुपात गुण होता है, तब FOC t() को हल करने के लिए पर्याप्त है। यदि नहीं, तब यह जांचना आवश्यक है कि आवंटन और शुल्क अनुसूचियों के समय एकरसता बाधा (ऊपर तंत्र डिजाइन#पर्याप्तता देखें) हर जगह संतुष्ट है या नहीं। यदि नहीं, तब डिज़ाइनर को मायर्सन इस्त्री का उपयोग करना चाहिए।
मायर्सन इस्त्री
कुछ अनुप्रयोगों में डिज़ाइनर मूल्य और आवंटन शेड्यूल के लिए प्रथम-क्रम की शर्तों को हल कर सकता है, फिर भी उन्हें पता चलता है कि यह मोनोटोनिक नहीं हैं। उदाहरण के लिए, क्वासिलिनियर सेटिंग में यह अधिकांशतः तब होता है जब खतरा अनुपात स्वयं समान नहीं होता है। स्पेंस-मिर्लीज़ शर्त के अनुसार इष्टतम मूल्य और आवंटन कार्यक्रम एकरस होना चाहिए, इसलिए डिज़ाइनर को किसी भी अंतराल को समाप्त करना होगा जिस पर शेड्यूल समतल करके दिशा बदलता है।
सहज रूप से, जो चल रहा है वह यह है कि डिजाइनर को कुछ प्रकारों को साथ जोड़ना और उन्हें ही अनुबंध देना सबसे अच्छा लगता है। सामान्यतः डिज़ाइनर उच्च प्रकारों को उत्तम डील देकर उन्हें भिन्न दिखने के लिए प्रेरित करते हैं। यदि मार्जिन पर अपर्याप्त रूप से कुछ उच्च प्रकार हैं तब डिज़ाइनर को उच्च प्रकार के विशिष्ट अनुबंध पर शुल्क लगाने के लिए निम्न प्रकार की रियायत (जिसे उनका सूचना किराया कहा जाता है) देना उचित नहीं लगता है।
ऊपर दिए गए उदाहरण में, एकाधिकारवादी प्रिंसिपल को क्वासिलिनियर उपयोगिता वाले एजेंटों को बेचने पर विचार करें। मान लीजिए आवंटन अनुसूची प्रथम-क्रम की शर्तों को संतुष्ट करने पर एकल आंतरिक शिखर होता है और आंतरिक गर्त , दाईं ओर चित्रित।
- मायरसन (1981) का अनुसरण करते हुए इसे चुनकर समतल करें संतुष्टि देने वाला कहाँ x मानचित्रण का व्युत्क्रम कार्य है और x मानचित्रण का व्युत्क्रम कार्य है . वह है, रिटर्न ए आंतरिक शिखर से पहले और रिटर्न ए आंतरिक गर्त के पश्चात्.
- यदि गैरमोनोटोनिक क्षेत्र टाइप स्पेस के किनारे को बॉर्डर करें, बस उपयुक्त सेट करें सीमा प्रकार के लिए फलन (या दोनों)। यदि अनेक क्षेत्र हैं, तब पुनरावृत्तीय प्रक्रिया के लिए पाठ्यपुस्तक देखें; ऐसा हो सकता है कि से अधिक कुंडों को साथ इस्त्री किया जाना चाहिए।
प्रमाण
प्रमाण इष्टतम नियंत्रण के सिद्धांत का उपयोग करता है। यह अंतरालों के समुच्चय पर विचार करता है के नॉनमोनोटोनिक क्षेत्र में जिस पर यह शेड्यूल को समतल कर सकता है। इसके पश्चात् यह आवश्यक शर्तों को प्राप्त करने के लिए हैमिल्टनियन लिखता है अंतराल के भीतर
- जो एकरसता को संतुष्ट करता है
- जिसके लिए एकरसता बाधा अंतराल की सीमाओं पर बाध्यकारी नहीं है
शर्त दो यह सुनिश्चित करती है कि इष्टतम नियंत्रण समस्या को संतुष्ट करने से अंतराल सीमाओं पर मूल समस्या में शेड्यूल फिर से जुड़ जाता है (कोई छलांग नहीं)। कोई आवश्यक शर्तों को पूरा करना समतल होना चाहिए जिससे कि यह एकरस होना चाहिए और फिर भी सीमाओं पर पुनः जुड़ना चाहिए।
पहले की तरह, मूलधन की अपेक्षित अदायगी को अधिकतम करें, किन्तु इस बार एकरसता की बाधा के अधीन
और इसे करने के लिए छाया मूल्य के साथ हैमिल्टनियन का उपयोग करें
कहाँ राज्य चर है और द कंट्रोल। इष्टतम नियंत्रण में हमेशा की तरह निवेश विकास समीकरण को संतुष्ट करना होगा
शर्त 2 का लाभ उठाते हुए, ध्यान दें कि एकरसता बाधा की सीमाओं पर बाध्यकारी नहीं है मध्यान्तर,
जिसका अर्थ है कि निवेश परिवर्तनीय स्थिति को एकीकृत किया जा सकता है और यह 0 के सामान्तर भी है
मूलधन के अधिशेष का औसत विरूपण 0 होना चाहिए। शेड्यूल को समतल करने के लिए, खोजें इस तरह कि इसकी उलटी छवि पर मैप होती है उपरोक्त शर्त को संतुष्ट करने वाला अंतराल।
यह भी देखें
- एल्गोरिदमिक तंत्र डिजाइन
- एल्विन ई. रोथ - नोबेल पुरस्कार, बाज़ार डिज़ाइन
- असाइनमेंट समस्या
- अनुबंध सिद्धांत
- कार्यान्वयन सिद्धांत
- प्रोत्साहन अनुकूलता
- रहस्योद्घाटन सिद्धांत
- स्मार्ट बाज़ार
- मेटागेम
टिप्पणियाँ
- ↑ L. Hurwicz & S. Reiter (2006) Designing Economic Mechanisms, p. 30
- ↑ "The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 2007" (Press release). Nobel Foundation. October 15, 2007. Retrieved 2008-08-15.
- ↑ In unusual circumstances some truth-telling games have more equilibria than the Bayesian game they mapped from. See Fudenburg-Tirole Ch. 7.2 for some references.
- ↑ Phillips, Matthew; Marden, Jason R. (July 2018). "अवतल लागत-साझाकरण खेलों में डिज़ाइन ट्रेडऑफ़". IEEE Transactions on Automatic Control (in English). 63 (7): 2242–2247. doi:10.1109/tac.2017.2765299. ISSN 0018-9286. S2CID 45923961.
संदर्भ
- क्लार्क, एडवर्ड एच. (1971). "सार्वजनिक वस्तुओं का बहुखण्डीय मूल्य निर्धारण" (PDF). सार्वजनिक पसंद. 11 (1): 17–33. doi:10.1007/BF01726210. JSTOR 30022651. S2CID 154860771.
- गिब्बार्ड, एलन (1973). "मतदान योजनाओं में हेरफेर: एक सामान्य परिणाम" (PDF). इकोनोमेट्रिका. 41 (4): 587–601. doi:10.2307/1914083. JSTOR 1914083.
- ग्रोव, थिओडोर (1973). "टीमों में प्रोत्साहन" (PDF). अर्थमिति. 41 (4): 617–631. doi:10.2307/1914085. JSTOR 1914085.
- हर्सेन्यि, जॉन सी. (1967). "अधूरी जानकारी वाले खेल "बायेसियन" खिलाड़ियों द्वारा खेले गए, I-III। भाग I. मूल मॉडल". प्रबंधन विज्ञान. 14 (3): 159–182. doi:10.1287/mnsc.14.3.159. JSTOR 2628393.
- मिर्र्लीस, जे. ए. (1971). "इष्टतम आय कराधान के सिद्धांत में एक अन्वेषण" (PDF). आर्थिक अध्ययन की समीक्षा. 38 (2): 175–208. doi:10.2307/2296779. JSTOR 2296779. Archived from the original (PDF) on 2017-05-10. Retrieved 2016-08-12.
{{cite journal}}: Invalid|url-status=मृत(help) - मायरसन, रोजर बी.; सैटरथवेट, मार्क ए. (1983). "द्विपक्षीय व्यापार के लिए कुशल तंत्र" (PDF). जर्नल ऑफ इकोनॉमिक थ्योरी. 29 (2): 265–281. doi:10.1016/0022-0531(83)90048-0. hdl:10419/220829.
{{cite journal}}: Invalid|hdl-access=मुक्त(help) - सैटरथवेट, मार्क एलन (1975). "रणनीति-प्रमाणता और तीर की शर्तें: मतदान प्रक्रियाओं और सामाजिक कल्याण कार्यों के लिए अस्तित्व और पत्राचार प्रमेय". जर्नल ऑफ़ इकोनॉमिक थ्योरी. 10 (2): 187–217. CiteSeerX 10.1.1.471.9842. doi:10.1016/0022-0531(75)90050-2.
- विक्रे, विलियम (1961). "प्रतिअटकलें, नीलामी, और प्रतिस्पर्धी मुहरबंद निविदाएं" (PDF). वित्त जर्नल. 16 (1): 8–37. doi:10.1111/j.1540-6261.1961.tb02789.x.
अग्रिम पठन
- अध्याय 7 का फुडेनबर्ग, ड्रयू; तिरोले, जीन (1991), खेल सिद्धांत, बोस्टान: एमआईटी प्रेस, ISBN 978-0-262-06141-4. स्नातक खेल सिद्धांत के लिए एक मानक पाठ।
- अध्याय 23 का मास-Colell; विंस्टन; हरा (1995), सूक्ष्म आर्थिक सिद्धांत, ऑक्सफ़ोर्ड: ऑक्सफोर्ड यूनिवरसिटि प्रेस, ISBN 978-0-19-507340-9. स्नातक सूक्ष्मअर्थशास्त्र के लिए एक मानक पाठ।
- मिलग्रोम, पॉल (2004), नीलामी सिद्धांत को कार्यान्वित करना, न्यूयॉर्क: कैम्ब्रिज यूनिवर्सिटी प्रेस, ISBN 978-0-521-55184-7. अनुप्रयोग नीलामी के संदर्भ में तंत्र डिजाइन सिद्धांतों की।
- नोआम निसान. एक गूगल तकनीक वार्ता तंत्र डिजाइन पर.
- लेग्रोस, पैट्रिक; कैंटिलोन, एस्टेले (2007). "तंत्र डिज़ाइन क्या है और यह नीति-निर्माण के लिए क्यों मायने रखता है?". आर्थिक नीति अनुसंधान केंद्र.
- रोजर बी मायर्सन (2008). "तंत्र डिज़ाइन," द न्यू पालग्रेव डिक्शनरी ऑफ़ इकोनॉमिक्स ऑनलाइन, अमूर्त.
- डायमंटारस, डिमिट्रायस (2009), आर्थिक डिज़ाइन के लिए एक टूलबॉक्स, न्यूयॉर्क: पालग्रेव मैकमिलन, ISBN 978-0-230-61060-6. एक स्नातक पाठ विशेष रूप से तंत्र डिजाइन पर केंद्रित है।
बाहरी संबंध
- एरिक मास्किन "नोबेल पुरस्कार व्याख्यान" 8 दिसंबर 2007 को औला मैग्ना, स्टॉकहोम विश्वविद्यालय में वितरित किया गया।
