रेखांकन का टेन्सर उत्पाद: Difference between revisions
No edit summary |
m (6 revisions imported from alpha:रेखांकन_का_टेन्सर_उत्पाद) |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Operation in graph theory}} | {{Short description|Operation in graph theory}} | ||
{{distinguish|टेंसर उत्पाद}} | {{distinguish|टेंसर उत्पाद}} | ||
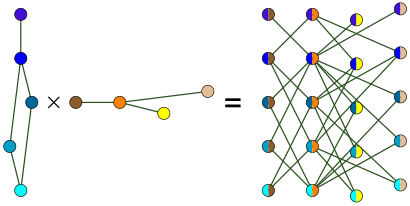
[[File:Graph-tensor-product.svg|thumb|upright=1.35|रेखांकन का टेंसर उत्पाद।]][[ग्राफ सिद्धांत]] में, टेंसर उत्पाद | [[File:Graph-tensor-product.svg|thumb|upright=1.35|रेखांकन का टेंसर उत्पाद।]][[ग्राफ सिद्धांत]] में, टेंसर उत्पाद {''G'' × ''H''} ग्राफ का (असतत गणित) {{mvar|G}} और {{mvar|H}} ऐसा ग्राफ है। | ||
* [[ शीर्ष (ग्राफ सिद्धांत) ]] का सेट {{math|''G'' × ''H''}} कार्टेशियन उत्पाद है {{math|''V''(''G'') × ''V''(''H'')}}; और | * [[ शीर्ष (ग्राफ सिद्धांत) | शीर्ष (ग्राफ सिद्धांत)]] का सेट {{math|''G'' × ''H''}} कार्टेशियन उत्पाद है {{math|''V''(''G'') × ''V''(''H'')}}; और | ||
* शिखर {{math|(''g'',''h'')}} और {{math|(''g''',''h' '')}} में सटे हुए हैं {{math|''G'' × ''H''}} [[अगर और केवल अगर|यदि और केवल यदि]] | * शिखर {{math|(''g'',''h'')}} और {{math|(''g''',''h' '')}} में सटे हुए हैं {{math|''G'' × ''H''}} [[अगर और केवल अगर|यदि और केवल यदि]] | ||
**{{mvar|g}} लगी हुई है {{mvar|g'}} में {{mvar|G}}, और | **{{mvar|g}} लगी हुई है {{mvar|g'}} में {{mvar|G}}, और | ||
**{{mvar|h}} लगी हुई है {{mvar|h'}} में {{mvar|H}}. | **{{mvar|h}} लगी हुई है {{mvar|h'}} में {{mvar|H}}. | ||
टेंसर उत्पाद को प्रत्यक्ष उत्पाद, क्रोनकर उत्पाद, श्रेणीबद्ध उत्पाद, कार्डिनल उत्पाद, संबंधपरक उत्पाद, कमजोर प्रत्यक्ष उत्पाद या संयोजन भी कहा जाता है। द्विआधारी संबंधों पर एक ऑपरेशन के रूप में, टेन्सर उत्पाद को [[अल्फ्रेड नॉर्थ व्हाइटहेड]] और [[बर्ट्रेंड रसेल]] द्वारा उनके [[ गणितीय सिद्धांत | प्रिंसिपिया मैथेमेटिका (1912)]] | टेंसर उत्पाद को प्रत्यक्ष उत्पाद, क्रोनकर उत्पाद, श्रेणीबद्ध उत्पाद, कार्डिनल उत्पाद, संबंधपरक उत्पाद, कमजोर प्रत्यक्ष उत्पाद या संयोजन भी कहा जाता है। द्विआधारी संबंधों पर एक ऑपरेशन के रूप में, टेन्सर उत्पाद को [[अल्फ्रेड नॉर्थ व्हाइटहेड]] और [[बर्ट्रेंड रसेल]] द्वारा उनके [[ गणितीय सिद्धांत |प्रिंसिपिया मैथेमेटिका (1912)]] में प्रस्तुत किया गया था। यह ग्राफ़ के आसन्न मैट्रिक्स के [[क्रोनकर उत्पाद|क्रोनकर गुणनफल]] के बराबर भी है।{{sfn|Weichsel|1962}} | ||
अंकन {{math|''G'' × ''H''}} भी (और पूर्व में सामान्य रूप से था) एक अन्य निर्माण का प्रतिनिधित्व करने के लिए उपयोग किया जाता है जिसे ग्राफ़ के कार्टेशियन उत्पाद के रूप में जाना जाता है, लेकिन आजकल अधिक सामान्यतः टेंसर उत्पाद को संदर्भित करता है। क्रॉस प्रतीक दो किनारों के टेन्सर उत्पाद से उत्पन्न दो किनारों को नेत्रहीन रूप से दिखाता है।{{sfn|Hahn|Sabidussi|1997}} इस उत्पाद को ग्राफ़ के मज़बूत गुणनफल के साथ भ्रमित नहीं होना चाहिए। | अंकन {{math|''G'' × ''H''}} भी (और पूर्व में सामान्य रूप से था) एक अन्य निर्माण का प्रतिनिधित्व करने के लिए उपयोग किया जाता है जिसे ग्राफ़ के कार्टेशियन उत्पाद के रूप में जाना जाता है, लेकिन आजकल अधिक सामान्यतः टेंसर उत्पाद को संदर्भित करता है। क्रॉस प्रतीक दो किनारों के टेन्सर उत्पाद से उत्पन्न दो किनारों को नेत्रहीन रूप से दिखाता है।{{sfn|Hahn|Sabidussi|1997}} इस उत्पाद को ग्राफ़ के मज़बूत गुणनफल के साथ भ्रमित नहीं होना चाहिए। | ||
== उदाहरण == | == उदाहरण == | ||
* टेंसर उत्पाद {{math|''G'' × ''K''<sub>2</sub>}} एक [[द्विपक्षीय ग्राफ]] है, जिसे [[द्विपक्षीय डबल कवर]] कहा जाता है {{mvar|G}} | * टेंसर उत्पाद {{math|''G'' × ''K''<sub>2</sub>}} एक [[द्विपक्षीय ग्राफ]] है, जिसे [[द्विपक्षीय डबल कवर]] कहा जाता है {{mvar|G}} [[पीटरसन ग्राफ]] का द्विदलीय डबल कवर [[Desargues ग्राफ|डेसार्गेस ग्राफ]] है: {{math|1=''K''<sub>2</sub> × ''G''(5,2) = ''G''(10,3)}}. एक पूर्ण ग्राफ का द्विदलीय दोहरा आवरण {{mvar|K<sub>n</sub>}} एक [[क्राउन ग्राफ]] (एक [[पूर्ण द्विदलीय ग्राफ]]) है {{math|''K''<sub>''n'',''n''</sub>}} माइनस [[ सही मिलान |सही मिलान है]]।) | ||
* स्वयं के साथ एक पूर्ण ग्राफ़ का टेंसर उत्पाद रूक के ग्राफ़ का पूरक (ग्राफ़ सिद्धांत) है। इसके शीर्षों को a में रखा जा सकता है {{nowrap|{{mvar|n}}-by-{{mvar|n}}}} ग्रिड, ताकि प्रत्येक शीर्ष उन शीर्षों के निकट हो जो ग्रिड की एक ही पंक्ति या स्तंभ में नहीं हैं। | * स्वयं के साथ एक पूर्ण ग्राफ़ का टेंसर उत्पाद रूक के ग्राफ़ का पूरक (ग्राफ़ सिद्धांत) है। इसके शीर्षों को a में रखा जा सकता है {{nowrap|{{mvar|n}}-by-{{mvar|n}}}} ग्रिड, ताकि प्रत्येक शीर्ष उन शीर्षों के निकट हो जो ग्रिड की एक ही पंक्ति या स्तंभ में नहीं हैं। | ||
== गुण == | == गुण == | ||
टेन्सर उत्पाद [[उत्पाद (श्रेणी सिद्धांत)]]| श्रेणी-सैद्धांतिक उत्पाद है जो रेखांकन और [[ग्राफ समरूपता]] की श्रेणी में है। यानी एक समरूपता {{math|''G'' × ''H''}} समरूपता की एक जोड़ी से मेल खाती है {{mvar|G}} और करने के लिए {{mvar|H}} | टेन्सर उत्पाद [[उत्पाद (श्रेणी सिद्धांत)]]| श्रेणी-सैद्धांतिक उत्पाद है जो रेखांकन और [[ग्राफ समरूपता]] की श्रेणी में है। यानी एक समरूपता {{math|''G'' × ''H''}} समरूपता की एक जोड़ी से मेल खाती है {{mvar|G}} और करने के लिए {{mvar|H}} विशेष रूप से, एक ग्राफ {{mvar|I}} एक समरूपता को स्वीकार करता है यदि और केवल अगर केवल यदि यह G और H में एक समाकारिता को स्वीकार करता है। | ||
इसे देखने के लिए, एक दिशा में, समरूपता की एक जोड़ी का निरीक्षण करें {{math|''f{{sub|G}}'' : ''I'' → ''G''}} और {{math|''f{{sub|H}}'' : ''I'' → ''H''}} एक समरूपता उत्पन करता | इसे देखने के लिए, एक दिशा में, समरूपता की एक जोड़ी का निरीक्षण करें {{math|''f{{sub|G}}'' : ''I'' → ''G''}} और {{math|''f{{sub|H}}'' : ''I'' → ''H''}} एक समरूपता उत्पन करता है। | ||
:<math>\begin{cases} f : I \to G \times H \\ f(v) = \left (f_G(v), f_H(v) \right ) \end{cases}</math> | :<math>\begin{cases} f : I \to G \times H \\ f(v) = \left (f_G(v), f_H(v) \right ) \end{cases}</math> | ||
दूसरी दिशा में, एक समरूपता {{math|''f'' : ''I'' → ''G'' × ''H''}} को अनुमानों के समरूपता के साथ बनाया जा सकता | दूसरी दिशा में, एक समरूपता {{math|''f'' : ''I'' → ''G'' × ''H''}} को अनुमानों के समरूपता के साथ बनाया जा सकता है। | ||
:<math>\begin{cases} \pi_G : G \times H \to G \\ \pi_G((u,u')) = u \end{cases} \qquad \qquad \begin{cases} \pi_H : G \times H \to H \\ \pi_H((u,u')) = u' \end{cases}</math> | :<math>\begin{cases} \pi_G : G \times H \to G \\ \pi_G((u,u')) = u \end{cases} \qquad \qquad \begin{cases} \pi_H : G \times H \to H \\ \pi_H((u,u')) = u' \end{cases}</math> | ||
समरूपता प्राप्त करने के लिए {{mvar|G}} और करने के लिए {{mvar|H}} का आसन्न मैट्रिक्स {{math|''G'' × ''H''}} | समरूपता प्राप्त करने के लिए {{mvar|G}} और करने के लिए {{mvar|H}} का आसन्न मैट्रिक्स {{math|''G'' × ''H''}} क्रोनकर उत्पाद है। | ||
यदि एक ग्राफ को टेंसर उत्पाद के रूप में प्रदर्शित किया जा सकता है, तो कई अलग-अलग प्रतिनिधित्व हो सकते हैं (टेंसर उत्पाद अद्वितीय गुणनखंड को संतुष्ट नहीं करते हैं) लेकिन प्रत्येक प्रतिनिधित्व में इरेड्यूसिबल कारकों की समान संख्या होती है। {{harvtxt|इमरिच|1998}} टेंसर उत्पाद ग्राफ़ को पहचानने और ऐसे किसी भी ग्राफ़ का गुणनखंड खोजने के लिए एक बहुपद समय एल्गोरिथ्म देता है। | यदि एक ग्राफ को टेंसर उत्पाद के रूप में प्रदर्शित किया जा सकता है, तो कई अलग-अलग प्रतिनिधित्व हो सकते हैं (टेंसर उत्पाद अद्वितीय गुणनखंड को संतुष्ट नहीं करते हैं) लेकिन प्रत्येक प्रतिनिधित्व में इरेड्यूसिबल कारकों की समान संख्या होती है। {{harvtxt|इमरिच|1998}} टेंसर उत्पाद ग्राफ़ को पहचानने और ऐसे किसी भी ग्राफ़ का गुणनखंड खोजने के लिए एक बहुपद समय एल्गोरिथ्म देता है। | ||
| Line 30: | Line 30: | ||
या तो {{mvar|G}} या {{mvar|H}} द्विपक्षीय ग्राफ है, तो उनका टेंसर उत्पाद भी है। {{math|''G'' × ''H''}} जुड़ा हुआ है अगर और केवल अगर दोनों कारक जुड़े हुए हैं और कम से कम एक कारक द्विदलीय नहीं है।<ref>{{harvnb|Imrich|Klavžar|2000|loc= Theorem 5.29}}</ref> विशेष रूप से द्विदलीय दोहरा आवरण {{mvar|G}} जुड़ा हुआ है अगर और केवल अगर {{mvar|G}} जुड़ा हुआ है और गैर-द्विपक्षीय है। | या तो {{mvar|G}} या {{mvar|H}} द्विपक्षीय ग्राफ है, तो उनका टेंसर उत्पाद भी है। {{math|''G'' × ''H''}} जुड़ा हुआ है अगर और केवल अगर दोनों कारक जुड़े हुए हैं और कम से कम एक कारक द्विदलीय नहीं है।<ref>{{harvnb|Imrich|Klavžar|2000|loc= Theorem 5.29}}</ref> विशेष रूप से द्विदलीय दोहरा आवरण {{mvar|G}} जुड़ा हुआ है अगर और केवल अगर {{mvar|G}} जुड़ा हुआ है और गैर-द्विपक्षीय है। | ||
हेडेटनीमी अनुमान, जिसने एक टेन्सर उत्पाद की [[रंगीन संख्या]] के लिए एक सूत्र दिया था, | हेडेटनीमी अनुमान, जिसने एक टेन्सर उत्पाद की [[रंगीन संख्या]] के लिए एक सूत्र दिया था, {{harvs|first=यारोस्लाव|last=शितोव|year=2019|txt}} द्वारा अप्रमाणित किया गया था। | ||
ग्राफ़ का टेन्सर उत्पाद ग्राफ़ और ग्राफ़ समरूपता की श्रेणी को एक [[सममित मोनोइडल श्रेणी]] [[बंद मोनोइडल श्रेणी]] की संरचना से लैस करता है। माना {{math|''G''{{sub|0}}}} ग्राफ़ के शीर्षों के अंतर्निहित सेट को निरूपित करता है {{mvar|G}}. आंतरिक होम {{math|[''G'', ''H'']}} के कार्य हैं {{math|''f'' : ''G''{{sub|0}} → ''H''{{sub|0}}}} शीर्ष और किनारे के रूप में | ग्राफ़ का टेन्सर उत्पाद ग्राफ़ और ग्राफ़ समरूपता की श्रेणी को एक [[सममित मोनोइडल श्रेणी]] [[बंद मोनोइडल श्रेणी]] की संरचना से लैस करता है। माना {{math|''G''{{sub|0}}}} ग्राफ़ के शीर्षों के अंतर्निहित सेट को निरूपित करता है {{mvar|G}}. आंतरिक होम {{math|[''G'', ''H'']}} के कार्य हैं {{math|''f'' : ''G''{{sub|0}} → ''H''{{sub|0}}}} शीर्ष और किनारे के रूप में {{math|''f'' : ''G''{{sub|0}} → ''H''{{sub|0}}}} को {{math|''f''' : ''G''{{sub|0}} → ''H''{{sub|0}}}} जब भी कोई किनारा {{math|{''x'', ''y''} }} में {{mvar|H}} तात्पर्य {{math|{''f'' (''x''), ''f ' ''(''y'')} }}से है।{{sfn|Brown|Morris|Shrimpton|Wensley|2008|ps=; see also [https://lovelylittlelemmas.rjprojects.net/internal-hom-in-the-category-of-graphs/ this proof]}} | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 98: | Line 98: | ||
*{{mathworld | title = Graph Categorical Product | urlname = GraphCategoricalProduct | author = Nicolas Bray}} | *{{mathworld | title = Graph Categorical Product | urlname = GraphCategoricalProduct | author = Nicolas Bray}} | ||
[[Category: ग्राफ उत्पाद]] [[Category: अल्फ्रेड नॉर्थ व्हाइटहेड]] [[Category: बर्ट्रेंड रसेल]] | [[Category: ग्राफ उत्पाद]] [[Category: अल्फ्रेड नॉर्थ व्हाइटहेड]] [[Category: बर्ट्रेंड रसेल]] | ||
| Line 105: | Line 104: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 08/05/2023]] | [[Category:Created On 08/05/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 06:27, 26 September 2023
ग्राफ सिद्धांत में, टेंसर उत्पाद {G × H} ग्राफ का (असतत गणित) G और H ऐसा ग्राफ है।
- शीर्ष (ग्राफ सिद्धांत) का सेट G × H कार्टेशियन उत्पाद है V(G) × V(H); और
- शिखर (g,h) और (g',h' ) में सटे हुए हैं G × H यदि और केवल यदि
- g लगी हुई है g' में G, और
- h लगी हुई है h' में H.
टेंसर उत्पाद को प्रत्यक्ष उत्पाद, क्रोनकर उत्पाद, श्रेणीबद्ध उत्पाद, कार्डिनल उत्पाद, संबंधपरक उत्पाद, कमजोर प्रत्यक्ष उत्पाद या संयोजन भी कहा जाता है। द्विआधारी संबंधों पर एक ऑपरेशन के रूप में, टेन्सर उत्पाद को अल्फ्रेड नॉर्थ व्हाइटहेड और बर्ट्रेंड रसेल द्वारा उनके प्रिंसिपिया मैथेमेटिका (1912) में प्रस्तुत किया गया था। यह ग्राफ़ के आसन्न मैट्रिक्स के क्रोनकर गुणनफल के बराबर भी है।[1]
अंकन G × H भी (और पूर्व में सामान्य रूप से था) एक अन्य निर्माण का प्रतिनिधित्व करने के लिए उपयोग किया जाता है जिसे ग्राफ़ के कार्टेशियन उत्पाद के रूप में जाना जाता है, लेकिन आजकल अधिक सामान्यतः टेंसर उत्पाद को संदर्भित करता है। क्रॉस प्रतीक दो किनारों के टेन्सर उत्पाद से उत्पन्न दो किनारों को नेत्रहीन रूप से दिखाता है।[2] इस उत्पाद को ग्राफ़ के मज़बूत गुणनफल के साथ भ्रमित नहीं होना चाहिए।
उदाहरण
- टेंसर उत्पाद G × K2 एक द्विपक्षीय ग्राफ है, जिसे द्विपक्षीय डबल कवर कहा जाता है G पीटरसन ग्राफ का द्विदलीय डबल कवर डेसार्गेस ग्राफ है: K2 × G(5,2) = G(10,3). एक पूर्ण ग्राफ का द्विदलीय दोहरा आवरण Kn एक क्राउन ग्राफ (एक पूर्ण द्विदलीय ग्राफ) है Kn,n माइनस सही मिलान है।)
- स्वयं के साथ एक पूर्ण ग्राफ़ का टेंसर उत्पाद रूक के ग्राफ़ का पूरक (ग्राफ़ सिद्धांत) है। इसके शीर्षों को a में रखा जा सकता है n-by-n ग्रिड, ताकि प्रत्येक शीर्ष उन शीर्षों के निकट हो जो ग्रिड की एक ही पंक्ति या स्तंभ में नहीं हैं।
गुण
टेन्सर उत्पाद उत्पाद (श्रेणी सिद्धांत)| श्रेणी-सैद्धांतिक उत्पाद है जो रेखांकन और ग्राफ समरूपता की श्रेणी में है। यानी एक समरूपता G × H समरूपता की एक जोड़ी से मेल खाती है G और करने के लिए H विशेष रूप से, एक ग्राफ I एक समरूपता को स्वीकार करता है यदि और केवल अगर केवल यदि यह G और H में एक समाकारिता को स्वीकार करता है।
इसे देखने के लिए, एक दिशा में, समरूपता की एक जोड़ी का निरीक्षण करें fG : I → G और fH : I → H एक समरूपता उत्पन करता है।
दूसरी दिशा में, एक समरूपता f : I → G × H को अनुमानों के समरूपता के साथ बनाया जा सकता है।
समरूपता प्राप्त करने के लिए G और करने के लिए H का आसन्न मैट्रिक्स G × H क्रोनकर उत्पाद है।
यदि एक ग्राफ को टेंसर उत्पाद के रूप में प्रदर्शित किया जा सकता है, तो कई अलग-अलग प्रतिनिधित्व हो सकते हैं (टेंसर उत्पाद अद्वितीय गुणनखंड को संतुष्ट नहीं करते हैं) लेकिन प्रत्येक प्रतिनिधित्व में इरेड्यूसिबल कारकों की समान संख्या होती है। इमरिच (1998) टेंसर उत्पाद ग्राफ़ को पहचानने और ऐसे किसी भी ग्राफ़ का गुणनखंड खोजने के लिए एक बहुपद समय एल्गोरिथ्म देता है।
या तो G या H द्विपक्षीय ग्राफ है, तो उनका टेंसर उत्पाद भी है। G × H जुड़ा हुआ है अगर और केवल अगर दोनों कारक जुड़े हुए हैं और कम से कम एक कारक द्विदलीय नहीं है।[3] विशेष रूप से द्विदलीय दोहरा आवरण G जुड़ा हुआ है अगर और केवल अगर G जुड़ा हुआ है और गैर-द्विपक्षीय है।
हेडेटनीमी अनुमान, जिसने एक टेन्सर उत्पाद की रंगीन संख्या के लिए एक सूत्र दिया था, यारोस्लाव शितोव (2019) द्वारा अप्रमाणित किया गया था।
ग्राफ़ का टेन्सर उत्पाद ग्राफ़ और ग्राफ़ समरूपता की श्रेणी को एक सममित मोनोइडल श्रेणी बंद मोनोइडल श्रेणी की संरचना से लैस करता है। माना G0 ग्राफ़ के शीर्षों के अंतर्निहित सेट को निरूपित करता है G. आंतरिक होम [G, H] के कार्य हैं f : G0 → H0 शीर्ष और किनारे के रूप में f : G0 → H0 को f' : G0 → H0 जब भी कोई किनारा {x, y} में H तात्पर्य {f (x), f ' (y)} से है।[4]
यह भी देखें
- ग्राफ उत्पाद
- रेखांकन का मजबूत उत्पाद
टिप्पणियाँ
- ↑ Weichsel 1962.
- ↑ Hahn & Sabidussi 1997.
- ↑ Imrich & Klavžar 2000, Theorem 5.29
- ↑ Brown et al. 2008; see also this proof
संदर्भ
- Brown, R.; Morris, I.; Shrimpton, J.; Wensley, C. D. (2008), "Graphs of Morphisms of Graphs", The Electronic Journal of Combinatorics, 15: A1.
- Hahn, Geňa; Sabidussi, Gert (1997), Graph symmetry: algebraic methods and applications, NATO Advanced Science Institutes Series, vol. 497, Springer, p. 116, ISBN 978-0-7923-4668-5.
- Imrich, W. (1998), "Factoring cardinal product graphs in polynomial time", Discrete Mathematics, 192: 119–144, doi:10.1016/S0012-365X(98)00069-7, MR 1656730
- Imrich, Wilfried; Klavžar, Sandi (2000), Product Graphs: Structure and Recognition, Wiley, ISBN 0-471-37039-8
- Shitov, Yaroslav (May 2019), Counterexamples to Hedetniemi's conjecture, arXiv:1905.02167
- Weichsel, Paul M. (1962), "The Kronecker product of graphs", Proceedings of the American Mathematical Society, 13 (1): 47–52, doi:10.2307/2033769, JSTOR 2033769, MR 0133816
- Whitehead, A. N.; Russell, B. (1912), Principia Mathematica, Cambridge University Press, vol. 2, p. 384
बाहरी संबंध
- Nicolas Bray. "Graph Categorical Product". MathWorld.