वर्णनात्मक फलन: Difference between revisions
m (7 revisions imported from alpha:वर्णनात्मक_फलन) |
|||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 40: | Line 40: | ||
| s2cid = 51646567 | | s2cid = 51646567 | ||
| id = | | id = | ||
}}</ref> '''वर्णनात्मक फलन''' (डीएफ) विधि, कुछ गैर-रेखीय नियंत्रण समस्याओं का विश्लेषण करने के लिए एक अनुमानित प्रक्रिया है। यह अर्ध-रैखिकीकरण पर आधारित है, जो एक रैखिक समय-अपरिवर्तनीय (एलटीआई) स्थानांतरण फलन द्वारा जांच के तहत गैर-रैखिक प्रणाली का अनुमान है जो इनपुट तरंग के [[आयाम]] पर निर्भर करता है। परिभाषा के अनुसार, एक वास्तविक एलटीआई प्रणाली का स्थानांतरण फलन इनपुट फलन के आयाम पर निर्भर नहीं हो सकता क्योंकि एक एलटीआई प्रणाली रैखिक है। इस प्रकार, आयाम पर यह निर्भरता रैखिक प्रणालियों का एक | }}</ref> '''वर्णनात्मक फलन''' (डीएफ) विधि, कुछ गैर-रेखीय नियंत्रण समस्याओं का विश्लेषण करने के लिए एक अनुमानित प्रक्रिया है। यह अर्ध-रैखिकीकरण पर आधारित है, जो एक रैखिक समय-अपरिवर्तनीय (एलटीआई) स्थानांतरण फलन द्वारा जांच के तहत गैर-रैखिक प्रणाली का अनुमान है जो इनपुट तरंग के [[आयाम]] पर निर्भर करता है। परिभाषा के अनुसार, एक वास्तविक एलटीआई प्रणाली का स्थानांतरण फलन इनपुट फलन के आयाम पर निर्भर नहीं हो सकता क्योंकि एक एलटीआई प्रणाली रैखिक है। इस प्रकार, आयाम पर यह निर्भरता रैखिक प्रणालियों का एक समूह उत्पन्न करती है जो गैर-रेखीय प्रणाली व्यवहार की मुख्य विशेषताओं को पकड़ने के प्रयास में संयुक्त होती है। वर्णन करने वाला फलन गैर-रेखीय प्रणालियों को डिजाइन करने के लिए कुछ व्यापक रूप से प्रयुक्त तरीकों में से एक है, और औद्योगिक प्रक्रिया नियंत्रण, सर्वोमैकेनिज्म और इलेक्ट्रॉनिक दोलक जैसे बंद-लूप नियंत्रकों में सीमा चक्रों का विश्लेषण करने के लिए एक मानक गणितीय उपकरण के रूप में बहुत व्यापक रूप से उपयोग किया जाता है। | ||
==विधि== | ==विधि== | ||
एक धीमी गति से स्थिर रैखिक प्रणाली के साथ कैस्केड किए गए एक असंतुलित (लेकिन टुकड़ों में निरंतर) गैर-रैखिकता (जैसे, संतृप्ति के साथ एक एम्पलीफायर, या [[डेडबैंड]] प्रभाव वाला एक तत्व) के आसपास प्रतिक्रिया पर विचार करें। निरंतर क्षेत्र जिसमें गैर-रैखिकता के लिए प्रतिपुष्टि प्रस्तुत किया जाता है, रैखिक प्रणाली के आउटपुट के आयाम पर निर्भर करता है। जैसे-जैसे रैखिक प्रणाली का आउटपुट आयाम कम होता जाता है, गैर-रैखिकता एक अलग निरंतर क्षेत्र में स्थानांतरित हो सकती है। एक सतत क्षेत्र से दूसरे क्षेत्र में यह स्विचिंग आवधिक दोलन उत्पन्न कर सकता है। वर्णन करने वाली फलन विधि यह मानकर उन दोलनों की विशेषताओं (उदाहरण के लिए, उनकी मौलिक आवृत्ति) की भविष्यवाणी करने का प्रयास करती है कि धीमी प्रणाली एक कम-पास या [[बैंडपास]] फिल्टर की तरह काम करती है जो सभी ऊर्जा को एक ही आवृत्ति के आसपास केंद्रित करती है। भले ही आउटपुट तरंग में कई मोड हों, फिर भी विधि आवृत्ति और संभवतः आयाम जैसी गुणों के बारे में अंतर्ज्ञान प्रदान कर सकती है; इस | एक धीमी गति से स्थिर रैखिक प्रणाली के साथ कैस्केड किए गए एक असंतुलित (लेकिन टुकड़ों में निरंतर) गैर-रैखिकता (जैसे, संतृप्ति के साथ एक एम्पलीफायर, या [[डेडबैंड]] प्रभाव वाला एक तत्व) के आसपास प्रतिक्रिया पर विचार करें। निरंतर क्षेत्र जिसमें गैर-रैखिकता के लिए प्रतिपुष्टि प्रस्तुत किया जाता है, रैखिक प्रणाली के आउटपुट के आयाम पर निर्भर करता है। जैसे-जैसे रैखिक प्रणाली का आउटपुट आयाम कम होता जाता है, गैर-रैखिकता एक अलग निरंतर क्षेत्र में स्थानांतरित हो सकती है। एक सतत क्षेत्र से दूसरे क्षेत्र में यह स्विचिंग आवधिक दोलन उत्पन्न कर सकता है। वर्णन करने वाली फलन विधि यह मानकर उन दोलनों की विशेषताओं (उदाहरण के लिए, उनकी मौलिक आवृत्ति) की भविष्यवाणी करने का प्रयास करती है कि धीमी प्रणाली एक कम-पास या [[बैंडपास]] फिल्टर की तरह काम करती है जो सभी ऊर्जा को एक ही आवृत्ति के आसपास केंद्रित करती है। भले ही आउटपुट तरंग में कई मोड हों, फिर भी विधि आवृत्ति और संभवतः आयाम जैसी गुणों के बारे में अंतर्ज्ञान प्रदान कर सकती है; इस स्थिति में, वर्णन फलन विधि को प्रतिपुष्टि प्रणाली के [[स्लाइडिंग मोड नियंत्रण|स्लाइडिंग मोड]] का वर्णन करने के रूप में सोचा जा सकता है। | ||
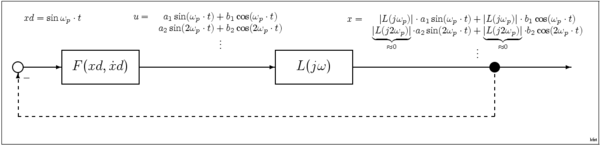
[[File:Function-block-harmonic-balance.png|thumb|center|600px|हार्मोनिक संतुलन की स्थिति में अरेखीय प्रणाली]]इस निम्न-पास धारणा का उपयोग करके, प्रणाली प्रतिक्रिया को साइनसॉइडल तरंगों के एक | [[File:Function-block-harmonic-balance.png|thumb|center|600px|हार्मोनिक संतुलन की स्थिति में अरेखीय प्रणाली]]इस निम्न-पास धारणा का उपयोग करके, प्रणाली प्रतिक्रिया को साइनसॉइडल तरंगों के एक समूह द्वारा वर्णित किया जा सकता है; इस स्थिति में प्रणाली को फलन (एसआईडीएफ) <math>H(j\omega)</math> का वर्णन करने वाले एक साइन इनपुट द्वारा चित्रित किया जाएगा, जो आयाम A और आवृत्ति <math>\omega</math> की साइन तरंग से युक्त इनपुट पर प्रणाली प्रतिक्रिया देता है। यह एसआईडीएफ ट्रांसफर फलन <math>H(A,\,j\omega)</math> का एक संशोधन है जिसका उपयोग रैखिक प्रणालियों को चिह्नित करने के लिए किया जाता है। एक अर्ध-रेखीय प्रणाली में, जब इनपुट एक साइन तरंग है, तो आउटपुट समान आवृत्ति की एक साइन तरंग होगी, लेकिन स्केल किए गए आयाम और स्थानांतरित चरण के साथ जैसा कि <math>H(A,\,j\omega)</math> द्वारा दिया गया है। कई प्रणालियाँ इस अर्थ में लगभग अर्ध-रैखिक हैं कि यद्यपि साइन तरंग की प्रतिक्रिया शुद्ध साइन तरंग नहीं है, लेकिन आउटपुट में अधिकांश ऊर्जा वास्तव में इनपुट के समान आवृत्ति <math>\omega</math> पर होती है। इसका कारण यह है कि ऐसी प्रणालियों में आंतरिक कम-पास या बैंडपास विशेषताएं हो सकती हैं जैसे कि हार्मोनिक्स स्वाभाविक रूप से क्षीण हो जाते हैं, या क्योंकि इस उद्देश्य के लिए बाहरी फ़िल्टर जोड़े जाते हैं। एसआईडीएफ तकनीक का एक महत्वपूर्ण अनुप्रयोग साइनसोइडल इलेक्ट्रॉनिक दोलक में दोलन आयाम का अनुमान लगाना है। | ||
अन्य प्रकार के वर्णनात्मक फलन का उपयोग किया गया है जो स्तर के इनपुट और गॉसियन नॉइज़ इनपुट के लिए डीएफ हैं। हालाँकि प्रणाली का पूरा विवरण नहीं है, लेकिन डीएफ | अन्य प्रकार के वर्णनात्मक फलन का उपयोग किया गया है जो स्तर के इनपुट और गॉसियन नॉइज़ इनपुट के लिए डीएफ हैं। हालाँकि प्रणाली का पूरा विवरण नहीं है, लेकिन डीएफ प्रायः नियंत्रण और स्थिरता के बारे में विशिष्ट प्रश्नों का उत्तर देने के लिए पर्याप्त होते हैं। अपेक्षाकृत कमजोर गैर-रेखीयताओं वाले प्रणाली का विश्लेषण करने के लिए डीएफ विधियां सर्वोत्तम हैं। उच्च क्रम के साइनसॉइडल इनपुट फलन का वर्णन करने वाले फलन (एचओएसआईडीएफ) के अतिरिक्त, एक साइनसॉइडल इनपुट की इनपुट आवृत्ति के हार्मोनिक्स पर नॉनलाइनियर प्रणाली के एक वर्ग की प्रतिक्रिया का वर्णन करता है। एचओएसआईडीएफ उन प्रणालियों के लिए एसआईडीएफ का एक विस्तार है जहां प्रतिक्रिया में गैर-रैखिकताएं महत्वपूर्ण हैं। | ||
==चेतावनी== | ==चेतावनी== | ||
यद्यपि वर्णन करने वाला फलन पद्धति विभिन्न प्रकार की प्रणालियों के लिए यथोचित सटीक परिणाम दे सकती है, लेकिन यह दूसरों के लिए बुरी तरह विफल हो सकती है। उदाहरण के लिए, विधि विफल हो सकती है यदि प्रणाली गैर-रैखिकता के उच्च हार्मोनिक्स पर जोर देता है। ऐसे उदाहरण बैंग-बैंग प्रणाली के लिए त्ज़िपकिन द्वारा प्रस्तुत किए गए हैं।<ref>{{cite book|last=Tsypkin|first=Yakov Z.|title=रिले नियंत्रण प्रणाली|publisher=Cambridge: Univ Press|year=1984}}</ref> एक काफी समान उदाहरण एक बंद-लूप थरथरानवाला है जिसमें एक गैर-इनवर्टिंग [[श्मिट ट्रिगर]] होता है जिसके बाद एक इनवर्टिंग इंटीग्रेटर होता है जो अपने आउटपुट को श्मिट ट्रिगर के इनपुट में वापस फीड करता है। श्मिट ट्रिगर का आउटपुट एक वर्गाकार तरंगरूप होने वाला है, जबकि इंटीग्रेटर (इसके बाद) का आउटपुट एक त्रिकोणीय तरंगरूप होने वाला है, जिसके शिखर वर्गाकार तरंग में ट्रांजिशन के साथ मेल खाते हैं। इन दो | यद्यपि वर्णन करने वाला फलन पद्धति विभिन्न प्रकार की प्रणालियों के लिए यथोचित सटीक परिणाम दे सकती है, लेकिन यह दूसरों के लिए बुरी तरह विफल हो सकती है। उदाहरण के लिए, विधि विफल हो सकती है यदि प्रणाली गैर-रैखिकता के उच्च हार्मोनिक्स पर जोर देता है। ऐसे उदाहरण बैंग-बैंग प्रणाली के लिए त्ज़िपकिन द्वारा प्रस्तुत किए गए हैं।<ref>{{cite book|last=Tsypkin|first=Yakov Z.|title=रिले नियंत्रण प्रणाली|publisher=Cambridge: Univ Press|year=1984}}</ref> एक काफी समान उदाहरण एक बंद-लूप थरथरानवाला है जिसमें एक गैर-इनवर्टिंग [[श्मिट ट्रिगर]] होता है जिसके बाद एक इनवर्टिंग इंटीग्रेटर होता है जो अपने आउटपुट को श्मिट ट्रिगर के इनपुट में वापस फीड करता है। श्मिट ट्रिगर का आउटपुट एक वर्गाकार तरंगरूप होने वाला है, जबकि इंटीग्रेटर (इसके बाद) का आउटपुट एक त्रिकोणीय तरंगरूप होने वाला है, जिसके शिखर वर्गाकार तरंग में ट्रांजिशन के साथ मेल खाते हैं। इन दो दोलक चरणों में से प्रत्येक सिग्नल से बिल्कुल 90 डिग्री (इसके इनपुट के सापेक्ष) पीछे है। यदि कोई इस सर्किट पर डीएफ विश्लेषण करता है, तो श्मिट ट्रिगर के इनपुट पर त्रिकोण तरंग को इसके मौलिक (साइन तरंग) द्वारा प्रतिस्थापित किया जाएगा, जो ट्रिगर से गुजरने पर 90 डिग्री से कम चरण बदलाव का कारण बनेगा (क्योंकि साइन तरंग यह इसे त्रिभुज तरंग की तुलना में जल्दी ट्रिगर करेगा) इसलिए प्रणाली उसी (सरल) तरीके से दोलन नहीं करता हुआ प्रतीत होगा।<ref name="LurieEnright2000">{{cite book|author1=Boris Lurie|author2=Paul Enright|title=Classical Feedback Control: With MATLAB|year=2000|publisher=CRC Press|isbn=978-0-8247-0370-7|pages=298–299}}</ref> | ||
साथ ही, ऐसे | साथ ही, ऐसे स्थिति में जहां एज़रमैन या कल्मन अनुमानों की शर्तें पूरी हो जाती हैं, फ़ंक्शन विधि का वर्णन करके कोई आवधिक समाधान नहीं होता है,<ref>{{cite journal | ||
|author1=Leonov G.A. |author2=Kuznetsov N.V. | year = 2011 | |author1=Leonov G.A. |author2=Kuznetsov N.V. | year = 2011 | ||
| title = Algorithms for Searching for Hidden Oscillations in the Aizerman and Kalman Problems | | title = Algorithms for Searching for Hidden Oscillations in the Aizerman and Kalman Problems | ||
| Line 107: | Line 107: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 10/08/2023]] | [[Category:Created On 10/08/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 21:53, 10 October 2023
नियंत्रण प्रणाली सिद्धांत में, 1930 के दशक में निकोले मित्रोफ़ानोविच क्रायलोव और निकोले बोगोलीबोव द्वारा विकसित,[1][2] और राल्फ कोचेनबर्गर द्वारा विस्तारित [3] वर्णनात्मक फलन (डीएफ) विधि, कुछ गैर-रेखीय नियंत्रण समस्याओं का विश्लेषण करने के लिए एक अनुमानित प्रक्रिया है। यह अर्ध-रैखिकीकरण पर आधारित है, जो एक रैखिक समय-अपरिवर्तनीय (एलटीआई) स्थानांतरण फलन द्वारा जांच के तहत गैर-रैखिक प्रणाली का अनुमान है जो इनपुट तरंग के आयाम पर निर्भर करता है। परिभाषा के अनुसार, एक वास्तविक एलटीआई प्रणाली का स्थानांतरण फलन इनपुट फलन के आयाम पर निर्भर नहीं हो सकता क्योंकि एक एलटीआई प्रणाली रैखिक है। इस प्रकार, आयाम पर यह निर्भरता रैखिक प्रणालियों का एक समूह उत्पन्न करती है जो गैर-रेखीय प्रणाली व्यवहार की मुख्य विशेषताओं को पकड़ने के प्रयास में संयुक्त होती है। वर्णन करने वाला फलन गैर-रेखीय प्रणालियों को डिजाइन करने के लिए कुछ व्यापक रूप से प्रयुक्त तरीकों में से एक है, और औद्योगिक प्रक्रिया नियंत्रण, सर्वोमैकेनिज्म और इलेक्ट्रॉनिक दोलक जैसे बंद-लूप नियंत्रकों में सीमा चक्रों का विश्लेषण करने के लिए एक मानक गणितीय उपकरण के रूप में बहुत व्यापक रूप से उपयोग किया जाता है।
विधि
एक धीमी गति से स्थिर रैखिक प्रणाली के साथ कैस्केड किए गए एक असंतुलित (लेकिन टुकड़ों में निरंतर) गैर-रैखिकता (जैसे, संतृप्ति के साथ एक एम्पलीफायर, या डेडबैंड प्रभाव वाला एक तत्व) के आसपास प्रतिक्रिया पर विचार करें। निरंतर क्षेत्र जिसमें गैर-रैखिकता के लिए प्रतिपुष्टि प्रस्तुत किया जाता है, रैखिक प्रणाली के आउटपुट के आयाम पर निर्भर करता है। जैसे-जैसे रैखिक प्रणाली का आउटपुट आयाम कम होता जाता है, गैर-रैखिकता एक अलग निरंतर क्षेत्र में स्थानांतरित हो सकती है। एक सतत क्षेत्र से दूसरे क्षेत्र में यह स्विचिंग आवधिक दोलन उत्पन्न कर सकता है। वर्णन करने वाली फलन विधि यह मानकर उन दोलनों की विशेषताओं (उदाहरण के लिए, उनकी मौलिक आवृत्ति) की भविष्यवाणी करने का प्रयास करती है कि धीमी प्रणाली एक कम-पास या बैंडपास फिल्टर की तरह काम करती है जो सभी ऊर्जा को एक ही आवृत्ति के आसपास केंद्रित करती है। भले ही आउटपुट तरंग में कई मोड हों, फिर भी विधि आवृत्ति और संभवतः आयाम जैसी गुणों के बारे में अंतर्ज्ञान प्रदान कर सकती है; इस स्थिति में, वर्णन फलन विधि को प्रतिपुष्टि प्रणाली के स्लाइडिंग मोड का वर्णन करने के रूप में सोचा जा सकता है।
इस निम्न-पास धारणा का उपयोग करके, प्रणाली प्रतिक्रिया को साइनसॉइडल तरंगों के एक समूह द्वारा वर्णित किया जा सकता है; इस स्थिति में प्रणाली को फलन (एसआईडीएफ) का वर्णन करने वाले एक साइन इनपुट द्वारा चित्रित किया जाएगा, जो आयाम A और आवृत्ति की साइन तरंग से युक्त इनपुट पर प्रणाली प्रतिक्रिया देता है। यह एसआईडीएफ ट्रांसफर फलन का एक संशोधन है जिसका उपयोग रैखिक प्रणालियों को चिह्नित करने के लिए किया जाता है। एक अर्ध-रेखीय प्रणाली में, जब इनपुट एक साइन तरंग है, तो आउटपुट समान आवृत्ति की एक साइन तरंग होगी, लेकिन स्केल किए गए आयाम और स्थानांतरित चरण के साथ जैसा कि द्वारा दिया गया है। कई प्रणालियाँ इस अर्थ में लगभग अर्ध-रैखिक हैं कि यद्यपि साइन तरंग की प्रतिक्रिया शुद्ध साइन तरंग नहीं है, लेकिन आउटपुट में अधिकांश ऊर्जा वास्तव में इनपुट के समान आवृत्ति पर होती है। इसका कारण यह है कि ऐसी प्रणालियों में आंतरिक कम-पास या बैंडपास विशेषताएं हो सकती हैं जैसे कि हार्मोनिक्स स्वाभाविक रूप से क्षीण हो जाते हैं, या क्योंकि इस उद्देश्य के लिए बाहरी फ़िल्टर जोड़े जाते हैं। एसआईडीएफ तकनीक का एक महत्वपूर्ण अनुप्रयोग साइनसोइडल इलेक्ट्रॉनिक दोलक में दोलन आयाम का अनुमान लगाना है।
अन्य प्रकार के वर्णनात्मक फलन का उपयोग किया गया है जो स्तर के इनपुट और गॉसियन नॉइज़ इनपुट के लिए डीएफ हैं। हालाँकि प्रणाली का पूरा विवरण नहीं है, लेकिन डीएफ प्रायः नियंत्रण और स्थिरता के बारे में विशिष्ट प्रश्नों का उत्तर देने के लिए पर्याप्त होते हैं। अपेक्षाकृत कमजोर गैर-रेखीयताओं वाले प्रणाली का विश्लेषण करने के लिए डीएफ विधियां सर्वोत्तम हैं। उच्च क्रम के साइनसॉइडल इनपुट फलन का वर्णन करने वाले फलन (एचओएसआईडीएफ) के अतिरिक्त, एक साइनसॉइडल इनपुट की इनपुट आवृत्ति के हार्मोनिक्स पर नॉनलाइनियर प्रणाली के एक वर्ग की प्रतिक्रिया का वर्णन करता है। एचओएसआईडीएफ उन प्रणालियों के लिए एसआईडीएफ का एक विस्तार है जहां प्रतिक्रिया में गैर-रैखिकताएं महत्वपूर्ण हैं।
चेतावनी
यद्यपि वर्णन करने वाला फलन पद्धति विभिन्न प्रकार की प्रणालियों के लिए यथोचित सटीक परिणाम दे सकती है, लेकिन यह दूसरों के लिए बुरी तरह विफल हो सकती है। उदाहरण के लिए, विधि विफल हो सकती है यदि प्रणाली गैर-रैखिकता के उच्च हार्मोनिक्स पर जोर देता है। ऐसे उदाहरण बैंग-बैंग प्रणाली के लिए त्ज़िपकिन द्वारा प्रस्तुत किए गए हैं।[4] एक काफी समान उदाहरण एक बंद-लूप थरथरानवाला है जिसमें एक गैर-इनवर्टिंग श्मिट ट्रिगर होता है जिसके बाद एक इनवर्टिंग इंटीग्रेटर होता है जो अपने आउटपुट को श्मिट ट्रिगर के इनपुट में वापस फीड करता है। श्मिट ट्रिगर का आउटपुट एक वर्गाकार तरंगरूप होने वाला है, जबकि इंटीग्रेटर (इसके बाद) का आउटपुट एक त्रिकोणीय तरंगरूप होने वाला है, जिसके शिखर वर्गाकार तरंग में ट्रांजिशन के साथ मेल खाते हैं। इन दो दोलक चरणों में से प्रत्येक सिग्नल से बिल्कुल 90 डिग्री (इसके इनपुट के सापेक्ष) पीछे है। यदि कोई इस सर्किट पर डीएफ विश्लेषण करता है, तो श्मिट ट्रिगर के इनपुट पर त्रिकोण तरंग को इसके मौलिक (साइन तरंग) द्वारा प्रतिस्थापित किया जाएगा, जो ट्रिगर से गुजरने पर 90 डिग्री से कम चरण बदलाव का कारण बनेगा (क्योंकि साइन तरंग यह इसे त्रिभुज तरंग की तुलना में जल्दी ट्रिगर करेगा) इसलिए प्रणाली उसी (सरल) तरीके से दोलन नहीं करता हुआ प्रतीत होगा।[5]
साथ ही, ऐसे स्थिति में जहां एज़रमैन या कल्मन अनुमानों की शर्तें पूरी हो जाती हैं, फ़ंक्शन विधि का वर्णन करके कोई आवधिक समाधान नहीं होता है,[6][7] लेकिन छिपे हुए आवधिक आकर्षण वाले प्रति उदाहरण ज्ञात होते हैं। जब एक विश्राम खंड पूर्वानुमानित सीमा चक्रों को नष्ट कर देता है, तो वर्णन करने वाला फलन विधि के प्रति उदाहरणों का निर्माण असंतत गतिशील प्रणालियों के लिए किया जा सकता है।[8] इसलिए, वर्णन करने वाला फलन विधि के अनुप्रयोग के लिए अतिरिक्त औचित्य की आवश्यकता होती है।[9][10]
संदर्भ
- ↑ Krylov, N. M.; N. Bogoliubov (1943). Introduction to Nonlinear Mechanics. Princeton, US: Princeton Univ. Press. ISBN 0691079854. Archived from the original on 2013-06-20.
- ↑ Blaquiere, Austin (2012-12-02). Nonlinear System Analysis. Elsevier Science. p. 177. ISBN 978-0323151665.
- ↑ Kochenburger, Ralph J. (January 1950). "A Frequency Response Method for Analyzing and Synthesizing Contactor Servomechanisms". Trans. AIEE. American Institute of Electrical Engineers. 69 (1): 270–284. doi:10.1109/t-aiee.1950.5060149. S2CID 51646567.
- ↑ Tsypkin, Yakov Z. (1984). रिले नियंत्रण प्रणाली. Cambridge: Univ Press.
- ↑ Boris Lurie; Paul Enright (2000). Classical Feedback Control: With MATLAB. CRC Press. pp. 298–299. ISBN 978-0-8247-0370-7.
- ↑ Leonov G.A.; Kuznetsov N.V. (2011). "Algorithms for Searching for Hidden Oscillations in the Aizerman and Kalman Problems" (PDF). Doklady Mathematics. 84 (1): 475–481. doi:10.1134/S1064562411040120. S2CID 120692391.,
- ↑ "Aizerman's and Kalman's conjectures and describing function method" (PDF).
- ↑ Leonov G.A.; Kuznetsov N.V. (2018). "On the Keldysh problem of flutter suppression". AIP Conference Proceedings. 1959: art. num. 020002. arXiv:1803.06920. doi:10.1063/1.5034578. S2CID 55340847.
- ↑ Bragin V.O.; Vagaitsev V.I.; Kuznetsov N.V.; Leonov G.A. (2011). "Algorithms for Finding Hidden Oscillations in Nonlinear Systems. The Aizerman and Kalman Conjectures and Chua's Circuits" (PDF). Journal of Computer and Systems Sciences International. 50 (4): 511–543. doi:10.1134/S106423071104006X. S2CID 21657305.
- ↑ Leonov G.A.; Kuznetsov N.V. (2013). "Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits". International Journal of Bifurcation and Chaos. 23 (1): 1330002–219. Bibcode:2013IJBC...2330002L. doi:10.1142/S0218127413300024.
अग्रिम पठन
- N. Krylov and N. Bogolyubov: Introduction to Nonlinear Mechanics, Princeton University Press, 1947
- A. Gelb and W. E. Vander Velde: Multiple-Input Describing Functions and Nonlinear System Design, McGraw Hill, 1968.
- James K. Roberge, Operational Amplifiers: Theory and Practice, chapter 6: Non-Linear Systems, 1975; free copy courtesy of MIT OpenCourseWare 6.010 (2013); see also (1985) video recording of Roberge's lecture on describing functions
- P.W.J.M. Nuij, O.H. Bosgra, M. Steinbuch, Higher Order Sinusoidal Input Describing Functions for the Analysis of Nonlinear Systems with Harmonic Responses, Mechanical Systems and Signal Processing, 20(8), 1883–1904, (2006)