फलन का शून्य: Difference between revisions
No edit summary |
m (14 revisions imported from alpha:फलन_का_शून्य) |
||
| (10 intermediate revisions by 3 users not shown) | |||
| Line 4: | Line 4: | ||
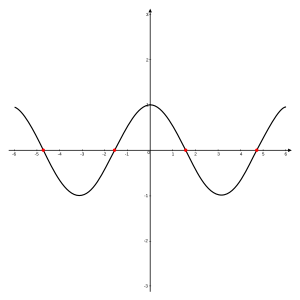
{{Css Image Crop |Image = X-intercepts.svg |bSize = 300 |cWidth = 300 |cHeight = 110 |oLeft = 0 |oTop = 100 |Location = right |Description = A graph of the function <math>\cos(x)</math> for <math>x</math> in <math>\left[-2\pi,2\pi\right]</math>, with '''zeros''' at <math>-\tfrac{3\pi}{2},\;-\tfrac{\pi}{2},\;\tfrac{\pi}{2}</math>, and <math>\tfrac{3\pi}{2},</math> marked in <span style="color:red">red</span>.}} | {{Css Image Crop |Image = X-intercepts.svg |bSize = 300 |cWidth = 300 |cHeight = 110 |oLeft = 0 |oTop = 100 |Location = right |Description = A graph of the function <math>\cos(x)</math> for <math>x</math> in <math>\left[-2\pi,2\pi\right]</math>, with '''zeros''' at <math>-\tfrac{3\pi}{2},\;-\tfrac{\pi}{2},\;\tfrac{\pi}{2}</math>, and <math>\tfrac{3\pi}{2},</math> marked in <span style="color:red">red</span>.}} | ||
गणित में, एक [[वास्तविक संख्या]], [[जटिल संख्या|सम्मिश्र | गणित में, एक [[वास्तविक संख्या]], [[जटिल संख्या|सम्मिश्र संख्या]] या सामान्यतः [[वेक्टर-मूल्यवान फ़ंक्शन|सदिश फलन]] का मान शून्य होता है, जिसे कभी-कभी रूट भी कहा जाता है और इस प्रकार <math>f</math> के डोमेन का एक सदस्य <math>x</math> के रूप में है, जैसे कि <math>f</math> ऐसा है कि <math>f(x)</math> पर वनिश हो जाता है अर्थात फलन <math>f</math>, <math>x</math> पर 0 का मान प्राप्त करता है <math>x</math>, या समकक्ष, <math>x</math> समीकरण का <math>f(x) = 0</math> सॉलूशन है.<ref name=":0">{{Cite web|url=http://tutorial.math.lamar.edu/Classes/Alg/ZeroesOfPolynomials.aspx | title=Algebra - Zeroes/Roots of Polynomials |website=tutorial.math.lamar.edu| access-date=2019-12-15}}</ref> इस प्रकार '''फलन का शून्य''' एक इनपुट मान होता है, जो 0 का आउटपुट उत्पन्न करता है।<ref name="Foerster">{{cite book | last = Foerster | first = Paul A. | title = Algebra and Trigonometry: Functions and Applications, Teacher's Edition | edition = Classics | year = 2006 | page = [https://archive.org/details/algebratrigonome00paul_0/page/535 535] | publisher = [[Prentice Hall]] | location = Upper Saddle River, NJ | url = https://archive.org/details/algebratrigonome00paul_0/page/535 | isbn = 0-13-165711-9 }}</ref> | ||
एक [[बहुपद]] का रूट संगत बहुपद फलन शून्य होता है।<ref name=":0" /> इस प्रकार बीजगणित के फंडामेंटल प्रमेय | एक [[बहुपद]] का रूट संगत बहुपद फलन शून्य होता है।<ref name=":0" /> इस प्रकार बीजगणित के फंडामेंटल प्रमेय से पता चलता है कि किसी भी गैर-शून्य बहुपद में [[बहुपद की डिग्री|बहुपद की घात]] के बराबर रूट की संख्या होती है और जब कोई सम्मिश्र रूट पर कंसीडर करता है तो रूट की संख्या और घात बराबर होती है और इस प्रकार सामान्यतः [[बीजगणितीय रूप से बंद विस्तार|बीजगणितीय क्लोज्ड एक्सटेंशन]] में रुट ें उनकी [[बहुलता (गणित)]] के साथ गिनी जाती हैं।<ref>{{Cite web|url=https://www.mathplanet.com/education/algebra-2/polynomial-functions/roots-and-zeros|title=Roots and zeros (Algebra 2, Polynomial functions)| website=Mathplanet |language=en|access-date=2019-12-15}}</ref> उदाहरण के लिए, <math>f(x)=x^2-5x+6</math> द्वारा परिभाषित घात दो के बहुपद <math>f</math> के दो रुट जो 2 और 3 के रूप में होते है या शून्य रूप में होते है। | ||
<math display="block">f(2)=2^2-5\times 2+6= 0\text{ and }f(3)=3^2-5\times 3+6=0.</math> | <math display="block">f(2)=2^2-5\times 2+6= 0\text{ and }f(3)=3^2-5\times 3+6=0.</math> | ||
यदि फलन | यदि फलन वास्तविक संख्याओं को वास्तविक संख्याओं में मैप करता है, तो इसके शून्य उन बिंदुओं के <math>x</math>- निर्देशांक होते हैं, जहां [[किसी फ़ंक्शन का ग्राफ़|इस फलन का ग्राफ़]] x-अक्ष से मिलता है। इस संदर्भ में ऐसे बिंदु <math>(x,0)</math> के लिए एक वैकल्पिक नाम <math>x</math>-इंटरसेप्ट के रूप में होता है | ||
==[[समीकरण]] का सॉलूशन == | ==[[समीकरण]] का सॉलूशन == | ||
अज्ञात | अज्ञात <math>x</math> में प्रत्येक समीकरण (गणित) को इस प्रकार पुनः लिखा जा सकता है, | ||
:<math>f(x)=0</math> | :<math>f(x)=0</math> | ||
बायीं ओर के सभी पदों को पुनः समूहित करते है। इससे निष्कर्ष यह निकलता है कि ऐसे समीकरण के सॉलूशन बिल्कुल फलन | बायीं ओर के सभी पदों को पुनः समूहित करते है। इससे निष्कर्ष यह निकलता है कि ऐसे समीकरण के सॉलूशन बिल्कुल फलन <math>f</math> के रूप में शून्य होते हैं और इस प्रकार दूसरे शब्दों में फलन का शून्य वास्तव में फलन को 0 के बराबर करके प्राप्त समीकरण का एक सॉलूशन होता है और फलन के शून्य का अध्ययन बिल्कुल समीकरणों के सॉलूशन के अध्ययन के समान होता है। | ||
== बहुपद रुट == | == बहुपद रुट == | ||
{{main|बहुपद रुट के गुण}} | {{main|बहुपद रुट के गुण}} | ||
बहुपद की विषम घात वाले प्रत्येक वास्तविक बहुपद में वास्तविक रुट | बहुपद की विषम घात वाले प्रत्येक वास्तविक बहुपद में वास्तविक रुट की एक विषम संख्या होती है और इस प्रकार बहुपद की एक रुट की बहुलता (गणित) बहुलता की काउंटिंग होती है। इसी प्रकार, सम घात वाले वास्तविक बहुपद में वास्तविक रुट की संख्या भी सम होनी चाहिए। फलस्वरूप वास्तविक विषम बहुपदों में कम से कम एक वास्तविक रूट होना चाहिए क्योंकि सबसे छोटी विषम पूर्ण संख्या 1 होती है। जबकि सम बहुपदों में कोई भी नहीं होता है। इस सिद्धांत को [[मध्यवर्ती मूल्य प्रमेय]] के संदर्भ से सिद्ध किया जाता है, चूंकि बहुपद फलन सतत फलन के रूप में होते है, इसलिए ऋणात्मक से धनात्मक या इसके विपरीत में बदलने की प्रक्रिया में फलन का मान शून्य को पार करना चाहिए, जो सदैव विषम कार्यों के लिए होता है। | ||
===बीजगणित का फंडामेंटल प्रमेय === | ===बीजगणित का फंडामेंटल प्रमेय === | ||
{{main| | {{main|बीजगणित का फंडामेंटल प्रमेय}} | ||
बीजगणित का फंडामेंटल प्रमेय | |||
बीजगणित के मौलिक प्रमेय में कहा गया है कि घात <math>n</math> के प्रत्येक बहुपद में <math>n</math> सम्मिश्र रुट के रूप में होती हैं, जिन्हें उनकी बहुलता के साथ गिना जाता है। वास्तविक गुणांक वाले बहुपदों की अवास्तविक रुट सम्मिश्र संयुग्मी युग्मों के रूप में होती है। विएटा के सूत्र एक बहुपद के गुणांकों को उसके रुट के योग और गुणन से जोड़ते हैं। | |||
== | == कंप्यूटिंग रूट == | ||
{{ | {{main|रुट फाइंडिंग कलन विधि|वास्तविक रुट आइसोलेशन|समीकरण हल करना}} | ||
फलन | फलन की रूट कंप्यूटिंग इस प्रकार होती है, उदाहरण के लिए बहुपद फलन के लिए अधिकांशतः विशेष या [[सन्निकटन]] प्रोद्योगिकीय के रूप में उपयोग की आवश्यकता होती है। उदाहरण के लिए न्यूटन की विधि आदि। चूंकि, कुछ बहुपद फलन जिनमें 4 से अधिक वाले बहुपद की सभी घातें सम्मलित होती है, उनके सभी रूट उनके गुणांकों के संदर्भ में बीजगणितीय फलन के रूप में व्यक्त किए जाते हैं और अधिक जानकारी के लिए, [[बीजगणितीय समाधान|बीजगणितीय]] सॉलूशन में दिखाया गया है। | ||
फलन | ==जीरो समुच्चय == | ||
{{redirect|जीरो सेट|म्यूजिकल एल्बम|जीरो सेट}} | |||
गणित के विभिन्न क्षेत्रों में, किसी [[फ़ंक्शन (गणित)|फलन (गणित)]] का शून्य समुच्चय उसके सभी शून्यों का समुच्चय होता है और इस प्रकार अधिक सटीक रूप से यदि <math>f:X\to\mathbb{R}</math> एक वास्तविक मूल्य फलन के रूप में होते है और सामान्यतः कुछ [[एड्डीटीव समूह]] में मान लेने वाले फलन होते है, इसका शून्य समुच्चय <math>f^{-1}(0)</math>, की व्युत्क्रम छवि <math>\{0\}</math> में <math>X</math>.के रूप में होती है | |||
फलन के [[कोडोमेन]] पर समान परिकल्पना के अनुसार फलन <math>f</math> का एक लेवेल समुच्चय फलन का शून्य समुच्चय होता है <math>f-c</math> के लिए <math>c</math> के कोडोमेन में <math>f.</math>होता है | |||
एक [[रेखीय मानचित्र]] के शून्य समुच्चय को उसके [[कर्नेल (बीजगणित)]] के रूप में भी जाना जाता है। | |||
फलन का कोज़ेरो समुच्चय <math>f:X\to\mathbb{R}</math> के शून्य समुच्चय का [[पूरक (सेट सिद्धांत)|पूरक ( समुच्चय सिद्धांत)]] है और इस प्रकार <math>f</math> का उपसमुच्चय <math>X</math> है, जिस पर <math>f</math> शून्येतर रूप में है। | |||
=== अनुप्रयोग === | === अनुप्रयोग === | ||
[[बीजगणितीय ज्यामिति]] में, बीजीय विविधता की | [[बीजगणितीय ज्यामिति]] में, बीजीय विविधता की पहली परिभाषा शून्य समुच्चय के माध्यम से होती है। विशेष रूप से, एक [[एफ़िन बीजगणितीय सेट|एफ़िन बीजगणितीय समुच्चय]] एक क्षेत्र पर (गणित) के बहुपद वलय <math>k\left[x_1,\ldots,x_n\right]</math> में कई बहुपदों के शून्य समुच्चय ों का प्रतिच्छेदन है। इस संदर्भ में, शून्य समुच्चय को कभी-कभी शून्य लोकस कहा जाता है। | ||
[[गणितीय विश्लेषण]] और [[ज्यामिति]] में, कोई भी [[बंद सेट|संवृत समुच्चय]] <math>\mathbb{R}^n</math> सभी पर परिभाषित एक सुचारु फलन का शून्य समुच्चय है <math>\mathbb{R}^n</math>. यह [[पैराकॉम्पैक्टनेस]] के परिणाम के रूप में किसी भी स्मूथ विविधता तक विस्तारित होता है। | |||
[[ | [[विभेदक ज्यामिति|अवकलन ज्यामिति]] में, शून्य समुच्चय का उपयोग अधिकांशतः [[ कई गुना |मैनिफोल्ड्स]] को परिभाषित करने के लिए किया जाता है। एक महत्वपूर्ण विशेष स्थिति यह है कि <math>f</math>, <math>\mathbb{R}^p</math> को <math>\mathbb{R}^n</math> से एक सुचारु फलन है, यदि शून्य एक नियमित मान है तो <math>f</math>, का शून्य समुच्चय और <math>f</math> आयाम का एक स्मूथ मैनिफोल्ड है, यदि <math>m=p-n</math> एक गणित नियमित मूल्य प्रमेय है। | ||
उदाहरण के लिए, इकाई <math>m</math>-गोले में <math>\mathbb{R}^{m+1}</math> वास्तविक | उदाहरण के लिए, इकाई <math>m</math>-गोले में <math>\mathbb{R}^{m+1}</math> वास्तविक मूल्यवान फलन का शून्य समुच्चय है <math>f(x)=\Vert x \Vert^2-1</math>. | ||
== यह भी देखें == | == यह भी देखें == | ||
*मार्डन | *मार्डन प्रमेय | ||
*[[जड़-खोज एल्गोरिथ्म|रुट - | *[[जड़-खोज एल्गोरिथ्म|रुट -फाइंडिंग कलन विधि]] | ||
*सेंडोव का अनुमान | *सेंडोव का अनुमान | ||
* [[अनंत पर लुप्त हो जाना]] | * वनिश [[अनंत पर लुप्त हो जाना|पर इनफिनिटी]] | ||
* [[जीबरा क्रोससिंग]] | * [[जीबरा क्रोससिंग|जीरो क्रोससिंग]] | ||
*[[शून्य और ध्रुव]] | *[[शून्य और ध्रुव|जीरो और ध्रुव]] | ||
== संदर्भ == | == संदर्भ == | ||
| Line 69: | Line 73: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 13/07/2023]] | [[Category:Created On 13/07/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 09:12, 9 November 2023
गणित में, एक वास्तविक संख्या, सम्मिश्र संख्या या सामान्यतः सदिश फलन का मान शून्य होता है, जिसे कभी-कभी रूट भी कहा जाता है और इस प्रकार के डोमेन का एक सदस्य के रूप में है, जैसे कि ऐसा है कि पर वनिश हो जाता है अर्थात फलन , पर 0 का मान प्राप्त करता है , या समकक्ष, समीकरण का सॉलूशन है.[1] इस प्रकार फलन का शून्य एक इनपुट मान होता है, जो 0 का आउटपुट उत्पन्न करता है।[2]
एक बहुपद का रूट संगत बहुपद फलन शून्य होता है।[1] इस प्रकार बीजगणित के फंडामेंटल प्रमेय से पता चलता है कि किसी भी गैर-शून्य बहुपद में बहुपद की घात के बराबर रूट की संख्या होती है और जब कोई सम्मिश्र रूट पर कंसीडर करता है तो रूट की संख्या और घात बराबर होती है और इस प्रकार सामान्यतः बीजगणितीय क्लोज्ड एक्सटेंशन में रुट ें उनकी बहुलता (गणित) के साथ गिनी जाती हैं।[3] उदाहरण के लिए, द्वारा परिभाषित घात दो के बहुपद के दो रुट जो 2 और 3 के रूप में होते है या शून्य रूप में होते है।
यदि फलन वास्तविक संख्याओं को वास्तविक संख्याओं में मैप करता है, तो इसके शून्य उन बिंदुओं के - निर्देशांक होते हैं, जहां इस फलन का ग्राफ़ x-अक्ष से मिलता है। इस संदर्भ में ऐसे बिंदु के लिए एक वैकल्पिक नाम -इंटरसेप्ट के रूप में होता है
समीकरण का सॉलूशन
अज्ञात में प्रत्येक समीकरण (गणित) को इस प्रकार पुनः लिखा जा सकता है,
बायीं ओर के सभी पदों को पुनः समूहित करते है। इससे निष्कर्ष यह निकलता है कि ऐसे समीकरण के सॉलूशन बिल्कुल फलन के रूप में शून्य होते हैं और इस प्रकार दूसरे शब्दों में फलन का शून्य वास्तव में फलन को 0 के बराबर करके प्राप्त समीकरण का एक सॉलूशन होता है और फलन के शून्य का अध्ययन बिल्कुल समीकरणों के सॉलूशन के अध्ययन के समान होता है।
बहुपद रुट
बहुपद की विषम घात वाले प्रत्येक वास्तविक बहुपद में वास्तविक रुट की एक विषम संख्या होती है और इस प्रकार बहुपद की एक रुट की बहुलता (गणित) बहुलता की काउंटिंग होती है। इसी प्रकार, सम घात वाले वास्तविक बहुपद में वास्तविक रुट की संख्या भी सम होनी चाहिए। फलस्वरूप वास्तविक विषम बहुपदों में कम से कम एक वास्तविक रूट होना चाहिए क्योंकि सबसे छोटी विषम पूर्ण संख्या 1 होती है। जबकि सम बहुपदों में कोई भी नहीं होता है। इस सिद्धांत को मध्यवर्ती मूल्य प्रमेय के संदर्भ से सिद्ध किया जाता है, चूंकि बहुपद फलन सतत फलन के रूप में होते है, इसलिए ऋणात्मक से धनात्मक या इसके विपरीत में बदलने की प्रक्रिया में फलन का मान शून्य को पार करना चाहिए, जो सदैव विषम कार्यों के लिए होता है।
बीजगणित का फंडामेंटल प्रमेय
बीजगणित के मौलिक प्रमेय में कहा गया है कि घात के प्रत्येक बहुपद में सम्मिश्र रुट के रूप में होती हैं, जिन्हें उनकी बहुलता के साथ गिना जाता है। वास्तविक गुणांक वाले बहुपदों की अवास्तविक रुट सम्मिश्र संयुग्मी युग्मों के रूप में होती है। विएटा के सूत्र एक बहुपद के गुणांकों को उसके रुट के योग और गुणन से जोड़ते हैं।
कंप्यूटिंग रूट
फलन की रूट कंप्यूटिंग इस प्रकार होती है, उदाहरण के लिए बहुपद फलन के लिए अधिकांशतः विशेष या सन्निकटन प्रोद्योगिकीय के रूप में उपयोग की आवश्यकता होती है। उदाहरण के लिए न्यूटन की विधि आदि। चूंकि, कुछ बहुपद फलन जिनमें 4 से अधिक वाले बहुपद की सभी घातें सम्मलित होती है, उनके सभी रूट उनके गुणांकों के संदर्भ में बीजगणितीय फलन के रूप में व्यक्त किए जाते हैं और अधिक जानकारी के लिए, बीजगणितीय सॉलूशन में दिखाया गया है।
जीरो समुच्चय
गणित के विभिन्न क्षेत्रों में, किसी फलन (गणित) का शून्य समुच्चय उसके सभी शून्यों का समुच्चय होता है और इस प्रकार अधिक सटीक रूप से यदि एक वास्तविक मूल्य फलन के रूप में होते है और सामान्यतः कुछ एड्डीटीव समूह में मान लेने वाले फलन होते है, इसका शून्य समुच्चय , की व्युत्क्रम छवि में .के रूप में होती है
फलन के कोडोमेन पर समान परिकल्पना के अनुसार फलन का एक लेवेल समुच्चय फलन का शून्य समुच्चय होता है के लिए के कोडोमेन में होता है
एक रेखीय मानचित्र के शून्य समुच्चय को उसके कर्नेल (बीजगणित) के रूप में भी जाना जाता है।
फलन का कोज़ेरो समुच्चय के शून्य समुच्चय का पूरक ( समुच्चय सिद्धांत) है और इस प्रकार का उपसमुच्चय है, जिस पर शून्येतर रूप में है।
अनुप्रयोग
बीजगणितीय ज्यामिति में, बीजीय विविधता की पहली परिभाषा शून्य समुच्चय के माध्यम से होती है। विशेष रूप से, एक एफ़िन बीजगणितीय समुच्चय एक क्षेत्र पर (गणित) के बहुपद वलय में कई बहुपदों के शून्य समुच्चय ों का प्रतिच्छेदन है। इस संदर्भ में, शून्य समुच्चय को कभी-कभी शून्य लोकस कहा जाता है।
गणितीय विश्लेषण और ज्यामिति में, कोई भी संवृत समुच्चय सभी पर परिभाषित एक सुचारु फलन का शून्य समुच्चय है . यह पैराकॉम्पैक्टनेस के परिणाम के रूप में किसी भी स्मूथ विविधता तक विस्तारित होता है।
अवकलन ज्यामिति में, शून्य समुच्चय का उपयोग अधिकांशतः मैनिफोल्ड्स को परिभाषित करने के लिए किया जाता है। एक महत्वपूर्ण विशेष स्थिति यह है कि , को से एक सुचारु फलन है, यदि शून्य एक नियमित मान है तो , का शून्य समुच्चय और आयाम का एक स्मूथ मैनिफोल्ड है, यदि एक गणित नियमित मूल्य प्रमेय है।
उदाहरण के लिए, इकाई -गोले में वास्तविक मूल्यवान फलन का शून्य समुच्चय है .
यह भी देखें
- मार्डन प्रमेय
- रुट -फाइंडिंग कलन विधि
- सेंडोव का अनुमान
- वनिश पर इनफिनिटी
- जीरो क्रोससिंग
- जीरो और ध्रुव
संदर्भ
- ↑ 1.0 1.1 "Algebra - Zeroes/Roots of Polynomials". tutorial.math.lamar.edu. Retrieved 2019-12-15.
- ↑ Foerster, Paul A. (2006). Algebra and Trigonometry: Functions and Applications, Teacher's Edition (Classics ed.). Upper Saddle River, NJ: Prentice Hall. p. 535. ISBN 0-13-165711-9.
- ↑ "Roots and zeros (Algebra 2, Polynomial functions)". Mathplanet (in English). Retrieved 2019-12-15.