गैम्बलिंग और सूचना सिद्धांत: Difference between revisions
No edit summary |
m (6 revisions imported from alpha:गैम्बलिंग_और_सूचना_सिद्धांत) |
||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
सांख्यिकीय अनुमान को हमारे आसपास की दुनिया पर लागू गैम्बलिंग सिद्धांत के रूप में माना जा सकता है। लघुगणकीय सूचना माप के असंख्य अनुप्रयोग हमें सटीक रूप से बताते हैं कि आंशिक जानकारी के सामने सर्वोत्तम अनुमान कैसे लगाया जाए।<ref>Jaynes, E.T. (1998/2003) [http://bayes.wustl.edu/ ''Probability Theory: The Logic of Science''] (Cambridge U. Press, New York).</ref> उस अर्थ में, सूचना सिद्धांत को | सांख्यिकीय अनुमान को हमारे आसपास की दुनिया पर लागू गैम्बलिंग सिद्धांत के रूप में माना जा सकता है। लघुगणकीय सूचना माप के असंख्य अनुप्रयोग हमें सटीक रूप से बताते हैं कि आंशिक जानकारी के सामने सर्वोत्तम अनुमान कैसे लगाया जाए।<ref>Jaynes, E.T. (1998/2003) [http://bayes.wustl.edu/ ''Probability Theory: The Logic of Science''] (Cambridge U. Press, New York).</ref> उस अर्थ में, सूचना सिद्धांत को गैंबलिंग के सिद्धांत की औपचारिक अभिव्यक्ति माना जा सकता है। इसलिए, इसमें कोई आश्चर्य की बात नहीं है कि सूचना सिद्धांत का संयोग के खेल में भी अनुप्रयोग होता है।<ref>{{Cite journal | last1 = Kelly | first1 = J. L. | author-link1 = John Larry Kelly, Jr.| title = सूचना दर की एक नई व्याख्या| doi = 10.1002/j.1538-7305.1956.tb03809.x | journal = [[Bell System Technical Journal]] | volume = 35 | issue = 4 | pages = 917–926 | year = 1956 | url = http://www.herrold.com/brokerage/kelly.pdf}}</ref> | ||
== केली शर्त == | == केली शर्त == | ||
{{main|केली मानदंड}} | {{main|केली मानदंड}} | ||
केली शर्त या आनुपातिक शर्त निवेश और | केली शर्त या आनुपातिक शर्त निवेश और गैंबलिंग पर सूचना सिद्धांत का एक अनुप्रयोग है। इसके आविष्कारक जॉन लैरी केली जूनियर थे। | ||
केली की अंतर्दृष्टि का एक हिस्सा यह था कि गैम्बलर प्रत्येक दांव से अपेक्षित लाभ के | केली की अंतर्दृष्टि का एक हिस्सा यह था कि गैम्बलर प्रत्येक दांव से अपेक्षित लाभ के स्थान पर, अपनी पूंजी के लघुगणक की अपेक्षा को अधिकतम कर दे। यह महत्वपूर्ण है, क्योंकि बाद वाले स्थिति में, अनुकूल दांव लगाए जाने पर व्यक्ति को अपना सब कुछ दांव पर लगाने के लिए प्रेरित किया जाएगा और यदि वह हार जाता है, तो उसके पास बाद में दांव लगाने के लिए कोई पूंजी नहीं होगी। केली को एहसास हुआ कि यह गैम्बलर की पूंजी का लघुगणक था जो क्रमिक दांवों में योगात्मक है, और "जिस पर बड़ी संख्या का कानून लागू होता है।" | ||
===अतिरिक्त जानकारी=== | ===अतिरिक्त जानकारी=== | ||
बिट दो संभावित परिणामों और यहां तक कि बाधाओं के साथ एक शर्त योग्य घटना में एन्ट्रापी की मात्रा है। जाहिर तौर पर हम अपना पैसा दोगुना कर सकते हैं अगर हमें पहले से पता हो कि उस घटना का परिणाम क्या होगा। केली की अंतर्दृष्टि यह थी कि | बिट दो संभावित परिणामों और यहां तक कि बाधाओं के साथ एक शर्त योग्य घटना में एन्ट्रापी की मात्रा है। जाहिर तौर पर हम अपना पैसा दोगुना कर सकते हैं अगर हमें पहले से पता हो कि उस घटना का परिणाम क्या होगा। केली की अंतर्दृष्टि यह थी कि शर्त का परिदृश्य कितना भी जटिल क्यों न हो, हम एक इष्टतम शर्त रणनीति का उपयोग कर सकते हैं, जिसे केली मानदंड कहा जाता है, ताकि हम जो भी जानकारी प्राप्त कर सकें, उसके साथ हमारे पैसे में तेजी से वृद्धि हो सके। इस "अवैध" पक्ष की जानकारी का मूल्य दांव पर लगाने योग्य घटना के परिणाम के सापेक्ष पारस्परिक जानकारी के रूप में मापा जाता है: | ||
:<math>\begin{align}I(X;Y) & = \mathbb{E}_Y \{D_{\mathrm{KL}}\big(P(X|Y) \| P(X|I) \big) \} \\ | :<math>\begin{align}I(X;Y) & = \mathbb{E}_Y \{D_{\mathrm{KL}}\big(P(X|Y) \| P(X|I) \big) \} \\ | ||
& = \mathbb{E}_Y \{D_{\mathrm{KL}}\big(P(X|\textrm{side}\ \textrm{information}\ Y) \| P(X|\textrm{stated}\ \textrm{odds}\ I) \big) | & = \mathbb{E}_Y \{D_{\mathrm{KL}}\big(P(X|\textrm{side}\ \textrm{information}\ Y) \| P(X|\textrm{stated}\ \textrm{odds}\ I) \big) | ||
\}, \end{align} </math> | \}, \end{align} </math> | ||
जहां Y पक्ष की जानकारी है, X दांव योग्य घटना का परिणाम है, और I | जहां Y पक्ष की जानकारी है, X दांव योग्य घटना का परिणाम है, और I बुकमेकर के ज्ञान की स्थिति है। यह X के पूर्ववर्ती संभाव्यता वितरण का औसत कुल्बैक-लीब्लर विचलन, या सूचना लाभ है, जिसे X पर पूर्व वितरण, या बताई गई बाधाओं के सापेक्ष वाई का मान दिया गया है। ध्यान दें कि अपेक्षा को वाई के स्थान पर वाई पर ले लिया गया है। X: X पर वास्तविक पैसे का दांव लगाना शुरू करने से पहले हमें यह मूल्यांकन करने की आवश्यकता है कि लंबी अवधि में हमारी ओर की जानकारी वाई कितनी सटीक है। यह बायेसियन अनुमान का एक सीधा अनुप्रयोग है। ध्यान दें कि पार्श्व जानकारी Y न केवल घटना X के बारे में हमारे ज्ञान को प्रभावित कर सकती है, बल्कि स्वयं घटना को भी प्रभावित कर सकती है। उदाहरण के लिए, Y एक घोड़ा हो सकता है जिसके पास बहुत अधिक जई थी या पर्याप्त पानी नहीं था। इस स्थिति में भी वही गणित लागू होता है, क्योंकि बुकमेकर के दृष्टिकोण से, जब वह अपना दांव लगाता है तो कभी-कभार होने वाली रेस फिक्सिंग को पहले से ही ध्यान में रखा जाता है। | ||
पार्श्व सूचना की प्रकृति अत्यंत सूक्ष्म है। हमने पहले ही देखा है कि यह वास्तविक घटना के साथ-साथ परिणाम के बारे में हमारे ज्ञान को भी प्रभावित कर सकता है। मान लीजिए हमारे पास एक मुखबिर है, जो हमें बताता है कि अमुक घोड़ा जीतने वाला है। हम निश्चित रूप से सिर्फ एक अफवाह के आधार पर उस घोड़े पर अपना सारा पैसा दांव पर नहीं लगाना चाहते: वह मुखबिर किसी अन्य घोड़े पर दांव लगा सकता है, और अफवाहें फैला रहा हो सकता है ताकि वह खुद बेहतर दांव लगा सके। इसके | पार्श्व सूचना की प्रकृति अत्यंत सूक्ष्म है। हमने पहले ही देखा है कि यह वास्तविक घटना के साथ-साथ परिणाम के बारे में हमारे ज्ञान को भी प्रभावित कर सकता है। मान लीजिए हमारे पास एक मुखबिर है, जो हमें बताता है कि अमुक घोड़ा जीतने वाला है। हम निश्चित रूप से सिर्फ एक अफवाह के आधार पर उस घोड़े पर अपना सारा पैसा दांव पर नहीं लगाना चाहते: वह मुखबिर किसी अन्य घोड़े पर दांव लगा सकता है, और अफवाहें फैला रहा हो सकता है ताकि वह खुद बेहतर दांव लगा सके। इसके स्थान पर, जैसा कि हमने संकेत दिया है, हमें लंबी अवधि में अपनी जानकारी का मूल्यांकन करने की आवश्यकता है ताकि यह देखा जा सके कि यह दौड़ के परिणामों के साथ कैसे संबंधित है। इस तरह से हम यह निर्धारित कर सकते हैं कि हमारा मुखबिर कितना विश्वसनीय है, और केली मानदंड के अनुसार हमारी पूंजी के अपेक्षित लघुगणक को अधिकतम करने के लिए अपना दांव सटीक रूप से लगाएं। भले ही हमारा मुखबिर हमसे झूठ बोल रहा हो, हम तब भी उसके झूठ से लाभ उठा सकते हैं यदि हम उसकी युक्तियों और वास्तविक दौड़ परिणामों के बीच कुछ विपरीत संबंध पा सकें। | ||
===दोगुना होने की दर=== | ===दोगुना होने की दर=== | ||
घुड़दौड़ पर गैंबलिंग खेलने की दर दोगुनी हो गई है<ref>[[Thomas M. Cover]], Joy A. Thomas. ''Elements of information theory'', 1st Edition. New York: Wiley-Interscience, 1991. {{ISBN|0-471-06259-6}}, Chapter 6.</ref> | घुड़दौड़ पर गैंबलिंग खेलने की दर दोगुनी हो गई है<ref>[[Thomas M. Cover]], Joy A. Thomas. ''Elements of information theory'', 1st Edition. New York: Wiley-Interscience, 1991. {{ISBN|0-471-06259-6}}, Chapter 6.</ref> | ||
: <math> W(b,p) = \mathbb E[\log_2 S(X)] = \sum_{i=1}^m p_i \log_2 b_i o_i </math> | : <math> W(b,p) = \mathbb E[\log_2 S(X)] = \sum_{i=1}^m p_i \log_2 b_i o_i </math> | ||
जहाँ <math>m</math> घोड़े हैं, iवें घोड़े के जीतने की प्रायिकता है <math>p_i</math>, घोड़े पर लगाए गए धन के दांव का अनुपात <math>b_i</math> है, और संभावना (भुगतान) <math>o_i</math>है (उदाहरण के लिए, <math>o_i=2</math> यदि जीतने वाला घोड़ा दांव की राशि से दोगुना भुगतान करता है)। यह मात्रा आनुपातिक (केली) | जहाँ <math>m</math> घोड़े हैं, iवें घोड़े के जीतने की प्रायिकता है <math>p_i</math>, घोड़े पर लगाए गए धन के दांव का अनुपात <math>b_i</math> है, और संभावना (भुगतान) <math>o_i</math>है (उदाहरण के लिए, <math>o_i=2</math> यदि जीतने वाला घोड़ा दांव की राशि से दोगुना भुगतान करता है)। यह मात्रा आनुपातिक (केली) गैंबलिंग से अधिकतम होती है: | ||
: <math> b = p \,</math> | : <math> b = p \,</math> | ||
| Line 29: | Line 29: | ||
===अपेक्षित लाभ=== | ===अपेक्षित लाभ=== | ||
एक गैम्बलर द्वारा प्राप्त की जाने वाली अतिरिक्त जानकारी की मात्रा और उसकी पूंजी (केली) की अपेक्षित घातीय वृद्धि के बीच एक महत्वपूर्ण लेकिन सरल संबंध | एक गैम्बलर द्वारा प्राप्त की जाने वाली अतिरिक्त जानकारी की मात्रा और उसकी पूंजी (केली) की अपेक्षित घातीय वृद्धि के बीच एक महत्वपूर्ण लेकिन सरल संबंध उपस्थित है: | ||
: <math> \mathbb E \log K_t = \log K_0 + \sum_{i=1}^t H_i </math> | : <math> \mathbb E \log K_t = \log K_0 + \sum_{i=1}^t H_i </math> | ||
| Line 38: | Line 38: | ||
==स्वयं जानकारी के लिए आवेदन== | ==स्वयं जानकारी के लिए आवेदन== | ||
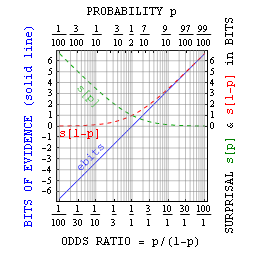
[[Image:Sandebits.png|thumb|256px|right|बिट्स में आश्चर्य और साक्ष्य, क्रमशः संभाव्यता और बाधाओं के लघुगणकीय माप के रूप में।]] | [[Image:Sandebits.png|thumb|256px|right|बिट्स में आश्चर्य और साक्ष्य, क्रमशः संभाव्यता और बाधाओं के लघुगणकीय माप के रूप में।]]लॉगरिदमिक संभाव्यता आत्म-सूचना या आश्चर्य को मापती है, <ref>Tribus, Myron (1961) ''Thermodynamics and Thermostatics: An Introduction to Energy, Information and States of Matter, with Engineering Applications'' (D. Van Nostrand Company Inc., 24 West 40 Street, New York 18, New York, U.S.A) ASIN: B000ARSH5S.</ref> जिसका औसत सूचना एन्ट्रापी/अनिश्चितता है और जिसका औसत अंतर केएल-विचलन है, इसमें अपने आप में बाधाओं-विश्लेषण के अनुप्रयोग होते हैं। इसकी दो प्राथमिक ताकतें यह हैं कि आश्चर्य: (i) छोटी संभावनाओं को प्रबंधनीय आकार की संख्याओं में कम करना, और (ii) जब भी संभावनाएं बढ़ जाती हैं, उन्हें जोड़ना। | ||
उदाहरण के लिए, कोई कह सकता है कि | उदाहरण के लिए, कोई कह सकता है कि "स्टेट्स की संख्या बिट्स की संख्या के दो के बराबर है" यानी #states = 2<sup>#bits</sup>। यहां जो मात्रा बिट्स में मापी गई है वह ऊपर उल्लिखित लघुगणकीय सूचना माप है। इसलिए एन सिक्कों को पहली बार उछालने पर सभी हेड्स आने में आश्चर्य की बात है। | ||
आश्चर्य की योगात्मक प्रकृति, और मुट्ठी भर सिक्कों के साथ उनके अर्थ को | आश्चर्य की योगात्मक प्रकृति, और मुट्ठी भर सिक्कों के साथ उनके अर्थ को अनुभूति करने की क्षमता, किसी को अप्रत्याशित घटनाओं (जैसे लॉटरी जीतना, या कोई दुर्घटना होना) को संदर्भ में रखने में मदद कर सकती है। उदाहरण के लिए, यदि 17 मिलियन टिकटों में से एक विजेता है, तो एकल यादृच्छिक चयन से जीतने का आश्चर्य लगभग 24 बिट है। 24 सिक्कों को कुछ बार उछालने से आपको पहली कोशिश में सभी चित आने के आश्चर्य का एहसास हो सकता है। | ||
विकल्पों का वजन करते समय इस माप की योगात्मक प्रकृति भी काम आती है। उदाहरण के लिए, कल्पना करें कि टीकाकरण से होने वाले नुकसान का आश्चर्य 20 बिट्स है। यदि किसी रोग के बिना पकड़ में आने का आश्चर्य 16 बिट है, लेकिन यदि आप रोग पकड़ लेते हैं तो उससे होने वाले नुकसान का आश्चर्य 2 बिट है, तो टीकाकरण न करवाने से होने वाले नुकसान का आश्चर्य केवल 16+2=18 बिट है। चाहे | विकल्पों का वजन करते समय इस माप की योगात्मक प्रकृति भी काम आती है। उदाहरण के लिए, कल्पना करें कि टीकाकरण से होने वाले नुकसान का आश्चर्य 20 बिट्स है। यदि किसी रोग के बिना पकड़ में आने का आश्चर्य 16 बिट है, लेकिन यदि आप रोग पकड़ लेते हैं तो उससे होने वाले नुकसान का आश्चर्य 2 बिट है, तो टीकाकरण न करवाने से होने वाले नुकसान का आश्चर्य केवल 16+2=18 बिट है। चाहे आपने टीकाकरण कराने का निर्णय लिया हो या नहीं (उदाहरण के लिए इसके लिए भुगतान की मौद्रिक लागत इस चर्चा में सम्मिलित नहीं है), आप कम से कम इस तथ्य से अवगत निर्णय की जिम्मेदारी ले सकते हैं कि टीकाकरण न करवाने में इससे अधिक सम्मिलित है अतिरिक्त जोखिम का एक सा. | ||
अधिक | अधिक सामान्यतः, कोई संभाव्यता पी को आश्चर्य की बिट्स के बिट्स से संबंधित कर सकता है क्योंकि संभावना = 1/2<sup>sbits</sup>। जैसा कि ऊपर सुझाव दिया गया है, यह मुख्य रूप से छोटी संभावनाओं के साथ उपयोगी है। हालाँकि, जेन्स ने बताया कि सच्चे-झूठे दावों के साथ साक्ष्य के अंशों को भी परिभाषित किया जा सकता है, जो कि आश्चर्य के विरुद्ध आश्चर्य के रूप में परिभाषित किया गया है। बिट्स में यह साक्ष्य केवल अंतर अनुपात = p/(1-p) = 2<sup>ebits</sup> से संबंधित है, और इसमें स्वयं-जानकारी के समान लाभ हैं। | ||
==संयोग के खेलों में अनुप्रयोग== | ==संयोग के खेलों में अनुप्रयोग== | ||
सूचना सिद्धांत को जानकारी | सूचना सिद्धांत को जानकारी को परिमाणित करने के एक तरीके के रूप में सोचा जा सकता है ताकि अपूर्ण जानकारी के सामने सर्वोत्तम निर्णय लिया जा सके। यानी, आपके पास उपलब्ध जानकारी का उपयोग करके सर्वोत्तम निर्णय कैसे लिया जाए। शर्त का उद्देश्य किसी अनिश्चित खेल/दौड़/मैच के सभी प्रासंगिक चरों का तर्कसंगत रूप से आकलन करना है, फिर उनकी तुलना बुकमेकर के आकलन से करना है, जो सामान्यतः ऑड्स या स्प्रेड के रूप में आता है और यदि आकलन पर्याप्त रूप से भिन्न हो तो उचित दांव लगाएं।<ref>Hansen, Kristen Brinch. (2006) [http://pure.au.dk/portal/files/1627/000145742-145742.pdf ''Sports Betting from a Behavioral Finance Point of View''] (Arhus School of Business).</ref> गैंबलिंग के जिस क्षेत्र में इसका सबसे अधिक उपयोग होता है वह खेल शर्त है। आंकड़ों की उपलब्धता के कारण खेल बाधाएं सूचना सिद्धांत को बहुत अच्छी तरह से उधार देती हैं। कई वर्षों से जाने-माने अर्थशास्त्रियों ने खेल को अपनी प्रयोगशाला के रूप में उपयोग करके विभिन्न गणितीय सिद्धांतों का परीक्षण किया है, जिसके परिणाम बहुत अलग-अलग रहे हैं। | ||
यदि आकलन पर्याप्त रूप से भिन्न हो तो उचित दांव लगाएं।<ref>Hansen, Kristen Brinch. (2006) [http://pure.au.dk/portal/files/1627/000145742-145742.pdf ''Sports Betting from a Behavioral Finance Point of View''] (Arhus School of Business).</ref> | |||
खेलों में शर्त के संबंध में एक सिद्धांत यह है कि यह एक यादृच्छिक चाल है। रैंडम वॉक एक ऐसा परिदृश्य है जहां नई जानकारी, कीमतें और रिटर्न में संयोग से उतार-चढ़ाव होगा, यह कुशल-बाजार परिकल्पना का हिस्सा है। कुशल बाज़ार परिकल्पना की अंतर्निहित धारणा यह है कि बाज़ार हमेशा किसी भी नई जानकारी के लिए समायोजन करेगा। इसलिए कोई भी बाजार को हरा नहीं सकता क्योंकि वे उसी जानकारी पर कारोबार कर रहे हैं जिससे बाजार समायोजित हुआ है। हालाँकि, फामा के अनुसार,<ref>Fama, E.F. (1970) "Efficient Capital Markets: A Review of Theory and Independent Work", ''Journal of Financial Economics'' Volume 25, 383-417</ref> एक कुशल बाज़ार के लिए तीन गुणों को पूरा करने की आवश्यकता है: | |||
* प्रतिभूतियों के व्यापार में कोई लेनदेन लागत नहीं होती है | * प्रतिभूतियों के व्यापार में कोई लेनदेन लागत नहीं होती है | ||
* सभी उपलब्ध जानकारी सभी बाज़ार सहभागियों के लिए निःशुल्क उपलब्ध है | * सभी उपलब्ध जानकारी सभी बाज़ार सहभागियों के लिए निःशुल्क उपलब्ध है | ||
* प्रत्येक सुरक्षा की वर्तमान कीमत और भविष्य की कीमतों के वितरण के लिए वर्तमान जानकारी के निहितार्थ पर सभी सहमत हैं | * प्रत्येक सुरक्षा की वर्तमान कीमत और भविष्य की कीमतों के वितरण के लिए वर्तमान जानकारी के निहितार्थ पर सभी सहमत हैं | ||
सांख्यिकीविदों ने दिखाया है कि यह तीसरी शर्त है जो सूचना सिद्धांत को | सांख्यिकीविदों ने दिखाया है कि यह तीसरी शर्त है जो खेल विकलांगता में सूचना सिद्धांत को उपयोगी बनाने की अनुमति देती है। जब हर कोई इस बात पर सहमत नहीं होता कि जानकारी घटना के परिणाम को कैसे प्रभावित करेगी, तो हमें अलग-अलग सम्मति मिलती है। | ||
==यह भी देखें== | ==यह भी देखें== | ||
* | * उदासीनता का सिद्धान्त | ||
* | * सांख्यिकीय संघ फुटबॉल भविष्यवाणियाँ | ||
* | * उन्नत एनएफ़एल आँकड़े | ||
==संदर्भ== | ==संदर्भ== | ||
| Line 81: | Line 79: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 04/12/2023]] | [[Category:Created On 04/12/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 09:14, 12 December 2023
सांख्यिकीय अनुमान को हमारे आसपास की दुनिया पर लागू गैम्बलिंग सिद्धांत के रूप में माना जा सकता है। लघुगणकीय सूचना माप के असंख्य अनुप्रयोग हमें सटीक रूप से बताते हैं कि आंशिक जानकारी के सामने सर्वोत्तम अनुमान कैसे लगाया जाए।[1] उस अर्थ में, सूचना सिद्धांत को गैंबलिंग के सिद्धांत की औपचारिक अभिव्यक्ति माना जा सकता है। इसलिए, इसमें कोई आश्चर्य की बात नहीं है कि सूचना सिद्धांत का संयोग के खेल में भी अनुप्रयोग होता है।[2]
केली शर्त
केली शर्त या आनुपातिक शर्त निवेश और गैंबलिंग पर सूचना सिद्धांत का एक अनुप्रयोग है। इसके आविष्कारक जॉन लैरी केली जूनियर थे।
केली की अंतर्दृष्टि का एक हिस्सा यह था कि गैम्बलर प्रत्येक दांव से अपेक्षित लाभ के स्थान पर, अपनी पूंजी के लघुगणक की अपेक्षा को अधिकतम कर दे। यह महत्वपूर्ण है, क्योंकि बाद वाले स्थिति में, अनुकूल दांव लगाए जाने पर व्यक्ति को अपना सब कुछ दांव पर लगाने के लिए प्रेरित किया जाएगा और यदि वह हार जाता है, तो उसके पास बाद में दांव लगाने के लिए कोई पूंजी नहीं होगी। केली को एहसास हुआ कि यह गैम्बलर की पूंजी का लघुगणक था जो क्रमिक दांवों में योगात्मक है, और "जिस पर बड़ी संख्या का कानून लागू होता है।"
अतिरिक्त जानकारी
बिट दो संभावित परिणामों और यहां तक कि बाधाओं के साथ एक शर्त योग्य घटना में एन्ट्रापी की मात्रा है। जाहिर तौर पर हम अपना पैसा दोगुना कर सकते हैं अगर हमें पहले से पता हो कि उस घटना का परिणाम क्या होगा। केली की अंतर्दृष्टि यह थी कि शर्त का परिदृश्य कितना भी जटिल क्यों न हो, हम एक इष्टतम शर्त रणनीति का उपयोग कर सकते हैं, जिसे केली मानदंड कहा जाता है, ताकि हम जो भी जानकारी प्राप्त कर सकें, उसके साथ हमारे पैसे में तेजी से वृद्धि हो सके। इस "अवैध" पक्ष की जानकारी का मूल्य दांव पर लगाने योग्य घटना के परिणाम के सापेक्ष पारस्परिक जानकारी के रूप में मापा जाता है:
जहां Y पक्ष की जानकारी है, X दांव योग्य घटना का परिणाम है, और I बुकमेकर के ज्ञान की स्थिति है। यह X के पूर्ववर्ती संभाव्यता वितरण का औसत कुल्बैक-लीब्लर विचलन, या सूचना लाभ है, जिसे X पर पूर्व वितरण, या बताई गई बाधाओं के सापेक्ष वाई का मान दिया गया है। ध्यान दें कि अपेक्षा को वाई के स्थान पर वाई पर ले लिया गया है। X: X पर वास्तविक पैसे का दांव लगाना शुरू करने से पहले हमें यह मूल्यांकन करने की आवश्यकता है कि लंबी अवधि में हमारी ओर की जानकारी वाई कितनी सटीक है। यह बायेसियन अनुमान का एक सीधा अनुप्रयोग है। ध्यान दें कि पार्श्व जानकारी Y न केवल घटना X के बारे में हमारे ज्ञान को प्रभावित कर सकती है, बल्कि स्वयं घटना को भी प्रभावित कर सकती है। उदाहरण के लिए, Y एक घोड़ा हो सकता है जिसके पास बहुत अधिक जई थी या पर्याप्त पानी नहीं था। इस स्थिति में भी वही गणित लागू होता है, क्योंकि बुकमेकर के दृष्टिकोण से, जब वह अपना दांव लगाता है तो कभी-कभार होने वाली रेस फिक्सिंग को पहले से ही ध्यान में रखा जाता है।
पार्श्व सूचना की प्रकृति अत्यंत सूक्ष्म है। हमने पहले ही देखा है कि यह वास्तविक घटना के साथ-साथ परिणाम के बारे में हमारे ज्ञान को भी प्रभावित कर सकता है। मान लीजिए हमारे पास एक मुखबिर है, जो हमें बताता है कि अमुक घोड़ा जीतने वाला है। हम निश्चित रूप से सिर्फ एक अफवाह के आधार पर उस घोड़े पर अपना सारा पैसा दांव पर नहीं लगाना चाहते: वह मुखबिर किसी अन्य घोड़े पर दांव लगा सकता है, और अफवाहें फैला रहा हो सकता है ताकि वह खुद बेहतर दांव लगा सके। इसके स्थान पर, जैसा कि हमने संकेत दिया है, हमें लंबी अवधि में अपनी जानकारी का मूल्यांकन करने की आवश्यकता है ताकि यह देखा जा सके कि यह दौड़ के परिणामों के साथ कैसे संबंधित है। इस तरह से हम यह निर्धारित कर सकते हैं कि हमारा मुखबिर कितना विश्वसनीय है, और केली मानदंड के अनुसार हमारी पूंजी के अपेक्षित लघुगणक को अधिकतम करने के लिए अपना दांव सटीक रूप से लगाएं। भले ही हमारा मुखबिर हमसे झूठ बोल रहा हो, हम तब भी उसके झूठ से लाभ उठा सकते हैं यदि हम उसकी युक्तियों और वास्तविक दौड़ परिणामों के बीच कुछ विपरीत संबंध पा सकें।
दोगुना होने की दर
घुड़दौड़ पर गैंबलिंग खेलने की दर दोगुनी हो गई है[3]
जहाँ घोड़े हैं, iवें घोड़े के जीतने की प्रायिकता है , घोड़े पर लगाए गए धन के दांव का अनुपात है, और संभावना (भुगतान) है (उदाहरण के लिए, यदि जीतने वाला घोड़ा दांव की राशि से दोगुना भुगतान करता है)। यह मात्रा आनुपातिक (केली) गैंबलिंग से अधिकतम होती है:
जिसके लिए
जहाँ सूचना एन्ट्रापी है.
अपेक्षित लाभ
एक गैम्बलर द्वारा प्राप्त की जाने वाली अतिरिक्त जानकारी की मात्रा और उसकी पूंजी (केली) की अपेक्षित घातीय वृद्धि के बीच एक महत्वपूर्ण लेकिन सरल संबंध उपस्थित है:
एक इष्टतम शर्त रणनीति के लिए, जहां प्रारंभिक पूंजी है, टीवें दांव के बाद की राजधानी है, और दांव के संबंध में प्राप्त अतिरिक्त जानकारी की मात्रा है (विशेष रूप से, प्रत्येक बीटेबल घटना के परिणाम के सापेक्ष पारस्परिक जानकारी)। यह समीकरण किसी भी लेनदेन लागत या न्यूनतम दांव के अभाव में लागू होता है। जब ये बाधाएं लागू होती हैं (जैसा कि वे वास्तविक जीवन में हमेशा करते हैं), एक और महत्वपूर्ण गैम्बलिंग अवधारणा खेल में आती है: गैम्बलर (या बेईमान निवेशक) को अंतिम बर्बादी की एक निश्चित संभावना का सामना करना पड़ता है, जिसे गैम्बलर के बर्बाद परिदृश्य के रूप में जाना जाता है। ध्यान दें कि भोजन, कपड़े और आश्रय को भी निश्चित लेनदेन लागत माना जा सकता है और इस प्रकार गैम्बलर की अंतिम बर्बादी की संभावना में योगदान होता है।
यह समीकरण डेटा संचार (पियर्स) के प्रचलित प्रतिमान के बाहर शैनन के सूचना सिद्धांत का पहला अनुप्रयोग था।
स्वयं जानकारी के लिए आवेदन
लॉगरिदमिक संभाव्यता आत्म-सूचना या आश्चर्य को मापती है, [4] जिसका औसत सूचना एन्ट्रापी/अनिश्चितता है और जिसका औसत अंतर केएल-विचलन है, इसमें अपने आप में बाधाओं-विश्लेषण के अनुप्रयोग होते हैं। इसकी दो प्राथमिक ताकतें यह हैं कि आश्चर्य: (i) छोटी संभावनाओं को प्रबंधनीय आकार की संख्याओं में कम करना, और (ii) जब भी संभावनाएं बढ़ जाती हैं, उन्हें जोड़ना।
उदाहरण के लिए, कोई कह सकता है कि "स्टेट्स की संख्या बिट्स की संख्या के दो के बराबर है" यानी #states = 2#bits। यहां जो मात्रा बिट्स में मापी गई है वह ऊपर उल्लिखित लघुगणकीय सूचना माप है। इसलिए एन सिक्कों को पहली बार उछालने पर सभी हेड्स आने में आश्चर्य की बात है।
आश्चर्य की योगात्मक प्रकृति, और मुट्ठी भर सिक्कों के साथ उनके अर्थ को अनुभूति करने की क्षमता, किसी को अप्रत्याशित घटनाओं (जैसे लॉटरी जीतना, या कोई दुर्घटना होना) को संदर्भ में रखने में मदद कर सकती है। उदाहरण के लिए, यदि 17 मिलियन टिकटों में से एक विजेता है, तो एकल यादृच्छिक चयन से जीतने का आश्चर्य लगभग 24 बिट है। 24 सिक्कों को कुछ बार उछालने से आपको पहली कोशिश में सभी चित आने के आश्चर्य का एहसास हो सकता है।
विकल्पों का वजन करते समय इस माप की योगात्मक प्रकृति भी काम आती है। उदाहरण के लिए, कल्पना करें कि टीकाकरण से होने वाले नुकसान का आश्चर्य 20 बिट्स है। यदि किसी रोग के बिना पकड़ में आने का आश्चर्य 16 बिट है, लेकिन यदि आप रोग पकड़ लेते हैं तो उससे होने वाले नुकसान का आश्चर्य 2 बिट है, तो टीकाकरण न करवाने से होने वाले नुकसान का आश्चर्य केवल 16+2=18 बिट है। चाहे आपने टीकाकरण कराने का निर्णय लिया हो या नहीं (उदाहरण के लिए इसके लिए भुगतान की मौद्रिक लागत इस चर्चा में सम्मिलित नहीं है), आप कम से कम इस तथ्य से अवगत निर्णय की जिम्मेदारी ले सकते हैं कि टीकाकरण न करवाने में इससे अधिक सम्मिलित है अतिरिक्त जोखिम का एक सा.
अधिक सामान्यतः, कोई संभाव्यता पी को आश्चर्य की बिट्स के बिट्स से संबंधित कर सकता है क्योंकि संभावना = 1/2sbits। जैसा कि ऊपर सुझाव दिया गया है, यह मुख्य रूप से छोटी संभावनाओं के साथ उपयोगी है। हालाँकि, जेन्स ने बताया कि सच्चे-झूठे दावों के साथ साक्ष्य के अंशों को भी परिभाषित किया जा सकता है, जो कि आश्चर्य के विरुद्ध आश्चर्य के रूप में परिभाषित किया गया है। बिट्स में यह साक्ष्य केवल अंतर अनुपात = p/(1-p) = 2ebits से संबंधित है, और इसमें स्वयं-जानकारी के समान लाभ हैं।
संयोग के खेलों में अनुप्रयोग
सूचना सिद्धांत को जानकारी को परिमाणित करने के एक तरीके के रूप में सोचा जा सकता है ताकि अपूर्ण जानकारी के सामने सर्वोत्तम निर्णय लिया जा सके। यानी, आपके पास उपलब्ध जानकारी का उपयोग करके सर्वोत्तम निर्णय कैसे लिया जाए। शर्त का उद्देश्य किसी अनिश्चित खेल/दौड़/मैच के सभी प्रासंगिक चरों का तर्कसंगत रूप से आकलन करना है, फिर उनकी तुलना बुकमेकर के आकलन से करना है, जो सामान्यतः ऑड्स या स्प्रेड के रूप में आता है और यदि आकलन पर्याप्त रूप से भिन्न हो तो उचित दांव लगाएं।[5] गैंबलिंग के जिस क्षेत्र में इसका सबसे अधिक उपयोग होता है वह खेल शर्त है। आंकड़ों की उपलब्धता के कारण खेल बाधाएं सूचना सिद्धांत को बहुत अच्छी तरह से उधार देती हैं। कई वर्षों से जाने-माने अर्थशास्त्रियों ने खेल को अपनी प्रयोगशाला के रूप में उपयोग करके विभिन्न गणितीय सिद्धांतों का परीक्षण किया है, जिसके परिणाम बहुत अलग-अलग रहे हैं।
खेलों में शर्त के संबंध में एक सिद्धांत यह है कि यह एक यादृच्छिक चाल है। रैंडम वॉक एक ऐसा परिदृश्य है जहां नई जानकारी, कीमतें और रिटर्न में संयोग से उतार-चढ़ाव होगा, यह कुशल-बाजार परिकल्पना का हिस्सा है। कुशल बाज़ार परिकल्पना की अंतर्निहित धारणा यह है कि बाज़ार हमेशा किसी भी नई जानकारी के लिए समायोजन करेगा। इसलिए कोई भी बाजार को हरा नहीं सकता क्योंकि वे उसी जानकारी पर कारोबार कर रहे हैं जिससे बाजार समायोजित हुआ है। हालाँकि, फामा के अनुसार,[6] एक कुशल बाज़ार के लिए तीन गुणों को पूरा करने की आवश्यकता है:
- प्रतिभूतियों के व्यापार में कोई लेनदेन लागत नहीं होती है
- सभी उपलब्ध जानकारी सभी बाज़ार सहभागियों के लिए निःशुल्क उपलब्ध है
- प्रत्येक सुरक्षा की वर्तमान कीमत और भविष्य की कीमतों के वितरण के लिए वर्तमान जानकारी के निहितार्थ पर सभी सहमत हैं
सांख्यिकीविदों ने दिखाया है कि यह तीसरी शर्त है जो खेल विकलांगता में सूचना सिद्धांत को उपयोगी बनाने की अनुमति देती है। जब हर कोई इस बात पर सहमत नहीं होता कि जानकारी घटना के परिणाम को कैसे प्रभावित करेगी, तो हमें अलग-अलग सम्मति मिलती है।
यह भी देखें
- उदासीनता का सिद्धान्त
- सांख्यिकीय संघ फुटबॉल भविष्यवाणियाँ
- उन्नत एनएफ़एल आँकड़े
संदर्भ
- ↑ Jaynes, E.T. (1998/2003) Probability Theory: The Logic of Science (Cambridge U. Press, New York).
- ↑ Kelly, J. L. (1956). "सूचना दर की एक नई व्याख्या" (PDF). Bell System Technical Journal. 35 (4): 917–926. doi:10.1002/j.1538-7305.1956.tb03809.x.
- ↑ Thomas M. Cover, Joy A. Thomas. Elements of information theory, 1st Edition. New York: Wiley-Interscience, 1991. ISBN 0-471-06259-6, Chapter 6.
- ↑ Tribus, Myron (1961) Thermodynamics and Thermostatics: An Introduction to Energy, Information and States of Matter, with Engineering Applications (D. Van Nostrand Company Inc., 24 West 40 Street, New York 18, New York, U.S.A) ASIN: B000ARSH5S.
- ↑ Hansen, Kristen Brinch. (2006) Sports Betting from a Behavioral Finance Point of View (Arhus School of Business).
- ↑ Fama, E.F. (1970) "Efficient Capital Markets: A Review of Theory and Independent Work", Journal of Financial Economics Volume 25, 383-417