बोसोनिक स्ट्रिंग सिद्धांत: Difference between revisions

Latest revision as of 09:17, 12 December 2023

बोसोनिक स्ट्रिंग सिद्धांत, स्ट्रिंग सिद्धांत का मूल वर्ज़न है, जिसे 1960 के दशक के अंत में विकसित किया गया और इसका नाम सत्येन्द्र नाथ बोस के नाम पर रखा गया था। इसे ऐसा इसलिए कहा जाता है क्योंकि इसके स्पेक्ट्रम में केवल बोसॉन होते हैं।

1980 के दशक में, स्ट्रिंग सिद्धांत के संदर्भ में सुपरसिमेट्री का अविष्कार किया गया, और स्ट्रिंग सिद्धांत का नया वर्ज़न जिसे सुपरस्ट्रिंग सिद्धांत (सुपरसिमेट्रिक स्ट्रिंग सिद्धांत) कहा जाता है, वास्तविक फोकस बन गया। फिर भी, बोसोनिक स्ट्रिंग सिद्धांत पर्टर्बेटिव स्ट्रिंग सिद्धांत की अनेक सामान्य विशेषताओं को समझने के लिए अत्यधिक उपयोगी मॉडल बना हुआ है, और सुपरस्ट्रिंग्स की अनेक सैद्धांतिक कठिनाइयाँ वास्तव में बोसोनिक स्ट्रिंग्स के संदर्भ में पूर्व में ही प्राप्त की जा सकती हैं।

समस्याएँ

चूँकि बोसोनिक स्ट्रिंग सिद्धांत में अनेक आकर्षक विशेषताएं हैं, यह दो महत्वपूर्ण क्षेत्रों में व्यवहार्य भौतिक मॉडल के रूप में कम है।

सर्वप्रथम, यह केवल बोसॉन के अस्तित्व की भविष्यवाणी करता है जबकि कई भौतिक कण फ़र्मिअन हैं।

दूसरा, यह काल्पनिक संख्या द्रव्यमान के साथ स्ट्रिंग के मोड के अस्तित्व की भविष्यवाणी करता है, जिसका अर्थ है कि सिद्धांत में टैचियन संक्षेपण नामक प्रक्रिया में अस्थिरता है।

इसके अतिरिक्त, सामान्य स्पेसटाइम आयाम में बोसोनिक स्ट्रिंग सिद्धांत अनुरूप विसंगति के कारण विसंगतियों को प्रदर्शित करता है। किन्तु, जैसा कि सर्वप्रथम क्लाउड लवलेस ने देखा था,^[1] 26 आयामों (स्पेस के 25 आयाम और समय का एक आयाम) के स्पेसटाइम में, सिद्धांत के लिए महत्वपूर्ण आयाम, विसंगति समाप्त हो जाती है। यह उच्च आयामीता आवश्यक रूप से स्ट्रिंग सिद्धांत के लिए समस्या नहीं है, क्योंकि इसे इस प्रकार से प्रस्तुत किया जा सकता है कि 22 अतिरिक्त आयामों के साथ स्पेसटाइम को छोटे टोरस या अन्य कॉम्पैक्ट मैनिफोल्ड बनाने के लिए फोल्ड कर दिया जाता है। इससे कम ऊर्जा प्रयोगों के लिए स्पेसटाइम के केवल परिचित चार आयाम ही दिखाई देंगे। महत्वपूर्ण आयाम का अस्तित्व जहां विसंगति समाप्त हो जाती है, सभी स्ट्रिंग सिद्धांतों की सामान्य विशेषता है।

बोसोनिक स्ट्रिंग के प्रकार

चार संभावित बोसोनिक स्ट्रिंग सिद्धांत हैं, जो इस पर निर्भर करता है कि ओपन स्ट्रिंग की अनुमति है या नहीं और क्या स्ट्रिंग में निर्दिष्ट अभिविन्यास है। याद रखें कि ओपन स्ट्रिंग के सिद्धांत में क्लोज्ड स्ट्रिंग भी सम्मिलित होनी चाहिए; ओपन स्ट्रिंग के विषय में अध्ययन किया जा सकता है कि उनके समापन बिंदु D25-ब्रेन पर निश्चित किए गए हैं जो सभी स्पेसटाइम को भरते हैं। स्ट्रिंग के विशिष्ट अभिविन्यास का अर्थ है कि केवल ओरिएंटेबिलिटी वर्ल्डशीट के अनुरूप इंटरैक्शन की अनुमति है (उदाहरण के लिए, दो स्ट्रिंग केवल समान अभिविन्यास के साथ विलय कर सकते हैं)। चार संभावित सिद्धांतों के स्पेक्ट्रा का रेखाचित्र इस प्रकार है:

बोसोनिक स्ट्रिंग सिद्धांत	गैर-सकारात्मक $M^{2}$ अवस्था
ओपन एंड क्लोज्ड, ओरिएंटेड	टैचियन, ग्रेविटॉन, डिलेटन, द्रव्यमान रहित एंटीसिमेट्रिक टेंसर
ओपन एंड क्लोज्ड, अनओरिएंटेड	टैचियन, ग्रेविटॉन, डिलेटन
क्लोज्ड, ओरिएंटेड	टैचियन, ग्रेविटॉन, डिलेटन, एंटीसिमेट्रिक टेंसर, U(1) वेक्टर बोसोन
क्लोज्ड, अनओरिएंटेड	टैचियन, ग्रेविटॉन, डिलेटन

ध्यान दें कि सभी चार सिद्धांतों में एक ऋणात्मक ऊर्जा टैचियन ( $M^{2}=-{\frac {1}{\alpha '}}$ ) है और एक द्रव्यमान रहित गुरुत्वाकर्षण है।

इस लेख का शेष भाग सीमाहीन, ओरिएंटेबल वर्डशीट के अनुरूप क्लोज्ड, ओरिएंटेड सिद्धांत पर प्रस्तावित होता है।

गणित

पाथ इंटेग्रल परटूरबेशन थ्योरी

कहा जा सकता है कि^[2] बोसोनिक स्ट्रिंग सिद्धांत को पॉलाकोव क्रिया के पाथ इंटेग्रल परिमाणीकरण द्वारा परिभाषित किया जा सकता है:

I_{0}[g,X]={\frac {T}{8\pi }}\int _{M}d^{2}\xi {\sqrt {g}}g^{mn}\partial _{m}x^{\mu }\partial _{n}x^{\nu }G_{\mu \nu }(x)

$x^{\mu }(\xi )$ वर्ल्डशीट पर वह क्षेत्र है जो 25+1 स्पेसटाइम में स्ट्रिंग के एम्बेडिंग का वर्णन करता है; पॉलाकोव सूत्रीकरण में, $g$ इसे एम्बेडिंग से प्रेरित मीट्रिक के रूप में नहीं, यद्यपि स्वतंत्र गतिशील क्षेत्र के रूप में समझा जाना चाहिए। $G$ लक्ष्य स्पेसटाइम पर मीट्रिक है, जिसे सामान्यतः पर्टर्बेटिव सिद्धांत में मिन्कोवस्की मीट्रिक माना जाता है। विक रोटेशन के अनुसार, इसे यूक्लिडियन मीट्रिक $G_{\mu \nu }=\delta _{\mu \nu }$ के रूप में प्राप्त किया जाता है। M टोपोलॉजिकल मैनिफ़ोल्ड पैरामीट्रिज्ड के रूप में वर्ल्डशीट $\xi$ निर्देशांक है। $T$ स्ट्रिंग टेंशन है और रेगे स्लोप $T={\frac {1}{2\pi \alpha '}}$ से संबंधित है।

$I_{0}$ इसमें डिफोमॉर्फिज्म और वेइल इनवेरिएंस है। वेइल समरूपता परिमाणीकरण (अनुरूप विसंगति) पर विभाजित हो जाती है और इसलिए इस क्रिया को काउंटरटर्म के साथ पूरक किया जाना चाहिए, साथ ही काल्पनिक विशुद्ध रूप से टोपोलॉजिकल पद, यूलर विशेषता के आनुपातिक होता है:

I=I_{0}+\lambda \chi (M)+\mu _{0}^{2}\int _{M}d^{2}\xi {\sqrt {g}}

काउंटरटर्म द्वारा वेइल इनवेरिएंस को स्पष्ट रूप से विभाजित करने पर महत्वपूर्ण आयाम 26 में समाप्त किया जा सकता है।

फिर भौतिक राशियों का निर्माण (यूक्लिडियन) विभाजन फ़ंक्शन N-पॉइंट फ़ंक्शन से किया जाता है:

Z=\sum _{h=0}^{\infty }\int {\frac {{\mathcal {D}}g_{mn}{\mathcal {D}}X^{\mu }}{\mathcal {N}}}\exp(-I[g,X])

\left\langle V_{i_{1}}(k_{1}^{\mu })\cdots V_{i_{p}}(k_{p}^{\mu })\right\rangle =\sum _{h=0}^{\infty }\int {\frac {{\mathcal {D}}g_{mn}{\mathcal {D}}X^{\mu }}{\mathcal {N}}}\exp(-I[g,X])V_{i_{1}}(k_{1}^{\mu })\cdots V_{i_{p}}(k_{p}^{\mu })

परटूरबेटिव श्रृंखला को जीनस द्वारा अनुक्रमित टोपोलॉजी के योग के रूप में व्यक्त किया जाता है।

असतत योग संभावित टोपोलॉजी पर योग है, जो यूक्लिडियन बोसोनिक ओरिएंटेबल क्लोज्ड स्ट्रिंग्स के लिए कॉम्पैक्ट ओरिएंटेबल रीमैनियन सतह हैं और इस प्रकार $h$ जीनस द्वारा पहचाने जाते हैं। सामान्यीकरण कारक ${\mathcal {N}}$ समरूपता से ओवरकाउंटिंग की क्षतिपूर्ति के लिए प्रस्तुत किया गया है। जबकि विभाजन फ़ंक्शन की गणना ब्रह्माण्ड संबंधी स्थिरांक से युग्मित होती है, जिसमें N-पॉइंट फ़ंक्शन भी सम्मिलित है $p$ वर्टेक्स ऑपरेटर्स, स्ट्रिंग्स के प्रकीर्णन आयाम का वर्णन करता है।

क्रिया का समरूपता समूह वास्तव में एकीकरण स्थान को सीमित आयामी मैनिफ़ोल्ड तक कम कर देता है। विभाजन फ़ंक्शन में $g$ पाथ इंटेग्रल, संभावित रीमैनियन संरचनाओं पर प्राथमिक योग है; चूँकि, वेइल ट्रांसफ़ॉर्मेशन के संबंध में उद्धरण हमें केवल अनुरूप संरचनाओं अर्थात, संबंधित आव्यूह की पहचान के अनुसार आव्यूह के समतुल्य वर्ग पर विचार करने की अनुमति देता है,

g'(\xi )=e^{\sigma (\xi )}g(\xi )

चूँकि वर्ड-शीट द्वि-आयामी है, अनुरूप संरचनाओं और जटिल संरचनाओं के मध्य 1-1 समानता है। अभी भी डिफोमॉर्फिज्म को दूर करना होगा। यह हमें सभी संभावित जटिल संरचनाओं मॉड्यूलो डिफोमॉर्फिज्म के स्थान पर एकीकरण के साथ त्याग देता है, जो कि दी गई टोपोलॉजिकल सतह का केवल मॉड्यूलि स्पेस है, और वास्तव में परिमित-आयामी जटिल मैनिफोल्ड है। इसलिए पर्टर्बेटिव बोसोनिक स्ट्रिंग्स की मूल समस्या मॉड्यूलि स्पेस का पैरामीट्रिजेशन बन जाती है, जो जीनस के लिए अशून्य $h\geq 4$ है।

h = 0

ट्री-लेवल पर, जीनस 0 के अनुरूप, ब्रह्माण्ड संबंधी स्थिरांक लुप्त हो जाता है: $Z_{0}=0$ .

चार टैच्योन के प्रकीर्णन के लिए चार-बिंदु कार्य शापिरो-विरासोरो आयाम है:

A_{4}\propto (2\pi )^{26}\delta ^{26}(k){\frac {\Gamma (-1-s/2)\Gamma (-1-t/2)\Gamma (-1-u/2)}{\Gamma (2+s/2)\Gamma (2+t/2)\Gamma (2+u/2)}}

जहाँ $k$ कुल संवेग है और $s$ , $t$ , $u$ मैंडेलस्टैम चर हैं।

h = 1

Fundamental domain for the modular group.

छायांकित क्षेत्र मॉड्यूलर समूह के लिए संभावित मौलिक डोमेन है।

जीनस 1 टोरस है, और वन-लूप स्तर से युग्मित होता है। विभाजन फलन की मात्रा इस प्रकार है:

Z_{1}=\int _{{\mathcal {M}}_{1}}{\frac {d^{2}\tau }{8\pi ^{2}\tau _{2}^{2}}}{\frac {1}{(4\pi ^{2}\tau _{2})^{12}}}\left|\eta (\tau )\right|^{-48}

$\tau$ सकारात्मक काल्पनिक भाग वाली सम्मिश्र संख्या $\tau _{2}$ ; ${\mathcal {M}}_{1}$ है, टोरस के मॉड्यूलि स्पेस के लिए होलोमोर्फिक, मॉड्यूलर समूह के लिए कोई मौलिक डोमेन $PSL(2,\mathbb {Z} )$ है, उदाहरण के लिए, $\left\{\tau _{2}>0,|\tau |^{2}>1,-{\frac {1}{2}}<\tau _{1}<{\frac {1}{2}}\right\}$ ऊपरी अर्ध तल पर कार्य करता है, $\eta (\tau )$ डेडेकाइंड ईटा फ़ंक्शन है। इंटीग्रैंड निश्चित रूप से मॉड्यूलर समूह के अनुसार अपरिवर्तनीय है: माप ${\frac {d^{2}\tau }{\tau _{2}^{2}}}$ बस पोंकारे मीट्रिक है जिसमें आइसोमेट्री समूह के रूप में PSL(2,R) है; शेष एकीकरण $\tau _{2}\rightarrow |c\tau +d|^{2}\tau _{2}$ भी गुण से अपरिवर्तनीय है और तथ्य यह है कि $\eta (\tau )$ भार 1/2 का मॉड्यूलर रूप है।

यह इंटेग्रल विचलन करता है। यह टैचियन की उपस्थिति के कारण है और पर्टर्बेटिव वैक्यूम की अस्थिरता से संबंधित है।

यह भी देखें

नंबू-गोटो क्रिया
पोल्याकोव क्रिया

संदर्भ

D'Hoker, Eric & Phong, D. H. (Oct 1988). "The geometry of string perturbation theory". Rev. Mod. Phys. American Physical Society. 60 (4): 917–1065. Bibcode:1988RvMP...60..917D. doi:10.1103/RevModPhys.60.917.

Belavin, A.A. & Knizhnik, V.G. (Feb 1986). "Complex geometry and the theory of quantum strings". ZhETF. 91 (2): 364–390. Bibcode:1986ZhETF..91..364B. Archived from the original on 2021-02-26. Retrieved 2015-04-24.

[PR-1] Lovelace, Claud (1971), "Pomeron form factors and dual Regge cuts", Physics Letters, B34 (6): 500–506, Bibcode:1971PhLB...34..500L, doi:10.1016/0370-2693(71)90665-4.

[2] D'Hoker, Phong

[1]

[2]

@@ Line 1: / Line 1: @@
-{{String theory|cTopic=Theory}}
+'''बोसोनिक [[स्ट्रिंग सिद्धांत]],''' स्ट्रिंग सिद्धांत का मूल वर्ज़न है, जिसे 1960 के दशक के अंत में विकसित किया गया और इसका नाम [[सत्येन्द्र नाथ बोस]] के नाम पर रखा गया था। इसे ऐसा इसलिए कहा जाता है क्योंकि इसके स्पेक्ट्रम में केवल [[बोसॉन]] होते हैं।
-बोसोनिक [[स्ट्रिंग सिद्धांत]], स्ट्रिंग सिद्धांत का मूल संस्करण है, जिसे 1960 के दशक के अंत में विकसित किया गया और इसका नाम [[सत्येन्द्र नाथ बोस]] के नाम पर रखा गया। इसे ऐसा इसलिए कहा जाता है क्योंकि इसके स्पेक्ट्रम में केवल [[बोसॉन]] होते हैं।
-के दशक में, स्ट्रिंग सिद्धांत के संदर्भ में [[अतिसममिति]] की खोज की गई, और स्ट्रिंग सिद्धांत का एक नया संस्करण जिसे [[सुपरस्ट्रिंग सिद्धांत]] (सुपरसिमेट्रिक स्ट्रिंग सिद्धांत) कहा जाता है, वास्तविक फोकस बन गया। फिर भी, बोसोनिक स्ट्रिंग सिद्धांत [[ विक्षुब्ध ]] स्ट्रिंग सिद्धांत की कई सामान्य विशेषताओं को समझने के लिए एक बहुत ही उपयोगी मॉडल बना हुआ है, और सुपरस्ट्रिंग्स की कई सैद्धांतिक कठिनाइयाँ वास्तव में बोसोनिक स्ट्रिंग्स के संदर्भ में पहले से ही पाई जा सकती हैं।
+के दशक में, स्ट्रिंग सिद्धांत के संदर्भ में [[अतिसममिति|सुपरसिमेट्री]] का अविष्कार किया गया, और स्ट्रिंग सिद्धांत का नया वर्ज़न जिसे [[सुपरस्ट्रिंग सिद्धांत]] (सुपरसिमेट्रिक स्ट्रिंग सिद्धांत) कहा जाता है, वास्तविक फोकस बन गया। फिर भी, बोसोनिक स्ट्रिंग सिद्धांत[[ विक्षुब्ध | पर्टर्बेटिव]] स्ट्रिंग सिद्धांत की अनेक सामान्य विशेषताओं को समझने के लिए अत्यधिक उपयोगी मॉडल बना हुआ है, और सुपरस्ट्रिंग्स की अनेक सैद्धांतिक कठिनाइयाँ वास्तव में बोसोनिक स्ट्रिंग्स के संदर्भ में पूर्व में ही प्राप्त की जा सकती हैं।
 == समस्याएँ ==
-हालाँकि बोसोनिक स्ट्रिंग सिद्धांत में कई आकर्षक विशेषताएं हैं, यह दो महत्वपूर्ण क्षेत्रों में एक व्यवहार्य [[भौतिक मॉडल]] के रूप में कम है।
+चूँकि बोसोनिक स्ट्रिंग सिद्धांत में अनेक आकर्षक विशेषताएं हैं, यह दो महत्वपूर्ण क्षेत्रों में व्यवहार्य [[भौतिक मॉडल]] के रूप में कम है।
-सबसे पहले, यह केवल [[बोसॉन]] के अस्तित्व की भविष्यवाणी करता है जबकि कई भौतिक कण फ़र्मिअन हैं।
+सर्वप्रथम, यह केवल [[बोसॉन]] के अस्तित्व की भविष्यवाणी करता है जबकि कई भौतिक कण फ़र्मिअन हैं।
-दूसरा, यह [[काल्पनिक संख्या]] द्रव्यमान के साथ स्ट्रिंग के एक मोड के अस्तित्व की भविष्यवाणी करता है, जिसका अर्थ है कि सिद्धांत में टैचियन संक्षेपण नामक प्रक्रिया में अस्थिरता है।
+दूसरा, यह [[काल्पनिक संख्या]] द्रव्यमान के साथ स्ट्रिंग के मोड के अस्तित्व की भविष्यवाणी करता है, जिसका अर्थ है कि सिद्धांत में टैचियन संक्षेपण नामक प्रक्रिया में अस्थिरता है।
-इसके अलावा, सामान्य स्पेसटाइम आयाम में बोसोनिक स्ट्रिंग सिद्धांत [[अनुरूप विसंगति]] के कारण विसंगतियों को प्रदर्शित करता है। लेकिन, जैसा कि सबसे पहले [[क्लाउड लवलेस]] ने देखा था,<ref name="PR">{{citation|last=Lovelace|first=Claud|title=Pomeron form factors and dual Regge cuts|journal=Physics Letters|volume=B34|issue=6|year=1971|pages=500–506|bibcode=1971PhLB...34..500L|doi=10.1016/0370-2693(71)90665-4}}.</ref> 26 आयामों (अंतरिक्ष के 25 आयाम और समय का एक आयाम) के अंतरिक्ष समय में, सिद्धांत के लिए [[महत्वपूर्ण आयाम]], विसंगति रद्द हो जाती है। यह उच्च आयामीता आवश्यक रूप से स्ट्रिंग सिद्धांत के लिए एक समस्या नहीं है, क्योंकि इसे इस तरह से तैयार किया जा सकता है कि 22 अतिरिक्त आयामों के साथ स्पेसटाइम को एक छोटे [[ टोरस्र्स ]] या अन्य कॉम्पैक्ट मैनिफोल्ड बनाने के लिए मोड़ दिया जाता है। इससे कम ऊर्जा प्रयोगों के लिए स्पेसटाइम के केवल परिचित चार आयाम ही दिखाई देंगे। एक महत्वपूर्ण आयाम का अस्तित्व जहां विसंगति रद्द हो जाती है, सभी स्ट्रिंग सिद्धांतों की एक सामान्य विशेषता है।
+इसके अतिरिक्त, सामान्य स्पेसटाइम आयाम में बोसोनिक स्ट्रिंग सिद्धांत [[अनुरूप विसंगति]] के कारण विसंगतियों को प्रदर्शित करता है। किन्तु, जैसा कि सर्वप्रथम [[क्लाउड लवलेस]] ने देखा था,<ref name="PR">{{citation|last=Lovelace|first=Claud|title=Pomeron form factors and dual Regge cuts|journal=Physics Letters|volume=B34|issue=6|year=1971|pages=500–506|bibcode=1971PhLB...34..500L|doi=10.1016/0370-2693(71)90665-4}}.</ref> 26 आयामों (स्पेस के 25 आयाम और समय का एक आयाम) के स्पेसटाइम में, सिद्धांत के लिए [[महत्वपूर्ण आयाम]], विसंगति समाप्त हो जाती है। यह उच्च आयामीता आवश्यक रूप से स्ट्रिंग सिद्धांत के लिए समस्या नहीं है, क्योंकि इसे इस प्रकार से प्रस्तुत किया जा सकता है कि 22 अतिरिक्त आयामों के साथ स्पेसटाइम को छोटे[[ टोरस्र्स | टोरस]] या अन्य कॉम्पैक्ट मैनिफोल्ड बनाने के लिए फोल्ड कर दिया जाता है। इससे कम ऊर्जा प्रयोगों के लिए स्पेसटाइम के केवल परिचित चार आयाम ही दिखाई देंगे। महत्वपूर्ण आयाम का अस्तित्व जहां विसंगति समाप्त हो जाती है, सभी स्ट्रिंग सिद्धांतों की सामान्य विशेषता है।
-== बोसोनिक तारों के प्रकार ==
+== बोसोनिक स्ट्रिंग के प्रकार ==
-चार संभावित बोसोनिक स्ट्रिंग सिद्धांत हैं, जो इस बात पर निर्भर करता है कि क्या स्ट्रिंग (भौतिकी) # बंद और खुले स्ट्रिंग की अनुमति है और क्या स्ट्रिंग में एक निर्दिष्ट [[ उन्मुखता ]] है # अलग-अलग मैनिफोल्ड्स की ओरिएंटेबिलिटी। याद रखें कि खुली स्ट्रिंग के सिद्धांत में बंद स्ट्रिंग भी शामिल होनी चाहिए; खुले तारों को [[ डी-brane ]]|डी25-ब्रेन पर तय किए गए उनके समापन बिंदु के रूप में सोचा जा सकता है जो पूरे स्पेसटाइम को भरता है। स्ट्रिंग के एक विशिष्ट अभिविन्यास का मतलब है कि केवल ओरिएंटेबिलिटी [[वर्ल्डशीट]] के अनुरूप इंटरैक्शन की अनुमति है (उदाहरण के लिए, दो स्ट्रिंग केवल समान अभिविन्यास के साथ विलय कर सकते हैं)। चार संभावित सिद्धांतों के स्पेक्ट्रा का एक रेखाचित्र इस प्रकार है:
+चार संभावित बोसोनिक स्ट्रिंग सिद्धांत हैं, जो इस पर निर्भर करता है कि ओपन स्ट्रिंग की अनुमति है या नहीं और क्या स्ट्रिंग में निर्दिष्ट[[ उन्मुखता | अभिविन्यास]] है। याद रखें कि ओपन स्ट्रिंग के सिद्धांत में क्लोज्ड स्ट्रिंग भी सम्मिलित होनी चाहिए; ओपन स्ट्रिंग के विषय में अध्ययन किया जा सकता है कि उनके समापन बिंदु [[ डी-brane |D25-ब्रेन]] पर निश्चित किए गए हैं जो सभी स्पेसटाइम को भरते हैं। स्ट्रिंग के विशिष्ट अभिविन्यास का अर्थ है कि केवल ओरिएंटेबिलिटी [[वर्ल्डशीट]] के अनुरूप इंटरैक्शन की अनुमति है (उदाहरण के लिए, दो स्ट्रिंग केवल समान अभिविन्यास के साथ विलय कर सकते हैं)। चार संभावित सिद्धांतों के स्पेक्ट्रा का रेखाचित्र इस प्रकार है:
 {| class="wikitable"
 |-
-! Bosonic string theory || Non-positive <math>M^2</math> states
+! बोसोनिक स्ट्रिंग सिद्धांत || गैर-सकारात्मक <math>M^2</math> अवस्था
 |-
-| Open and closed, oriented || tachyon, [[graviton]], [[dilaton]], massless antisymmetric tensor
+| ओपन एंड क्लोज्ड, ओरिएंटेड || टैचियन, [[graviton|ग्रेविटॉन]], [[dilaton|डिलेटन]], द्रव्यमान रहित एंटीसिमेट्रिक टेंसर
 |-
-| Open and closed, unoriented || tachyon, graviton, dilaton
+| ओपन एंड क्लोज्ड, अनओरिएंटेड || टैचियन, ग्रेविटॉन, डिलेटन
 |-
-| Closed, oriented || tachyon, graviton, dilaton, antisymmetric tensor, [[U(1)]] [[vector boson]]
+| क्लोज्ड, ओरिएंटेड || टैचियन, ग्रेविटॉन, डिलेटन, एंटीसिमेट्रिक टेंसर, [[U(1)]] [[vector boson|वेक्टर बोसोन]]
 |-
-| Closed, unoriented || tachyon, graviton, dilaton
+| क्लोज्ड, अनओरिएंटेड || टैचियन, ग्रेविटॉन, डिलेटन
 |}
-ध्यान दें कि सभी चार सिद्धांतों में एक नकारात्मक ऊर्जा टैचियन है (<math>M^2 = - \frac{1}{\alpha'}</math>) और एक द्रव्यमान रहित गुरुत्वाकर्षण।
+ध्यान दें कि सभी चार सिद्धांतों में एक ऋणात्मक ऊर्जा टैचियन (<math>M^2 = - \frac{1}{\alpha'}</math>) है और एक द्रव्यमान रहित गुरुत्वाकर्षण है।
-इस लेख का शेष भाग सीमाहीन, उन्मुख विश्वपत्रकों के अनुरूप, बंद, उन्मुख सिद्धांत पर लागू होता है।
+इस लेख का शेष भाग सीमाहीन, ओरिएंटेबल वर्डशीट के अनुरूप क्लोज्ड, ओरिएंटेड सिद्धांत पर प्रस्तावित होता है।
 == गणित ==
-=== पथ अभिन्न गड़बड़ी सिद्धांत ===
+=== पाथ इंटेग्रल परटूरबेशन थ्योरी ===
-बोसोनिक स्ट्रिंग सिद्धांत कहा जा सकता है<ref>D'Hoker, Phong</ref> [[पॉलाकोव कार्रवाई]] के [[पथ अभिन्न सूत्रीकरण]] द्वारा परिभाषित किया जाना है:
+कहा जा सकता है कि<ref>D'Hoker, Phong</ref> बोसोनिक स्ट्रिंग सिद्धांत को [[पॉलाकोव कार्रवाई|पॉलाकोव क्रिया]] के [[पथ अभिन्न सूत्रीकरण|पाथ इंटेग्रल परिमाणीकरण]] द्वारा परिभाषित किया जा सकता है:
 : <math> I_0[g,X] = \frac{T}{8\pi} \int_M d^2 \xi \sqrt{g} g^{mn} \partial_m x^\mu \partial_n x^\nu G_{\mu\nu}(x) </math>
-<math>x^\mu(\xi)</math> वर्ल्डशीट पर वह फ़ील्ड है जो 25+1 स्पेसटाइम में स्ट्रिंग के एम्बेडिंग का वर्णन करता है; पॉलाकोव सूत्रीकरण में, <math>g</math> इसे एम्बेडिंग से प्रेरित मीट्रिक के रूप में नहीं, बल्कि एक स्वतंत्र गतिशील क्षेत्र के रूप में समझा जाना चाहिए। <math>G</math> लक्ष्य स्पेसटाइम पर मीट्रिक है, जिसे आमतौर पर पर्टर्बेटिव सिद्धांत में [[मिन्कोवस्की मीट्रिक]] माना जाता है। [[ बाती घुमाना ]] के तहत, इसे यूक्लिडियन मीट्रिक में लाया जाता है <math>G_{\mu\nu} = \delta_{\mu\nu}</math>. एम एक [[ टोपोलॉजिकल मैनिफ़ोल्ड ]] पैरामीट्रिज्ड के रूप में वर्ल्डशीट है <math>\xi</math> निर्देशांक <math>T</math> स्ट्रिंग तनाव है और रेगे ढलान से संबंधित है <math>T = \frac{1}{2\pi\alpha'}</math>.
+<math>x^\mu(\xi)</math> वर्ल्डशीट पर वह क्षेत्र है जो 25+1 स्पेसटाइम में स्ट्रिंग के एम्बेडिंग का वर्णन करता है; पॉलाकोव सूत्रीकरण में, <math>g</math> इसे एम्बेडिंग से प्रेरित मीट्रिक के रूप में नहीं, यद्यपि स्वतंत्र गतिशील क्षेत्र के रूप में समझा जाना चाहिए। <math>G</math> लक्ष्य स्पेसटाइम पर मीट्रिक है, जिसे सामान्यतः पर्टर्बेटिव सिद्धांत में [[मिन्कोवस्की मीट्रिक]] माना जाता है। [[ बाती घुमाना |विक रोटेशन]] के अनुसार, इसे यूक्लिडियन मीट्रिक  <math>G_{\mu\nu} = \delta_{\mu\nu}</math> के रूप में प्राप्त किया जाता है। M[[ टोपोलॉजिकल मैनिफ़ोल्ड |  टोपोलॉजिकल मैनिफ़ोल्ड]] पैरामीट्रिज्ड के रूप में वर्ल्डशीट <math>\xi</math> निर्देशांक है। <math>T</math> स्ट्रिंग टेंशन है और रेगे स्लोप <math>T = \frac{1}{2\pi\alpha'}</math> से संबंधित है।
-<math>I_0</math> इसमें [[डिफोमॉर्फिज्म इनवेरिएंस]] और [[वेइल परिवर्तन]] है। वेइल समरूपता परिमाणीकरण (अनुरूप विसंगति) पर टूट जाती है और इसलिए इस क्रिया को एक काउंटरटर्म के साथ पूरक किया जाना चाहिए, साथ ही एक काल्पनिक विशुद्ध रूप से टोपोलॉजिकल शब्द, [[यूलर विशेषता]] के आनुपातिक:
+<math>I_0</math> इसमें [[डिफोमॉर्फिज्म इनवेरिएंस|डिफोमॉर्फिज्म]] और [[वेइल परिवर्तन|वेइल इनवेरिएंस]] है। वेइल समरूपता परिमाणीकरण (अनुरूप विसंगति) पर विभाजित हो जाती है और इसलिए इस क्रिया को काउंटरटर्म के साथ पूरक किया जाना चाहिए, साथ ही काल्पनिक विशुद्ध रूप से टोपोलॉजिकल पद, [[यूलर विशेषता]] के आनुपातिक होता है:
 : <math> I = I_0 + \lambda \chi(M) + \mu_0^2 \int_M d^2\xi \sqrt{g} </math>
-काउंटरटर्म द्वारा वेइल इनवेरिएंस को स्पष्ट रूप से तोड़ने को महत्वपूर्ण आयाम 26 में रद्द किया जा सकता है।
+काउंटरटर्म द्वारा वेइल इनवेरिएंस को स्पष्ट रूप से विभाजित करने पर महत्वपूर्ण आयाम 26 में समाप्त किया जा सकता है।
-फिर भौतिक मात्राओं का निर्माण (यूक्लिडियन) विभाजन फ़ंक्शन (क्वांटम फ़ील्ड सिद्धांत) और सहसंबंध फ़ंक्शन (क्वांटम फ़ील्ड सिद्धांत) | एन-पॉइंट फ़ंक्शन से किया जाता है:
+फिर भौतिक राशियों का निर्माण (यूक्लिडियन) विभाजन फ़ंक्शन N-पॉइंट फ़ंक्शन से किया जाता है:
 : <math> Z = \sum_{h=0}^\infty \int \frac{\mathcal{D}g_{mn} \mathcal{D}X^\mu}{\mathcal{N}} \exp ( - I[g,X] ) </math>
 : <math> \left\langle V_{i_1} (k^\mu_1) \cdots V_{i_p}(k_p^\mu) \right\rangle = \sum_{h=0}^\infty \int \frac{\mathcal{D}g_{mn} \mathcal{D}X^\mu}{\mathcal{N}} \exp ( - I[g,X] ) V_{i_1} (k_1^\mu) \cdots V_{i_p} (k^\mu_p) </math>
-[[File:Sum over genera.png|thumb|right|परेशान करने वाली श्रृंखला को जीनस द्वारा अनुक्रमित टोपोलॉजी के योग के रूप में व्यक्त किया जाता है।]]असतत योग संभावित टोपोलॉजी पर एक योग है, जो यूक्लिडियन बोसोनिक ओरिएंटेबल बंद स्ट्रिंग्स के लिए कॉम्पैक्ट ओरिएंटेबल [[रीमैनियन मैनिफोल्ड]] हैं और इस प्रकार एक जीनस द्वारा पहचाने जाते हैं <math>h</math>. एक सामान्यीकरण कारक <math>\mathcal{N}</math> समरूपता से ओवरकाउंटिंग की भरपाई के लिए पेश किया गया है। जबकि विभाजन फ़ंक्शन की गणना [[ब्रह्माण्ड संबंधी स्थिरांक]] से मेल खाती है, जिसमें एन-पॉइंट फ़ंक्शन भी शामिल है <math>p</math> वर्टेक्स ऑपरेटर्स, स्ट्रिंग्स के प्रकीर्णन आयाम का वर्णन करता है।
+[[File:Sum over genera.png|thumb|right|परटूरबेटिव श्रृंखला को जीनस द्वारा अनुक्रमित टोपोलॉजी के योग के रूप में व्यक्त किया जाता है।]]असतत योग संभावित टोपोलॉजी पर योग है, जो यूक्लिडियन बोसोनिक ओरिएंटेबल क्लोज्ड स्ट्रिंग्स के लिए कॉम्पैक्ट ओरिएंटेबल [[रीमैनियन मैनिफोल्ड|रीमैनियन सतह]] हैं और इस प्रकार <math>h</math> जीनस द्वारा पहचाने जाते हैं। सामान्यीकरण कारक <math>\mathcal{N}</math> समरूपता से ओवरकाउंटिंग की क्षतिपूर्ति के लिए प्रस्तुत किया गया है। जबकि विभाजन फ़ंक्शन की गणना [[ब्रह्माण्ड संबंधी स्थिरांक]] से युग्मित होती है, जिसमें N-पॉइंट फ़ंक्शन भी सम्मिलित है <math>p</math> वर्टेक्स ऑपरेटर्स, स्ट्रिंग्स के प्रकीर्णन आयाम का वर्णन करता है।
-क्रिया का समरूपता समूह वास्तव में एकीकरण स्थान को एक सीमित आयामी कई गुना तक कम कर देता है। <math>g</math> h> विभाजन फ़ंक्शन में पथ-अभिन्न, संभावित रीमानियन संरचनाओं पर एक प्राथमिक योग है; हालाँकि, वेइल ट्रांसफ़ॉर्मेशन के संबंध में [[भागफल स्थान (टोपोलॉजी)]] हमें केवल [[अनुरूप संरचना]]ओं पर विचार करने की अनुमति देता है, अर्थात, संबंधित मेट्रिक्स की पहचान के तहत मेट्रिक्स के समतुल्य वर्ग
+क्रिया का समरूपता समूह वास्तव में एकीकरण स्थान को सीमित आयामी मैनिफ़ोल्ड तक कम कर देता है। विभाजन फ़ंक्शन में <math>g</math> पाथ इंटेग्रल, संभावित रीमैनियन संरचनाओं पर प्राथमिक योग है; चूँकि, वेइल ट्रांसफ़ॉर्मेशन के संबंध में [[भागफल स्थान (टोपोलॉजी)|उद्धरण]] हमें केवल [[अनुरूप संरचना|अनुरूप संरचनाओं]] अर्थात, संबंधित आव्यूह की पहचान के अनुसार आव्यूह के समतुल्य वर्ग पर विचार करने की अनुमति देता है,
 : <math> g'(\xi) = e^{\sigma(\xi)} g(\xi) </math>
-चूँकि विश्व-पत्र द्वि-आयामी है, अनुरूप संरचनाओं और जटिल मैनिफोल्ड के बीच 1-1 पत्राचार है। किसी को अभी भी भिन्नताओं को दूर करना होगा। यह हमें सभी संभावित जटिल संरचनाओं मॉड्यूलो डिफोमॉर्फिज्म के स्थान पर एकीकरण के साथ छोड़ देता है, जो कि दी गई टोपोलॉजिकल सतह का केवल मॉड्यूलि स्थान है, और वास्तव में एक परिमित-आयामी जटिल मैनिफोल्ड है। इसलिए पर्टर्बेटिव बोसोनिक स्ट्रिंग्स की मूल समस्या [[ मॉड्यूलि स्पेस ]] का पैरामीट्रिजेशन बन जाती है, जो जीनस के लिए गैर-तुच्छ है <math>h \geq 4</math>.
+चूँकि वर्ड-शीट द्वि-आयामी है, अनुरूप संरचनाओं और जटिल संरचनाओं के मध्य 1-1 समानता है। अभी भी डिफोमॉर्फिज्म को दूर करना होगा। यह हमें सभी संभावित जटिल संरचनाओं मॉड्यूलो डिफोमॉर्फिज्म के स्थान पर एकीकरण के साथ त्याग देता है, जो कि दी गई टोपोलॉजिकल सतह का केवल मॉड्यूलि स्पेस है, और वास्तव में परिमित-आयामी जटिल मैनिफोल्ड है। इसलिए पर्टर्बेटिव बोसोनिक स्ट्रिंग्स की मूल समस्या [[ मॉड्यूलि स्पेस |मॉड्यूलि स्पेस]] का पैरामीट्रिजेशन बन जाती है, जो जीनस के लिए अशून्य <math>h \geq 4</math> है।
-<!-- The single most important quantity in first quantized bosonic string theory is the N-point scattering amplitude. This treats the incoming and outgoing strings as points, which in string theory are [[tachyon]]s, with momentum ''k''<sub>''i''</sub> which connect to a string world surface at the surface points ''z''<sub>''i''</sub>. It is given by the following [[functional integral]] over all possible embeddings of this 2D surface in 26 dimensions:<ref>Polchinski, Joseph. ''String Theory: Volume I''. Cambridge University Press, p. 173.</ref>
+'''h = 0'''
-: <math> A_N = \int  D\mu \int  D[X] \exp \left( -\frac{1}{4\pi\alpha} \int \partial_z X_\mu(z,\overline{z}) \partial_{\overline{z}}  X^\mu(z,\overline{z}) \, dz^2 + i \sum_{i=1}^N  k_{i \mu} X^\mu (z_i,\overline{z}_i) \right) </math>
+ट्री-लेवल पर, जीनस 0 के अनुरूप, ब्रह्माण्ड संबंधी स्थिरांक लुप्त हो जाता है: <math> Z_0 = 0 </math>.
-The functional integral can be done because it is a Gaussian to become:
+चार टैच्योन के प्रकीर्णन के लिए चार-बिंदु कार्य शापिरो-विरासोरो आयाम है:
-: <math> A_N = \int  D\mu \prod_{0<i<j<N+1} |z_i-z_j|^{2\alpha k_i.k_j} </math>
-This is integrated over the various points ''z''<sub>''i''</sub>. Special care must be taken because two parts of this complex region may represent the same point on the 2D surface and you don't want to integrate over them twice. Also you need to make sure you are not integrating multiple times over different parameterizations of the surface. When this is taken into account it can be used to calculate the 4-point scattering amplitude (the 3-point amplitude is simply a delta function):
-: <math> A_4 = \frac{ \Gamma (-1+\frac12(k_1+k_2)^2) \Gamma (-1+\frac12(k_2+k_3)^2)  } { \Gamma (-2+\frac12((k_1+k_2)^2+(k_2+k_3)^2)) } </math>
-Which is a [[beta function]], known as [[Veneziano amplitude]]. It was this beta function which was apparently found before full string theory was developed. With superstrings the equations contain not only the 10D space-time coordinates X but also the Grassmann coordinates&nbsp;''&theta;''. Since there are various ways this can be done this leads to different string theories.
-When integrating over surfaces such as the torus, we end up with equations in terms of [[theta functions]] and elliptic functions such as the [[Dedekind eta function]]. This is smooth everywhere, which it has to be to make physical sense, only when raised to the 24th power. This is the origin of needing 26 dimensions of space-time for bosonic string theory. The extra two dimensions arise as degrees of freedom of the string surface. -->
-==== एच = 0 ====
-वृक्ष-स्तर पर, जीनस 0 के अनुरूप, ब्रह्माण्ड संबंधी स्थिरांक गायब हो जाता है: <math> Z_0 = 0 </math>.
-चार टैच्योन के बिखरने के लिए चार-बिंदु कार्य शापिरो-विरासोरो आयाम है:
 : <math> A_4 \propto (2\pi)^{26} \delta^{26}(k) \frac{\Gamma(-1-s/2) \Gamma(-1-t/2) \Gamma(-1-u/2)}{\Gamma(2+s/2) \Gamma(2+t/2) \Gamma(2+u/2)} </math>
-कहाँ <math>k</math> कुल गति है और <math>s</math>, <math>t</math>, <math>u</math> मैंडेलस्टैम चर हैं।
+जहाँ <math>k</math> कुल संवेग है और <math>s</math>, <math>t</math>, <math>u</math> मैंडेलस्टैम चर हैं।
-==== एच = 1 ====
+==== h = 1 ====
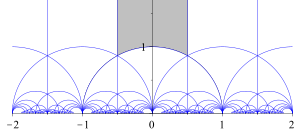
-[[File:ModularGroup-FundamentalDomain.svg|thumb|right|alt=Fundamental domain for the modular group.| छायांकित क्षेत्र मॉड्यूलर समूह के लिए एक संभावित मौलिक डोमेन है।]]जीनस 1 टोरस है, और वन-लूप फेनमैन आरेख|वन-लूप स्तर से मेल खाता है। विभाजन फ़ंक्शन की मात्रा इस प्रकार है:
+[[File:ModularGroup-FundamentalDomain.svg|thumb|right|alt=Fundamental domain for the modular group.| छायांकित क्षेत्र मॉड्यूलर समूह के लिए संभावित मौलिक डोमेन है।]]जीनस 1 टोरस है, और वन-लूप स्तर से युग्मित होता है। विभाजन फलन की मात्रा इस प्रकार है:
 : <math> Z_1 = \int_{\mathcal{M}_1} \frac{d^2 \tau}{8\pi^2 \tau_2^2} \frac{1}{(4\pi^2 \tau_2)^{12}} \left| \eta(\tau) \right| ^{-48} </math>
-<math>\tau</math> सकारात्मक काल्पनिक भाग वाली एक सम्मिश्र संख्या है <math>\tau_2</math>; <math>\mathcal{M}_1</math>, टोरस के मॉड्यूलि स्पेस के लिए होलोमोर्फिक, [[मॉड्यूलर समूह]] के लिए कोई [[मौलिक डोमेन]] है <math>PSL(2,\mathbb{Z})</math> उदाहरण के लिए, ऊपरी आधे तल पर कार्य करना <math> \left\{ \tau_2 > 0, |\tau|^2 > 1, -\frac{1}{2} < \tau_1 < \frac{1}{2}  \right\} </math>. <math>\eta(\tau)</math> [[डेडेकाइंड और फ़ंक्शन]] है। इंटीग्रैंड निश्चित रूप से मॉड्यूलर समूह के तहत अपरिवर्तनीय है: माप <math> \frac{d^2 \tau}{\tau_2^2} </math> बस पोंकारे मीट्रिक है जिसमें आइसोमेट्री समूह के रूप में SL2(R)|PSL(2,R) है; शेष एकीकरण भी गुण से अपरिवर्तनीय है <math>\tau_2 \rightarrow |c \tau + d|^2 \tau_2 </math> और तथ्य यह है कि <math>\eta(\tau)</math> वजन 1/2 का एक [[मॉड्यूलर रूप]] है।
+<math>\tau</math> सकारात्मक काल्पनिक भाग वाली सम्मिश्र संख्या <math>\tau_2</math>; <math>\mathcal{M}_1</math> है, टोरस के मॉड्यूलि स्पेस के लिए होलोमोर्फिक, [[मॉड्यूलर समूह]] के लिए कोई [[मौलिक डोमेन]] <math>PSL(2,\mathbb{Z})</math> है, उदाहरण के लिए, <math> \left\{ \tau_2 > 0, |\tau|^2 > 1, -\frac{1}{2} < \tau_1 < \frac{1}{2}  \right\} </math>ऊपरी अर्ध तल पर कार्य करता है, <math>\eta(\tau)</math> [[डेडेकाइंड और फ़ंक्शन|डेडेकाइंड ईटा फ़ंक्शन]] है। इंटीग्रैंड निश्चित रूप से मॉड्यूलर समूह के अनुसार अपरिवर्तनीय है: माप <math> \frac{d^2 \tau}{\tau_2^2} </math> बस पोंकारे मीट्रिक है जिसमें आइसोमेट्री समूह के रूप में PSL(2,R) है; शेष एकीकरण <math>\tau_2 \rightarrow |c \tau + d|^2 \tau_2 </math>  भी गुण से अपरिवर्तनीय है और तथ्य यह है कि <math>\eta(\tau)</math> भार 1/2 का [[मॉड्यूलर रूप]] है।
-यह अभिन्न विचलन करता है. यह टैचियन की उपस्थिति के कारण है और पर्टर्बेटिव वैक्यूम की अस्थिरता से संबंधित है।
+यह इंटेग्रल विचलन करता है। यह टैचियन की उपस्थिति के कारण है और पर्टर्बेटिव वैक्यूम की अस्थिरता से संबंधित है।
 ==यह भी देखें==
 *नंबू-गोटो क्रिया
-*पोल्याकोव कार्रवाई
+*पोल्याकोव क्रिया
 ==टिप्पणियाँ==
 {{reflist}}
+== संदर्भ ==
-==संदर्भ==
 {{cite journal
 |  title = The geometry of string perturbation theory
@@ Line 135: / Line 116: @@
   |url-status      = dead
 }}
-==बाहरी संबंध==
-* [https://web.archive.org/web/20101008035958/http://superstringtheory.com/basics/basic5a.html How many string theories are there?]
-* [http://pirsa.org/C09001 PIRSA:C09001 - Introduction to the Bosonic String]
 [[Category: स्ट्रिंग सिद्धांत]]
@@ Line 146: / Line 122: @@
 [[Category: Machine Translated Page]]
 [[Category:Created On 18/11/2023]]
+[[Category:Vigyan Ready]]

Anonymous

Search

बोसोनिक स्ट्रिंग सिद्धांत: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 09:17, 12 December 2023

Contents

समस्याएँ

बोसोनिक स्ट्रिंग के प्रकार

गणित

पाथ इंटेग्रल परटूरबेशन थ्योरी

h = 1

यह भी देखें

टिप्पणियाँ

संदर्भ

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

बोसोनिक स्ट्रिंग सिद्धांत: Difference between revisions

Latest revision as of 09:17, 12 December 2023

समस्याएँ

बोसोनिक स्ट्रिंग के प्रकार

गणित

पाथ इंटेग्रल परटूरबेशन थ्योरी

h = 1

यह भी देखें

टिप्पणियाँ

संदर्भ

Navigation

Wiki tools

Page tools

Other projects

Categories