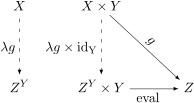घातीय ऑब्जेक्ट: Difference between revisions
No edit summary |
No edit summary |
||
| (9 intermediate revisions by 4 users not shown) | |||
| Line 24: | Line 24: | ||
== उदाहरण == | == उदाहरण == | ||
सेट की श्रेणी में, एक घातीय वस्तु <math>Z^Y</math> सभी कार्यों (गणित) का सेट | सेट की श्रेणी में, एक घातीय वस्तु <math>Z^Y</math> सभी कार्यों (गणित) का सेट <math>Y \to Z</math> है.<ref name="Lane">{{cite book|title=कामकाजी गणितज्ञ के लिए श्रेणियाँ|volume = 5|last=Mac Lane|first=Saunders|publisher=Springer-Verlag|year=1978|isbn=978-0387984032|edition=2nd|series=graduate texts in mathematics|page=98|chapter=Chapter 4: Adjoints|author-link=Saunders Mac Lane|doi = 10.1007/978-1-4757-4721-8_5}}</ref> नक्शा <math>\mathrm{eval}\colon (Z^Y \times Y) \to Z</math> केवल वह लागू होता है, जो जोड़ी <math>(f, y)</math> प्रति <math>f(y)</math> भेजता है. किसी भी नक्शे के लिए <math>g\colon X \times Y \to Z</math> नक्शा <math>\lambda g\colon X \to Z^Y</math> का करी रूप <math>g</math> है: | ||
:<math>\lambda g(x)(y) = g(x,y).\,</math> | :<math>\lambda g(x)(y) = g(x,y).\,</math> | ||
एक हेटिंग बीजगणित <math>H</math> केवल एक बंधी हुई जाली (क्रम) है जिसमें सभी घातीय वस्तुएँ हैं। हेटिंग निहितार्थ, <math>Y \Rightarrow Z</math>, के लिए | एक हेटिंग बीजगणित <math>H</math> केवल एक बंधी हुई जाली (क्रम) है जिसमें सभी घातीय वस्तुएँ हैं। हेटिंग निहितार्थ, <math>Y \Rightarrow Z</math>, के लिए <math>Z^Y</math>एक वैकल्पिक संकेतन है. उपरोक्त संयोजन परिणाम निहितार्थ में अनुवाद करते हैं (<math>\Rightarrow : H \times H \to H</math>) मिलने के लिए सही आसन्न होने के नाते (<math>\wedge : H \times H \to H</math>). इस संयोजन को <math>(- \wedge Y) \dashv (Y \Rightarrow -)</math>इस प्रकार लिखा जा सकता है, या अधिक पूर्ण रूप से इस प्रकार लिखा जा सकता है: | ||
<math display="block">(- \wedge Y): H \stackrel {\longrightarrow} {\underset {\longleftarrow}{\top}} H: (Y \Rightarrow -)</math> | <math display="block">(- \wedge Y): H \stackrel {\longrightarrow} {\underset {\longleftarrow}{\top}} H: (Y \Rightarrow -)</math> | ||
टोपोलॉजिकल स्पेस की श्रेणी में, | टोपोलॉजिकल स्पेस की श्रेणी में, घातीय वस्तु <math>Z^Y</math> उपस्थित है शर्त यह है कि कि <math>Y</math> एक स्थानीय रूप से विनिमेय स्पेस हौसडॉर्फ स्पेस है। उस स्थिति में, स्पेस <math>Z^Y</math> विनिमेय-खुला टोपोलॉजी के साथ <math>Y</math> से <math>Z</math> से सभी निरंतर कार्य (टोपोलॉजी) का सेट है। मूल्यांकन मानचित्र सेट की श्रेणी के समान ही है; यह उपरोक्त टोपोलॉजी के साथ निरंतर है।<ref>[[Joseph J. Rotman]], ''An Introduction to Algebraic Topology'' (1988) Springer-Verlag {{ISBN|0-387-96678-1}} ''(See Chapter 11 for proof.)''</ref> यदि <math>Y</math> हॉसडॉर्फ स्थानीय रूप से विनिमेय नहीं है, घातीय वस्तु उपस्थित नहीं हो सकती है (स्पेस <math>Z^Y</math> अभी भी मौजूद है, लेकिन यह एक एक्सपोनेंशियल ऑब्जेक्ट होने में विफल हो सकता है क्योंकि मूल्यांकन फलन को निरंतर होने की आवश्यकता नहीं है)। इस कारण से टोपोलॉजिकल रिक्त स्थान की श्रेणी कार्तीय बंद होने में विफल रहती है। | ||
कार्यात्मक | चूँकि, <math>Z^Y</math> स्थानीय रूप से विनिमेय रिक्त स्थान <math>Z</math> तथा <math>Y</math> के लिए स्थानीय रूप से विनिमेय होने की आवश्यकता नहीं है. रिक्त स्थान की एक कार्तीय बंद श्रेणी, उदाहरण के लिए, रिक्त स्थान की एक कार्तीय बंद श्रेणी, दृढ़तापूर्वक उत्पन्न किए गए हौसडॉर्फ रिक्त स्थान द्वारा फैली पूर्ण उपश्रेणी द्वारा दी गई है। | ||
कार्यात्मक कार्यरचना भाषाओं में, आकृतिवाद <math>\operatorname{eval}</math> अधिकांश होता है| बुलाया <math>\operatorname{apply}</math>, और वाक्य रचना <math>\lambda g</math> अक्सर कार्य अनुप्रयोग # प्रतिनिधित्व | लिखा जाता है <math>\operatorname{curry}(g)</math>. रूपवाद <math>\operatorname{eval}</math> यहाँ मान के साथ भ्रमित नहीं होना चाहिए <code>eval</code>कुछ प्रोग्रामिंग भाषाओं में कार्य करता है, जो उद्धृत भावों का मूल्यांकन करता है। | |||
== यह भी देखें == | == यह भी देखें == | ||
| Line 47: | Line 48: | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
| Line 53: | Line 65: | ||
{{Category theory}} | {{Category theory}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Articles with redirect hatnotes needing review]] | |||
[[Category:Articles with short description]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 30/11/2022]] | [[Category:Created On 30/11/2022]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Missing redirects]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:ऑब्जेक्ट्स (Category सिद्धांत)]] | |||
Latest revision as of 15:34, 29 December 2022
गणित में, विशेष रूप से श्रेणी सिद्धांत में, एक घातीय वस्तु या मानचित्र वस्तु सेट सिद्धांत में एक कार्य स्थान का श्रेणीबद्ध सामान्यीकरण है। सभी परिमित उत्पादों और घातीय वस्तुओं वाली श्रेणियों को कार्तीय बंद श्रेणियां कहा जाता है। संलग्न उत्पादों के बिना श्रेणियाँ (जैसे शीर्ष की उपश्रेणियाँ) अभी भी एक घातीय नियम हो सकती हैं।[1][2]
परिभाषा
मान लीजिये एक श्रेणी हो, और तथा की वस्तु (श्रेणी सिद्धांत) हो, और के पास के साथ सभी बाइनरी उत्पाद (श्रेणी सिद्धांत) हैं. एक वस्तु एक साथ एक आकारिकी के साथ किसी भी वस्तु के लिए एक चरघातीय वस्तु है किसी वस्तु के लिये और एक अद्वितीय आकारिकी (का स्थानांतरण कहा जाता है ) है, जैसे कि निम्न आरेख क्रमविनिमेय आरेख में बदलना:
प्रत्येक के लिए एक अद्वितीय का यह कार्य होम-सेट का एक समरूपता (आक्षेप) को स्थापित करता है
यदि सभी वस्तुओं के लिए उपस्थित है में , फिर गुणन द्वारा वस्तुओं पर परिभाषित और तीर पर , उत्पाद फ़ंक्टर के लिए एक सही आसन्न है . इस कारण से, आकारिकी तथा कभी-कभी एक दूसरे के चरघातांकी संलग्नक कहलाते हैं।[3]
समान परिभाषा
वैकल्पिक रूप से, घातीय वस्तु को समीकरणों के माध्यम से परिभाषित किया जा सकता है:
- की उपस्थितगी के अस्तित्व की आश्वस्त संचालन के मौजूद होने से मिलती है।
- उपरोक्त आरेखों की क्रमविनिमेयता समानता द्वारा आश्वस्तकृत है।
- की विशिष्टता की आश्वस्त समानता . द्वारा दी जाती है।
सार्वभौमिक संपत्ति
घातीय उत्पाद प्रकार्यक से एक सार्वभौमिक आकारिकी वस्तु को द्वारा दिया गया है. इस सार्वभौमिक रूपवाद में एक वस्तु और एक रूपवाद होती है.
उदाहरण
सेट की श्रेणी में, एक घातीय वस्तु सभी कार्यों (गणित) का सेट है.[4] नक्शा केवल वह लागू होता है, जो जोड़ी प्रति भेजता है. किसी भी नक्शे के लिए नक्शा का करी रूप है:
एक हेटिंग बीजगणित केवल एक बंधी हुई जाली (क्रम) है जिसमें सभी घातीय वस्तुएँ हैं। हेटिंग निहितार्थ, , के लिए एक वैकल्पिक संकेतन है. उपरोक्त संयोजन परिणाम निहितार्थ में अनुवाद करते हैं () मिलने के लिए सही आसन्न होने के नाते (). इस संयोजन को इस प्रकार लिखा जा सकता है, या अधिक पूर्ण रूप से इस प्रकार लिखा जा सकता है:
चूँकि, स्थानीय रूप से विनिमेय रिक्त स्थान तथा के लिए स्थानीय रूप से विनिमेय होने की आवश्यकता नहीं है. रिक्त स्थान की एक कार्तीय बंद श्रेणी, उदाहरण के लिए, रिक्त स्थान की एक कार्तीय बंद श्रेणी, दृढ़तापूर्वक उत्पन्न किए गए हौसडॉर्फ रिक्त स्थान द्वारा फैली पूर्ण उपश्रेणी द्वारा दी गई है।
कार्यात्मक कार्यरचना भाषाओं में, आकृतिवाद अधिकांश होता है| बुलाया , और वाक्य रचना अक्सर कार्य अनुप्रयोग # प्रतिनिधित्व | लिखा जाता है . रूपवाद यहाँ मान के साथ भ्रमित नहीं होना चाहिए evalकुछ प्रोग्रामिंग भाषाओं में कार्य करता है, जो उद्धृत भावों का मूल्यांकन करता है।
यह भी देखें
- बंद मोनोइडल श्रेणी
टिप्पणियाँ
- ↑ Exponential law for spaces at the nLab
- ↑ Convenient category of topological spaces at the nLab
- ↑ Goldblatt, Robert (1984). "Chapter 3: Arrows instead of epsilon". टोपोई: तर्क का श्रेणीबद्ध विश्लेषण. Studies in Logic and the Foundations of Mathematics #98 (Revised ed.). North-Holland. p. 72. ISBN 978-0-444-86711-7.
- ↑ Mac Lane, Saunders (1978). "Chapter 4: Adjoints". कामकाजी गणितज्ञ के लिए श्रेणियाँ. graduate texts in mathematics. Vol. 5 (2nd ed.). Springer-Verlag. p. 98. doi:10.1007/978-1-4757-4721-8_5. ISBN 978-0387984032.
- ↑ Joseph J. Rotman, An Introduction to Algebraic Topology (1988) Springer-Verlag ISBN 0-387-96678-1 (See Chapter 11 for proof.)
संदर्भ
- Adámek, Jiří; Horst Herrlich; George Strecker (2006) [1990]. Abstract and Concrete Categories (The Joy of Cats). John Wiley & Sons.
- Awodey, Steve (2010). "Chapter 6: Exponentials". Category theory. Oxford New York: Oxford University Press. ISBN 978-0199237180.
- Mac Lane, Saunders (1998). "Chapter 4: Adjoints". Categories for the working mathematician. New York: Springer. ISBN 978-0387984032.
बाहरी संबंध
- Interactive Web page which generates examples of exponential objects and other categorical constructions. Written by Jocelyn Paine.