हेविसाइड चरण फलन: Difference between revisions
No edit summary |
No edit summary |
||
| (10 intermediate revisions by 4 users not shown) | |||
| Line 4: | Line 4: | ||
| image = Dirac distribution CDF.svg | | image = Dirac distribution CDF.svg | ||
| imagesize = 325px | | imagesize = 325px | ||
| caption = अर्ध-अधिकतम परिपाटी का उपयोग करते हुए हीविसाइड | | caption = अर्ध-अधिकतम परिपाटी का उपयोग करते हुए हीविसाइड चरण फलन | ||
| general_definition = <math display="block">H(x) := \begin{cases} 1, & x > 0 \\ 0, & x < 0 \end{cases}</math> | | general_definition = <math display="block">H(x) := \begin{cases} 1, & x > 0 \\ 0, & x < 0 \end{cases}</math> | ||
| fields_of_application = परिचालन गणना | | fields_of_application = परिचालन गणना | ||
}} | }} | ||
हेविसाइड | '''हेविसाइड चरण फलन''', या इकाई चरण फलन, जिसे सामान्यतः '''{{mvar|H}}''' '''या {{mvar|θ}}''' से निरूपित किया जाता है (लेकिन कभी कभी {{mvar|u}}, {{math|'''1'''}} या {{math|{{not a typo|𝟙}}}}), एक चरण फलन है, जिसका नाम [[ओलिवर हेविसाइड]] (1850-1925) के नाम पर रखा गया है, जिसका मान ऋणात्मक तर्कों के लिए [[0 (संख्या)]] और सकारात्मक तर्कों के लिए [[1 (संख्या)]] है यह चरण कार्यों के सामान्य वर्ग का उदाहरण है, जिनमें से सभी को इस एक के अनुवादों के [[रैखिक संयोजन]] के रूप में दर्शाया जा सकता है। | ||
फलन मूल रूप से [[अंतर समीकरण|अंतर समीकरणों]] के समाधान के लिए परिचालन कलन में विकसित किया गया था, जहां यह संकेत का प्रतिनिधित्व करता है जो एक निर्दिष्ट समय पर बदलता है और अनिश्चित काल के लिए बदलता है। ओलिवर हेविसाइड, जिन्होंने टेलीग्राफिक संचार के विश्लेषण में एक उपकरण के रूप में परिचालन गणना विकसित किया, ने {{math|'''1'''}} के रूप में कार्य का प्रतिनिधित्व किया। | |||
हेविसाइड | हेविसाइड फलन को परिभाषित किया जा सकता है: | ||
* एक टुकड़ा | * एक टुकड़ा फलन: <math display="block">H(x) := \begin{cases} 1, & x > 0 \\ 0, & x \le 0 \end{cases}</math> | ||
* [[इवरसन ब्रैकेट]] | * [[इवरसन ब्रैकेट|इवरसन कोष्ठक]] अंकन का उपयोग करना: <math display="block">H(x) := [x>0]</math> | ||
* एक संकेतक | * एक संकेतक फलन: <math display="block">H(x) := \mathbf{1}_{x > 0}=\mathbf 1_{\mathbb R_+}(x)</math> | ||
* [[रैंप समारोह]] का व्युत्पन्न: <math display="block">H(x) := \frac{d}{dx} \max \{ x, 0 \}\quad \mbox{for } x \ne 0</math> | * [[रैंप समारोह|रैंप फलन]] का व्युत्पन्न: <math display="block">H(x) := \frac{d}{dx} \max \{ x, 0 \}\quad \mbox{for } x \ne 0</math> | ||
डीआईआरएसी डेल्टा | डीआईआरएसी डेल्टा फलन हेविसाइड फलन का व्युत्पन्न है | ||
<math display="block">\delta(x)= \frac{d}{dx} H(x)</math> | <math display="block">\delta(x)= \frac{d}{dx} H(x)</math> | ||
इसलिए हेविसाइड | इसलिए हेविसाइड फलन को डीआईआरएसी डेल्टा फलन का [[अभिन्न]] माना जा सकता है। यह कभी-कभी लिखा जाता है | ||
<math display="block">H(x) := \int_{-\infty}^x \delta(s)\,ds</math> | <math display="block">H(x) := \int_{-\infty}^x \delta(s)\,ds</math> | ||
यह विस्तार x = 0 के लिए हो सकता है (या यहां तक कि समझ में नहीं आता), इस पर निर्भर करता है कि किस औपचारिकता का उपयोग δ से जुड़े इंटीग्रल को अर्थ देने के लिए किया जाता है। इस संदर्भ में, हीविसाइड | यह विस्तार x = 0 के लिए हो सकता है (या यहां तक कि समझ में नहीं आता), इस पर निर्भर करता है कि किस औपचारिकता का उपयोग δ से जुड़े इंटीग्रल को अर्थ देने के लिए किया जाता है। इस संदर्भ में, हीविसाइड फलन एक यादृच्छिक चर का संचयी वितरण फलन है जो [[लगभग निश्चित रूप से]] 0 है। ([[निरंतर यादृच्छिक चर]] देखें।) | ||
परिचालन कलन में, उपयोगी उत्तर सम्भवतः ही कभी इस बात पर निर्भर करते हैं कि {{math|''H''(0)}} के लिए किस मूल्य का उपयोग किया जाता है , क्योंकि {{mvar|H}} अधिकतर एक [[वितरण (गणित)]] के रूप में उपयोग किया जाता है।चूँकि, विकल्प कार्यात्मक विश्लेषण और खेल सिद्धांत में कुछ महत्वपूर्ण परिणाम हो सकते हैं, जहां निरंतरता के अधिक सामान्य रूपों पर विचार किया जाता है। कुछ सामान्य विकल्पों को 0 कारण देखा जा सकता है। | |||
हेविसाइड चरण फलन के लिए सन्निकटन [[जीव रसायन|बायोकेमिस्ट्री]] और [[तंत्रिका विज्ञान|न्यूरोसाइंस]] में उपयोग किए जाते हैं, जहां रासायनिक संकेतों के उत्तर में चरण फलन (जैसे कि हिल और माइकलिस-मेंटेन समीकरण) के [[लॉजिस्टिक फ़ंक्शन|लॉजिस्टिक फलन]] सन्निकटन का उपयोग लगभग बाइनरी सेल्युलर बदलने के लिए किया जा सकता है। | |||
हेविसाइड | |||
== विश्लेषणात्मक सन्निकटन == | == विश्लेषणात्मक सन्निकटन == | ||
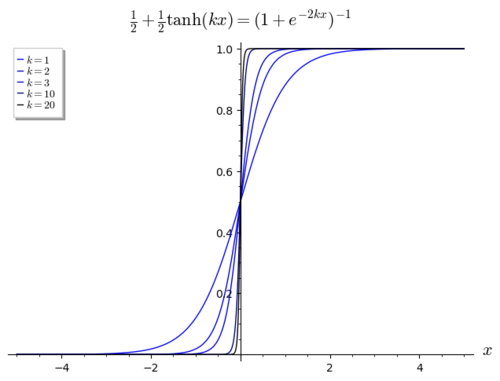
[[File:Step function approximation.png|alt=A set of functions that successively approach the step function|thumb|500x500px |<math>\tfrac{1}{2} + \tfrac{1}{2} \tanh(kx) = \frac{1}{1+e^{-2kx}}</math><br> के रूप में चरण | [[File:Step function approximation.png|alt=A set of functions that successively approach the step function|thumb|500x500px |<math>\tfrac{1}{2} + \tfrac{1}{2} \tanh(kx) = \frac{1}{1+e^{-2kx}}</math><br> के रूप में चरण फलन के पास पहुंचता है {{math|''k'' → ∞}}।]]चरण फलन के लिए चिकनी फलन सन्निकटन के लिए, कोई लॉजिस्टिक फलन का उपयोग कर सकता है | ||
<math display="block">H(x) \approx \tfrac{1}{2} + \tfrac{1}{2}\tanh kx = \frac{1}{1+e^{-2kx}},</math> | <math display="block">H(x) \approx \tfrac{1}{2} + \tfrac{1}{2}\tanh kx = \frac{1}{1+e^{-2kx}},</math> | ||
जहां बड़ा {{mvar|k}}, {{math|''x'' {{=}} 0}} पर तीव्र संक्रमण के संगत है। यदि हम लेते हैं {{math|''H''(0) {{=}} {{sfrac|1|2}}}}, समानता सीमा में है: | जहां बड़ा {{mvar|k}}, {{math|''x'' {{=}} 0}} पर तीव्र संक्रमण के संगत है। यदि हम लेते हैं {{math|''H''(0) {{=}} {{sfrac|1|2}}}}, समानता सीमा में है: | ||
<math display="block">H(x)=\lim_{k \to \infty}\tfrac{1}{2}(1+\tanh kx)=\lim_{k \to \infty}\frac{1}{1+e^{-2kx}}.</math> | <math display="block">H(x)=\lim_{k \to \infty}\tfrac{1}{2}(1+\tanh kx)=\lim_{k \to \infty}\frac{1}{1+e^{-2kx}}.</math> | ||
चरण फलन के लिए कई अन्य सहज, विश्लेषणात्मक सन्निकटन हैं।<ref>{{MathWorld | urlname=HeavisideStepFunction | title=Heaviside Step Function}}</ref> संभावनाओं में से हैं: | |||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
H(x) &= \lim_{k \to \infty} \left(\tfrac{1}{2} + \tfrac{1}{\pi}\arctan kx\right)\\ | H(x) &= \lim_{k \to \infty} \left(\tfrac{1}{2} + \tfrac{1}{\pi}\arctan kx\right)\\ | ||
H(x) &= \lim_{k \to \infty}\left(\tfrac{1}{2} + \tfrac12\operatorname{erf} kx\right) | H(x) &= \lim_{k \to \infty}\left(\tfrac{1}{2} + \tfrac12\operatorname{erf} kx\right) | ||
\end{align}</math> | \end{align}</math> | ||
ये सीमाएँ [[नुकीला|बिंदुवार]] और वितरण (गणित) के अर्थ में हैं। सामान्य तौर पर, चूँकि, पॉइंटवाइज कन्वर्जेंस को वितरणात्मक अभिसरण की आवश्यकता नहीं है, और इसके विपरीत वितरणात्मक अभिसरण को इंगित करने की आवश्यकता नहीं होती है।(चूँकि, यदि | ये सीमाएँ [[नुकीला|बिंदुवार]] और वितरण (गणित) के अर्थ में हैं। सामान्य तौर पर, चूँकि, पॉइंटवाइज कन्वर्जेंस को वितरणात्मक अभिसरण की आवश्यकता नहीं है, और इसके विपरीत वितरणात्मक अभिसरण को इंगित करने की आवश्यकता नहीं होती है।(चूँकि, यदि फलन के पॉइंटवाइज कन्वर्जेंट अनुक्रम के सभी सदस्य समान रूप से कुछ अच्छे फलन से बंधे होते हैं, तो अभिसरण भी वितरण के अर्थ में होता है।) | ||
सामान्य तौर पर, [[निरंतर वितरण]] संभावना वितरण का कोई भी संचयी वितरण | सामान्य तौर पर, [[निरंतर वितरण]] संभावना वितरण का कोई भी संचयी वितरण फलन जो शून्य के आसपास होता है और इसमें पैरामीटर होता है जो विचरण के लिए नियंत्रण करता है, एक अनुमान के रूप में काम कर सकता है, सीमा में विचरण शून्य तक पहुंचता है। उदाहरण के लिए, उपरोक्त सभी तीनों सन्निकटन सामान्य संभावना वितरण के संचयी वितरण कार्य हैं: क्रमशः लॉजिस्टिक वितरण, कॉची वितरण और [[सामान्य वितरण]] वितरण। | ||
== अभिन्न प्रतिनिधित्व == | == अभिन्न प्रतिनिधित्व == | ||
अधिकतर [[एकीकरण]] (गणित) हेविसाइड चरण | अधिकतर [[एकीकरण]] (गणित) हेविसाइड चरण फलन का प्रतिनिधित्व उपयोगी होता है: | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
H(x)&=\lim_{ \varepsilon \to 0^+} -\frac{1}{2\pi i}\int_{-\infty}^\infty \frac{1}{\tau+i\varepsilon} e^{-i x \tau} d\tau \\ | H(x)&=\lim_{ \varepsilon \to 0^+} -\frac{1}{2\pi i}\int_{-\infty}^\infty \frac{1}{\tau+i\varepsilon} e^{-i x \tau} d\tau \\ | ||
&=\lim_{ \varepsilon \to 0^+} \frac{1}{2\pi i}\int_{-\infty}^\infty \frac{1}{\tau-i\varepsilon} e^{i x \tau} d\tau. | &=\lim_{ \varepsilon \to 0^+} \frac{1}{2\pi i}\int_{-\infty}^\infty \frac{1}{\tau-i\varepsilon} e^{i x \tau} d\tau. | ||
\end{align}</math> | \end{align}</math> | ||
जहां दूसरा प्रतिनिधित्व पहले से कम करना आसान है, यह देखते हुए कि चरण | जहां दूसरा प्रतिनिधित्व पहले से कम करना आसान है, यह देखते हुए कि चरण फलन वास्तविक है और इस प्रकार इसका अपना जटिल संयुग्म है। | ||
== शून्य तर्क == | == शून्य तर्क == | ||
{{mvar|H}} सामान्यतः एकीकरण में उपयोग किया जाता है, और एक ही बिंदु पर | {{mvar|H}} सामान्यतः एकीकरण में उपयोग किया जाता है, और एक ही बिंदु पर फलन का मूल्य इसके अभिन्न को प्रभावित नहीं करता है, यह सम्भवतः ही कभी अर्थ रखता है कि {{math|''H''(0)}} का विशेष मान क्या चुना जाता है। वास्तव में जब {{mvar|H}} एक वितरण (गणित) या एक तत्व के रूप में माना जाता है {{math|''L''{{isup|∞}}}} ({{math|''L{{isup|p}}''}} अंतरिक्ष देखें) यह भी शून्य पर मान की बात करने का कोई अर्थ नहीं बनता है, क्योंकि ऐसी वस्तुओं को केवल हर जगह लगभग परिभाषित किया जाता है। यदि कुछ विश्लेषणात्मक सन्निकटन (जैसा कि ऊपर के उदाहरणों में) का उपयोग किया जाता है, तो अधिकांशतः जो कुछ भी होता है वह शून्य पर प्रासंगिक सीमा का उपयोग किया जाता है। | ||
किसी विशेष मूल्य को चुनने के विभिन्न कारण उपस्थित हैं। | किसी विशेष मूल्य को चुनने के विभिन्न कारण उपस्थित हैं। | ||
* {{math|''H''(0) {{=}} {{sfrac|1|2}}}} का उपयोग अधिकांशतः | * {{math|''H''(0) {{=}} {{sfrac|1|2}}}} का उपयोग अधिकांशतः फलन के ग्राफ के बाद से किया जाता है, फिर घूर्णी समरूपता होती है; दूसरे विधि से रखो, {{math|''H'' − {{sfrac|1|2}}}} तब एक विषम कार्य है। इस स्थिति में [[हस्ताक्षर समारोह|हस्ताक्षर फलन]] के साथ निम्नलिखित संबंध सभी के लिए है {{mvar|x}}: <math display="block"> H(x) = \tfrac12(1 + \sgn x).</math> | ||
* {{math|''H''(0) {{=}} 1}} जब उपयोग किया जाता है {{mvar|H}} दाएं-निरंतर होने की आवश्यकता है। उदाहरण के लिए, संचयी वितरण कार्यों को सामान्यतः [[सही]] निरंतर होने के लिए लिया जाता है, क्योंकि लेबेसग्यू -स्टिल्टजेस एकीकरण के विपरीत एकीकृत कार्य हैं। इस स्थिति में {{mvar|H}} [[बंद सेट]] अर्ध-अनंत अंतराल का संकेतक | * {{math|''H''(0) {{=}} 1}} जब उपयोग किया जाता है {{mvar|H}} दाएं-निरंतर होने की आवश्यकता है। उदाहरण के लिए, संचयी वितरण कार्यों को सामान्यतः [[सही]] निरंतर होने के लिए लिया जाता है, क्योंकि लेबेसग्यू -स्टिल्टजेस एकीकरण के विपरीत एकीकृत कार्य हैं। इस स्थिति में {{mvar|H}} [[बंद सेट]] अर्ध-अनंत अंतराल का संकेतक फलन है: <math display="block"> H(x) = \mathbf{1}_{[0,\infty)}(x).</math> इसी संभावना वितरण में [[पतित वितरण]] है। | ||
* {{math|''H''(0) {{=}} 0}} जब उपयोग किया जाता है {{mvar|H}} बचे रहने की आवश्यकता है। इस स्थिति में {{mvar|H}} खुले सेट अर्ध-अनंत अंतराल का एक संकेतक | * {{math|''H''(0) {{=}} 0}} जब उपयोग किया जाता है {{mvar|H}} बचे रहने की आवश्यकता है। इस स्थिति में {{mvar|H}} खुले सेट अर्ध-अनंत अंतराल का एक संकेतक फलन है: <math display="block"> H(x) = \mathbf{1}_{(0,\infty)}(x).</math> | ||
* | * अनुकूलन और खेल सिद्धांत से कार्यात्मक-विश्लेषण संदर्भों में, यह अधिकांशतः उपयोगी होता है कि बहुउद्देशीय फलन के रूप में हेविसाइड फलन को परिभाषित करना है। सीमित कार्यों की निरंतरता को संरक्षित करने और कुछ समाधानों के अस्तित्व को सुनिश्चित करने के लिए निर्धारित-मूल्य फलन है। इन स्थितियों में, हेविसाइड फलन संभावित समाधानों का एक पूरा अंतराल लौटाता है, {{math|''H''(0) {{=}} [0,1]}}। | ||
== असतत रूप == | == असतत रूप == | ||
इकाई चरण का एक वैकल्पिक रूप, फलन के रूप में इसके अतिरिक्त परिभाषित किया गया {{math|''H'' : ℤ → ℝ}} (अर्थात, असतत चर में ले जाना {{mvar|n}}), है: | |||
<math display="block">H[n]=\begin{cases} 0, & n < 0, \\ 1, & n \ge 0, \end{cases} </math> | <math display="block">H[n]=\begin{cases} 0, & n < 0, \\ 1, & n \ge 0, \end{cases} </math> | ||
| Line 69: | Line 67: | ||
<math display="block">H[n]=\begin{cases} 0, & n < 0, \\ \tfrac12, & n = 0,\\ 1, & n > 0, \end{cases} </math> | <math display="block">H[n]=\begin{cases} 0, & n < 0, \\ \tfrac12, & n = 0,\\ 1, & n > 0, \end{cases} </math> | ||
जहाँ पर {{mvar|n}} एक [[पूर्णांक]] है। यदि {{mvar|n}} पूर्णांक है, तो {{math|''n'' < 0}} इसका तात्पर्य यह होना चाहिए {{math|''n'' ≤ −1}}, जबकि {{math|''n'' > 0}} इसका तात्पर्य यह होना चाहिए कि | जहाँ पर {{mvar|n}} एक [[पूर्णांक]] है। यदि {{mvar|n}} पूर्णांक है, तो {{math|''n'' < 0}} इसका तात्पर्य यह होना चाहिए {{math|''n'' ≤ −1}}, जबकि {{math|''n'' > 0}} इसका तात्पर्य यह होना चाहिए कि फलन एकता को प्राप्त करता है {{math|1=''n'' = 1}}। इसलिए चरण फलन के डोमेन पर रैंप जैसा व्यवहार प्रदर्शित करता है {{closed-closed|−1, 1}}, और आधे-अधिकतम सम्मेलन का उपयोग करके प्रामाणिक रूप से एक चरण फलन नहीं हो सकता है। | ||
निरंतर स्थिति के विपरीत, की परिभाषा {{math|''H''[0]}} महत्वपूर्ण है। | निरंतर स्थिति के विपरीत, की परिभाषा {{math|''H''[0]}} महत्वपूर्ण है। | ||
असतत-समय इकाई आवेग असतत-समय | असतत-समय इकाई आवेग असतत-समय चरण का पहला अंतर है | ||
<math display="block"> \delta[n] = H[n] - H[n-1].</math> | <math display="block"> \delta[n] = H[n] - H[n-1].</math> | ||
यह | यह फलन [[क्रोनकर डेल्टा]] का संचयी योग है: | ||
<math display="block"> H[n] = \sum_{k=-\infty}^{n} \delta[k] </math> | <math display="block"> H[n] = \sum_{k=-\infty}^{n} \delta[k] </math> | ||
| Line 84: | Line 82: | ||
पतित वितरण है। | पतित वितरण है। | ||
== [[antiderivative| | == [[antiderivative|प्रतिपक्षी]] और व्युत्पन्न == | ||
रैंप | रैंप फलन हेविसाइड चरण फलन का एक प्रतिपक्षी है: | ||
<math display="block">\int_{-\infty}^{x} H(\xi)\,d\xi = x H(x) = \max\{0,x\} \,.</math> | |||
हेविसाइड चरण | हेविसाइड चरण फलन का वितरण व्युत्पन्न डीआईआरएसी डेल्टा फलन है: | ||
<math display="block"> \frac{d H(x)}{dx} = \delta(x) \,.</math> | <math display="block"> \frac{d H(x)}{dx} = \delta(x) \,.</math> | ||
== फूरियर | == फूरियर रूपांतरण == | ||
हेविसाइड चरण | हेविसाइड चरण फलन का [[फूरियर रूपांतरण]] एक वितरण है। हमारे पास फूरियर रूपांतरण की परिभाषा के लिए स्थिरांक की पसंद का उपयोग करना | ||
<math display="block">\hat{H}(s) = \lim_{N\to\infty}\int^N_{-N} e^{-2\pi i x s} H(x)\,dx = \frac{1}{2} \left( \delta(s) - \frac{i}{\pi} \operatorname{p.v.}\frac{1}{s} \right).</math> | <math display="block">\hat{H}(s) = \lim_{N\to\infty}\int^N_{-N} e^{-2\pi i x s} H(x)\,dx = \frac{1}{2} \left( \delta(s) - \frac{i}{\pi} \operatorname{p.v.}\frac{1}{s} \right).</math> | ||
यहां {{math|p.v.{{sfrac|1|''s''}}}} वितरण (गणित) है जो एक परीक्षण | यहां {{math|p.v.{{sfrac|1|''s''}}}} वितरण (गणित) है जो एक परीक्षण फलन लेता है {{mvar|φ}} के कौची प्रमुख मूल्य के लिए <math>\textstyle\int_{-\infty}^\infty \frac{\varphi(s)}{s} \, ds</math>। अभिन्न में दिखाई देने वाली सीमा भी वितरण के अर्थ में ली गई है। | ||
== | == एकपक्षीय लाप्लास रूपांतरण == | ||
हेविसाइड चरण | हेविसाइड चरण फलन का [[लाप्लास रूपांतरण]] एक [[मेरोमॉर्फिक फ़ंक्शन|मेरोमॉर्फिक फलन]] है। एक ओर लाप्लास रूपांतरण का उपयोग करना हमारे पास है: | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
\hat{H}(s) &= \lim_{N\to\infty}\int^N_{0} e^{-sx} H(x)\,dx\\ | \hat{H}(s) &= \lim_{N\to\infty}\int^N_{0} e^{-sx} H(x)\,dx\\ | ||
| Line 107: | Line 105: | ||
== अन्य भाव == | == अन्य भाव == | ||
हेविसाइड | हेविसाइड चरण फलन को [[हाइपरफंक्शन|हाइपरफलन]] के रूप में दर्शाया जा सकता है | ||
<math display="block">H(x) = \left(1-\frac{1}{2\pi i}\log z,\ -\frac{1}{2\pi i}\log z\right).</math> | <math display="block">H(x) = \left(1-\frac{1}{2\pi i}\log z,\ -\frac{1}{2\pi i}\log z\right).</math> | ||
जहाँ log z, z के जटिल लघुगणक का मुख्य मान है। | जहाँ log z, z के जटिल लघुगणक का मुख्य मान है। | ||
इस {{math|''x'' ≠ 0}} के लिए | इस {{math|''x'' ≠ 0}} के लिए [[निरपेक्ष मूल्य|निरपेक्ष मान]] फलन के रूप में भी व्यक्त किया जा सकता है | ||
<math display="block"> H(x) = \frac{x + |x|}{2x} \,.</math> | <math display="block"> H(x) = \frac{x + |x|}{2x} \,.</math> | ||
| Line 117: | Line 115: | ||
== यह भी देखें == | == यह भी देखें == | ||
{{Div col|colwidth=25em}} | {{Div col|colwidth=25em}} | ||
* | * डीरेक डेल्टा फलन | ||
* संकेतक | * संकेतक फलन | ||
* आइवरसन | * आइवरसन कोष्ठक | ||
* लाप्लास | * लाप्लास रूपांतरण | ||
* संकेतक के लाप्लासियन | * संकेतक के लाप्लासियन | ||
* [[गणितीय कार्यों की सूची]] | * [[गणितीय कार्यों की सूची]] | ||
* [[मैकाउले | * [[मैकाउले कोष्ठक]] | ||
* [[ऋणात्मक संख्या]] | * [[ऋणात्मक संख्या]] | ||
* आयताकार | * आयताकार फलन | ||
* साइन | * साइन फलन | ||
* [[साइन | * [[साइन एकीकरण]] | ||
* [[ | * [[चरण की प्रतिक्रिया]] | ||
{{Div col end}} | {{Div col end}} | ||
| Line 145: | Line 143: | ||
*{{cite book |first1=George F. D. |last1=Duff |author-link=George F. D. Duff |first2=D. |last2=Naylor |year=1966 |title=Differential Equations of Applied Mathematics |page=42 |chapter=Heaviside unit function |publisher=[[John Wiley & Sons]] }} | *{{cite book |first1=George F. D. |last1=Duff |author-link=George F. D. Duff |first2=D. |last2=Naylor |year=1966 |title=Differential Equations of Applied Mathematics |page=42 |chapter=Heaviside unit function |publisher=[[John Wiley & Sons]] }} | ||
{{DEFAULTSORT:Heaviside Step Function}} | {{DEFAULTSORT:Heaviside Step Function}} | ||
[[Category: | [[Category:CS1 English-language sources (en)]] | ||
[[Category:Created On 25/01/2023]] | [[Category:Commons category link is locally defined|Heaviside Step Function]] | ||
[[Category:Created On 25/01/2023|Heaviside Step Function]] | |||
[[Category:Lua-based templates|Heaviside Step Function]] | |||
[[Category:Machine Translated Page|Heaviside Step Function]] | |||
[[Category:Multi-column templates|Heaviside Step Function]] | |||
[[Category:Pages using div col with small parameter|Heaviside Step Function]] | |||
[[Category:Pages with script errors|Heaviside Step Function]] | |||
[[Category:Short description with empty Wikidata description|Heaviside Step Function]] | |||
[[Category:Templates Vigyan Ready|Heaviside Step Function]] | |||
[[Category:Templates that add a tracking category|Heaviside Step Function]] | |||
[[Category:Templates that generate short descriptions|Heaviside Step Function]] | |||
[[Category:Templates using TemplateData|Heaviside Step Function]] | |||
[[Category:Templates using under-protected Lua modules|Heaviside Step Function]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:विशेष कार्य|Heaviside Step Function]] | |||
[[Category:सामान्यीकृत कार्य|Heaviside Step Function]] | |||
Latest revision as of 17:02, 3 February 2023
| हेविसाइड स्टेप | |
|---|---|
 अर्ध-अधिकतम परिपाटी का उपयोग करते हुए हीविसाइड चरण फलन | |
| General information | |
| सामान्य परिभाषा | |
| आवेदन के क्षेत्र | परिचालन गणना |
हेविसाइड चरण फलन, या इकाई चरण फलन, जिसे सामान्यतः H या θ से निरूपित किया जाता है (लेकिन कभी कभी u, 1 या 𝟙), एक चरण फलन है, जिसका नाम ओलिवर हेविसाइड (1850-1925) के नाम पर रखा गया है, जिसका मान ऋणात्मक तर्कों के लिए 0 (संख्या) और सकारात्मक तर्कों के लिए 1 (संख्या) है यह चरण कार्यों के सामान्य वर्ग का उदाहरण है, जिनमें से सभी को इस एक के अनुवादों के रैखिक संयोजन के रूप में दर्शाया जा सकता है।
फलन मूल रूप से अंतर समीकरणों के समाधान के लिए परिचालन कलन में विकसित किया गया था, जहां यह संकेत का प्रतिनिधित्व करता है जो एक निर्दिष्ट समय पर बदलता है और अनिश्चित काल के लिए बदलता है। ओलिवर हेविसाइड, जिन्होंने टेलीग्राफिक संचार के विश्लेषण में एक उपकरण के रूप में परिचालन गणना विकसित किया, ने 1 के रूप में कार्य का प्रतिनिधित्व किया।
हेविसाइड फलन को परिभाषित किया जा सकता है:
- एक टुकड़ा फलन:
- इवरसन कोष्ठक अंकन का उपयोग करना:
- एक संकेतक फलन:
- रैंप फलन का व्युत्पन्न:
डीआईआरएसी डेल्टा फलन हेविसाइड फलन का व्युत्पन्न है
परिचालन कलन में, उपयोगी उत्तर सम्भवतः ही कभी इस बात पर निर्भर करते हैं कि H(0) के लिए किस मूल्य का उपयोग किया जाता है , क्योंकि H अधिकतर एक वितरण (गणित) के रूप में उपयोग किया जाता है।चूँकि, विकल्प कार्यात्मक विश्लेषण और खेल सिद्धांत में कुछ महत्वपूर्ण परिणाम हो सकते हैं, जहां निरंतरता के अधिक सामान्य रूपों पर विचार किया जाता है। कुछ सामान्य विकल्पों को 0 कारण देखा जा सकता है।
हेविसाइड चरण फलन के लिए सन्निकटन बायोकेमिस्ट्री और न्यूरोसाइंस में उपयोग किए जाते हैं, जहां रासायनिक संकेतों के उत्तर में चरण फलन (जैसे कि हिल और माइकलिस-मेंटेन समीकरण) के लॉजिस्टिक फलन सन्निकटन का उपयोग लगभग बाइनरी सेल्युलर बदलने के लिए किया जा सकता है।
विश्लेषणात्मक सन्निकटन
चरण फलन के लिए चिकनी फलन सन्निकटन के लिए, कोई लॉजिस्टिक फलन का उपयोग कर सकता है
सामान्य तौर पर, निरंतर वितरण संभावना वितरण का कोई भी संचयी वितरण फलन जो शून्य के आसपास होता है और इसमें पैरामीटर होता है जो विचरण के लिए नियंत्रण करता है, एक अनुमान के रूप में काम कर सकता है, सीमा में विचरण शून्य तक पहुंचता है। उदाहरण के लिए, उपरोक्त सभी तीनों सन्निकटन सामान्य संभावना वितरण के संचयी वितरण कार्य हैं: क्रमशः लॉजिस्टिक वितरण, कॉची वितरण और सामान्य वितरण वितरण।
अभिन्न प्रतिनिधित्व
अधिकतर एकीकरण (गणित) हेविसाइड चरण फलन का प्रतिनिधित्व उपयोगी होता है:
शून्य तर्क
H सामान्यतः एकीकरण में उपयोग किया जाता है, और एक ही बिंदु पर फलन का मूल्य इसके अभिन्न को प्रभावित नहीं करता है, यह सम्भवतः ही कभी अर्थ रखता है कि H(0) का विशेष मान क्या चुना जाता है। वास्तव में जब H एक वितरण (गणित) या एक तत्व के रूप में माना जाता है L∞ (Lp अंतरिक्ष देखें) यह भी शून्य पर मान की बात करने का कोई अर्थ नहीं बनता है, क्योंकि ऐसी वस्तुओं को केवल हर जगह लगभग परिभाषित किया जाता है। यदि कुछ विश्लेषणात्मक सन्निकटन (जैसा कि ऊपर के उदाहरणों में) का उपयोग किया जाता है, तो अधिकांशतः जो कुछ भी होता है वह शून्य पर प्रासंगिक सीमा का उपयोग किया जाता है।
किसी विशेष मूल्य को चुनने के विभिन्न कारण उपस्थित हैं।
- H(0) = 1/2 का उपयोग अधिकांशतः फलन के ग्राफ के बाद से किया जाता है, फिर घूर्णी समरूपता होती है; दूसरे विधि से रखो, H − 1/2 तब एक विषम कार्य है। इस स्थिति में हस्ताक्षर फलन के साथ निम्नलिखित संबंध सभी के लिए है x:
- H(0) = 1 जब उपयोग किया जाता है H दाएं-निरंतर होने की आवश्यकता है। उदाहरण के लिए, संचयी वितरण कार्यों को सामान्यतः सही निरंतर होने के लिए लिया जाता है, क्योंकि लेबेसग्यू -स्टिल्टजेस एकीकरण के विपरीत एकीकृत कार्य हैं। इस स्थिति में H बंद सेट अर्ध-अनंत अंतराल का संकेतक फलन है: इसी संभावना वितरण में पतित वितरण है।
- H(0) = 0 जब उपयोग किया जाता है H बचे रहने की आवश्यकता है। इस स्थिति में H खुले सेट अर्ध-अनंत अंतराल का एक संकेतक फलन है:
- अनुकूलन और खेल सिद्धांत से कार्यात्मक-विश्लेषण संदर्भों में, यह अधिकांशतः उपयोगी होता है कि बहुउद्देशीय फलन के रूप में हेविसाइड फलन को परिभाषित करना है। सीमित कार्यों की निरंतरता को संरक्षित करने और कुछ समाधानों के अस्तित्व को सुनिश्चित करने के लिए निर्धारित-मूल्य फलन है। इन स्थितियों में, हेविसाइड फलन संभावित समाधानों का एक पूरा अंतराल लौटाता है, H(0) = [0,1]।
असतत रूप
इकाई चरण का एक वैकल्पिक रूप, फलन के रूप में इसके अतिरिक्त परिभाषित किया गया H : ℤ → ℝ (अर्थात, असतत चर में ले जाना n), है:
निरंतर स्थिति के विपरीत, की परिभाषा H[0] महत्वपूर्ण है।
असतत-समय इकाई आवेग असतत-समय चरण का पहला अंतर है
प्रतिपक्षी और व्युत्पन्न
रैंप फलन हेविसाइड चरण फलन का एक प्रतिपक्षी है:
फूरियर रूपांतरण
हेविसाइड चरण फलन का फूरियर रूपांतरण एक वितरण है। हमारे पास फूरियर रूपांतरण की परिभाषा के लिए स्थिरांक की पसंद का उपयोग करना
एकपक्षीय लाप्लास रूपांतरण
हेविसाइड चरण फलन का लाप्लास रूपांतरण एक मेरोमॉर्फिक फलन है। एक ओर लाप्लास रूपांतरण का उपयोग करना हमारे पास है:
अन्य भाव
हेविसाइड चरण फलन को हाइपरफलन के रूप में दर्शाया जा सकता है
इस x ≠ 0 के लिए निरपेक्ष मान फलन के रूप में भी व्यक्त किया जा सकता है
यह भी देखें
- डीरेक डेल्टा फलन
- संकेतक फलन
- आइवरसन कोष्ठक
- लाप्लास रूपांतरण
- संकेतक के लाप्लासियन
- गणितीय कार्यों की सूची
- मैकाउले कोष्ठक
- ऋणात्मक संख्या
- आयताकार फलन
- साइन फलन
- साइन एकीकरण
- चरण की प्रतिक्रिया
संदर्भ
- ↑ Weisstein, Eric W. "Heaviside Step Function". MathWorld.
- ↑ Bracewell, Ronald Newbold (2000). The Fourier transform and its applications (in English) (3rd ed.). New York: McGraw-Hill. p. 61. ISBN 0-07-303938-1.
बाहरी कड़ियाँ
- Digital Library of Mathematical Functions, NIST, [1].
- Berg, Ernst Julius (1936). "Unit function". Heaviside's Operational Calculus, as applied to Engineering and Physics. McGraw-Hill Education. p. 5.
- Calvert, James B. (2002). "Heaviside, Laplace, and the Inversion Integral". University of Denver.
- Davies, Brian (2002). "Heaviside step function". Integral Transforms and their Applications (3rd ed.). Springer. p. 28.
- Duff, George F. D.; Naylor, D. (1966). "Heaviside unit function". Differential Equations of Applied Mathematics. John Wiley & Sons. p. 42.