कर्रिएर जनरेशन एंड रीकॉम्बिनेशन: Difference between revisions
No edit summary |
|||
| (22 intermediate revisions by 3 users not shown) | |||
| Line 2: | Line 2: | ||
अर्धचालकों की ठोस-अवस्था भौतिकी में, वाहक उत्पादन और वाहक पुनर्संयोजन ऐसी प्रक्रियाएं हैं जिनके द्वारा चल आवेश वाहक ([[इलेक्ट्रॉन]] और इलेक्ट्रॉन छिद्र) उत्पन्न और निष्कासित किए जाते हैं। वाहक उत्पादन और पुनर्संयोजन प्रक्रियाएं कई [[Optoelectronics|ऑप्टो इलेक्ट्रॉनिकीय प्रौद्योगिकी]] अर्धचालक उपकरणों जैसे कि [[डायोड|प्रकाश डायोड]], [[प्रकाश उत्सर्जक डायोड]] और [[लेज़र डायोड]] संचालन के लिए मूल सिद्धान्त हैं। वे [[द्विध्रुवी जंक्शन ट्रांजिस्टर|द्विध्रुवी संधि (जंक्शन) ट्रांजिस्टर]] और [[पी-एन जंक्शन|पी-एन संधि]] डायोड जैसे पी-एन संधि उपकरणों के पूर्ण विश्लेषण के लिए भी महत्वपूर्ण हैं। | अर्धचालकों की ठोस-अवस्था भौतिकी में, वाहक उत्पादन और वाहक पुनर्संयोजन ऐसी प्रक्रियाएं हैं जिनके द्वारा चल आवेश वाहक ([[इलेक्ट्रॉन]] और इलेक्ट्रॉन छिद्र) उत्पन्न और निष्कासित किए जाते हैं। वाहक उत्पादन और पुनर्संयोजन प्रक्रियाएं कई [[Optoelectronics|ऑप्टो इलेक्ट्रॉनिकीय प्रौद्योगिकी]] अर्धचालक उपकरणों जैसे कि [[डायोड|प्रकाश डायोड]], [[प्रकाश उत्सर्जक डायोड]] और [[लेज़र डायोड]] संचालन के लिए मूल सिद्धान्त हैं। वे [[द्विध्रुवी जंक्शन ट्रांजिस्टर|द्विध्रुवी संधि (जंक्शन) ट्रांजिस्टर]] और [[पी-एन जंक्शन|पी-एन संधि]] डायोड जैसे पी-एन संधि उपकरणों के पूर्ण विश्लेषण के लिए भी महत्वपूर्ण हैं। | ||
[[इलेक्ट्रॉन होल]] जोड़ी अकार्बनिक [[सेमीकंडक्टर|अर्धचालकों]] में उत्पादन और पुनर्संयोजन की मूलभूत इकाई है, जो संयोजी बंध (वैलेंस | [[इलेक्ट्रॉन होल|इलेक्ट्रॉन छिद्र]] जोड़ी अकार्बनिक [[सेमीकंडक्टर|अर्धचालकों]] में उत्पादन और पुनर्संयोजन की मूलभूत इकाई है, जो संयोजी बंध (वैलेंस बंध) और संवाहन बंध (कंडक्शन बंध) के मध्य एक इलेक्ट्रॉन संक्रमण के अनुरूप होती है, जहां इलेक्ट्रॉन की उत्पादन संयोजी बंध से संवाहन बंध में संक्रमण होता है और पुनर्संयोजन एक उत्क्रम संक्रमण की ओर अग्रसर करता है । | ||
== अवलोकन == | == अवलोकन == | ||
{{See also|इलेक्ट्रॉनिक बंध संरचना}} | {{See also|इलेक्ट्रॉनिक बंध संरचना}} | ||
[[Image:Electronic band diagram.svg|thumb|upright=1.7|एक अर्धचालक सामग्री की इलेक्ट्रॉनिक | [[Image:Electronic band diagram.svg|thumb|upright=1.7|एक अर्धचालक सामग्री की इलेक्ट्रॉनिक बंध संरचना।]]अन्य ठोस पदार्थों की तरह, अर्धचालक पदार्थों में एक [[इलेक्ट्रॉनिक बैंड संरचना|इलेक्ट्रॉनिक बंध संरचना]] होती है जो सामग्री के क्रिस्टल गुणों द्वारा निर्धारित होती है। इलेक्ट्रॉनों के बीच ऊर्जा वितरण को [[फर्मी स्तर]] और इलेक्ट्रॉनों के [[तापमान]] द्वारा वर्णित किया गया है। निरपेक्ष शून्य तापमान पर, सभी इलेक्ट्रॉन की ऊर्जा फर्मी स्तर से नीचे होती है; लेकिन गैर-शून्य तापमान पर फर्मी-डिराक वितरण के अनुगामी ऊर्जा स्तर भरे जाते हैं। | ||
आंतरिक (अनडोप्ड) अर्धचालकों में फर्मी स्तर दो अनुमत | आंतरिक (अनडोप्ड) अर्धचालकों में फर्मी स्तर दो अनुमत बंध के मध्य ऊर्जा अंतराल या एक वर्जित बंध के बीच में होता है जिसे [[संयोजी बंध]] और [[चालन बैंड|संवाहन]] [[संयोजी बंध|बंध]] कहा जाता है। सामान्यतः संयोजी बंध, निषिद्ध बंध के ठीक नीचे पूर्णतया व्याप्त होता है। सामान्य रूप से फर्मी स्तर के ऊपर संवाहन बंध लगभग पूर्णतया रिक्त होता है। चूंकि संयोजी बंध प्रायः इतना भरा होता है, कि इसके इलेक्ट्रॉन गतिहीन होते हैं, और विद्युत प्रवाह के रूप में प्रवाहित नहीं हो सकते हैं। | ||
यद्यपि, अगर | यद्यपि, अगर संयोजी बंध में एक इलेक्ट्रॉन संवाहन बंध तक पहुंचने के लिए पर्याप्त ऊर्जा प्राप्त करता है (अन्य इलेक्ट्रॉन, छिद्रों, फोटॉन या कंपन क्रिस्टल जाली के साथ परस्पर क्रिया के परिणामस्वरूप), प्रायः यह रिक्त संवाहन बंध ऊर्जा स्तर के बीच स्वतंत्र रूप से प्रवाह कर सकता है। इसके अतिरिक्त, यह एक छिद्र भी पीछे छोड़ देगा जो ठीक एक भौतिक आवेशित कण जैसा विद्युत प्रवाह की तरह प्रवाहित हो सकता है। | ||
वाहक उत्पादन ('कैरियर जेनरेशन') उन प्रक्रियाओं का वर्णन करती है जिनके द्वारा इलेक्ट्रॉन ऊर्जा प्राप्त करते हैं और संयोजी बंध से संवाहन बंध की ओर बढ़ते हैं, जिससे दो मोबाइल वाहक उत्पन्न होते हैं; जबकि पुनर्संयोजन उन प्रक्रियाओं का वर्णन करता है जिनके द्वारा एक संवाहन बंध इलेक्ट्रॉन ऊर्जा | वाहक उत्पादन ('कैरियर जेनरेशन') उन प्रक्रियाओं का वर्णन करती है जिनके द्वारा इलेक्ट्रॉन ऊर्जा प्राप्त करते हैं और संयोजी बंध से संवाहन बंध की ओर बढ़ते हैं, जिससे दो मोबाइल वाहक उत्पन्न होते हैं; जबकि पुनर्संयोजन उन प्रक्रियाओं का वर्णन करता है जिनके द्वारा एक संवाहन बंध इलेक्ट्रॉन ऊर्जा नष्ट कर देता है और संयोजी बंध में एक इलेक्ट्रॉन छिद्र की ऊर्जा अवस्था को पुनः प्राप्त कर लेता है। | ||
इन प्रक्रियाओं को क्वांटीकृत ऊर्जा और [[क्रिस्टल गति|क्रिस्टल संवेग]] [[फ़ोनन]] का संरक्षण करना चाहिए, और कंपन जाली संवेग के संरक्षण में एक विशाल भूमिका निभाती है, क्योंकि संघट्टन में, फोटॉन अपनी ऊर्जा के संबंध में बहुत कम संवेग स्थानांतरित कर सकते हैं। | इन प्रक्रियाओं को क्वांटीकृत ऊर्जा और [[क्रिस्टल गति|क्रिस्टल संवेग]] [[फ़ोनन]] का संरक्षण करना चाहिए, और कंपन जाली संवेग के संरक्षण में एक विशाल भूमिका निभाती है, क्योंकि संघट्टन में, फोटॉन अपनी ऊर्जा के संबंध में बहुत कम संवेग स्थानांतरित कर सकते हैं। | ||
== | == उत्पादन और पुनर्संयोजन में संबंध == | ||
[[File:diffusion center.gif|thumb|upright=1.6|right|निम्नलिखित छवि | [[File:diffusion center.gif|thumb|upright=1.6|right|निम्नलिखित छवि आंतरिक अर्धचालक बार के केंद्र में बढ़ती प्रकाश तीव्रता (पीढ़ी दर / सेमी<sup>3</sup>) के साथ उत्पन्न होने वाले अतिरिक्त वाहक (हरा: इलेक्ट्रॉन और बैंगनी: छेद) में परिवर्तन दिखाती है। छिद्रों की तुलना में इलेक्ट्रॉनों का विसरण स्थिरांक अधिक होता है जिसके कारण केंद्र में छिद्रों की तुलना में इलेक्ट्रॉनों की संख्या कम होती है।]]वाहक उत्पादन और पुनर्संयोजन अर्धचालकों में सदैव उष्मा इकाई के रूप मे और प्रकाशतः दोनों तरह से हो रही है। जैसा कि [[ऊष्मप्रवैगिकी]] द्वारा भविष्यवाणी की गई है, [[थर्मल संतुलन|ऊष्मीय संतुलन]] में एक सामग्री में उत्पादन और पुनर्संयोजन दरें संतुलित होंगी जिससे रिणामी आवेश वाहक घनत्व स्थिर रहे। प्रत्येक ऊर्जा बंध में ऊर्जा स्तर के वास की परिणामी संभावना फर्मी-डिराक सांख्यिकी द्वारा दी गई है। | ||
इलेक्ट्रॉन और छिद्र घनत्व का उत्पाद (<math>n</math> और <math>p</math>) एक स्थिरांक है <math>(n_o p_o=n_i^2)</math> संतुलन में, वाहक उत्पादन और पुनर्संयोजन को समान दरों पर अनुरक्षण किया जाता है। जब वाहक का अधिशेष होता है (यानी, <math>n p>n_i^2</math>), तो पुनर्संयोजन की दर पीढ़ी की दर से अधिक हो जाती है जो सिस्टम को वापस संतुलन की ओर ले जाती है। इसी तरह, जब वाहकों की कमी होती है ( | इलेक्ट्रॉन और छिद्र घनत्व का उत्पाद (<math>n</math> और <math>p</math>) एक स्थिरांक है <math>(n_o p_o=n_i^2)</math> संतुलन में, वाहक उत्पादन और पुनर्संयोजन को समान दरों पर अनुरक्षण किया जाता है। जब वाहक का अधिशेष होता है (यानी, <math>n p>n_i^2</math>), तो पुनर्संयोजन की दर पीढ़ी की दर से अधिक हो जाती है जो सिस्टम को वापस संतुलन की ओर ले जाती है। इसी तरह, जब वाहकों की कमी होती है (अथार्त, <math>n p<n_i^2</math>), तो उत्पादन दर पुनर्संयोजन दर से अधिक हो जाती है जो प्रणाली को फिर से संतुलन की ओर ले जाती है।<ref>{{cite journal | doi = 10.1109/LED.2014.2345058 | volume=35 | issue=10 | title=Optically Excited MOS-Capacitor for Recombination Lifetime Measurement | year=2014 | journal=IEEE Electron Device Letters | pages=986–988 | last1 = Elhami Khorasani | first1 = Arash | last2 = Schroder | first2 = Dieter K. | last3 = Alford | first3 = T. L.| bibcode=2014IEDL...35..986K | s2cid=19785166 }}</ref> जैसे ही इलेक्ट्रॉन एक ऊर्जा बंध से दूसरे में प्रवेश करता है तो ऊर्जा और संवेग जिसे उसने खो दिया है या प्राप्त कर लिया है उसे प्रक्रिया में सम्मिलित अन्य कणों (जैसे फोटॉन, इलेक्ट्रॉन, या कंपन जाली परमाणुओं की प्रणाली) में जाना या आना चाहिए। | ||
== वाहक | == वाहक उत्पादन == | ||
{{See also|अवशोषण (विद्युत चुम्बकीय विकिरण)|}} | {{See also|अवशोषण (विद्युत चुम्बकीय विकिरण)|}} | ||
| Line 28: | Line 28: | ||
अर्धचालकों में प्रकाश उत्तेजन वाहक के अलावा एक बाहरी विद्युत क्षेत्र द्वारा भी उत्पन्न किया जा सकता है, उदाहरण के लिए प्रकाश उत्सर्जक डायोड और [[ट्रांजिस्टर]] में। | अर्धचालकों में प्रकाश उत्तेजन वाहक के अलावा एक बाहरी विद्युत क्षेत्र द्वारा भी उत्पन्न किया जा सकता है, उदाहरण के लिए प्रकाश उत्सर्जक डायोड और [[ट्रांजिस्टर]] में। | ||
जब पर्याप्त ऊर्जा वाला प्रकाश एक अर्धचालक से टकराता है तो यह | जब पर्याप्त ऊर्जा वाला प्रकाश एक अर्धचालक से टकराता है तो यह ऊर्जा अंतराल में इलेक्ट्रॉनों को उत्तेजित कर सकता है। यह सामग्री के विद्युत प्रतिरोध को अस्थायी रूप से कम करने वाले अतिरिक्त आवेश वाहक उत्पन्न करता है। प्रकाश की उपस्थिति में यह उच्च चालकता [[फोटोकॉन्डक्टिविटी|प्रकाशिक चालकता]] के रूप में जाना जाता है। बिजली में प्रकाश के इस रूपांतरण का व्यापक रूप से फोटोडायोड में उपयोग किया जाता है। | ||
== पुनर्संयोजन तंत्र == | == पुनर्संयोजन तंत्र == | ||
{{main| | {{main|वाहक जीवनकाल}} | ||
वाहक पुनर्संयोजन | |||
वाहक पुनर्संयोजन अनेक शिथिलिकरण आयोजनों के माध्यम से हो सकता है। बंध-टू-बंध पुनर्संयोजन, शॉक्ले-रीड-हॉल (एसआरएच) ट्रैप-असिस्टेड पुनर्संयोजन, बरमा पुनर्संयोजन और सतह पुनर्संयोजन मुख्य हैं। इन क्षय मार्ग को विकिरण और गैर-विकिरण में अलग किया जा सकता है। उत्तरार्द्ध तब होता है जब औसत जीवनकाल के बाद अतिरिक्त ऊर्जा को फोनन उत्सर्जन <math>\tau_{nr}</math> द्वारा ऊष्मा में परिवर्तित किया जाता है, जबकि पूर्व में ऊर्जा का कम से कम हिस्सा एक विकिरण जीवनकाल के बाद में प्रकाश उत्सर्जन या [[चमक|प्रदीप्ति]] <math>\tau_{r}</math> द्वारा जारी किया जाता है। इसके बाद [[वाहक जीवनकाल]] <math>\tau </math> दोनों प्रकार की घटनाओं की दर से प्राप्त किया जाता है:<ref>{{Citation |last1=Pelant|first1=Ivan |title=Luminescence of disordered semiconductors |date=2012-02-09| work=Luminescence Spectroscopy of Semiconductors |pages=242–262 |publisher=Oxford University Press| isbn=9780199588336 |last2=Valenta|first2=Jan| doi=10.1093/acprof:oso/9780199588336.003.0009}}</ref> | |||
<math display="block">\frac{1}{\tau}=\frac{1}{\tau_{r}}+\frac{1}{\tau_{nr}}</math> | <math display="block">\frac{1}{\tau}=\frac{1}{\tau_{r}}+\frac{1}{\tau_{nr}}</math> | ||
| Line 42: | Line 43: | ||
== विकिरण पुनर्संयोजन == | == विकिरण पुनर्संयोजन == | ||
=== | === बंध-टू-बंध रेडिएटिव पुनर्संयोजन === | ||
बंध-से-बंध पुनर्संयोजन एक रेडिएटिव प्रक्रिया से संवाहन बंध से संयोजी बंध तक इलेक्ट्रॉनों की झंपन प्रक्रिया का नाम है। बंध-से-बंध पुनर्संयोजन के समय अवशोषित ऊर्जा को फोटॉन के रूप में सहज उत्सर्जन का एक रूप सामग्री द्वारा जारी किया जाता है। इन फोटॉन में उतनी ही या कम ऊर्जा होती है जितनी पहले अवशोषित की गई थी। यह प्रभाव है कि एल ई डी प्रकाश कैसे बनाते हैं। क्योंकि फोटॉन अपेक्षाकृत कम [[गति|संवेग]] वहन करता है, विकिरण पुनर्संयोजन केवल [[प्रत्यक्ष बैंडगैप|प्रत्यक्ष ऊर्जा अंतराल]] सामग्री में महत्वपूर्ण है। इस प्रक्रिया को द्विध्रुवीय पुनर्संयोजन के रूप में भी जाना जाता है<ref>{{Cite journal |last1=Stranks|first1=Samuel D.| last2=Burlakov|first2=Victor M.| last3=Leijtens|first3=Tomas |last4=Ball|first4=James M. |last5=Goriely|first5=Alain| last6=Snaith|first6=Henry J. |date=2014-09-11| title=Recombination Kinetics in Organic-Inorganic Perovskites: Excitons, Free Charge, and Subgap States |journal=Physical Review Applied |volume=2 |issue=3|pages=034007 |doi=10.1103/PhysRevApplied.2.034007|bibcode=2014PhRvP...2c4007S}}</ref>। | |||
इस प्रकार का पुनर्संयोजन | इस प्रकार का पुनर्संयोजन उत्तेजित अवस्था में इलेक्ट्रॉनों और छिद्रों के घनत्व पर निर्भर करता है, जिसे क्रमशः <math>n(t)</math> और <math>p(t)</math> से निरूपित किया जाता है। आइए हम विकिरण पुनर्संयोजन को <math>R_r</math> और वाहक उत्पादन दर को (G) जी के रूप में प्रस्तुत करते हैं। | ||
संपूर्ण उत्पादन थर्मल उत्पादन G<sub>0</sub> और अर्धचालक G<sub>L</sub> पर प्रकाश उद्दीप्त के कारण उत्पादन का योग है: | |||
<math display="block"> G = G_0 + G_L</math> | <math display="block"> G = G_0 + G_L</math> | ||
यहां हम उस | यहां हम उस स्थिति पर विचार करेंगे जिसमें अर्धचालक पर कोई द्युति नहीं है। इसलिए <math> G_L = 0</math> और <math> G = G_0 </math>, और हम वाहक घनत्व में परिवर्तन को समय के फलन के रूप में व्यक्त कर सकते हैं | ||
<math display="block"> {dn \over dt}= G-R_r = G_0 - R_r</math> | <math display="block"> {dn \over dt}= G-R_r = G_0 - R_r</math> | ||
क्योंकि पुनर्संयोजन की दर मुक्त इलेक्ट्रॉनों की | क्योंकि पुनर्संयोजन की दर मुक्त इलेक्ट्रॉनों की सांद्रता और उनके लिए उपलब्ध छिद्रों की सांद्रता दोनों से प्रभावित होती है, हम जानते हैं कि R<sub>r</sub> को np के समानुपाती होना चाहिए: | ||
<math display="block">R_r \propto np</math> | <math display="block">R_r \propto np</math> | ||
और हम | और हम <math>\propto</math> संकेत को हटाने के लिए आनुपातिकता स्थिरांक B<sub>r</sub> जोड़ते हैं : | ||
<math display="block">R_r=B_r np</math> | <math display="block">R_r=B_r np</math> | ||
यदि अर्धचालक | यदि अर्धचालक ऊष्मीय साम्यावस्था में है, तो जिस दर पर इलेक्ट्रॉनों और छिद्रों का पुनर्संयोजन उस दर से संतुलित होना चाहिए, जिस पर वे संयोजी बंध से संवाहन बंध तक एक इलेक्ट्रॉन के सहज संक्रमण से उत्पन्न होते हैं। पुनर्संयोजन दर <math>R_0</math> ऊष्मीय उत्पादन दर <math>G_0</math> से यथार्थत: संतुलित होना चाहिए। <ref name="sheng-p1402">{{Cite book| url=http://cds.cern.ch/record/1066014 |title=Semiconductor Physical Electronics |date=2006|isbn=978-0-387-28893-2|editor-last=Li|editor-first=Sheng S.|pages=140 |language=en-gb|doi=10.1007/0-387-37766-2}}</ref> | ||
इसलिए: | इसलिए: | ||
<math display="block"> R_0 = G_0 = B_r n_0 p_0 </math> | <math display="block"> R_0 = G_0 = B_r n_0 p_0 </math> | ||
जहाँ <math>n_0</math> और <math>p_0</math> संतुलन वाहक घनत्व हैं। मास एक्शन लॉ (इलेक्ट्रॉनिक्स) <math>np=n_i^2</math> का उपयोग करना , <math>n_i</math> आंतरिक वाहक घनत्व होने की स्थिति में, हम इसे पुनः लिख सकते हैं | |||
मास एक्शन लॉ (इलेक्ट्रॉनिक्स) | |||
<math display="block"> R_0 = G_0 = B_r n_0 p_0= B_r n_i^2 </math> | <math display="block"> R_0 = G_0 = B_r n_0 p_0= B_r n_i^2 </math> | ||
| Line 76: | Line 77: | ||
<math>R_\text{net}= B_r(\Delta n p_0 +\Delta p n_0)</math> | <math>R_\text{net}= B_r(\Delta n p_0 +\Delta p n_0)</math> | ||
एक एन-प्रकार | |||
एक एन-प्रकार अर्धचालक में, | |||
<math>p_0 \ll n_0 </math> और <math>\Delta p \ll n_0 </math> | <math>p_0 \ll n_0 </math> और <math>\Delta p \ll n_0 </math> | ||
| Line 82: | Line 85: | ||
<math>R_{net} \approx B_r\Delta p n_0</math> | <math>R_{net} \approx B_r\Delta p n_0</math> | ||
शुद्ध पुनर्संयोजन वह दर है जिस पर अतिरिक्त | |||
शुद्ध पुनर्संयोजन वह दर है जिस पर अतिरिक्त छिद्र <math>\Delta p</math> लुप्त हो जाते हैं | |||
<math>\frac{d\Delta p}{dt} = - R_\text{net} \approx - B_r\Delta p n_0</math> | <math>\frac{d\Delta p}{dt} = - R_\text{net} \approx - B_r\Delta p n_0</math> | ||
एक मानक | |||
एक मानक चरघातांकी विघटन प्राप्त करने के लिए इस अवकल समीकरण को हल कीजिए | |||
<math>\Delta p = p_{\max}e^{-B_rn_0t}</math> | <math>\Delta p = p_{\max}e^{-B_rn_0t}</math> | ||
कब <math>t = \frac{1}{Bn_0}</math>, सभी अतिरिक्त | जहां T = 0 होने पर P<sub>max</sub> अधिकतम अतिरिक्त छिद्र सांद्रता है। (यह सिद्ध किया जा सकता है कि <math>p_{\max}=\frac{G_L}{Bn_0}</math>, लेकिन यहां हम उस पर चर्चा नहीं करेंगे)। | ||
कब <math>t = \frac{1}{Bn_0}</math>, सभी अतिरिक्त छिद्र लुप्त हो गए होंगे। इसलिए, हम सामग्री में अतिरिक्त छिद्र के जीवनकाल को परिभाषित कर सकते हैं <math>\tau_p = \frac{1}{Bn_0}</math> | |||
इसलिए अल्पसंख्यक वाहक का जीवनकाल बहुसंख्यक वाहक एकाग्रता पर निर्भर है। | इसलिए अल्पसंख्यक वाहक का जीवनकाल बहुसंख्यक वाहक एकाग्रता पर निर्भर है। | ||
=== उत्तेजित उत्सर्जन === | === उत्तेजित उत्सर्जन === | ||
{{See also| | {{See also|प्रेरित उत्सर्जन|लेजर}} | ||
प्रेरित उत्सर्जन एक ऐसी प्रक्रिया है जिसमें एक आपतित फोटॉन एक उत्तेजित इलेक्ट्रॉन के साथ संपर्क करता है, जिससे यह चरण (तरंगों), [[आवृत्ति]], [[ध्रुवीकरण]] (तरंगों) और संचारण दिशा के संदर्भ में घटना के समान गुणों के साथ एक फोटॉन को पुन: संयोजित और उत्सर्जित करता है। उत्तेजनित उत्सर्जन के साथ-साथ जनसंख्या व्युत्क्रमण का सिद्धांत [[लेज़र]] और मेसर्स के संचालन के केंद्र में है। यह बीसवीं शताब्दी की शुरुआत में [[आइंस्टीन गुणांक]] द्वारा दिखाया गया है कि यदि उत्साहित और मूल स्तर डीजेनरेसी ([[वंशीय यांत्रिकी]]) हैं तो अवशोषण दर <math>W_{12}</math>और उत्तेजित उत्सर्जन दर <math>W_{21}</math>समान हैं।<ref>{{Cite book |title=Principles of Lasers ...| last=Svelto.| date=1989| pages=3| oclc=249201544}}</ref> यदि स्तर 1 और स्तर 2 क्रमशः <math>g_1</math>-गुना और <math>g_2</math>गुना पतित हैं, तो नया संबंध है:<math display="block">g_1 W_{12}= g_2 W_{21}.</math> | |||
=== | === अनुग्राही उत्सर्जन === | ||
अनुग्राही उत्सर्जन एक बहुपदीय प्रक्रिया है जिसमें एक वाहक ऊर्जा अंतराल के बीच में त्रुटि-संबंधित वेवस्टेट्स में गिर जाता है। अनुग्राही एक ऐसा दोष है जो वाहक धारण करने में सक्षम है। अनुग्राही उत्सर्जन प्रक्रिया छिद्र के साथ इलेक्ट्रॉनों को पुन: संयोजित करती है और ऊर्जा के संरक्षण के लिए फोटॉन का उत्सर्जन करती है। अनुग्राही उत्सर्जन की बहुपदीय प्रकृति के कारण प्रायः एक फोनन भी उत्सर्जित होता है। अनुग्राही उत्सर्जन अधिकांश त्रुटि या आवरण त्रुटि के उपयोग से आगे बढ़ सकता है। <ref>{{cite journal |last1=Blumenau |title=Dislocation Related Photoluminescence in Silicon |journal=Physical Review Letters |date=2001 |volume=87 |issue=18 |page=187404 |doi=10.1103/PhysRevLett.87.187404 |bibcode=2001PhRvL..87r7404B |url=https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.87.187404}}</ref> <ref>{{cite journal |last1=van Dijken |first1=Addy |last2=Meulenkamp |first2=Eric A. |last3=Vanmaekelbergh |first3=Daniël |last4=Meijerink |first4=Andries |title=The Kinetics of the Radiative and Nonradiative Processes in Nanocrystalline ZnO Particles upon Photoexcitation |journal=The Journal of Physical Chemistry B |date=2000-03-01 |volume=104 |issue=8 |pages=1715–1723 |doi=10.1021/jp993327z |url=https://pubs.acs.org/doi/10.1021/jp993327z |issn=1520-6106}}</ref> | |||
== गैर-[[विकिरण पुनर्संयोजन]] == | == गैर-[[विकिरण पुनर्संयोजन]] == | ||
गैर-विकिरण पुनर्संयोजन [[भास्वर]] और अर्धचालक में एक प्रक्रिया है, जिससे | गैर-विकिरण पुनर्संयोजन [[भास्वर|फॉस्फोर]] और अर्धचालक में एक प्रक्रिया है, जिससे आवेश वाहक फोटॉन के स्थान पर फोनन विमोचन करने का पुनर्संयोजन करते हैं। ऑप्टोइलेक्ट्रॉनिक्स और फॉस्फोर में गैर-विकिरणात्मक पुनर्संयोजन एक अवांछित प्रक्रिया है, जो प्रकाश उत्पादन क्षमता को अवनमन करती है और ऊष्मा हास में वृद्धि करती है। | ||
एक अर्धचालक के चालन बंध में इलेक्ट्रॉन एक छिद्र के साथ पुनर्संयोजित होने से पूर्व गैर-विकिरणात्मक जीवन काल औसतकाल होता है। ऑप्टोइलेक्ट्रॉनिक्स में यह एक महत्वपूर्ण मापदण्ड है जहां एक फोटॉन का उत्पादन करने के लिए विकिरणात्मक पुनर्संयोजन की आवश्यकता होती है; यदि गैर-विकिरणात्मक जीवन काल विकिरण से कम है, तो एक वाहक के गैर-विकिरणीय रूप से पुनर्संयोजित होने की संभावना अधिक होती है। इसका परिणाम न्यून आंतरिक क्वांटम दक्षता में होता है। | |||
=== शॉक्ले -रीड -हॉल (एसआरएच) === | === शॉक्ले -रीड -हॉल (एसआरएच) === | ||
शॉकले-रीड-हॉल पुनर्संयोजन(एसआरएच) में, जिसे ट्रैप-सहायक पुनर्संयोजन भी कहा जाता है, बंध के बीच संक्रमण में इलेक्ट्रॉन एक [[डोपेंट]] या [[क्रिस्टल दोष|क्रिस्टल जाली]] में त्रुटि द्वारा ऊर्जा अंतराल के भीतर बनाई गई एक नई ऊर्जा स्तर (स्थानीय स्तर) से पारित होता है; ऐसी ऊर्जा अवस्थाओं को विपाश कहा जाता हैं। गैर-विकिरणात्मक पुनर्संयोजन मुख्य रूप से ऐसे स्थलों पर होता है। ऊर्जा का आदान-प्रदान जाली कंपन के रूप में होता है, फोनन सामग्री के साथ तापीय ऊर्जा का आदान-प्रदान करता है। | |||
चूंकि जाल वाहक के बीच गति में अंतर को अवशोषित कर सकते हैं, एसआरएच [[सिलिकॉन]] और अन्य [[प्रत्यक्ष और अप्रत्यक्ष बैंड अंतराल]] सामग्री में प्रमुख पुनर्संयोजन प्रक्रिया | चूंकि जाल वाहक के बीच गति में अंतर को अवशोषित कर सकते हैं, एसआरएच [[सिलिकॉन]] और अन्य [[प्रत्यक्ष और अप्रत्यक्ष बैंड अंतराल|प्रत्यक्ष और अप्रत्यक्ष बंध अंतराल]] सामग्री में प्रमुख पुनर्संयोजन प्रक्रिया है। हालांकि, ट्रैप-असिस्टेड पुनर्संयोजन भी बहुत कम चार्ज वाहक घनत्व (बहुत निम्न स्तर के इंजेक्शन) की स्थितियों के तहत प्रत्यक्ष और अप्रत्यक्ष बंध अंतराल सामग्री में या [[पेरोव्साइट सोलर सेल]] जैसे जाल के उच्च घनत्व वाली सामग्री में हावी हो सकता है। इस प्रक्रिया का नाम [[विलियम शॉक्ले]], [[विलियम थॉर्नटन पढ़ा|विलियम थॉर्नटन रीड]] और रॉबर्ट एन हॉल<ref>{{cite journal|last1=Shockley|first1=W.|last2=Read|first2=W. T.|title=Statistics of the Recombinations of Holes and Electrons|journal=Physical Review|date=1 September 1952|volume=87|issue=5|pages=835–842|doi=10.1103/PhysRev.87.835|bibcode = 1952PhRv...87..835S }}</ref> के नाम पर रखा गया है,<ref>{{cite journal|last1=Hall|first1=R.N.|title=Germanium rectifier characteristics|journal=Physical Review|date=1951|volume=83|issue=1|page=228}}</ref> जिन्होंने इसे वर्ष 1952 में प्रकाशित किया था। | ||
==== प्रकार के जाल ==== | ==== प्रकार के जाल ==== | ||
===== इलेक्ट्रॉन जाल बनाम | ===== इलेक्ट्रॉन जाल बनाम छिद्र जाल ===== | ||
यद्यपि सभी पुनर्संयोजन की घटनाओं को इलेक्ट्रॉन आंदोलनों के संदर्भ में वर्णित किया जा सकता है, लेकिन उत्साहित इलेक्ट्रॉन और उनके द्वारा छोड़े गए इलेक्ट्रॉन छिद्र के संदर्भ में विभिन्न प्रक्रियाओं की कल्पना करना सामान्य है। इस संदर्भ में, यदि जाल का स्तर संवाहन बंध के निकट है, तो वे अस्थायी रूप से उत्साहित इलेक्ट्रॉन या अन्य शब्दों में, वे इलेक्ट्रॉन जाल हैं। दूसरी ओर, यदि उनकी ऊर्जा संयोजी बंध के निकट है, तो वे छिद्र जाल बन जाते हैं। | |||
===== उथले जाल बनाम गहरे जाल ===== | ===== उथले जाल बनाम गहरे जाल ===== | ||
{{See also| | {{See also|गहरे स्तर का जाल|डैथनियम}} | ||
सामान्यत: उथले और गहरे जाल के बीच अंतर इस बात पर निर्भर करता है कि इलेक्ट्रॉन जाल संवाहन बंध और छिद्र जाल संयोजी बंध के कितने निकट हैं। यदि अनुग्राही और बंध के बीच का अंतर kt (ऊर्जा) से छोटा है। ऊष्मीय ऊर्जा k<sub>B</sub>t, प्रायः यह कहा जाता है कि यह एक उथला जाल है। वैकल्पिक रूप से यदि अंतर ऊष्मीय ऊर्जा से बड़ा है तो इसे गहरा जाल कहा जाता है। यह अंतर उपयोगी है क्योंकि उथले जाल का अधिक सरलता से रिक्तीकरण किया जा सकता है और प्रायः इस प्रकार ऑप्टोइलेक्ट्रोनिक उपकरणों के प्रदर्शन के लिए हानिकारक नहीं होते हैं। | |||
==== | ==== एसआरएच मॉडल ==== | ||
[[File:Shockley-Read-Hall_model_inorganic_semiconductors.png|thumb|शॉक्ले-रीड-हॉल मॉडल में इलेक्ट्रॉन और | [[File:Shockley-Read-Hall_model_inorganic_semiconductors.png|thumb|शॉक्ले-रीड-हॉल मॉडल में इलेक्ट्रॉन और छिद्र अनुग्राही]]एसआरएच मॉडल में चार घटनायें अनुग्राही स्तर में सम्मिलित हो सकती हैं:<ref>{{Cite book|title=SEMICONDUCTOR PHOTONICS.|last=NISOLI, MAURO.|date=2016|publisher=SOCIETA EDITRICE ESCULAPIO|isbn=978-8893850025|oclc=964380194}}</ref> | ||
* | * संवाहन बंध में इलेक्ट्रॉन एक इंट्रागैप अवस्था में विपाशित किया सकता है। | ||
* एक इलेक्ट्रॉन को एक जाल स्तर से | * एक इलेक्ट्रॉन को एक जाल स्तर से संवाहन बंध में उत्सर्जित किया जा सकता है। | ||
* | * संयोजी बंध में छिद्र को एक जाल द्वारा प्रग्रहण किया जा सकता है। यह एक पूरित जाल के अनुरूप है जो एक इलेक्ट्रॉन को संयोजी बंध में अवमुक्त करता है। | ||
* एक | * एक प्रग्रहण किए गए छिद्र को संयोजी बंध में विमुक्त किया जा सकता है। संयोजी बंध से एक इलेक्ट्रॉन के प्रग्रहण के अनुरूप किया जा सकता है। | ||
जब वाहक पुनर्संयोजन जाल के माध्यम से होता है, तो हम इंट्रागैप | जब वाहक पुनर्संयोजन जाल के माध्यम से उत्पन्न होता है, तो हम इंट्रागैप संयोजी द्वारा स्थितियों के संयोजी घनत्व को परिवर्तित कर सकते हैं।<ref name=":1">{{Citation|last1=Kandada|first1=Ajay Ram Srimath|title=Chapter 4. Photophysics of Hybrid Perovskites|date=2016|work=Unconventional Thin Film Photovoltaics|pages=107–140|editor-last=Da Como|editor-first=Enrico|publisher=Royal Society of Chemistry|language=en|doi=10.1039/9781782624066-00107|isbn=9781782622932|last2=D'Innocenzo|first2=Valerio|last3=Lanzani|first3=Guglielmo|last4=Petrozza|first4=Annamaria|editor2-last=De Angelis|editor2-first=Filippo|editor3-last=Snaith|editor3-first=Henry|editor4-last=Walker|editor4-first=Alison}}</ref> अवधि <math>p(n)</math>फंसे हुए इलेक्ट्रॉनों/छिद्रों <math>N_t(1-f_t)</math> के घनत्व से बदल दिया जाता है। | ||
<math display="block">R_{nt}=B_n n N_t (1-f_t)</math> | <math display="block">R_{nt}=B_n n N_t (1-f_t)</math> | ||
जहां <math>N_t</math> सम्पीडित अवस्थाओं का घनत्व है और <math>f_t</math> उस अधिकृत अवस्था की प्रायिकता है। दोनों प्रकार के प्रग्रहण अवस्था को ध्यान में रखते हुए, हम दो प्रग्रहण गुणांक <math>B_n, B_p</math> को परिभाषित कर सकते हैं और दो असम्पीडित (डी-ट्रैपिंग) गुणांक <math>G_n, G_p</math> में परिभाषित कर सकते हैं। साम्यावस्था में, सम्पीडित और असम्पीडित {{nowrap|(<math>R_{nt}=G_{n}</math>}} और <math>R_{pt}=G_{p}</math>) दोनों को संतुलित किया जाना चाहिए। फिर, एक फलन के रूप में चार दरें <math>f_t</math>होना: | |||
<math display="block">\begin{array}{l l} R_{nt}=B_nnN_{t}(1-f_t)& G_n=B_n n_t N_t f_t \\ R_{pt}=B_p p N_t f_t&G_p=B_p p_t N_t (1-f_t) \end{array}</math> | <math display="block">\begin{array}{l l} R_{nt}=B_nnN_{t}(1-f_t)& G_n=B_n n_t N_t f_t \\ R_{pt}=B_p p N_t f_t&G_p=B_p p_t N_t (1-f_t) \end{array}</math> | ||
जहां <math>n_t </math> और <math>p_t </math> जब अर्ध फर्मी स्तर पाश ऊर्जा से सुमेलित होती है तो इलेक्ट्रॉन और छिद्र घनत्व होते हैं। स्थिर स्थिति में इलेक्ट्रॉनों की शुद्ध पुनर्संयोजन दर छिद्रों के लिए शुद्ध पुनर्संयोजन दर से सुमेलित होनी चाहिए, दूसरे शब्दों में: <math>R_{nt}-G_n =R_{pt}-G_p</math>। यह व्यावृति <math>f_t</math> की संभावना को समाप्त करता है और ट्रैप-सहायता पुनर्संयोजन के लिए शॉकली-रीड-हॉल अभिव्यक्ति की ओर जाता है: | |||
स्थिर | |||
<math display="block">R=\frac {np}{\tau_n(p+p_t)+\tau_p(n+n_t)}</math> | <math display="block">R=\frac {np}{\tau_n(p+p_t)+\tau_p(n+n_t)}</math> | ||
जहां इलेक्ट्रॉनों और | जहां इलेक्ट्रॉनों और छिद्रों के लिए औसत जीवनकाल को परिभाषित किया गया है:<ref name=":1" /> | ||
<math display="block">\tau_n=\frac{1}{B_n N_t},\quad \tau_p=\frac{1}{B_p N_t}.</math> | <math display="block">\tau_n=\frac{1}{B_n N_t},\quad \tau_p=\frac{1}{B_p N_t}.</math> | ||
| Line 143: | Line 153: | ||
=== बरमा पुनर्संयोजन === | === बरमा पुनर्संयोजन === | ||
{{main| | {{main|बरमा प्रभाव}} | ||
बरमा पुनर्संयोजन में ऊर्जा | बरमा पुनर्संयोजन में ऊर्जा एक तीसरे वाहक को दी जाती है जो किसी अन्य ऊर्जा बंध में जाए बिना ही उच्च ऊर्जा स्तर तक उत्साहित होता है। पारस्परिक क्रिया के पश्चात, तीसरा वाहक सामान्य रूप से ऊष्मीय कंपन के लिए अपनी अतिरिक्त ऊर्जा नष्ट कर देता है। यह प्रक्रिया एक तीन-कण अंतःक्रिया होने के कारण सामान्यतः यह केवल असंतुलित स्थितियों में महत्वपूर्ण होती है जब वाहक घनत्व बहुत अधिक होता है। [[बरमा प्रभाव]] प्रक्रिया आसानी से उत्पन्न नहीं होती है, क्योंकि तीसरे कण को अस्थिर उच्च-ऊर्जा अवस्था में प्रक्रिया शुरू करनी होगी। | ||
ऊष्मीय संतुलन में बरमा पुनर्संयोजन <math>R_A</math> और ऊष्मीय उत्पादन दर <math>G_0</math> एक दूसरे के बराबर होती है<ref name="sheng-p143">{{Cite book|date=2006|editor-last=Li|editor-first=Sheng S.|title=Semiconductor Physical Electronics|language=en-gb|pages=143|doi=10.1007/0-387-37766-2|isbn=978-0-387-28893-2|url=http://cds.cern.ch/record/1066014}}</ref> | |||
<math display="block"> | <math display="block"> | ||
R_{A0} = G_0 = C_n n_0^2 p_0 + C_p n_0 p_0^2 | R_{A0} = G_0 = C_n n_0^2 p_0 + C_p n_0 p_0^2 | ||
</math> | </math> | ||
जहां <math>C_n,C_p</math> बरमा अधिकृत संभावनाएं हैं। असाम्य अवस्था बरमा पुनर्संयोजन दर <math>r_A</math> और परिणामस्वरूप शुद्ध पुनर्संयोजन दर <math>U_A</math> स्थिर-राज्य की स्थिति के अधीन हैं<ref name="sheng-p143"/> | |||
<math display="block"> | <math display="block"> | ||
| Line 163: | Line 173: | ||
\tau_A = \frac{\Delta n}{R_A} = \frac{1}{ n^2C_n + 2n_i^2(C_n+C_p) +p^2C_p } \,. | \tau_A = \frac{\Delta n}{R_A} = \frac{1}{ n^2C_n + 2n_i^2(C_n+C_p) +p^2C_p } \,. | ||
</math> | </math> | ||
वर्ष 2007 में एलईडी दक्षता में अवनति लाने वाले तंत्र की पहचान बरमा पुनर्संयोजन के रूप में की गई थी जो मिश्रित प्रतिक्रिया के साथ हुई थी।<ref name=stevenson>Stevenson, Richard (August 2009) [https://spectrum.ieee.org/semiconductors/optoelectronics/the-leds-dark-secret "The LED's Dark Secret: Solid-state lighting won't supplant the lightbulb until it can overcome the mysterious malady known as droop"]. IEEE Spectrum</ref> वर्ष 2013 में एक प्रायोगिक अध्ययन में अधियाचित किया गया था कि बरमा पुनर्संयोजन को दक्षता में अवनति लाने के कारण के रूप में पहचाना गया है।<ref>{{cite web|author1=Justin Iveland |author2=Lucio Martinelli |author3=Jacques Peretti |author4=James S. Speck |author5=Claude Weisbuch. |title=Cause of LED Efficiency Droop Finally Revealed|url=https://www.sciencedaily.com/releases/2013/04/130423102328.htm|website=Physical Review Letters, 2013|publisher=Science Daily|access-date=23 April 2013}}</ref> हालांकि, यह विवादित है कि क्या इस अध्ययन में पाए गए बरमा हानि की मात्रा अवनति को समझाने के लिए पर्याप्त है। अन्य अक्सर उद्धृत किए गए साक्ष्य के खिलाफ मुख्य ड्रॉप-पैदा करने वाले तंत्र के रूप में इस तंत्र का कम तापमान निर्भरता है, जो ड्रॉप के लिए पाए जाने वाले के विपरीत है। | |||
=== सतह पुनर्संयोजन === | === सतह पुनर्संयोजन === | ||
अर्धचालक की सतह पर संपाश (ट्रैप)-सहायता प्राप्त पुनर्संयोजन को सतह पुनर्संयोजन के रूप में जाना जाता है। | अर्धचालक की सतह पर संपाश (ट्रैप)-सहायता प्राप्त पुनर्संयोजन को सतह पुनर्संयोजन के रूप में जाना जाता है। यह तब होता है जब अर्धचालक क्रिस्टल के अचानक बंद होने से लटकने वाले बंध के कारण अर्धचालक फॉर्म की सतह पर या उसके पास जाल होता है। सतह पुनर्संयोजन को सतह पुनर्संयोजन वेग की विशेषता है जो सतह दोषों के घनत्व पर निर्भर करता है।<ref>{{Cite book|title=The Physics of Solar Cells|last=Nelson|first=Jenny|publisher=Imperial College Press|year=2003|isbn=978-1-86094-340-9|location=London|pages=116}}</ref> सतह पर मुक्त वाहकों के संग्रह और निष्कर्षण के कारण सौर कोशिकाओं की सतह पुनर्संयोजन जैसे अनुप्रयोगों में पुनर्संयोजन का प्रमुख तंत्र हो सकता है। सौर कोशिकाओं के कुछ अनुप्रयोगों में एक बड़े ऊर्जा अंतराल के साथ पारदर्शी सामग्री की एक परत जिसे विंडो लेयर के रूप में भी जाना जाता है तथा जिसका उपयोग सतह के पुनर्संयोजन को कम करने के लिए किया जाता है। सतह के पुनर्संयोजन को कम करने के लिए निष्क्रियता तकनीक भी कार्यरत हैं।<ref>{{Cite journal|last1=Eades|first1=W.D.|last2=Swanson|first2=R.M.|date=1985|title=Calculation of surface generation and recombination velocities at the Si-SiO2 interface|journal=Journal of Applied Physics|volume=58|issue=11|pages=4267–4276|issn=0021-8979|doi=10.1063/1.335562|bibcode=1985JAP....58.4267E}}</ref> | ||
=== लैंग्विन पुनः संयोजन === | === लैंग्विन पुनः संयोजन === | ||
सामान्य विचलता प्रणालियों में मुक्त वाहकों के लिए पुनर्संयोजन दर को प्रायः लैंग्विन पुनर्संयोजन दर के साथ वर्णित किया जाता है।<ref>{{Cite web|url=https://blog.disorderedmatter.eu/2008/04/04/recombination-in-low-mobility-semiconductors-langevin-theory/|title = Recombination in low mobility semiconductors: Langevin theory|date = 4 April 2008}}</ref> प्रायः प्रतिरूपों का उपयोग अव्यवस्थित प्रणालियों जैसे कि जैविक सामग्री (और इसलिए कार्बनिक सौर कोशिकाओं के लिए प्रासंगिक है) और अन्य ऐसी प्रणालियों के लिए किया जाता है।<ref name="LakhwaniRao2014">{{cite journal|last1=Lakhwani|first1=Girish|last2=Rao|first2=Akshay|last3=Friend|first3=Richard H.|title=Bimolecular Recombination in Organic Photovoltaics|journal=Annual Review of Physical Chemistry|volume=65|issue=1|year=2014|pages=557–581|issn=0066-426X|doi=10.1146/annurev-physchem-040513-103615|pmid=24423376|bibcode=2014ARPC...65..557L}}</ref> लैंग्विन पुनर्संयोजन शक्ति | सामान्य विचलता प्रणालियों में मुक्त वाहकों के लिए पुनर्संयोजन दर को प्रायः लैंग्विन पुनर्संयोजन दर के साथ वर्णित किया जाता है।<ref>{{Cite web|url=https://blog.disorderedmatter.eu/2008/04/04/recombination-in-low-mobility-semiconductors-langevin-theory/|title = Recombination in low mobility semiconductors: Langevin theory|date = 4 April 2008}}</ref> प्रायः प्रतिरूपों का उपयोग अव्यवस्थित प्रणालियों जैसे कि जैविक सामग्री (और इसलिए कार्बनिक सौर कोशिकाओं के लिए प्रासंगिक है) और अन्य ऐसी प्रणालियों के लिए किया जाता है।<ref name="LakhwaniRao2014">{{cite journal|last1=Lakhwani|first1=Girish|last2=Rao|first2=Akshay|last3=Friend|first3=Richard H.|title=Bimolecular Recombination in Organic Photovoltaics|journal=Annual Review of Physical Chemistry|volume=65|issue=1|year=2014|pages=557–581|issn=0066-426X|doi=10.1146/annurev-physchem-040513-103615|pmid=24423376|bibcode=2014ARPC...65..557L}}</ref> लैंग्विन पुनर्संयोजन शक्ति <math>\gamma = \tfrac{q}{\varepsilon}\mu</math> के रूप में परिभाषित किया गया है। | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 188: | Line 198: | ||
* [http://www.pvlighthouse.com.au/calculators/Band%20gap%20calculator/Band%20gap%20calculator.aspx PV Lighthouse Band Gap Calculator] | * [http://www.pvlighthouse.com.au/calculators/Band%20gap%20calculator/Band%20gap%20calculator.aspx PV Lighthouse Band Gap Calculator] | ||
*[https://www.pveducation.org/pvcdrom/design-of-silicon-cells/surface-recombination PV Education] | *[https://www.pveducation.org/pvcdrom/design-of-silicon-cells/surface-recombination PV Education] | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:CS1 British English-language sources (en-gb)]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:Created On 01/02/2023]] | [[Category:Created On 01/02/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Optoelectronics]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:अर्धचालकों]] | |||
[[Category:चार्ज वाहक]] | |||
Latest revision as of 10:10, 15 February 2023
अर्धचालकों की ठोस-अवस्था भौतिकी में, वाहक उत्पादन और वाहक पुनर्संयोजन ऐसी प्रक्रियाएं हैं जिनके द्वारा चल आवेश वाहक (इलेक्ट्रॉन और इलेक्ट्रॉन छिद्र) उत्पन्न और निष्कासित किए जाते हैं। वाहक उत्पादन और पुनर्संयोजन प्रक्रियाएं कई ऑप्टो इलेक्ट्रॉनिकीय प्रौद्योगिकी अर्धचालक उपकरणों जैसे कि प्रकाश डायोड, प्रकाश उत्सर्जक डायोड और लेज़र डायोड संचालन के लिए मूल सिद्धान्त हैं। वे द्विध्रुवी संधि (जंक्शन) ट्रांजिस्टर और पी-एन संधि डायोड जैसे पी-एन संधि उपकरणों के पूर्ण विश्लेषण के लिए भी महत्वपूर्ण हैं।
इलेक्ट्रॉन छिद्र जोड़ी अकार्बनिक अर्धचालकों में उत्पादन और पुनर्संयोजन की मूलभूत इकाई है, जो संयोजी बंध (वैलेंस बंध) और संवाहन बंध (कंडक्शन बंध) के मध्य एक इलेक्ट्रॉन संक्रमण के अनुरूप होती है, जहां इलेक्ट्रॉन की उत्पादन संयोजी बंध से संवाहन बंध में संक्रमण होता है और पुनर्संयोजन एक उत्क्रम संक्रमण की ओर अग्रसर करता है ।
अवलोकन
अन्य ठोस पदार्थों की तरह, अर्धचालक पदार्थों में एक इलेक्ट्रॉनिक बंध संरचना होती है जो सामग्री के क्रिस्टल गुणों द्वारा निर्धारित होती है। इलेक्ट्रॉनों के बीच ऊर्जा वितरण को फर्मी स्तर और इलेक्ट्रॉनों के तापमान द्वारा वर्णित किया गया है। निरपेक्ष शून्य तापमान पर, सभी इलेक्ट्रॉन की ऊर्जा फर्मी स्तर से नीचे होती है; लेकिन गैर-शून्य तापमान पर फर्मी-डिराक वितरण के अनुगामी ऊर्जा स्तर भरे जाते हैं।
आंतरिक (अनडोप्ड) अर्धचालकों में फर्मी स्तर दो अनुमत बंध के मध्य ऊर्जा अंतराल या एक वर्जित बंध के बीच में होता है जिसे संयोजी बंध और संवाहन बंध कहा जाता है। सामान्यतः संयोजी बंध, निषिद्ध बंध के ठीक नीचे पूर्णतया व्याप्त होता है। सामान्य रूप से फर्मी स्तर के ऊपर संवाहन बंध लगभग पूर्णतया रिक्त होता है। चूंकि संयोजी बंध प्रायः इतना भरा होता है, कि इसके इलेक्ट्रॉन गतिहीन होते हैं, और विद्युत प्रवाह के रूप में प्रवाहित नहीं हो सकते हैं।
यद्यपि, अगर संयोजी बंध में एक इलेक्ट्रॉन संवाहन बंध तक पहुंचने के लिए पर्याप्त ऊर्जा प्राप्त करता है (अन्य इलेक्ट्रॉन, छिद्रों, फोटॉन या कंपन क्रिस्टल जाली के साथ परस्पर क्रिया के परिणामस्वरूप), प्रायः यह रिक्त संवाहन बंध ऊर्जा स्तर के बीच स्वतंत्र रूप से प्रवाह कर सकता है। इसके अतिरिक्त, यह एक छिद्र भी पीछे छोड़ देगा जो ठीक एक भौतिक आवेशित कण जैसा विद्युत प्रवाह की तरह प्रवाहित हो सकता है।
वाहक उत्पादन ('कैरियर जेनरेशन') उन प्रक्रियाओं का वर्णन करती है जिनके द्वारा इलेक्ट्रॉन ऊर्जा प्राप्त करते हैं और संयोजी बंध से संवाहन बंध की ओर बढ़ते हैं, जिससे दो मोबाइल वाहक उत्पन्न होते हैं; जबकि पुनर्संयोजन उन प्रक्रियाओं का वर्णन करता है जिनके द्वारा एक संवाहन बंध इलेक्ट्रॉन ऊर्जा नष्ट कर देता है और संयोजी बंध में एक इलेक्ट्रॉन छिद्र की ऊर्जा अवस्था को पुनः प्राप्त कर लेता है।
इन प्रक्रियाओं को क्वांटीकृत ऊर्जा और क्रिस्टल संवेग फ़ोनन का संरक्षण करना चाहिए, और कंपन जाली संवेग के संरक्षण में एक विशाल भूमिका निभाती है, क्योंकि संघट्टन में, फोटॉन अपनी ऊर्जा के संबंध में बहुत कम संवेग स्थानांतरित कर सकते हैं।
उत्पादन और पुनर्संयोजन में संबंध
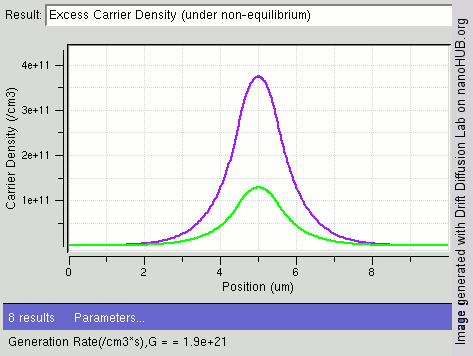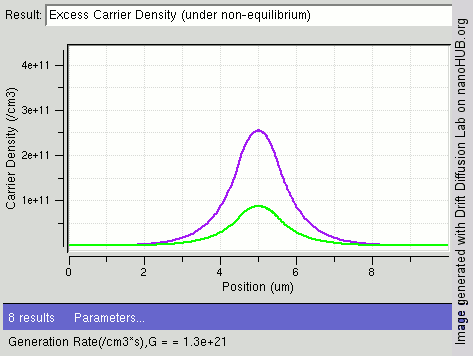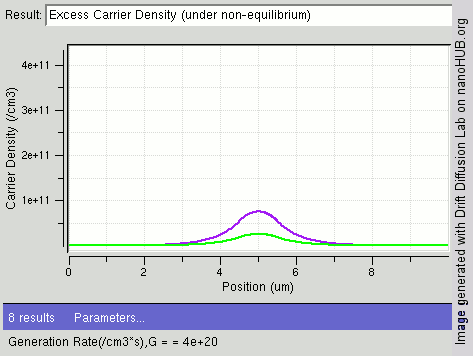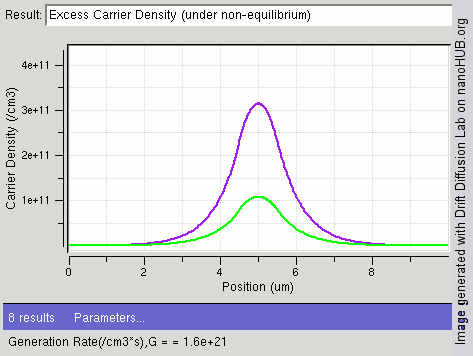
वाहक उत्पादन और पुनर्संयोजन अर्धचालकों में सदैव उष्मा इकाई के रूप मे और प्रकाशतः दोनों तरह से हो रही है। जैसा कि ऊष्मप्रवैगिकी द्वारा भविष्यवाणी की गई है, ऊष्मीय संतुलन में एक सामग्री में उत्पादन और पुनर्संयोजन दरें संतुलित होंगी जिससे रिणामी आवेश वाहक घनत्व स्थिर रहे। प्रत्येक ऊर्जा बंध में ऊर्जा स्तर के वास की परिणामी संभावना फर्मी-डिराक सांख्यिकी द्वारा दी गई है।
इलेक्ट्रॉन और छिद्र घनत्व का उत्पाद ( और ) एक स्थिरांक है संतुलन में, वाहक उत्पादन और पुनर्संयोजन को समान दरों पर अनुरक्षण किया जाता है। जब वाहक का अधिशेष होता है (यानी, ), तो पुनर्संयोजन की दर पीढ़ी की दर से अधिक हो जाती है जो सिस्टम को वापस संतुलन की ओर ले जाती है। इसी तरह, जब वाहकों की कमी होती है (अथार्त, ), तो उत्पादन दर पुनर्संयोजन दर से अधिक हो जाती है जो प्रणाली को फिर से संतुलन की ओर ले जाती है।[1] जैसे ही इलेक्ट्रॉन एक ऊर्जा बंध से दूसरे में प्रवेश करता है तो ऊर्जा और संवेग जिसे उसने खो दिया है या प्राप्त कर लिया है उसे प्रक्रिया में सम्मिलित अन्य कणों (जैसे फोटॉन, इलेक्ट्रॉन, या कंपन जाली परमाणुओं की प्रणाली) में जाना या आना चाहिए।
वाहक उत्पादन
जब प्रकाश एक सामग्री के साथ सूचना का आदान प्रदान करता है, तो यह या तो अवशोषित (विद्युत चुम्बकीय विकिरण) हो सकता है (मुक्त वाहक या एक एक्सिटॉन की एक जोड़ी उत्पन्न करना) या यह एक पुनर्संयोजन घटना को उत्तेजित कर सकता है। जनित फोटॉन में घटना के लिए जिम्मेदार एक समान गुण हैं। अवशोषण फोटोडायोड्स, सौर कोशिकाओं और अन्य अर्धचालक फोटोडिटेक्टर में सक्रिय प्रक्रिया है, जबकि उत्तेजित उत्सर्जन लेजर डायोड में संचालन का सिद्धांत है।
अर्धचालकों में प्रकाश उत्तेजन वाहक के अलावा एक बाहरी विद्युत क्षेत्र द्वारा भी उत्पन्न किया जा सकता है, उदाहरण के लिए प्रकाश उत्सर्जक डायोड और ट्रांजिस्टर में।
जब पर्याप्त ऊर्जा वाला प्रकाश एक अर्धचालक से टकराता है तो यह ऊर्जा अंतराल में इलेक्ट्रॉनों को उत्तेजित कर सकता है। यह सामग्री के विद्युत प्रतिरोध को अस्थायी रूप से कम करने वाले अतिरिक्त आवेश वाहक उत्पन्न करता है। प्रकाश की उपस्थिति में यह उच्च चालकता प्रकाशिक चालकता के रूप में जाना जाता है। बिजली में प्रकाश के इस रूपांतरण का व्यापक रूप से फोटोडायोड में उपयोग किया जाता है।
पुनर्संयोजन तंत्र
वाहक पुनर्संयोजन अनेक शिथिलिकरण आयोजनों के माध्यम से हो सकता है। बंध-टू-बंध पुनर्संयोजन, शॉक्ले-रीड-हॉल (एसआरएच) ट्रैप-असिस्टेड पुनर्संयोजन, बरमा पुनर्संयोजन और सतह पुनर्संयोजन मुख्य हैं। इन क्षय मार्ग को विकिरण और गैर-विकिरण में अलग किया जा सकता है। उत्तरार्द्ध तब होता है जब औसत जीवनकाल के बाद अतिरिक्त ऊर्जा को फोनन उत्सर्जन द्वारा ऊष्मा में परिवर्तित किया जाता है, जबकि पूर्व में ऊर्जा का कम से कम हिस्सा एक विकिरण जीवनकाल के बाद में प्रकाश उत्सर्जन या प्रदीप्ति द्वारा जारी किया जाता है। इसके बाद वाहक जीवनकाल दोनों प्रकार की घटनाओं की दर से प्राप्त किया जाता है:[2]
विकिरण पुनर्संयोजन
बंध-टू-बंध रेडिएटिव पुनर्संयोजन
बंध-से-बंध पुनर्संयोजन एक रेडिएटिव प्रक्रिया से संवाहन बंध से संयोजी बंध तक इलेक्ट्रॉनों की झंपन प्रक्रिया का नाम है। बंध-से-बंध पुनर्संयोजन के समय अवशोषित ऊर्जा को फोटॉन के रूप में सहज उत्सर्जन का एक रूप सामग्री द्वारा जारी किया जाता है। इन फोटॉन में उतनी ही या कम ऊर्जा होती है जितनी पहले अवशोषित की गई थी। यह प्रभाव है कि एल ई डी प्रकाश कैसे बनाते हैं। क्योंकि फोटॉन अपेक्षाकृत कम संवेग वहन करता है, विकिरण पुनर्संयोजन केवल प्रत्यक्ष ऊर्जा अंतराल सामग्री में महत्वपूर्ण है। इस प्रक्रिया को द्विध्रुवीय पुनर्संयोजन के रूप में भी जाना जाता है[3]।
इस प्रकार का पुनर्संयोजन उत्तेजित अवस्था में इलेक्ट्रॉनों और छिद्रों के घनत्व पर निर्भर करता है, जिसे क्रमशः और से निरूपित किया जाता है। आइए हम विकिरण पुनर्संयोजन को और वाहक उत्पादन दर को (G) जी के रूप में प्रस्तुत करते हैं।
संपूर्ण उत्पादन थर्मल उत्पादन G0 और अर्धचालक GL पर प्रकाश उद्दीप्त के कारण उत्पादन का योग है:
इसलिए:
एक एन-प्रकार अर्धचालक में,
और
इस प्रकार
शुद्ध पुनर्संयोजन वह दर है जिस पर अतिरिक्त छिद्र लुप्त हो जाते हैं
एक मानक चरघातांकी विघटन प्राप्त करने के लिए इस अवकल समीकरण को हल कीजिए
जहां T = 0 होने पर Pmax अधिकतम अतिरिक्त छिद्र सांद्रता है। (यह सिद्ध किया जा सकता है कि , लेकिन यहां हम उस पर चर्चा नहीं करेंगे)।
कब , सभी अतिरिक्त छिद्र लुप्त हो गए होंगे। इसलिए, हम सामग्री में अतिरिक्त छिद्र के जीवनकाल को परिभाषित कर सकते हैं इसलिए अल्पसंख्यक वाहक का जीवनकाल बहुसंख्यक वाहक एकाग्रता पर निर्भर है।
उत्तेजित उत्सर्जन
प्रेरित उत्सर्जन एक ऐसी प्रक्रिया है जिसमें एक आपतित फोटॉन एक उत्तेजित इलेक्ट्रॉन के साथ संपर्क करता है, जिससे यह चरण (तरंगों), आवृत्ति, ध्रुवीकरण (तरंगों) और संचारण दिशा के संदर्भ में घटना के समान गुणों के साथ एक फोटॉन को पुन: संयोजित और उत्सर्जित करता है। उत्तेजनित उत्सर्जन के साथ-साथ जनसंख्या व्युत्क्रमण का सिद्धांत लेज़र और मेसर्स के संचालन के केंद्र में है। यह बीसवीं शताब्दी की शुरुआत में आइंस्टीन गुणांक द्वारा दिखाया गया है कि यदि उत्साहित और मूल स्तर डीजेनरेसी (वंशीय यांत्रिकी) हैं तो अवशोषण दर और उत्तेजित उत्सर्जन दर समान हैं।[6] यदि स्तर 1 और स्तर 2 क्रमशः -गुना और गुना पतित हैं, तो नया संबंध है:
अनुग्राही उत्सर्जन
अनुग्राही उत्सर्जन एक बहुपदीय प्रक्रिया है जिसमें एक वाहक ऊर्जा अंतराल के बीच में त्रुटि-संबंधित वेवस्टेट्स में गिर जाता है। अनुग्राही एक ऐसा दोष है जो वाहक धारण करने में सक्षम है। अनुग्राही उत्सर्जन प्रक्रिया छिद्र के साथ इलेक्ट्रॉनों को पुन: संयोजित करती है और ऊर्जा के संरक्षण के लिए फोटॉन का उत्सर्जन करती है। अनुग्राही उत्सर्जन की बहुपदीय प्रकृति के कारण प्रायः एक फोनन भी उत्सर्जित होता है। अनुग्राही उत्सर्जन अधिकांश त्रुटि या आवरण त्रुटि के उपयोग से आगे बढ़ सकता है। [7] [8]
गैर-विकिरण पुनर्संयोजन
गैर-विकिरण पुनर्संयोजन फॉस्फोर और अर्धचालक में एक प्रक्रिया है, जिससे आवेश वाहक फोटॉन के स्थान पर फोनन विमोचन करने का पुनर्संयोजन करते हैं। ऑप्टोइलेक्ट्रॉनिक्स और फॉस्फोर में गैर-विकिरणात्मक पुनर्संयोजन एक अवांछित प्रक्रिया है, जो प्रकाश उत्पादन क्षमता को अवनमन करती है और ऊष्मा हास में वृद्धि करती है।
एक अर्धचालक के चालन बंध में इलेक्ट्रॉन एक छिद्र के साथ पुनर्संयोजित होने से पूर्व गैर-विकिरणात्मक जीवन काल औसतकाल होता है। ऑप्टोइलेक्ट्रॉनिक्स में यह एक महत्वपूर्ण मापदण्ड है जहां एक फोटॉन का उत्पादन करने के लिए विकिरणात्मक पुनर्संयोजन की आवश्यकता होती है; यदि गैर-विकिरणात्मक जीवन काल विकिरण से कम है, तो एक वाहक के गैर-विकिरणीय रूप से पुनर्संयोजित होने की संभावना अधिक होती है। इसका परिणाम न्यून आंतरिक क्वांटम दक्षता में होता है।
शॉक्ले -रीड -हॉल (एसआरएच)
शॉकले-रीड-हॉल पुनर्संयोजन(एसआरएच) में, जिसे ट्रैप-सहायक पुनर्संयोजन भी कहा जाता है, बंध के बीच संक्रमण में इलेक्ट्रॉन एक डोपेंट या क्रिस्टल जाली में त्रुटि द्वारा ऊर्जा अंतराल के भीतर बनाई गई एक नई ऊर्जा स्तर (स्थानीय स्तर) से पारित होता है; ऐसी ऊर्जा अवस्थाओं को विपाश कहा जाता हैं। गैर-विकिरणात्मक पुनर्संयोजन मुख्य रूप से ऐसे स्थलों पर होता है। ऊर्जा का आदान-प्रदान जाली कंपन के रूप में होता है, फोनन सामग्री के साथ तापीय ऊर्जा का आदान-प्रदान करता है।
चूंकि जाल वाहक के बीच गति में अंतर को अवशोषित कर सकते हैं, एसआरएच सिलिकॉन और अन्य प्रत्यक्ष और अप्रत्यक्ष बंध अंतराल सामग्री में प्रमुख पुनर्संयोजन प्रक्रिया है। हालांकि, ट्रैप-असिस्टेड पुनर्संयोजन भी बहुत कम चार्ज वाहक घनत्व (बहुत निम्न स्तर के इंजेक्शन) की स्थितियों के तहत प्रत्यक्ष और अप्रत्यक्ष बंध अंतराल सामग्री में या पेरोव्साइट सोलर सेल जैसे जाल के उच्च घनत्व वाली सामग्री में हावी हो सकता है। इस प्रक्रिया का नाम विलियम शॉक्ले, विलियम थॉर्नटन रीड और रॉबर्ट एन हॉल[9] के नाम पर रखा गया है,[10] जिन्होंने इसे वर्ष 1952 में प्रकाशित किया था।
प्रकार के जाल
इलेक्ट्रॉन जाल बनाम छिद्र जाल
यद्यपि सभी पुनर्संयोजन की घटनाओं को इलेक्ट्रॉन आंदोलनों के संदर्भ में वर्णित किया जा सकता है, लेकिन उत्साहित इलेक्ट्रॉन और उनके द्वारा छोड़े गए इलेक्ट्रॉन छिद्र के संदर्भ में विभिन्न प्रक्रियाओं की कल्पना करना सामान्य है। इस संदर्भ में, यदि जाल का स्तर संवाहन बंध के निकट है, तो वे अस्थायी रूप से उत्साहित इलेक्ट्रॉन या अन्य शब्दों में, वे इलेक्ट्रॉन जाल हैं। दूसरी ओर, यदि उनकी ऊर्जा संयोजी बंध के निकट है, तो वे छिद्र जाल बन जाते हैं।
उथले जाल बनाम गहरे जाल
सामान्यत: उथले और गहरे जाल के बीच अंतर इस बात पर निर्भर करता है कि इलेक्ट्रॉन जाल संवाहन बंध और छिद्र जाल संयोजी बंध के कितने निकट हैं। यदि अनुग्राही और बंध के बीच का अंतर kt (ऊर्जा) से छोटा है। ऊष्मीय ऊर्जा kBt, प्रायः यह कहा जाता है कि यह एक उथला जाल है। वैकल्पिक रूप से यदि अंतर ऊष्मीय ऊर्जा से बड़ा है तो इसे गहरा जाल कहा जाता है। यह अंतर उपयोगी है क्योंकि उथले जाल का अधिक सरलता से रिक्तीकरण किया जा सकता है और प्रायः इस प्रकार ऑप्टोइलेक्ट्रोनिक उपकरणों के प्रदर्शन के लिए हानिकारक नहीं होते हैं।
एसआरएच मॉडल
एसआरएच मॉडल में चार घटनायें अनुग्राही स्तर में सम्मिलित हो सकती हैं:[11]
- संवाहन बंध में इलेक्ट्रॉन एक इंट्रागैप अवस्था में विपाशित किया सकता है।
- एक इलेक्ट्रॉन को एक जाल स्तर से संवाहन बंध में उत्सर्जित किया जा सकता है।
- संयोजी बंध में छिद्र को एक जाल द्वारा प्रग्रहण किया जा सकता है। यह एक पूरित जाल के अनुरूप है जो एक इलेक्ट्रॉन को संयोजी बंध में अवमुक्त करता है।
- एक प्रग्रहण किए गए छिद्र को संयोजी बंध में विमुक्त किया जा सकता है। संयोजी बंध से एक इलेक्ट्रॉन के प्रग्रहण के अनुरूप किया जा सकता है।
जब वाहक पुनर्संयोजन जाल के माध्यम से उत्पन्न होता है, तो हम इंट्रागैप संयोजी द्वारा स्थितियों के संयोजी घनत्व को परिवर्तित कर सकते हैं।[12] अवधि फंसे हुए इलेक्ट्रॉनों/छिद्रों के घनत्व से बदल दिया जाता है।
बरमा पुनर्संयोजन
बरमा पुनर्संयोजन में ऊर्जा एक तीसरे वाहक को दी जाती है जो किसी अन्य ऊर्जा बंध में जाए बिना ही उच्च ऊर्जा स्तर तक उत्साहित होता है। पारस्परिक क्रिया के पश्चात, तीसरा वाहक सामान्य रूप से ऊष्मीय कंपन के लिए अपनी अतिरिक्त ऊर्जा नष्ट कर देता है। यह प्रक्रिया एक तीन-कण अंतःक्रिया होने के कारण सामान्यतः यह केवल असंतुलित स्थितियों में महत्वपूर्ण होती है जब वाहक घनत्व बहुत अधिक होता है। बरमा प्रभाव प्रक्रिया आसानी से उत्पन्न नहीं होती है, क्योंकि तीसरे कण को अस्थिर उच्च-ऊर्जा अवस्था में प्रक्रिया शुरू करनी होगी।
ऊष्मीय संतुलन में बरमा पुनर्संयोजन और ऊष्मीय उत्पादन दर एक दूसरे के बराबर होती है[13]
सतह पुनर्संयोजन
अर्धचालक की सतह पर संपाश (ट्रैप)-सहायता प्राप्त पुनर्संयोजन को सतह पुनर्संयोजन के रूप में जाना जाता है। यह तब होता है जब अर्धचालक क्रिस्टल के अचानक बंद होने से लटकने वाले बंध के कारण अर्धचालक फॉर्म की सतह पर या उसके पास जाल होता है। सतह पुनर्संयोजन को सतह पुनर्संयोजन वेग की विशेषता है जो सतह दोषों के घनत्व पर निर्भर करता है।[17] सतह पर मुक्त वाहकों के संग्रह और निष्कर्षण के कारण सौर कोशिकाओं की सतह पुनर्संयोजन जैसे अनुप्रयोगों में पुनर्संयोजन का प्रमुख तंत्र हो सकता है। सौर कोशिकाओं के कुछ अनुप्रयोगों में एक बड़े ऊर्जा अंतराल के साथ पारदर्शी सामग्री की एक परत जिसे विंडो लेयर के रूप में भी जाना जाता है तथा जिसका उपयोग सतह के पुनर्संयोजन को कम करने के लिए किया जाता है। सतह के पुनर्संयोजन को कम करने के लिए निष्क्रियता तकनीक भी कार्यरत हैं।[18]
लैंग्विन पुनः संयोजन
सामान्य विचलता प्रणालियों में मुक्त वाहकों के लिए पुनर्संयोजन दर को प्रायः लैंग्विन पुनर्संयोजन दर के साथ वर्णित किया जाता है।[19] प्रायः प्रतिरूपों का उपयोग अव्यवस्थित प्रणालियों जैसे कि जैविक सामग्री (और इसलिए कार्बनिक सौर कोशिकाओं के लिए प्रासंगिक है) और अन्य ऐसी प्रणालियों के लिए किया जाता है।[20] लैंग्विन पुनर्संयोजन शक्ति के रूप में परिभाषित किया गया है।
यह भी देखें
- पंजर प्रभाव
- ओज़े प्रभाव
संदर्भ
- ↑ Elhami Khorasani, Arash; Schroder, Dieter K.; Alford, T. L. (2014). "Optically Excited MOS-Capacitor for Recombination Lifetime Measurement". IEEE Electron Device Letters. 35 (10): 986–988. Bibcode:2014IEDL...35..986K. doi:10.1109/LED.2014.2345058. S2CID 19785166.
- ↑ Pelant, Ivan; Valenta, Jan (2012-02-09), "Luminescence of disordered semiconductors", Luminescence Spectroscopy of Semiconductors, Oxford University Press, pp. 242–262, doi:10.1093/acprof:oso/9780199588336.003.0009, ISBN 9780199588336
- ↑ Stranks, Samuel D.; Burlakov, Victor M.; Leijtens, Tomas; Ball, James M.; Goriely, Alain; Snaith, Henry J. (2014-09-11). "Recombination Kinetics in Organic-Inorganic Perovskites: Excitons, Free Charge, and Subgap States". Physical Review Applied. 2 (3): 034007. Bibcode:2014PhRvP...2c4007S. doi:10.1103/PhysRevApplied.2.034007.
- ↑ 4.0 4.1 Li, Sheng S., ed. (2006). Semiconductor Physical Electronics (in British English). p. 140. doi:10.1007/0-387-37766-2. ISBN 978-0-387-28893-2.
- ↑ 5.0 5.1 NISOLI, MAURO. (2016). SEMICONDUCTOR PHOTONICS. SOCIETA EDITRICE ESCULAPIO. ISBN 978-8893850025. OCLC 964380194.
- ↑ Svelto. (1989). Principles of Lasers ... p. 3. OCLC 249201544.
- ↑ Blumenau (2001). "Dislocation Related Photoluminescence in Silicon". Physical Review Letters. 87 (18): 187404. Bibcode:2001PhRvL..87r7404B. doi:10.1103/PhysRevLett.87.187404.
- ↑ van Dijken, Addy; Meulenkamp, Eric A.; Vanmaekelbergh, Daniël; Meijerink, Andries (2000-03-01). "The Kinetics of the Radiative and Nonradiative Processes in Nanocrystalline ZnO Particles upon Photoexcitation". The Journal of Physical Chemistry B. 104 (8): 1715–1723. doi:10.1021/jp993327z. ISSN 1520-6106.
- ↑ Shockley, W.; Read, W. T. (1 September 1952). "Statistics of the Recombinations of Holes and Electrons". Physical Review. 87 (5): 835–842. Bibcode:1952PhRv...87..835S. doi:10.1103/PhysRev.87.835.
- ↑ Hall, R.N. (1951). "Germanium rectifier characteristics". Physical Review. 83 (1): 228.
- ↑ NISOLI, MAURO. (2016). SEMICONDUCTOR PHOTONICS. SOCIETA EDITRICE ESCULAPIO. ISBN 978-8893850025. OCLC 964380194.
- ↑ 12.0 12.1 Kandada, Ajay Ram Srimath; D'Innocenzo, Valerio; Lanzani, Guglielmo; Petrozza, Annamaria (2016), Da Como, Enrico; De Angelis, Filippo; Snaith, Henry; Walker, Alison (eds.), "Chapter 4. Photophysics of Hybrid Perovskites", Unconventional Thin Film Photovoltaics (in English), Royal Society of Chemistry, pp. 107–140, doi:10.1039/9781782624066-00107, ISBN 9781782622932
- ↑ 13.0 13.1 Li, Sheng S., ed. (2006). Semiconductor Physical Electronics (in British English). p. 143. doi:10.1007/0-387-37766-2. ISBN 978-0-387-28893-2.
- ↑ Li, Sheng S., ed. (2006). Semiconductor Physical Electronics (in British English). p. 144. doi:10.1007/0-387-37766-2. ISBN 978-0-387-28893-2.
- ↑ Stevenson, Richard (August 2009) "The LED's Dark Secret: Solid-state lighting won't supplant the lightbulb until it can overcome the mysterious malady known as droop". IEEE Spectrum
- ↑ Justin Iveland; Lucio Martinelli; Jacques Peretti; James S. Speck; Claude Weisbuch. "Cause of LED Efficiency Droop Finally Revealed". Physical Review Letters, 2013. Science Daily. Retrieved 23 April 2013.
- ↑ Nelson, Jenny (2003). The Physics of Solar Cells. London: Imperial College Press. p. 116. ISBN 978-1-86094-340-9.
- ↑ Eades, W.D.; Swanson, R.M. (1985). "Calculation of surface generation and recombination velocities at the Si-SiO2 interface". Journal of Applied Physics. 58 (11): 4267–4276. Bibcode:1985JAP....58.4267E. doi:10.1063/1.335562. ISSN 0021-8979.
- ↑ "Recombination in low mobility semiconductors: Langevin theory". 4 April 2008.
- ↑ Lakhwani, Girish; Rao, Akshay; Friend, Richard H. (2014). "Bimolecular Recombination in Organic Photovoltaics". Annual Review of Physical Chemistry. 65 (1): 557–581. Bibcode:2014ARPC...65..557L. doi:10.1146/annurev-physchem-040513-103615. ISSN 0066-426X. PMID 24423376.
आगे की पढाई
- N.W. Ashcroft and N.D. Mermin, Solid State Physics, Brooks Cole, 1976
