भिड़ंत (कलिश़्‌न्‌): Difference between revisions

Revision as of 23:54, 27 August 2022

भौतिकी में, एक भिड़ंत (कलिश़्‌न्‌) कोई भी घटना है जिसमें दो या दो से अधिक निकाय अपेक्षाकृत कम समय में एक दूसरे पर बलों को बढ़ाते हैं।यद्यपि शब्द भिड़ंत'का सबसे आम उपयोग उन घटनाओं को संदर्भित करता है जिनमें दो या दो से अधिक वस्तुएं महान बल से टकराती हैं, शब्द के वैज्ञानिक उपयोग का तात्पर्य बल की भयावहता के बारे में कुछ भी नहीं है।^[1] भौतिक बातचीत के कुछ उदाहरण जो वैज्ञानिकों पर विचार करेंगे, वे निम्नलिखित हैं:

जब कोई कीट किसी पौधे की पत्ती पर उतरता है, तो कहा जाता है कि उसके पैर पत्ते से टकराते हैं।
जब एक बिल्ली एक लॉन में घूमती है, तो उसके पंजे जमीन के साथ किए गए प्रत्येक संपर्क को भिड़ंत माना जाता है, साथ ही साथ उसके फर के प्रत्येक ब्रश को घास के ब्लेड के खिलाफ माना जाता है।
जब कोई मुक्केबाज मुक्का मारता है, तो कहा जाता है कि उसकी मुट्ठी विरोधियों के शरीर से टकराती है।
जब कोई खगोलीय पिंड ब्लैक होल में विलीन हो जाता है, तो उन्हें टकराने वाला माना जाता है।

भिड़ंत शब्द के कुछ बोलचाल की भाषा में उपयोग निम्नलिखित हैं:

यातायात भिड़ंत में कम से कम एक ऑटोमोबाइल शामिल है।
हवाई जहाजों के बीच मध्य हवा में भिड़ंत होती है।
जहाज की भिड़ंत में कम से कम दो गतिमान समुद्री जहाज एक दूसरे से टकराते हैं; संबंधित शब्द, गठबंधन, वर्णन करता है कि जब एक चलती जहाज एक स्थिर वस्तु पर हमला करता है (अक्सर, लेकिन हमेशा नहीं, एक और जहाज)।

भौतिकी में, भिड़ंत से पहले और बाद में सिस्टम की कुल गतिज ऊर्जा में परिवर्तन द्वारा भिड़ंतों को वर्गीकृत किया जा सकता है:

यदि कुल गतिज ऊर्जा का अधिकांश या सभी भाग नष्ट हो जाता है (गर्मी, ध्वनि आदि के रूप में नष्ट हो जाता है या स्वयं वस्तुओं द्वारा अवशोषित हो जाता है), तो भिड़ंत को बेलोचदार कहा जाता है; इस तरह के भिड़ंत में पूर्ण विराम पर आने वाली वस्तुएं शामिल होती हैं। इस तरह की भिड़ंत का एक उदाहरण कार दुर्घटना है, क्योंकि दुर्घटनाग्रस्त होने पर कारें एक-दूसरे से उछलने के बजाय अंदर की ओर उखड़ जाती हैं। यह डिज़ाइन द्वारा है, रहने वालों और दर्शकों की सुरक्षा के लिए एक दुर्घटना होनी चाहिए - कार का फ्रेम इसके बजाय दुर्घटना की ऊर्जा को अवशोषित करता है।
यदि अधिकांश गतिज ऊर्जा संरक्षित है (अर्थात वस्तुएं बाद में चलती रहती हैं), तो भिड़ंत को लोचदार कहा जाता है। इसका एक उदाहरण बेसबॉल का बल्ला बेसबॉल से टकराना है - बल्ले की गतिज ऊर्जा गेंद को स्थानांतरित कर दी जाती है, जिससे गेंद का वेग बहुत बढ़ जाता है। बल्ले की गेंद से टकराने की आवाज ऊर्जा के नुकसान का प्रतिनिधित्व करती है।
और यदि कुल गतिज ऊर्जा संरक्षित रहती है (अर्थात ध्वनि, ऊष्मा आदि के रूप में कोई ऊर्जा नहीं निकलती है), तो भिड़ंत को पूरी तरह से लोचदार कहा जाता है। थर्मोडायनामिक्स के दूसरे नियम के कारण ऐसी प्रणाली एक आदर्शीकरण है और वास्तविकता में नहीं हो सकती है।

भौतिकी

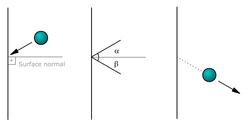
विक्षेपण तब होता है जब कोई वस्तु एक विमान की सतह को मारती है। यदि प्रभाव के बाद गतिज ऊर्जा प्रभाव से पहले समान है, तो यह एक लोचदार भिड़ंतहै।यदि गतिज ऊर्जा खो जाती है, तो यह एक अयोग्य भिड़ंत है।आरेख यह नहीं दिखाता है कि सचित्र भिड़ंतलोचदार थी या इनलेस्टिक थी, क्योंकि कोई वेग प्रदान नहीं किया जाता है।सबसे अधिक कह सकते हैं कि भिड़ंतपूरी तरह से अयोग्य नहीं थी, क्योंकि उस स्थिति में गेंद दीवार से चिपक गई होगी।

भिड़ंत दो निकायों या दो से अधिक निकायों के बीच एक साथ छोटी अवधि की बातचीत है, जिसके दौरान उनके बीच कार्य करने वाले आंतरिक बलों के कारण शामिल निकायों की गति में परिवर्तन होता है। भिड़ंत में बल शामिल होते हैं ( वेग में परिवर्तन होता है)। प्रभाव से ठीक पहले वेग अंतर के परिमाण को समापन गति कहा जाता है। सभी भिड़ंत संवेग का संरक्षण करते हैं। विभिन्न प्रकार के भिड़ंतों में जो अंतर होता है वह यह है कि क्या वे गतिज ऊर्जा का संरक्षण भी करते हैं। प्रभाव की रेखा वह रेखा है जो प्रभाव के दौरान निकटतम या संपर्क में आने वाली सतहों के सामान्य सामान्य के समान होती है। यह वह रेखा है जिसके साथ भिड़ंत की आंतरिक शक्ति प्रभाव के दौरान कार्य करती है, और न्यूटन के बहाली के गुणांक को केवल इसी रेखा के साथ परिभाषित किया जाता है। भिड़ंत तीन प्रकार की होती है:

पूरी तरह से लोचदार भिड़ंत
बेलोचदार भिड़ंत
पूरी तरह से बेलोचदार भिड़ंत

विशेष रूप से, भिड़ंत या तो लोचदार हो सकते हैं, जिसका अर्थ है कि वे गति और गतिज ऊर्जा दोनों को संरक्षित करते हैं, या अकुशल , जिसका अर्थ है कि वे गति का संरक्षण करते हैं लेकिन गतिज ऊर्जा नहीं होती है।

एक बेलोचदार भिड़ंत को कभी-कभी प्लास्टिक की भिड़ंत भी कहा जाता है। एक "पूरी तरह से बेलोचदार" भिड़ंत (जिसे "पूरी तरह से प्लास्टिक" भिड़ंत भी कहा जाता है) बेलोचदार भिड़ंत का एक सीमित मामला है जिसमें दो शरीर प्रभाव के बाद आपस में जुड़ जाते हैं।

जिस डिग्री तक भिड़ंत लोचदार या बेलोचदार होती है, उसे पुनर्स्थापन के गुणांक द्वारा निर्धारित किया जाता है, एक मान जो आम तौर पर शून्य और एक के बीच होता है। एक पूरी तरह से लोचदार भिड़ंत में एक की बहाली का गुणांक होता है; एक पूरी तरह से बेलोचदार भिड़ंत में शून्य की बहाली का गुणांक होता है।

भिड़ंत के प्रकार

दो निकायों के बीच दो प्रकार के भिड़ंत होते हैं - 1) हेड-ऑन भिड़ंत या एक-आयामी भिड़ंत - जहां प्रभाव से ठीक पहले प्रत्येक शरीर का वेग प्रभाव की रेखा के साथ होता है, और 2) गैर-सिर पर भिड़ंत, तिरछी भिड़ंत या द्वि-आयामी भिड़ंत - जहां प्रभाव से ठीक पहले प्रत्येक पिंड का वेग प्रभाव की रेखा के साथ नहीं होता है।

बहाली के गुणांक के अनुसार, किसी भी भिड़ंत के दो विशेष मामले नीचे लिखे गए हैं:

एक पूरी तरह से लोचदार भिड़ंत को एक के रूप में परिभाषित किया जाता है जिसमें भिड़ंत में गतिज ऊर्जा का कोई नुकसान नहीं होता है। वास्तव में, वस्तुओं के बीच कोई भी मैक्रोस्कोपिक भिड़ंत कुछ गतिज ऊर्जा को आंतरिक ऊर्जा और ऊर्जा के अन्य रूपों में बदल देगी, इसलिए कोई भी बड़े पैमाने पर प्रभाव पूरी तरह से लोचदार नहीं होता है। हालांकि, कुछ समस्याएं पूरी तरह से लोचदार के काफी करीब हैं कि उन्हें इस तरह अनुमानित किया जा सकता है। इस मामले में, बहाली का गुणांक एक के बराबर है।
एक बेलोचदार भिड़ंत वह है जिसमें गतिज ऊर्जा का हिस्सा भिड़ंत में ऊर्जा के किसी अन्य रूप में बदल जाता है। गतिहीन भिड़ंतों में संवेग संरक्षित होता है (जैसा कि यह लोचदार भिड़ंतों के लिए होता है), लेकिन कोई भिड़ंत के माध्यम से गतिज ऊर्जा को ट्रैक नहीं कर सकता क्योंकि इसमें से कुछ ऊर्जा के अन्य रूपों में परिवर्तित हो जाती है। इस मामले में, बहाली का गुणांक एक के बराबर नहीं है।

किसी भी प्रकार की भिड़ंत में एक ऐसा चरण होता है जब एक क्षण के लिए टकराने वाले पिंडों का वेग रेखा के साथ समान वेग होता है। तब इस चरण के दौरान निकायों की गतिज ऊर्जा कम हो जाती है और इसे अधिकतम विरूपण चरण कहा जा सकता है जिसके लिए क्षणिक रूप से बहाली का गुणांक एक हो जाता है।

आदर्श गैसों में भिड़ंत पूरी तरह से लोचदार भिड़ंत तक पहुंचते हैं, जैसे कि उप-परमाणु कणों की बिखरने वाली बातचीत जो विद्युत चुम्बकीय बल द्वारा विक्षेपित होती है। उपग्रहों और ग्रहों के बीच गुलेल प्रकार के गुरुत्वाकर्षण अंतःक्रियाओं जैसे कुछ बड़े पैमाने पर अंतःक्रियाएं लगभग पूरी तरह से लोचदार होती हैं।

कठोर गोले के बीच भिड़ंत लगभग लोचदार हो सकती है, इसलिए लोचदार भिड़ंत के सीमित मामले की गणना करना उपयोगी होता है। संवेग के संरक्षण की धारणा के साथ-साथ गतिज ऊर्जा के संरक्षण से दो-पिंडों के भिड़ंत में अंतिम वेगों की गणना संभव हो जाती है।

गठबंधन (ऑलिसिस)

समुद्री कानून में, एक चलती वस्तु से टकराने वाले जहाज की स्थिति और एक स्थिर वस्तु से टकराने की स्थिति के बीच अंतर करना कभी-कभी वांछनीय होता है। "गठबंधन" शब्द का उपयोग तब एक स्थिर वस्तु के प्रहार के लिए किया जाता है, जबकि "भिड़ंत" का अर्थ किसी चलती हुई वस्तु से टकराने के लिए किया जाता है। ^[2] ^[3] ^[4] इस प्रकार, जब दो जहाज एक-दूसरे के खिलाफ दौड़ते हैं, तो कोर्ट आमतौर पर भिड़ंत शब्द का इस्तेमाल करते हैं, जबकि जब एक जहाज दूसरे के खिलाफ चलता है, तो वे आम तौर पर गठबंधन शब्द का इस्तेमाल करते हैं। ^[5] स्थिर वस्तु एक पुल या गोदी भी हो सकती है। जबकि दो शब्दों के बीच कोई बड़ा अंतर नहीं है और अक्सर उनका परस्पर उपयोग भी किया जाता है, अंतर का निर्धारण करने से आपात स्थिति की परिस्थितियों को स्पष्ट करने और उसके अनुसार अनुकूलन करने में मदद मिलती है। ^[6] वेन लाइन बंकरिंग, इंक. के मामले में वी. नेटली डीएम / वी, यह स्थापित किया गया था कि यह अनुमान था कि चलती पोत गलती पर है, जिसमें कहा गया है कि "अनुमान सामान्य ज्ञान के अवलोकन से निकला है कि चलती जहाजों आमतौर पर स्थिर वस्तुओं से नहीं टकराती हैं जब तक कि चलती पोत को गलत तरीके से नियंत्रित नहीं किया जाता है। किसी तरह"। ^[7] यह भी ओरेगन नियम के रूप में कहा जाता है।^[8]

विश्लेषणात्मक बनाम संख्यात्मक दृष्टिकोण भिड़ंत को हल करने की दिशा में

भिड़ंत से जुड़ी अपेक्षाकृत कुछ समस्याओं को विश्लेषणात्मक रूप से हल किया जा सकता है; शेष को संख्यात्मक विधियों की आवश्यकता होती है। भिड़ंत का अनुकरण करने में एक महत्वपूर्ण समस्या यह निर्धारित करना है कि क्या दो वस्तुएं वास्तव में टकराई हैं। इस समस्या को भिड़ंत का पता लगाना कहा जाता है।

भिड़ंत के उदाहरण जो विश्लेषणात्मक रूप से हल किए जा सकते हैं

बिलियर्ड्स

क्यू स्पोर्ट्स में भिड़ंत महत्वपूर्ण भूमिका निभाते हैं। क्योंकि बिलियर्ड गेंदों के बीच भिड़ंत लगभग लोचदार होते हैं, और गेंदें एक ऐसी सतह पर लुढ़कती हैं जो कम रोलिंग घर्षण पैदा करती है, उनके व्यवहार का उपयोग अक्सर न्यूटन के गति के नियमों को स्पष्ट करने के लिए किया जाता है। एक समान द्रव्यमान वाली एक गतिमान गेंद के शून्य-घर्षण भिड़ंत के बाद, दो गेंदों की दिशाओं के बीच का कोण 90 डिग्री है। यह एक महत्वपूर्ण तथ्य है जिसे पेशेवर बिलियर्ड्स खिलाड़ी ध्यान में रखते हैं, ^[9] हालांकि यह मानता है कि गेंद घर्षण के साथ लुढ़कने के बजाय टेबल पर घर्षण के किसी भी प्रभाव के बिना आगे बढ़ रही है। संबंधित प्रारंभिक वेग u ₁ और u ₂ के साथ किन्हीं दो द्रव्यमान m ₁ और m ₂ के दो आयामों में एक लोचदार भिड़ंत पर विचार करें, जहां u ₂ = 0, और अंतिम वेग V ₁ और V ₂ । संवेग का संरक्षण m ₁ u ₁ = m ₁ V ₁ + m ₂ V ₂ देता है। लोचदार भिड़ंत के लिए ऊर्जा का संरक्षण देता है (1/2) m ₁ | यू ₁ | ² = (1/2) मी ₁ | वी ₁ | ² + (1/2) मी ₂ | वी ₂ | ² . अब स्थिति m ₁ = m ₂ पर विचार करें: हम u ₁ = V ₁ + V ₂ और | . प्राप्त करते हैं यू ₁ | ² = | वी ₁ | ² + | वी ₂ | ² . पूर्व समीकरण के प्रत्येक पक्ष के डॉट उत्पाद को अपने साथ लेते हुए, | यू ₁ | ² = यू ₁ • यू ₁ = | वी ₁ | ² + | वी ₂ | ² + 2 वी ₁ • वी ₂ । बाद के समीकरण के साथ इसकी तुलना करने पर V ₁ • V ₂ = 0 मिलता है, इसलिए वे लंबवत होते हैं जब तक कि V ₁ शून्य वेक्टर न हो (जो तब होता है जब और केवल भिड़ंत आमने-सामने होता है)।

सही इनलैस्टिक भिड़ंत

एक पूर्ण बेलोचदार भिड़ंत में, यानी, बहाली का एक शून्य गुणांक, टकराने वाले कण आपस में जुड़ जाते हैं। संवेग के संरक्षण पर विचार करना आवश्यक है:

$m_{a}\mathbf {u} _{a}+m_{b}\mathbf {u} _{b}=\left(m_{a}+m_{b}\right)\mathbf {v} \,$

जहाँ v अंतिम वेग है, जो इसलिए द्वारा दिया गया है

$\mathbf {v} ={\frac {m_{a}\mathbf {u} _{a}+m_{b}\mathbf {u} _{b}}{m_{a}+m_{b}}}$

कुल गतिज ऊर्जा में कमी दो कणों के निकाय के संबंध में संवेग फ्रेम के केंद्र में भिड़ंत से पहले की कुल गतिज ऊर्जा के बराबर होती है, क्योंकि ऐसे फ्रेम में भिड़ंत के बाद गतिज ऊर्जा शून्य होती है। इस फ्रेम में भिड़ंत से पहले अधिकांश गतिज ऊर्जा छोटे द्रव्यमान वाले कण की होती है। दूसरे फ्रेम में, गतिज ऊर्जा में कमी के अलावा गतिज ऊर्जा का एक कण से दूसरे कण में स्थानांतरण हो सकता है; तथ्य यह है कि यह फ्रेम पर निर्भर करता है यह दर्शाता है कि यह कितना सापेक्ष है। समय के उलट होने के साथ हमारे पास दो वस्तुओं की स्थिति होती है जो एक दूसरे से दूर धकेल दी जाती हैं, उदाहरण के लिए एक प्रक्षेप्य की शूटिंग, या एक रॉकेट जो जोर लगा रहा है ( Tsiolkovsky रॉकेट समीकरण की व्युत्पत्ति की तुलना करें)।

m_{a}\mathbf {u} _{a}+m_{b}\mathbf {u} _{b}=\left(m_{a}+m_{b}\right)\mathbf {v} \,

जहां v अंतिम वेग है, जो इसलिए द्वारा दिया गया है

कुल गतिज ऊर्जा की कमी दो कणों की प्रणाली के संबंध में गति के फ्रेम के केंद्र में भिड़ंत से पहले कुल गतिज ऊर्जा के बराबर है, क्योंकि इस तरह के फ्रेम में भिड़ंतके बाद गतिज ऊर्जा शून्य है।इस फ्रेम में भिड़ंतसे पहले अधिकांश गतिज ऊर्जा छोटे द्रव्यमान के साथ कण का है।एक अन्य फ्रेम में, गतिज ऊर्जा की कमी के अलावा एक कण से दूसरे में गतिज ऊर्जा का हस्तांतरण हो सकता है;तथ्य यह है कि यह फ्रेम पर निर्भर करता है दिखाता है कि यह कितना सापेक्ष है। समय के साथ हमारे पास दो वस्तुओं की स्थिति है जो एक दूसरे से दूर धकेलती हैं, उदा।एक प्रोजेक्टाइल की शूटिंग, या थ्रस्ट को लागू करने वाला एक रॉकेट (Tsiolkovsky रॉकेट समीकरण की व्युत्पत्ति की तुलना करें)।

संख्यात्मक रूप से विश्लेषण किए गए भिड़ंतों के उदाहरण

पशु हरकत (लोकोमोशन)

अंतर्निहित सब्सट्रेट के साथ किसी जानवर के पैर या पंजा के भिड़ंत को आम तौर पर जमीनी प्रतिक्रिया बल कहा जाता है। ये भिड़ंत बेलोचदार होते हैं, क्योंकि गतिज ऊर्जा संरक्षित नहीं होती है। प्रोस्थेटिक्स में एक महत्वपूर्ण शोध विषय विकलांग और गैर-विकलांग दोनों चाल से जुड़े पैर-ग्राउंड भिड़ंत के दौरान उत्पन्न बलों की मात्रा निर्धारित कर रहा है। इस परिमाणीकरण के लिए आम तौर पर विषयों को एक बल मंच (कभी-कभी "बल प्लेट" कहा जाता है) के साथ-साथ विस्तृत गतिज और गतिशील (कभी-कभी गतिज कहा जाता है) विश्लेषण की आवश्यकता होती है।

एक प्रयोगात्मक उपकरण के रूप में उपयोग किए जाने वाले भिड़ंत

वस्तुओं और अन्य भौतिक घटनाओं के भौतिक गुणों का अध्ययन करने के लिए टकराव को एक प्रयोगात्मक तकनीक के रूप में प्रयोग किया जा सकता है।

अंतरिक्ष की खोज

किसी वस्तु को जानबूझकर किसी अन्य खगोलीय पिंड पर क्रैश-लैंड करने के लिए बनाया जा सकता है, माप करने के लिए और नष्ट होने से पहले उन्हें पृथ्वी पर भेजने के लिए, या कहीं और उपकरणों को प्रभाव का निरीक्षण करने की अनुमति देने के लिए बनाया जा सकता है। उदाहरण देखें:

अपोलो 13, अपोलो 14, अपोलो 15, अपोलो 16 और अपोलो 17 के दौरान, एस-आईवीबी (रॉकेट का तीसरा चरण) चंद्र कोर को चिह्नित करने के लिए उपयोग किए जाने वाले भूकंपीय माप करने के लिए चंद्रमा में दुर्घटनाग्रस्त हो गया था।
गहरा प्रभाव
स्मार्ट-1 - यूरोपीय अंतरिक्ष एजेंसी उपग्रह
चंद्रमा प्रभाव जांच - इसरो जांच और एलसीआरओएसएस अपने खर्च किए गए सेंटौर ऊपरी चरण के साथ - नासा प्रोब
ग्रहों की रक्षा के लिए दोहरा क्षुद्रग्रह पुनर्निर्देशन परीक्षण (योजनाबद्ध)

आणविक भिड़ंतों का गणितीय विवरण

मान लीजिए किसी अणु का रैखिक, कोणीय और आंतरिक संवेग r चरों { p _i } के समुच्चय द्वारा दिया जाता है। एक अणु की स्थिति को तब श्रेणी w _i = δ p ₁ δ p ₂ δ p ₃ ... p _r द्वारा वर्णित किया जा सकता है। विभिन्न राज्यों के अनुरूप कई ऐसी श्रेणियां हैं; एक विशिष्ट राज्य को सूचकांक i द्वारा दर्शाया जा सकता है। इस प्रकार टकराने वाले दो अणुओं को ( i, j ) द्वारा निरूपित किया जा सकता है (ऐसे क्रमित जोड़े को कभी-कभी एक नक्षत्र के रूप में जाना जाता है। ) यह मान लेना सुविधाजनक है कि दो अणु एक दूसरे पर नगण्य प्रभाव डालते हैं जब तक कि उनका गुरुत्वाकर्षण केंद्र एक महत्वपूर्ण दूरी b के भीतर न पहुंच जाए। इसलिए टकराव तब शुरू होता है जब गुरुत्वाकर्षण के संबंधित केंद्र इस महत्वपूर्ण दूरी पर पहुंच जाते हैं, और जब वे फिर से इस महत्वपूर्ण दूरी पर अपने रास्ते पर पहुंचते हैं तो पूरा हो जाता है। इस मॉडल के तहत, एक टक्कर पूरी तरह से मैट्रिक्स द्वारा वर्णित है ${\begin{pmatrix}i&j\\k&l\end{pmatrix}}$ , जो टकराव से पहले नक्षत्र ( i, j ) और टकराव के बाद (सामान्य रूप से भिन्न) नक्षत्र ( k, l ) को संदर्भित करता है। यह अंकन सांख्यिकीय यांत्रिकी के बोल्ट्जमान के एच-प्रमेय को सिद्ध करने में सुविधाजनक है।

जानबूझकर भिड़ंत के माध्यम से हमला

जानबूझकर टक्कर के माध्यम से हमले के प्रकारों में शामिल हैं:

किसी वस्तु या वाहन के साथ रगड़ना, उदा।:

राम-छड़ी, एक इमारत में एक कार चलाने की प्रथा को तोड़ने के लिए

एक दूर की वस्तु के साथ एक हमलावर भिड़ंत एक प्रक्षेप्य को फेंकने या लॉन्च करके प्राप्त किया जा सकता है।

यह भी देखें

बैलिस्टिक पेंडुलम
कार दुर्घटना
बहाली का गुणांक
टक्कर (दूरसंचार)
टक्कर की पहचान हुई है
मामूली टक्कर
टकराव
सीधी टक्कर
प्रभाव क्रेटर
प्रभाव घटना
अयोग्य टकराव
गैसों का गतिज सिद्धांत - अणुओं के बीच टकराव
मिड-एयर टक्कर
प्रक्षेप्य
उपग्रह टक्कर
अंतरिक्ष का कचरा
ट्रेन दुर्घटना

↑ Schmidt, Paul W. (2019). "Collision (physics)". Access Science (in English). doi:10.1036/1097-8542.149000.
↑ merriam-webster.com, "Allision". Accessed November 7, 2014.
↑ "Admiralty Court Rejects Equal Division Rule and Apportions Damages Unequally in Multiple Fault Collision Case". Columbia Law Review. 63 (3): 554 footnote 1. March 1963. doi:10.2307/1120603. JSTOR 1120603. The striking by a vessel of a fixed object such as a bridge, technically termed 'allision' rather than 'collision'.
↑ Talley, Wayne K. (January 1995). "Safety Investments and Operating Conditions: Determinants of Accident Passenger-Vessel Damage Cost". Southern Economic Journal. 61 (3): 823, note 11. doi:10.2307/1061000. JSTOR 1061000. collision—vessel struck or was struck by another vessel on the water surface, or struck a stationary object, not another ship (an allision).
↑ Healy, Nicholas J.; Sweeney, Joseph C. (July–October 1991). "Basic Principles of the Law of Collision". Journal of Maritme Law and Commerce. 22 (3): 359.
↑ "You Say Collision, I Say Allision; Let's Sort the Whole Thing Out | response.restoration.noaa.gov". response.restoration.noaa.gov (in English). Retrieved 2018-08-28.
↑ Judge, ELDON E. FALLON, District. "Vane Line Bunkering, Inc. | Civil Action No. 17-1882. | 20180222d82 | Leagle.com". Leagle (in English). Retrieved 2018-08-28.{{cite news}}: CS1 maint: multiple names: authors list (link)
↑ See 158 U.S. 186 - The Oregon, especially paragraph 10.
↑ Alciatore, David G. (January 2006). "TP 3.1 90° rule" (PDF). Retrieved 2008-03-08.

संदर्भ

Tolman, R. C. (1938). The Principles of Statistical Mechanics. Oxford: Clarendon Press. Reissued (1979) New York: Dover ISBN 0-486-63896-0.

बाहरी संबंध

Three Dimensional Collision - Oblique inelastic collision between two homogeneous spheres.
One Dimensional Collision - One Dimensional Collision Flash Applet.
Two Dimensional Collision - Two Dimensional Collision Flash Applet.

हू: भिड़ंत

[1] Schmidt, Paul W. (2019). "Collision (physics)". Access Science (in English). doi:10.1036/1097-8542.149000.

[2] rriam-webster.com, "Allision". Accessed November 7, 2014.

[3] "Admiralty Court Rejects Equal Division Rule and Apportions Damages Unequally in Multiple Fault Collision Case". Columbia Law Review. 63 (3): 554 footnote 1. March 1963. doi:10.2307/1120603. JSTOR 1120603. The striking by a vessel of a fixed object such as a bridge, technically termed 'allision' rather than 'collision'.

[4] Talley, Wayne K. (January 1995). "Safety Investments and Operating Conditions: Determinants of Accident Passenger-Vessel Damage Cost". Southern Economic Journal. 61 (3): 823, note 11. doi:10.2307/1061000. JSTOR 1061000. collision—vessel struck or was struck by another vessel on the water surface, or struck a stationary object, not another ship (an allision).

[5] Healy, Nicholas J.; Sweeney, Joseph C. (July–October 1991). "Basic Principles of the Law of Collision". Journal of Maritme Law and Commerce. 22 (3): 359.

[6] "You Say Collision, I Say Allision; Let's Sort the Whole Thing Out | response.restoration.noaa.gov". response.restoration.noaa.gov (in English). Retrieved 2018-08-28.

[7] Judge, ELDON E. FALLON, District. "Vane Line Bunkering, Inc. | Civil Action No. 17-1882. | 20180222d82 | Leagle.com". Leagle (in English). Retrieved 2018-08-28.{{cite news}}: CS1 maint: multiple names: authors list (link)

[8] See 158 U.S. 186 - The Oregon, especially paragraph 10.

[9] Alciatore, David G. (January 2006). "TP 3.1 90° rule" (PDF). Retrieved 2008-03-08.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

@@ Line 80: / Line 80: @@
 समय के साथ हमारे पास दो वस्तुओं की स्थिति है जो एक दूसरे से दूर धकेलती हैं, उदा।एक प्रोजेक्टाइल की शूटिंग, या थ्रस्ट को लागू करने वाला एक रॉकेट (Tsiolkovsky रॉकेट समीकरण की व्युत्पत्ति की तुलना करें)।
-== भिड़ंत के उदाहरण संख्यात्मक रूप से विश्लेषण किया गया ==
+== संख्यात्मक रूप से विश्लेषण किए गए भिड़ंतों के उदाहरण ==
-=== पशु लोकोमोशन ===
+=== पशु हरकत (लोकोमोशन) ===
-अंतर्निहित सब्सट्रेट के साथ एक जानवर के पैर या पंजा के भिड़ंत को आमतौर पर जमीनी प्रतिक्रिया बल कहा जाता है।ये भिड़ंत अयोग्य हैं, क्योंकि गतिज ऊर्जा का संरक्षण नहीं है।प्रोस्थेटिक्स में एक महत्वपूर्ण शोध विषय विकलांग और गैर-विकलांग दोनों गेट से जुड़े फुट-ग्राउंड भिड़ंत के दौरान उत्पन्न बलों को निर्धारित कर रहा है।इस परिमाणीकरण में आम तौर पर एक बल प्लेटफॉर्म (कभी -कभी एक बल प्लेट कहा जाता है) के साथ -साथ विस्तृत कीनेमेटिक और गतिशील (कभी -कभी गतिज कहा जाता है) विश्लेषण के लिए विषयों की आवश्यकता होती है।
+अंतर्निहित सब्सट्रेट के साथ किसी जानवर के पैर या पंजा के भिड़ंत को आम तौर पर जमीनी प्रतिक्रिया बल कहा जाता है। ये भिड़ंत बेलोचदार होते हैं, क्योंकि गतिज ऊर्जा संरक्षित नहीं होती है। [[:hi:कृत्रिम अंग|प्रोस्थेटिक्स]] में एक महत्वपूर्ण शोध विषय विकलांग और गैर-विकलांग दोनों चाल से जुड़े पैर-ग्राउंड भिड़ंत के दौरान उत्पन्न बलों की मात्रा निर्धारित कर रहा है। इस परिमाणीकरण के लिए आम तौर पर विषयों को एक [[:hi:बल मंच|बल मंच]] (कभी-कभी "बल प्लेट" कहा जाता है) के साथ-साथ विस्तृत [[:hi:शुद्ध गतिविज्ञान|गतिज]] और [[:hi:गति विज्ञान|गतिशील]] (कभी-कभी गतिज कहा जाता है) विश्लेषण की आवश्यकता होती है।
 == एक प्रयोगात्मक उपकरण के रूप में उपयोग किए जाने वाले भिड़ंत ==
-भिड़ंत का उपयोग वस्तुओं और अन्य भौतिक घटनाओं के भौतिक गुणों का अध्ययन करने के लिए एक प्रयोगात्मक तकनीक के रूप में किया जा सकता है।
+वस्तुओं और अन्य भौतिक घटनाओं के भौतिक गुणों का अध्ययन करने के लिए टकराव को एक प्रयोगात्मक तकनीक के रूप में प्रयोग किया जा सकता है।
+=== अंतरिक्ष की खोज ===
+किसी वस्तु को जानबूझकर किसी अन्य खगोलीय पिंड पर क्रैश-लैंड करने के लिए बनाया जा सकता है, माप करने के लिए और नष्ट होने से पहले उन्हें पृथ्वी पर भेजने के लिए, या कहीं और उपकरणों को प्रभाव का निरीक्षण करने की अनुमति देने के लिए बनाया जा सकता है। उदाहरण देखें:
+* [[:hi:अपोलो 13|अपोलो 13]], [[:hi:अपोलो 14|अपोलो 14]], [[:hi:अपोलो 15|अपोलो 15]], [[:hi:अपोलो 16|अपोलो 16]] और [[:hi:अपोलो 17|अपोलो 17]] के दौरान, [[:hi:एस-आईवीबी|एस-आईवीबी]] (रॉकेट का तीसरा चरण) चंद्र कोर को चिह्नित करने के लिए उपयोग किए जाने वाले भूकंपीय माप करने के लिए [[:hi:चन्द्रमा|चंद्रमा]] में दुर्घटनाग्रस्त हो गया था।
+* [[:hi:गहरा प्रभाव (अंतरिक्ष यान)|''गहरा प्रभाव'']]
+* [[:hi:स्मार्ट-1|स्मार्ट-1]] - [[:hi:यूरोपीय अंतरिक्ष अभिकरण|यूरोपीय अंतरिक्ष एजेंसी]] उपग्रह
+* [[:hi:चंद्रमा प्रभाव जांच|चंद्रमा प्रभाव जांच]] - [[:hi:भारतीय अंतरिक्ष अनुसंधान संगठन|इसरो]] जांच और [[:hi:एलक्रॉस|एलसीआरओएसएस]] अपने खर्च किए गए [[:hi:सेंटौर (रॉकेट स्टेज)|सेंटौर ऊपरी चरण]] के साथ - नासा प्रोब
+* [[:hi:ग्रह रक्षा|ग्रहों की रक्षा]] के लिए [[:hi:डबल क्षुद्रग्रह पुनर्निर्देशन परीक्षण|दोहरा क्षुद्रग्रह पुनर्निर्देशन परीक्षण]] (योजनाबद्ध)
-=== अंतरिक्ष अन्वेषण ===
-एक वस्तु को जानबूझकर एक और खगोलीय शरीर पर क्रैश-लैंड के लिए बनाया जा सकता है, माप करने के लिए और उन्हें नष्ट होने से पहले पृथ्वी पर भेजने के लिए, या उपकरणों को कहीं और प्रभाव का निरीक्षण करने की अनुमति देने के लिए।उदा: देखें:
-*अपोलो 13, अपोलो 14, अपोलो 15, अपोलो 16 और अपोलो 17 के दौरान, एस-आईवीबी (रॉकेट का तीसरा चरण) चंद्रमा में दुर्घटनाग्रस्त हो गया था ताकि लूनर कोर की विशेषता के लिए उपयोग किए जाने वाले भूकंपीय माप को करने के लिए।
-* गहरा प्रभाव
-* स्मार्ट -1 - यूरोपीय अंतरिक्ष एजेंसी उपग्रह
-* चंद्रमा प्रभाव जांच - इसरो जांच और अपने खर्च किए गए सेंटोर ऊपरी चरण के साथ lcross - नासा जांच
-* ग्रह रक्षा के लिए डबल क्षुद्रग्रह पुनर्निर्देशन परीक्षण (योजनाबद्ध)
 === आणविक भिड़ंतों का गणितीय विवरण ===
-एक अणु के रैखिक, कोणीय और आंतरिक क्षण को आर चर के सेट द्वारा दिया जाना चाहिए {पी<sub>''i''</sub> }।एक अणु की स्थिति तब रेंज ΔW द्वारा वर्णित की जा सकती है<sub>''i''</sub> = Δp<sub>1</sub>ΔP<sub>2</sub>ΔP<sub>3</sub> ... Δp<sub>''r''</sub>।विभिन्न राज्यों के अनुरूप ऐसी कई सीमाएं हैं;एक विशिष्ट राज्य को सूचकांक i द्वारा निरूपित किया जा सकता है।भिड़ंतसे गुजरने वाले दो अणुओं को इस प्रकार (i, j) द्वारा निरूपित किया जा सकता है (इस तरह की एक आदेशित जोड़ी को कभी -कभी एक नक्षत्र के रूप में जाना जाता है।)
+मान लीजिए किसी [[:hi:अणु|अणु]] का रैखिक, कोणीय और आंतरिक संवेग ''r'' चरों { ''p'' <sub>''i''</sub> } के समुच्चय द्वारा दिया जाता है। एक अणु की स्थिति को तब श्रेणी ''w'' <sub>''i''</sub> = δ ''p'' <sub>1</sub> δ ''p'' <sub>2</sub> δ ''p'' <sub>3</sub> ... ''p'' <sub>''r''</sub> द्वारा वर्णित किया जा सकता है। विभिन्न राज्यों के अनुरूप कई ऐसी श्रेणियां हैं; एक विशिष्ट राज्य को सूचकांक ''i'' द्वारा दर्शाया जा सकता है। इस प्रकार टकराने वाले दो अणुओं को ( ''i'', ''j'' ) द्वारा निरूपित किया जा सकता है (ऐसे क्रमित जोड़े को कभी-कभी एक ''नक्षत्र'' के रूप में जाना जाता है। ) यह मान लेना सुविधाजनक है कि दो अणु एक दूसरे पर नगण्य प्रभाव डालते हैं जब तक कि उनका गुरुत्वाकर्षण केंद्र एक महत्वपूर्ण दूरी ''b'' के भीतर न पहुंच जाए। इसलिए टकराव तब शुरू होता है जब गुरुत्वाकर्षण के संबंधित केंद्र इस महत्वपूर्ण दूरी पर पहुंच जाते हैं, और जब वे फिर से इस महत्वपूर्ण दूरी पर अपने रास्ते पर पहुंचते हैं तो पूरा हो जाता है। इस मॉडल के तहत, एक टक्कर पूरी तरह से मैट्रिक्स द्वारा वर्णित है <math>\begin{pmatrix}i&j\\k&l\end{pmatrix} </math>, जो टकराव से पहले नक्षत्र ( ''i'', ''j'' ) और टकराव के बाद (सामान्य रूप से भिन्न) नक्षत्र ( ''k'', ''l'' ) को संदर्भित करता है। यह अंकन [[:hi:सांख्यिकीय यांत्रिकी|सांख्यिकीय यांत्रिकी]] के बोल्ट्जमान के [[:hi:H-theorem|एच-प्रमेय]] को सिद्ध करने में सुविधाजनक है।
-यह मानने के लिए सुविधाजनक है कि दो अणु एक दूसरे पर एक नगण्य प्रभाव डालते हैं जब तक कि एक महत्वपूर्ण दूरी के भीतर गुरुत्वाकर्षण के दृष्टिकोण का केंद्र नहीं।इसलिए भिड़ंत तब शुरू होता है जब गुरुत्वाकर्षण के संबंधित केंद्र इस महत्वपूर्ण दूरी पर आते हैं, और तब पूरा हो जाता है जब वे फिर से इस महत्वपूर्ण दूरी पर अपने रास्ते पर पहुंच जाते हैं।इस मॉडल के तहत, मैट्रिक्स द्वारा एक भिड़ंतपूरी तरह से वर्णित है<math>\begin{pmatrix}i&j\\k&l\end{pmatrix} </math>, जो भिड़ंतसे पहले नक्षत्र (i, j) को संदर्भित करता है, और भिड़ंतके बाद (सामान्य रूप से अलग) नक्षत्र (k, l)।
-यह संकेतन बोल्ट्जमैन के सांख्यिकीय यांत्रिकी के एच-थ्योरम को साबित करने में सुविधाजनक है।
+== जानबूझकर भिड़ंत के माध्यम से हमला ==
+जानबूझकर टक्कर के माध्यम से हमले के प्रकारों में शामिल हैं:
+किसी वस्तु या वाहन के साथ रगड़ना, उदा।:
+राम-छड़ी, एक इमारत में एक कार चलाने की प्रथा को तोड़ने के लिए
-== एक जानबूझकर भिड़ंतके माध्यम से हमला ==
-एक जानबूझकर भिड़ंतके माध्यम से हमले के प्रकार में शामिल हैं:
-* शरीर के साथ हड़ताली: निहत्थे हड़ताली, छिद्रण, किकिंग
-* एक हथियार के साथ हड़ताली, जैसे कि तलवार, क्लब या कुल्हाड़ी
-* किसी वस्तु या वाहन के साथ रगड़ना, उदा।:
-** राम-छड़ी, एक इमारत में एक कार चलाने की प्रथा को तोड़ने के लिए
-** बड़े दरवाजों को तोड़ने के लिए इस्तेमाल किया जाने वाला एक राम, मध्ययुगीन हथियार, भी एक आधुनिक संस्करण का उपयोग पुलिस बलों द्वारा छापे के दौरान किया जाता है
 एक दूर की वस्तु के साथ एक हमलावर भिड़ंत एक प्रक्षेप्य को फेंकने या लॉन्च करके प्राप्त किया जा सकता है।

Anonymous

Search

भिड़ंत (कलिश़्‌न्‌): Difference between revisions

Namespaces

More

Page actions

Revision as of 23:54, 27 August 2022

Contents

भौतिकी

भिड़ंत के प्रकार

गठबंधन (ऑलिसिस)

विश्लेषणात्मक बनाम संख्यात्मक दृष्टिकोण भिड़ंत को हल करने की दिशा में