तंत्रिका विज्ञान में सॉलिटॉन मॉडल: Difference between revisions

From Vigyanwiki
No edit summary
Line 76: Line 76:
[[Category: Machine Translated Page]]
[[Category: Machine Translated Page]]
[[Category:Created On 16/02/2023]]
[[Category:Created On 16/02/2023]]
[[Category:Vigyan Ready]]

Revision as of 16:30, 10 March 2023

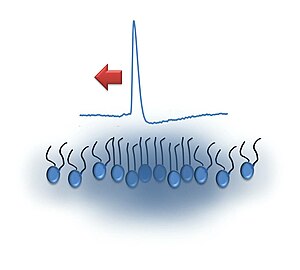
कृत्रिम लिपिड प्रणाली में मापी गई अरैखिक विद्युत-यांत्रिक तरंग

तंत्रिका विज्ञान में सॉलिटॉन परिकल्पना जैविक न्यूरॉन मॉडल है जो यह समझाने का दावा करता है कि तंत्रिका पल्स प्रसार के थर्मोडायनामिक सिद्धांत के आधार पर कार्यवाही संभावना कैसे प्रारंभ किए जाते हैं और अक्षतंतु के साथ संचालित किए जाते हैं। [1] यह प्रस्तावित करता है कि सिग्नल सेल की कोशिका झिल्ली के साथ कुछ प्रकार की एकान्त तरंग (जल तरंगों) ध्वनि (या घनत्व) दालों के रूप में यात्रा करते हैं जिन्हें सॉलिटन के रूप में मॉडल किया जा सकता है। मॉडल को हॉजकिन-हक्सले मॉडल के विकल्प के रूप में प्रस्तावित किया गया है [2] जिसमें संभावित कार्रवाई: मेम्ब्रेन में वोल्टेज-गेटेड आयन चैनल खुलते हैं और सोडियम आयनों को सेल (इनवर्ड करंट) में प्रवेश करने की अनुमति देते हैं। झिल्ली क्षमता में परिणामी कमी पास के वोल्टेज-गेटेड सोडियम चैनल खोलती है, इस प्रकार क्रिया क्षमता का प्रचार करती है। पोटेशियम चैनलों के देरी से खुलने से ट्रांसमेम्ब्रेन क्षमता बहाल हो जाती है। सॉलिटॉन परिकल्पना समर्थकों का दावा है कि अपव्यय हानि को छोड़कर मुख्य रूप से प्रसार के रोचक ऊर्जा का संरक्षण किया जाता है; मापा तापमान परिवर्तन हॉजकिन-हक्सले मॉडल के साथ पूरी तरह से असंगत हैं।

सॉलिटॉन मॉडल (और सामान्य रूप से ध्वनि तरंगें) रूद्धोष्म प्रसार पर निर्भर करता है जिसमें उत्तेजना के स्रोत पर प्रदान की गई ऊर्जा को माध्यम, अर्थात प्लाज्मा झिल्ली के माध्यम से रूद्धोष्म रूप से ले जाया जाता है। तापमान स्पंद का मापन और ऐक्शन पोटेंशिअल के रोचक ताप निर्मुक्त होने का दावा किया गया अभाव [3] [4] प्रस्ताव के आधार थे कि तंत्रिका आवेग ध्वनि तरंगों की तरह रुद्धोष्म घटना है। इलेक्ट्रिक ईल के विद्युत अंग में सिनैप्टिक रूप से विकसित ऐक्शन पोटेंशिअल पर्याप्त सकारात्मक (केवल) ताप उत्पादन के साथ जुड़ा हुआ है, जिसके बाद परिवेश के तापमान पर सक्रिय शीतलन होता है। [5] गारफिश घ्राण तंत्रिका में, ऐक्शन पोटेंशिअल द्विध्रुवीय तापमान परिवर्तन के साथ जुड़ा हुआ है; यद्यपि, गर्मी का शुद्ध उत्पादन होता है। [6] ये प्रकाशित परिणाम हॉजकिन-हक्सले मॉडल के साथ असंगत हैं और लेखक उस मॉडल के संदर्भ में अपने काम की व्याख्या करते हैं: झिल्ली समाई के निर्वहन के रूप में प्रारंभिक सोडियम वर्तमान गर्मी जारी करता है; झिल्ली समाई के पुनर्भरण के रोचक गर्मी अवशोषित होती है क्योंकि पोटेशियम आयन अपनी सांद्रता प्रवणता के साथ किन्तु झिल्ली क्षमता के विरुद्ध चलते हैं। इस तंत्र को संघनित्र सिद्धांत कहा जाता है। झिल्ली क्षमता में परिवर्तन द्वारा संचालित झिल्ली विन्यास परिवर्तन से अतिरिक्त गर्मी उत्पन्न हो सकती है। विध्रुवण के रोचक एन्ट्रापी में वृद्धि से ऊष्मा मुक्त होगी; पुनर्ध्रुवीकरण के रोचक एन्ट्रापी वृद्धि गर्मी को अवशोषित करेगी। हालाँकि, ऐसा कोई भी एंट्रोपिक योगदान हॉजकिन और हक्सले मॉडल के साथ असंगत है [7]


इतिहास

अस्थायी ताजकी ने तंत्रिका स्पंद प्रसार की घटना के लिए थर्मोडायनामिक दृष्टिकोण का बीड़ा उठाया, जिसने कई घटनाओं की पहचान की जो हॉजकिन-हक्सले मॉडल में सम्मिलित नहीं थे। [8] तंत्रिका आवेग के विभिन्न गैर-विद्युत घटकों को मापने के साथ, तसाकी ने तंत्रिका तंतुओं में चरण संक्रमण के भौतिक रसायन विज्ञान और तंत्रिका नाड़ी प्रसार के लिए इसके महत्व की जांच की। तासाकी के काम के आधार पर, कोनराड कौफमैन ने अप्रकाशित पांडुलिपि में ध्वनि तरंगों को तंत्रिका नाड़ी प्रसार के भौतिक आधार के रूप में प्रस्तावित किया। [9] सॉलिटॉन मॉडल के मूल में मूल विचार चरण संक्रमण के पास गैर-रैखिक लोचदार गुणों द्वारा झिल्ली में दो आयामी ध्वनि तरंगों के आंतरिक फैलाव का संतुलन है। प्रारंभिक आवेग ऐसी परिस्थितियों में स्थिर आकार प्राप्त कर सकता है, जिसे सामान्य रूप से एकान्त तरंग के रूप में जाना जाता है।[10] सॉलिटॉन इस तरह की घटना को नियंत्रित करने वाले गैर-रैखिक तरंग समीकरणों के सेट का सबसे सरल समाधान है और 2005 में थॉमस हेमबर्ग और एंड्रयू डी. जैक्सन द्वारा मॉडल तंत्रिका आवेग पर प्रयुक्त किया गया था। [11] [12] [13] दोनों कोपेनहेगन विश्वविद्यालय के नील्स बोह्र संस्थान में है। हेमबर्ग संस्थान के मेम्ब्रेन बायोफिजिक्स ग्रुप के प्रमुख हैं। मैथियास श्नाइडर के जैविक भौतिकी समूह ने लिपिड इंटरफेस में द्वि-आयामी ध्वनि तरंगों के प्रसार और जैविक संकेतन में उनकी संभावित भूमिका का अध्ययन किया है। [14] [15] [16] [17]


औचित्य

मॉडल अवलोकन के साथ प्रारंभ होता है कि कोशिका झिल्लियों में हमेशा एक गलनांक होता है (तापमान जिसके नीचे स्थिरता द्रव से जेल की तरह बदलती है) जीव के शरीर के तापमान से थोड़ा ही कम होता है, और यह सॉलिटॉन के प्रसार की अनुमति देता है। मिश्रित तंत्रिका के साथ यात्रा करने वाली क्रिया क्षमता के परिणामस्वरूप तापमान में मामूली वृद्धि होती है और तापमान में कमी आती है। [18] सोलिटॉन मॉडल समर्थकों का दावा है कि समग्र पल्स के रोचक कोई शुद्ध गर्मी जारी नहीं होती है और देखा गया तापमान परिवर्तन हॉजकिन-हक्सले मॉडल के साथ असंगत हैं। यद्यपि, यह असत्य है: हॉजकिन हक्सले मॉडल द्विध्रुवीय रिलीज और गर्मी के अवशोषण की भविष्यवाणी करता है। [7] इसके अतिरिक्त, ऐक्शन पोटेंशिअल के कारण झिल्ली का थोड़ा स्थानीय मोटा होना और बाहर की ओर कार्य करने वाला बल होता है; [19] हॉजकिन-हक्सले मॉडल द्वारा इस प्रभाव की भविष्यवाणी नहीं की गई है, किन्तुइसका खंडन भी नहीं करता है।

सॉलिटॉन मॉडल एक्शन पोटेंशिअल से जुड़े विद्युत धाराओं को निम्नानुसार समझाने का प्रयास करता है: ट्रैवलिंग सॉलिटॉन स्थानीय रूप से झिल्ली के घनत्व और मोटाई को बदलता है, और चूंकि झिल्ली में कई आवेशित और रासायनिक ध्रुवीय पदार्थ होते हैं, इसका परिणाम पिजोइलेक्ट्रिसिटी के समान विद्युत प्रभाव होगा। के लिए। दरअसल, ऐसी अरैखिक ध्वनि तरंगें अब लिपिड इंटरफेस पर उपस्थित दिखाई गई हैं जो ऐक्शन पोटेंशिअल (इलेक्ट्रो-ऑप्टो-मैकेनिकल कपलिंग, वेलोसिटीज, बाइफैसिक पल्स शेप, एक्साइटेशन के लिए थ्रेसहोल्ड आदि) के लिए सतही समानता दिखाती हैं। [15] इसके अतिरिक्त, लहरें झिल्ली में स्थानीयकृत रहती हैं और प्रतिबाधा बेमेल के कारण आसपास में फैलती नहीं हैं। [20]


औपचारिकता

तंत्रिकाओं की क्रिया क्षमता का प्रतिनिधित्व करने वाला सॉलिटॉन आंशिक अंतर समीकरण का समाधान है

कहाँ t समय है और x तंत्रिका अक्षतंतु के साथ स्थिति है। Δρ क्रिया क्षमता के प्रभाव में झिल्ली घनत्व में परिवर्तन है, c0 तंत्रिका झिल्ली का ध्वनि वेग है, p और q चरण संक्रमण की प्रकृति का वर्णन करें और इस प्रकार तंत्रिका झिल्ली के लोचदार स्थिरांक की गैर-रैखिकता। पैरामीटर c0, p और q तंत्रिका झिल्ली के थर्मोडायनामिक गुणों द्वारा निर्धारित होते हैं और स्वतंत्र रूप से समायोजित नहीं किए जा सकते हैं। उन्हें प्रयोगात्मक रूप से निर्धारित किया जाना है। पैरामीटर h झिल्ली के ध्वनि वेग की आवृत्ति निर्भरता (फैलाव संबंध) का वर्णन करता है। उपरोक्त समीकरण में कोई फिट पैरामीटर नहीं है। यह औपचारिक रूप से पानी की नहरों में सॉलिटॉन के लिए बूसिन्सक सन्निकटन (जल तरंगों) से संबंधित है। उपरोक्त समीकरण के समाधान में सीमित अधिकतम आयाम और न्यूनतम प्रसार वेग होता है जो माइलिनेटेड नसों में पल्स वेग के समान होता है। प्रतिबंधात्मक धारणाओं के अनुसार, आवधिक समाधान उपस्थित हैं जो हाइपरप्लोरीकरण और दुर्दम्य अवधि प्रदर्शित करते हैं। [21]


आयन चैनल की भूमिका

सॉलिटॉन मॉडल के समर्थकों का दावा है कि यह एक्शन पोटेंशिअल के कई पहलुओं की व्याख्या करता है, जिन्हें हॉजकिन-हक्सले मॉडल द्वारा नहीं समझाया गया है। चूंकि यह थर्मोडायनामिक प्रकृति का है, यह आणविक माप पर आयन चैनल प्रोटीन जैसे एकल मैक्रोमोलेक्युलस के गुणों को संबोधित नहीं करता है। बल्कि यह माना जाता है कि तंत्रिका झिल्ली के मैक्रोस्कोपिक थर्मोडायनामिक गुणों में उनके गुण अंतर्निहित रूप से निहित हैं। सॉलिटॉन मॉडल ऐक्शन पोटेंशिअल के रोचक मेम्ब्रेन करंट उतार-चढ़ाव की भविष्यवाणी करता है। ये धाराएँ समान रूप से दिखाई देती हैं जैसा कि आयन चैनल प्रोटीन के लिए रिपोर्ट किया गया है।[22] ऐसा माना जाता है कि वे थर्मल उतार-चढ़ाव से अनायास उत्पन्न होने वाले लिपिड झिल्ली छिद्रों के कारण होते हैं। इस तरह के थर्मल उतार-चढ़ाव विशिष्ट आयनिक चयनात्मकता या सिस्टम की मैक्रोस्कोपिक संवेदनशीलता पर उनके प्रभाव के आधार पर वोल्टेज परिवर्तनों की प्रतिक्रिया के विशिष्ट समय-पाठ्यक्रम की व्याख्या करते हैं।

संज्ञाहरण के लिए आवेदन

लेखकों का दावा है कि उनका मॉडल कई चतनाशून्य करनेवाली औषधि की कार्रवाई के पहले अस्पष्ट तरीके की व्याख्या करता है। न्यूनतम वायुकोशीय सांद्रता #मेयेर-ओवरटन परिकल्पना | मेयर-ओवरटन अवलोकन का मानना ​​है कि रासायनिक रूप से विविध एनेस्थेटिक्स की विस्तृत विविधता की ताकत उनके लिपिड विलेयता के समानुपाती होती है, यह सुझाव देते हुए कि वे विशिष्ट प्रोटीन जैसे आयन चैनलों के लिए बाध्य होकर कार्य नहीं करते हैं बल्कि इसके अतिरिक्त लिपिड झिल्ली के गुणों में घुलने और बदलने से। झिल्ली में घुलने वाले पदार्थ झिल्ली के हिमांक को कम करते हैं, और परिणामस्वरूप शरीर के तापमान और हिमांक के बीच बड़ा अंतर सॉलिटॉन के प्रसार को रोकता है। [23] दबाव बढ़ाकर, पीएच को कम करके या तापमान को कम करके, इस अंतर को वापस सामान्य पर बहाल किया जा सकता है, जो एनेस्थेटिक्स की क्रिया को रद्द कर देना चाहिए: यह वास्तव में देखा गया है। किसी दिए गए लिपिड घुलनशीलता के एनेस्थेटिक की क्रिया को रद्द करने के लिए आवश्यक दबाव की मात्रा सॉलिटॉन मॉडल से गणना की जा सकती है और प्रयोगात्मक अवलोकनों के साथ उचित रूप से सहमत है।

मॉडल भविष्यवाणियों और प्रयोगात्मक टिप्पणियों के बीच अंतर

सॉलिटन्स का टकराव

प्रायोगिक प्रेक्षणों और सॉलिटॉन मॉडल के बीच कुछ असहमतियों की सूची निम्नलिखित है:

एक्सोन से सोमा का एंटीड्रोमिक आक्रमण: एक्सोन पर कहीं भी प्रारंभ की गई एक्शन पोटेंशिअल एंटीड्रोमिक (पिछड़ी) दिशा में न्यूरॉन सोमा (सेल बॉडी) में आयाम के हानि के बिना यात्रा करेगी और सोमा में पूर्ण-आयाम एक्शन पोटेंशिअल उत्पन्न करेगी। चूंकि सोमा का झिल्ली क्षेत्र अक्षतंतु के क्षेत्र की तुलना में अधिक परिमाण का क्रम है, ऊर्जा के संरक्षण के लिए आवश्यक है कि आयाम में रुद्धोष्म यांत्रिक तरंग कम हो। चूंकि गर्मी उत्पादन की अनुपस्थिति 'सोलिटॉन मॉडल' के दावा किए गए औचित्य में से है, इसलिए उस मॉडल के भीतर इसकी व्याख्या करना विशेष रूप से कठिन है। [24]

व्यापक तापमान सीमा पर क्रिया क्षमता की दृढ़ता: सॉलिटॉन मॉडल की महत्वपूर्ण धारणा अक्षतंतु के परिवेश तापमान के पास चरण संक्रमण की उपस्थिति है (औपचारिकता, ऊपर)। फिर, चरण संक्रमण तापमान से दूर तापमान में तेजी से परिवर्तन आवश्यक रूप से ऐक्शन पोटेंशिअल में बड़े बदलाव का कारण होगा। चरण संक्रमण तापमान के नीचे, सॉलिटॉन तरंग संभव नहीं होगी। फिर भी, ऐक्शन पोटेंशिअल 0 डिग्री सेल्सियस पर उपस्थित हैं। हॉजकिन-हक्सले आयन चैनलों के मापा उद्घाटन और समापन कैनेटीक्स द्वारा अनुमानित तरीके से समय पाठ्यक्रम धीमा हो गया है। [25]

टकराव:विपरीत दिशाओं में यात्रा करने वाले तंत्रिका आवेग टक्कर पर एक दूसरे को नष्ट कर देते हैं। [26] दूसरी ओर, यांत्रिक तरंगें नष्ट नहीं होतीं बल्कि एक दूसरे से होकर गुजरती हैं। सॉलिटॉन मॉडल के समर्थकों ने यह दिखाने का प्रयास किया है कि ऐक्शन पोटेंशिअल टक्कर से गुजर सकता है; [27] हालाँकि, ऑर्थोड्रोमिक और एंटीड्रोमिक एक्शन पोटेंशिअल का टकराव विनाश तंत्रिका विज्ञान प्रयोगशालाओं में नियमित रूप से देखी जाने वाली घटना है और न्यूरॉन्स की पहचान के लिए मानक विधि का आधार है। [28] टक्कर होने पर सॉलिटॉन एक-दूसरे से गुजरते हैं (चित्र-- सॉलिटॉन की टक्कर), सामान्य रूप से एकान्त तरंगें एक-दूसरे को पार कर सकती हैं, नष्ट कर सकती हैं या उछाल सकती हैं [29] और सॉलिटॉन ऐसी एकान्त तरंगों का केवल विशेष मामला है। [30]

वोल्टेज क्लैंप के अनुसार आयनिक धाराएं: हॉजकिन और हक्सले (1952) (हॉजकिन-हक्सले मॉडल) द्वारा उपयोग किए जाने वाले वोल्टेज क्लैंप, स्क्वीड विशाल अक्षतंतु में क्रिया क्षमता को प्रयोगात्मक रूप से विच्छेदित करने के लिए, झिल्ली वोल्टेज स्थिर रखने के लिए आवश्यक वर्तमान को मापने के लिए इलेक्ट्रॉनिक प्रतिक्रिया का उपयोग करता है। आदेशित मूल्य पर। अक्षतंतु के आंतरिक भाग में डाला गया चांदी का तार, अक्षतंतु की लंबाई के साथ स्थिर झिल्ली वोल्टेज को बल देता है। इन परिस्थितियों में, यात्रा 'सोलिटन' की कोई संभावना नहीं है। कोई भी उष्मागतिकीय परिवर्तन क्रिया विभव से उत्पन्न होने वाले परिवर्तनों से बहुत भिन्न होता है। फिर भी, मापा धाराएँ क्रिया क्षमता को त्रुटिहीन रूप से पुन: उत्पन्न करती हैं।

एकल चैनल धाराएं: पैच क्लैंप विधि ग्लास पिपेट की नोक पर झिल्ली के सूक्ष्म पैच को अलग करती है। तब एकल आयनिक चैनलों से धाराओं को रिकॉर्ड करना संभव है। सॉलिटॉन्स या थर्मोडायनामिक परिवर्तनों के प्रचार की कोई संभावना नहीं है। फिर भी, इन चैनलों के गुण (वोल्टेज छलांग के लिए अस्थायी प्रतिक्रिया, आयनिक चयनात्मकता) पारंपरिक वोल्टेज क्लैंप के अनुसार मापी गई मैक्रोस्कोपिक धाराओं के गुणों की त्रुटिहीन भविष्यवाणी करते हैं। [31]

चयनात्मक आयनिक चालकता: एक्शन पोटेंशिअल विध्रुवण में अंतर्निहित धारा सोडियम के लिए चयनात्मक है। पुनर्ध्रुवीकरण चयनात्मक पोटेशियम वर्तमान पर निर्भर करता है। इन धाराओं में वोल्टेज परिवर्तनों के लिए बहुत विशिष्ट प्रतिक्रियाएँ होती हैं जो मात्रात्मक रूप से क्रिया क्षमता की व्याख्या करती हैं। सोडियम के लिए गैर-पारगम्य आयनों का प्रतिस्थापन क्रिया क्षमता को समाप्त कर देता है। 'सोलिटॉन मॉडल' या तो आयनिक चयनात्मकता या वोल्टेज परिवर्तनों की प्रतिक्रियाओं की व्याख्या नहीं कर सकता है।

फार्माकोलॉजी: दवा टेट्रोडोटॉक्सिन (टीटीएक्स) अत्यधिक कम सांद्रता पर कार्रवाई क्षमता को अवरुद्ध करती है। सोडियम चैनल पर टीटीएक्स की कार्रवाई के स्थल की पहचान कर ली गई है। [32] डेंड्रोटॉक्सिन पोटेशियम चैनलों को अवरुद्ध करते हैं। ये दवाएं क्रिया क्षमता में मात्रात्मक रूप से अनुमानित परिवर्तन उत्पन्न करती हैं। [31] 'सोलिटॉन मॉडल' इन औषधीय प्रभावों के लिए कोई स्पष्टीकरण प्रदान नहीं करता है।

क्रिया तरंगें

अहमद एल हदी और बेंजामिन माच्टा द्वारा प्रस्तावित हालिया सैद्धांतिक मॉडल का प्रस्ताव है कि एक यांत्रिक सतह तरंग है जो विद्युत क्रिया क्षमता के साथ सह-प्रचार करती है। इन धरातलीय तरंगों को क्रिया तरंगें कहते हैं। [33] एल हदी-मचता के मॉडल में, ये सह-प्रसार तरंगें ऐक्शन पोटेंशिअल के कारण झिल्ली में वोल्टेज परिवर्तन द्वारा संचालित होती हैं।

यह भी देखें

स्रोत

संदर्भ

  1. ↑ Andersen, S; Jackson, A; Heimburg, T (2009). "Towards a thermodynamic theory of nerve pulse propagation" (PDF). Progress in Neurobiology. 88 (2): 104–113. doi:10.1016/j.pneurobio.2009.03.002. PMID 19482227. S2CID 2218193.
  2. ↑ Hodgkin AL, Huxley AF, Katz B (1952). "लोलिगो के विशाल अक्षतंतु की झिल्ली के माध्यम से सोडियम और पोटेशियम आयनों द्वारा प्रवाहित होने वाली धाराएँ". Journal of Physiology. 116 (4): 424–448. doi:10.1113/jphysiol.1952.sp004717. PMC 1392213. PMID 14946713.{{cite journal}}: CS1 maint: multiple names: authors list (link)
    Hodgkin AL, Huxley AF (1952). "लोलिगो के विशाल अक्षतंतु की झिल्ली के माध्यम से सोडियम और पोटेशियम आयनों द्वारा प्रवाहित होने वाली धाराएँ". Journal of Physiology. 116 (4): 449–472. doi:10.1113/jphysiol.1952.sp004717. PMC 1392213. PMID 14946713.
    Hodgkin AL, Huxley AF (1952). "लोलिगो के विशाल अक्षतंतु में झिल्ली चालन के घटक". J Physiol. 116 (4): 473–496. doi:10.1113/jphysiol.1952.sp004718. PMC 1392209. PMID 14946714.
    Hodgkin AL, Huxley AF (1952). "लोलिगो के विशाल अक्षतंतु में सोडियम चालन पर झिल्ली क्षमता का दोहरा प्रभाव". J Physiol. 116 (4): 497–506. doi:10.1113/jphysiol.1952.sp004719. PMC 1392212. PMID 14946715.
    Hodgkin AL, Huxley AF (1952). "मेम्ब्रेन करंट का मात्रात्मक विवरण और तंत्रिका में प्रवाहकत्त्व और उत्तेजना के लिए इसका अनुप्रयोग". J Physiol. 117 (4): 500–544. doi:10.1113/jphysiol.1952.sp004764. PMC 1392413. PMID 12991237.
  3. ↑ Tasaki, Ichiji (13 October 1995). "Mechanical and Thermal Changes in the Torpedo Electric Organ Associated with Its Postsynaptic Potentials". Biochemical and Biophysical Research Communications. 215 (2): 654–658. doi:10.1006/bbrc.1995.2514. PMID 7488005.
  4. ↑ Howarth, J V; Keynes, R D; Ritchie, J M; Muralt, A von (1 Jul 1975). "The heat production associated with the passage of a single impulse in pike olfactory nerve fibres". The Journal of Physiology. 249 (2): 349–368. doi:10.1113/jphysiol.1975.sp011019. PMC 1309578. PMID 1236946.
  5. ↑ Tasaki, I; Byrne, P. M. (1993). "Rapid heat production associated with electrical excitation of the electric organs of the electric eel". Biochem Biophys Res Commun. 197 (2): 910–915. doi:10.1006/bbrc.1993.2565. PMID 8267630.
  6. ↑ Tasaki, K; Kusano, K; Byrne, PM (1989). "Rapid thermal and mechanical changes in garfish olfactory nerve associated with a propagated impulse". Biophys J. 55 (6): 1033–1040. Bibcode:1989BpJ....55.1033T. doi:10.1016/s0006-3495(89)82902-9. PMC 1330571. PMID 2765644.
  7. ↑ 7.0 7.1 Howarth, J. V. (1975). "Heat Production in Non-Myelinated Nerves". Philosophical Transactions of the Royal Society. 270 (908): 425–432. Bibcode:1975RSPTB.270..425H. doi:10.1098/rstb.1975.0020. JSTOR 2417341. PMID 238239.
  8. ↑ Tasaki, Ichiji (1982). Physiology and Electrochemistry of Nerve Fibers. Bethesda, Maryland: Academic Press Inc. (London). ISBN 978-0-12-683780-3.
  9. ↑ Kaufmann, Konrad (1989). Action Potentials and Electrochemical Coupling in the Macroscopic Chiral Phospholipid Membrane. Caruaru, Brazil.{{cite book}}: CS1 maint: location missing publisher (link)
  10. ↑ Xin-Yi, Wang (1985). "Solitary wave and nonequilibrium phase transition in liquid crystals". Physical Review A. 32 (5): 3126–3129. Bibcode:1985PhRvA..32.3126X. doi:10.1103/PhysRevA.32.3126. PMID 9896466.
  11. ↑ Heimburg, T., Jackson, A.D. (12 July 2005). "On soliton propagation in biomembranes and nerves". Proc. Natl. Acad. Sci. U.S.A. 102 (2): 9790–9795. Bibcode:2005PNAS..102.9790H. doi:10.1073/pnas.0503823102. PMC 1175000. PMID 15994235.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  12. ↑ Heimburg, T., Jackson, A.D. (2007). "On the action potential as a propagating density pulse and the role of anesthetics". Biophys. Rev. Lett. 2: 57–78. arXiv:physics/0610117. Bibcode:2006physics..10117H. doi:10.1142/S179304800700043X. S2CID 1295386.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  13. ↑ Andersen, S.S.L., Jackson, A.D., Heimburg, T. (2009). "Towards a thermodynamic theory of nerve pulse propagation". Prog. Neurobiol. 88 (2): 104–113. doi:10.1016/j.pneurobio.2009.03.002. PMID 19482227. S2CID 2218193.{{cite journal}}: CS1 maint: multiple names: authors list (link)[dead link]
  14. ↑ Griesbauer, J; Bossinger, S; Wixforth, A; Schneider, M (9 May 2012). "Propagation of 2D Pressure Pulses in Lipid Monolayers and Its Possible Implications for Biology". Physical Review Letters. 108 (19): 198103. arXiv:1211.4104. Bibcode:2012PhRvL.108s8103G. doi:10.1103/PhysRevLett.108.198103. PMID 23003093.
  15. ↑ 15.0 15.1 Shrivastava, Shamit; Schneider, Matthias (18 June 2014). "Evidence for two-dimensional solitary sound waves in a lipid controlled interface and its implications for biological signalling". Journal of the Royal Society Interface. 11 (97): 20140098. doi:10.1098/rsif.2014.0098. PMC 4078894. PMID 24942845.
  16. ↑ Griesbauer, J; Bossinger, S; Wixforth, A; Schneider, M (19 Dec 2012). "Simultaneously propagating voltage and pressure pulses in lipid monolayers of pork brain and synthetic lipids". Physical Review E. 86 (6): 061909. arXiv:1211.4105. Bibcode:2012PhRvE..86f1909G. doi:10.1103/PhysRevE.86.061909. PMID 23367978. S2CID 25259498.
  17. ↑ Shrivastava, Shamit (Jan 2014). NON-LINEAR SOLITARY SOUND WAVES IN LIPID MEMBRANES AND THEIR POSSIBLE ROLE IN BIOLOGICAL SIGNALING (1st ed.). Boston, MA 02215 US: Thesis, Boston University.{{cite book}}: CS1 maint: location (link)
  18. ↑ Abbott, B.C., Hill, A.V., Howarth, J.V. (1958). "The positive and negative heat associated with a nerve impulse". Proceedings of the Royal Society B. 148 (931): 149–187. Bibcode:1958RSPSB.148..149A. doi:10.1098/rspb.1958.0012. PMID 13518134. S2CID 2252017.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  19. ↑ Iwasa, K., Tasaki I., Gibbons, R. (1980). "Swelling of nerve fibres associated with action potentials". Science. 210 (4467): 338–9. Bibcode:1980Sci...210..338I. doi:10.1126/science.7423196. PMID 7423196.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  20. ↑ Griesbauer, J; Wixforth, A; Schneider, M F (15 Nov 2009). "Wave Propagation in Lipid Monolayers". Biophysical Journal. 97 (10): 2710–2716. Bibcode:2009BpJ....97.2710G. doi:10.1016/j.bpj.2009.07.049. PMC 2776282. PMID 19917224.
  21. ↑ Villagran Vargas, E., Ludu, A., Hustert, R., Gumrich, P., Jackson, A.D., Heimburg, T. (2011). "Periodic solutions and refractory periods in the soliton theory for nerves and the locust femoral nerve". Biophysical Chemistry. 153 (2–3): 159–167. arXiv:1006.3281. doi:10.1016/j.bpc.2010.11.001. PMID 21177017. S2CID 15106768.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  22. ↑ Heimburg, T. (2010). "Lipid Ion Channels". Biophys. Chem. 150 (1–3): 2–22. arXiv:1001.2524. Bibcode:2010arXiv1001.2524H. doi:10.1016/j.bpc.2010.02.018. PMID 20385440. S2CID 926828.
  23. ↑ Heimburg, T., Jackson, A.D. (2007). "The thermodynamics of general anesthesia". Biophys. J. 92 (9): 3159–65. arXiv:physics/0610147. Bibcode:2007BpJ....92.3159H. doi:10.1529/biophysj.106.099754. PMC 1852341. PMID 17293400.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  24. ↑ Rall, W and Shepherd, GM (1968) Theoretical reconstructions of dendrodendritic synaptic interactions in the olfactory bulb. J Neurophysiol 31, 884-915.http://jn.physiology.org/content/jn/31/6/884.full.pdf
  25. ↑ Hodgkin; Katz (1949). "The Effect of Temperature on the Electrical Activity of the Giant Axon of the Squid". J. Physiol. 109 (1–2): 240–249. doi:10.1113/jphysiol.1949.sp004388. PMC 1392577. PMID 15394322.
  26. ↑ Tasaki, Ichiji (1949). "Collision of two nerve impulses in the nerve fiber". Biochim Biophys Acta. 3: 494–497. doi:10.1016/0006-3002(49)90121-3.
  27. ↑ Gonzalez, Alfredo; Budvytyte, Rima; Mosgaard, Lars D; Nissen, Søren; Heimburg, Thomas (10 Sep 2014). "Penetration of Action Potentials During Collision in the Median and Lateral Giant Axons of Invertebrates". Physical Review X. 4 (3): 031047. arXiv:1404.3643. Bibcode:2014PhRvX...4c1047G. doi:10.1103/PhysRevX.4.031047. S2CID 17503341.
  28. ↑ Sander, HW, Collision Testing in J Kimura Peripheral Nerve Diseases https://books.google.com/books?id=jp05zU9vxo8C&pg=PA359&lpg=PA359&dq=collision+test+neurophysiology&source=bl&ots=PTz3H5Mn-t&sig=LUtPKvs1ad8q0wX8zIQ712mNG7E&hl=en&sa=X&ei=dE9iVfvlENOMyASFz4OQAg&ved=0CB0Q6AEwADgK#v=onepage&q=collision%20test%20neurophysiology&f=false
  29. ↑ Eckl, C; Mayer, A P; Kovalev, A S (3 August 1998). "Do Surface Acoustic Solitons Exist?". Physical Review Letters. 81 (5): 983–986. Bibcode:1998PhRvL..81..983E. doi:10.1103/PhysRevLett.81.983.
  30. ↑ Shrivastava, Shamit; Kang, Kevin; Schneider, Matthias F (30 Jan 2015). "Solitary shock waves and adiabatic phase transition in lipid interfaces and nerves". Physical Review E. 91 (12715): 012715. arXiv:1411.2454. Bibcode:2015PhRvE..91a2715S. doi:10.1103/PhysRevE.91.012715. PMID 25679650. S2CID 12034915.
  31. ↑ 31.0 31.1 Hille, Bertil (2001). Ion channels of excitable membranes (3. ed. ed.). Sunderland, Massachusetts: Sinauer. ISBN 9780878933211.
  32. ↑ Catterall, WA (2014). "Structure and function of voltage-gated sodium channels at atomic resolution". Experimental Physiology. 99 (1): 35–51. doi:10.1113/expphysiol.2013.071969. PMC 3885250. PMID 24097157.
  33. ↑ El Hady, A., Machta, B. (2015). "Mechanical surface waves accompany action potential propagation". Nature Communications. 6: 6697. arXiv:1407.7600. Bibcode:2015NatCo...6.6697E. doi:10.1038/ncomms7697. PMID 25819404. S2CID 17462621.{{cite journal}}: CS1 maint: multiple names: authors list (link)
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=तंत्रिका_विज्ञान_में_सॉलिटॉन_मॉडल&oldid=104766’