विश्लेषणात्मक संकेत: Difference between revisions
(Created page with "{{Distinguish|analytic expression|analytic function}} गणित और संकेत आगे बढ़ाना में, एक विश्लेषणात...") |
No edit summary |
||
| Line 3: | Line 3: | ||
गणित और [[ संकेत आगे बढ़ाना ]] में, एक विश्लेषणात्मक सिग्नल एक जटिल-मूल्यवान फ़ंक्शन होता है जिसमें कोई [[नकारात्मक आवृत्ति]] घटक नहीं होता है।<ref>Smith, J.O. "Analytic Signals and Hilbert Transform Filters", in Mathematics of the Discrete Fourier Transform (DFT) with Audio Applications, Second Edition, https://ccrma.stanford.edu/~jos/r320/Analytic_Signals_Hilbert_Transform.html, or https://www.dsprelated.com/freebooks/mdft/Analytic_Signals_Hilbert_Transform.html, online book, 2007 edition, accessed 2021-04-29.</ref>एक विश्लेषणात्मक संकेत के वास्तविक और काल्पनिक भाग हिल्बर्ट परिवर्तन द्वारा एक दूसरे से संबंधित वास्तविक-मूल्यवान कार्य हैं। | गणित और [[ संकेत आगे बढ़ाना ]] में, एक विश्लेषणात्मक सिग्नल एक जटिल-मूल्यवान फ़ंक्शन होता है जिसमें कोई [[नकारात्मक आवृत्ति]] घटक नहीं होता है।<ref>Smith, J.O. "Analytic Signals and Hilbert Transform Filters", in Mathematics of the Discrete Fourier Transform (DFT) with Audio Applications, Second Edition, https://ccrma.stanford.edu/~jos/r320/Analytic_Signals_Hilbert_Transform.html, or https://www.dsprelated.com/freebooks/mdft/Analytic_Signals_Hilbert_Transform.html, online book, 2007 edition, accessed 2021-04-29.</ref>एक विश्लेषणात्मक संकेत के वास्तविक और काल्पनिक भाग हिल्बर्ट परिवर्तन द्वारा एक दूसरे से संबंधित वास्तविक-मूल्यवान कार्य हैं। | ||
[[वास्तविक संख्या]] का विश्लेषणात्मक प्रतिनिधित्व | वास्तविक-मूल्यवान कार्य एक ''विश्लेषणात्मक संकेत'' है, जिसमें मूल कार्य और उसका हिल्बर्ट रूपांतरण | [[वास्तविक संख्या]] का विश्लेषणात्मक प्रतिनिधित्व | वास्तविक-मूल्यवान कार्य एक ''विश्लेषणात्मक संकेत'' है, जिसमें मूल कार्य और उसका हिल्बर्ट रूपांतरण सम्मलित है। यह प्रतिनिधित्व कई गणितीय जोड़तोड़ की सुविधा देता है। मूल विचार यह है कि ऐसे [[स्पेक्ट्रम]] के [[हर्मिटियन समरूपता]] के कारण वास्तविक-मूल्यवान फ़ंक्शन के [[फूरियर रूपांतरण]] (या स्पेक्ट्रम) के नकारात्मक आवृत्ति घटक अनावश्यक हैं। इन नकारात्मक आवृत्ति घटकों को सूचना की हानि के बिना त्याग दिया जा सकता है, बशर्ते कोई जटिल-मूल्यवान फ़ंक्शन से निपटने के लिए तैयार हो। यह फ़ंक्शन की कुछ विशेषताओं को अधिक सुलभ बनाता है और मॉड्यूलेशन और डिमॉड्यूलेशन तकनीकों की व्युत्पत्ति की सुविधा देता है, जैसे सिंगल-साइडबैंड। | ||
जब तक हेरफेर किए गए फ़ंक्शन में कोई नकारात्मक आवृत्ति घटक नहीं होता है (अर्थात, यह अभी भी '' विश्लेषणात्मक '' है), जटिल से वास्तविक में रूपांतरण केवल काल्पनिक भाग को छोड़ने का | जब तक हेरफेर किए गए फ़ंक्शन में कोई नकारात्मक आवृत्ति घटक नहीं होता है (अर्थात, यह अभी भी '' विश्लेषणात्मक '' है), जटिल से वास्तविक में रूपांतरण केवल काल्पनिक भाग को छोड़ने का स्थिति है। विश्लेषणात्मक प्रतिनिधित्व चरण (साइन तरंगों) अवधारणा का एक सामान्यीकरण है:<ref name=Bracewell>Bracewell, Ron. ''The Fourier Transform and Its Applications''. McGraw-Hill, 1965. p 269</ref> जबकि चरण समय-अपरिवर्तनीय आयाम, चरण और आवृत्ति तक सीमित है, विश्लेषणात्मक संकेत समय-परिवर्तनीय पैरामीटर के लिए अनुमति देता है। | ||
== परिभाषा == | == परिभाषा == | ||
[[File:Analytisches-signal-uebertragungsfunktion-en.svg|thumb|250px|एक विश्लेषणात्मक संकेत बनाने के लिए स्थानांतरण समारोह]] | [[File:Analytisches-signal-uebertragungsfunktion-en.svg|thumb|250px|एक विश्लेषणात्मक संकेत बनाने के लिए स्थानांतरण समारोह]]यदि <math>s(t)</math> फूरियर रूपांतरण के साथ एक वास्तविक-मूल्यवान कार्य है <math>S(f)</math>, तब परिवर्तन में [[हर्मिटियन फ़ंक्शन]] समरूपता है <math>f = 0</math> एक्सिस: | ||
:<math>S(-f) = S(f)^*,</math> | :<math>S(-f) = S(f)^*,</math> | ||
कहाँ <math>S(f)^*</math> का जटिल संयुग्म है <math>S(f)</math>. | कहाँ <math>S(f)^*</math> का जटिल संयुग्म है <math>S(f)</math>. | ||
| Line 27: | Line 27: | ||
*<math>\sgn(f)</math> [[साइन समारोह]] है, | *<math>\sgn(f)</math> [[साइन समारोह]] है, | ||
के केवल गैर-नकारात्मक आवृत्ति घटक | के केवल गैर-नकारात्मक आवृत्ति घटक सम्मलित हैं <math>S(f)</math>. और ऑपरेशन प्रतिवर्ती है, की हर्मिटियन समरूपता के कारण <math>S(f)</math>: | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 60: | Line 60: | ||
===नकारात्मक आवृत्ति घटक=== | ===नकारात्मक आवृत्ति घटक=== | ||
तब से <math>s(t) = \operatorname{Re}[s_\mathrm{a}(t)]</math>, नकारात्मक आवृत्ति घटकों को पुनर्स्थापित करना त्यागने का एक साधारण | तब से <math>s(t) = \operatorname{Re}[s_\mathrm{a}(t)]</math>, नकारात्मक आवृत्ति घटकों को पुनर्स्थापित करना त्यागने का एक साधारण स्थिति है <math>\operatorname{Im}[s_\mathrm{a}(t)]</math> जो प्रति-सहज लग सकता है। हम यह भी नोट कर सकते हैं कि जटिल संयुग्म <math>s_\mathrm{a}^*(t)</math> केवल नकारात्मक आवृत्ति घटक सम्मलित हैं। और इसलिए <math>s(t) = \operatorname{Re}[s_\mathrm{a}^*(t)]</math> दबा हुआ सकारात्मक आवृत्ति घटकों को पुनर्स्थापित करता है। एक अन्य दृष्टिकोण यह है कि किसी भी स्थिति में काल्पनिक घटक एक ऐसा शब्द है जो आवृत्ति घटकों को घटाता है <math>s(t).</math> <math>\operatorname{Re}</math> h> ऑपरेटर नए घटकों को जोड़ने का आभास देते हुए, घटाव को हटा देता है। | ||
== उदाहरण == | == उदाहरण == | ||
| Line 71: | Line 71: | ||
s_\mathrm{a}(t) &= s(t) + j\hat{s}(t) = \cos(\omega t) + j\sin(\omega t) = e^{j\omega t}. | s_\mathrm{a}(t) &= s(t) + j\hat{s}(t) = \cos(\omega t) + j\sin(\omega t) = e^{j\omega t}. | ||
\end{align}</math> | \end{align}</math> | ||
अंतिम समानता यूलर का सूत्र है, जिसका एक उपप्रमेय है <math display="inline">\cos(\omega t) = \frac{1}{2} \left(e^{j\omega t} + e^{j (-\omega) t}\right).</math> | अंतिम समानता यूलर का सूत्र है, जिसका एक उपप्रमेय है <math display="inline">\cos(\omega t) = \frac{1}{2} \left(e^{j\omega t} + e^{j (-\omega) t}\right).</math> सामान्यतः , एक साधारण साइनसॉइड का विश्लेषणात्मक प्रतिनिधित्व इसे जटिल-घातीयों के संदर्भ में व्यक्त करके, नकारात्मक आवृत्ति घटक को छोड़कर, सकारात्मक आवृत्ति घटक को दोगुना करके प्राप्त किया जाता है। और साइनसोइड्स के योग का विश्लेषणात्मक प्रतिनिधित्व व्यक्तिगत साइनसोइड्स के विश्लेषणात्मक प्रतिनिधित्वों का योग है। | ||
=== उदाहरण 2 === | === उदाहरण 2 === | ||
| Line 103: | Line 103: | ||
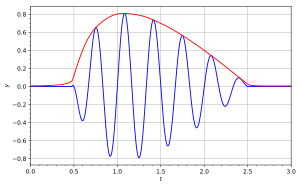
[[Image:analytic.svg|thumb|300px|नीले रंग में एक फ़ंक्शन और लाल रंग में इसके विश्लेषणात्मक प्रतिनिधित्व का परिमाण, लिफाफा प्रभाव दिखा रहा है।]]ध्रुवीय निर्देशांक में एक विश्लेषणात्मक संकेत भी व्यक्त किया जा सकता है: | [[Image:analytic.svg|thumb|300px|नीले रंग में एक फ़ंक्शन और लाल रंग में इसके विश्लेषणात्मक प्रतिनिधित्व का परिमाण, लिफाफा प्रभाव दिखा रहा है।]]ध्रुवीय निर्देशांक में एक विश्लेषणात्मक संकेत भी व्यक्त किया जा सकता है: | ||
:<math>s_\mathrm{a}(t) = s_\mathrm{m}(t)e^{j\phi(t)},</math> | :<math>s_\mathrm{a}(t) = s_\mathrm{m}(t)e^{j\phi(t)},</math> | ||
जहां निम्नलिखित समय-भिन्न मात्राएं | जहां निम्नलिखित समय-भिन्न मात्राएं प्रस्तुत की जाती हैं: | ||
*<math>s_\mathrm{m}(t) \triangleq |s_\mathrm{a}(t)|</math> तात्कालिक आयाम या आवरण (तरंगें) कहा जाता है; | *<math>s_\mathrm{m}(t) \triangleq |s_\mathrm{a}(t)|</math> तात्कालिक आयाम या आवरण (तरंगें) कहा जाता है; | ||
*<math>\phi(t) \triangleq \arg\!\left[s_\mathrm{a}(t)\right]</math> [[तात्कालिक चरण]] या चरण कोण कहा जाता है। | *<math>\phi(t) \triangleq \arg\!\left[s_\mathrm{a}(t)\right]</math> [[तात्कालिक चरण]] या चरण कोण कहा जाता है। | ||
| Line 116: | Line 116: | ||
=== {{anchor|Complex envelope}} जटिल लिफाफा/बेसबैंड === | === {{anchor|Complex envelope}} जटिल लिफाफा/बेसबैंड === | ||
विश्लेषणात्मक संकेतों को | विश्लेषणात्मक संकेतों को अधिकांशतः 0 हर्ट्ज की ओर आवृत्ति (नीचे-रूपांतरित) में स्थानांतरित किया जाता है, संभवतः [गैर-सममित] नकारात्मक आवृत्ति घटक बनाते हैं: | ||
<math display="block">{s_\mathrm{a}}_{\downarrow}(t) \triangleq s_\mathrm{a}(t)e^{-j\omega_0 t} = s_\mathrm{m}(t)e^{j(\phi(t) - \omega_0 t)},</math> | <math display="block">{s_\mathrm{a}}_{\downarrow}(t) \triangleq s_\mathrm{a}(t)e^{-j\omega_0 t} = s_\mathrm{m}(t)e^{j(\phi(t) - \omega_0 t)},</math> | ||
कहाँ <math>\omega_0</math> एक मनमाना संदर्भ कोणीय आवृत्ति है।<ref name=Bracewell/> | कहाँ <math>\omega_0</math> एक मनमाना संदर्भ कोणीय आवृत्ति है।<ref name=Bracewell/> | ||
यह फ़ंक्शन विभिन्न नामों से जाता है, जैसे जटिल लिफाफा और जटिल [[बेसबैंड]]। जटिल लिफाफा अद्वितीय नहीं है; यह की पसंद से निर्धारित होता है <math>\omega_0</math>. इस अवधारणा का प्रयोग | यह फ़ंक्शन विभिन्न नामों से जाता है, जैसे जटिल लिफाफा और जटिल [[बेसबैंड]]। जटिल लिफाफा अद्वितीय नहीं है; यह की पसंद से निर्धारित होता है <math>\omega_0</math>. इस अवधारणा का प्रयोग अधिकांशतः [[पासबैंड संकेत]]ों के साथ काम करते समय किया जाता है। यदि <math>s(t)</math> एक संग्राहक संकेत है, <math>\omega_0</math> इसकी [[वाहक आवृत्ति]] के बराबर हो सकता है। | ||
अन्य | अन्य स्थितियों ं में, <math>\omega_0</math> वांछित पासबैंड के बीच में कहीं चुना गया है। फिर वास्तविक गुणांक के साथ एक साधारण निम्न-पास फ़िल्टर ब्याज के हिस्से को बढ़ा सकता है। एक अन्य मकसद उच्चतम आवृत्ति को कम करना है, जो कि उपनाम-मुक्त नमूनाकरण के लिए न्यूनतम दर को कम करता है। एक आवृत्ति बदलाव जटिल सिग्नल प्रतिनिधित्व के गणितीय ट्रैक्टेबिलिटी को कम नहीं करता है। तो उस मायने में, डाउन-कन्वर्टेड सिग्नल अभी भी विश्लेषणात्मक है। चूँकि , वास्तविक-मूल्यवान प्रतिनिधित्व को पुनर्स्थापित करना अब केवल वास्तविक घटक को निकालने का सरल स्थिति नहीं है। अप-रूपांतरण की आवश्यकता हो सकती है, और यदि सिग्नल [[upsampling]] (सिग्नल प्रोसेसिंग) (असतत-समय) किया गया है, तो [[अलियासिंग]] से बचने के लिए [[ प्रक्षेप ]] (अपसैंपलिंग) भी आवश्यक हो सकता है। | ||
यदि <math>\omega_0</math> की उच्चतम आवृत्ति से बड़ा चुना जाता है <math>s_\mathrm{a}(t),</math> तब <math>{s_\mathrm{a}}_{\downarrow}(t)</math> कोई सकारात्मक आवृत्तियाँ नहीं हैं। उस स्थिति में, वास्तविक घटक निकालने से उन्हें पुनर्स्थापित किया जाता है, लेकिन विपरीत क्रम में; कम आवृत्ति वाले घटक अब उच्च वाले हैं और इसके विपरीत। इसका उपयोग एक प्रकार के [[सिंगल-साइडबैंड मॉड्यूलेशन]]|सिंगल-साइडबैंड सिग्नल को लोअर साइडबैंड या इनवर्टेड साइडबैंड कहा जाता है। | |||
संदर्भ आवृत्ति के अन्य विकल्पों पर कभी-कभी विचार किया जाता है: | संदर्भ आवृत्ति के अन्य विकल्पों पर कभी-कभी विचार किया जाता है: | ||
| Line 130: | Line 130: | ||
* वैकल्पिक रूप से,<ref>{{Cite journal|last=Justice|first=J.|date=1979-12-01|title=संगीत संगणना में विश्लेषणात्मक सिग्नल प्रोसेसिंग| journal=IEEE Transactions on Acoustics, Speech, and Signal Processing|volume=27|issue=6|pages=670–684| doi=10.1109/TASSP.1979.1163321| issn=0096-3518}}</ref> <math>\omega_0</math> अलिखित तात्कालिक चरण को रैखिक रूप से अनुमानित करने में औसत वर्ग त्रुटि को कम करने के लिए चुना जा सकता है <math>\phi(t)</math>: <math display="block">\int_{-\infty}^{+\infty}[\omega(t) - \omega_0]^2 |s_\mathrm{a}(t)|^2\, dt</math> | * वैकल्पिक रूप से,<ref>{{Cite journal|last=Justice|first=J.|date=1979-12-01|title=संगीत संगणना में विश्लेषणात्मक सिग्नल प्रोसेसिंग| journal=IEEE Transactions on Acoustics, Speech, and Signal Processing|volume=27|issue=6|pages=670–684| doi=10.1109/TASSP.1979.1163321| issn=0096-3518}}</ref> <math>\omega_0</math> अलिखित तात्कालिक चरण को रैखिक रूप से अनुमानित करने में औसत वर्ग त्रुटि को कम करने के लिए चुना जा सकता है <math>\phi(t)</math>: <math display="block">\int_{-\infty}^{+\infty}[\omega(t) - \omega_0]^2 |s_\mathrm{a}(t)|^2\, dt</math> | ||
* या कोई अन्य विकल्प (कुछ इष्टतम के लिए <math>\theta</math>): <math display="block">\int_{-\infty}^{+\infty}[\phi(t) - (\omega_0 t + \theta)]^2\, dt.</math> | * या कोई अन्य विकल्प (कुछ इष्टतम के लिए <math>\theta</math>): <math display="block">\int_{-\infty}^{+\infty}[\phi(t) - (\omega_0 t + \theta)]^2\, dt.</math> | ||
समय-आवृत्ति सिग्नल प्रोसेसिंग के क्षेत्र में, यह दिखाया गया था कि विग्नर-विले वितरण की परिभाषा में विश्लेषणात्मक सिग्नल की आवश्यकता थी | समय-आवृत्ति सिग्नल प्रोसेसिंग के क्षेत्र में, यह दिखाया गया था कि विग्नर-विले वितरण की परिभाषा में विश्लेषणात्मक सिग्नल की आवश्यकता थी जिससे कि व्यावहारिक अनुप्रयोगों के लिए आवश्यक वांछित गुण हो सकें।<ref>B. Boashash, “Notes on the use of the Wigner distribution for time frequency signal analysis”, IEEE Trans. on Acoustics, Speech, and Signal Processing , vol. 26, no. 9, 1987</ref> | ||
कभी-कभी वाक्यांश जटिल लिफाफे को एक (निरंतर-आवृत्ति) चरण के [[जटिल आयाम]] का सरल अर्थ दिया जाता है;{{efn|"the complex envelope (or complex amplitude)"<ref>{{Cite book|url=https://books.google.com/books?id=tOeeJyP95IQC |title=Time-Frequency Analysis|last1=Hlawatsch|first1=Franz|last2=Auger|first2=François|date=2013-03-01|publisher=John Wiley & Sons |isbn=9781118623831|language=en}}</ref>}}{{efn|"the complex envelope (or complex amplitude)", p. 586 <ref>{{Cite book |url=https://books.google.com/books?id=kxICp6t-CDAC&q=%2522complex%2520amplitude%2522%2520%2522complex%2520envelope%2522&pg=RA1-PA586 |title=Encyclopedia of Optical Engineering: Abe-Las, pages 1-1024|last=Driggers|first=Ronald G.|date=2003-01-01 |publisher=CRC Press|isbn=9780824742508|language=en}}</ref>}} | कभी-कभी वाक्यांश जटिल लिफाफे को एक (निरंतर-आवृत्ति) चरण के [[जटिल आयाम]] का सरल अर्थ दिया जाता है;{{efn|"the complex envelope (or complex amplitude)"<ref>{{Cite book|url=https://books.google.com/books?id=tOeeJyP95IQC |title=Time-Frequency Analysis|last1=Hlawatsch|first1=Franz|last2=Auger|first2=François|date=2013-03-01|publisher=John Wiley & Sons |isbn=9781118623831|language=en}}</ref>}}{{efn|"the complex envelope (or complex amplitude)", p. 586 <ref>{{Cite book |url=https://books.google.com/books?id=kxICp6t-CDAC&q=%2522complex%2520amplitude%2522%2520%2522complex%2520envelope%2522&pg=RA1-PA586 |title=Encyclopedia of Optical Engineering: Abe-Las, pages 1-1024|last=Driggers|first=Ronald G.|date=2003-01-01 |publisher=CRC Press|isbn=9780824742508|language=en}}</ref>}} | ||
दूसरी बार जटिल लिफाफा <math> s_m(t)</math> जैसा कि ऊपर परिभाषित किया गया है, जटिल आयाम के समय-निर्भर सामान्यीकरण के रूप में व्याख्या की गई है।{{efn|"Complex envelope is an extended interpretation of complex amplitude as a function of time." p. 85<ref>{{Cite book|url=https://books.google.com/books?id=tXQy5JdQyZoC|title=Global Environment Remote Sensing| last=Okamoto|first=Kenʼichi|date=2001-01-01|publisher=IOS Press|isbn=9781586031015|language=en}}</ref>}} वास्तविक-मूल्य वाले | दूसरी बार जटिल लिफाफा <math> s_m(t)</math> जैसा कि ऊपर परिभाषित किया गया है, जटिल आयाम के समय-निर्भर सामान्यीकरण के रूप में व्याख्या की गई है।{{efn|"Complex envelope is an extended interpretation of complex amplitude as a function of time." p. 85<ref>{{Cite book|url=https://books.google.com/books?id=tXQy5JdQyZoC|title=Global Environment Remote Sensing| last=Okamoto|first=Kenʼichi|date=2001-01-01|publisher=IOS Press|isbn=9781586031015|language=en}}</ref>}} वास्तविक-मूल्य वाले स्थिति में उनका संबंध उससे अलग नहीं है: अलग-अलग लिफाफा (तरंगें) निरंतर [[आयाम]] को सामान्य करता है। | ||
== एकाधिक चर के संकेतों के लिए विश्लेषणात्मक संकेत का विस्तार == | == एकाधिक चर के संकेतों के लिए विश्लेषणात्मक संकेत का विस्तार == | ||
विश्लेषणात्मक संकेत की अवधारणा एकल चर के संकेतों के लिए अच्छी तरह से परिभाषित है जो | विश्लेषणात्मक संकेत की अवधारणा एकल चर के संकेतों के लिए अच्छी तरह से परिभाषित है जो सामान्यतः समय है। दो या दो से अधिक चर के संकेतों के लिए, एक विश्लेषणात्मक संकेत को अलग-अलग विधियों से परिभाषित किया जा सकता है, और दो दृष्टिकोण नीचे प्रस्तुत किए गए हैं। | ||
=== तदर्थ दिशा === के आधार पर बहु-आयामी विश्लेषणात्मक संकेत | === तदर्थ दिशा === के आधार पर बहु-आयामी विश्लेषणात्मक संकेत | ||
एक बार यह स्थापित हो जाने के बाद कि इस | एक बार यह स्थापित हो जाने के बाद कि इस स्थिति के लिए नकारात्मक आवृत्तियों का क्या मतलब है, एक बहु-आयामी संकेत के लिए विश्लेषणात्मक संकेत का एक सीधा सामान्यीकरण किया जा सकता है। यह एक [[इकाई वेक्टर]] की शुरुआत करके किया जा सकता है <math>\boldsymbol \hat{u}</math> फूरियर डोमेन में और किसी आवृत्ति वेक्टर को लेबल करें <math>\boldsymbol \xi</math> नकारात्मक के रूप में यदि <math>\boldsymbol \xi \cdot \boldsymbol \hat{u} < 0</math>. एक-चर संकेतों के स्थिति में वर्णित प्रक्रिया के अनुसार, सभी नकारात्मक आवृत्तियों को हटाकर और परिणाम को 2 से गुणा करके विश्लेषणात्मक संकेत उत्पन्न किया जाता है। चूँकि , इसके लिए कोई विशेष दिशा नहीं है <math>\boldsymbol \hat{u}</math> जिसे तब तक चुना जाना चाहिए जब तक कि कुछ अतिरिक्त बाधाएँ न हों। इसलिए, का चुनाव <math>\boldsymbol \hat{u}</math> तदर्थ है, या अनुप्रयोग विशिष्ट है। | ||
=== [[ मोनोजेनिक संकेत ]] === | === [[ मोनोजेनिक संकेत ]] === | ||
विश्लेषणात्मक संकेत के वास्तविक और काल्पनिक भाग वेक्टर-मूल्यवान मोनोजेनिक सिग्नल के दो तत्वों के अनुरूप होते हैं, क्योंकि यह एक-चर संकेतों के लिए परिभाषित किया गया है। | <nowiki>विश्लेषणात्मक संकेत के वास्तविक और काल्पनिक भाग वेक्टर-मूल्यवान मोनोजेनिक सिग्नल के दो तत्वों के अनुरूप होते हैं, क्योंकि यह एक-चर संकेतों के लिए परिभाषित किया गया है। चूँकि , मोनोजेनिक सिग्नल को एक सीधे विधि से चर की मनमानी संख्या तक बढ़ाया जा सकता है, जिससे एक उत्पादन होता है {{nobreak|(</nowiki>''n'' + 1)}एन-वैरिएबल सिग्नल के स्थिति में }-डायमेंशनल वेक्टर-वैल्यू फंक्शन। | ||
== यह भी देखें == | == यह भी देखें == | ||
Revision as of 22:04, 16 March 2023
गणित और संकेत आगे बढ़ाना में, एक विश्लेषणात्मक सिग्नल एक जटिल-मूल्यवान फ़ंक्शन होता है जिसमें कोई नकारात्मक आवृत्ति घटक नहीं होता है।[1]एक विश्लेषणात्मक संकेत के वास्तविक और काल्पनिक भाग हिल्बर्ट परिवर्तन द्वारा एक दूसरे से संबंधित वास्तविक-मूल्यवान कार्य हैं।
वास्तविक संख्या का विश्लेषणात्मक प्रतिनिधित्व | वास्तविक-मूल्यवान कार्य एक विश्लेषणात्मक संकेत है, जिसमें मूल कार्य और उसका हिल्बर्ट रूपांतरण सम्मलित है। यह प्रतिनिधित्व कई गणितीय जोड़तोड़ की सुविधा देता है। मूल विचार यह है कि ऐसे स्पेक्ट्रम के हर्मिटियन समरूपता के कारण वास्तविक-मूल्यवान फ़ंक्शन के फूरियर रूपांतरण (या स्पेक्ट्रम) के नकारात्मक आवृत्ति घटक अनावश्यक हैं। इन नकारात्मक आवृत्ति घटकों को सूचना की हानि के बिना त्याग दिया जा सकता है, बशर्ते कोई जटिल-मूल्यवान फ़ंक्शन से निपटने के लिए तैयार हो। यह फ़ंक्शन की कुछ विशेषताओं को अधिक सुलभ बनाता है और मॉड्यूलेशन और डिमॉड्यूलेशन तकनीकों की व्युत्पत्ति की सुविधा देता है, जैसे सिंगल-साइडबैंड।
जब तक हेरफेर किए गए फ़ंक्शन में कोई नकारात्मक आवृत्ति घटक नहीं होता है (अर्थात, यह अभी भी विश्लेषणात्मक है), जटिल से वास्तविक में रूपांतरण केवल काल्पनिक भाग को छोड़ने का स्थिति है। विश्लेषणात्मक प्रतिनिधित्व चरण (साइन तरंगों) अवधारणा का एक सामान्यीकरण है:[2] जबकि चरण समय-अपरिवर्तनीय आयाम, चरण और आवृत्ति तक सीमित है, विश्लेषणात्मक संकेत समय-परिवर्तनीय पैरामीटर के लिए अनुमति देता है।
परिभाषा
यदि फूरियर रूपांतरण के साथ एक वास्तविक-मूल्यवान कार्य है , तब परिवर्तन में हर्मिटियन फ़ंक्शन समरूपता है एक्सिस:
कहाँ का जटिल संयुग्म है . कार्यक्रम:
कहाँ
- हैवीसाइड स्टेप फंक्शन है,
- साइन समारोह है,
के केवल गैर-नकारात्मक आवृत्ति घटक सम्मलित हैं . और ऑपरेशन प्रतिवर्ती है, की हर्मिटियन समरूपता के कारण :
का विश्लेषणात्मक संकेत का व्युत्क्रम फूरियर रूपांतरण है :
कहाँ
- का हिल्बर्ट रूपांतरण है ;
- बाइनरी कनवल्शन ऑपरेटर है;
- काल्पनिक इकाई है।
नोट किया कि इसे फ़िल्टरिंग ऑपरेशन के रूप में भी व्यक्त किया जा सकता है जो नकारात्मक आवृत्ति घटकों को सीधे हटा देता है:
नकारात्मक आवृत्ति घटक
तब से , नकारात्मक आवृत्ति घटकों को पुनर्स्थापित करना त्यागने का एक साधारण स्थिति है जो प्रति-सहज लग सकता है। हम यह भी नोट कर सकते हैं कि जटिल संयुग्म केवल नकारात्मक आवृत्ति घटक सम्मलित हैं। और इसलिए दबा हुआ सकारात्मक आवृत्ति घटकों को पुनर्स्थापित करता है। एक अन्य दृष्टिकोण यह है कि किसी भी स्थिति में काल्पनिक घटक एक ऐसा शब्द है जो आवृत्ति घटकों को घटाता है h> ऑपरेटर नए घटकों को जोड़ने का आभास देते हुए, घटाव को हटा देता है।
उदाहरण
उदाहरण 1
- कहाँ
तब:
अंतिम समानता यूलर का सूत्र है, जिसका एक उपप्रमेय है सामान्यतः , एक साधारण साइनसॉइड का विश्लेषणात्मक प्रतिनिधित्व इसे जटिल-घातीयों के संदर्भ में व्यक्त करके, नकारात्मक आवृत्ति घटक को छोड़कर, सकारात्मक आवृत्ति घटक को दोगुना करके प्राप्त किया जाता है। और साइनसोइड्स के योग का विश्लेषणात्मक प्रतिनिधित्व व्यक्तिगत साइनसोइड्स के विश्लेषणात्मक प्रतिनिधित्वों का योग है।
उदाहरण 2
यहां हम नकारात्मक आवृत्ति को पहचानने और त्यागने के लिए यूलर के सूत्र का उपयोग करते हैं।
तब:
उदाहरण 3
नकारात्मक आवृत्ति घटकों को हटाने के लिए हिल्बर्ट ट्रांसफ़ॉर्म विधि का उपयोग करने का यह एक और उदाहरण है। हम ध्यान दें कि कुछ भी हमें गणना करने से नहीं रोकता है एक जटिल-मूल्यवान के लिए . लेकिन यह प्रतिवर्ती प्रतिनिधित्व नहीं हो सकता है, क्योंकि मूल स्पेक्ट्रम सामान्य रूप से सममित नहीं है। इसलिए इस उदाहरण को छोड़कर, सामान्य चर्चा वास्तविक-मूल्यवान है .
- , कहाँ .
तब:
गुण
तात्कालिक आयाम और चरण
ध्रुवीय निर्देशांक में एक विश्लेषणात्मक संकेत भी व्यक्त किया जा सकता है:
जहां निम्नलिखित समय-भिन्न मात्राएं प्रस्तुत की जाती हैं:
- तात्कालिक आयाम या आवरण (तरंगें) कहा जाता है;
- तात्कालिक चरण या चरण कोण कहा जाता है।
संलग्न आरेख में, नीला वक्र दर्शाता है और लाल वक्र इसी को दर्शाता है .
चरण लपेटन तात्कालिक चरण के समय व्युत्पन्न में रेडियन/सेकंड की इकाइयाँ होती हैं, और इसे तात्कालिक कोणीय आवृत्ति कहा जाता है:
तात्कालिक चरण # तात्कालिक आवृत्ति (हेटर्स में) इसलिए है:
तात्कालिक आयाम, और तात्कालिक चरण और आवृत्ति सिग्नल की स्थानीय विशेषताओं को मापने और पता लगाने के लिए उपयोग किए जाने वाले कुछ अनुप्रयोगों में होती है। सिग्नल के विश्लेषणात्मक प्रतिनिधित्व का एक अन्य अनुप्रयोग मॉडुलन के विमॉडुलन से संबंधित है। ध्रुवीय निर्देशांक आसानी से आयाम मॉडुलन और चरण (या आवृत्ति) मॉडुलन के प्रभावों को अलग करते हैं, और कुछ प्रकार के संकेतों को प्रभावी ढंग से ध्वस्त करते हैं।
जटिल लिफाफा/बेसबैंड
विश्लेषणात्मक संकेतों को अधिकांशतः 0 हर्ट्ज की ओर आवृत्ति (नीचे-रूपांतरित) में स्थानांतरित किया जाता है, संभवतः [गैर-सममित] नकारात्मक आवृत्ति घटक बनाते हैं:
यह फ़ंक्शन विभिन्न नामों से जाता है, जैसे जटिल लिफाफा और जटिल बेसबैंड। जटिल लिफाफा अद्वितीय नहीं है; यह की पसंद से निर्धारित होता है . इस अवधारणा का प्रयोग अधिकांशतः पासबैंड संकेतों के साथ काम करते समय किया जाता है। यदि एक संग्राहक संकेत है, इसकी वाहक आवृत्ति के बराबर हो सकता है।
अन्य स्थितियों ं में, वांछित पासबैंड के बीच में कहीं चुना गया है। फिर वास्तविक गुणांक के साथ एक साधारण निम्न-पास फ़िल्टर ब्याज के हिस्से को बढ़ा सकता है। एक अन्य मकसद उच्चतम आवृत्ति को कम करना है, जो कि उपनाम-मुक्त नमूनाकरण के लिए न्यूनतम दर को कम करता है। एक आवृत्ति बदलाव जटिल सिग्नल प्रतिनिधित्व के गणितीय ट्रैक्टेबिलिटी को कम नहीं करता है। तो उस मायने में, डाउन-कन्वर्टेड सिग्नल अभी भी विश्लेषणात्मक है। चूँकि , वास्तविक-मूल्यवान प्रतिनिधित्व को पुनर्स्थापित करना अब केवल वास्तविक घटक को निकालने का सरल स्थिति नहीं है। अप-रूपांतरण की आवश्यकता हो सकती है, और यदि सिग्नल upsampling (सिग्नल प्रोसेसिंग) (असतत-समय) किया गया है, तो अलियासिंग से बचने के लिए प्रक्षेप (अपसैंपलिंग) भी आवश्यक हो सकता है।
यदि की उच्चतम आवृत्ति से बड़ा चुना जाता है तब कोई सकारात्मक आवृत्तियाँ नहीं हैं। उस स्थिति में, वास्तविक घटक निकालने से उन्हें पुनर्स्थापित किया जाता है, लेकिन विपरीत क्रम में; कम आवृत्ति वाले घटक अब उच्च वाले हैं और इसके विपरीत। इसका उपयोग एक प्रकार के सिंगल-साइडबैंड मॉड्यूलेशन|सिंगल-साइडबैंड सिग्नल को लोअर साइडबैंड या इनवर्टेड साइडबैंड कहा जाता है।
संदर्भ आवृत्ति के अन्य विकल्पों पर कभी-कभी विचार किया जाता है:
- कभी-कभी कम करने के लिए चुना गया है
- वैकल्पिक रूप से,[4] अलिखित तात्कालिक चरण को रैखिक रूप से अनुमानित करने में औसत वर्ग त्रुटि को कम करने के लिए चुना जा सकता है :
- या कोई अन्य विकल्प (कुछ इष्टतम के लिए ):
समय-आवृत्ति सिग्नल प्रोसेसिंग के क्षेत्र में, यह दिखाया गया था कि विग्नर-विले वितरण की परिभाषा में विश्लेषणात्मक सिग्नल की आवश्यकता थी जिससे कि व्यावहारिक अनुप्रयोगों के लिए आवश्यक वांछित गुण हो सकें।[5] कभी-कभी वाक्यांश जटिल लिफाफे को एक (निरंतर-आवृत्ति) चरण के जटिल आयाम का सरल अर्थ दिया जाता है;[lower-alpha 1][lower-alpha 2] दूसरी बार जटिल लिफाफा जैसा कि ऊपर परिभाषित किया गया है, जटिल आयाम के समय-निर्भर सामान्यीकरण के रूप में व्याख्या की गई है।[lower-alpha 3] वास्तविक-मूल्य वाले स्थिति में उनका संबंध उससे अलग नहीं है: अलग-अलग लिफाफा (तरंगें) निरंतर आयाम को सामान्य करता है।
एकाधिक चर के संकेतों के लिए विश्लेषणात्मक संकेत का विस्तार
विश्लेषणात्मक संकेत की अवधारणा एकल चर के संकेतों के लिए अच्छी तरह से परिभाषित है जो सामान्यतः समय है। दो या दो से अधिक चर के संकेतों के लिए, एक विश्लेषणात्मक संकेत को अलग-अलग विधियों से परिभाषित किया जा सकता है, और दो दृष्टिकोण नीचे प्रस्तुत किए गए हैं।
=== तदर्थ दिशा === के आधार पर बहु-आयामी विश्लेषणात्मक संकेत एक बार यह स्थापित हो जाने के बाद कि इस स्थिति के लिए नकारात्मक आवृत्तियों का क्या मतलब है, एक बहु-आयामी संकेत के लिए विश्लेषणात्मक संकेत का एक सीधा सामान्यीकरण किया जा सकता है। यह एक इकाई वेक्टर की शुरुआत करके किया जा सकता है फूरियर डोमेन में और किसी आवृत्ति वेक्टर को लेबल करें नकारात्मक के रूप में यदि . एक-चर संकेतों के स्थिति में वर्णित प्रक्रिया के अनुसार, सभी नकारात्मक आवृत्तियों को हटाकर और परिणाम को 2 से गुणा करके विश्लेषणात्मक संकेत उत्पन्न किया जाता है। चूँकि , इसके लिए कोई विशेष दिशा नहीं है जिसे तब तक चुना जाना चाहिए जब तक कि कुछ अतिरिक्त बाधाएँ न हों। इसलिए, का चुनाव तदर्थ है, या अनुप्रयोग विशिष्ट है।
मोनोजेनिक संकेत
विश्लेषणात्मक संकेत के वास्तविक और काल्पनिक भाग वेक्टर-मूल्यवान मोनोजेनिक सिग्नल के दो तत्वों के अनुरूप होते हैं, क्योंकि यह एक-चर संकेतों के लिए परिभाषित किया गया है। चूँकि , मोनोजेनिक सिग्नल को एक सीधे विधि से चर की मनमानी संख्या तक बढ़ाया जा सकता है, जिससे एक उत्पादन होता है {{nobreak|(n + 1)}एन-वैरिएबल सिग्नल के स्थिति में }-डायमेंशनल वेक्टर-वैल्यू फंक्शन।
यह भी देखें
- हिल्बर्ट ट्रांसफॉर्म#असतत हिल्बर्ट ट्रांसफॉर्म
- नकारात्मक आवृत्ति
अनुप्रयोग
- सिंगल-साइडबैंड मॉड्यूलेशन
- चतुर्भुज फ़िल्टर
- कारण फ़िल्टर
टिप्पणियाँ
संदर्भ
- ↑ Smith, J.O. "Analytic Signals and Hilbert Transform Filters", in Mathematics of the Discrete Fourier Transform (DFT) with Audio Applications, Second Edition, https://ccrma.stanford.edu/~jos/r320/Analytic_Signals_Hilbert_Transform.html, or https://www.dsprelated.com/freebooks/mdft/Analytic_Signals_Hilbert_Transform.html, online book, 2007 edition, accessed 2021-04-29.
- ↑ 2.0 2.1 Bracewell, Ron. The Fourier Transform and Its Applications. McGraw-Hill, 1965. p 269
- ↑ B. Boashash, "Estimating and Interpreting the Instantaneous Frequency of a Signal-Part I: Fundamentals", Proceedings of the IEEE, Vol. 80, No. 4, pp. 519–538, April 1992
- ↑ Justice, J. (1979-12-01). "संगीत संगणना में विश्लेषणात्मक सिग्नल प्रोसेसिंग". IEEE Transactions on Acoustics, Speech, and Signal Processing. 27 (6): 670–684. doi:10.1109/TASSP.1979.1163321. ISSN 0096-3518.
- ↑ B. Boashash, “Notes on the use of the Wigner distribution for time frequency signal analysis”, IEEE Trans. on Acoustics, Speech, and Signal Processing , vol. 26, no. 9, 1987
- ↑ Hlawatsch, Franz; Auger, François (2013-03-01). Time-Frequency Analysis (in English). John Wiley & Sons. ISBN 9781118623831.
- ↑ Driggers, Ronald G. (2003-01-01). Encyclopedia of Optical Engineering: Abe-Las, pages 1-1024 (in English). CRC Press. ISBN 9780824742508.
- ↑ Okamoto, Kenʼichi (2001-01-01). Global Environment Remote Sensing (in English). IOS Press. ISBN 9781586031015.
अग्रिम पठन
This further reading section may contain inappropriate or excessive suggestions that may not follow Wikipedia's guidelines. Please ensure that only a reasonable number of balanced, topical, reliable, and notable further reading suggestions are given; removing less relevant or redundant publications with the same point of view where appropriate. Consider utilising appropriate texts as inline sources or creating a separate bibliography article. (October 2014) (Learn how and when to remove this template message) |
- Leon Cohen, Time-frequency analysis, Prentice Hall, Upper Saddle River, 1995.
- Frederick W. King, Hilbert Transforms, vol. II, Cambridge University Press, Cambridge, 2009.
- B. Boashash, Time-Frequency Signal Analysis and Processing: A Comprehensive Reference, Elsevier Science, Oxford, 2003.