तिर्यक रेखा (ज्यामिति): Difference between revisions
(Created page with "{{Short description|Line intersecting 2 coplanar lines at 2 points}} {{Angles}} ज्यामिति में, एक तिर्यक रेखा एक रे...") |
m (Abhishek moved page अनुप्रस्थ (ज्यामिति) to तिर्यक रेखा (ज्यामिति) without leaving a redirect) |
(No difference)
| |
Revision as of 14:16, 10 March 2023
| Types of angles |
|---|
| 2D angles |
| Exterior |
| 2D angle pairs |
|
Adjacent |
| 3D angles |
| Dihedral |
ज्यामिति में, एक तिर्यक रेखा एक रेखा (गणित) है जो रेखा-रेखा दो रेखाओं को एक ही तल (ज्यामिति) में दो भिन्न बिंदु (ज्यामिति) पर काटती है। ट्रांसवर्सल्स यह स्थापित करने में एक भूमिका निभाते हैं कि यूक्लिडियन विमान में दो या दो से अधिक अन्य रेखाएं समानांतर (ज्यामिति) हैं या नहीं। दो रेखाओं के साथ एक तिर्यक रेखा के प्रतिच्छेदन विभिन्न प्रकार के कोणों के जोड़े बनाते हैं: लगातार आंतरिक कोण, लगातार बाहरी कोण, संगत कोण और वैकल्पिक कोण। यूक्लिड के समानांतर अभिधारणा के परिणामस्वरूप, यदि दो रेखाएँ समानांतर हैं, तो लगातार आंतरिक कोण पूरक कोण होते हैं, संगत कोण बराबर होते हैं, और एकांतर कोण बराबर होते हैं।
|

|

| |
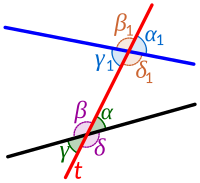
| Eight angles of a transversal. (Vertical angles such as and are always congruent.) |
Transversal between non-parallel lines. Consecutive angles are not supplementary. |
Transversal between parallel lines. Consecutive angles are supplementary. |
तिर्यक रेखा के कोण
एक तिर्यक रेखा 8 कोण बनाती है, जैसा कि ऊपर बाईं ओर ग्राफ में दिखाया गया है:
- 4 दो पंक्तियों में से प्रत्येक के साथ, अर्थात् α, β, γ और δ और फिर α1, बी1, सी1 और δ1; और
- जिनमें से 4 आंतरिक हैं (दो रेखाओं के बीच), अर्थात् α, β, γ1 और δ1 और जिनमें से 4 बाहरी हैं, अर्थात् α1, बी1, γ और δ।
एक तिर्यक रेखा जो दो समान्तर रेखाओं को समकोण पर काटती है, लंब तिर्यक रेखा कहलाती है। इस स्थिति में, सभी 8 कोण समकोण हैं [1] जब रेखाएँ समानांतर रेखाएँ होती हैं, एक ऐसा मामला जिस पर अक्सर विचार किया जाता है, एक तिर्यक रेखा कई सर्वांगसमता (ज्यामिति) पूरक कोण उत्पन्न करती है। इनमें से कुछ कोण युग्मों के विशिष्ट नाम हैं और नीचे उनकी चर्चा की गई है: संगत कोण, एकांतर कोण और क्रमागत कोण।[2][3]: Art. 87
एकांतर कोण
वैकल्पिक कोण कोणों के चार युग्म हैं जो:
- भिन्न वर्टेक्स (ज्यामिति) बिंदु हैं,
- तिर्यक रेखा के विपरीत दिशा में लेटें और
- दोनों कोण आंतरिक हैं या दोनों कोण बाहरी हैं।
यह गणित का एक बहुत ही उपयोगी विषय है
यदि एक युग्म के दो कोण सर्वांगसम (माप में बराबर) हैं, तो अन्य युग्मों में से प्रत्येक के कोण भी सर्वांगसम होते हैं।
यूक्लिड के तत्वों का प्रस्ताव 1.27 | यूक्लिड के तत्व, निरपेक्ष ज्यामिति का एक प्रमेय (इसलिए अतिशयोक्तिपूर्ण ज्यामिति और यूक्लिडियन ज्यामिति दोनों में मान्य), यह साबित करता है कि यदि एक तिर्यक रेखा के वैकल्पिक कोणों की एक जोड़ी के कोण सर्वांगसम हैं तो दो रेखाएँ समानांतर (गैर) हैं - प्रतिच्छेदन)।
यह यूक्लिड के समानांतर अभिधारणा से अनुसरण करता है कि यदि दो रेखाएँ समानांतर हैं, तो एक तिर्यक रेखा के वैकल्पिक कोणों के एक युग्म के कोण सर्वांगसम होते हैं (यूक्लिड के तत्वों की प्रस्तावना 1.29)।
संगत कोण
संगत कोण कोणों के वे चार युग्म हैं जो:
- विभिन्न शीर्ष बिंदु हैं,
- तिर्यक रेखा के एक ही तरफ लेटें और
- एक कोण आंतरिक है और दूसरा बाहरी है।
दो रेखाएँ समानांतर होती हैं यदि और केवल यदि किसी तिर्यक रेखा के संगत कोणों के किसी युग्म के दो कोण सर्वांगसम (माप में बराबर) हों।
यूक्लिड के तत्वों का प्रस्ताव 1.28, निरपेक्ष ज्यामिति का एक प्रमेय (इसलिए अतिशयोक्तिपूर्ण ज्यामिति और यूक्लिडियन ज्यामिति दोनों में मान्य), यह साबित करता है कि यदि एक अनुप्रस्थ के संगत कोणों की एक जोड़ी के कोण सर्वांगसम हैं तो दो रेखाएँ समानांतर (गैर-प्रतिच्छेदन) हैं। .
यह यूक्लिड के समानांतर अभिधारणा से अनुसरण करता है कि यदि दो रेखाएँ समानांतर हैं, तो एक तिर्यक रेखा के संगत कोणों के एक युग्म के कोण सर्वांगसम होते हैं (यूक्लिड के तत्वों की प्रस्तावना 1.29)।
यदि संगत कोणों के एक युग्म के कोण सर्वांगसम हैं, तो अन्य युग्मों के प्रत्येक युग्म के कोण भी सर्वांगसम होते हैं। इस पृष्ठ पर समानांतर रेखाओं वाली विभिन्न छवियों में, संगत कोण जोड़े हैं: α=α1, β = β1, γ=γ1 और δ=δ1.
लगातार आंतरिक कोण
लगातार आंतरिक कोण कोणों के दो युग्म हैं जो:[4][2]
- विभिन्न शीर्ष बिंदु हैं,
- तिर्यक रेखा के एक ही तरफ लेटें और
- दोनों आंतरिक हैं।
दो रेखाएँ समानांतर होती हैं यदि और केवल यदि किसी तिर्यक रेखा के लगातार आंतरिक कोणों के किसी भी युग्म के दो कोण संपूरक हों (योग 180°)।
यूक्लिड के तत्वों का प्रस्ताव 1.28, निरपेक्ष ज्यामिति का एक प्रमेय (इसलिए अतिशयोक्तिपूर्ण ज्यामिति और यूक्लिडियन ज्यामिति दोनों में मान्य), यह साबित करता है कि यदि लगातार आंतरिक कोणों की एक जोड़ी के कोण पूरक हैं तो दो रेखाएँ समानांतर (गैर-प्रतिच्छेदन) हैं।
यह यूक्लिड के समानांतर अभिधारणा से अनुसरण करता है कि यदि दो रेखाएँ समानांतर हैं, तो एक तिर्यक रेखा के लगातार आंतरिक कोणों की एक जोड़ी के कोण पूरक होते हैं (यूक्लिड के तत्वों का प्रस्ताव 1.29)।
यदि क्रमागत आंतरिक कोणों का एक युग्म संपूरक है, तो दूसरा युग्म भी संपूरक है।
तिर्यक रेखाओं की अन्य विशेषताएं
यदि सामान्य स्थिति में तीन रेखाएँ एक त्रिभुज बनाती हैं और फिर एक तिर्यक रेखा द्वारा काटी जाती हैं, तो छह परिणामी खंडों की लंबाई मेनेलॉस प्रमेय को संतुष्ट करती है।
संबंधित प्रमेय
समानांतर अभिधारणा के यूक्लिड के सूत्रीकरण को एक तिर्यक रेखा के रूप में बताया जा सकता है। विशेष रूप से, यदि तिर्यक रेखा के एक ही ओर के आंतरिक कोण दो समकोणों से कम हैं तो रेखाओं को प्रतिच्छेद करना चाहिए। वास्तव में, यूक्लिड ग्रीक में उसी वाक्यांश का उपयोग करता है जिसे आमतौर पर ट्रांसवर्सल के रूप में अनुवादित किया जाता है।[5]: 308, nfote 1
यूक्लिड के प्रस्ताव 27 में कहा गया है कि यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार काटती है कि वैकल्पिक आंतरिक कोण सर्वांगसम हों, तो रेखाएँ समानांतर होती हैं। यूक्लिड इस उपपत्ति को विरोधाभास द्वारा सिद्ध करता है: यदि रेखाएँ समानांतर नहीं हैं तो उन्हें प्रतिच्छेद करना चाहिए और एक त्रिभुज बनता है। फिर एकांतर कोण दूसरे कोण के बराबर एक बाहरी कोण होता है जो त्रिभुज में एक विपरीत आंतरिक कोण होता है। यह प्रस्ताव 16 का खंडन करता है जिसमें कहा गया है कि त्रिभुज का एक बाहरी कोण हमेशा विपरीत आंतरिक कोणों से बड़ा होता है।[5]: 307 [3]: Art. 88
यूक्लिड का प्रस्ताव 28 इस परिणाम को दो तरह से विस्तारित करता है। सबसे पहले, यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार काटती है कि संगत कोण सर्वांगसम हों, तो रेखाएँ समानांतर होती हैं। दूसरा, यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार काटती है कि तिर्यक रेखा के एक ही ओर के आंतरिक कोण संपूरक हों, तो रेखाएँ समानांतर होती हैं। ये पिछले प्रस्ताव से इस तथ्य को लागू करते हैं कि प्रतिच्छेदी रेखाओं के विपरीत कोण बराबर होते हैं (प्रस्ताव 15) और एक रेखा पर आसन्न कोण पूरक होते हैं (प्रस्तावना 13)। जैसा कि बंद किया हुआ ने उल्लेख किया है, यूक्लिड समानांतर रेखाओं के लिए संभावित छह में से केवल तीन मानदंड देता है।[5]: 309–310 [3]: Art. 89-90
यूक्लिड का प्रस्ताव 29 पिछले दो का विलोम है। सबसे पहले, यदि एक तिर्यक रेखा दो समानांतर रेखाओं को काटती है, तो एकांतर आंतरिक कोण सर्वांगसम होते हैं। यदि नहीं, तो एक दूसरे से बड़ा है, जिसका अर्थ है कि इसका पूरक दूसरे कोण के पूरक से कम है। इसका तात्पर्य यह है कि तिर्यक रेखा के एक ही ओर आंतरिक कोण होते हैं जो दो समकोणों से कम होते हैं, जो पांचवें अभिधारणा के विपरीत होते हैं। प्रस्ताव यह कहते हुए जारी रहता है कि दो समानांतर रेखाओं के एक अनुप्रस्थ पर, संगत कोण सर्वांगसम होते हैं और एक ही तरफ के आंतरिक कोण दो समकोण के बराबर होते हैं। ये कथन उसी तरह अनुसरण करते हैं जैसे प्रस्ताव 28 प्रस्ताव 27 का अनुसरण करता है।[5]: 311–312 [3]: Art. 93-95
यूक्लिड का प्रमाण पाँचवीं अभिधारणा का आवश्यक उपयोग करता है, हालाँकि, ज्यामिति के आधुनिक उपचार इसके बजाय प्लेफेयर के स्वयंसिद्ध का उपयोग करते हैं। Playfair के स्वयंसिद्ध को मानते हुए प्रस्ताव 29 को सिद्ध करने के लिए, एक तिर्यक रेखा को दो समानांतर रेखाओं को पार करने दें और मान लें कि वैकल्पिक आंतरिक कोण बराबर नहीं हैं। उस बिंदु से एक तीसरी रेखा खींचें जहां तिर्यक रेखा पहली रेखा को काटती है, लेकिन तिर्यक रेखा द्वारा दूसरी रेखा के साथ बनाए गए कोण के बराबर कोण के साथ। यह एक बिंदु के माध्यम से दो अलग-अलग रेखाएँ पैदा करता है, दोनों दूसरी रेखा के समानांतर, स्वयंसिद्ध के विपरीत।[5]: 313 [6]
उच्च आयामों में
उच्च आयामी स्थानों में, एक रेखा जो अलग-अलग बिंदुओं में रेखाओं के प्रत्येक सेट को प्रतिच्छेद करती है, वह रेखाओं के उस सेट का अनुप्रस्थ है। द्वि-आयामी (विमान) मामले के विपरीत, दो से अधिक पंक्तियों के सेट के लिए ट्रांसवर्सल मौजूद होने की गारंटी नहीं है।
यूक्लिडियन 3-स्पेस में, रेगुलस (ज्यामिति) तिरछी रेखाओं का एक सेट है, R, जैसे कि की प्रत्येक पंक्ति पर प्रत्येक बिंदु के माध्यम से R, का एक अनुप्रस्थ गुजरता है R और के तिर्यक रेखा के प्रत्येक बिंदु के माध्यम से R की एक रेखा गुजरती है R. एक रेगुलस के ट्रांसवर्सल का सेट R भी एक रेगुलस है, जिसे विपरीत रेगुलस कहा जाता है, Ro. इस स्थान में, तीन परस्पर तिरछी रेखाओं को हमेशा एक रेगुलस तक बढ़ाया जा सकता है।
संदर्भ
- ↑ "आड़ा". Math Open Reference. 2009. (interactive)
- ↑ 2.0 2.1 Rod Pierce (2011). "समानांतर रेखाएं". MathisFun. (interactive)
- ↑ 3.0 3.1 3.2 3.3 Holgate, Thomas Franklin (1901). Elementary Geometry. Macmillan.
- ↑ C.Clapham, J.Nicholson (2009). "गणित का ऑक्सफोर्ड संक्षिप्त शब्दकोश" (PDF). Addison-Wesley. p. 582.
- ↑ 5.0 5.1 5.2 5.3 5.4 Heath, T.L. (1908). The thirteen books of Euclid's Elements. Vol. 1. The University Press.
- ↑ A similar proof is given in Holgate 1901, Art. 93


