स्पर्शरेखा का नियम: Difference between revisions
m (8 revisions imported from alpha:स्पर्शरेखा_का_नियम) |
No edit summary |
||
| Line 77: | Line 77: | ||
[[श्रेणी:त्रिकोणों के बारे में प्रमेय]] | [[श्रेणी:त्रिकोणों के बारे में प्रमेय]] | ||
[[Category:Created On 17/12/2022]] | [[Category:Created On 17/12/2022]] | ||
[[Category:Vigyan Ready]] | [[Category:Machine Translated Page]] | ||
[[Category:Mathematics sidebar templates]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Templates Vigyan Ready]] | |||
Latest revision as of 11:48, 24 April 2023
| त्रिकोणमिति |
|---|
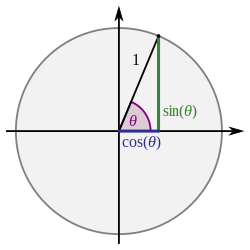 |
| संदर्भ |
| कानून और सिद्धांत |
| पथरी |
त्रिकोणमिति में कोटिस्पर्श का नियम[1] त्रिभुज की भुजाओं की लंबाई और तीनों कोणों के अर्धभागों की कोटिस्पर्श रेखाओं के बीच संबंध है। इसे कॉट प्रमेय के रूप में भी जाना जाता है।
जिस प्रकार तीन मात्राएँ जिनकी समानता जीवा के नियम द्वारा व्यक्त की जाती है। वे त्रिभुज के परिबद्ध वृत्त के व्यास के बराबर होती हैं (या इसके व्युत्क्रम के आधार पर इस बात पर निर्भर करता है कि नियम कैसे व्यक्त किया जाता है)। उसी प्रकार कोस्पर्शी नियम भी त्रिज्या से संबंधित है। त्रिभुज (अंतर्त्रिज्या) का गहरा हुआ चक्र उसके पक्षों और कोणों के लिए इसको प्रदर्शित करता है।
कथन
त्रिकोण के लिए सामान्य अंकन का उपयोग करना (ऊपरी दाईं ओर की आकृति देखें)। जहां a, b, c तीन भुजाओं की लंबाई हैं, A, B, C उन तीन संबंधित भुजाओं के विपरीत शीर्ष हैं, α, β, γ शीर्षों पर संगत कोण हैं, s अर्ध-परिधि है। अर्थात् s = a + b + c/2 और r उत्कीर्ण वृत्त की त्रिज्या है। त्रिकोणमितीय कार्यों का नियम यह जानकारी प्रदान करता है कि-
और इसके अतिरिक्त अंतःत्रिज्या द्वारा दिया जाता है। कि-
प्रमाण
उपरोक्त आकृति में त्रिभुज की भुजाओं के साथ अंतर्वृत्त की स्पर्शरेखा के बिंदु परिधि को 6 खंडों में और 3 जोड़े में विभाजित करते हैं। प्रत्येक जोड़ी में खंड समान लंबाई के होते हैं। उदाहरण के लिए शीर्ष से सटे हुए 2 खंड A बराबर हैं। यदि हम प्रत्येक जोड़ी से एक खंड चुनते हैं। तो उनका योग अर्धपरिमाप s होगा। इसका एक उदाहरण चित्र में रंग में दिखाए गए खंड हैं। लाल रेखा बनाने वाले दो खंडों का योग a होता है। इसलिए नीले खंड की लंबाई s − a होनी चाहिए। अन्य पांच खंडों की भी लंबाई s − a, s − b, या s − c होनी चाहिए। जैसा कि नीचे चित्र में दिखाया गया है।
कोटैंजेंट फलन की परिभाषा का उपयोग करते हुए आकृति का निरीक्षण करके हमारे पास है-
और इसी प्रकार अन्य दो कोणों के लिये पहले अभिकथन को सिद्ध करते हुए।
दूसरे के लिए अंतःत्रिज्या सूत्र - हम त्रिकोणमितीय सर्वसमिकाओं की सूची से प्रारम्भ करते हैं। स्पर्श और राशियों की कोटिस्पर्श रेखाएँ:
के लिए आवेदन cot(α/2 + β/2 + γ/2) = cot π/2= 0, हम प्राप्त करते हैं:
(यह त्रिकोणमितीय सर्वसमिकाओं का प्रमाण भी है। विविध -- त्रिकोटि स्पर्शरेखा पहचान)
पहले भाग में प्राप्त मूल्यों को प्रतिस्थापित करते हुए हम प्राप्त करते हैं:
r3/s द्वारा गुणा करना r2 का मान देता है। दूसरा प्रमाण सिद्ध करना।
कोटिस्पर्श के नियम का उपयोग करते हुए कुछ प्रमाण
कोटैंगेंट्स के नियम से कई अन्य परिणाम प्राप्त किए जा सकते हैं।
- हीरो का सूत्र: ध्यान दें कि त्रिभुज का क्षेत्रफल ABC को 6 छोटे त्रिभुजों और 3 जोड़े में भी विभाजित किया गया है। प्रत्येक जोड़ी में समान क्षेत्रफल वाले त्रिभुजों के साथ विभाजित किया गया है। उदाहरण के लिए A शीर्ष के निकट दो त्रिभुज , s − a चौड़ाई का समकोण त्रिभुज होना और ऊंचाई r, प्रत्येक का एक क्षेत्र 1/2r(s − a) है। तो उन दो त्रिभुजों का एक साथ क्षेत्रफल r(s − a) है और क्षेत्र पूरे त्रिकोण का S है। इसलिए- यह परिणाम देता हैआवश्यकता अनुसार।
- मोलवीड का सूत्र: हमारे पास योग सूत्र और कोटिस्पर्श के नियम से है- यह परिणाम देता है-आवश्यकता अनुसार।
- मोलवीड का सूत्र: हमारे पास योग सूत्र और कोटिस्पर्श के नियम से है-यहां योग/उत्पाद सूत्र के अनुसार किसी उत्पाद को योग में बदलने के लिए एक अतिरिक्त चरण की आवश्यकता होती है। यह परिणाम देता है-आवश्यकता अनुसार।
- स्पर्शरेखा के नियम को भी इससे प्राप्त किया जा सकता है।
यह भी देखें
- ज्या का नियम
- कोसाइन का नियम
- स्पर्शरेखा का नियम
- मोलवीड का सूत्र
- हीरो का सूत्र
इस पेज में अनुपस्थित आंतरिक लिंक की सूची
- केंद्र में
- त्रिभुज के अंतःवृत्त और बहिर्वृत्त
- त्रिकोण
- अंकित घेरा
- से कम
- ज्या का नियम
- परिबद्ध घेरा
- त्रिकोणमितीय समारोह
- स्पर्शरेखा का नियम
संदर्भ
- ↑ The Universal Encyclopaedia of Mathematics, Pan Reference Books, 1976, page 530. English version George Allen and Unwin, 1964. Translated from the German version Meyers Rechenduden, 1960.
- Silvester, John R. (2001). Geometry: Ancient and Modern. Oxford University Press. p. 313. ISBN 9780198508250.

