क्षण वितरण विधि: Difference between revisions
No edit summary |
No edit summary |
||
| Line 79: | Line 79: | ||
|- style="background-color:#EEEEEE;" | |- style="background-color:#EEEEEE;" | ||
|style="text-align:center; font-weight:normal;"| | |style="text-align:center; font-weight:normal;"| | ||
|style="text-align:right; width:50px; padding:1px;"| | |style="text-align:right; width:50px; padding:1px;"|संयुक्त | ||
|style="text-align:left; width:82px; padding:1px;"|A | |style="text-align:left; width:82px; padding:1px;"|A | ||
|style="text-align:center; width:31px; padding:1px;"| | |style="text-align:center; width:31px; padding:1px;"| | ||
|style="text-align:right; width:82px; padding:1px;"| | |style="text-align:right; width:82px; padding:1px;"|संयुक्त | ||
|style="text-align:left; width:82px; padding:1px;"|B | |style="text-align:left; width:82px; padding:1px;"|B | ||
|style="text-align:center; width:31px; padding:1px;"| | |style="text-align:center; width:31px; padding:1px;"| | ||
|style="text-align:right; width:82px; padding:1px;"| | |style="text-align:right; width:82px; padding:1px;"|संयुक्त | ||
|style="text-align:left; width:82px; padding:1px;"|C | |style="text-align:left; width:82px; padding:1px;"|C | ||
|style="text-align:center; width:31px; padding:1px;"| | |style="text-align:center; width:31px; padding:1px;"| | ||
|style="text-align:right; width:82px; padding:1px;"| | |style="text-align:right; width:82px; padding:1px;"|संयुक्त | ||
|style="text-align:left; width:44px; padding:1px;"|D | |style="text-align:left; width:44px; padding:1px;"|D | ||
|- style="background-color:#EEEEEE; font-weight:bold;" | |- style="background-color:#EEEEEE; font-weight:bold;" | ||
|style="text-align:center; font-weight:normal;"| | |style="text-align:center; font-weight:normal;"|वितरण कारक | ||
|style="text-align:right; width:50px; padding:1px;"|0 | |style="text-align:right; width:50px; padding:1px;"|0 | ||
|style="text-align:left; width:82px; padding:1px;"|1 | |style="text-align:left; width:82px; padding:1px;"|1 | ||
| Line 104: | Line 104: | ||
|style="text-align:left; width:44px; padding:1px;"|0 | |style="text-align:left; width:44px; padding:1px;"|0 | ||
|- style="background-color:#EEEEEE; font-weight:bold;" | |- style="background-color:#EEEEEE; font-weight:bold;" | ||
|style="text-align:center; font-weight:normal;"| | |style="text-align:center; font-weight:normal;"|निश्चित-अंत क्षण | ||
|style="text-align:right; width:50px; padding:1px;"| | |style="text-align:right; width:50px; padding:1px;"| | ||
|style="text-align:left; width:82px; padding:1px;"|-14.700 | |style="text-align:left; width:82px; padding:1px;"|-14.700 | ||
| Line 117: | Line 117: | ||
|style="text-align:left; width:44px; padding:1px;"| | |style="text-align:left; width:44px; padding:1px;"| | ||
|- | |- | ||
|style="text-align:center;"| | |style="text-align:center;"|स्टेप 1 | ||
|style="text-align:right; width:50px; padding:1px;"| | |style="text-align:right; width:50px; padding:1px;"| | ||
|style="text-align:left; width:82px; background-color:#F8F8F8; padding:1px;"|+14.700 | |style="text-align:left; width:82px; background-color:#F8F8F8; padding:1px;"|+14.700 | ||
| Line 130: | Line 130: | ||
|style="text-align:left; width:44px; padding:1px;"| | |style="text-align:left; width:44px; padding:1px;"| | ||
|- | |- | ||
|style="text-align:center;"| | |style="text-align:center;"|स्टेप 2 | ||
|style="text-align:right; width:50px; padding:1px;"| | |style="text-align:right; width:50px; padding:1px;"| | ||
|style="text-align:left; width:82px; padding:1px;"| | |style="text-align:left; width:82px; padding:1px;"| | ||
| Line 143: | Line 143: | ||
|style="text-align:left; width:44px; padding:1px;"| | |style="text-align:left; width:44px; padding:1px;"| | ||
|- | |- | ||
|style="text-align:center;"| | |style="text-align:center;"|स्टेप 3 | ||
|style="text-align:right; width:50px; padding:1px;"| | |style="text-align:right; width:50px; padding:1px;"| | ||
|style="text-align:left; width:82px; padding:1px;"| | |style="text-align:left; width:82px; padding:1px;"| | ||
| Line 156: | Line 156: | ||
|style="text-align:left; width:44px; padding:1px;"| | |style="text-align:left; width:44px; padding:1px;"| | ||
|- | |- | ||
|style="text-align:center;"| | |style="text-align:center;"|स्टेप 4 | ||
|style="text-align:right; width:50px; padding:1px;"| | |style="text-align:right; width:50px; padding:1px;"| | ||
|style="text-align:left; width:82px; padding:1px;"| | |style="text-align:left; width:82px; padding:1px;"| | ||
| Line 169: | Line 169: | ||
|style="text-align:left; width:44px; padding:1px;"| | |style="text-align:left; width:44px; padding:1px;"| | ||
|- | |- | ||
|style="text-align:center;"| | |style="text-align:center;"|स्टेप 5 | ||
|style="text-align:right; width:50px; padding:1px;"| | |style="text-align:right; width:50px; padding:1px;"| | ||
|style="text-align:left; width:82px; padding:1px;"| | |style="text-align:left; width:82px; padding:1px;"| | ||
| Line 182: | Line 182: | ||
|style="text-align:left; width:44px; padding:1px;"| | |style="text-align:left; width:44px; padding:1px;"| | ||
|- | |- | ||
|style="text-align:center;"| | |style="text-align:center;"|स्टेप 6 | ||
|style="text-align:right; width:50px; padding:1px;"| | |style="text-align:right; width:50px; padding:1px;"| | ||
|style="text-align:left; width:82px; padding:1px;"| | |style="text-align:left; width:82px; padding:1px;"| | ||
| Line 195: | Line 195: | ||
|style="text-align:left; width:44px; padding:1px;"| | |style="text-align:left; width:44px; padding:1px;"| | ||
|- | |- | ||
|style="text-align:center;"| | |style="text-align:center;"|स्टेप 7 | ||
|style="text-align:right; width:50px; padding:1px;"| | |style="text-align:right; width:50px; padding:1px;"| | ||
|style="text-align:left; width:82px; padding:1px;"| | |style="text-align:left; width:82px; padding:1px;"| | ||
| Line 208: | Line 208: | ||
|style="text-align:left; width:44px; padding:1px;"| | |style="text-align:left; width:44px; padding:1px;"| | ||
|- | |- | ||
|style="text-align:center;"| | |style="text-align:center;"|स्टेप 8 | ||
|style="text-align:right; width:50px; padding:1px;"| | |style="text-align:right; width:50px; padding:1px;"| | ||
|style="text-align:left; width:82px; padding:1px;"| | |style="text-align:left; width:82px; padding:1px;"| | ||
| Line 221: | Line 221: | ||
|style="text-align:left; width:44px; padding:1px;"| | |style="text-align:left; width:44px; padding:1px;"| | ||
|- | |- | ||
|style="text-align:center;"| | |style="text-align:center;"|स्टेप 9 | ||
|style="text-align:right; width:50px; padding:1px;"| | |style="text-align:right; width:50px; padding:1px;"| | ||
|style="text-align:left; width:82px; padding:1px;"| | |style="text-align:left; width:82px; padding:1px;"| | ||
| Line 234: | Line 234: | ||
|style="text-align:left; width:44px; padding:1px;"| | |style="text-align:left; width:44px; padding:1px;"| | ||
|- | |- | ||
|style="text-align:center;"| | |style="text-align:center;"|स्टेप 10 | ||
|style="text-align:right; width:50px; padding:1px;"| | |style="text-align:right; width:50px; padding:1px;"| | ||
|style="text-align:left; width:82px; padding:1px;"| | |style="text-align:left; width:82px; padding:1px;"| | ||
| Line 247: | Line 247: | ||
|style="text-align:left; width:44px; padding:1px;"| | |style="text-align:left; width:44px; padding:1px;"| | ||
|- | |- | ||
|style="background-color:#EEEEEE; font-weight:bold;"| | |style="background-color:#EEEEEE; font-weight:bold;"|क्षणों का योग | ||
|style="text-align:right; width:50px; padding:1px;"| | |style="text-align:right; width:50px; padding:1px;"| | ||
|style="text-align:left; width:82px; padding:1px;"|0 | |style="text-align:left; width:82px; padding:1px;"|0 | ||
Revision as of 10:56, 26 March 2023
क्षण वितरण विधि हार्डी क्रॉस द्वारा विकसित सांख्यिकीय रूप से अनिश्चित बीम (संरचना) और फ़्रेमिंग (निर्माण) के लिए संरचनात्मक विश्लेषण पद्धति है। यह 1930 में अमेरिकन सोसायटी ऑफ सिविल इंजीनियर्स जर्नल में प्रकाशित हुआ था।[1] यह विधि केवल वंक संबंधी प्रभावों के लिए उत्तरदायी है और अक्षीय अपरूपण प्रभावों की उपेक्षा करती है। 1930 के दशक से जब तक संरचनाओं के डिजाइन और विश्लेषण में कंप्यूटर का व्यापक रूप से उपयोग नहीं किया जाने लगा था और क्षण वितरण विधि सबसे व्यापक रूप से प्रचलित विधि थी।
परिचय
क्षण वितरण पद्धति में विश्लेषण की जाने वाली संरचना के प्रत्येक जोड़ को स्थिर किया जाता है, जिससे कि निश्चित-अंत क्षणों को विकसित किया जा सके। फिर प्रत्येक निश्चित जोड़ को क्रमिक रूप से जारी किया जाता है और निश्चित-अंत क्षण जो रिलीज के समय तक संतुलन में नहीं होते हैं, यांत्रिक संतुलन प्राप्त होने तक आसन्न सदस्यों को वितरित किए जाते हैं। गणितीय शब्दों में आघूर्ण वितरण पद्धति को पुनरावृति के माध्यम से साथ समीकरणों के समुच्चय को हल करने की प्रक्रिया के रूप में प्रदर्शित किया जा सकता है।
आघूर्ण वितरण पद्धति संरचनात्मक विश्लेषण की विस्थापन पद्धति की श्रेणी में आती है।
कार्यान्वयन
संरचना का विश्लेषण करने के लिए क्षण वितरण पद्धति को लागू करने के लिए, निम्नलिखित बातों पर विचार किया जाना चाहिए।
निश्चित अंत क्षण
निश्चित अंत क्षण बाहरी भार द्वारा सदस्य के सिरों पर उत्पन्न होने वाले क्षण होते हैं।
झुकने की कठोरता
किसी सदस्य की झुकने वाली कठोरता (EI/L) को सदस्य की लचीली कठोरता के रूप में दर्शाया जाता है। लोच के मापांक का उत्पाद (E) और क्षेत्र का दूसरा क्षण (I)) सदस्य की लंबाई (L) से विभाजित होता है। पल वितरण पद्धति में जो आवश्यक है वह विशिष्ट मूल्य नहीं है जबकि सभी सदस्यों के बीच झुकने की कठोरता का अनुपात है।
वितरण कारक
जब जोड़ जारी किया जा रहा है और असंतुलित पल के अनुसार घूमना प्रारंभ कर देता है, तो संयुक्त में साथ तैयार किए गए प्रत्येक सदस्य पर प्रतिरोधी बल विकसित होते हैं। चूंकि कुल प्रतिरोध असंतुलित पल के बराबर है, प्रत्येक सदस्य पर विकसित प्रतिरोधी बलों की परिमाण सदस्यों की झुकने वाली कठोरता से भिन्न होती है। वितरण कारकों को प्रत्येक सदस्य द्वारा किए गए असंतुलित क्षणों के अनुपात के रूप में परिभाषित किया जा सकता है। गणितीय शब्दों में, सदस्य का वितरण कारक संयुक्त रूप से बनाया गया के रूप में दिया गया है।
जहाँ n संयुक्त में बनाए गए सदस्यों की संख्या है।
कैरीओवर कारक
जब जोड़ जारी किया जाता है, तो असंतुलित क्षण को प्रतिसंतुलित करने के लिए संतुलन क्षण होता है। संतुलन क्षण प्रारंभ में निश्चित अंत क्षण के समान होता है। यह संतुलन क्षण तब सदस्य के दूसरे छोर तक ले जाया जाता है। प्रारंभिक अंत के निश्चित-अंत क्षण के लिए दूसरे छोर पर ले जाए गए पल का अनुपात कैरीओवर कारक है।
कैरीओवर कारकों का निर्धारण
निश्चित बीम के छोर अंत A को छोड़ दें और क्षण लागू करें जबकि दूसरा सिरा अंत B स्थिर रहता है। यह अंत A को कोण से घुमाने का कारण बनेगा । बार का परिमाण अंत B पर विकसित पाया जाता है, इस सदस्य के कैरीओवर कारक को अनुपात के रूप में दिया जाता है ऊपर ।
एल लंबाई के बीम के स्थितियों में निरंतर क्रॉस-सेक्शन के साथ जिसकी वंक संबंधी कठोरता है ,
इसलिए कैरीओवर कारक
संधिपत्र पर हस्ताक्षर
बार चिह्न परिपाटी का चयन हो जाने के बाद, इसे संपूर्ण संरचना के लिए बनाए रखना होता है। क्षण वितरण पद्धति की गणना में पारंपरिक अभियंता के हस्ताक्षर सम्मेलन का उपयोग नहीं किया जाता है, चूंकि परिणाम पारंपरिक विधियों से व्यक्त किए जा सकते हैं। बीएमडी स्थितियों में बाईं ओर का क्षण घड़ी की दिशा में होता है और दूसरा वामावर्त दिशा में होता है इसलिए झुकना सकारात्मक होता है और इसे शिथिलता कहा जाता है।
फ़्रेमयुक्त संरचना
साइडवे के साथ या उसके अतिरिक्त फ़्रेमयुक्त संरचना का पल वितरण विधि का उपयोग करके विश्लेषण किया जा सकता है।
उदाहरण
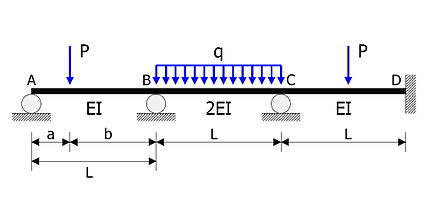
आंकड़े में दिखाए गए सांख्यिकीय रूप से अनिश्चित बीम का विश्लेषण किया जाना है।
बीम को तीन अलग-अलग सदस्यों, AB, BC और CD माना जाता है, जो बी और सी पर निश्चित अंत आघूर्ण प्रतिरोधी जोड़ों से जुड़े होते हैं।
- सदस्य AB, BC, CD का विस्तार समान है .
- आनमन कठोरताएँ क्रमशः EI, 2EI, EI हैं।
- परिमाण का केंद्रित भार दूरी पर कार्य करता है समर्थन ए से
- तीव्रता का समान भार BC पर कार्य करता है।
- सदस्य CD परिमाण के केंद्रित भार के साथ अपने मध्यकाल में भरी हुई है .
निम्नलिखित गणनाओं में, दक्षिणावर्त क्षण धनात्मक हैं।
निश्चित अंत क्षण
झुकने की कठोरता और वितरण कारक
AB, BC और CD सदस्यों की झुकने की कठोरता होती है, क्रमश , और , इसलिए, दशमलव संकेतन को दोहराने में परिणाम व्यक्त करना।
जोड़ों A और D के वितरण कारक हैं और .
कैरीओवर कारक
कैरीओवर कारक हैं , D निश्चित समर्थन से C तक कैरीओवर कारक को छोड़कर जो शून्य है।
पल वितरण
नंबर ग्रे में संतुलित क्षण हैं; तीर ( → / ← ) किसी के छोर से दूसरे छोर तक के पल को ले जाने का प्रतिनिधित्व करते हैं सदस्य। * चरण 1: जैसे ही संयुक्त ए जारी किया जाता है, निश्चित अंत क्षण के बराबर परिमाण का संतुलन क्षण विकसित होता है और संयुक्त A से संयुक्त B तक ले जाया जाता है। * चरण 2: संयुक्त B पर असंतुलित क्षण अब निश्चित अंत क्षणों का योग है , और संयुक्त ए से कैरी-ओवर पल। यह असंतुलित पल वितरण कारकों के अनुसार सदस्यों बीए और बीसी को वितरित किया जाता है और . चरण 2 संतुलित क्षण के आगे बढ़ने के साथ समाप्त होता है संयुक्त सी के लिए। संयुक्त ए रोलर समर्थन है जिसमें कोई घूर्णी संयम नहीं है, इसलिए संयुक्त बी से संयुक्त ए तक ले जाने का क्षण शून्य है। * चरण 3: संयुक्त सी पर असंतुलित पल अब निश्चित अंत क्षणों का योग है , और संयुक्त बी से कैरीओवर पल। पिछले चरण के रूप में, यह असंतुलित पल प्रत्येक सदस्य को वितरित किया जाता है और फिर संयुक्त डी और वापस संयुक्त बी में ले जाया जाता है। संयुक्त डी इस संयुक्त इच्छा के लिए निश्चित समर्थन और आगे बढ़ने वाले क्षण हैं वितरित नहीं किया जाएगा और न ही संयुक्त C पर ले जाया जाएगा। * चरण 4: संयुक्त B में अभी भी संतुलित क्षण है जिसे चरण 3 में संयुक्त C से आगे ले जाया गया था। क्षण वितरण को प्रेरित करने और संतुलन प्राप्त करने के लिए संयुक्त B को बार फिर से जारी किया गया है। * चरण 5 - 10: जोड़ों को तब तक जारी किया जाता है और फिर से स्थिर किया जाता है जब तक कि प्रत्येक जोड़ में शून्य आकार के असंतुलित क्षण या आवश्यक परिशुद्धता में उपेक्षात्मक रूप से छोटा न हो। अंकगणितीय रूप से प्रत्येक संबंधित कॉलम में सभी क्षणों को जोड़ना अंतिम क्षण मान देता है।
परिणाम
- पल वितरण विधि द्वारा निर्धारित जोड़ों पर क्षण
- पारंपरिक अभियंता के संधिपत्र पर हस्ताक्षर का उपयोग यहां किया जाता है, अर्थात बीम सदस्य के निचले हिस्से में सकारात्मक क्षण बढ़ाव का कारण बनते हैं।
तुलनात्मक उद्देश्यों के लिए, मैट्रिक्स विधि का उपयोग करके उत्पन्न परिणाम निम्नलिखित हैं। ध्यान दें कि ऊपर दिए गए विश्लेषण में, पुनरावृत्त प्रक्रिया को >0.01 परिशुद्धता तक ले जाया गया था। तथ्य यह है कि मैट्रिक्स विश्लेषण के परिणाम और क्षण वितरण विश्लेषण के परिणाम 0.001 सटीकता से मेल खाते हैं, मात्र संयोग है।
- मैट्रिक्स विधि द्वारा निर्धारित जोड़ों पर क्षण
ध्यान दें कि क्षण वितरण पद्धति केवल जोड़ों पर क्षणों को निर्धारित करती है। पूर्ण झुकने वाले क्षण आरेखों को विकसित करने के लिए निर्धारित संयुक्त क्षणों और आंतरिक खंड संतुलन का उपयोग करके अतिरिक्त गणना की आवश्यकता होती है।
विस्थापन विधि के माध्यम से परिणाम
जैसा कि हार्डी क्रॉस विधि केवल अनुमानित परिणाम प्रदान करती है, पुनरावृत्तियों की संख्या के व्युत्क्रमानुपाती त्रुटि के मार्जिन के साथ, यह महत्वपूर्ण है[citation needed] यह अंदाजा लगाने के लिए कि यह तरीका कितना सटीक हो सकता है। इसे ध्यान में रखते हुए, यहाँ सटीक विधि का उपयोग करके प्राप्त किया गया परिणाम है: विस्थापन विधि
इसके लिए, विस्थापन विधि समीकरण निम्नलिखित रूप ग्रहण करता है:
इस उदाहरण में वर्णित संरचना के लिए, कठोरता मैट्रिक्स इस प्रकार है:
समतुल्य नोडल बल वेक्टर:
ऊपर प्रस्तुत मूल्यों को समीकरण में बदलना और इसके लिए इसे हल करना निम्नलिखित परिणाम की ओर जाता है:
इसलिए, नोड बी में मूल्यांकन किए गए क्षण इस प्रकार हैं:
नोड सी में मूल्यांकन किए गए क्षण इस प्रकार हैं:
यह भी देखें
- सीमित तत्व विधि
- ढाल विक्षेपण विधि
टिप्पणियाँ
- ↑ Cross, Hardy (1930). "फिक्स्ड-एंड मोमेंट्स को डिस्ट्रीब्यूट करके कंटीन्यूअस फ्रेम्स का विश्लेषण". Proceedings of the American Society of Civil Engineers. ASCE. pp. 919–928.
संदर्भ
- Błaszkowiak, Stanisław; Zbigniew Kączkowski (1966). Iterative Methods in Structural Analysis. Pergamon Press, Państwowe Wydawnictwo Naukowe.
- Norris, Charles Head; John Benson Wilbur; Senol Utku (1976). Elementary Structural Analysis (3rd ed.). McGraw-Hill. pp. 327–345. ISBN 0-07-047256-4.
- McCormac, Jack C.; Nelson, James K. Jr. (1997). Structural Analysis: A Classical and Matrix Approach (2nd ed.). Addison-Wesley. pp. 488–538. ISBN 0-673-99753-7.
- Yang, Chang-hyeon (2001-01-10). Structural Analysis (in Korean) (4th ed.). Seoul: Cheong Moon Gak Publishers. pp. 391–422. ISBN 89-7088-709-1. Archived from the original on 2007-10-08. Retrieved 2007-08-31.
{{cite book}}: CS1 maint: unrecognized language (link) - Volokh, K.Y. (2002). "On foundations of the Hardy Cross method". International Journal of Solids and Structures. International Journal of Solids and Structures, volume 39, issue 16, August 2002, Pages 4197-4200. 39 (16): 4197–4200. doi:10.1016/S0020-7683(02)00345-1.