इलेक्ट्रॉन प्रकाशिकी: Difference between revisions
No edit summary |
No edit summary |
||
| Line 8: | Line 8: | ||
{{main|इलेक्ट्रॉन}} | {{main|इलेक्ट्रॉन}} | ||
इलेक्ट्रॉन आवेशित कण सामान्य द्रव्यमान वाले बिंदु आवेश [[स्पिन (भौतिकी)|स्पिन (भौतिकी]] 1/2 के साथ होते हैं, इसलिए वे [[फर्मियन]] रूप में होते है। इलेक्ट्रॉन उपयुक्त [[विद्युत क्षेत्र]] | इलेक्ट्रॉन आवेशित कण सामान्य द्रव्यमान वाले बिंदु आवेश [[स्पिन (भौतिकी)|स्पिन (भौतिकी]] 1/2 के साथ होते हैं, इसलिए वे [[फर्मियन]] रूप में होते है। इलेक्ट्रॉन उपयुक्त [[विद्युत क्षेत्र]] या [[चुंबकीय क्षेत्र]] क्षेत्रों द्वारा [[कण त्वरक]] के रूप में हो सकते हैं, जिससे [[गतिज ऊर्जा]] प्राप्त होती है। पर्याप्त वोल्टेज दिए जाने पर मापने योग्य सापेक्षतावादी प्रभावों को प्रदर्शित करने के लिए इलेक्ट्रॉन को पर्याप्त तेजी से त्वरित किया जाता है। [[तरंग कण द्वैत|तरंग कण डुअलिटी]] के अनुसार इलेक्ट्रॉनों को [[तरंग दैर्ध्य]] चरण तरंगों और [[आयाम]] जैसे गुणों के साथ पदार्थ तरंगों के रूप में भी माना जा सकता है। | ||
== ज्यामितीय इलेक्ट्रॉन प्रकाशिकी == | == ज्यामितीय इलेक्ट्रॉन प्रकाशिकी == | ||
=== चुंबकीय क्षेत्र === | === चुंबकीय क्षेत्र === | ||
लोरेंत्ज़ बल की दूसरी अवधि के अनुसार चुंबकीय क्षेत्र और इलेक्ट्रॉन वेग के बीच एक क्रॉस उत्पाद के अनुसार इलेक्ट्रॉन चुंबकीय क्षेत्र के साथ क्रिया करते हैं। इस प्रकार एक अनंत समान क्षेत्र में इसका परिणाम क्षेत्र की दिशा के चारों ओर इलेक्ट्रॉन की एक गोलाकार गति के रूप में होता है, जिसके द्वारा दी गई त्रिज्या इस रूप में होती है | |||
:<math> r = \frac{mv_\perp}{eB}</math> | :<math> r = \frac{mv_\perp}{eB}</math> | ||
जहाँ r कक्षा की त्रिज्या है, m [[इलेक्ट्रॉन द्रव्यमान]] है, <math>v_\perp</math>क्षेत्र के लंबवत इलेक्ट्रॉन वेग का घटक है, ई इलेक्ट्रॉन आवेश है और बी लागू चुंबकीय क्षेत्र का परिमाण है। चुंबकीय क्षेत्र के समानांतर एक वेग घटक वाले इलेक्ट्रॉन [[ कुंडलित वक्रता ]] | जहाँ r कक्षा की त्रिज्या होती है, m [[इलेक्ट्रॉन द्रव्यमान]] होती है, <math>v_\perp</math>क्षेत्र के लंबवत इलेक्ट्रॉन वेग का घटक के रूप में होता है, ई इलेक्ट्रॉन आवेश है और बी लागू चुंबकीय क्षेत्र का परिमाण के रूप में है। चुंबकीय क्षेत्र के समानांतर एक वेग घटक वाले इलेक्ट्रॉन [[ कुंडलित वक्रता ]] प्रक्षेप वक्र के साथ आगे बढ़ते है। | ||
=== विद्युत क्षेत्र === | === विद्युत क्षेत्र === | ||
एक | एक प्रयुक्त स्थिर वैद्युत विक्षेप क्षेत्र के स्थितियों में, एक इलेक्ट्रॉन क्षेत्र के सकारात्मक ढाल की ओर विक्षेपित होगा। विशेष रूप से, स्थिर वैद्युत विक्षेप फ़ील्ड लाइनों के इस क्रॉसिंग का अर्थ है कि स्थिर वैद्युत विक्षेप फ़ील्ड के माध्यम से चलने वाले इलेक्ट्रॉन अपने वेग के परिमाण को बदलते हैं, जबकि चुंबकीय क्षेत्र में, केवल वेग की दिशा को संशोधित किया जाता है। | ||
चूंकि इलेक्ट्रॉन [[विवर्तन]] जैसे गैर-कण (तरंग-जैसे) प्रभाव प्रदर्शित कर सकते हैं, मैक्सवेल के समीकरण को हल करके इलेक्ट्रॉन पथों का एक पूर्ण विश्लेषण प्राप्त किया जा सकता है - चूंकि कई स्थितियों में, कण व्याख्या जटिलता में बड़ी कमी के साथ पर्याप्त सन्निकटन प्रदान कर सकती है। | चूंकि इलेक्ट्रॉन [[विवर्तन]] जैसे गैर-कण (तरंग-जैसे) प्रभाव प्रदर्शित कर सकते हैं, मैक्सवेल के समीकरण को हल करके इलेक्ट्रॉन पथों का एक पूर्ण विश्लेषण प्राप्त किया जा सकता है - चूंकि कई स्थितियों में, कण व्याख्या जटिलता में बड़ी कमी के साथ पर्याप्त सन्निकटन प्रदान कर सकती है। | ||
| Line 47: | Line 47: | ||
|url = https://cds.cern.ch/record/2128406 | |url = https://cds.cern.ch/record/2128406 | ||
}} | }} | ||
</ref> मोटाई-संग्राहक [[सिलिकॉन नाइट्राइड]] झिल्ली और प्रोग्रामेबल फेज शिफ्ट डिवाइसेस ने दूर-क्षेत्र स्थानिक तीव्रता और इलेक्ट्रॉन तरंग के चरण को नियंत्रित करने के लिए स्थानिक रूप से भिन्न चरण शिफ्टों को लागू करने के लिए इन गुणों का शोषण किया है। इस तरह के उपकरणों को इलेक्ट्रॉन वेवफ्रंट को मनमाने ढंग से आकार देने के लिए लागू किया गया है, इलेक्ट्रॉन सूक्ष्मदर्शी में निहित [[ऑप्टिकल विपथन]] को सही ककिरण ं, [[मुक्त इलेक्ट्रॉनों की कक्षीय कोणीय गति]] को हल ककिरण ं, और मुक्त इलेक्ट्रॉनों और चुंबकीय पदार्थ या प्लास्मोनिक नैनोस्ट्रक्चर के बीच बातचीत में | </ref> मोटाई-संग्राहक [[सिलिकॉन नाइट्राइड]] झिल्ली और प्रोग्रामेबल फेज शिफ्ट डिवाइसेस ने दूर-क्षेत्र स्थानिक तीव्रता और इलेक्ट्रॉन तरंग के चरण को नियंत्रित करने के लिए स्थानिक रूप से भिन्न चरण शिफ्टों को लागू करने के लिए इन गुणों का शोषण किया है। इस तरह के उपकरणों को इलेक्ट्रॉन वेवफ्रंट को मनमाने ढंग से आकार देने के लिए लागू किया गया है, इलेक्ट्रॉन सूक्ष्मदर्शी में निहित [[ऑप्टिकल विपथन]] को सही ककिरण ं, [[मुक्त इलेक्ट्रॉनों की कक्षीय कोणीय गति]] को हल ककिरण ं, और मुक्त इलेक्ट्रॉनों और चुंबकीय पदार्थ या प्लास्मोनिक नैनोस्ट्रक्चर के बीच बातचीत में डुअलिटी वाद को मापने के लिए।<ref name="ShilohLu2019"> | ||
{{cite journal|last1=Shiloh|first1=Roy|last2=Lu|first2=Peng-Han|last3=Remez|first3=Roei|last4=Tavabi|first4=Amir H|last5=Pozzi|first5=Giulio|last6=Dunin-Borkowski|first6=Rafal E|last7=Arie|first7=Ady|title=Nanostructuring of electron beams|journal=Physica Scripta|volume=94|issue=3|year=2019|pages=034004|issn=0031-8949|doi=10.1088/1402-4896/aaf258|bibcode=2019PhyS...94c4004S|doi-access=free}} | {{cite journal|last1=Shiloh|first1=Roy|last2=Lu|first2=Peng-Han|last3=Remez|first3=Roei|last4=Tavabi|first4=Amir H|last5=Pozzi|first5=Giulio|last6=Dunin-Borkowski|first6=Rafal E|last7=Arie|first7=Ady|title=Nanostructuring of electron beams|journal=Physica Scripta|volume=94|issue=3|year=2019|pages=034004|issn=0031-8949|doi=10.1088/1402-4896/aaf258|bibcode=2019PhyS...94c4004S|doi-access=free}} | ||
</ref> | </ref> | ||
Revision as of 23:42, 13 April 2023
इलेक्ट्रॉन प्रकाशिकी विद्युत चुम्बकीय क्षेत्र के साथ इलेक्ट्रॉन प्रक्षेप वक्र की गणना के लिए एक गणितीय रूपकिरण खा के रूप में है। प्रकाश विज्ञान शब्द का प्रयोग इसलिए किया जाता है क्योंकि चुंबकीय लेंस और स्थिर वैद्युत विक्षेप लेंस प्रकाश किरण पर ऑप्टिकल लेंस के समान आवेशित कण किरणपुंज के रूप में कार्य करते हैं।
इलेक्ट्रॉन सूक्ष्मदर्शी और कण त्वरक के डिजाइन के लिए इलेक्ट्रॉन प्रकाशिकी की गणना महत्वपूर्ण होती है। पैराएक्सियल सन्निकटन में, किरण ट्रांसफर मैट्रिक्स विश्लेषण का उपयोग करके प्रक्षेप वक्र की गणना की जा सकती है।
इलेक्ट्रॉन गुण
इलेक्ट्रॉन आवेशित कण सामान्य द्रव्यमान वाले बिंदु आवेश स्पिन (भौतिकी 1/2 के साथ होते हैं, इसलिए वे फर्मियन रूप में होते है। इलेक्ट्रॉन उपयुक्त विद्युत क्षेत्र या चुंबकीय क्षेत्र क्षेत्रों द्वारा कण त्वरक के रूप में हो सकते हैं, जिससे गतिज ऊर्जा प्राप्त होती है। पर्याप्त वोल्टेज दिए जाने पर मापने योग्य सापेक्षतावादी प्रभावों को प्रदर्शित करने के लिए इलेक्ट्रॉन को पर्याप्त तेजी से त्वरित किया जाता है। तरंग कण डुअलिटी के अनुसार इलेक्ट्रॉनों को तरंग दैर्ध्य चरण तरंगों और आयाम जैसे गुणों के साथ पदार्थ तरंगों के रूप में भी माना जा सकता है।
ज्यामितीय इलेक्ट्रॉन प्रकाशिकी
चुंबकीय क्षेत्र
लोरेंत्ज़ बल की दूसरी अवधि के अनुसार चुंबकीय क्षेत्र और इलेक्ट्रॉन वेग के बीच एक क्रॉस उत्पाद के अनुसार इलेक्ट्रॉन चुंबकीय क्षेत्र के साथ क्रिया करते हैं। इस प्रकार एक अनंत समान क्षेत्र में इसका परिणाम क्षेत्र की दिशा के चारों ओर इलेक्ट्रॉन की एक गोलाकार गति के रूप में होता है, जिसके द्वारा दी गई त्रिज्या इस रूप में होती है
जहाँ r कक्षा की त्रिज्या होती है, m इलेक्ट्रॉन द्रव्यमान होती है, क्षेत्र के लंबवत इलेक्ट्रॉन वेग का घटक के रूप में होता है, ई इलेक्ट्रॉन आवेश है और बी लागू चुंबकीय क्षेत्र का परिमाण के रूप में है। चुंबकीय क्षेत्र के समानांतर एक वेग घटक वाले इलेक्ट्रॉन कुंडलित वक्रता प्रक्षेप वक्र के साथ आगे बढ़ते है।
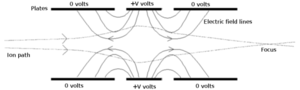
विद्युत क्षेत्र
एक प्रयुक्त स्थिर वैद्युत विक्षेप क्षेत्र के स्थितियों में, एक इलेक्ट्रॉन क्षेत्र के सकारात्मक ढाल की ओर विक्षेपित होगा। विशेष रूप से, स्थिर वैद्युत विक्षेप फ़ील्ड लाइनों के इस क्रॉसिंग का अर्थ है कि स्थिर वैद्युत विक्षेप फ़ील्ड के माध्यम से चलने वाले इलेक्ट्रॉन अपने वेग के परिमाण को बदलते हैं, जबकि चुंबकीय क्षेत्र में, केवल वेग की दिशा को संशोधित किया जाता है।
चूंकि इलेक्ट्रॉन विवर्तन जैसे गैर-कण (तरंग-जैसे) प्रभाव प्रदर्शित कर सकते हैं, मैक्सवेल के समीकरण को हल करके इलेक्ट्रॉन पथों का एक पूर्ण विश्लेषण प्राप्त किया जा सकता है - चूंकि कई स्थितियों में, कण व्याख्या जटिलता में बड़ी कमी के साथ पर्याप्त सन्निकटन प्रदान कर सकती है।
इलेक्ट्रॉनों की एक और संपत्ति यह है कि वे पदार्थ के साथ दृढ़ता से संपर्क करते हैं क्योंकि वे न केवल नाभिक के प्रति संवेदनशील होते हैं, बल्कि पदार्थ के इलेक्ट्रॉन चार्ज क्लाउड के प्रति भी संवेदनशील होते हैं। इसलिए, इलेक्ट्रॉनों को किसी भी उचित दूरी को प्रसारित करने के लिए खालीपन की आवश्यकता होती है, जैसे इलेक्ट्रॉन ऑप्टिक सिस्टम में वांछनीय होगा।
निर्वात में प्रवेश औसत मुक्त पथ द्वारा तय किया जाता है, इलेक्ट्रॉनों और पदार्थ के बीच टकराव की संभावना का एक उपाय, अनुमानित मान जिसके लिए पॉइसन सांख्यिकी से प्राप्त किया जा सकता है।
सापेक्षवादी सिद्धांत
चूंकि बहुत आम नहीं है, डायराक समीकरण से प्रारंभ होने वाले आवेशित कणों पर चुंबकीय संरचनाओं के प्रभावों को प्राप्त करना भी संभव है।[1]
विवर्तनिक इलेक्ट्रॉन प्रकाशिकी
निर्वात में प्रसार करने वाले एक उप-सापेक्षवादी मुक्त इलेक्ट्रॉन को यथार्थ रूप से एक ब्रोगली का पदार्थ तरंग के रूप में वर्णित किया जा सकता है, जिसकी तरंग दैर्ध्य इसके अनुदैर्ध्य गति के व्युत्क्रमानुपाती होती है। इलेक्ट्रॉन द्वारा किए गए आवेश के परिणामस्वरूप, विद्युत क्षेत्र, चुंबकीय क्षेत्र, या स्थिर वैद्युत विक्षेप मतलब पतली, कमजोर रूप से परस्पर क्रिया करने वाली पदार्थ की आंतरिक क्षमता एक इलेक्ट्रॉन के तरंगाग्र को एक चरण बदलाव प्रदान कर सकती है।[2] मोटाई-संग्राहक सिलिकॉन नाइट्राइड झिल्ली और प्रोग्रामेबल फेज शिफ्ट डिवाइसेस ने दूर-क्षेत्र स्थानिक तीव्रता और इलेक्ट्रॉन तरंग के चरण को नियंत्रित करने के लिए स्थानिक रूप से भिन्न चरण शिफ्टों को लागू करने के लिए इन गुणों का शोषण किया है। इस तरह के उपकरणों को इलेक्ट्रॉन वेवफ्रंट को मनमाने ढंग से आकार देने के लिए लागू किया गया है, इलेक्ट्रॉन सूक्ष्मदर्शी में निहित ऑप्टिकल विपथन को सही ककिरण ं, मुक्त इलेक्ट्रॉनों की कक्षीय कोणीय गति को हल ककिरण ं, और मुक्त इलेक्ट्रॉनों और चुंबकीय पदार्थ या प्लास्मोनिक नैनोस्ट्रक्चर के बीच बातचीत में डुअलिटी वाद को मापने के लिए।[3]
यह भी देखें
- आवेशित कण किरण
- मजबूत फोकसिंग
- इलेक्ट्रॉन किरण प्रौद्योगिकी
- इलेक्ट्रॉन सूक्ष्मदर्शी
- किरण उत्सर्जन
- अर्नेस्ट रसा
- अर्धगोल इलेक्ट्रॉन ऊर्जा विश्लेषक
अग्रिम पठन
- Hawkes, P. W. & Kasper, E. (1994). Principles of Electron Optics. Academic Press. ISBN 9780080984162.
- Pozzi, G. (2016). Particles and Waves in Electron Optics and Microscopy. Academic Press. ISBN 9780128048146.
संदर्भ
- ↑ Jagannathan, R.; Simon, R.; Sudarshan, E. C. G.; Mukunda, N. (1989). "डायराक समीकरण के आधार पर चुंबकीय इलेक्ट्रॉन लेंस का क्वांटम सिद्धांत" (PDF). Physics Letters A. 134 (8–9): 457. Bibcode:1989PhLA..134..457J. doi:10.1016/0375-9601(89)90685-3.
- ↑ Pozzi, Giulio; Peter Hawkes (2016). "Particles and waves in electron optics and microscopy". Advances in Imaging and Electron Physics. 194 (2): 1–336. doi:10.1016/bs.aiep.2016.02.001.
- ↑ Shiloh, Roy; Lu, Peng-Han; Remez, Roei; Tavabi, Amir H; Pozzi, Giulio; Dunin-Borkowski, Rafal E; Arie, Ady (2019). "Nanostructuring of electron beams". Physica Scripta. 94 (3): 034004. Bibcode:2019PhyS...94c4004S. doi:10.1088/1402-4896/aaf258. ISSN 0031-8949.
