|
|
| Line 43: |
Line 43: |
| त्रिकोणमितीय कार्यों का विभेदन एक त्रिकोणमितीय फलन के व्युत्पन्न को खोजने की गणितीय प्रक्रिया है, या चर के संबंध में इसकी परिवर्तन की दर है। उदाहरण के लिए, साइन फलन का व्युत्पन्न sin′(''a'') = cos(''a'') लिखा जाता है, जिसका अर्थ है कि किसी विशेष कोण x = a पर sin(''x'') के परिवर्तन की दर उस कोण के कोज्या द्वारा दिया जाता है। | | त्रिकोणमितीय कार्यों का विभेदन एक त्रिकोणमितीय फलन के व्युत्पन्न को खोजने की गणितीय प्रक्रिया है, या चर के संबंध में इसकी परिवर्तन की दर है। उदाहरण के लिए, साइन फलन का व्युत्पन्न sin′(''a'') = cos(''a'') लिखा जाता है, जिसका अर्थ है कि किसी विशेष कोण x = a पर sin(''x'') के परिवर्तन की दर उस कोण के कोज्या द्वारा दिया जाता है। |
|
| |
|
| tan(''x'') = sin(x)/cos(x) जैसे कार्यों पर प्रयुक्त [[भागफल नियम]] के माध्यम से वृत्ताकार त्रिकोणमितीय कार्यों के सभी [[ यौगिक | यौगिक]] sin(x) और cos(x) से पाए जा सकते हैं, इन व्युत्पत्तियों को जानने के बाद, व्युत्क्रम त्रिकोणमितीय कार्यों के यौगिक [[निहित भेदभाव|निहित विभेदन]] का उपयोग करते हुए पाए जाते हैं। | | tan(''x'') = sin(x)/cos(x) जैसे कार्यों पर प्रयुक्त [[भागफल नियम]] के माध्यम से वृत्ताकार त्रिकोणमितीय कार्यों के सभी [[ यौगिक |यौगिक]] sin(x) और cos(x) से पाए जा सकते हैं, इन व्युत्पत्तियों को जानने के बाद, व्युत्क्रम त्रिकोणमितीय कार्यों के यौगिक [[निहित भेदभाव|निहित विभेदन]] का उपयोग करते हुए पाए जाते हैं। |
|
| |
|
| ==त्रिकोणमितीय कार्यों के यौगिक का प्रमाण== | | ==त्रिकोणमितीय कार्यों के यौगिक का प्रमाण== |
|
| |
|
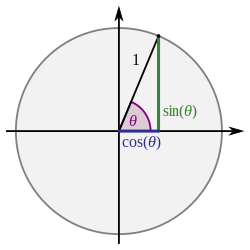
| sin(θ)/θ की सीमा जब θ 0 की ओर जाता है | | sin(θ)/θ की सीमा जब θ 0 की ओर जाता है |
| [[File:limit circle FbN.jpeg|thumb|वृत्त, केंद्र O, त्रिज्या 1]]दाईं ओर का आरेख केंद्र O और त्रिज्या r = 1 के साथ एक वृत्त दिखाता है। मान लें कि दो त्रिज्या OA और OB θ रेडियन का एक चाप बनाते हैं। चूंकि हम सीमा पर विचार कर रहे हैं क्योंकि θ शून्य की ओर जाता है, हम मान सकते हैं कि θ एक छोटी सकारात्मक संख्या है, मान लीजिए 0 < θ < ½ π पहले चतुर्थांश में। | | [[File:limit circle FbN.jpeg|thumb|वृत्त, केंद्र O, त्रिज्या 1]]दाईं ओर का आरेख केंद्र O और त्रिज्या r = 1 के साथ एक वृत्त दिखाता है। मान लें कि दो त्रिज्या OA और OB θ रेडियन का एक चाप बनाते हैं। चूंकि हम सीमा पर विचार कर रहे हैं क्योंकि θ शून्य की ओर जाता है, हम मान सकते हैं कि θ एक छोटी सकारात्मक संख्या है, मान लीजिए 0 < θ < ½ π पहले चतुर्थांश में। |
|
| |
|
| आरेख में, R<sub>1</sub> को त्रिभुज OAB, R<sub>2</sub> हो वृत्ताकार क्षेत्र OAB, और R<sub>3</sub> त्रिभुज OAC होने दे । त्रिभुज OAB के क्षेत्रफल है: | | आरेख में, R<sub>1</sub> को त्रिभुज OAB, R<sub>2</sub> हो वृत्ताकार क्षेत्र OAB, और R<sub>3</sub> त्रिभुज OAC होने दे । त्रिभुज OAB के क्षेत्रफल है: |
|
| |
|
| :<math> \mathrm{Area}(R_1 | | :<math> \mathrm{Area}(R_1 |
| Line 70: |
Line 70: |
| [[File:Squeeze FbN.png|thumb|निचोड़: घटता y = 1 और y = cos θ लाल रंग में दिखाया गया है, वक्र y = sin(θ)/θ नीले रंग में दिखाया गया है। | | [[File:Squeeze FbN.png|thumb|निचोड़: घटता y = 1 और y = cos θ लाल रंग में दिखाया गया है, वक्र y = sin(θ)/θ नीले रंग में दिखाया गया है। |
|
| |
|
| ]]हम यह निष्कर्ष निकालते हैं कि 0 < θ < ½ π के लिए, {{nowrap|sin(''θ'')/''θ''}} सदैव 1 से कम और सदैव cos(θ) से बड़ा होता है। इस प्रकार, जैसे-जैसे θ 0 के नजदीक आता जाता है, {{nowrap|sin(''θ'')/''θ''}} ऊंचाई 1 पर छत और ऊंचाई {{nowrap|cos ''θ''}} पर मंजिल के बीच [[निचोड़ प्रमेय]] है , जो 1 की ओर बढ़ता है; इसलिए sin(θ)/θ को 1 की ओर प्रवृत्त होना चाहिए क्योंकि θ धनात्मक पक्ष से 0 की ओर प्रवृत्त होता है:<blockquote><math>\lim_{\theta \to 0^+} \frac{\sin\theta}{\theta} = 1 \, . </math></blockquote>उस स्थिति लिए जहां θ एक छोटी ऋणात्मक संख्या है -½ π < θ < 0, हम इस तथ्य का उपयोग करते हैं कि ज्या एक विषम फलन है: | | ]]हम यह निष्कर्ष निकालते हैं कि 0 < θ < ½ π के लिए, {{nowrap|sin(''θ'')/''θ''}} सदैव 1 से कम और सदैव cos(θ) से बड़ा होता है। इस प्रकार, जैसे-जैसे θ 0 के नजदीक आता जाता है, {{nowrap|sin(''θ'')/''θ''}} ऊंचाई 1 पर छत और ऊंचाई {{nowrap|cos ''θ''}} पर मंजिल के बीच [[निचोड़ प्रमेय]] है , जो 1 की ओर बढ़ता है; इसलिए sin(θ)/θ को 1 की ओर प्रवृत्त होना चाहिए क्योंकि θ धनात्मक पक्ष से 0 की ओर प्रवृत्त होता है:<blockquote><math>\lim_{\theta \to 0^+} \frac{\sin\theta}{\theta} = 1 \, . </math></blockquote>उस स्थिति लिए जहां θ एक छोटी ऋणात्मक संख्या है -½ π < θ < 0, हम इस तथ्य का उपयोग करते हैं कि ज्या एक विषम फलन है: |
|
| |
|
| :<math>\lim_{\theta \to 0^-}\! \frac{\sin\theta}{\theta} | | :<math>\lim_{\theta \to 0^-}\! \frac{\sin\theta}{\theta} |
| Line 80: |
Line 80: |
| \lim_{\theta\to 0^+}\!\frac{\sin\theta}{\theta} \ =\ | | \lim_{\theta\to 0^+}\!\frac{\sin\theta}{\theta} \ =\ |
| 1 \, . </math> | | 1 \, . </math> |
|
| |
|
| |
|
| |
|
| |
|
|
| |
|
| Line 118: |
Line 115: |
| \ =\ | | \ =\ |
| 1 \, . </math> | | 1 \, . </math> |
|
| |
|
| |
|
| === [[साइन समारोह]] का व्युत्पन्न === | | === [[साइन समारोह]] का व्युत्पन्न === |
| हम व्युत्पन्न परिभाषा से अंतर उद्धरण के माध्यम से साइन फलन के व्युत्पन्न की गणना करते हैं: | | हम व्युत्पन्न परिभाषा से अंतर उद्धरण के माध्यम से साइन फलन के व्युत्पन्न की गणना करते हैं: |
| :<math> \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\sin\theta = \lim_{\delta \to 0} \frac{\sin(\theta + \delta) - \sin \theta}{\delta} . </math> | | :<math> \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\sin\theta = \lim_{\delta \to 0} \frac{\sin(\theta + \delta) - \sin \theta}{\delta} . </math> |
| त्रिकोणमितीय सर्वसमिकाओं की सूची का उपयोग करना कोण योग और अंतर सर्वसमिका {{nowrap|1=sin(α+β) = sin α cos β + sin β cos α}}, अपने पास: | | त्रिकोणमितीय सर्वसमिकाओं की सूची का उपयोग करना कोण योग और अंतर सर्वसमिका {{nowrap|1=sin(α+β) = sin α cos β + sin β cos α}}, अपने पास: |
| Line 136: |
Line 132: |
| = | | = |
| \cos\theta \, . </math> | | \cos\theta \, . </math> |
|
| |
|
| |
|
| === कोसाइन फलन का व्युत्पन्न === | | === कोसाइन फलन का व्युत्पन्न === |
| Line 156: |
Line 151: |
| = (0) \cos\theta - (1) \sin\theta = -\sin\theta \, . </math> | | = (0) \cos\theta - (1) \sin\theta = -\sin\theta \, . </math> |
|
| |
|
| | | ===श्रृंखला नियम से=== |
| ====श्रृंखला नियम से====
| |
| श्रृंखला नियम से कोसाइन फलन के व्युत्पन्न की गणना करने के लिए, पहले निम्नलिखित तीन तथ्यों का पालन करें: | | श्रृंखला नियम से कोसाइन फलन के व्युत्पन्न की गणना करने के लिए, पहले निम्नलिखित तीन तथ्यों का पालन करें: |
| :<math>\cos\theta = \sin\left(\tfrac{\pi}{2}-\theta\right)</math> | | :<math>\cos\theta = \sin\left(\tfrac{\pi}{2}-\theta\right)</math> |
| Line 218: |
Line 212: |
|
| |
|
| == व्युत्क्रम त्रिकोणमितीय कार्यों के यौगिक का प्रमाण == | | == व्युत्क्रम त्रिकोणमितीय कार्यों के यौगिक का प्रमाण == |
| निम्नलिखित यौगिक को व्युत्क्रम त्रिकोणमितीय फलन के समान एक [[चर (गणित)]] y समुच्चय करके पाया जाता है जिसे हम व्युत्पन्न करना चाहते हैं। अंतर्निहित अवकलन का उपयोग करना और फिर dy/dx के लिए हल करना, व्युत्क्रम फलन का अवकलज y के संदर्भ में पाया जाता है। dy/dx को वापस x के संदर्भ में परिवर्तित करने के लिए, हम यूनिट सर्कल पर एक संदर्भ त्रिकोण बना सकते हैं, जिससे θ y हो। [[पाइथागोरस प्रमेय]] और नियमित त्रिकोणमितीय कार्यों की परिभाषा का उपयोग करके, हम अंत में x के संदर्भ में dy/dx को व्यक्त कर सकते हैं। | | निम्नलिखित यौगिक को व्युत्क्रम त्रिकोणमितीय फलन के समान एक [[चर (गणित)]] y समुच्चय करके पाया जाता है जिसे हम व्युत्पन्न करना चाहते हैं। अंतर्निहित अवकलन का उपयोग करना और फिर dy/dx के लिए हल करना, व्युत्क्रम फलन का अवकलज y के संदर्भ में पाया जाता है। dy/dx को वापस x के संदर्भ में परिवर्तित करने के लिए, हम यूनिट सर्कल पर एक संदर्भ त्रिकोण बना सकते हैं, जिससे θ y हो। [[पाइथागोरस प्रमेय]] और नियमित त्रिकोणमितीय कार्यों की परिभाषा का उपयोग करके, हम अंत में x के संदर्भ में dy/dx को व्यक्त कर सकते हैं। |
|
| |
|
| ===प्रतिलोम ज्या फलन में अंतर करना=== | | ===प्रतिलोम ज्या फलन में अंतर करना=== |
| Line 399: |
Line 393: |
| = -\frac{1}{\sqrt{x^2}\sqrt{x^2-1}} | | = -\frac{1}{\sqrt{x^2}\sqrt{x^2-1}} |
| = -\frac{1}{|x|\sqrt{x^2-1}} </math> | | = -\frac{1}{|x|\sqrt{x^2-1}} </math> |
|
| |
| '''त्रिकोणमितीय कार्यों का विभेदन एक त्रिकोणमितीय फलन के व्युत्पन्न को खोजने की गणितीय प्रक्रिया है, या चर के संबंध में इसकी परिवर्तन की दर है। उदाहरण के लिए, साइन फलन का<br />'''
| |
| == यह भी देखें == | | == यह भी देखें == |
|
| |
|
| Function
|
Derivative
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
त्रिकोणमितीय कार्यों का विभेदन एक त्रिकोणमितीय फलन के व्युत्पन्न को खोजने की गणितीय प्रक्रिया है, या चर के संबंध में इसकी परिवर्तन की दर है। उदाहरण के लिए, साइन फलन का व्युत्पन्न sin′(a) = cos(a) लिखा जाता है, जिसका अर्थ है कि किसी विशेष कोण x = a पर sin(x) के परिवर्तन की दर उस कोण के कोज्या द्वारा दिया जाता है।
tan(x) = sin(x)/cos(x) जैसे कार्यों पर प्रयुक्त भागफल नियम के माध्यम से वृत्ताकार त्रिकोणमितीय कार्यों के सभी यौगिक sin(x) और cos(x) से पाए जा सकते हैं, इन व्युत्पत्तियों को जानने के बाद, व्युत्क्रम त्रिकोणमितीय कार्यों के यौगिक निहित विभेदन का उपयोग करते हुए पाए जाते हैं।
त्रिकोणमितीय कार्यों के यौगिक का प्रमाण
sin(θ)/θ की सीमा जब θ 0 की ओर जाता है

वृत्त, केंद्र O, त्रिज्या 1
दाईं ओर का आरेख केंद्र O और त्रिज्या r = 1 के साथ एक वृत्त दिखाता है। मान लें कि दो त्रिज्या OA और OB θ रेडियन का एक चाप बनाते हैं। चूंकि हम सीमा पर विचार कर रहे हैं क्योंकि θ शून्य की ओर जाता है, हम मान सकते हैं कि θ एक छोटी सकारात्मक संख्या है, मान लीजिए 0 < θ < ½ π पहले चतुर्थांश में।
आरेख में, R1 को त्रिभुज OAB, R2 हो वृत्ताकार क्षेत्र OAB, और R3 त्रिभुज OAC होने दे । त्रिभुज OAB के क्षेत्रफल है:

वृत्ताकार सेक्टर क्षेत्रफल OAB है  , जबकि त्रिभुज OAC का क्षेत्रफल इसके द्वारा दिया गया है
, जबकि त्रिभुज OAC का क्षेत्रफल इसके द्वारा दिया गया है

चूंकि प्रत्येक क्षेत्र अगले में समाहित है, एक के पास:

इसके अतिरिक्त, चूंकि पहले चतुर्थांश में sin θ > 0 , हम ½ sin θ से विभाजित कर सकते हैं :

अंतिम चरण में हमने असमानताओं को उलटते हुए तीन सकारात्मक शब्दों के व्युत्क्रमों को लिया।

निचोड़: घटता y = 1 और y = cos θ लाल रंग में दिखाया गया है, वक्र y = sin(θ)/θ नीले रंग में दिखाया गया है।
हम यह निष्कर्ष निकालते हैं कि 0 < θ < ½ π के लिए, sin(θ)/θ सदैव 1 से कम और सदैव cos(θ) से बड़ा होता है। इस प्रकार, जैसे-जैसे θ 0 के नजदीक आता जाता है, sin(θ)/θ ऊंचाई 1 पर छत और ऊंचाई cos θ पर मंजिल के बीच निचोड़ प्रमेय है , जो 1 की ओर बढ़ता है; इसलिए sin(θ)/θ को 1 की ओर प्रवृत्त होना चाहिए क्योंकि θ धनात्मक पक्ष से 0 की ओर प्रवृत्त होता है:

उस स्थिति लिए जहां θ एक छोटी ऋणात्मक संख्या है -½ π < θ < 0, हम इस तथ्य का उपयोग करते हैं कि ज्या एक विषम फलन है:

(cos(θ)-1)/θ की सीमा जब θ 0 की ओर जाता है
अंतिम खंड हमें अपेक्षाकृत आसानी से इस नई सीमा की गणना करने में सक्षम बनाता है। यह एक साधारण ट्रिक को नियोजित करके किया जाता है। इस गणना में, θ का चिह्न महत्वहीन है।

का उपयोग करते हुए cos2θ – 1 = –sin2θ,
तथ्य यह है कि किसी उत्पाद की सीमा सीमाओं का गुणनफल है, और पिछले अनुभाग से सीमा परिणाम, हम पाते हैं कि:

tan(θ)/θ की सीमा जब θ 0 की ओर जाता है
- साइन फलन के लिए सीमा का उपयोग करना, यह तथ्य कि स्पर्शरेखा फलन विषम है, और यह तथ्य कि उत्पाद की सीमा सीमा का उत्पाद है, हम पाते हैं:

हम व्युत्पन्न परिभाषा से अंतर उद्धरण के माध्यम से साइन फलन के व्युत्पन्न की गणना करते हैं:

त्रिकोणमितीय सर्वसमिकाओं की सूची का उपयोग करना कोण योग और अंतर सर्वसमिका sin(α+β) = sin α cos β + sin β cos α, अपने पास:

- साइन और कोसाइन कार्यों के लिए सीमाओं का उपयोग करना:

कोसाइन फलन का व्युत्पन्न
व्युत्पन्न की परिभाषा से
हम फिर से सीमा परिभाषा से कोसाइन समारोह के व्युत्पन्न की गणना करते हैं:

कोण योग सूत्र का उपयोग करना cos(α+β) = cos α cos β – sin α sin β, अपने पास:

- साइन और कोसाइन कार्यों के लिए सीमाओं का उपयोग करना:

श्रृंखला नियम से
श्रृंखला नियम से कोसाइन फलन के व्युत्पन्न की गणना करने के लिए, पहले निम्नलिखित तीन तथ्यों का पालन करें:



पहला और दूसरा त्रिकोणमितीय सर्वसमिकाओं की सूची समरूपता है, और तीसरा ऊपर सिद्ध किया गया है। इन तीन तथ्यों का उपयोग करते हुए हम निम्नलिखित लिख सकते हैं,

हम श्रृंखला नियम का उपयोग करके इसे अलग कर सकते हैं। दे  , अपने पास:
, अपने पास:
 .
.
इसलिए, हमने यह सिद्ध किया है
 .
.
स्पर्शरेखा समारोह का व्युत्पन्न
व्युत्पन्न की परिभाषा से
स्पर्शरेखा फलन tan θ के व्युत्पन्न की गणना करने के लिए, हम अंतर भागफल के माध्यम से व्युत्पन्न परिभाषा का उपयोग करते हैं। परिभाषा से:

प्रसिद्ध कोण सूत्र का उपयोग करना tan(α+β) = (tan α + tan β) / (1 - tan α tan β), अपने पास:
![{\displaystyle {\frac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\tan \theta =\lim _{\delta \to 0}\left[{\frac {{\frac {\tan \theta +\tan \delta }{1-\tan \theta \tan \delta }}-\tan \theta }{\delta }}\right]=\lim _{\delta \to 0}\left[{\frac {\tan \theta +\tan \delta -\tan \theta +\tan ^{2}\theta \tan \delta }{\delta \left(1-\tan \theta \tan \delta \right)}}\right].}](/index.php?title=Special:MathShowImage&hash=a5893fd35d613ee50fc17749fe02252d&mode=mathml)
इस तथ्य का उपयोग करना कि किसी उत्पाद की सीमा सीमा का उत्पाद है:

- 3 फलन के लिए सीमा का उपयोग करना, और तथ्य यह है कि tan δ 0 की ओर जाता है क्योंकि δ 0 की ओर जाता है:

हम तुरंत देखते हैं कि:

भागफल नियम से
कोई भागफल नियम का उपयोग करके स्पर्शरेखा फलन के अवकलज की गणना भी कर सकता है।

त्रिकोणमितीय सर्वसमिकाओं की सूची पाइथागोरस की सर्वसमिकाओं द्वारा अंश को 1 तक सरल बनाया जा सकता है, जो हमें देता है,

इसलिए,

व्युत्क्रम त्रिकोणमितीय कार्यों के यौगिक का प्रमाण
निम्नलिखित यौगिक को व्युत्क्रम त्रिकोणमितीय फलन के समान एक चर (गणित) y समुच्चय करके पाया जाता है जिसे हम व्युत्पन्न करना चाहते हैं। अंतर्निहित अवकलन का उपयोग करना और फिर dy/dx के लिए हल करना, व्युत्क्रम फलन का अवकलज y के संदर्भ में पाया जाता है। dy/dx को वापस x के संदर्भ में परिवर्तित करने के लिए, हम यूनिट सर्कल पर एक संदर्भ त्रिकोण बना सकते हैं, जिससे θ y हो। पाइथागोरस प्रमेय और नियमित त्रिकोणमितीय कार्यों की परिभाषा का उपयोग करके, हम अंत में x के संदर्भ में dy/dx को व्यक्त कर सकते हैं।
प्रतिलोम ज्या फलन में अंतर करना
हम जाने

कहाँ

तब

व्युत्पन्न के संबंध में लेना  दोनों तरफ और डीई/डीएक्स के लिए हल करना:
दोनों तरफ और डीई/डीएक्स के लिए हल करना:


स्थानापन्न  में ऊपर से,
में ऊपर से,

स्थानापन्न  में ऊपर से,
में ऊपर से,


प्रतिलोम कोज्या फलन में अंतर करना
हम जाने

कहाँ

तब

व्युत्पन्न के संबंध में लेना  दोनों तरफ और डीई/डीएक्स के लिए हल करना:
दोनों तरफ और डीई/डीएक्स के लिए हल करना:


स्थानापन्न  ऊपर से, हम प्राप्त करते हैं
ऊपर से, हम प्राप्त करते हैं

स्थानापन्न  ऊपर से, हम प्राप्त करते हैं
ऊपर से, हम प्राप्त करते हैं


वैकल्पिक रूप से, एक बार के व्युत्पन्न  स्थापित है, का व्युत्पन्न है
स्थापित है, का व्युत्पन्न है  पहचान को अलग करके तुरंत अनुसरण करता है
पहचान को अलग करके तुरंत अनुसरण करता है  ताकि
ताकि  .
.
प्रतिलोम स्पर्शरेखा फलन में अंतर करना
हम जाने

कहाँ

तब

व्युत्पन्न के संबंध में लेना  दोनों तरफ और डीई/डीएक्स के लिए हल करना:
दोनों तरफ और डीई/डीएक्स के लिए हल करना:

बाईं तरफ:
 पायथागॉरियन पहचान का उपयोग करना
पायथागॉरियन पहचान का उपयोग करना
दाईं ओर:

इसलिए,

स्थानापन्न  ऊपर से, हम प्राप्त करते हैं
ऊपर से, हम प्राप्त करते हैं


प्रतिलोम कोटिस्पर्श फलन में अंतर करना
हम जाने

कहाँ  . तब
. तब

व्युत्पन्न के संबंध में लेना  दोनों तरफ और डीई/डीएक्स के लिए हल करना:
दोनों तरफ और डीई/डीएक्स के लिए हल करना:

बाईं तरफ:
 पायथागॉरियन पहचान का उपयोग करना
पायथागॉरियन पहचान का उपयोग करना
दाईं ओर:

इसलिए,

स्थानापन्न  ,
,


वैकल्पिक रूप से, के व्युत्पन्न के रूप में  जैसा कि ऊपर दिखाया गया है, फिर पहचान का उपयोग करके व्युत्पन्न किया गया है
जैसा कि ऊपर दिखाया गया है, फिर पहचान का उपयोग करके व्युत्पन्न किया गया है  उसका तुरंत पालन करता है
उसका तुरंत पालन करता है

प्रतिलोम छेदक फलन में अंतर करना
अंतर्निहित विभेदन का उपयोग करना
होने देना

तब
![{\displaystyle x=\sec y\mid \ y\in \left[0,{\frac {\pi }{2}}\right)\cup \left({\frac {\pi }{2}},\pi \right]}](/index.php?title=Special:MathShowImage&hash=6837f27c6ded7ea86cf61108dc195276&mode=mathml)

(अभिव्यक्ति में निरपेक्ष मान आवश्यक है क्योंकि y के अंतराल में छेदक और स्पर्शरेखा का गुणनफल सदैव गैर-ऋणात्मक होता है, जबकि मूलांक  मुख्य वर्गमूल की परिभाषा के अनुसार सदैव गैर-नकारात्मक होता है, इसलिए शेष गुणक भी गैर-ऋणात्मक होना चाहिए, जिसे x के निरपेक्ष मान का उपयोग करके प्राप्त किया जाता है।)
मुख्य वर्गमूल की परिभाषा के अनुसार सदैव गैर-नकारात्मक होता है, इसलिए शेष गुणक भी गैर-ऋणात्मक होना चाहिए, जिसे x के निरपेक्ष मान का उपयोग करके प्राप्त किया जाता है।)

शृंखला नियम का उपयोग करना
वैकल्पिक रूप से, चापसेकेंट का व्युत्पन्न श्रृंखला नियम का उपयोग करके आर्ककोसाइन के व्युत्पन्न से प्राप्त किया जा सकता है।
होने देना

कहाँ
 और
और ![{\displaystyle y\in \left[0,{\frac {\pi }{2}}\right)\cup \left({\frac {\pi }{2}},\pi \right]}](/index.php?title=Special:MathShowImage&hash=1165087dee67405c9eda3fb48e7f1199&mode=mathml)
फिर, चेन नियम को प्रयुक्त करना  :
:

प्रतिलोम व्युत्क्रमज्या फलन में अंतर करना
अंतर्निहित विभेदन का उपयोग करना
होने देना

तब
![{\displaystyle x=\csc y\ \mid \ y\in \left[-{\frac {\pi }{2}},0\right)\cup \left(0,{\frac {\pi }{2}}\right]}](/index.php?title=Special:MathShowImage&hash=1ceced66968453312f098771f63a1a25&mode=mathml)

(व्यंजक में निरपेक्ष मान आवश्यक है क्योंकि y के अंतराल में व्युत्क्रमज्या और स्पर्शरेखा का गुणनफल सदैव गैर-नकारात्मक होता है, जबकि रेडिकल  मुख्य वर्गमूल की परिभाषा के अनुसार सदैव गैर-नकारात्मक होता है, इसलिए शेष गुणक भी गैर-ऋणात्मक होना चाहिए, जिसे x के निरपेक्ष मान का उपयोग करके प्राप्त किया जाता है।)
मुख्य वर्गमूल की परिभाषा के अनुसार सदैव गैर-नकारात्मक होता है, इसलिए शेष गुणक भी गैर-ऋणात्मक होना चाहिए, जिसे x के निरपेक्ष मान का उपयोग करके प्राप्त किया जाता है।)

शृंखला नियम का उपयोग करना
वैकल्पिक रूप से, चापकोसेकेंट का व्युत्पन्न श्रृंखला नियम का उपयोग करके आर्कसीन के व्युत्पन्न से प्राप्त किया जा सकता है।
होने देना

कहाँ
 और
और ![{\displaystyle y\in \left[-{\frac {\pi }{2}},0\right)\cup \left(0,{\frac {\pi }{2}}\right]}](/index.php?title=Special:MathShowImage&hash=e9af644a6253e4ceca8d081478dd764b&mode=mathml)
फिर, चेन नियम को प्रयुक्त करना  :
:

यह भी देखें
- गणना
- यौगिक
- विभेदन नियम
- जनरल लीबनिज नियम
- व्युत्क्रम कार्य और विभेदन
- भिन्नता की रैखिकता
- प्रतिलोम त्रिकोणमितीय फलनों के समाकलों की सूची
- त्रिकोणमितीय सर्वसमिकाओं की सूची
- व्युत्पन्न तालिका
- त्रिकोणमिति
संदर्भ
ग्रन्थसूची