अणु कक्षीय सिद्धांत

रसायन विज्ञान में, अणु कक्षीय सिद्धांत (एमओ सिद्धांत या एमओटी) क्वांटम यांत्रिकी का उपयोग करके अणुओं की इलेक्ट्रॉनिक संरचना का वर्णन करने की एक विधि है। यह 20वीं शताब्दी के प्रारंभ में प्रस्तावित किया गया था।

आणविक कक्षीय सिद्धांत में, एक अणु में इलेक्ट्रॉनों को परमाणुओं के बीच अलग-अलग रासायनिक बंधनों को नहीं सौंपा जाता है, लेकिन पूरे अणु में परमाणु नाभिक के प्रभाव में चलने के लिए माना जाता है। क्वांटम यांत्रिकी इलेक्ट्रॉनों के स्थानिक और ऊर्जावान गुणों का वर्णन आणविक कक्षाओं के रूप में करती है जो एक अणु में दो या दो से अधिक परमाणुओं को घेरते हैं और परमाणुओं के बीच रासायनिक संयोजन इलेक्ट्रॉन होते हैं।

आणविक कक्षीय सिद्धांत ने परमाणु कक्षाओं (एलसीओ) के रैखिक संयोजन के रूप में बंधुआ इलेक्ट्रॉनों-आणविक कक्षाओं के स्थिति को अनुमानित करके रासायनिक बंधन के अध्ययन में क्रांतिकारी बदलाव किया। श्रोडिंगर समीकरण में घनत्व कार्यात्मक सिद्धांत (डीएफटी) या हार्ट्री-फॉक (एचएफ) मॉडल को प्रयुक्त करके ये अनुमान लगाए गए हैं।

आणविक कक्षीय सिद्धांत और संयोजकता आबंध सिद्धांत क्वांटम रसायन विज्ञान के मूलभूत सिद्धांत हैं।

परमाणु कक्षाओं (LCAO) विधि का रैखिक संयोजन

एलसीएओ पद्धति में, प्रत्येक अणु में आणविक कक्षाओं का एक समूह होता है। यह माना जाता है कि आण्विक कक्षीय तरंग फलन ψ_j को निम्न समीकरण के अनुसार n घटक परमाणु कक्षकों χ_i के सरल भारित योग के रूप में लिखा जा सकता है:

$$\psi _{j}=\sum _{i=1}^{n}c_{ij}\chi _{i}.$$

श्रोडिंगर समीकरण में इस समीकरण को प्रतिस्थापित करके और परिवर्तनशील सिद्धांत को प्रयुक्त करके कोई भी c_ij गुणांकों को संख्यात्मक रूप से निर्धारित कर सकता है। परिवर्तनशील सिद्धांत एक गणितीय तकनीक है जिसका उपयोग क्वांटम यांत्रिकी में प्रत्येक परमाणु कक्षीय आधार के गुणांकों के निर्माण के लिए किया जाता है। एक बड़े गुणांक का मतलब है कि कक्षीय आधार उस विशेष योगदान देने वाले परमाणु कक्षीय से अधिक बना है- इसलिए, आणविक कक्षीय उस प्रकार की सबसे अच्छी विशेषता है। परमाणु कक्षकों के एक रैखिक संयोजन के रूप में कक्षीय योगदान की मात्रा निर्धारित करने की इस पद्धति का उपयोग कम्प्यूटेशनल रसायन विज्ञान में किया जाता है। कुछ कम्प्यूटेशनल योजनाओं में अभिसरण में तेजी लाने के लिए पद्धति पर एक अतिरिक्त एकात्मक परिवर्तन प्रयुक्त किया जा सकता है। 1930 के दशक में आणविक कक्षीय सिद्धांत को संयोजकता आबंध सिद्धांत के एक प्रतियोगी के रूप में देखा गया था, इससे पहले कि यह महसूस किया गया कि दो विधियां निकटता से संबंधित हैं और जब विस्तारित होती हैं तो वे समकक्ष हो जाती हैं।

अनुमानित आणविक कक्षकों के रूप में उपयुक्त होने के लिए परमाणु कक्षीय संयोजनों के लिए तीन मुख्य आवश्यकताएं हैं।

1. परमाणु कक्षीय संयोजन में सही समरूपता होनी चाहिए, जिसका अर्थ है कि यह आणविक समरूपता के सही अलघुकरणीय प्रतिनिधित्व से संबंधित होना चाहिए। परमाणु कक्षाओं , या SALCs के रैखिक संयोजन का उपयोग करके, सही समरूपता के आणविक कक्षाओं का निर्माण किया जा सकता है।
2. अंतरिक्ष के भीतर परमाणु कक्षाओं को भी अधिव्यापन करना चाहिए। यदि वे एक दूसरे से बहुत दूर हैं तो वे आणविक कक्षा बनाने के लिए गठबंधन नहीं कर सकते हैं।
3. परमाणु कक्षाओं को आणविक कक्षाओं के रूप में संयोजित करने के लिए समान ऊर्जा स्तरों पर होना चाहिए।

इतिहास

मुख्य रूप से फ्रेडरिक हंड, रॉबर्ट मुल्लिकेन, जॉन सी. स्लेटर और जॉन लेनार्ड-जोन्स के प्रयासों के माध्यम से वैलेंस बांड सिद्धांत की स्थापना (1927) के बाद आणविक कक्षीय सिद्धांत विकसित किया गया था। एमओ सिद्धांत को मूल रूप से हंड-मुल्लिकेन सिद्धांत कहा जाता था। भौतिक विज्ञानी और भौतिक रसायनज्ञ एरिच हुकेल के अनुसार, आणविक कक्षीय सिद्धांत का पहला मात्रात्मक उपयोग जॉन लेनार्ड-जोन्स | लेनार्ड-जोन्स का 1929 का लेख्य था। इस लेख्य ने डाइऑक्सीजन अणु के लिए एक त्रिक अवस्था निम्नतम अवस्था की भविष्यवाणी की जिसने इसके अनुचुम्बकत्व की व्याख्या की (देखना अणु कक्षीय आरेख § डाइऑक्सीजन) संयोजकता आबंध सिद्धांत से पहले, जो 1931 में अपनी व्याख्या के साथ आया था। कक्षीय शब्द 1932 में मुल्लिकेन द्वारा पेश किया गया था।1933 तक, आणविक कक्षीय सिद्धांत को एक मान्य और उपयोगी सिद्धांत के रूप में स्वीकार कर लिया गया था।

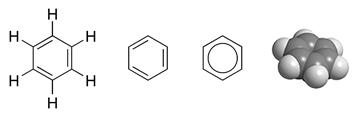
Erich Hückel ने 1931 में अपने Hückel method आणविक कक्षीय (एचएमओ) विधि के साथ असंतृप्त हाइड्रोकार्बन अणुओं के लिए आणविक कक्षीय सिद्धांत प्रयुक्त किया, जो कि पाई इलेक्ट्रॉन के लिए एमओ ऊर्जा के निर्धारण के लिए था, जिसे उन्होंने संयुग्मित और सुगंधित हाइड्रोकार्बन पर प्रयुक्त किया था। इस पद्धति ने बेंजीन जैसे छह पाई-इलेक्ट्रॉनों के साथ अणुओं की स्थिरता की व्याख्या प्रदान की थी।

आणविक कक्षीय तरंग की पहली सटीक गणना 1938 में चार्ल्स कूलसन द्वारा हाइड्रोजन अणु पर की गई थी। 1950 तक, आणविक कक्षाओं को पूरी तरह से स्व-सुसंगत क्षेत्र हैमिल्टनियन (क्वांटम यांत्रिकी) के ईजेनफलन (वेव फलन) के रूप में परिभाषित किया गया था और यह इस बिंदु पर था कि आणविक कक्षीय सिद्धांत पूरी तरह से कठोर और सुसंगत हो गया। इस कठोर दृष्टिकोण को अणुओं के लिए हार्ट्री-फॉक विधि के रूप में जाना जाता है, हालांकि इसकी उत्पत्ति परमाणुओं पर गणना में हुई थी। अणुओं पर गणना में, आणविक कक्षाओं को एक परमाणु कक्षीय आधार सेट (रसायन विज्ञान) के संदर्भ में विस्तारित किया जाता है, जिससे रूथान समीकरण बनते हैं। इससे कई आरंभिक क्वांटम रसायन विधियों का विकास हुआ। समानांतर में, आणविक कक्षीय सिद्धांत को कुछ अनुभवजन्य रूप से व्युत्पन्न मापदंडों का उपयोग करके अधिक अनुमानित तरीके से प्रयुक्त किया गया था, जिसे अब अर्ध-अनुभवजन्य क्वांटम रसायन विज्ञान विधियों के रूप में जाना जाता है।

आणविक कक्षीय सिद्धांत की सफलता ने लिगेंड क्षेत्र सिद्धांत को भी जन्म दिया, जिसे 1930 और 1940 के दशक के दौरान क्रिस्टल क्षेत्र सिद्धांत के विकल्प के रूप में विकसित किया गया था।

कक्षकों के प्रकार

H के आणविक कक्षकों के निर्माण को दर्शाने वाला MO आरेख₂ (केंद्र) दो H परमाणुओं के परमाणु कक्षाओं से। निम्न-ऊर्जा MO दो H नाभिकों के बीच केंद्रित इलेक्ट्रॉन घनत्व के साथ बंध रहा है। उच्च-ऊर्जा MO प्रत्येक इंच नाभिक के पीछे केंद्रित इलेक्ट्रॉन घनत्व के साथ प्रति-बंधक है।

आणविक कक्षीय (एमओ) सिद्धांत परमाणुओं के बीच बंधन से उत्पन्न आणविक कक्षाओं का प्रतिनिधित्व करने के लिए परमाणु कक्षाओं (एलसीएओ) के रैखिक संयोजन का उपयोग करता है। इन्हें प्रायः तीन प्रकारों में विभाजित किया जाता है, बॉन्डिंग, एंटीबांडिंग और नॉन-बॉन्डिंग। एक बॉन्डिंग ऑर्बिटल परमाणुओं की एक जोड़ी के बीच क्षेत्र में इलेक्ट्रॉन घनत्व को केंद्रित करता है, ताकि इसका इलेक्ट्रॉन घनत्व दो नाभिकों में से प्रत्येक को दूसरे की ओर आकर्षित करे और दोनों परमाणुओं को एक साथ जोड़े रखे। एक प्रति-बंधक कक्षीय प्रत्येक नाभिक के पीछे इलेक्ट्रॉन घनत्व को केंद्रित करता है (अर्थात प्रत्येक परमाणु की तरफ जो दूसरे परमाणु से सबसे दूर होता है), और इसलिए दो नाभिकों में से प्रत्येक को दूसरे से दूर खींचता है और वास्तव में दोनों के बीच के बंधन को कमजोर करता है। नॉन-बॉन्डिंग ऑर्बिटल्स में इलेक्ट्रॉन परमाणु ऑर्बिटल्स से जुड़े होते हैं जो एक दूसरे के साथ सकारात्मक या नकारात्मक रूप से इंटरैक्ट नहीं करते हैं, और इन ऑर्बिटल्स में इलेक्ट्रॉन न तो बॉन्ड स्ट्रेंथ में योगदान करते हैं और न ही इससे अलग होते हैं।

आणविक कक्षाओं को उन परमाणु कक्षाओं के प्रकार के अनुसार विभाजित किया जाता है जिनसे वे बनते हैं। यदि रासायनिक पदार्थ एक-दूसरे के साथ परस्पर क्रिया करते हैं, तो उनके कक्षाओं ऊर्जा में कम हो जाते हैं, तो वे बंधन बनाते हैं। अलग-अलग बंधन कक्षाओं को प्रतिष्ठित किया जाता है जो ऋणावेशित सूक्ष्म अणु का विन्यास (इलेक्ट्रॉन अभ्र आकार) और ऊर्जा स्तरों से भिन्न होते हैं।

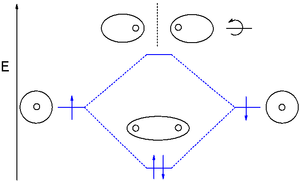
अणु के आणविक कक्षकों को आणविक कक्षीय आरेखों में चित्रित किया जा सकता है।

सामान्य बंधन ऑर्बिटल्स सिग्मा (σ) ऑर्बिटल्स हैं जो बांड अक्ष के बारे में सममित हैं, और या पीआई (Π) ऑर्बिटल्स बांड अक्ष के साथ एक नोडल सतह के साथ हैं। बांड अक्ष के साथ क्रमशः दो और तीन नोडल विमानों के साथ डेल्टा (δ) ऑर्बिटल्स और फाई (φ) ऑर्बिटल्स कम हैं। एंटीबाइंडिंग ऑर्बिटल्स को एक तारक के जोड़ के द्वारा दर्शाया गया है। उदाहरण के लिए, एक प्रतिरक्षी पाई कक्षक को π* के रूप में दिखाया जा सकता है

अवलोकन

एमओटी रासायनिक आबंधन पर एक वैश्विक, स्थानीयकृत दृष्टिकोण प्रदान करता है। एमओ सिद्धांत में, अणु में कोई भी इलेक्ट्रॉन अणु में कहीं भी पाया जा सकता है, क्योंकि क्वांटम स्थितियां इलेक्ट्रॉनों को एक मनमाने ढंग से बड़ी संख्या में नाभिक के प्रभाव में यात्रा करने की अनुमति देती हैं, जब तक कि वे कुछ क्वांटम नियमों द्वारा अनुमत आइजेनस्टेट्स में हैं। इस प्रकार, जब उच्च-आवृत्ति वाले प्रकाश या अन्य साधनों के माध्यम से आवश्यक मात्रा में ऊर्जा से उत्साहित होते हैं, तो इलेक्ट्रॉन उच्च-ऊर्जा आणविक कक्षा में संक्रमण कर सकते हैं। उदाहरण के लिए, हाइड्रोजन डायटोमिक अणु के साधारण मामले में, यूवी विकिरण के तहत बॉन्डिंग ऑर्बिटल से एंटीबॉन्डिंग ऑर्बिटल में एक इलेक्ट्रॉन का प्रचार हो सकता है। यह पदोन्नति दो हाइड्रोजन परमाणुओं के बीच के बंधन को कमजोर करती है और प्रकाश के अवशोषण के कारण एक रासायनिक बंधन को तोड़ते हुए फोटोडिसोसिएशन का कारण बन सकती है।

आणविक कक्षीय सिद्धांत का उपयोग पराबैंगनी-दृश्य स्पेक्ट्रोस्कोपी (यूवी-विज़) की व्याख्या के लिए किया जाता है। अणुओं की इलेक्ट्रॉनिक संरचना में परिवर्तन को विशिष्ट तरंग दैर्ध्य पर प्रकाश के अवशोषण से देखा जा सकता है। निम्न ऊर्जा वाले एक कक्षीय से उच्च ऊर्जा वाले कक्षक में जाने वाले इलेक्ट्रॉनों के संक्रमण द्वारा दर्शाए गए इन संकेतों के लिए असाइनमेंट किए जा सकते हैं। अंतिम स्थिति के लिए आणविक कक्षीय आरेख एक उत्तेजित अवस्था में अणु की इलेक्ट्रॉनिक प्रकृति का वर्णन करता है।

यद्यपि एमओ सिद्धांत में कुछ आणविक ऑर्बिटल्स इलेक्ट्रॉनों को धारण कर सकते हैं जो आणविक परमाणुओं के विशिष्ट जोड़े के बीच अधिक स्थानीय होते हैं, अन्य ऑर्बिटल्स इलेक्ट्रॉनों को पकड़ सकते हैं जो अणु पर अधिक समान रूप से फैले हुए हैं। इस प्रकार, कुल मिलाकर, बॉन्डिंग एमओ सिद्धांत में कहीं अधिक स्पष्ट है, जो इसे गुंजयमान अणुओं के लिए अधिक प्रयुक्त करता है, जिनके पास वैलेंस बॉन्ड (वीबी) सिद्धांत की तुलना में गैर-पूर्णांक बॉन्ड ऑर्डर हैं। यह विस्तारित प्रणालियों के वर्णन के लिए एमओ सिद्धांत को अधिक उपयोगी बनाता है।

रॉबर्ट एस मुल्लिकेन, जिन्होंने आणविक कक्षीय सिद्धांत के आगमन में सक्रिय रूप से भाग लिया, प्रत्येक अणु को एक आत्मनिर्भर इकाई मानते हैं। वह अपने लेख में दावा करता है:

...अणु को विशिष्ट परमाणु या आयनिक इकाइयों के रूप में मानने के प्रयासों को बंधन इलेक्ट्रॉनों या इलेक्ट्रॉन-जोड़ों की असतत संख्या द्वारा एक साथ रखा जाता है, विशेष मामलों में सन्निकटन के अलावा, या गणना की एक विधि के रूप में, अधिक या कम अर्थहीन माना जाता है। यहां एक अणु को नाभिकों का एक समूह माना जाता है, जिनमें से प्रत्येक के चारों ओर एक बाहरी क्षेत्र में एक मुक्त परमाणु के समान एक इलेक्ट्रॉन विन्यास को समूहीकृत किया जाता है, सिवाय इसके कि प्रत्येक नाभिक के आसपास के इलेक्ट्रॉन विन्यास के बाहरी हिस्से आमतौर पर भाग में होते हैं। संयुक्त रूप से दो या अधिक नाभिकों के लिए .....

एक उदाहरण बेंजीन, C₆H₆ का एमओ विवरण है, जो छह कार्बन परमाणुओं और तीन दोहरे बंधनों का एक सुगंधित हेक्सागोनल वलय है। इस अणु में, 30 कुल वैलेंस बॉन्डिंग इलेक्ट्रॉनों में से 24 - कार्बन परमाणुओं से आने वाले 24 और हाइड्रोजन परमाणुओं से आने वाले 6 - 12 σ (सिग्मा) बॉन्डिंग ऑर्बिटल्स में स्थित होते हैं, जो ज्यादातर परमाणुओं के जोड़े (CC या C-H) के बीच स्थित होते हैं। वैलेंस बॉन्ड विवरण में इलेक्ट्रॉनों के समान। हालांकि, बेंजीन में शेष छह बॉन्डिंग इलेक्ट्रॉन तीन π (पीआई/pi) आणविक बॉन्डिंग ऑर्बिटल्स में स्थित होते हैं जो कि रिंग के चारों ओर डेलोकलाइज्ड होते हैं। इनमें से दो इलेक्ट्रॉन एक एमओ में हैं जिसका सभी छह परमाणुओं से समान कक्षीय योगदान है। अन्य चार इलेक्ट्रॉन एक दूसरे से समकोण पर लंबवत नोड्स वाले ऑर्बिटल्स में हैं। जैसा कि वीबी सिद्धांत में है, ये सभी छह डेलोकलाइज़्ड π इलेक्ट्रॉन एक बड़े स्थान में रहते हैं जो रिंग प्लेन के ऊपर और नीचे उपस्थित होता है। बेंजीन में सभी कार्बन-कार्बन बांड रासायनिक रूप से समतुल्य हैं। एमओ सिद्धांत में यह इस तथ्य का प्रत्यक्ष परिणाम है कि तीन आणविक π ऑर्बिटल्स छह कार्बन परमाणुओं पर अतिरिक्त छह इलेक्ट्रॉनों को जोड़ते हैं और समान रूप से फैलाते हैं।

मीथेन और CH
₄ जैसे अणुओं में, आठ वैलेंस इलेक्ट्रॉन चार एमओ में पाए जाते हैं जो सभी पांच परमाणुओं में फैले हुए हैं। MOs को चार स्थानीयकृत sp3 कक्षकों में बदलना संभव है। लाइनस पॉलिंग ने 1931 में कार्बन 2s और 2p ऑर्बिटल्स को संकरणित किया ताकि वे सीधे हाइड्रोजन 1s आधार कार्यों की ओर संकेत करें और अधिकतम ओवरलैप को प्रदर्शित करें। हालांकि, आयनीकरण ऊर्जा और वर्णक्रमीय अवशोषण बैंड की स्थिति की भविष्यवाणी करने के लिए डेलोकलाइज्ड एमओ विवरण अधिक उपयुक्त है। जब मीथेन को आयनित किया जाता है, तो वैलेंस एमओ से एक एकल इलेक्ट्रॉन लिया जाता है, जो एस बॉन्डिंग या ट्रिपल डीजनरेट पी बॉन्डिंग स्तरों से आ सकता है, जिससे दो आयनीकरण ऊर्जा उत्पन्न होती है। इसकी तुलना में, वैलेंस बॉन्ड थ्योरी में स्पष्टीकरण अधिक जटिल है। जब एक इलेक्ट्रॉन को एक sp³ ऑर्बिटल से हटा दिया जाता है, तो चार वैलेंस बॉन्ड संरचनाओं के बीच प्रतिध्वनि उत्पन्न होती है, जिनमें से प्रत्येक में एक एकल-इलेक्ट्रॉन बॉन्ड और तीन दो-इलेक्ट्रॉन बॉन्ड होते हैं। इन चार संरचनाओं के विभिन्न रैखिक संयोजनों से त्रिगुणित पतित T₂ और A₁ आयनित अवस्थाएँ (CH₄⁺) उत्पन्न होती हैं। आयनित और जमीनी अवस्था के बीच ऊर्जा का अंतर दो आयनीकरण ऊर्जा देता है।

बेंजीन की तरह, बीटा कैरोटीन, क्लोरोफिल, या हीम जैसे पदार्थों में, π ऑर्बिटल्स में कुछ इलेक्ट्रॉन एक अणु में लंबी दूरी पर आणविक ऑर्बिटल्स में फैले होते हैं, जिसके परिणामस्वरूप कम ऊर्जा (दृश्य स्पेक्ट्रम) में प्रकाश अवशोषण होता है। जो इन पदार्थों के चारित्रिक रंगों को दर्शाता है। यह और अणुओं के लिए अन्य स्पेक्ट्रोस्कोपिक डेटा को एमओ सिद्धांत में अच्छी तरह से समझाया गया है, जिसमें बहुकेंद्रीय कक्षाओं से जुड़े इलेक्ट्रॉनिक राज्यों पर जोर दिया गया है, जिसमें कक्षीय समरूपता मिलान के सिद्धांतों पर आधारित कक्षाओं का मिश्रण भी सम्मिलित है। वही एमओ सिद्धांत भी स्वाभाविक रूप से कुछ विद्युत घटनाओं की व्याख्या करते हैं, जैसे ग्रेफाइट में उपस्थित हेक्सागोनल परमाणु शीट्स की प्लेनर दिशा में उच्च विद्युत चालकता है। यह आधे भरे पी ऑर्बिटल्स के निरंतर बैंड ओवरलैप का परिणाम है और विद्युत चालन की व्याख्या करता है। एमओ सिद्धांत मानता है कि ग्रेफाइट परमाणु शीट में कुछ इलेक्ट्रॉन मनमानी दूरी पर पूरी तरह से विभाजित होते हैं और बहुत बड़े आणविक ऑर्बिटल्स में रहते हैं जो पूरे ग्रेफाइट शीट को कवर करते हैं, और कुछ इलेक्ट्रॉन इस प्रकार स्वतंत्र रूप से स्थानांतरित होते हैं और इसलिए शीट प्लेन में बिजली का संचालन करते हैं जैसे कि वे एक धातु में रहते थे।

यह भी देखें

• सीआईएस प्रभाव
• कॉन्फ़िगरेशन इंटरैक्शन
• युग्मित क्लस्टर
• सीमांत आणविक कक्षीय सिद्धांत
• लिगैंड क्षेत्र सिद्धांत (संक्रमण धातु परिसरों के लिए एमओ सिद्धांत)
• मोलर-प्लेसेट पर्टर्बेशन थ्योरी
• क्वांटम रसायन विज्ञान कंप्यूटर प्रोग्राम
• अर्ध-अनुभवजन्य क्वांटम रसायन पद्धति

बाहरी संबंध

• Molecular Orbital Theory - Purdue University
• Molecular Orbital Theory - Sparknotes
• Molecular Orbital Theory - Mark Bishop's Chemistry Site
• Introduction to MO Theory - Queen Mary, London University
• Molecular Orbital Theory - a related terms table
• An introduction to Molecular Group Theory - Oxford University