भौगोलिक समन्वय रूपांतरण: Difference between revisions
No edit summary |
No edit summary |
||
| Line 31: | Line 31: | ||
एक समन्वय प्रणाली रूपांतरण एक समन्वय प्रणाली से दूसरे में रूपांतरण है, दोनों समन्वय प्रणालियों के साथ एक ही भौगोलिक डेटा पर आधारित है। सामान्य रूपांतरण कार्यों में जियोडेटिक और पृथ्वी-केंद्रित, पृथ्वी-स्थिर ([[ECEF]]) निर्देशांक के बीच रूपांतरण और एक प्रकार के मानचित्र प्रक्षेपण से दूसरे में रूपांतरण शामिल हैं। | एक समन्वय प्रणाली रूपांतरण एक समन्वय प्रणाली से दूसरे में रूपांतरण है, दोनों समन्वय प्रणालियों के साथ एक ही भौगोलिक डेटा पर आधारित है। सामान्य रूपांतरण कार्यों में जियोडेटिक और पृथ्वी-केंद्रित, पृथ्वी-स्थिर ([[ECEF]]) निर्देशांक के बीच रूपांतरण और एक प्रकार के मानचित्र प्रक्षेपण से दूसरे में रूपांतरण शामिल हैं। | ||
'''<big><u>जियोडेटिक से ईसीईएफ निर्देशांक तक-</u></big>''' | |||
[[Image:Geodetic latitude and the length of Normal.svg|thumb|लंबाई PQ, जिसे | [[Image:Geodetic latitude and the length of Normal.svg|thumb|लंबाई PQ, जिसे प्रमुख ऊर्ध्वाधर त्रिज्या कहा जाता है। <math>N(\phi)</math>. IQ लंबाई <math>\, e^2 N(\phi) </math> के बराबर है। <math>R = (X,\, Y,\, Z)</math>.]]जिओडेटिक निर्देशांक (अक्षांश <math>\ \phi</math>, देशांतर <math>\ \lambda</math>, ऊंचाई <math>h</math>) निम्नलिखित समीकरण का उपयोग करके ईसीईएफ निर्देशांक में परिवर्तित किया जा सकता है:<ref name="gps-chap10">{{cite book|title=जीपीएस - सिद्धांत और व्यवहार|author1=B. Hofmann-Wellenhof |author2=H. Lichtenegger |author3=J. Collins |isbn=3-211-82839-7|page=282|others=Section 10.2.1|year=1997 }}</ref> | ||
: <math>\begin{align} | : <math>\begin{align} | ||
X & = \left( N(\phi) + h\right)\cos{\phi}\cos{\lambda} \\ | X & = \left( N(\phi) + h\right)\cos{\phi}\cos{\lambda} \\ | ||
| Line 40: | Line 40: | ||
& = \left( (1 - f)^2 N(\phi) + h\right)\sin{\phi} | & = \left( (1 - f)^2 N(\phi) + h\right)\sin{\phi} | ||
\end{align}</math> | \end{align}</math> | ||
जहाँ- | |||
: <math> | : <math> | ||
N(\phi) = \frac{a^2}{\sqrt{a^2 \cos^2 \phi + b^2 \sin^2 \phi }} | N(\phi) = \frac{a^2}{\sqrt{a^2 \cos^2 \phi + b^2 \sin^2 \phi }} | ||
= \frac{a}{\sqrt{1 - e^2\sin^2\phi}}, | = \frac{a}{\sqrt{1 - e^2\sin^2\phi}}, | ||
</math> | </math> | ||
और <math>a</math> और <math>b</math> क्रमशः विषुवतीय त्रिज्या (अर्ध-प्रमुख अक्ष) और ध्रुवीय त्रिज्या ([[अर्ध-लघु अक्ष]]) हैं। <math>e^2 = 1 - \frac{b^2}{a^2}</math> दीर्घवृत्ताभ की | और <math>a</math> और <math>b</math> क्रमशः विषुवतीय त्रिज्या (अर्ध-प्रमुख अक्ष) और ध्रुवीय त्रिज्या ([[अर्ध-लघु अक्ष]]) हैं। <math>e^2 = 1 - \frac{b^2}{a^2}</math> दीर्घवृत्ताभ की प्रथम संख्यात्मक उत्केन्द्रता का वर्ग है। <math>f = 1 - \frac{b}{a}</math> दीर्घवृत्ताभ का चपटा होना है। [[वक्रता की प्रमुख ऊर्ध्वाधर त्रिज्या]] <math>\, N(\phi) </math> दीर्घवृत्ताभ सामान्य के साथ सतह से Z-अक्ष की दूरी है। | ||
==== गुण ==== | ==== गुण ==== | ||
निम्नलिखित स्थिति देशांतर के लिए उसी प्रकार संचालित होती है। जैसे कि भूकेंद्रीय निर्देशांक प्रणाली में होती है: | |||
:<math>\frac{X}{\cos\lambda} - \frac{Y}{\sin\lambda} = 0.</math> | :<math>\frac{X}{\cos\lambda} - \frac{Y}{\sin\lambda} = 0.</math> | ||
और निम्नलिखित अक्षांश के लिए है: | और निम्नलिखित अक्षांश के लिए है: | ||
:<math>\frac{p}{\cos\phi} - \frac{Z}{\sin\phi} - e^2 N(\phi) = 0,</math> | :<math>\frac{p}{\cos\phi} - \frac{Z}{\sin\phi} - e^2 N(\phi) = 0,</math> | ||
जहाँ <math>p = \sqrt{X^2 + Y^2}</math> पैरामीटर के रूप में <math>h</math> में कमी करके समाप्त कर दिया जाता है। | |||
:<math>\frac{p}{\cos\phi} = N + h</math> | :<math>\frac{p}{\cos\phi} = N + h</math> | ||
और | और | ||
| Line 247: | Line 247: | ||
डेटम के जियोडेटिक कोऑर्डिनेट से ट्रांसफॉर्मेशन में हेल्मर्ट ट्रांसफॉर्म का उपयोग <math>A</math> डेटम के भूगर्भीय निर्देशांक के लिए <math>B</math> तीन-चरणीय प्रक्रिया के संदर्भ में होता है:<ref name=HelmertNZ>{{cite web|title=डेटम रूपांतरणों के लिए प्रयुक्त समीकरण|url=http://www.linz.govt.nz/geodetic/conversion-coordinates/geodetic-datum-conversion/datum-transformation-equations/index.aspx|publisher=Land Information New Zealand (LINZ)|access-date=5 March 2014}}</ref> | डेटम के जियोडेटिक कोऑर्डिनेट से ट्रांसफॉर्मेशन में हेल्मर्ट ट्रांसफॉर्म का उपयोग <math>A</math> डेटम के भूगर्भीय निर्देशांक के लिए <math>B</math> तीन-चरणीय प्रक्रिया के संदर्भ में होता है:<ref name=HelmertNZ>{{cite web|title=डेटम रूपांतरणों के लिए प्रयुक्त समीकरण|url=http://www.linz.govt.nz/geodetic/conversion-coordinates/geodetic-datum-conversion/datum-transformation-equations/index.aspx|publisher=Land Information New Zealand (LINZ)|access-date=5 March 2014}}</ref> | ||
# डेटम के लिए जियोडेटिक निर्देशांक से ईसीईएफ निर्देशांक में कनवर्ट करें <math>A</math> | # डेटम के लिए जियोडेटिक निर्देशांक से ईसीईएफ निर्देशांक में कनवर्ट करें <math>A</math> | ||
# उपयुक्त के साथ हेल्मर्ट ट्रांसफ़ॉर्म | # उपयुक्त के साथ हेल्मर्ट ट्रांसफ़ॉर्म संचालित करें <math>A\to B</math> डेटाम से बदलने के लिए, पैरामीटर बदलें <math>A</math> ईसीईएफ डेटाम के लिए समन्वय करता है <math>B</math> ईसीईएफ समन्वय करता है | ||
# डेटाम के लिए ईसीईएफ निर्देशांक से जियोडेटिक निर्देशांक में कनवर्ट करें <math>B</math> | # डेटाम के लिए ईसीईएफ निर्देशांक से जियोडेटिक निर्देशांक में कनवर्ट करें <math>B</math> | ||
ईसीईएफ एक्सवाईजेड वैक्टर के संदर्भ में, हेल्मर्ट ट्रांसफॉर्म का रूप है (स्थिति वेक्टर परिवर्तन सम्मेलन और बहुत छोटा रोटेशन कोण सरलीकरण)<ref name=HelmertNZ/> | ईसीईएफ एक्सवाईजेड वैक्टर के संदर्भ में, हेल्मर्ट ट्रांसफॉर्म का रूप है (स्थिति वेक्टर परिवर्तन सम्मेलन और बहुत छोटा रोटेशन कोण सरलीकरण)<ref name=HelmertNZ/> | ||
| Line 268: | Line 268: | ||
हेल्मर्ट रूपांतरण के घुमावों और अनुवादों के बीच युग्मन को समाप्त करने के लिए, रूपांतरण किए जा रहे निर्देशांकों के निकट घूर्णन का एक नया XYZ केंद्र देने के लिए तीन अतिरिक्त पैरामीटर पेश किए जा सकते हैं। इस दस-पैरामीटर मॉडल को मोलोडेंस्की-बडेकास रूपांतरण कहा जाता है और इसे अधिक बुनियादी मोलोडेंस्की रूपांतरण के साथ भ्रमित नहीं किया जाना चाहिए।{{r|OGP7_2|page1=133-134}} | हेल्मर्ट रूपांतरण के घुमावों और अनुवादों के बीच युग्मन को समाप्त करने के लिए, रूपांतरण किए जा रहे निर्देशांकों के निकट घूर्णन का एक नया XYZ केंद्र देने के लिए तीन अतिरिक्त पैरामीटर पेश किए जा सकते हैं। इस दस-पैरामीटर मॉडल को मोलोडेंस्की-बडेकास रूपांतरण कहा जाता है और इसे अधिक बुनियादी मोलोडेंस्की रूपांतरण के साथ भ्रमित नहीं किया जाना चाहिए।{{r|OGP7_2|page1=133-134}} | ||
हेल्मर्ट रूपांतरण की | हेल्मर्ट रूपांतरण की प्रकार, मोलोडेंस्की-बडेकास रूपांतरण का उपयोग करना तीन चरणों वाली प्रक्रिया है: | ||
# डेटम के लिए जियोडेटिक निर्देशांक से ईसीईएफ निर्देशांक में कनवर्ट करें <math>A</math> | # डेटम के लिए जियोडेटिक निर्देशांक से ईसीईएफ निर्देशांक में कनवर्ट करें <math>A</math> | ||
# उपयुक्त के साथ मोलोडेंस्की-बडेकास परिवर्तन | # उपयुक्त के साथ मोलोडेंस्की-बडेकास परिवर्तन संचालित करें <math>A\to B</math> डेटाम से बदलने के लिए, पैरामीटर बदलें <math>A</math> ईसीईएफ डेटाम के लिए समन्वय करता है <math>B</math> ईसीईएफ समन्वय करता है | ||
# डेटाम के लिए ईसीईएफ निर्देशांक से जियोडेटिक निर्देशांक में कनवर्ट करें <math>B</math> | # डेटाम के लिए ईसीईएफ निर्देशांक से जियोडेटिक निर्देशांक में कनवर्ट करें <math>B</math> | ||
परिवर्तन का रूप है<ref name=MB_NGA>{{cite web|title=मोलोडेंस्की-बडेका का (7+3) परिवर्तन|url=http://earth-info.nga.mil/GandG/coordsys/datums/molodensky.html|publisher=National Geospatial Intelligence Agency (NGA)|access-date=5 March 2014}}</ref> | परिवर्तन का रूप है<ref name=MB_NGA>{{cite web|title=मोलोडेंस्की-बडेका का (7+3) परिवर्तन|url=http://earth-info.nga.mil/GandG/coordsys/datums/molodensky.html|publisher=National Geospatial Intelligence Agency (NGA)|access-date=5 March 2014}}</ref> | ||
| Line 300: | Line 300: | ||
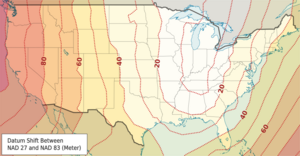
[[File:Datum Shift Between NAD27 and NAD83.png|thumb|स्थान के कार्य के रूप में NAD27 और NAD83 डेटम के बीच स्थिति में बदलाव का परिमाण।]]ग्रिड-आधारित ट्रांसफ़ॉर्मेशन सीधे मैप निर्देशांक को एक (मैप-प्रोजेक्शन, जियोडेटिक डेटाम) जोड़ी से दूसरे (मैप-प्रोजेक्शन, जियोडेटिक डेटाम) जोड़ी के मैप निर्देशांक में परिवर्तित करते हैं। एक उदाहरण उत्तरी अमेरिकी डेटम (एनएडी) 1927 से एनएडी 1983 डेटम में बदलने के लिए एनएडीकॉन विधि है।<ref name=ESRI_grid>{{cite web|title=ArcGIS सहायता 10.1: ग्रिड-आधारित विधियाँ|url=http://resources.arcgis.com/en/help/main/10.1/index.html#//003r00000013000000|publisher=ESRI|access-date=5 March 2014}</ref> हाई एक्यूरेसी रेफरेंस नेटवर्क (HARN), NADCON ट्रांसफॉर्म का एक उच्च सटीकता वाला संस्करण है, जिसकी सटीकता लगभग 5 सेंटीमीटर है। राष्ट्रीय परिवर्तन संस्करण 2 ([[NTv2]]) NAD 1927 और NAD 1983 के बीच रूपांतरण के लिए NADCON का एक कनाडाई संस्करण है। HARN को NAD 83/91 और उच्च परिशुद्धता ग्रिड नेटवर्क (HPGN) के रूप में भी जाना जाता है।<ref name=nadcon_harn>{{cite web|title=NADCON/HARN डेट शिफ्ट मेथड|url=http://www.bluemarblegeo.com/knowledgebase/geocalc/classdef/datumshift/datumshifts/nadcon.html|publisher=bluemarblegeo.com|access-date=5 March 2014}</ref> इसके बाद, ऑस्ट्रेलिया और न्यूज़ीलैंड ने अपने स्वयं के स्थानीय डेटा के बीच रूपांतरण के लिए ग्रिड-आधारित विधियाँ बनाने के लिए NTv2 प्रारूप को अपनाया। | [[File:Datum Shift Between NAD27 and NAD83.png|thumb|स्थान के कार्य के रूप में NAD27 और NAD83 डेटम के बीच स्थिति में बदलाव का परिमाण।]]ग्रिड-आधारित ट्रांसफ़ॉर्मेशन सीधे मैप निर्देशांक को एक (मैप-प्रोजेक्शन, जियोडेटिक डेटाम) जोड़ी से दूसरे (मैप-प्रोजेक्शन, जियोडेटिक डेटाम) जोड़ी के मैप निर्देशांक में परिवर्तित करते हैं। एक उदाहरण उत्तरी अमेरिकी डेटम (एनएडी) 1927 से एनएडी 1983 डेटम में बदलने के लिए एनएडीकॉन विधि है।<ref name=ESRI_grid>{{cite web|title=ArcGIS सहायता 10.1: ग्रिड-आधारित विधियाँ|url=http://resources.arcgis.com/en/help/main/10.1/index.html#//003r00000013000000|publisher=ESRI|access-date=5 March 2014}</ref> हाई एक्यूरेसी रेफरेंस नेटवर्क (HARN), NADCON ट्रांसफॉर्म का एक उच्च सटीकता वाला संस्करण है, जिसकी सटीकता लगभग 5 सेंटीमीटर है। राष्ट्रीय परिवर्तन संस्करण 2 ([[NTv2]]) NAD 1927 और NAD 1983 के बीच रूपांतरण के लिए NADCON का एक कनाडाई संस्करण है। HARN को NAD 83/91 और उच्च परिशुद्धता ग्रिड नेटवर्क (HPGN) के रूप में भी जाना जाता है।<ref name=nadcon_harn>{{cite web|title=NADCON/HARN डेट शिफ्ट मेथड|url=http://www.bluemarblegeo.com/knowledgebase/geocalc/classdef/datumshift/datumshifts/nadcon.html|publisher=bluemarblegeo.com|access-date=5 March 2014}</ref> इसके बाद, ऑस्ट्रेलिया और न्यूज़ीलैंड ने अपने स्वयं के स्थानीय डेटा के बीच रूपांतरण के लिए ग्रिड-आधारित विधियाँ बनाने के लिए NTv2 प्रारूप को अपनाया। | ||
एकाधिक प्रतिगमन समीकरण रूपांतरण की | एकाधिक प्रतिगमन समीकरण रूपांतरण की प्रकार, ग्रिड-आधारित विधियाँ मानचित्र निर्देशांकों को परिवर्तित करने के लिए एक निम्न-क्रम प्रक्षेप विधि का उपयोग करती हैं, लेकिन तीन के बजाय दो आयामों में। [[एनओएए]] एनएडीसीओएन ट्रांसफॉर्मेशन करने के लिए एक सॉफ्टवेयर टूल (एनजीएस जियोडेटिक टूलकिट के हिस्से के रूप में) प्रदान करता है।<ref name=NOAA_NADCON>{{cite web|title=नैडकॉन - संस्करण 4.2|url=http://www.ngs.noaa.gov/PC_PROD/NADCON/|publisher=NOAA|access-date=5 March 2014}}</ref><ref name=Mulcare>{{cite web|last=Mulcare |first=Donald M. |title=NGS Toolkit, Part 8: The National Geodetic Survey NADCON Tool |url=http://www.profsurv.com/magazine/article.aspx?i=1193 |publisher=Professional Surveyor Magazine |access-date=5 March 2014 |url-status=dead |archive-url=https://web.archive.org/web/20140306001134/http://www.profsurv.com/magazine/article.aspx?i=1193 |archive-date=6 March 2014 }}</ref> | ||
Revision as of 14:00, 26 April 2023
जियोडेसी में विश्व भर में और समय के साथ उपयोग में आने वाले विभिन्न भौगोलिक समन्वय प्रणालियों द्वारा विभिन्न भौगोलिक समन्वय प्रणालियों के बीच रूपांतरण को महत्वपूर्ण बनाया जाता है। निर्देशांक रूपांतरण कई विभिन्न प्रकार के रूपांतरणों से बना हुआ है। जो निम्न हैं- भौगोलिक निर्देशांकों का प्रारूप परिवर्तन, समन्वय प्रणालियों का रूपांतरण या विभिन्न भू-गणितीय डेटा में परिवर्तन। भौगोलिक समन्वय रूपांतरण में कार्टोग्राफी, सर्वेक्षण, मार्गदर्शन और भौगोलिक सूचना प्रणाली में अनेक अनुप्रयोग हैं।
जियोडेसी में भौगोलिक निर्देशांक रूपांतरण को विभिन्न प्रकार की समन्वय प्रारूपों या मानचित्र अनुमानों के बीच अनुवाद के रूप में परिभाषित किया जाता है। जो सभी एक ही जियोडेटिक डेटाम के संदर्भ में होते हैं।[1] भौगोलिक समन्वय परिवर्तन विभिन्न भौगोलिक आंकड़ों के बीच एक अनुवाद होता है। इस लेख में भौगोलिक समन्वय रूपांतरण और परिवर्तन दोनों पर विचार किया जाएगा।
यह लेख प्रदर्शित करता है कि पाठक पहले से ही लेखों की भौगोलिक समन्वय प्रणाली और जियोडेटिक डेटम की सामग्री से पूर्णतयः परिचित हैं।
इकाइयों और प्रारूप का परिवर्तन
अनौपचारिक रूप से भौगोलिक स्थान निर्दिष्ट करने का अर्थ सामान्यतः स्थान का अक्षांश और देशांतर को प्रदर्शित करना होता है। अक्षांश और देशांतर के लिए संख्यात्मक मान कई विभिन्न प्रकार की इकाइयों या स्वरूपों में हो सकते हैं:[2]
- सेक्सजेसिमल डिग्री: डिग्री (कोण), मिनट और सेकेण्ड: 40° 26' 46" N 79° 58' 56" W
- डिग्री और दशमलव मिनट: 40° 26.767′ N 79° 58.933′ W
- दशमलव डिग्री: +40.446 -79.982
एक डिग्री में 60 मिनट और एक मिनट में 60 सेकंड होते हैं। इसलिए डिग्री मिनट सेकेंड प्रारूप से दशमलव डिग्री प्रारूप में बदलने के लिए निम्नलिखित सूत्र का उपयोग किया जा सकता है।
- .
दशमलव डिग्री प्रारूप से डिग्री मिनट सेकेंड प्रारूप में वापस बदलने के लिए,
जहाँ और धनात्मक और श्रणात्मक दोनों मूल्यों को सही प्रकार से संभालने के लिए केवल अस्थायी चर हैं।
समन्वय प्रणाली रूपांतरण
एक समन्वय प्रणाली रूपांतरण एक समन्वय प्रणाली से दूसरे में रूपांतरण है, दोनों समन्वय प्रणालियों के साथ एक ही भौगोलिक डेटा पर आधारित है। सामान्य रूपांतरण कार्यों में जियोडेटिक और पृथ्वी-केंद्रित, पृथ्वी-स्थिर (ECEF) निर्देशांक के बीच रूपांतरण और एक प्रकार के मानचित्र प्रक्षेपण से दूसरे में रूपांतरण शामिल हैं।
जियोडेटिक से ईसीईएफ निर्देशांक तक-
जिओडेटिक निर्देशांक (अक्षांश , देशांतर , ऊंचाई ) निम्नलिखित समीकरण का उपयोग करके ईसीईएफ निर्देशांक में परिवर्तित किया जा सकता है:[3]
जहाँ-
और और क्रमशः विषुवतीय त्रिज्या (अर्ध-प्रमुख अक्ष) और ध्रुवीय त्रिज्या (अर्ध-लघु अक्ष) हैं। दीर्घवृत्ताभ की प्रथम संख्यात्मक उत्केन्द्रता का वर्ग है। दीर्घवृत्ताभ का चपटा होना है। वक्रता की प्रमुख ऊर्ध्वाधर त्रिज्या दीर्घवृत्ताभ सामान्य के साथ सतह से Z-अक्ष की दूरी है।
गुण
निम्नलिखित स्थिति देशांतर के लिए उसी प्रकार संचालित होती है। जैसे कि भूकेंद्रीय निर्देशांक प्रणाली में होती है:
और निम्नलिखित अक्षांश के लिए है:
जहाँ पैरामीटर के रूप में में कमी करके समाप्त कर दिया जाता है।
और
आगे:
ऑर्थोगोनलिटी
निर्देशांक के ऑर्थोगोनल निर्देशांक की पुष्टि भेदभाव के माध्यम से की जाती है:
कहाँ
(यह भी देखें मेरिडियन चाप # दीर्घवृत्त पर मेरिडियन दूरी)।
=== ईसीईएफ से जियोडेटिक निर्देशांक === तक
देशांतर के लिए ईसीईएफ निर्देशांक का रूपांतरण है:
- .
जहां atan2 चतुष्कोण-संकल्प चाप-स्पर्शरेखा फलन है। भूकेन्द्रीय देशांतर और भूगणितीय देशांतर का मान समान होता है; यह पृथ्वी और अन्य समान आकार के ग्रहों के लिए सच है क्योंकि उनके स्पिन अक्ष के चारों ओर बड़ी मात्रा में घूर्णी समरूपता है (सामान्यीकरण के लिए त्रिअक्षीय दीर्घवृत्ताकार देशांतर देखें)।
अक्षांश और ऊंचाई के रूपांतरण में N से जुड़ा एक गोलाकार संबंध शामिल है, जो अक्षांश का एक कार्य है:
- ,
- .
इसे पुनरावृत्त रूप से हल किया जा सकता है,[4][5] उदाहरण के लिए, पहले अनुमान h≈0 से शुरू करके N को अपडेट करना। अधिक विस्तृत तरीके नीचे दिखाए गए हैं। हालाँकि, प्रक्रिया छोटी सटीकता के प्रति संवेदनशील है और शायद 10 हो रहा है6 अलग।[6][7]
न्यूटन-रेफसन विधि
निम्नलिखित बॉरिंग का अपरिमेय भूगणितीय-अक्षांश समीकरण,[8] उपर्युक्त गुणों से व्युत्पन्न, न्यूटन-रफसन पुनरावृति विधि द्वारा हल करने के लिए कुशल है:[9][10]
कहाँ और पहले जैसा। ऊंचाई की गणना इस प्रकार की जाती है:
पुनरावृत्ति को निम्नलिखित गणना में बदला जा सकता है:
कहाँ अटल पुनरावृत्ति के लिए एक अच्छा स्टार्टर मान है जब . बॉरिंग ने दिखाया कि एकल पुनरावृति पर्याप्त सटीक समाधान उत्पन्न करती है। उन्होंने अपने मूल सूत्रीकरण में अतिरिक्त त्रिकोणमितीय कार्यों का उपयोग किया।
फेरारी का समाधान
का चतुर्थक समीकरण , ऊपर से व्युत्पन्न, क्वार्टिक समीकरण द्वारा हल किया जा सकता है#Ferrari.27s हल|फेरारी का हल[11][12] उपज:
फेरारी के समाधान का अनुप्रयोग
झू के अनुसार, कई तकनीकें और एल्गोरिदम उपलब्ध हैं लेकिन सबसे सटीक हैं,[13] Heikkinen द्वारा स्थापित निम्नलिखित प्रक्रिया है,[14] जैसा कि झू ने उद्धृत किया है। यह माना जाता है कि जियोडेटिक पैरामीटर ज्ञात हैं
नोट: atan2[Y, X] चार-चतुर्थांश व्युत्क्रम स्पर्शरेखा फलन है।
शक्ति श्रृंखला
छोटे के लिए e2 शक्ति श्रृंखला
इसके साथ आरंभ होता है
=== ईएनयू निर्देशांक === से/से जियोडेटिक
जियोडेटिक निर्देशांक से स्थानीय स्पर्शरेखा विमान में परिवर्तित करने के लिए (एक्सिस कन्वेंशन # ग्राउंड रेफरेंस फ्रेम: ईएनयू और एनईडी) निर्देशांक एक दो चरण की प्रक्रिया है:
- जियोडेटिक निर्देशांक को ईसीईएफ निर्देशांक में बदलें
- ईसीईएफ निर्देशांक को स्थानीय ईएनयू निर्देशांक में बदलें
==== ईसीईएफ से ईएनयू ==== तक
ईसीईएफ निर्देशांक से स्थानीय निर्देशांक में बदलने के लिए हमें स्थानीय संदर्भ बिंदु की आवश्यकता होती है। सामान्यतः, यह एक राडार का स्थान हो सकता है। यदि एक रडार स्थित है और एक विमान पर , तो ENU फ्रेम में रडार से विमान की ओर इशारा करने वाला वेक्टर है
टिप्पणी: भूगणितीय अक्षांश है; भूकेन्द्रिक अक्षांश स्थानीय स्पर्शरेखा तल के लिए ऊर्ध्वाधर दिशा का प्रतिनिधित्व करने के लिए अनुपयुक्त है और यदि आवश्यक हो तो भूकेन्द्रिक अक्षांश होना चाहिए।
ईएनयू से ईसीईएफ तक
यह ईसीईएफ से ईएनयू परिवर्तन का उलटा है
नक्शा अनुमानों में रूपांतरण
एक ही डेटा के संदर्भ में अलग-अलग मानचित्र अनुमानों के बीच निर्देशांक और मानचित्र स्थिति का रूपांतरण या तो एक प्रक्षेपण से दूसरे प्रक्षेपण में प्रत्यक्ष अनुवाद सूत्रों के माध्यम से या पहले प्रक्षेपण से परिवर्तित करके पूरा किया जा सकता है। एक मध्यवर्ती समन्वय प्रणाली, जैसे ईसीईएफ, फिर ईसीईएफ से प्रक्षेपण में परिवर्तित करना . इसमें शामिल सूत्र जटिल हो सकते हैं और कुछ मामलों में, जैसे ईसीईएफ में उपरोक्त जियोडेटिक रूपांतरण के लिए, रूपांतरण का कोई बंद-रूप समाधान नहीं है और अनुमानित विधियों का उपयोग किया जाना चाहिए। डीएमए तकनीकी मैनुअल 8358.1 जैसे संदर्भ[15] और यूएसजीएस पेपर मैप प्रोजेक्शंस: ए वर्किंग मैनुअल[16] मानचित्र अनुमानों के रूपांतरण के लिए सूत्र शामिल हैं। समन्वय रूपांतरण कार्यों को करने के लिए कंप्यूटर प्रोग्राम का उपयोग करना आम है, जैसे कि DoD और NGA समर्थित GEOTRANS प्रोग्राम के साथ।[17]
डेटा परिवर्तन
डेटाम के बीच रूपांतरण कई तरीकों से पूरा किया जा सकता है। ऐसे परिवर्तन हैं जो सीधे जियोडेटिक निर्देशांक को एक डेटा से दूसरे में परिवर्तित करते हैं। अधिक अप्रत्यक्ष रूपांतरण हैं जो जियोडेटिक निर्देशांक से ईसीईएफ निर्देशांक में परिवर्तित होते हैं, ईसीईएफ निर्देशांक को एक डेटाम से दूसरे में परिवर्तित करते हैं, फिर नए डेटा के ईसीईएफ निर्देशांक को वापस जियोडेटिक निर्देशांक में बदलते हैं। ग्रिड-आधारित परिवर्तन भी हैं जो सीधे एक (डेटाम, मैप प्रोजेक्शन) जोड़ी से दूसरे (डेटाम, मैप प्रोजेक्शन) जोड़ी में बदलते हैं।
हेल्मर्ट परिवर्तन
डेटम के जियोडेटिक कोऑर्डिनेट से ट्रांसफॉर्मेशन में हेल्मर्ट ट्रांसफॉर्म का उपयोग डेटम के भूगर्भीय निर्देशांक के लिए तीन-चरणीय प्रक्रिया के संदर्भ में होता है:[18]
- डेटम के लिए जियोडेटिक निर्देशांक से ईसीईएफ निर्देशांक में कनवर्ट करें
- उपयुक्त के साथ हेल्मर्ट ट्रांसफ़ॉर्म संचालित करें डेटाम से बदलने के लिए, पैरामीटर बदलें ईसीईएफ डेटाम के लिए समन्वय करता है ईसीईएफ समन्वय करता है
- डेटाम के लिए ईसीईएफ निर्देशांक से जियोडेटिक निर्देशांक में कनवर्ट करें
ईसीईएफ एक्सवाईजेड वैक्टर के संदर्भ में, हेल्मर्ट ट्रांसफॉर्म का रूप है (स्थिति वेक्टर परिवर्तन सम्मेलन और बहुत छोटा रोटेशन कोण सरलीकरण)[18]
हेल्मर्ट ट्रांस्फ़ॉर्म एक सात-पैरामीटर ट्रांसफ़ॉर्म है जिसमें तीन ट्रांसलेशन (शिफ्ट) पैरामीटर हैं , तीन रोटेशन पैरामीटर और एक स्केलिंग (फैलाव) पैरामीटर . हेल्मर्ट ट्रांसफ़ॉर्म एक अनुमानित तरीका है जो सटीक है जब ट्रांसफ़ॉर्म पैरामीटर ईसीईएफ़ वैक्टर के परिमाण के सापेक्ष छोटे होते हैं। इन शर्तों के तहत, परिवर्तन को प्रतिवर्ती माना जाता है।[19]
चौदह-पैरामीटर हेल्मर्ट रूपांतरण, प्रत्येक पैरामीटर के लिए रैखिक समय निर्भरता के साथ,[19]: 131-133 भू-आकृतिक प्रक्रियाओं, जैसे कि महाद्वीपीय बहाव, के भौगोलिक निर्देशांक बकाया के समय के विकास को पकड़ने के लिए इस्तेमाल किया जा सकता है[20] और भूकंप।[21] इसे सॉफ्टवेयर में शामिल किया गया है, जैसे यू.एस. एनजीएस से हॉरिजॉन्टल टाइम डिपेंडेंट पोजिशनिंग (एचटीडीपी) टूल। रेफरी नाम = एचटीडीपी>"एचटीडीपी - हॉरिजॉन्टल टाइम-डिपेंडेंट पोजिशनिंग". U.S. National Geodetic Survey (NGS). Retrieved 5 March 2014.</ref>
मोलोडेंस्की-बडेकास परिवर्तन
हेल्मर्ट रूपांतरण के घुमावों और अनुवादों के बीच युग्मन को समाप्त करने के लिए, रूपांतरण किए जा रहे निर्देशांकों के निकट घूर्णन का एक नया XYZ केंद्र देने के लिए तीन अतिरिक्त पैरामीटर पेश किए जा सकते हैं। इस दस-पैरामीटर मॉडल को मोलोडेंस्की-बडेकास रूपांतरण कहा जाता है और इसे अधिक बुनियादी मोलोडेंस्की रूपांतरण के साथ भ्रमित नहीं किया जाना चाहिए।[19]: 133-134
हेल्मर्ट रूपांतरण की प्रकार, मोलोडेंस्की-बडेकास रूपांतरण का उपयोग करना तीन चरणों वाली प्रक्रिया है:
- डेटम के लिए जियोडेटिक निर्देशांक से ईसीईएफ निर्देशांक में कनवर्ट करें
- उपयुक्त के साथ मोलोडेंस्की-बडेकास परिवर्तन संचालित करें डेटाम से बदलने के लिए, पैरामीटर बदलें ईसीईएफ डेटाम के लिए समन्वय करता है ईसीईएफ समन्वय करता है
- डेटाम के लिए ईसीईएफ निर्देशांक से जियोडेटिक निर्देशांक में कनवर्ट करें
परिवर्तन का रूप है[22]
कहाँ रोटेशन और स्केलिंग ट्रांसफॉर्म के लिए मूल है और स्केलिंग कारक है।
Molodensky-Badekas ट्रांस्फ़ॉर्म का उपयोग स्थानीय जियोडेटिक डेटा को वैश्विक जियोडेटिक डेटा में बदलने के लिए किया जाता है, जैसे कि WGS 84। हेल्मर्ट ट्रांसफ़ॉर्म के विपरीत, मोलोडेंस्की-बडेकास ट्रांसफ़ॉर्मेशन मूल डेटा के साथ घूर्णी मूल होने के कारण प्रतिवर्ती नहीं है।[19]: 134
मोलोडेंस्की परिवर्तन
मोलोडेंस्की परिवर्तन भूस्थैतिक निर्देशांक (ईसीईएफ) में परिवर्तित करने के मध्यवर्ती चरण के बिना सीधे विभिन्न डेटा के भूगर्भीय समन्वय प्रणालियों के बीच परिवर्तित होता है।[23] इसके लिए डेटम केंद्रों और संदर्भ दीर्घवृत्ताभ अर्ध-प्रमुख अक्षों और चपटे मापदंडों के बीच अंतर के बीच तीन पारियों की आवश्यकता होती है।
मोलोडेंस्की परिवर्तन का उपयोग राष्ट्रीय भू-स्थानिक-खुफिया एजेंसी (NGA) द्वारा उनके मानक TR8350.2 और NGA समर्थित GEOTRANS प्रोग्राम में किया जाता है।[24] मोलोडेंस्की पद्धति आधुनिक कंप्यूटरों के आगमन से पहले लोकप्रिय थी और यह विधि कई जियोडेटिक कार्यक्रमों का हिस्सा है।
ग्रिड-आधारित विधि
ग्रिड-आधारित ट्रांसफ़ॉर्मेशन सीधे मैप निर्देशांक को एक (मैप-प्रोजेक्शन, जियोडेटिक डेटाम) जोड़ी से दूसरे (मैप-प्रोजेक्शन, जियोडेटिक डेटाम) जोड़ी के मैप निर्देशांक में परिवर्तित करते हैं। एक उदाहरण उत्तरी अमेरिकी डेटम (एनएडी) 1927 से एनएडी 1983 डेटम में बदलने के लिए एनएडीकॉन विधि है।[25] हाई एक्यूरेसी रेफरेंस नेटवर्क (HARN), NADCON ट्रांसफॉर्म का एक उच्च सटीकता वाला संस्करण है, जिसकी सटीकता लगभग 5 सेंटीमीटर है। राष्ट्रीय परिवर्तन संस्करण 2 (NTv2) NAD 1927 और NAD 1983 के बीच रूपांतरण के लिए NADCON का एक कनाडाई संस्करण है। HARN को NAD 83/91 और उच्च परिशुद्धता ग्रिड नेटवर्क (HPGN) के रूप में भी जाना जाता है।[26] इसके बाद, ऑस्ट्रेलिया और न्यूज़ीलैंड ने अपने स्वयं के स्थानीय डेटा के बीच रूपांतरण के लिए ग्रिड-आधारित विधियाँ बनाने के लिए NTv2 प्रारूप को अपनाया।
एकाधिक प्रतिगमन समीकरण रूपांतरण की प्रकार, ग्रिड-आधारित विधियाँ मानचित्र निर्देशांकों को परिवर्तित करने के लिए एक निम्न-क्रम प्रक्षेप विधि का उपयोग करती हैं, लेकिन तीन के बजाय दो आयामों में। एनओएए एनएडीसीओएन ट्रांसफॉर्मेशन करने के लिए एक सॉफ्टवेयर टूल (एनजीएस जियोडेटिक टूलकिट के हिस्से के रूप में) प्रदान करता है।[27][28]
एकाधिक प्रतिगमन समीकरण
मानक मोलोडेंस्की परिवर्तनों की तुलना में छोटे भौगोलिक क्षेत्रों में उच्च सटीकता परिणाम प्राप्त करने के लिए अनुभवजन्य एकाधिक प्रतिगमन विधियों के उपयोग के माध्यम से डेटा परिवर्तन किए गए थे। MRE ट्रांस्फ़ॉर्म का उपयोग स्थानीय डेटा को महाद्वीप के आकार या छोटे क्षेत्रों में वैश्विक डेटा में बदलने के लिए किया जाता है, जैसे WGS 84।[29] मानक NIMA TM 8350.2, परिशिष्ट D,[30] लगभग 2 मीटर की सटीकता के साथ MRE को कई स्थानीय डेटा से WGS 84 में रूपांतरित करता है।[31]
एमआरई बिना किसी मध्यवर्ती ईसीईएफ कदम के जियोडेटिक निर्देशांक का प्रत्यक्ष परिवर्तन है। जियोडेटिक निर्देशांक नए डेटम में जियोडेटिक निर्देशांक में नौवीं डिग्री तक के बहुपदों के रूप में तैयार किए गए हैं मूल डेटा का . उदाहरण के लिए, में परिवर्तन के रूप में परिचालित किया जा सकता है (केवल द्विघात शब्दों तक दिखाया गया है)[29]: 9
कहाँ
- एकाधिक प्रतिगमन द्वारा फिट किए गए पैरामीटर
- पैमाने का कारक
- डेटा की उत्पत्ति,
के लिए समान समीकरणों के साथ और . पर्याप्त संख्या में दिया गया अच्छे आँकड़ों के लिए दोनों डेटा में स्थलों के लिए समन्वय जोड़े, इन बहुपदों के मापदंडों को फिट करने के लिए कई प्रतिगमन विधियों का उपयोग किया जाता है। बहुपद, फिट किए गए गुणांक के साथ, कई प्रतिगमन समीकरण बनाते हैं।
यह भी देखें
- गॉस-क्रुगर समन्वय प्रणाली
- नक्शा अनुमानों की सूची
- स्थानिक संदर्भ प्रणाली
- स्थलाकृतिक समन्वय प्रणाली
- यूनिवर्सल पोलर स्टीरियोग्राफिक कोऑर्डिनेट सिस्टम
- यूनिवर्सल ट्रांसवर्स मर्केटर समन्वय प्रणाली
संदर्भ
- ↑ Roger Foster; Dan Mullaney. "Basic Geodesy Article 018: Conversions and Transformations" (PDF). National Geospatial Intelligence Agency. Retrieved 4 March 2014.
- ↑ "समन्वय ट्रांसफार्मर". Ordnance Survey Great Britain. Retrieved 4 March 2014.
- ↑ B. Hofmann-Wellenhof; H. Lichtenegger; J. Collins (1997). जीपीएस - सिद्धांत और व्यवहार. Section 10.2.1. p. 282. ISBN 3-211-82839-7.
- ↑ A guide to coordinate systems in Great Britain. This is available as a pdf document at "ordnancesurvey.co.uk". Archived from the original on 2012-02-11. Retrieved 2012-01-11. Appendices B1, B2
- ↑ Osborne, P (2008). The Mercator Projections Archived 2012-01-18 at the Wayback Machine Section 5.4
- ↑ R. Burtch, A Comparison of Methods Used in Rectangular to Geodetic Coordinate Transformations.
- ↑ Featherstone, W. E.; Claessens, S. J. (2008). "जिओडेटिक और एलिपोसाइडल निर्देशांक के बीच क्लोज्ड-फॉर्म ट्रांसफॉर्मेशन". Stud. Geophys. Geod. 52 (1): 1–18. Bibcode:2008StGG...52....1F. doi:10.1007/s11200-008-0002-6. hdl:20.500.11937/11589. S2CID 59401014.
- ↑ Bowring, B. R. (1976). "स्थानिक से भौगोलिक निर्देशांक में परिवर्तन". Surv. Rev. 23 (181): 323–327. doi:10.1179/003962676791280626.
- ↑ Fukushima, T. (1999). "जियोसेंट्रिक से जियोडेटिक कोऑर्डिनेट में तेजी से रूपांतरण". J. Geod. 73 (11): 603–610. Bibcode:1999JGeod..73..603F. doi:10.1007/s001900050271. S2CID 121816294. (Appendix B)
- ↑ Sudano, J. J. (1997). "An exact conversion from an earth-centered coordinate system to latitude, longitude and altitude". Proceedings of the IEEE 1997 National Aerospace and Electronics Conference. NAECON 1997. Vol. 2. pp. 646–650. doi:10.1109/NAECON.1997.622711. ISBN 0-7803-3725-5. S2CID 111028929.
- ↑ Vermeille, H., H. (2002). "जियोसेंट्रिक से जियोडेटिक निर्देशांक में प्रत्यक्ष परिवर्तन". J. Geod. 76 (8): 451–454. doi:10.1007/s00190-002-0273-6. S2CID 120075409.
- ↑ Gonzalez-Vega, Laureano; PoloBlanco, Irene (2009). "A symbolic analysis of Vermeille and Borkowski polynomials for transforming 3D Cartesian to geodetic coordinates". J. Geod. 83 (11): 1071–1081. Bibcode:2009JGeod..83.1071G. doi:10.1007/s00190-009-0325-2. S2CID 120864969.
- ↑ Zhu, J. (1994). "पृथ्वी-केंद्रित पृथ्वी-स्थिर निर्देशांकों का भूगणितीय निर्देशांकों में रूपांतरण". IEEE Transactions on Aerospace and Electronic Systems. 30 (3): 957–961. Bibcode:1994ITAES..30..957Z. doi:10.1109/7.303772.
- ↑ Heikkinen, M. (1982). "Geschlossene formeln zur berechnung räumlicher geodätischer koordinaten aus rechtwinkligen koordinaten". Z. Vermess. (in Deutsch). 107: 207–211.
- ↑ "TM8358.2: The Universal Grids: Universal Transverse Mercator (UTM) and Universal Polar Stereographic (UPS)" (PDF). National Geospatial-Intelligence Agency. Retrieved 4 March 2014.
- ↑ Snyder, John P. (1987). Map Projections: A Working Manual. USGS Professional Paper: 1395.
- ↑ "MSP GEOTRANS 3.3 (भौगोलिक अनुवादक)". NGA: Coordinate Systems Analysis Branch. Retrieved 4 March 2014.
- ↑ 18.0 18.1 "डेटम रूपांतरणों के लिए प्रयुक्त समीकरण". Land Information New Zealand (LINZ). Retrieved 5 March 2014.
- ↑ 19.0 19.1 19.2 19.3 "जियोमैटिक्स गाइडेंस नोट नंबर 7, भाग 2 समन्वय रूपांतरण और सूत्र सहित परिवर्तन" (PDF). International Association of Oil and Gas Producers (OGP). Archived from the original (PDF) on 6 March 2014. Retrieved 5 March 2014.
- ↑ Bolstad, Paul (2012). GIS Fundamentals, 4th Edition (PDF). Atlas books. p. 93. ISBN 978-0-9717647-3-6. Archived from the original (PDF) on 2016-02-02.
- ↑ {{cite web|title=NIMA TR 8350.2 का परिशिष्ट: वर्ल्ड जियोडेटिक सिस्टम 1984 का कार्यान्वयन (WGS 84) संदर्भ फ़्रेम G1150|url=http://gis-lab.info/docs/nima-tr8350.2-addendum.pdf%7Cpublisher=National Geospatial-Intelligence Agency|access-date=6 March 2014}
- ↑ "मोलोडेंस्की-बडेका का (7+3) परिवर्तन". National Geospatial Intelligence Agency (NGA). Retrieved 5 March 2014.
- ↑ "ArcGIS सहायता 10.1: समीकरण-आधारित विधियाँ". ESRI. Retrieved 5 March 2014.
- ↑ {{cite web|title=डेटम ट्रांसफॉर्मेशन|url=http://earth-info.nga.mil/GandG/coordsys/datums/index.html%7Cpublisher=National Geospatial-Intelligence Agency|access-date=5 March 2014}
- ↑ {{cite web|title=ArcGIS सहायता 10.1: ग्रिड-आधारित विधियाँ|url=http://resources.arcgis.com/en/help/main/10.1/index.html#//003r00000013000000%7Cpublisher=ESRI%7Caccess-date=5 March 2014}
- ↑ {{cite web|title=NADCON/HARN डेट शिफ्ट मेथड|url=http://www.bluemarblegeo.com/knowledgebase/geocalc/classdef/datumshift/datumshifts/nadcon.html%7Cpublisher=bluemarblegeo.com%7Caccess-date=5 March 2014}
- ↑ "नैडकॉन - संस्करण 4.2". NOAA. Retrieved 5 March 2014.
- ↑ Mulcare, Donald M. "NGS Toolkit, Part 8: The National Geodetic Survey NADCON Tool". Professional Surveyor Magazine. Archived from the original on 6 March 2014. Retrieved 5 March 2014.
- ↑ 29.0 29.1 User's Handbook on Datum Transformations Involving WGS 84 (PDF) (Report). Special Publication No. 60 (3rd ed.). Monaco: International Hydrographic Bureau. August 2008. Retrieved 2017-01-10.
- ↑ {{cite web|title=डिफेन्स वर्ल्ड जियोडेटिक सिस्टम 1984 विभाग इसकी परिभाषा और स्थानीय जियोडेटिक सिस्टम के साथ संबंध|url=http://earth-info.nga.mil/GandG/publications/tr8350.2/wgs84fin.pdf%7Cpublisher=National Imagery and Mapping Agency (NIMA)|access-date=5 March 2014}
- ↑ Taylor, Chuck. "उच्च-सटीकता डेटा परिवर्तन". Retrieved 5 March 2014.