परिमेय फलन: Difference between revisions
No edit summary |
No edit summary |
||
| Line 55: | Line 55: | ||
:<math>f(x) = \frac{x^2 + 2}{x^2 + 1}</math> | :<math>f(x) = \frac{x^2 + 2}{x^2 + 1}</math> | ||
सभी [[ वास्तविक संख्या | वास्तविक संख्या]] ओं के लिए परिभाषित किया गया है, लेकिन सभी जटिल संख्याओं के लिए नहीं, क्योंकि यदि x का वर्गमूल <math>-1</math> था (अर्थात [[ काल्पनिक इकाई ]] या नकारात्मक इकाई), तो औपचारिक मूल्यांकन शून्य से विभाजन की ओर ले जाएगा: | |||
:<math>f(i) = \frac{i^2 + 2}{i^2 + 1} = \frac{-1 + 2}{-1 + 1} = \frac{1}{0},</math> | :<math>f(i) = \frac{i^2 + 2}{i^2 + 1} = \frac{-1 + 2}{-1 + 1} = \frac{1}{0},</math> | ||
जो अपरिभाषित है। | जो कि अपरिभाषित है। | ||
एक | एक स्थिर फलन जैसे f(x) =π एक परिमेय फलन है क्योंकि अचर बहुपद होते हैं। फलन स्वयं परिमेय है, भले ही f(x) का मान सभी x के लिए अपरिमेय हो। | ||
प्रत्येक बहुपद फलन <math>f(x) = P(x)</math> | प्रत्येक बहुपद फलन<math>f(x) = P(x)</math>, <math>Q(x) = 1.</math> के साथ एक परिमेय फलन है। एक फ़ंक्शन जिसे इस रूप में नहीं लिखा जा सकता है, जैसे <math>f(x) = \sin(x),</math> एक परिमेय फलन नहीं है। | ||
हालांकि, विशेषण "तर्कहीन" आमतौर पर कार्यों के लिए उपयोग नहीं किया जाता है। | |||
परिमेय फलन <math>f(x) = \tfrac{x}{x}</math> 0 को छोड़कर सभी x के लिए 1 के बराबर है, जहां [[ हटाने योग्य विलक्षणता |हटाने योग्य विलक्षणता]] है। दो परिमेय फलनों का योग, गुणनफल या भागफल (शून्य बहुपद द्वारा भाग को छोड़कर) अपने आप में एक परिमेय फलन है। हालांकि, मानक रूप में कमी की प्रक्रिया अनजाने में ऐसी विलक्षणताओं को हटाने में परिणत हो सकती है जब तक कि सावधानी न बरती जाए। परिमेय फलन की परिभाषा का उपयोग करते हुए तुल्यता वर्ग इसके आसपास हो जाता है, क्योंकि x/x, 1/1 के बराबर है। | |||
== [[ टेलर श्रृंखला ]] == | == [[ टेलर श्रृंखला ]] == | ||
किसी भी परिमेय फलन की टेलर | किसी भी परिमेय फलन की टेलर श्रेणी के गुणांक एक रेखीय पुनरावर्तन संबंध को संतुष्ट करते हैं, जो कि परिमेय फलन को एक टेलर श्रृंखला के अनिश्चित गुणांकों के साथ जोड़कर और हर के मान को खत्म करने के बाद समान पदों को एकत्रित करके पाया जा सकता है। | ||
उदाहरण के लिए, | उदाहरण के लिए, | ||
| Line 76: | Line 78: | ||
:<math>1 = (x^2 - x + 2) \sum_{k=0}^{\infty} a_k x^k</math> | :<math>1 = (x^2 - x + 2) \sum_{k=0}^{\infty} a_k x^k</math> | ||
:<math>1 = \sum_{k=0}^{\infty} a_k x^{k+2} - \sum_{k=0}^{\infty} a_k x^{k+1} + 2\sum_{k=0}^{\infty} a_k x^k.</math> | :<math>1 = \sum_{k=0}^{\infty} a_k x^{k+2} - \sum_{k=0}^{\infty} a_k x^{k+1} + 2\sum_{k=0}^{\infty} a_k x^k.</math> | ||
x की समान | x की घात को समान करने के लिए योगों के सूचकांकों को समायोजित किया जाता हैं जैसे- | ||
:<math>1 = \sum_{k=2}^{\infty} a_{k-2} x^k - \sum_{k=1}^{\infty} a_{k-1} x^k + 2\sum_{k=0}^{\infty} a_k x^k.</math> | :<math>1 = \sum_{k=2}^{\infty} a_{k-2} x^k - \sum_{k=1}^{\infty} a_{k-1} x^k + 2\sum_{k=0}^{\infty} a_k x^k.</math> | ||
| Line 82: | Line 84: | ||
:<math>1 = 2a_0 + (2a_1 - a_0)x + \sum_{k=2}^{\infty} (a_{k-2} - a_{k-1} + 2a_k) x^k.</math> | :<math>1 = 2a_0 + (2a_1 - a_0)x + \sum_{k=2}^{\infty} (a_{k-2} - a_{k-1} + 2a_k) x^k.</math> | ||
चूंकि यह मूल टेलर श्रृंखला के अभिसरण की त्रिज्या में सभी x के लिए | चूंकि यह मूल टेलर श्रृंखला के अभिसरण की त्रिज्या में सभी मान x के लिए उपयुक्त है, इस प्रकार हम निम्नानुसार इसकी गणना कर सकते हैं। इस प्रकार बायीं ओर का अचर पद दायीं ओर के अचर पद के बराबर होना चाहिए, जो कि इस प्रकार है | ||
:<math>a_0 = \frac{1}{2}.</math> | :<math>a_0 = \frac{1}{2}.</math> | ||
इस प्रकार बाईं ओर x की कोई घात नहीं है इसलिए दाईं ओर के सभी गुणांक शून्य होने चाहिए, इसे हम इस प्रकार प्रदर्शित कर सकते हैं- | |||
:<math>a_1 = \frac{1}{4}</math> | :<math>a_1 = \frac{1}{4}</math> | ||
:<math>a_k = \frac{1}{2} (a_{k-1} - a_{k-2})\quad \text{for}\ k \ge 2.</math> | :<math>a_k = \frac{1}{2} (a_{k-1} - a_{k-2})\quad \text{for}\ k \ge 2.</math> | ||
इसके विपरीत, कोई भी अनुक्रम जो एक रैखिक पुनरावृत्ति को संतुष्ट करता है, एक टेलर श्रृंखला के गुणांक के रूप में उपयोग किए जाने पर एक तर्कसंगत कार्य निर्धारित करता है। यह ऐसी पुनरावृत्तियों को हल करने में उपयोगी है, | इसके विपरीत, कोई भी अनुक्रम जो एक रैखिक पुनरावृत्ति को संतुष्ट करता है, एक टेलर श्रृंखला के गुणांक के रूप में उपयोग किए जाने पर एक तर्कसंगत कार्य निर्धारित करता है। यह ऐसी पुनरावृत्तियों को हल करने में उपयोगी है, चूंकि आंशिक अंश अपघटन का उपयोग करके हम किसी भी उचित परिमेय फलन को {{nowrap|1 / (''ax'' + ''b'')}} के रूप के गुणनखंडों के योग के रूप में लिख सकते हैं। और हम इनका विस्तार ज्यामितीय श्रृंखला के रूप में भी कर सकते हैं, जो टेलर गुणांकों के लिए एक स्पष्ट सूत्र देता है; यह कार्यों को उत्पन्न करने की विधि है। | ||
==सार बीजगणित और ज्यामितीय धारणा == <!-- Rational expression redirects here --> | ==सार बीजगणित और ज्यामितीय धारणा == <!-- Rational expression redirects here --> | ||
अमूर्त बीजगणित में बहुपद की अवधारणा को औपचारिक अभिव्यक्तियों को शामिल करने के लिए विस्तारित किया जाता है जिसमें बहुपद के गुणांक किसी भी क्षेत्र (गणित) से लिए जा सकते हैं। इस सेटिंग में एक फ़ील्ड F और कुछ अनिश्चित X दिया गया है, एक 'तर्कसंगत व्यंजक' [[ बहुपद वलय ]] F[X] के भिन्नों के क्षेत्र का कोई भी तत्व है। किसी भी परिमेय व्यंजक को Q 0 वाले दो बहुपद P/Q के भागफल के रूप में लिखा जा सकता है, हालाँकि यह निरूपण अद्वितीय नहीं है। P/Q बहुपदों P, Q, R, और S के लिए R/S के समतुल्य है, जब PS = QR है। हालांकि, चूंकि एफ [एक्स] एक अद्वितीय कारक डोमेन है, इसलिए किसी भी तर्कसंगत अभिव्यक्ति पी/क्यू के लिए सबसे कम डिग्री के पी और क्यू बहुपद और क्यू को [[ मोनिक बहुपद ]] के लिए चुना गया है। यह उसी तरह है जैसे पूर्णांकों का एक [[ अंश (गणित) ]] हमेशा सामान्य कारकों को रद्द करके सबसे कम शब्दों में विशिष्ट रूप से लिखा जा सकता है। | '''अमूर्त बीजगणित में बहुपद की अवधारणा को औपचारिक''' अभिव्यक्तियों को शामिल करने के लिए विस्तारित किया जाता है जिसमें बहुपद के गुणांक किसी भी क्षेत्र (गणित) से लिए जा सकते हैं। इस सेटिंग में एक फ़ील्ड F और कुछ अनिश्चित X दिया गया है, एक 'तर्कसंगत व्यंजक' [[ बहुपद वलय ]] F[X] के भिन्नों के क्षेत्र का कोई भी तत्व है। किसी भी परिमेय व्यंजक को Q 0 वाले दो बहुपद P/Q के भागफल के रूप में लिखा जा सकता है, हालाँकि यह निरूपण अद्वितीय नहीं है। P/Q बहुपदों P, Q, R, और S के लिए R/S के समतुल्य है, जब PS = QR है। हालांकि, चूंकि एफ [एक्स] एक अद्वितीय कारक डोमेन है, इसलिए किसी भी तर्कसंगत अभिव्यक्ति पी/क्यू के लिए सबसे कम डिग्री के पी और क्यू बहुपद और क्यू को [[ मोनिक बहुपद ]] के लिए चुना गया है। यह उसी तरह है जैसे पूर्णांकों का एक [[ अंश (गणित) ]] हमेशा सामान्य कारकों को रद्द करके सबसे कम शब्दों में विशिष्ट रूप से लिखा जा सकता है। | ||
परिमेय व्यंजकों के क्षेत्र को F(X) से दर्शाया जाता है। कहा जाता है कि इस क्षेत्र को एफ पर (एक [[ पारलौकिक तत्व ]]) एक्स द्वारा उत्पन्न (एक क्षेत्र के रूप में) किया जाता है, क्योंकि एफ (एक्स) में एफ और तत्व एक्स दोनों युक्त कोई उचित उपक्षेत्र नहीं होता है। | परिमेय व्यंजकों के क्षेत्र को F(X) से दर्शाया जाता है। कहा जाता है कि इस क्षेत्र को एफ पर (एक [[ पारलौकिक तत्व ]]) एक्स द्वारा उत्पन्न (एक क्षेत्र के रूप में) किया जाता है, क्योंकि एफ (एक्स) में एफ और तत्व एक्स दोनों युक्त कोई उचित उपक्षेत्र नहीं होता है। | ||
Revision as of 21:31, 7 October 2022
This article includes a list of general references, but it lacks sufficient corresponding inline citations. (September 2015) (Learn how and when to remove this template message) |
गणित में, एक परिमेय फलन कोई भी फलन है जिसे परिमेय भिन्न द्वारा परिभाषित किया जा सकता है, जो एक बीजीय भिन्न इस प्रकार है कि अंश और हर दोनों बहुपद हैं। बहुपदों के गुणांकों का परिमेय संख्या होना आवश्यक नहीं है; उन्हें किसी भी क्षेत्र (गणित) K में लिया जा सकता है। इस मामले में, हम K के ऊपर एक परिमेय फलन और एक परिमेय भिन्न की बात करते हैं। चरों के मान K वाले किसी भी क्षेत्र L में लिए जा सकते हैं। तब डोमेन (फ़ंक्शन) का प्रांत चरों के मानों का समुच्चय होता है जिसके लिए हर शून्य नहीं है, और कोडोमेन L है।
एक क्षेत्र K पर परिमेय फलनों का समुच्चय एक क्षेत्र है, जो K के ऊपर बहुपद फलनों के वलय (गणित) के भिन्नों का क्षेत्र है।
परिभाषाएं
एक फलन को परिमेय फलन हम तभी कह सकते है जब इसे इस रूप में लिखा जाता है
जहाँ और के बहुपद फलन हैं, और शून्य फलन नहीं है। का प्रांत के सभी मानों का समुच्चय है, जिसके लिए हर शून्य नहीं है।
हालाँकि, यदि और में एक गैर-स्थिर बहुपद सबसे बड़ा सामान्य भाजक है, तब और को सेट करने से एक परिमेय फलन उत्पन्न होता है
जिसका डोमेन से बड़ा हो सकता है और यह के प्रांत पर के बराबर है। यह और की पहचान करने के लिए एक सामान्य उपयोग है, यानी के डोमेन को "निरंतरता से" के डोमेन तक विस्तारित करना है। उसके इस मान के लिए वास्तव में, एक परिमेय भिन्न को बहुपदों के भिन्नों के तुल्यता वर्ग के रूप में परिभाषित किया जा सकता है, जहाँ दो भिन्न तथा को यदि हो तब इन्हें समकक्ष माना जाता है। इस मामले में के बराबर है .
एक उचित परिमेय फलन एक परिमेय फलन है जिसमें के बहुपद की घात की डिग्री से कम है और दोनों वास्तविक बहुपद हैं, जिन्हें एक भिन्न के सादृश्य द्वारा नामित किया गया है जिसमें उचित और अनुचित भिन्न है।[1]
डिग्री
एक तर्कसंगत कार्य की डिग्री के बारे में कई गैर समकक्ष परिभाषाएं हैं।
सामान्यतः, एक परिमेय फलन की घात उसके संघटक बहुपदों P और Q की घातों का अधिकतम होता है। जब भिन्न को निम्नतम पदों पर घटाया जाता है। यदि f की घात d है, तो समीकरण कुछ इस प्रकार होगा-
w के कुछ मानों को छोड़कर z में d विशिष्ट समाधान हैं, जिसे हम महत्वपूर्ण मूल्य कहते हैं, जहां दो या दो से अधिक समाधान मेल खाते हैं या जहां कुछ समाधान अनंत पर बिंदु को खारिज कर दिया जाता है (अर्थात, जब हर को साफ करने के बाद समीकरण की डिग्री घट जाती है)।
जटिल संख्या के मामले में डिग्री एक के साथ एक तर्कसंगत कार्य एक मोबियस परिवर्तन है।
एक परिमेय फलन के ग्राफ की डिग्री वह डिग्री नहीं है जैसा कि ऊपर परिभाषित किया गया है, यह अंश की डिग्री का अधिकतम और हर की डिग्री का एक प्लस है।
कुछ संदर्भों में, जैसे कि स्पर्शोन्मुख विश्लेषण में, एक तर्कसंगत कार्य की डिग्री अंश और हर की डिग्री के बीच का अंतर है। नेटवर्क संश्लेषण और नेटवर्क विश्लेषण (विद्युत सर्किट) में, डिग्री दो का एक तर्कसंगत कार्य (अर्थात, घात के दो बहुपदों का अनुपात अधिकतम दो) को अक्सर द्विघात फलन कहा जाता है।[2]
उदाहरण
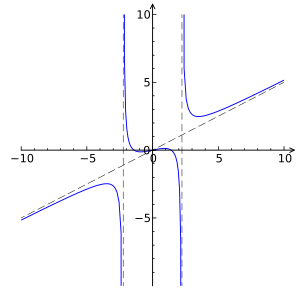
तर्कसंगत कार्य
पर परिभाषित नहीं है
यह स्पर्शोन्मुख है जैसा तर्कसंगत कार्य
सभी वास्तविक संख्या ओं के लिए परिभाषित किया गया है, लेकिन सभी जटिल संख्याओं के लिए नहीं, क्योंकि यदि x का वर्गमूल था (अर्थात काल्पनिक इकाई या नकारात्मक इकाई), तो औपचारिक मूल्यांकन शून्य से विभाजन की ओर ले जाएगा:
जो कि अपरिभाषित है।
एक स्थिर फलन जैसे f(x) =π एक परिमेय फलन है क्योंकि अचर बहुपद होते हैं। फलन स्वयं परिमेय है, भले ही f(x) का मान सभी x के लिए अपरिमेय हो।
प्रत्येक बहुपद फलन, के साथ एक परिमेय फलन है। एक फ़ंक्शन जिसे इस रूप में नहीं लिखा जा सकता है, जैसे एक परिमेय फलन नहीं है।
हालांकि, विशेषण "तर्कहीन" आमतौर पर कार्यों के लिए उपयोग नहीं किया जाता है।
परिमेय फलन 0 को छोड़कर सभी x के लिए 1 के बराबर है, जहां हटाने योग्य विलक्षणता है। दो परिमेय फलनों का योग, गुणनफल या भागफल (शून्य बहुपद द्वारा भाग को छोड़कर) अपने आप में एक परिमेय फलन है। हालांकि, मानक रूप में कमी की प्रक्रिया अनजाने में ऐसी विलक्षणताओं को हटाने में परिणत हो सकती है जब तक कि सावधानी न बरती जाए। परिमेय फलन की परिभाषा का उपयोग करते हुए तुल्यता वर्ग इसके आसपास हो जाता है, क्योंकि x/x, 1/1 के बराबर है।
टेलर श्रृंखला
किसी भी परिमेय फलन की टेलर श्रेणी के गुणांक एक रेखीय पुनरावर्तन संबंध को संतुष्ट करते हैं, जो कि परिमेय फलन को एक टेलर श्रृंखला के अनिश्चित गुणांकों के साथ जोड़कर और हर के मान को खत्म करने के बाद समान पदों को एकत्रित करके पाया जा सकता है।
उदाहरण के लिए,
हर से गुणा करना और बांटना,
x की घात को समान करने के लिए योगों के सूचकांकों को समायोजित किया जाता हैं जैसे-
समान पदों का संयोजन देता है
चूंकि यह मूल टेलर श्रृंखला के अभिसरण की त्रिज्या में सभी मान x के लिए उपयुक्त है, इस प्रकार हम निम्नानुसार इसकी गणना कर सकते हैं। इस प्रकार बायीं ओर का अचर पद दायीं ओर के अचर पद के बराबर होना चाहिए, जो कि इस प्रकार है
इस प्रकार बाईं ओर x की कोई घात नहीं है इसलिए दाईं ओर के सभी गुणांक शून्य होने चाहिए, इसे हम इस प्रकार प्रदर्शित कर सकते हैं-
इसके विपरीत, कोई भी अनुक्रम जो एक रैखिक पुनरावृत्ति को संतुष्ट करता है, एक टेलर श्रृंखला के गुणांक के रूप में उपयोग किए जाने पर एक तर्कसंगत कार्य निर्धारित करता है। यह ऐसी पुनरावृत्तियों को हल करने में उपयोगी है, चूंकि आंशिक अंश अपघटन का उपयोग करके हम किसी भी उचित परिमेय फलन को 1 / (ax + b) के रूप के गुणनखंडों के योग के रूप में लिख सकते हैं। और हम इनका विस्तार ज्यामितीय श्रृंखला के रूप में भी कर सकते हैं, जो टेलर गुणांकों के लिए एक स्पष्ट सूत्र देता है; यह कार्यों को उत्पन्न करने की विधि है।
सार बीजगणित और ज्यामितीय धारणा
अमूर्त बीजगणित में बहुपद की अवधारणा को औपचारिक अभिव्यक्तियों को शामिल करने के लिए विस्तारित किया जाता है जिसमें बहुपद के गुणांक किसी भी क्षेत्र (गणित) से लिए जा सकते हैं। इस सेटिंग में एक फ़ील्ड F और कुछ अनिश्चित X दिया गया है, एक 'तर्कसंगत व्यंजक' बहुपद वलय F[X] के भिन्नों के क्षेत्र का कोई भी तत्व है। किसी भी परिमेय व्यंजक को Q 0 वाले दो बहुपद P/Q के भागफल के रूप में लिखा जा सकता है, हालाँकि यह निरूपण अद्वितीय नहीं है। P/Q बहुपदों P, Q, R, और S के लिए R/S के समतुल्य है, जब PS = QR है। हालांकि, चूंकि एफ [एक्स] एक अद्वितीय कारक डोमेन है, इसलिए किसी भी तर्कसंगत अभिव्यक्ति पी/क्यू के लिए सबसे कम डिग्री के पी और क्यू बहुपद और क्यू को मोनिक बहुपद के लिए चुना गया है। यह उसी तरह है जैसे पूर्णांकों का एक अंश (गणित) हमेशा सामान्य कारकों को रद्द करके सबसे कम शब्दों में विशिष्ट रूप से लिखा जा सकता है।
परिमेय व्यंजकों के क्षेत्र को F(X) से दर्शाया जाता है। कहा जाता है कि इस क्षेत्र को एफ पर (एक पारलौकिक तत्व ) एक्स द्वारा उत्पन्न (एक क्षेत्र के रूप में) किया जाता है, क्योंकि एफ (एक्स) में एफ और तत्व एक्स दोनों युक्त कोई उचित उपक्षेत्र नहीं होता है।
जटिल तर्कसंगत कार्य
<गैलरी कैप्शन = जूलिया तर्कसंगत मानचित्रों के लिए सेट करता है> जूलिया सेट f(z)=1 over az5+z3+bz.png| जूलिया सेट f(z)=1 over z3+z*(-3-3*I).png| जूलिया के लिए f(z)=(z2+a) over (z2+b) a=-0.2+0.7i , b=0.917.png| जूलिया f(z)= . के लिए सेटz2 over (z9-z+0.025).png| </गैलरी> जटिल विश्लेषण में, एक तर्कसंगत कार्य
जटिल गुणांक वाले दो बहुपदों का अनुपात है, जहां Q शून्य बहुपद नहीं है और P तथा Q कोई सामान्य कारक नहीं है (इससे बचा जाता है f अनिश्चित मान 0/0) लेना।
का डोमेन f सम्मिश्र संख्याओं का समुच्चय ऐसा है कि . प्रत्येक परिमेय फलन को स्वाभाविक रूप से एक ऐसे फलन तक बढ़ाया जा सकता है जिसका डोमेन और परास संपूर्ण रीमैन क्षेत्र (जटिल प्रक्षेप्य रेखा ) है।
परिमेय फलन मेरोमॉर्फिक फ़ंक्शन के प्रतिनिधि उदाहरण हैं।
तर्कसंगत कार्यों का पुनरावृत्ति (मानचित्र)[3] रीमैन क्षेत्र पर असतत गतिशील प्रणाली बनाता है।
एक बीजीय किस्म पर एक परिमेय फलन की धारणा
बहुपद वलय की तरह# कई चरों में बहुपद वलय, परिमेय व्यंजकों को n अनिश्चित X के लिए भी सामान्यीकृत किया जा सकता है1,..., एक्सn, F[X . के भिन्नों का क्षेत्र लेकर1,..., एक्सn], जिसे F(X .) द्वारा निरूपित किया जाता है1,..., एक्सn)
बीजगणितीय ज्यामिति में परिमेय फलन के अमूर्त विचार का एक विस्तारित संस्करण प्रयोग किया जाता है। वहां एक बीजीय किस्म वी का कार्य क्षेत्र वी के समन्वय रिंग के अंशों के क्षेत्र के रूप में बनता है (अधिक सटीक रूप से कहा जाता है, एक ज़रिस्की-घने एफ़िन ओपन सेट वी में)। इसके तत्वों f को गैर-रिक्त खुले सेट U पर बीजीय ज्यामिति के अर्थ में नियमित कार्यों के रूप में माना जाता है, और इसे प्रक्षेप्य रेखा के रूप के रूप में भी देखा जा सकता है।
आवेदन
परिमेय कार्यों का उपयोग संख्यात्मक विश्लेषण में कार्यों के प्रक्षेप और सन्निकटन के लिए किया जाता है, उदाहरण के लिए हेनरी पैड द्वारा पेश किए गए पैड सन्निकटन। तर्कसंगत कार्यों के संदर्भ में अनुमान कंप्यूटर बीजगणित प्रणालियों और अन्य संख्यात्मक सॉफ़्टवेयर के लिए उपयुक्त हैं। बहुपदों की तरह, उनका सीधा मूल्यांकन किया जा सकता है, और साथ ही वे बहुपदों की तुलना में अधिक विविध व्यवहार व्यक्त करते हैं। तर्कसंगत कार्यों का उपयोग विज्ञान और इंजीनियरिंग में अधिक जटिल समीकरणों को अनुमानित या मॉडल करने के लिए किया जाता है जिसमें भौतिकी में क्षेत्र और बल, विश्लेषणात्मक रसायन विज्ञान में स्पेक्ट्रोस्कोपी, जैव रसायन में एंजाइम कैनेटीक्स, इलेक्ट्रॉनिक सर्किटरी, वायुगतिकी, विवो में दवा सांद्रता, परमाणुओं और अणुओं के लिए तरंग कार्य, प्रकाशिकी शामिल हैं। और छवि संकल्प, और ध्वनिकी और ध्वनि में सुधार करने के लिए फोटोग्राफी[citation needed].
संकेत का प्रक्रमण में, लाप्लास ट्रांसफॉर्म (निरंतर सिस्टम के लिए) या z-परिणत (असतत-समय सिस्टम के लिए) आमतौर पर उपयोग किए जाने वाले रैखिक समय-अपरिवर्तनीय सिस्टम (फिल्टर) की आवेग प्रतिक्रिया के साथ अनंत आवेग प्रतिक्रिया जटिल संख्याओं पर तर्कसंगत कार्य हैं .
यह भी देखें
- भिन्नों का क्षेत्र
- आंशिक अंश अपघटन
- एकीकरण में आंशिक अंश
- एक बीजीय किस्म का कार्य क्षेत्र
- बीजीय भिन्न – तर्कसंगत कार्यों का एक सामान्यीकरण जो पूर्णांक जड़ों को लेने की अनुमति देता है
संदर्भ
- ↑ Martin J. Corless, Art Frazho, Linear Systems and Control, p. 163, CRC Press, 2003 ISBN 0203911377.
- Malcolm W. Pownall, Functions and Graphs: Calculus Preparatory Mathematics, p. 203, Prentice-Hall, 1983 ISBN 0133323048.
- ↑ Glisson, Tildon H., Introduction to Circuit Analysis and Design, Springer, 2011 ISBN ISBN 9048194431.
- ↑ Iteration of Rational Functions by Omar Antolín Camarena
- "Rational function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. (2007), "Section 3.4. Rational Function Interpolation and Extrapolation", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
इस पृष्ठ में अनुपलब्ध आंतरिक कड़ियों की सूची
- रैखिक फिल्टर
- मूर्ति प्रोद्योगिकी
- करणीय
- खास समय
- सिग्नल (इलेक्ट्रॉनिक्स)
- लगातार कश्मीर फिल्टर
- चरण विलंब
- एम-व्युत्पन्न फ़िल्टर
- स्थानांतरण प्रकार्य
- बहुपदीय फलन
- लो पास फिल्टर
- अंतःप्रतीक हस्तक्षेप
- फ़िल्टर (प्रकाशिकी)
- युग्मित उपकरण को चार्ज करें
- गांठदार तत्व
- पतली फिल्म थोक ध्वनिक गुंजयमान यंत्र
- लोहा
- परमाणु घड़ी
- फुरियर रूपांतरण
- लहर (फ़िल्टर)
- कार्तीय समन्वय प्रणाली
- अंक शास्त्र
- यूक्लिडियन स्पेस
- मामला
- ब्रम्हांड
- कद
- द्वि-आयामी अंतरिक्ष
- निर्देशांक तरीका
- अदिश (गणित)
- शास्त्रीय हैमिल्टनियन quaternions
- quaternions
- पार उत्पाद
- उत्पत्ति (गणित)
- दो प्रतिच्छेद रेखाएँ
- तिरछी रेखाएं
- समानांतर पंक्ति
- रेखीय समीकरण
- समानांतर चतुर्भुज
- वृत्त
- शंकु खंड
- विकृति (गणित)
- निर्देशांक वेक्टर
- लीनियर अलजेब्रा
- सीधा
- भौतिक विज्ञान
- लेट बीजगणित
- एक क्षेत्र पर बीजगणित
- जोड़नेवाला
- समाकृतिकता
- कार्तीय गुणन
- अंदरूनी प्रोडक्ट
- आइंस्टीन योग सम्मेलन
- इकाई वेक्टर
- टुकड़े-टुकड़े चिकना
- द्विभाजित
- आंशिक व्युत्पन्न
- आयतन तत्व
- समारोह (गणित)
- रेखा समाकलन का मौलिक प्रमेय
- खंड अनुसार
- सौम्य सतह
- फ़ानो विमान
- प्रक्षेप्य स्थान
- प्रक्षेप्य ज्यामिति
- चार आयामी अंतरिक्ष
- विद्युत प्रवाह
- उच्च लाभ एंटीना
- सर्वदिशात्मक एंटीना
- गामा किरणें
- विद्युत संकेत
- वाहक लहर
- आयाम अधिमिश्रण
- चैनल क्षमता
- आर्थिक अच्छा
- आधार - सामग्री संकोचन
- शोर उन्मुक्ति
- कॉल चिह्न
- शिशु की देखरेख करने वाला
- आईएसएम बैंड
- लंबी लहर
- एफएम प्रसारण
- सत्य के प्रति निष्ठा
- जमीनी लहर
- कम आवृत्ति
- श्रव्य विकृति
- वह-एएसी
- एमपीईजी-4
- संशोधित असतत कोसाइन परिवर्तन
- भू-स्थिर
- प्रत्यक्ष प्रसारण उपग्रह टेलीविजन
- माध्यमिक आवृत्ति
- परमाणु घड़ी
- बीपीसी (समय संकेत)
- फुल डुप्लेक्स
- बिट प्रति सेकंड
- पहला प्रतिसादकर्ता
- हवाई गलियारा
- नागरिक बंद
- विविधता स्वागत
- शून्य (रेडियो)
- बिजली का मीटर
- जमीन (बिजली)
- हवाई अड्डे की निगरानी रडार
- altimeter
- समुद्री रडार
- देशान्तर
- तोपखाने का खोल
- बचाव बीकन का संकेत देने वाली आपातकालीन स्थिति
- अंतर्राष्ट्रीय कॉस्पास-सरसैट कार्यक्रम
- संरक्षण जीवविज्ञान
- हवाई आलोक चित्र विद्या
- गैराज का दरवाज़ा
- मुख्य जेब
- अंतरिक्ष-विज्ञान
- ध्वनि-विज्ञान
- निरंतर संकेत
- मिड-रेंज स्पीकर
- फ़िल्टर (सिग्नल प्रोसेसिंग)
- उष्ण ऊर्जा
- विद्युतीय प्रतिरोध
- लंबी लाइन (दूरसंचार)
- इलास्टेंस
- गूंज
- ध्वनिक प्रतिध्वनि
- प्रत्यावर्ती धारा
- आवृत्ति विभाजन बहुसंकेतन
- छवि फ़िल्टर
- वाहक लहर
- ऊष्मा समीकरण
- प्रतिक दर
- विद्युत चालकता
- आवृति का उतार - चढ़ाव
- निरंतर कश्मीर फिल्टर
- जटिल विमान
- फासर (साइन वेव्स)
- पोर्ट (सर्किट सिद्धांत)
- लग्रांगियन यांत्रिकी
- जाल विश्लेषण
- पॉइसन इंटीग्रल
- affine परिवर्तन
- तर्कसंगत कार्य
- शोर अनुपात का संकेत
- मिलान फ़िल्टर
- रैखिक-द्विघात-गाऊसी नियंत्रण
- राज्य स्थान (नियंत्रण)
- ऑपरेशनल एंप्लीफायर
- एलटीआई प्रणाली सिद्धांत
- विशिष्ट एकीकृत परिपथ आवेदन
- सतत समय
- एंटी - एलियासिंग फ़िल्टर
- भाजक
- निश्चित बिंदु अंकगणित
- फ्लोटिंग-पॉइंट अंकगणित
- डिजिटल बाइकैड फ़िल्टर
- अनुकूली फिल्टर
- अध्यारोपण सिद्धांत
- कदम की प्रतिक्रिया
- राज्य स्थान (नियंत्रण)
- नियंत्रण प्रणाली
- वोल्टेज नियंत्रित थरथरानवाला
- कंपंडोर
- नमूना और पकड़
- संगणक
- अनेक संभावनाओं में से चुनी हूई प्रक्रिया
- प्रायिकता वितरण
- वर्तमान परिपथ
- गूंज रद्दीकरण
- सुविधा निकासी
- छवि उन्नीतकरण
- एक प्रकार की प्रोग्रामिंग की पर्त
- ओ एस आई मॉडल
- समानता (संचार)
- आंकड़ा अधिग्रहण
- रूपांतरण सिद्धांत
- लीनियर अलजेब्रा
- स्टचास्तिक प्रोसेसेज़
- संभावना
- गैर-स्थानीय साधन
- घटना (सिंक्रनाइज़ेशन आदिम)
- एंटीलोक ब्रेक
- उद्यम प्रणाली
- सुरक्षा-महत्वपूर्ण प्रणाली
- डेटा सामान्य
- आर टी -11
- डंब टर्मिनल
- समय बताना
- सेब II
- जल्द से जल्द समय सीमा पहले शेड्यूलिंग
- अनुकूली विभाजन अनुसूचक
- वीडियो गेम कंसोल की चौथी पीढ़ी
- वीडियो गेम कंसोल की तीसरी पीढ़ी
- नमूनाकरण दर
- अंकगणित औसत
- उच्च प्रदर्शन कंप्यूटिंग
- भयावह विफलता
- हुड विधि
- प्रणाली विश्लेषण
- समय अपरिवर्तनीय
- औद्योगिक नियंत्रण प्रणाली
- निर्देशयोग्य तर्क नियंत्रक
- प्रक्रिया अभियंता)
- नियंत्रण पाश
- संयंत्र (नियंत्रण सिद्धांत)
- क्रूज नियंत्रण
- अनुक्रमिक कार्य चार्ट
- नकारात्मक प्रतिपुष्टि
- अन्देंप्त
- नियंत्रण वॉल्व
- पीआईडी नियंत्रक
- यौगिक
- फिल्टर (सिग्नल प्रोसेसिंग)
- वितरित कोटा पद्धति
- महाकाव्यों
- डूप गति नियंत्रण
- हवाई जहाज
- संक्षिप्त और प्रारंभिकवाद
- मोटर गाड़ी
- संयुक्त राज्य नौसेना
- निर्देशित मिसाइलें
- भूभाग-निम्नलिखित रडार
- अवरक्त किरणे
- प्रेसिजन-निर्देशित युद्धपोत
- विमान भेदी युद्ध
- शाही रूसी नौसेना
- हस्तक्षेप हरा
- सेंट पीटर्सबर्ग
- योण क्षेत्र
- आकाशीय बिजली
- द्वितीय विश्वयुद्ध
- संयुक्त राज्य सेना
- डेथ रे
- पर्ल हार्बर पर हमला
- ओबाउ (नेविगेशन)
- जमीन नियंत्रित दृष्टिकोण
- भूविज्ञानी
- आंधी तूफान
- मौसम पूर्वानुमान
- बहुत बुरा मौसम
- सर्दियों का तूफान
- संकेत पहचान
- बिखरने
- इलेक्ट्रिकल कंडक्टीविटी
- पराबैगनी प्रकाश
- खालीपन
- भूसा (प्रतिमाप)
- पारद्युतिक स्थिरांक
- विद्युत चुम्बकीय विकिरण
- विद्युतीय प्रतिरोध
- प्रतिचुम्बकत्व
- बहुपथ प्रसार
- तरंग दैर्ध्य
- अर्ध-सक्रिय रडार होमिंग
- Nyquist आवृत्ति
- ध्रुवीकरण (लहरें)
- अपवर्तक सूचकांक
- नाड़ी पुनरावृत्ति आवृत्ति
- शोर मचाने वाला फ़र्श
- प्रकाश गूंज
- रेत का तूफान
- स्वत: नियंत्रण प्राप्त करें
- जय स्पाइक
- घबराना
- आयनमंडलीय परावर्तन
- वायुमंडलीय वाहिनी
- व्युत्क्रम वर्ग नियम
- इलेक्ट्रानिक युद्ध
- उड़ान का समय
- प्रकाश कि गति
- पूर्व चेतावनी रडार
- रफ़्तार
- निरंतर-लहर रडार
- स्पेकट्रूम विशेष्यग्य
- रेंज अस्पष्टता संकल्प
- मिलान फ़िल्टर
- रोटेशन
- चरणबद्ध व्यूह रचना
- मैमथ राडार
- निगरानी करना
- स्क्रीन
- पतला सरणी अभिशाप
- हवाई रडार प्रणाली
- परिमाणक्रम
- इंस्टीट्यूट ऑफ़ इलेक्ट्रिकल एंड इलेक्ट्रॉनिक्स इंजीनियर्स
- क्षितिज राडार के ऊपर
- पल्स बनाने वाला नेटवर्क
- अमेरिका में प्रदूषण की रोकथाम
- आईटी रेडियो विनियम
- रडार संकेत विशेषताएं
- हैस (रडार)
- एवियोनिक्स में एक्रोनिम्स और संक्षिप्ताक्षर
- समय की इकाई
- गुणात्मक प्रतिलोम
- रोशनी
- दिल की आवाज
- हिलाना
- सरल आवर्त गति
- नहीं (पत्र)
- एसआई व्युत्पन्न इकाई
- इंटरनेशनल इलेक्ट्रोटेक्नीकल कमीशन
- प्रति मिनट धूर्णन
- हवा की लहर
- एक समारोह का तर्क
- चरण (लहरें)
- आयामहीन मात्रा
- असतत समय संकेत
- विशेष मामला
- मध्यम (प्रकाशिकी)
- कोई भी त्रुटि
- ध्वनि की तरंग
- दृश्यमान प्रतिबिम्ब
- लय
- सुनवाई की दहलीज
- प्रजातियाँ
- मुख्य विधुत
- नाबालिग तीसरा
- माप की इकाइयां
- आवधिकता (बहुविकल्पी)
- परिमाण के आदेश (आवृत्ति)
- वर्णक्रमीय घटक
- रैखिक समय-अपरिवर्तनीय प्रणाली
- असतत समय फिल्टर
- ऑटोरेग्रेसिव मॉडल
- डिजिटल डाटा
- डिजिटल देरी लाइन
- बीआईबीओ स्थिरता
- फोरियर श्रेणी
- दोषी
- दशमलव (सिग्नल प्रोसेसिंग)
- असतत फूरियर रूपांतरण
- एफआईआर ट्रांसफर फंक्शन
- 3डी परीक्षण मॉडल
- ब्लेंडर (सॉफ्टवेयर)
- वैज्ञानिक दृश्य
- प्रतिपादन (कंप्यूटर ग्राफिक्स)
- विज्ञापन देना
- चलचित्र
- अनुभूति
- निहित सतह
- विमानन
- भूतपूर्व छात्र
- छिपी सतह निर्धारण
- अंतरिक्ष आक्रमणकारी
- लकीर खींचने की क्रिया
- एनएमओएस तर्क
- उच्च संकल्प
- एमओएस मेमोरी
- पूरक राज्य मंत्री
- नक्षत्र-भवन
- वैश्विक चमक
- मैकिंटोश कंप्यूटर
- प्रथम व्यक्ति शूटर
- साधारण मानचित्रण
- हिमयुग (2002 फ़िल्म)
- मेडागास्कर (2005 फ़िल्म)
- बायोइनफॉरमैटिक्स
- शारीरिक रूप से आधारित प्रतिपादन
- हीरे की थाली
- प्रतिबिंब (कंप्यूटर ग्राफिक्स)
- 2010 की एनिमेटेड फीचर फिल्मों की सूची
- परिवेशी बाधा
- वास्तविक समय (मीडिया)
- जानकारी
- कंकाल एनिमेशन
- भीड़ अनुकरण
- प्रक्रियात्मक एनिमेशन
- अणु प्रणाली
- कैमरा
- माइक्रोस्कोप
- इंजीनियरिंग के चित्र
- रेखापुंज छवि
- नक्शा
- हार्डवेयर एक्सिलरेशन
- अंधेरा
- गैर-समान तर्कसंगत बी-तख़्ता
- नक्शा टक्कर
- चुम्बकीय अनुनाद इमेजिंग
- नमूनाकरण (सिग्नल प्रोसेसिंग)
- sculpting
- आधुनिक कला का संग्रहालय
- गेम डेवलपर्स कांफ्रेंस
- शैक्षिक
- आपूर्ती बंद करने की आवृत्ति
- प्रतिक्रिया (इलेक्ट्रॉनिक्स)
- अण्डाकार फिल्टर
- सीरिज़ सर्किट)
- मिलान जेड-ट्रांसफॉर्म विधि
- कंघी फ़िल्टर
- समूह देरी
- सप्टक
- दूसरों से अलग
- लो पास फिल्टर
- निर्देश प्रति सेकंड
- अंकगणित अतिप्रवाह
- चरण (लहरें)
- हस्तक्षेप (लहर प्रसार)
- बीट (ध्वनिक)
- अण्डाकार तर्कसंगत कार्य
- जैकोबी अण्डाकार कार्य
- क्यू कारक
- यूनिट सर्कल
- फी (पत्र)
- सुनहरा अनुपात
- मोनोटोनिक
- Immittance
- ऑप एंप
- आवेग invariance
- बेसेल फ़ंक्शन
- जटिल सन्युग्म
- संकेत प्रतिबिंब
- विद्युतीय ऊर्जा
- इनपुट उपस्थिति
- एकदिश धारा
- जटिल संख्या
- भार प्रतिबाधा
- विद्युतचुंबकीय व्यवधान
- बिजली की आपूर्ति
- आम-कैथोड
- अवमन्दन कारक
- ध्वनिरोधन
- गूंज (घटना)
- फ्रेस्नेल समीकरण
- रोड़ी
- लोडिंग कॉइल
- आर एस होयतो
- लोड हो रहा है कॉइल
- चेबीशेव बहुपद
- एक बंदरगाह
- सकारात्मक-वास्तविक कार्य
- आपूर्ती बंद करने की आवृत्ति
- उच्च मार्ग
- रैखिक फ़िल्टर
- प्रतिक दर
- घेरा
- नॉन-रिटर्न-टू-जीरो
- अनियमित चर
- संघ बाध्य
- एकाधिक आवृत्ति-शिफ्ट कुंजीयन
- COMPARATOR
- द्विआधारी जोड़
- असंबद्ध संचरण
- त्रुटि समारोह
- आपसी जानकारी
- बिखरा हुआ1
- डिजिटल मॉडुलन
- डिमॉड्युलेटर
- कंघा
- खड़ी तरंगें
- नमूना दर
- प्रक्षेप
- ऑडियो सिग्नल प्रोसेसिंग
- खगोल-कंघी
- खास समय
- पोल (जटिल विश्लेषण)
- दुर्लभ
- आरसी सर्किट
- अवरोध
- स्थिर समय
- एक घोड़ा
- पुनरावृत्ति संबंध
- निष्क्रिय फिल्टर
- श्रव्य सीमा
- मिक्सिंग कंसोल
- एसी कपलिंग
- क्यूएससी ऑडियो
- संकट
- दूसरों से अलग
- डीएसएल मॉडम
- फाइबर ऑप्टिक संचार
- व्यावर्तित जोड़ी
- बातचीत का माध्यम
- समाक्षीय तार
- लंबी दूरी का टेलीफोन कनेक्शन
- डाउनस्ट्रीम (कंप्यूटर विज्ञान)
- आवृत्ति द्वैध
- आवृत्ति प्रतिक्रिया
- आकड़ों की योग्यता
- परीक्षण के अंतर्गत उपकरण
- कंघी फिल्टर
- निष्क्रियता (इंजीनियरिंग)
- लाभ (इलेक्ट्रॉनिक्स)
- कोने की आवृत्ति
- फील्ड इफ़ेक्ट ट्रांजिस्टर
- कम आवृत्ति दोलन
- एकीकृत परिपथ
- निरंतर-प्रतिरोध नेटवर्क
- यूनिट सर्कल
- अधिकतम प्रयोग करने योग्य आवृत्ति
- विशेषता समीकरण (कलन)
- लहर संख्या
- वेवगाइड (प्रकाशिकी)
- लाप्लासियान
- वेवनंबर
- अपवर्तन तरंग
- एकतरफा बहुपद
- एकपदी की डिग्री
- एक बहुपद का क्रम (बहुविकल्पी)
- रैखिक प्रकार्य
- कामुक समीकरण
- चतुर्थक कार्य
- क्रमसूचक अंक
- त्रिनाम
- इंटीग्रल डोमेन
- सदिश स्थल
- फील्ड (गणित)
- सेट (गणित)
- अंगूठी (गणित)
- पूर्णांक मॉड्यूल n
- लोगारित्म
- घातांक प्रकार्य
- एल्गोरिदम का विश्लेषण
- बीजगणित का मौलिक प्रमेय
- डिजिटल डाटा
- प्रारंभ करनेवाला
- ध्वनि दाब स्तर
- साधारण सेल
- निरंतर संकेत
- व्यावर्तित जोड़ी
- आवृत्ति स्पेक्ट्रम
- जुड़वां सीसा
- नेटवर्क विश्लेषण (विद्युत सर्किट)
- सैटेलाइट टेलीविज़न
- एक बहुपद की घात
- क्यू कारक
- निविष्टी की हानि
- खड़ी लहर
- गांठदार घटक
- गांठदार तत्व मॉडल
- विरोधी गूंज
- वितरित तत्व फ़िल्टर
- मिटटी तेल
- बहुपथ हस्तक्षेप
- पहली पीढ़ी का कंप्यूटर
- ऊर्जा परिवर्तन
- उपकरण को मापना
- ऊर्जा का रूप
- repeatability
- प्रतिक्रिया (इंजीनियरिंग)
- बिजली का शोर
- संचार प्रणाली
- चुंबकीय कारतूस
- स्पर्श संवेदक
- ध्वनि परावर्तन
- उज्ज्वल दीपक
- द्वितीय विश्व युद्ध के दौरान प्रौद्योगिकी
- शोर (इलेक्ट्रॉनिक्स)
- फिल्टर सिद्धांत
- डिप्लेक्सर
- हार्मोनिक विकृति
- आस्पेक्ट अनुपात
- लॉर्ड रेले
- हंस बेथे
- संतुलित जोड़ी
- असंतुलित रेखा
- भिन्नात्मक बैंडविड्थ
- स्वतंत्रता की डिग्री (भौतिकी और रसायन विज्ञान)
- देरी बराबरी
- अधिष्ठापन
- लाइनों के संचालन पर संकेतों का प्रतिबिंब
- परावर्तन गुणांक
- कसने वाला नट
- कम तापमान सह-निकाल दिया सिरेमिक
- हवाई जहाज
- परावैद्युतांक
- ऊष्मीय चालकता
- वैफ़ल आयरन
- नकारात्मक प्रतिरोध एम्पलीफायर
- आधार मिलान
- इस्पात मिश्र धातु
- लाउडस्पीकर बाड़े
- ताकत
- दोहरी प्रतिबाधा
- गांठदार-तत्व मॉडल
- गैरपेशेवर रेडियो
- भंवर धारा
- चीनी मिट्टी
- विद्युत यांत्रिक युग्मन गुणांक
- भाग प्रति अरब
- आपसी अधिष्ठापन
- शिखर से शिखर तक
- वारैक्टर
- पीस (अपघर्षक काटने)
- स्पंदित लेजर बयान
- ध्रुव (जटिल विश्लेषण)
- कम उत्तीर्ण
- ऑपरेशनल एंप्लीफायर
- YIG क्षेत्र
- अनुरूप संकेत
- सभा की भाषा
- घुमाव
- निश्चित बिंदु अंकगणित
- डेटा पथ
- पता पीढ़ी इकाई
- बुंदाडा इटाकुरा
- मोशन वेक्टर
- SE444
- गति मुआवजा
- भाषा संकलन
- पीएमओएस तर्क
- तंग पाश
- अंकगणितीय तर्क इकाई
- ट्राईमीडिया (मीडिया प्रोसेसर)
- कृत्रिम होशियारी
- एक चिप पर सिस्टम
- पुनर्निर्माण फिल्टर
- नमूनाकरण (सिग्नल प्रोसेसिंग)
- तेजी से अनुमानित एंटी-अलियासिंग
- नमूनाचयन आवृत्ति
- डिजीटल
- फ़िल्टर बैंक
- स्थानीय थरथरानवाला
- सुपरहेटरोडाइन रिसीवर
- यव (रोटेशन)
- चूरा लहर
- पीजोइलेक्ट्रिक सामग्री की सूची
- स्कैनिंग जांच माइक्रोस्कोपी
- पिकअप (संगीत प्रौद्योगिकी)
- विद्युतीय संभाव्यता
- टोपाज़
- पहला विश्व युद्ध
- गूंज (घटना)
- गन्ना की चीनी
- वेक्टर क्षेत्र
- चार्ज का घनत्व
- खिसकाना
- वोइगट नोटेशन
- मैडेलुंग स्थिरांक
- लिथियम टैंटलेट
- पीतल
- काल्कोजन
- ध्रुवीय अर्धचालकों में गैर रेखीय पीजोइलेक्ट्रिक प्रभाव
- पैरीलीन
- फोजी
- संपर्क माइक्रोफ़ोन
- गैर विनाशकारी परीक्षण
- उठाओ (संगीत प्रौद्योगिकी)
- स्कैनिंग टनलिंग माइक्रोस्कोप
- रॉबर्ट बॉश GmbH
- चुम्बकीय अनुनाद इमेजिंग
- सार्वजनिक रेल
- गुहिकायन
- उच्च तीव्रता केंद्रित अल्ट्रासाउंड
- थरथरानवाला
- घड़ी की नाड़ी
- टकराव
- तार की रस्सी
- अत्यंत सहनशक्ति
- उपज (इंजीनियरिंग)
- लोहे के अपरूप
- समुंद्री जहाज
- क्रिस्टल लैटिस
- हथियार, शस्त्र
- आधारभूत संरचना
- रॉकेट्स
- अस्थिभंग बेरहमी
- एनीलिंग (धातु विज्ञान)
- तड़के (धातु विज्ञान)
- औजार
- ग्रीनहाउस गैस का उत्सर्जन
- बोरान
- अलॉय स्टील
- ताँबा
- नरम लोहा
- क्रस्ट (भूविज्ञान)
- लकड़ी का कोयला
- धातु थकान
- निष्क्रियता (रसायन विज्ञान)
- उच्च गति स्टील
- प्रमुख
- कमरे का तापमान
- शरीर केंद्रित घन
- चेहरा केंद्रित घन
- अनाज सीमाएं
- तलछट
- शरीर केंद्रित चतुष्कोणीय
- अपरूपण तनाव
- काम सख्त
- शारीरिक संपीड़न
- अनाज के आकार में वृद्धि
- वसूली (धातु विज्ञान)
- उष्मा उपचार
- निरंतर ढलाई
- इनगट
- कास्टिंग (धातु का काम)
- हॉट रोलिंग
- इबेरिआ का प्रायद्वीप
- श्री लंका
- युद्धरत राज्यों की अवधि
- हान साम्राज्य
- क्लासिकल एंटिक्विटी
- Tissamaharama तमिल ब्राह्मी शिलालेख
- चेरा डायनेस्टी
- पैगोपोलिस के ज़ोसिमोस
- तत्व का पता लगाएं
- कम कार्बन अर्थव्यवस्था
- गीत राजवंश
- फाइनरी फोर्ज
- तुलसी ब्रुक (धातुकर्मी)
- मामले को मजबूत बनाना
- लौह अयस्क
- खुली चूल्हा भट्टी
- उत्थान और पतन
- इस्पात उत्पादकों की सूची
- कम मिश्र धातु स्टील
- एचएसएलए स्टील
- दोहरे चरण स्टील
- हॉट डिप गल्वनाइजिंग
- तेजी से सख्त होना
- बढ़ने की योग्यता
- जिंदगी के जबड़े
- नाखून (इंजीनियरिंग)
- हाथ - या
- खुदाई
- लुढ़का सजातीय कवच
- सफेद वस्तुओं
- इस्पात की पतली तारें
- छुरा
- ओवरहेड पावर लाइन
- घड़ी
- परमाणु हथियार परीक्षण
- मशीन की
- ताप विस्तार प्रसार गुणांक
- नकारात्मक प्रतिपुष्टि
- गर्म करने वाला तत्व
- घड़ी
- कैल्शियम मानक
- अरेखीय प्रकाशिकी
- धरती
- मणि पत्थर
- मोह पैमाने की कठोरता
- खरोंच कठोरता
- पूर्व मध्य जर्मन
- मध्य उच्च जर्मन
- प्राचीन यूनानी
- पारदर्शिता और पारदर्शिता
- सकल (भूविज्ञान)
- कैल्सेडनी
- सुलेमानी पत्थर
- बिल्लौर
- बैंगनी रंग)
- नीला रंग)
- खनिज कठोरता का मोह पैमाना
- क्षुद्रग्रह (रत्न विज्ञान)
- मैंने
- एराइड आइलैंड
- सेशल्स
- तलछटी पत्थर
- रूपांतरित चट्टान
- धरती
- परिपक्वता (तलछट विज्ञान)
- नस (भूविज्ञान)
- सेमीकंडक्टर
- बटन लगाना
- पत्थर का औजार
- पाषाण प्रौद्योगिकी
- आयरलैंड का गणराज्य
- पूर्व-कोलंबियाई युग
- पियर्स थरथरानवाला
- पतली फिल्म मोटाई मॉनिटर
- ट्यूनेड सर्किट
- पेंडुलम क्लॉक
- बेल लेबोरेटरीज
- ट्यूनिंग कांटा
- एलसी थरथरानवाला
- सामरिक सामग्री
- एचिंग
- सतह ध्वनिक तरंग
- समावेशन (खनिज)
- जिंक आक्साइड
- नव युवक
- गैस निकालना
- शॉक (यांत्रिकी)
- जी बल
- रासायनिक चमकाने
- प्रति-चुंबकीय
- रैंडम संख्या जनरेटर
- दिमाग
- कंपन
- विवेक
- लोंगिट्युडिनल वेव
- डायाफ्राम (ध्वनिकी)
- प्रतिबिंब (भौतिकी)
- श्यानता
- वस्तुस्थिति
- विरल करना
- समतल लहर
- ध्वनि का दबाव
- ध्वनि तीव्रता
- रुद्धोष्म प्रक्रिया
- आपेक्षिक यूलर समीकरण
- वर्गमूल औसत का वर्ग
- वर्गमूल औसत का वर्ग
- जवाबदेही
- आवृत्तियों
- बर्ड वोकलिज़ेशन
- समुद्री स्तनधारियों
- सस्तन प्राणी
- हीड्रास्फीयर
- प्रबलता
- शिकार
- भाषण संचार
- श्वेत रव
- ध्वनिरोधन
- सोनार
- रॉयल सोसाइटी के फेलो
- रडार अनुसंधान प्रतिष्ठान
- रॉयल सिग्नल और रडार स्थापना
- रेले तरंगें
- एचएफई वंशानुगत हेमोक्रोमैटोसिस
- लौह अधिभार
- ध्वनिकी संस्थान (यूनाइटेड किंगडम)
- गैबर मेडल
- हाइब्रिड इंटीग्रेटेड सर्किट
- खास समय
- समय क्षेत्र
- मैक्सिम इंटीग्रेटेड प्रोडक्ट्स
- प्यार की तरंगे
- लोंगिट्युडिनल वेव
- देखा फिल्टर
- एलसी फिल्टर
- सतह ध्वनिक तरंग सेंसर
- टॉर्कः
- चरण बंद लूप
- भूकंप का झटका
- फोनोन
- qubit
- स्पिन वेव
- क्वांटम जानकारी
- ध्वनिक-विद्युत प्रभाव
- बहाव का वेग
- जेट (द्रव)
- मिश्रण (प्रक्रिया इंजीनियरिंग)
- छोटी बूंद आधारित माइक्रोफ्लुइडिक्स
- अर्ध-लहर द्विध्रुव
- सकारात्मक आरोप
- प्रेरित तत्व
- विकिरण स्वरुप
- विद्युतचुम्बकीय तरंगें
- लॉग-आवधिक एंटीना
- चरणबद्ध व्यूह रचना
- चुंबकीय पाश एंटीना
- काउंटरपोइज़ (ग्राउंड सिस्टम)
- जमीन (बिजली)
- तांबे का नुकसान
- फोकस (प्रकाशिकी)
- गैरपेशेवर रेडियो
- दिशिकता
- लाभ (विद्युत चुम्बकीय)
- कम शोर एम्पलीफायर
- शून्य (रेडियो)
- चरणबद्ध
- वोर्सिगट एंटीना
- फील्ड की छमता
- प्रतिबाधा मैच
- लाइन-ऑफ़-विज़न प्रसार
- दाहिने हाथ का नियम
- विशिष्टता (तकनीकी मानक)
- आकाश की लहर
- परावर्तक प्रतिबिंब
- व्युत्क्रम वर्ग नियम
- ऊर्जा घटक
- एंटीना प्रकार
- लौहचुंबकीय
- स्थिर हरा
- रेखा की चौडाई
- YIG फ़िल्टर
- प्रकाश तरंगदैर्घ्य
- solenoid
- इन्सुलेटर (बिजली)
- चुंबकीय क्षेत्र
- गति देनेवाला
- पार्टिकल एक्सेलेटर
- प्रेरण ऊष्मन
- चुंबकीय ताला
- एम्पीयर-टर्न
- अरेखीय
- सीमित तत्व विधि
- remanence
- चुंबकीय परिपथ
- टेस्ला (इकाई)
- चुम्बकीय भेद्यता
- वयर्थ ऊष्मा
- एकदिश धारा
- इलेक्ट्रिक आर्क
- चुंबकीय क्षेत्र रेखाएं
- फाड़ना
- भंवर धारा
- हिस्टैरिसीस हानि
- क्षेत्र रेखा
- प्रत्यारोपण (यांत्रिक प्रक्रिया)
- पदार्थ विज्ञान
- परमाणु क्रमांक
- आइसोटोप
- श्वसन संबंधी रोग
- तत्व का पता लगाएं
- Ytterby
- वैद्युतीयऋणात्मकता
- समूह 3 तत्व
- भाप
- संयोजकता (रसायन विज्ञान)
- यट्रियम (III) ऑक्साइड
- घुलनशीलता
- यट्रियम (III) फ्लोराइड
- यट्रियम (III) क्लोराइड
- ऑर्गेनोयट्रियम केमिस्ट्री
- ट्रिमराइज़ेशन
- सौर प्रणाली
- न्यूट्रॉन कैप्चर
- मीरा
- परमाणु कचरा
- हाफ लाइफ
- निम्नतम अवस्था
- समावयवी संक्रमण
- जोहान गैडोलिन
- पृथ्वी (रसायन विज्ञान)
- येट्रियम बेरियम कॉपर ऑक्साइड
- ज़ेनोटाइम
- भाग प्रति दस लाख
- स्तन का दूध
- पत्ता गोभी
- परमाणु भार
- माउंटेन पास रेयर अर्थ माइन
- येट्रियम फ्लोराइड
- सीआरटी टेलीविजन
- यत्रियम आयरन गार्नेट
- हीरा
- दोपंत
- थर्मल विस्तार
- नस
- मेरुदण्ड
- रूमेटाइड गठिया
- वाईबीसीओ
- बिजली के वाहन
- रंग
- फुफ्फुसीय शोथ
- व्यावसायिक सुरक्षा और स्वास्थ्य प्रसाशन
- अनुशंसित जोखिम सीमा
- अनाज की सीमा
- क्रिस्टलोग्राफी
- क्रिस्टलोग्राफिक दोष
- एनिस्ट्रोपिक
- अपवित्रता
- पुन: क्रिस्टलीकरण (रसायन विज्ञान)
- किरोपोलोस विधि
- वर्न्यूइल विधि
- तरल चरण एपिटॉक्सी
- फील्ड इफ़ेक्ट ट्रांजिस्टर
- राष्ट्रीय प्रज्वलन सुविधा
- अतिसंतृप्ति
- इलेक्ट्रिकल कंडक्टीविटी
- इंटरनेशनल एनील्ड कॉपर स्टैंडर्ड
- भूतल विज्ञान
- संघनित पदार्थ भौतिकी
- हीलियम परमाणु प्रकीर्णन
- क्रिस्टल की संरचना
- कम ऊर्जा इलेक्ट्रॉन विवर्तन
- कोण-समाधानित प्रकाश उत्सर्जन स्पेक्ट्रोस्कोपी
- आंशिक क्रिस्टलीकरण (रसायन विज्ञान)
- अलकाली धातु
- सीज़ियम-133
- नापाक
- दूसरा
- रेडियोआइसोटोप
- उत्सर्जन चित्र
- लचीलापन
- चमक (खनिज)
- प्रकाश द्वारा सहज प्रभावित
- दाढ़ एकाग्रता
- क्षारीय धातु
- कटियन
- ऋणायन
- अरहेनियस बेस
- काल्कोजन
- लुईस बेस
- सीज़ियम फ्लोराइड
- आदिम कोशिका
- जन अंक
- नाभिकीय चुबकीय अनुनाद
- परमाणु समावयवी
- विखंडन उत्पाद उपज
- खर्च किया गया परमाणु ईंधन
- आयोडीन के समस्थानिक
- पृथ्वी का वातावरण
- परमाणु नतीजा
- भाग प्रति दस लाख
- फिटकिरी
- निक्षालन (धातु विज्ञान)
- शुद्ध पानी
- एल्कलाइन अर्थ मेटल
- परमाण्विक भार
- माध्यमिक आयन मास स्पेक्ट्रोमेट्री
- तौल और माप पर सामान्य सम्मेलन
- निष्कर्षण तेल उद्योग
- पूर्णता (तेल और गैस के कुएं)
- डिफरेंशियल सेंट्रीफ्यूजेशन
- ऑर्गेनेल
- कार्बनिक रसायन शास्त्र
- विकिरण उपचार
- सीज़ियम के समस्थानिक
- भड़कना (आतिशबाजी)
- मिरगी
- फेशबैक प्रतिध्वनि
- क्वांटम तकनीक
- हृदय गति रुकना
- ऑटो ज्वलन ताप
- बीओस्फिअ
- अंतरराष्ट्रीय परमाणु ऊर्जा एजेंसी
- गंदा बम
- मेपल के पेड़ दुर्घटना
- बिल्लौर
- रोशनी
- चमक (खनिज)
- सुसंगतता (भौतिकी)
- पराग
- समलौत जिला
- उत्तर मैसेडोनिया गणराज्य
- उत्तरी केरोलिना
- दोपंत
- धारियाँ
- नियामक माप मशीन
- प्राकृतिक इतिहास का राष्ट्रीय संग्रहालय
- प्रेरित उत्सर्जन
- ईसा पूर्व
- उत्तर सिल्क रोड
- पुराना वसीयतनामा
- नीतिवचन की किताब
- पलायन की किताब
- रवि
- एनीओलाइट
- चौगुनी आयन जाल
- संगति (भौतिकी)
- भौतिकी में नोबेल पुरस्कार
- कोलम्बिया विश्वविद्यालय
- कानाफूसी-गैलरी लहर
- पेंटासीन
- भौतिक विज्ञान की ठोस अवस्था
- राष्ट्रीय भौतिक प्रयोगशाला (यूनाइटेड किंगडम)
- पी-टेरफिनाइल
- कृत्रिम हीरा
- अंतरिक्ष यान
- मंगल ग्रह
- जनसंख्या का ह्रास
- चरण बंद लूप
- कट्टरपंथी (रसायन विज्ञान)
- विद्युत चुम्बकीय वर्णक्रम
- सितारा
- सक्रिय गांगेय नाभिक
- दृश्य प्रकाश
- उपनाम (सीजन 3)
- काइजु
- उपनाम (टीवी श्रृंखला)
- गुणक
- मीटर
- शून्य समारोह
- फ़ंक्शन का डोमेन
- कम शर्तें
- समाशोधन भाजक
- एक बीजीय किस्म की डिग्री
- मूल्य (गणित)
- निरंतर कार्य
- समान शब्द
- पुनरावृत्ति संबंध
- स्थायी अवधि
- आंशिक अंश
- जियोमीट्रिक श्रंखला
- निर्माण कार्य
- अद्वितीय गुणनखंड डोमेन
- अपरिवर्तनीय अंश
- सार बीजगणित
- समन्वय की अंगूठी
- एक बीजीय किस्म का कार्य क्षेत्र
- कंप्यूटर बीजगणित प्रणाली