सांकेतिक ग्राफ: Difference between revisions
(TEXT) |
(TEXT) |
||
| Line 1: | Line 1: | ||
{{Short description|Graph with sign-labeled edges}} | {{Short description|Graph with sign-labeled edges}} | ||
[[File:Pox.jpg|thumb|एक त्रिकोण की भुजाओं के लिए चिन्हों को आठ | [[File:Pox.jpg|thumb|एक त्रिकोण की भुजाओं के लिए चिन्हों को आठ प्रकार से निर्दिष्ट किया जा सकता है। [[फ्रिट्ज हैडर]] के सिद्धांत के अनुसार, विषम संख्या में ऋणात्मक चिह्न एक असंतुलित त्रिभुज बनाते हैं।]]गणित में आलेख सिद्धांत के क्षेत्र में, चिन्हित आलेख एक आलेख होता है जिसमें प्रत्येक किनारे पर एक धनात्मक या ऋणात्मक चिह्न होता है। | ||
एक | एक चिन्हित आरेख संतुलित होता है यदि हर चक्र के किनारे के संकेतों का उत्पाद धनात्मक होता है। <nowiki>''चिन्हित आरेख''</nowiki> नाम और संतुलन की धारणा पहली बार 1953 में [[फ्रैंक हैरिस|फ्श्रेणी हैरी]] के एक गणितीय लेख में दिखाई देती है।<ref name=harnb>{{citation|last=Harary |first=Frank |author-link=Frank Harary |journal=[[Michigan Mathematical Journal]] |mr=0067468 |pages=143–146 |title=On the notion of balance of a signed graph |url=http://projecteuclid.org/getRecord?id=euclid.mmj/1028989917 |archive-url=https://archive.today/20130415153307/http://projecteuclid.org/getRecord?id=euclid.mmj/1028989917 |url-status=dead |archive-date=2013-04-15 |volume=2 |year=1955}}</ref> डेन्स कोनिग ने पहले से ही 1936 में एक अलग शब्दावली के अंतर्गत समतुल्य धारणाओं का अध्ययन किया था, लेकिन चिन्ह समूह की प्रासंगिकता को पहचाने बिना किया था।<ref name=koenig>{{citation | last = Kőnig | first = Dénes | author-link = Dénes Kőnig | editor = [[Akademische Verlagsgesellschaft]] | title = Theorie der endlichen und unendlichen Graphen | year = 1936 }}</ref> मिशिगन विश्वविद्यालय में समूह गतिशीलता के केंद्र में, [[डोरविन कार्टराईट]] और हैरी ने फ्रिट्ज हैडर के मनोवैज्ञानिक सिद्धांत के त्रिकोण में संतुलन के मनोवैज्ञानिक सिद्धांत को चिन्हित रेखांकन में [[संतुलन सिद्धांत|संतुलन]] के मनोवैज्ञानिक सिद्धांत के रूप में सामान्यीकृत किया था।<ref name=carhar>{{cite journal |last1=Cartwright |first1=D. |first2=Frank |last2=Harary |year=1956 |title=Structural balance: a generalization of Heider's theory |journal=[[Psychological Review]] |volume=63 |issue=5 |pages=277–293 |doi=10.1037/h0046049 |pmid=13359597 |url=https://snap.stanford.edu/class/cs224w-readings/cartwright56balance.pdf }}</ref><ref>[[Steven Strogatz]] (2010), [http://opinionator.blogs.nytimes.com/2010/02/14/the-enemy-of-my-enemy/?ref=opinion&_r=0 The enemy of my enemy], The [[New York Times]], February 14, 2010</ref> | ||
चिन्हित रेखांकन बहुत बार पुनः खोजे गए हैं क्योंकि वे कई असंबद्ध क्षेत्रों में स्वाभाविक रूप से सामने आते हैं।<ref>{{citation | |||
| last = Zaslavsky | first = Thomas | | last = Zaslavsky | first = Thomas | ||
| journal = Electronic Journal of Combinatorics | | journal = Electronic Journal of Combinatorics | ||
| Line 15: | Line 15: | ||
== मूलभूत प्रमेय == | == मूलभूत प्रमेय == | ||
एक पथ का चिह्न उसके किनारों के चिह्नों का गुणनफल होता है। इस प्रकार एक पथ तभी धनात्मक होता है जब उसमें सम संख्या में ऋणात्मक किनारे हों (जहाँ शून्य सम है)। | एक पथ का चिह्न उसके किनारों के चिह्नों का गुणनफल होता है। इस प्रकार एक पथ तभी धनात्मक होता है जब उसमें सम संख्या में ऋणात्मक किनारे हों (जहाँ शून्य सम है)। फ्श्रेणी हैरी के गणितीय संतुलन सिद्धांत में, प्रत्येक चक्र धनात्मक होने पर एक चिन्हित आरेख संतुलित होता है। हैरी सिद्ध करता है कि एक चिन्हित आरेख संतुलित होता है जब (1) नोड्स के प्रत्येक जोड़े के लिए, उनके मध्य के सभी पंथ का एक ही चिह्न होता है, या (2) शीर्षों को उपसमुच्चय (संभवतः रिक्त) की एक जोड़ी में विभाजित किया जाता है, प्रत्येक में केवल धनात्मक किनारे होते हैं, लेकिन ऋणात्मक किनारों से जुड़े होते हैं।<ref name="harnb" /> यह प्रमेय का सामान्यीकरण करता है कि एक साधारण (अचिन्हित) आरेख द्विभाज्य होता है यदि और केवल यदि प्रत्येक चक्र की लंबाई समान होती है। | ||
एक साधारण प्रमाण स्विचिंग की विधि का उपयोग करता है। एक | एक साधारण प्रमाण स्विचिंग की विधि का उपयोग करता है। एक चिन्हित आलेख को स्विच करने का अर्थ है शीर्ष उपसमुच्चय और उसके पूरक के मध्य सभी किनारों के संकेतों को उत्क्रम कर देना है। हैरी के प्रमेय को सिद्ध करने के लिए, प्रेरण द्वारा दिखाया गया है कि Σ को सभी धनात्मक होने के लिए स्विच किया जा सकता है अगर यह संतुलित है। | ||
एक मंद प्रमेय, लेकिन एक सरल प्रमाण के साथ, यह है कि यदि | एक मंद प्रमेय, लेकिन एक सरल प्रमाण के साथ, यह है कि यदि चिन्हित पूर्ण आलेख में प्रत्येक 3-चक्र धनात्मक है, तो आलेख संतुलित है। प्रमाण के लिए, एक स्वेच्छाचारी नोड ''n'' का चयन करे और इसे और उन सभी नोड्स को रखें जो ''n'' से एक समूह में धनात्मक किनारे से जुड़े होते हैं, जिन्हें ''A'' कहा जाता है, और वे सभी जो n से दूसरे में एक ऋणात्मक किनारे से जुड़े हैं, जिसे ''B'' कहा जाता है क्योंकि यह एक पूर्ण आरेख है, ''A'' में प्रत्येक दो नोड मित्र होने चाहिए और ''B'' में प्रत्येक दो नोड मित्र होने चाहिए, अन्यथा एक 3-चक्र होगा जो असंतुलित था। (क्योंकि यह एक पूर्ण आरेख है, कोई भी ऋणात्मक किनारा असंतुलित 3-चक्र का कारण होगा।) इसी तरह, सभी ऋणात्मक किनारों को दो समूहों के मध्य जाना चाहिए।<ref>[http://www.scienceoftheweb.org/15-396/lectures/lecture03.pdf Luis Von Ahn Science of the Web Lecture 3 p. 28]</ref> | ||
== कुंठा == | == कुंठा == | ||
| Line 29: | Line 29: | ||
एक और समतुल्य परिभाषा है (जिसे स्विच करके आसानी से सिद्ध किया जा सकता है)। प्रत्येक शीर्ष को +1 या -1 का मान दें; हम इसे Σ की स्थिति कहते हैं। एक किनारे को संतुष्ट कहा जाता है यदि यह धनात्मक है और दोनों समापन बिंदुओं का मान समान है, या यह ऋणात्मक है और अंत बिंदुओं के विपरीत मान हैं। एक किनारा जो संतुष्ट नहीं होता है उसे कुंठा कहा जाता है। सभी अवस्था में कुंठित किनारों की सबसे छोटी संख्या कुंठा सूचकांक है। यह परिभाषा पहली बार एबेलसन और रोसेनबर्ग द्वारा (अप्रचलित) नाम सम्मिश्रता के अंतर्गत एक अलग संकेतन में प्रस्तावित की गई थी।<ref>Robert P. Abelson; Milton J. Rosenberg (1958), Symbolic psycho-logic: a model of attitudinal cognition, ''Behavioral Science'' 3, 1–13.</ref> ऐसे समुच्चय का पूरक सबसे संभावित किनारों के साथ Σ का संतुलित उपआरेख है। | एक और समतुल्य परिभाषा है (जिसे स्विच करके आसानी से सिद्ध किया जा सकता है)। प्रत्येक शीर्ष को +1 या -1 का मान दें; हम इसे Σ की स्थिति कहते हैं। एक किनारे को संतुष्ट कहा जाता है यदि यह धनात्मक है और दोनों समापन बिंदुओं का मान समान है, या यह ऋणात्मक है और अंत बिंदुओं के विपरीत मान हैं। एक किनारा जो संतुष्ट नहीं होता है उसे कुंठा कहा जाता है। सभी अवस्था में कुंठित किनारों की सबसे छोटी संख्या कुंठा सूचकांक है। यह परिभाषा पहली बार एबेलसन और रोसेनबर्ग द्वारा (अप्रचलित) नाम सम्मिश्रता के अंतर्गत एक अलग संकेतन में प्रस्तावित की गई थी।<ref>Robert P. Abelson; Milton J. Rosenberg (1958), Symbolic psycho-logic: a model of attitudinal cognition, ''Behavioral Science'' 3, 1–13.</ref> ऐसे समुच्चय का पूरक सबसे संभावित किनारों के साथ Σ का संतुलित उपआरेख है। | ||
कुंठा सूचकांक खोजना एक [[NP-कठिन]] समस्या है। अरेफ एट अल द्विआधारी क्रमादेश निदर्श का सुझाव देते हैं जो उचित समय में 105 किनारों तक आरेख के कुंठा सूचकांक की गणना करने में सक्षम हैं।<ref>{{cite arXiv|last1=Aref|first1=Samin|last2=Mason|first2=Andrew J.|last3=Wilson|first3=Mark C.|date=2019|title=हस्ताक्षरित नेटवर्क में हताशा सूचकांक का एक मॉडलिंग और कम्प्यूटेशनल अध्ययन|eprint=1611.09030|class=cs.SI}}</ref><ref>{{Citation|last1=Aref|first1=Samin|title=Computing the Line Index of Balance Using Integer Programming Optimisation|date=2018|work=Optimization Problems in Graph Theory: In Honor of Gregory Z. Gutin's 60th Birthday|pages=65–84|editor-last=Goldengorin|editor-first=Boris|series=Springer Optimization and Its Applications|publisher=Springer International Publishing|language=en|doi=10.1007/978-3-319-94830-0_3|isbn=9783319948300|last2=Mason|first2=Andrew J.|last3=Wilson|first3=Mark C.|arxiv=1710.09876|s2cid=27936778}}</ref><ref>{{Cite journal|last1=Aref|first1=Samin|last2=Wilson|first2=Mark C|date=2019-04-01|editor-last=Estrada|editor-first=Ernesto|title=हस्ताक्षरित नेटवर्क में संतुलन और हताशा|journal=Journal of Complex Networks|language=en|volume=7|issue=2|pages=163–189|doi=10.1093/comnet/cny015|issn=2051-1329|arxiv=1712.04628}}</ref> कोई भी [[NP-कठिन]] सम्मिश्रता देख सकता है कि सभी-ऋणात्मक | कुंठा सूचकांक खोजना एक [[NP-कठिन]] समस्या है। अरेफ एट अल द्विआधारी क्रमादेश निदर्श का सुझाव देते हैं जो उचित समय में 105 किनारों तक आरेख के कुंठा सूचकांक की गणना करने में सक्षम हैं।<ref>{{cite arXiv|last1=Aref|first1=Samin|last2=Mason|first2=Andrew J.|last3=Wilson|first3=Mark C.|date=2019|title=हस्ताक्षरित नेटवर्क में हताशा सूचकांक का एक मॉडलिंग और कम्प्यूटेशनल अध्ययन|eprint=1611.09030|class=cs.SI}}</ref><ref>{{Citation|last1=Aref|first1=Samin|title=Computing the Line Index of Balance Using Integer Programming Optimisation|date=2018|work=Optimization Problems in Graph Theory: In Honor of Gregory Z. Gutin's 60th Birthday|pages=65–84|editor-last=Goldengorin|editor-first=Boris|series=Springer Optimization and Its Applications|publisher=Springer International Publishing|language=en|doi=10.1007/978-3-319-94830-0_3|isbn=9783319948300|last2=Mason|first2=Andrew J.|last3=Wilson|first3=Mark C.|arxiv=1710.09876|s2cid=27936778}}</ref><ref>{{Cite journal|last1=Aref|first1=Samin|last2=Wilson|first2=Mark C|date=2019-04-01|editor-last=Estrada|editor-first=Ernesto|title=हस्ताक्षरित नेटवर्क में संतुलन और हताशा|journal=Journal of Complex Networks|language=en|volume=7|issue=2|pages=163–189|doi=10.1093/comnet/cny015|issn=2051-1329|arxiv=1712.04628}}</ref> कोई भी [[NP-कठिन]] सम्मिश्रता देख सकता है कि सभी-ऋणात्मक चिन्हित आलेख की कुंठा सूचकांक आलेख सिद्धांत में [[मैक्सकट|अधिकतम]] कमी समस्या के समान है, जो [[NP-कठिन]] है। | ||
[[स्पिन ग्लास|प्रचक्रण ग्लास]] के एक निदर्श, मिश्रित आइसिंग निदर्श में कुंठा सूचकांक महत्वपूर्ण है। इस निदर्श में, | [[स्पिन ग्लास|प्रचक्रण ग्लास]] के एक निदर्श, मिश्रित आइसिंग निदर्श में कुंठा सूचकांक महत्वपूर्ण है। इस निदर्श में, चिन्हित आरेख निश्चित है। एक स्थिति में प्रत्येक शीर्ष पर "प्रचक्रण", या तो "ऊपर" या "नीचे" सम्मलित है। हम प्रचक्रण अप को +1 और प्रचक्रण डाउन को -1 मानते हैं। इस प्रकार, प्रत्येक अवस्था में कई कुंठित किनारे हैं। एक अवस्था की ऊर्जा तब बड़ी होती है जब उसके पास अधिक कुंठित किनारे होते हैं, इसलिए एक मूल अवस्था सबसे कम कुंठित ऊर्जा वाली अवस्था होती है। इस प्रकार, $$\ $ की मूल अवस्था ऊर्जा का पता लगाने के लिए किसी को कुंठा सूचकांक का पता लगाना होता है। | ||
=== कुंठा संख्या === | === कुंठा संख्या === | ||
| Line 37: | Line 37: | ||
== कलनविधीय समस्याएं == | == कलनविधीय समस्याएं == | ||
चिन्हित आलेख के विषय में तीन मूलभूत प्रश्न हैं: क्या यह संतुलित है? इसमें समुच्चय किए गए संतुलित किनारे का सबसे बड़ा आकार क्या है? इसे संतुलित करने के लिए हटाए जाने वाले[[ शीर्ष (ग्राफ सिद्धांत) | शीर्षों]] की सबसे छोटी संख्या क्या है? बहुपद काल में पहला प्रश्न का समाधान करना आसान है। दूसरे प्रश्न को कुंठा सूचकांक या अधिकतम संतुलित उपआरेख समस्या कहा जाता है। यह NP-कठिन है क्योंकि इसका विशेष प्रकरण (जब आरेख के सभी किनारे ऋणात्मक हैं) NP-कठिन समस्या अधिकतम कमी है। तीसरे प्रश्न को कुंठा संख्या या अधिकतम संतुलित प्रेरित उपआरेख समस्या कहा जाता है, यह NP-कठिन भी है; उदाहरण देखें<ref name=ggmz>{{cite journal |last1=Gülpinar |first1=N. |first2=G. |last2=Gutin |author-link2=Gregory Gutin|first3=G. |last3=Mitra |first4=A. |last4=Zverovitch |year=2004 |title=हस्ताक्षरित रेखांकन का उपयोग करके रैखिक कार्यक्रमों में शुद्ध नेटवर्क सबमैट्रिसेस निकालना|journal=[[Discrete Appl. Math.]] |volume=137 |issue=3 |pages=359–372|doi=10.1016/S0166-218X(03)00361-5 }}</ref> | |||
== मैट्रोइड सिद्धांत == | == मैट्रोइड सिद्धांत == | ||
एक | एक चिन्हित आलेख से जुड़े दो मैट्रोइड्स हैं, जिन्हें चिन्ह-आलेखिक [[ matroid |मैट्रॉइड]] कहा जाता है (जिसे फ़्रेम मैट्रॉइड या कभी-कभी अभिनति मैट्रोइड भी कहा जाता है) और लिफ्ट मैट्रोइड, जो दोनों एक आलेख के चक्र मैट्रॉइड को सामान्य करते हैं। वे [[पक्षपाती ग्राफ|अभिनत आरेख]] के समान मैट्रोइड्स के विशेष प्रकरण हैं। | ||
'फ़्रेम मेट्रॉइड' (या 'चिन्ह-आलेखिक मैट्रॉइड') M(G) ने | 'फ़्रेम मेट्रॉइड' (या 'चिन्ह-आलेखिक मैट्रॉइड') M(G) ने इसके आधार समुच्चय के लिए कोर समुच्चय E के लिए है।<ref>{{citation | last = Zaslavsky | first = Thomas|author-link=Thomas Zaslavsky| doi = 10.1016/0166-218X(82)90033-6 | issue = 1 | journal = [[Discrete Applied Mathematics]] | mr = 676405 | pages = 47–74 | title = Signed graphs | volume = 4 | year = 1982| hdl = 10338.dmlcz/127957 | hdl-access = free }}. Erratum. ''Discrete Applied Mathematics'', '''5''' (1983), 248</ref> एक कोर समुच्चय स्वतंत्र होता है यदि प्रत्येक घटक में या तो कोई वृत्त नहीं होता है या केवल एक वृत्त होता है, जो ऋणात्मक होता है। ([[ मैट्रोइड सिद्धांत |मैट्रोइड सिद्धांत]] में एक अर्ध-कोर यथार्थत: ऋणात्मक लूप की तरह काम करता है।) मैट्रॉइड का एक परिपथ या तो एक धनात्मक वृत्त होता है, या एक संयोजक सामान्य पाथ के साथ ऋणात्मक वृत्त का एक जोड़ा होता है, जैसे कि दो वृत्त या तो अलग हो जाते हैं (फिर संयोजक पथ में प्रत्येक वृत्त के साथ सामान्य एक अंत होता है और अन्यथा दोनों से अलग होता है) या केवल एक सामान्य शीर्ष अनुकरण करें (इस प्रकरण में संयोजक पथ वह एकल शीर्ष है)। कोर समुच्चय S की कोटि n - b है, जहाँ n, G के शीर्षों की संख्या है और b, S के संतुलित घटकों की संख्या है, पृथक शीर्षों को संतुलित घटकों के रूप में गिना जाता है। यह मेट्रॉइड चिन्हित आलेख के आपतन आव्यूह का स्तंभ मेट्रॉइड है। यही कारण है कि यह प्राचीन मूल तंत्र की मूलांश की रैखिक निर्भरताओं का वर्णन करता है। | ||
यह | |||
यही कारण है कि यह प्राचीन | |||
'विस्तारित लिफ्ट मैट्रॉइड' | 'विस्तारित लिफ्ट मैट्रॉइड' ''L''<sub>0</sub>(''G'') ने अपने आधार के लिए समुच्चय ''E''<sub>0</sub> को कोर समुच्चय E के एक अतिरिक्त बिंदु के साथ समुच्चय किया है, जिसे हम ''e''<sub>0</sub> से निरूपित करते है। लिफ्ट मैट्रॉइड ''L''(''G'') ''E'' तक सीमित विस्तारित लिफ्ट मैट्रॉइड है। अतिरिक्त बिंदु यथार्थत: ऋणात्मक लूप की तरह फलन करता है, इसलिए हम केवल लिफ्ट मैट्रॉइड का वर्णन करते हैं। एक किनारे का समुच्चय स्वतंत्र होता है यदि इसमें या तो कोई वृत्त नहीं होता है या केवल एक वृत्त होता है, जो ऋणात्मक होता है। (यह वही नियम है जो चिन्हित-आलेखिक मैट्रोइड में प्रत्येक घटक के लिए अलग से उपयोजित होता है।) एक मैट्रॉइड परिपथ या तो एक धनात्मक वृत्त या ऋणात्मक वृत्तों की एक जोड़ा होता है जो या तो अलग हैं या केवल एक सामान्य शीर्ष है। कोर समुच्चय ''S'' की श्रेणी ''n'' - ''c'' + ε है, जहां ''c'' वियुक्त शीर्षों की गणना करते हुए ''S'' के घटकों की संख्या है, और ε 0 है यदि S संतुलित है और 1 यदि यह नहीं है। | ||
== अन्य प्रकार के | == अन्य प्रकार के चिन्हित आरेख == | ||
कभी-कभी संकेतों को +1 और -1 मान लिया जाता है। यह केवल अंकन का अंतर है, यदि संकेतों को अभी भी एक वृत्त के चारों ओर गुणा किया जाता है और गुणनफल का चिह्न महत्वपूर्ण है। हालांकि, किनारे के लेबल का | कभी-कभी संकेतों को +1 और -1 मान लिया जाता है। यह केवल अंकन का अंतर है, यदि संकेतों को अभी भी एक वृत्त के चारों ओर गुणा किया जाता है और गुणनफल का चिह्न महत्वपूर्ण है। हालांकि, किनारे के लेबल का उपचारण करने के दो अन्य प्रकार हैं जो चिन्हित आरेख सिद्धांत में फिट नहीं होते हैं। | ||
चिन्हित आलेख शब्द को कभी-कभी आलेख पर उपयोजित किया जाता है जिसमें प्रत्येक किनारे का भार होता है, w(e) = +1 या -1 होता है। ये एक ही प्रकार के चिन्हित आलेख नहीं हैं; वे एक प्रतिबंधित भार समुच्चय के साथ भारित [[ग्राफ (असतत गणित)|आरेख (असतत गणित)]] हैं। अंतर यह है कि भार जोड़ा जाता है, गुणा नहीं किया जाता है। समस्याएं और प्रकार पूरी तरह से अलग हैं। | |||
नाम उन आलेखों पर भी उपयोजित होता है जिनमें संकेत किनारों पर रंगों के रूप में | नाम उन आलेखों पर भी उपयोजित होता है जिनमें संकेत किनारों पर रंगों के रूप में फलन करते हैं। रंग का महत्व यह है कि यह किनारे पर लगाए गए विभिन्न भारों को निर्धारित करता है, और ऐसा नहीं है कि इसका चिन्ह आंतरिक रूप से महत्वपूर्ण है। [[गाँठ सिद्धांत|ग्रंथि सिद्धांत]] में यह स्थिति है, जहाँ संकेतों का केवल महत्व यह है कि उन्हें दो-तत्व समूह द्वारा परस्पर बदला जा सकता है, लेकिन धनात्मक और ऋणात्मक के मध्य कोई आंतरिक अंतर नहीं है। सांकेतिक रंग के आलेख का मैट्रोइड अंतर्निहित आलेख का चक्र मैट्रोइड है; यह चिन्हित आरेख का फ्रेम या लिफ्ट मैट्रॉइड नहीं है। चिन्ह लेबल, मैट्रोइड को बदलने के बदले, मैट्रोइड के तत्वों पर संकेत बन जाते हैं। | ||
इस लेख में हम | इस लेख में हम यथार्थ अर्थों में केवल चिन्हित आरेख सिद्धांत पर विचार करते हैं। सांकेतिक रंग के आलेख के लिए [[रंगीन मैट्रोइड|रंगीन मैट्रोइड्स]] देखें। | ||
=== | ===चिन्हित दिशा आरेख === | ||
एक | एक चिन्हित दिशा आरेख चिन्हित चाप के साथ एक [[निर्देशित ग्राफ|निर्देशित आरेख]] है। चिन्हित दिशा आरेख चिन्हित आलेख की तुलना में कहीं अधिक सम्मिश्र हैं, क्योंकि केवल निर्देशित चक्रों के संकेत ही महत्वपूर्ण हैं। उदाहरण के लिए, संतुलन की कई परिभाषाएँ हैं, जिनमें से प्रत्येक को चित्रित करना कठिन है, चिन्हित अप्रत्यक्ष रेखांकन की स्थिति के विपरीत हैं। | ||
चिन्हित द्विलेखों को अभिविन्यस्त के साथ अस्पष्ट नहीं होना चाहिए। उत्तरार्द्ध द्विदिश रेखांकन हैं, निर्देशित रेखांकन नहीं (सभी धनात्मक संकेतों के तुच्छ प्रकरण को छोड़कर)। | |||
== | == शीर्ष संकेत == | ||
एक शीर्ष- | एक शीर्ष-चिन्हित आलेख, जिसे कभी-कभी चिह्नित आलेख कहा जाता है, एक आलेख होता है जिसके शीर्षों को संकेत दिए जाते हैं। एक वृत्त को संगत कहा जाता है (लेकिन यह तार्किक स्थिरता से असंबंधित है) या सामंजस्यपूर्ण कहा जाता है यदि इसके शीर्ष संकेतों का गुणनफल धनात्मक है, और भिन्न या असंगत है यदि उत्पाद ऋणात्मक है। हरारी के संतुलन प्रमेय के अनुरूप सामंजस्यपूर्ण शीर्ष-चिन्हित रेखांकन का कोई सरल लक्षण वर्णन नहीं है; इसके बदले, अभिलक्षण एक कठिन समस्या रही है, जोगलेकर, शाह और दीवान (2012) द्वारा सबसे अच्छा समाधान (और भी सामान्यतः) किया गया है।<ref name="JSD">Manas Joglekar, Nisarg Shah, and Ajit A. Diwan (2012), "Balanced group labeled graphs", ''Discrete Mathematics'', vol. 312, no. 9, pp. 1542–1549.</ref> | ||
प्रमुख परिवर्तन के बिना शीर्ष संकेतों के सिद्धांत में किनारे के संकेतों को जोड़ना प्रायः आसान होता है; इस प्रकार, शीर्ष-चिन्हित आलेख (या चिह्नित चिन्हित आलेख) के लिए कई परिणाम स्वाभाविक रूप से शीर्ष-और-किनारे-चिन्हित आलेख तक विस्तारित होते हैं। जोगलेकर, शाह और दीवान (2012) द्वारा सद्भाव के अभिलक्षणन वर्णन के लिए यह विशेष रूप से सत्य है। | |||
ध्यान दें कि [[चिह्नित ग्राफ|चिह्नित आरेख]] शब्द [[पेट्री नेट]] में | एक चिह्नित चिन्हित आरेख और एक अवस्था फलन के साथ एक चिन्हित आरेख के मध्य का अंतर (§ कुंठा के रूप में) यह है कि पूर्व में शीर्ष संकेत आवश्यक संरचना का भाग हैं, जबकि एक अवस्था फलन चिन्हित आरेख पर एक चर फलन है। | ||
ध्यान दें कि <nowiki>''</nowiki>[[चिह्नित ग्राफ|चिह्नित आरेख<nowiki>''</nowiki>]] शब्द का व्यापक रूप से [[पेट्री नेट]] में पूरी तरह से अलग अर्थ में उपयोग किया जाता है; चिह्नित रेखांकन पर लेख देखें। | |||
== रंग == | == रंग == | ||
अचिन्हित आलेख सिद्धांत के साथ, चिन्हित आलेख रंग की एक धारणा है। जहाँ आलेख का [[ग्राफ रंग|रंग]] शीर्ष समुच्चय से प्राकृतिक संख्याओं तक मानचित्रण है, एक चिन्हित आलेख का रंग शीर्ष समुच्चय से पूर्णांकों तक मानचित्रण है। उचित रंगों पर प्रतिबंध चिन्हित आलेख के किनारों से आती हैं। दो शीर्षों को निर्दिष्ट पूर्णांक भिन्न होने चाहिए यदि वे एक धनात्मक किनारे से जुड़े होते है। यदि कोने एक ऋणात्मक किनारे से जुड़े हुए हैं, तो आसन्न कोने पर लेबल योगात्मक व्युत्क्रम नहीं होना चाहिए। धनात्मक लूप के साथ चिन्हित आरेख का कोई उचित रंग नहीं हो सकता है। | |||
अधिकतम प्राकृतिक संख्या k पर परिमाण के साथ पूर्णांक के समुच्चय पर | अधिकतम प्राकृतिक संख्या k पर परिमाण के साथ पूर्णांक के समुच्चय पर शीर्ष लेबल को प्रतिबंधित करते समय, एक चिन्हित आलेख के उचित रंगों का समुच्चय परिमित होता है। ऐसे उचित रंगों की संख्या और k के मध्य का संबंध k में एक बहुपद है; जब इसे <math>2k+1</math> के संदर्भ में व्यक्त किया गया है तो इसे चिन्हित आरेख का [[रंगीन बहुपद]] कहा जाता है। यह एक अचिन्हित आरेख के रंगीन बहुपद के अनुरूप है। | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
===[[सामाजिक मनोविज्ञान]]=== | ===[[सामाजिक मनोविज्ञान]]=== | ||
सामाजिक मनोविज्ञान में, | सामाजिक मनोविज्ञान में, चिन्हित रेखांकन का उपयोग सामाजिक स्थितियों को निदर्श करने के लिए किया गया है, धनात्मक किनारों के साथ दोस्ती का प्रतिनिधित्व करते हैं और नोड्स के मध्य ऋणात्मक किनारों की द्वेष, जो लोगों का प्रतिनिधित्व करते हैं।<ref name=carhar/> फिर, उदाहरण के लिए, एक धनात्मक 3-चक्र या तो तीन परस्पर मित्र हैं, या एक सामान्य शत्रु वाले दो मित्र हैं; जबकि एक ऋणात्मक 3-चक्र या तो तीन परस्पर शत्रु हैं, या दो शत्रु हैं जो एक पारस्परिक मित्र साझा करते हैं। संतुलन सिद्धांत के अनुसार, धनात्मक चक्र संतुलित होते हैं और इन्हें स्थिर सामाजिक स्थिति माना जाता है, जबकि ऋणात्मक चक्र असंतुलित होते हैं और इन्हें अस्थिर माना जाता है। सिद्धांत के अनुसार, तीन पारस्परिक शत्रुओं के प्रकरण में, ऐसा इसलिए है क्योंकि एक सामान्य शत्रु को साझा करने से दो शत्रुओं के मित्र बनने की संभावना होती है। एक दोस्त को साझा करने वाले दो दुश्मनों के प्रकरण में, साझा दोस्त एक दूसरे को चयन करने की संभावना रखता है और अपनी दोस्ती में से एक को दुश्मन में बदल देता है। | ||
एंटल, क्रैपीव्स्की और रेडर [[सामाजिक गतिशीलता]] को एक | एंटल, क्रैपीव्स्की और रेडर [[सामाजिक गतिशीलता]] को एक चिन्हित आरेख के किनारे पर चिन्ह इन परिवर्तन के रूप में मानते हैं।<ref>T. Antal, P.L. Krapivsky & S. Redner (2006) [https://arxiv.org/abs/physics/0605183 Social Balance on Networks: The Dynamics of Friendship and Enmity]</ref> एक तलाकशुदा जोड़े के पिछले दोस्तों के साथ सामाजिक संबंधों का उपयोग समाज में एक चिन्हित आरेख के विकास को दर्शाने के लिए किया जाता है। एक अन्य दृष्टांत [[प्रथम विश्व युद्ध]] से पहले के दशकों में यूरोपीय शक्तियों के मध्य बदलते अंतरराष्ट्रीय समझौते का वर्णन करता है। वे स्थानीय त्रय गतिकी और विवश त्रय गतिकी पर विचार करते हैं, जहां बाद वाले प्रकरण में एक संबंध परिवर्तन तभी किया जाता है जब असंतुलित त्रय की कुल संख्या कम हो जाती है। अनुकरण ने परिवर्तन के लिए चयन किए गए यादृच्छिक असंतुलित त्रिभुज वाले यादृच्छिक संबंधों के साथ एक पूर्ण आरेख माना जाता है। इस प्रक्रिया के अंतर्गत ''N'' नोड्स के साथ चिन्हित आरेख के विकास का अध्ययन किया जाता है और उपयोगी लिंक के स्थिर घनत्व का वर्णन करने के लिए अनुकरण किया जाता है। | ||
संतुलन सिद्धांत को गंभीर रूप से चुनौती दी गई है, विशेष रूप से बड़ी प्रणालियों के लिए इसके आवेदन में, सैद्धांतिक आधार पर कि | संतुलन सिद्धांत को गंभीर रूप से चुनौती दी गई है, विशेष रूप से बड़ी प्रणालियों के लिए इसके आवेदन में, सैद्धांतिक आधार पर कि उपयोगी संबंध समाज को एक साथ बांधते हैं, जबकि शत्रु के दो कैंप में विभाजित समाज अत्यधिक अस्थिर होता है।<ref>B. Anderson, in ''Perspectives on Social Network Research'', ed. P.W. Holland and S. Leinhardt. New York: Academic Press, 1979.</ref> प्रायोगिक अध्ययनों ने भी संरचनात्मक संतुलन सिद्धांत की भविष्यवाणियों की केवल कमजोर पुष्टि प्रदान की है।<ref>{{cite journal | last1 = Morrissette | first1 = Julian O. | last2 = Jahnke | first2 = John C. | year = 1967 | title = संरचनात्मक संतुलन के सिद्धांत में शक्ति शून्य का कोई संबंध और संबंध नहीं| journal = Human Relations | volume = 20 | issue = 2| pages = 189–195 | doi = 10.1177/001872676702000207 | s2cid = 143210382 }}</ref> | ||
प्रायोगिक अध्ययनों ने भी संरचनात्मक संतुलन सिद्धांत की भविष्यवाणियों की केवल कमजोर पुष्टि प्रदान की है।<ref>{{cite journal | last1 = Morrissette | first1 = Julian O. | last2 = Jahnke | first2 = John C. | year = 1967 | title = संरचनात्मक संतुलन के सिद्धांत में शक्ति शून्य का कोई संबंध और संबंध नहीं| journal = Human Relations | volume = 20 | issue = 2| pages = 189–195 | doi = 10.1177/001872676702000207 | s2cid = 143210382 }}</ref> | === प्रचक्रण ग्लास === | ||
=== | भौतिकी में, चिन्हित रेखांकन अलोहचुंबकीय आइसिंग निदर्श के लिए एक प्राकृतिक संदर्भ है, जो प्रचक्रण ग्लास के अध्ययन के लिए उपयोजित होता है। | ||
भौतिकी में, | |||
=== | === सम्मिश्र पद्धति === | ||
[[File:Simple 3-level trophic system.png|thumb|right|एक साधारण | [[File:Simple 3-level trophic system.png|thumb|right|एक साधारण पोषी स्तर का प्रतिनिधित्व करने वाला एक तीन-चर चिन्हित दिशा आरेख ]]प्रारंभिक रूप से जनसंख्या जीव विज्ञान और पारिस्थितिकी में विकसित एक विश्लेषणात्मक पद्धति का उपयोग करना, लेकिन अब कई वैज्ञानिक विषयों में उपयोग किया जाता है, चिन्हित दिशा आरेख ने सम्मिश्र कारण प्रणालियों के व्यवहार के तर्क में आवेदन पाया है।<ref>Puccia, Charles J. and [[Richard Levins|Levins, Richard]] (1986). ''[http://www.hup.harvard.edu/catalog.php?isbn=9780674435070 Qualitative Modeling of Complex Systems: An Introduction to Loop Analysis and Time Averaging]''. Harvard University Press, Cambridge, MA.</ref><ref>{{cite journal | last1 = Dambacher | first1 = Jeffrey M. | last2 = Li | first2 = Hiram W. | last3 = Rossignol | first3 = Philippe A. | year = 2002 | title = पारिस्थितिक भविष्यवाणियों की अनिश्चितता का आकलन करने में सामुदायिक संरचना की प्रासंगिकता| journal = Ecology | volume = 83 | issue = 5| pages = 1372–1385 | doi = 10.1890/0012-9658(2002)083[1372:rocsia]2.0.co;2 | jstor = 3071950 }}</ref> इस तरह के विश्लेषण पद्धति के दिए गए स्तरों पर प्रतिक्रिया के बारे में प्रश्नो के उत्तर देते हैं, और एक या एक से अधिक बिंदुओं पर एक पद्धति को दी गई चर प्रतिक्रियाओं की दिशा के बारे में, इस तरह के क्षोभ के चर सहसंबंध, पद्धति में विचरण का वितरण, और संवेदनशीलता या पद्धति क्षोभ के लिए विशेष चर की असंवेदनशीलता देते हैं। | ||
=== डेटा गुच्छन === | === डेटा गुच्छन === | ||
सहसंबंध गुच्छन समानता द्वारा डेटा के प्राकृतिक गुच्छन की | सहसंबंध गुच्छन समानता द्वारा डेटा के प्राकृतिक गुच्छन की रूप में है। डेटा बिंदुओं को एक आलेख के कोने के रूप में दर्शाया जाता है, जिसमें समान वस्तुओं को जोड़ने वाला एक धनात्मक किनारा और असमान वस्तुओं को जोड़ने वाला एक ऋणात्मक किनारा होता है। | ||
===तंत्रिका विज्ञान=== | ===तंत्रिका विज्ञान=== | ||
मस्तिष्क को एक | मस्तिष्क को एक चिन्हित आरेख के रूप में माना जा सकता है जहां मस्तिष्क क्षेत्रों के गतिविधि प्रतिरुप के मध्य एककालता और प्रति एककालता धनात्मक और ऋणात्मक किनारों को निर्धारित करते हैं। इस संबंध में, मस्तिष्क संजाल की स्थिरता और ऊर्जा का पता लगाया जा सकता है।<ref name= 10.1038/s41598-021-81767-7>{{cite journal | vauthors = Saberi M, Khosrowabadi R, Khatibi A, Misic B, Jafari G | title = रेस्टिंग-स्टेट ब्रेन नेटवर्क की स्थिरता पर नकारात्मक लिंक का सामयिक प्रभाव| journal = Scientific Reports | date = January 2021 | volume = 11 | issue = 1 | page = 2176 | pmid = 33500525 | pmc = 7838299 | doi = 10.1038/s41598-021-81767-7 | bibcode = 2021NatSR..11.2176S | url = }</ref> इसके अलावा, हाल ही में, तंत्रिका संयोजन के गैर-तुच्छ संयोजन की पहचान करने और मस्तिष्क के समायोज्य तत्वों को उजागर करने के लिए मस्तिष्क संजाल विश्लेषण में कुंठा की अवधारणा का उपयोग किया गया है।<ref name= https://doi.org /10.1162/netn_a_00268 >{{cite journal | vauthors = Saberi M, Khosrowabadi R, Khatibi A, Misic B, Jafari G | title = कार्यात्मक मस्तिष्क नेटवर्क में हताशा गठन का पैटर्न| journal = Network Neuroscience | date = October 2022 | volume = 6 | issue = 4 | page = 1334-1356 | doi = 10.1162/netn_a_00268 | url = https://direct.mit.edu/netn/article/6/4/1334/112207/Pattern-of-frustration-formation-in-the-functional| doi-access = free }}</ref> | ||
== सामान्यीकरण == | == सामान्यीकरण == | ||
एक | एक चिन्हित आरेख एक विशेष प्रकार का [[लाभ ग्राफ|लाभ आरेख]] है जिसमें लाभ समूह का क्रम 2 होता है। जोड़ी (''G'', '''''B'''''(Σ)) एक चिन्हित आरेख Σ द्वारा निर्धारित एक विशेष प्रकार का अभिनत आरेख है। संकेत समूह की विशेष गुण है, जो बड़े लाभ समूहों द्वारा साझा नहीं की जाती है, कि किनारे के संकेत संतुलित चक्रों के समुच्चय '''''B'''''(Σ) द्वारा स्विच करने के लिए निर्धारित किए जाते हैं।<ref>{{cite journal | ||
| last1=Zaslavsky | first1=Thomas | authorlink1=Thomas Zaslavsky | | last1=Zaslavsky | first1=Thomas | authorlink1=Thomas Zaslavsky | ||
| title=Characterizations of signed graphs | | title=Characterizations of signed graphs | ||
| Line 113: | Line 110: | ||
*{{citation | *{{citation | ||
| last1 = Cartwright | first1 = D. | | last1 = Cartwright | first1 = D. | ||
| last2 = | | last2 = हरारी | first2 = F. | author2-link = फ्रैंक हैरी | ||
| journal = | | journal = मनोवैज्ञानिक समीक्षा | ||
| pages = 277–293 | | pages = 277–293 | ||
| title = | | title = संरचनात्मक संतुलन: हीडर के सिद्धांत का एक सामान्यीकरण | ||
| volume = 63 | | volume = 63 | ||
| issue = 5 | | issue = 5 | ||
| Line 122: | Line 119: | ||
}}. | }}. | ||
*{{citation | *{{citation | ||
| last = | | last = साइडेल | first = J. J. | ||
| contribution = | | contribution = दो-ग्राफ का एक सर्वेक्षण | ||
| location = | | location = रोम | ||
| mr = 0550136 | | mr = 0550136 | ||
| pages = 481–511 | | pages = 481–511 | ||
| series = | | series = अट्टी देई कन्वेग्नी लिंसी | ||
| volume = 17 | | volume = 17 | ||
| publisher = [[ | | publisher = [[एकेडेमिया नाजियोनेल देई लिंसी]] | ||
| title = Colloquio Internazionale sulle Teorie Combinatorie ( | | title = Colloquio Internazionale sulle Teorie Combinatorie (रोम, 1973), टोमो I | ||
| year = 1976}}. | | year = 1976}}. | ||
*{{citation | *{{citation | ||
| last = | | last = ज़स्लावस्की | first = थॉमस | ||
| journal = | | journal = कॉम्बिनेटरिक्स का इलेक्ट्रॉनिक जर्नल | ||
| mr = 1744869 | | mr = 1744869 | ||
| at = | | at = गतिशील सर्वेक्षण 8, 124 पीपी। | ||
| title = | | title = हस्ताक्षरित और लाभ रेखांकन और संबद्ध क्षेत्रों की एक गणितीय ग्रंथ सूची | ||
| url = http://www.combinatorics.org/ojs/index.php/eljc/article/view/DS8 | | url = http://www.combinatorics.org/ojs/index.php/eljc/article/view/DS8 | ||
| volume = 5 | | volume = 5 | ||
Revision as of 11:53, 15 May 2023
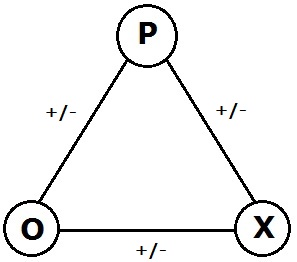
गणित में आलेख सिद्धांत के क्षेत्र में, चिन्हित आलेख एक आलेख होता है जिसमें प्रत्येक किनारे पर एक धनात्मक या ऋणात्मक चिह्न होता है।
एक चिन्हित आरेख संतुलित होता है यदि हर चक्र के किनारे के संकेतों का उत्पाद धनात्मक होता है। ''चिन्हित आरेख'' नाम और संतुलन की धारणा पहली बार 1953 में फ्श्रेणी हैरी के एक गणितीय लेख में दिखाई देती है।[1] डेन्स कोनिग ने पहले से ही 1936 में एक अलग शब्दावली के अंतर्गत समतुल्य धारणाओं का अध्ययन किया था, लेकिन चिन्ह समूह की प्रासंगिकता को पहचाने बिना किया था।[2] मिशिगन विश्वविद्यालय में समूह गतिशीलता के केंद्र में, डोरविन कार्टराईट और हैरी ने फ्रिट्ज हैडर के मनोवैज्ञानिक सिद्धांत के त्रिकोण में संतुलन के मनोवैज्ञानिक सिद्धांत को चिन्हित रेखांकन में संतुलन के मनोवैज्ञानिक सिद्धांत के रूप में सामान्यीकृत किया था।[3][4]
चिन्हित रेखांकन बहुत बार पुनः खोजे गए हैं क्योंकि वे कई असंबद्ध क्षेत्रों में स्वाभाविक रूप से सामने आते हैं।[5] उदाहरण के लिए, वे प्राचीन मूल प्रक्रिया के उपसमुच्चय की ज्यामिति का वर्णन और विश्लेषण करने में सक्षम बनाते हैं। वे सांस्थितिक मानचित्र सिद्धांत और समूह सिद्धांत में दिखाई देते हैं। वे आलेख में विषम और सम चक्रों के बारे में प्रश्नों के लिए एक स्वाभाविक संदर्भ हैं। वे अलोहचुंबकीय आइसिंग निदर्श में आधार अवस्था ऊर्जा की गणना में दिखाई देते हैं; इसके लिए Σ में सबसे बड़े संतुलित किनारे समुच्चय खोजने की आवश्यकता है। उन्हें सहसंबंध गुच्छन में डेटा वर्गीकरण पर उपयोजित किया गया है।
मूलभूत प्रमेय
एक पथ का चिह्न उसके किनारों के चिह्नों का गुणनफल होता है। इस प्रकार एक पथ तभी धनात्मक होता है जब उसमें सम संख्या में ऋणात्मक किनारे हों (जहाँ शून्य सम है)। फ्श्रेणी हैरी के गणितीय संतुलन सिद्धांत में, प्रत्येक चक्र धनात्मक होने पर एक चिन्हित आरेख संतुलित होता है। हैरी सिद्ध करता है कि एक चिन्हित आरेख संतुलित होता है जब (1) नोड्स के प्रत्येक जोड़े के लिए, उनके मध्य के सभी पंथ का एक ही चिह्न होता है, या (2) शीर्षों को उपसमुच्चय (संभवतः रिक्त) की एक जोड़ी में विभाजित किया जाता है, प्रत्येक में केवल धनात्मक किनारे होते हैं, लेकिन ऋणात्मक किनारों से जुड़े होते हैं।[1] यह प्रमेय का सामान्यीकरण करता है कि एक साधारण (अचिन्हित) आरेख द्विभाज्य होता है यदि और केवल यदि प्रत्येक चक्र की लंबाई समान होती है।
एक साधारण प्रमाण स्विचिंग की विधि का उपयोग करता है। एक चिन्हित आलेख को स्विच करने का अर्थ है शीर्ष उपसमुच्चय और उसके पूरक के मध्य सभी किनारों के संकेतों को उत्क्रम कर देना है। हैरी के प्रमेय को सिद्ध करने के लिए, प्रेरण द्वारा दिखाया गया है कि Σ को सभी धनात्मक होने के लिए स्विच किया जा सकता है अगर यह संतुलित है।
एक मंद प्रमेय, लेकिन एक सरल प्रमाण के साथ, यह है कि यदि चिन्हित पूर्ण आलेख में प्रत्येक 3-चक्र धनात्मक है, तो आलेख संतुलित है। प्रमाण के लिए, एक स्वेच्छाचारी नोड n का चयन करे और इसे और उन सभी नोड्स को रखें जो n से एक समूह में धनात्मक किनारे से जुड़े होते हैं, जिन्हें A कहा जाता है, और वे सभी जो n से दूसरे में एक ऋणात्मक किनारे से जुड़े हैं, जिसे B कहा जाता है क्योंकि यह एक पूर्ण आरेख है, A में प्रत्येक दो नोड मित्र होने चाहिए और B में प्रत्येक दो नोड मित्र होने चाहिए, अन्यथा एक 3-चक्र होगा जो असंतुलित था। (क्योंकि यह एक पूर्ण आरेख है, कोई भी ऋणात्मक किनारा असंतुलित 3-चक्र का कारण होगा।) इसी तरह, सभी ऋणात्मक किनारों को दो समूहों के मध्य जाना चाहिए।[6]
कुंठा
कुंठा सूचकांक
Σ का कुंठा सूचकांक (प्रारंभिक रूप से संतुलन की रेखा सूचकांक कहा जाता है)[7] किनारों की सबसे छोटी संख्या है जिसका विलोपन, या समतुल्य जिसका चिन्ह उत्क्रमण (हैरी का एक प्रमेय[7]), Σ को संतुलित बनाता है। तुल्यता का कारण यह है कि कुंठा सूचकांक किनारों की सबसे छोटी संख्या के समान होता है जिसका निषेध (या, समतुल्य, विलोपन; Σ संतुलित बनाता है।
कुंठा सूचकांक का वर्णन करने का दूसरा प्रकार यह है कि यह किनारों की सबसे छोटी संख्या है जो सभी ऋणात्मक चक्रों को समाविष्ट करती है। इस मात्रा को ऋणात्मक चक्र आवरण संख्या कहा गया है।
एक और समतुल्य परिभाषा है (जिसे स्विच करके आसानी से सिद्ध किया जा सकता है)। प्रत्येक शीर्ष को +1 या -1 का मान दें; हम इसे Σ की स्थिति कहते हैं। एक किनारे को संतुष्ट कहा जाता है यदि यह धनात्मक है और दोनों समापन बिंदुओं का मान समान है, या यह ऋणात्मक है और अंत बिंदुओं के विपरीत मान हैं। एक किनारा जो संतुष्ट नहीं होता है उसे कुंठा कहा जाता है। सभी अवस्था में कुंठित किनारों की सबसे छोटी संख्या कुंठा सूचकांक है। यह परिभाषा पहली बार एबेलसन और रोसेनबर्ग द्वारा (अप्रचलित) नाम सम्मिश्रता के अंतर्गत एक अलग संकेतन में प्रस्तावित की गई थी।[8] ऐसे समुच्चय का पूरक सबसे संभावित किनारों के साथ Σ का संतुलित उपआरेख है।
कुंठा सूचकांक खोजना एक NP-कठिन समस्या है। अरेफ एट अल द्विआधारी क्रमादेश निदर्श का सुझाव देते हैं जो उचित समय में 105 किनारों तक आरेख के कुंठा सूचकांक की गणना करने में सक्षम हैं।[9][10][11] कोई भी NP-कठिन सम्मिश्रता देख सकता है कि सभी-ऋणात्मक चिन्हित आलेख की कुंठा सूचकांक आलेख सिद्धांत में अधिकतम कमी समस्या के समान है, जो NP-कठिन है।
प्रचक्रण ग्लास के एक निदर्श, मिश्रित आइसिंग निदर्श में कुंठा सूचकांक महत्वपूर्ण है। इस निदर्श में, चिन्हित आरेख निश्चित है। एक स्थिति में प्रत्येक शीर्ष पर "प्रचक्रण", या तो "ऊपर" या "नीचे" सम्मलित है। हम प्रचक्रण अप को +1 और प्रचक्रण डाउन को -1 मानते हैं। इस प्रकार, प्रत्येक अवस्था में कई कुंठित किनारे हैं। एक अवस्था की ऊर्जा तब बड़ी होती है जब उसके पास अधिक कुंठित किनारे होते हैं, इसलिए एक मूल अवस्था सबसे कम कुंठित ऊर्जा वाली अवस्था होती है। इस प्रकार, $$\ $ की मूल अवस्था ऊर्जा का पता लगाने के लिए किसी को कुंठा सूचकांक का पता लगाना होता है।
कुंठा संख्या
अनुरूप शीर्ष संख्या कुंठा संख्या है, जिसे सबसे छोटी संख्या के रूप में परिभाषित किया गया है जिसका Σ से विलोपन संतुलन में होता है। समतुल्य रूप से, कोई Σ के संतुलित प्रेरित उपआरेख का सबसे बड़ा क्रम चाहता है।
कलनविधीय समस्याएं
चिन्हित आलेख के विषय में तीन मूलभूत प्रश्न हैं: क्या यह संतुलित है? इसमें समुच्चय किए गए संतुलित किनारे का सबसे बड़ा आकार क्या है? इसे संतुलित करने के लिए हटाए जाने वाले शीर्षों की सबसे छोटी संख्या क्या है? बहुपद काल में पहला प्रश्न का समाधान करना आसान है। दूसरे प्रश्न को कुंठा सूचकांक या अधिकतम संतुलित उपआरेख समस्या कहा जाता है। यह NP-कठिन है क्योंकि इसका विशेष प्रकरण (जब आरेख के सभी किनारे ऋणात्मक हैं) NP-कठिन समस्या अधिकतम कमी है। तीसरे प्रश्न को कुंठा संख्या या अधिकतम संतुलित प्रेरित उपआरेख समस्या कहा जाता है, यह NP-कठिन भी है; उदाहरण देखें[12]
मैट्रोइड सिद्धांत
एक चिन्हित आलेख से जुड़े दो मैट्रोइड्स हैं, जिन्हें चिन्ह-आलेखिक मैट्रॉइड कहा जाता है (जिसे फ़्रेम मैट्रॉइड या कभी-कभी अभिनति मैट्रोइड भी कहा जाता है) और लिफ्ट मैट्रोइड, जो दोनों एक आलेख के चक्र मैट्रॉइड को सामान्य करते हैं। वे अभिनत आरेख के समान मैट्रोइड्स के विशेष प्रकरण हैं।
'फ़्रेम मेट्रॉइड' (या 'चिन्ह-आलेखिक मैट्रॉइड') M(G) ने इसके आधार समुच्चय के लिए कोर समुच्चय E के लिए है।[13] एक कोर समुच्चय स्वतंत्र होता है यदि प्रत्येक घटक में या तो कोई वृत्त नहीं होता है या केवल एक वृत्त होता है, जो ऋणात्मक होता है। (मैट्रोइड सिद्धांत में एक अर्ध-कोर यथार्थत: ऋणात्मक लूप की तरह काम करता है।) मैट्रॉइड का एक परिपथ या तो एक धनात्मक वृत्त होता है, या एक संयोजक सामान्य पाथ के साथ ऋणात्मक वृत्त का एक जोड़ा होता है, जैसे कि दो वृत्त या तो अलग हो जाते हैं (फिर संयोजक पथ में प्रत्येक वृत्त के साथ सामान्य एक अंत होता है और अन्यथा दोनों से अलग होता है) या केवल एक सामान्य शीर्ष अनुकरण करें (इस प्रकरण में संयोजक पथ वह एकल शीर्ष है)। कोर समुच्चय S की कोटि n - b है, जहाँ n, G के शीर्षों की संख्या है और b, S के संतुलित घटकों की संख्या है, पृथक शीर्षों को संतुलित घटकों के रूप में गिना जाता है। यह मेट्रॉइड चिन्हित आलेख के आपतन आव्यूह का स्तंभ मेट्रॉइड है। यही कारण है कि यह प्राचीन मूल तंत्र की मूलांश की रैखिक निर्भरताओं का वर्णन करता है।
'विस्तारित लिफ्ट मैट्रॉइड' L0(G) ने अपने आधार के लिए समुच्चय E0 को कोर समुच्चय E के एक अतिरिक्त बिंदु के साथ समुच्चय किया है, जिसे हम e0 से निरूपित करते है। लिफ्ट मैट्रॉइड L(G) E तक सीमित विस्तारित लिफ्ट मैट्रॉइड है। अतिरिक्त बिंदु यथार्थत: ऋणात्मक लूप की तरह फलन करता है, इसलिए हम केवल लिफ्ट मैट्रॉइड का वर्णन करते हैं। एक किनारे का समुच्चय स्वतंत्र होता है यदि इसमें या तो कोई वृत्त नहीं होता है या केवल एक वृत्त होता है, जो ऋणात्मक होता है। (यह वही नियम है जो चिन्हित-आलेखिक मैट्रोइड में प्रत्येक घटक के लिए अलग से उपयोजित होता है।) एक मैट्रॉइड परिपथ या तो एक धनात्मक वृत्त या ऋणात्मक वृत्तों की एक जोड़ा होता है जो या तो अलग हैं या केवल एक सामान्य शीर्ष है। कोर समुच्चय S की श्रेणी n - c + ε है, जहां c वियुक्त शीर्षों की गणना करते हुए S के घटकों की संख्या है, और ε 0 है यदि S संतुलित है और 1 यदि यह नहीं है।
अन्य प्रकार के चिन्हित आरेख
कभी-कभी संकेतों को +1 और -1 मान लिया जाता है। यह केवल अंकन का अंतर है, यदि संकेतों को अभी भी एक वृत्त के चारों ओर गुणा किया जाता है और गुणनफल का चिह्न महत्वपूर्ण है। हालांकि, किनारे के लेबल का उपचारण करने के दो अन्य प्रकार हैं जो चिन्हित आरेख सिद्धांत में फिट नहीं होते हैं।
चिन्हित आलेख शब्द को कभी-कभी आलेख पर उपयोजित किया जाता है जिसमें प्रत्येक किनारे का भार होता है, w(e) = +1 या -1 होता है। ये एक ही प्रकार के चिन्हित आलेख नहीं हैं; वे एक प्रतिबंधित भार समुच्चय के साथ भारित आरेख (असतत गणित) हैं। अंतर यह है कि भार जोड़ा जाता है, गुणा नहीं किया जाता है। समस्याएं और प्रकार पूरी तरह से अलग हैं।
नाम उन आलेखों पर भी उपयोजित होता है जिनमें संकेत किनारों पर रंगों के रूप में फलन करते हैं। रंग का महत्व यह है कि यह किनारे पर लगाए गए विभिन्न भारों को निर्धारित करता है, और ऐसा नहीं है कि इसका चिन्ह आंतरिक रूप से महत्वपूर्ण है। ग्रंथि सिद्धांत में यह स्थिति है, जहाँ संकेतों का केवल महत्व यह है कि उन्हें दो-तत्व समूह द्वारा परस्पर बदला जा सकता है, लेकिन धनात्मक और ऋणात्मक के मध्य कोई आंतरिक अंतर नहीं है। सांकेतिक रंग के आलेख का मैट्रोइड अंतर्निहित आलेख का चक्र मैट्रोइड है; यह चिन्हित आरेख का फ्रेम या लिफ्ट मैट्रॉइड नहीं है। चिन्ह लेबल, मैट्रोइड को बदलने के बदले, मैट्रोइड के तत्वों पर संकेत बन जाते हैं।
इस लेख में हम यथार्थ अर्थों में केवल चिन्हित आरेख सिद्धांत पर विचार करते हैं। सांकेतिक रंग के आलेख के लिए रंगीन मैट्रोइड्स देखें।
चिन्हित दिशा आरेख
एक चिन्हित दिशा आरेख चिन्हित चाप के साथ एक निर्देशित आरेख है। चिन्हित दिशा आरेख चिन्हित आलेख की तुलना में कहीं अधिक सम्मिश्र हैं, क्योंकि केवल निर्देशित चक्रों के संकेत ही महत्वपूर्ण हैं। उदाहरण के लिए, संतुलन की कई परिभाषाएँ हैं, जिनमें से प्रत्येक को चित्रित करना कठिन है, चिन्हित अप्रत्यक्ष रेखांकन की स्थिति के विपरीत हैं।
चिन्हित द्विलेखों को अभिविन्यस्त के साथ अस्पष्ट नहीं होना चाहिए। उत्तरार्द्ध द्विदिश रेखांकन हैं, निर्देशित रेखांकन नहीं (सभी धनात्मक संकेतों के तुच्छ प्रकरण को छोड़कर)।
शीर्ष संकेत
एक शीर्ष-चिन्हित आलेख, जिसे कभी-कभी चिह्नित आलेख कहा जाता है, एक आलेख होता है जिसके शीर्षों को संकेत दिए जाते हैं। एक वृत्त को संगत कहा जाता है (लेकिन यह तार्किक स्थिरता से असंबंधित है) या सामंजस्यपूर्ण कहा जाता है यदि इसके शीर्ष संकेतों का गुणनफल धनात्मक है, और भिन्न या असंगत है यदि उत्पाद ऋणात्मक है। हरारी के संतुलन प्रमेय के अनुरूप सामंजस्यपूर्ण शीर्ष-चिन्हित रेखांकन का कोई सरल लक्षण वर्णन नहीं है; इसके बदले, अभिलक्षण एक कठिन समस्या रही है, जोगलेकर, शाह और दीवान (2012) द्वारा सबसे अच्छा समाधान (और भी सामान्यतः) किया गया है।[14]
प्रमुख परिवर्तन के बिना शीर्ष संकेतों के सिद्धांत में किनारे के संकेतों को जोड़ना प्रायः आसान होता है; इस प्रकार, शीर्ष-चिन्हित आलेख (या चिह्नित चिन्हित आलेख) के लिए कई परिणाम स्वाभाविक रूप से शीर्ष-और-किनारे-चिन्हित आलेख तक विस्तारित होते हैं। जोगलेकर, शाह और दीवान (2012) द्वारा सद्भाव के अभिलक्षणन वर्णन के लिए यह विशेष रूप से सत्य है।
एक चिह्नित चिन्हित आरेख और एक अवस्था फलन के साथ एक चिन्हित आरेख के मध्य का अंतर (§ कुंठा के रूप में) यह है कि पूर्व में शीर्ष संकेत आवश्यक संरचना का भाग हैं, जबकि एक अवस्था फलन चिन्हित आरेख पर एक चर फलन है।
ध्यान दें कि ''चिह्नित आरेख'' शब्द का व्यापक रूप से पेट्री नेट में पूरी तरह से अलग अर्थ में उपयोग किया जाता है; चिह्नित रेखांकन पर लेख देखें।
रंग
अचिन्हित आलेख सिद्धांत के साथ, चिन्हित आलेख रंग की एक धारणा है। जहाँ आलेख का रंग शीर्ष समुच्चय से प्राकृतिक संख्याओं तक मानचित्रण है, एक चिन्हित आलेख का रंग शीर्ष समुच्चय से पूर्णांकों तक मानचित्रण है। उचित रंगों पर प्रतिबंध चिन्हित आलेख के किनारों से आती हैं। दो शीर्षों को निर्दिष्ट पूर्णांक भिन्न होने चाहिए यदि वे एक धनात्मक किनारे से जुड़े होते है। यदि कोने एक ऋणात्मक किनारे से जुड़े हुए हैं, तो आसन्न कोने पर लेबल योगात्मक व्युत्क्रम नहीं होना चाहिए। धनात्मक लूप के साथ चिन्हित आरेख का कोई उचित रंग नहीं हो सकता है।
अधिकतम प्राकृतिक संख्या k पर परिमाण के साथ पूर्णांक के समुच्चय पर शीर्ष लेबल को प्रतिबंधित करते समय, एक चिन्हित आलेख के उचित रंगों का समुच्चय परिमित होता है। ऐसे उचित रंगों की संख्या और k के मध्य का संबंध k में एक बहुपद है; जब इसे के संदर्भ में व्यक्त किया गया है तो इसे चिन्हित आरेख का रंगीन बहुपद कहा जाता है। यह एक अचिन्हित आरेख के रंगीन बहुपद के अनुरूप है।
अनुप्रयोग
सामाजिक मनोविज्ञान
सामाजिक मनोविज्ञान में, चिन्हित रेखांकन का उपयोग सामाजिक स्थितियों को निदर्श करने के लिए किया गया है, धनात्मक किनारों के साथ दोस्ती का प्रतिनिधित्व करते हैं और नोड्स के मध्य ऋणात्मक किनारों की द्वेष, जो लोगों का प्रतिनिधित्व करते हैं।[3] फिर, उदाहरण के लिए, एक धनात्मक 3-चक्र या तो तीन परस्पर मित्र हैं, या एक सामान्य शत्रु वाले दो मित्र हैं; जबकि एक ऋणात्मक 3-चक्र या तो तीन परस्पर शत्रु हैं, या दो शत्रु हैं जो एक पारस्परिक मित्र साझा करते हैं। संतुलन सिद्धांत के अनुसार, धनात्मक चक्र संतुलित होते हैं और इन्हें स्थिर सामाजिक स्थिति माना जाता है, जबकि ऋणात्मक चक्र असंतुलित होते हैं और इन्हें अस्थिर माना जाता है। सिद्धांत के अनुसार, तीन पारस्परिक शत्रुओं के प्रकरण में, ऐसा इसलिए है क्योंकि एक सामान्य शत्रु को साझा करने से दो शत्रुओं के मित्र बनने की संभावना होती है। एक दोस्त को साझा करने वाले दो दुश्मनों के प्रकरण में, साझा दोस्त एक दूसरे को चयन करने की संभावना रखता है और अपनी दोस्ती में से एक को दुश्मन में बदल देता है।
एंटल, क्रैपीव्स्की और रेडर सामाजिक गतिशीलता को एक चिन्हित आरेख के किनारे पर चिन्ह इन परिवर्तन के रूप में मानते हैं।[15] एक तलाकशुदा जोड़े के पिछले दोस्तों के साथ सामाजिक संबंधों का उपयोग समाज में एक चिन्हित आरेख के विकास को दर्शाने के लिए किया जाता है। एक अन्य दृष्टांत प्रथम विश्व युद्ध से पहले के दशकों में यूरोपीय शक्तियों के मध्य बदलते अंतरराष्ट्रीय समझौते का वर्णन करता है। वे स्थानीय त्रय गतिकी और विवश त्रय गतिकी पर विचार करते हैं, जहां बाद वाले प्रकरण में एक संबंध परिवर्तन तभी किया जाता है जब असंतुलित त्रय की कुल संख्या कम हो जाती है। अनुकरण ने परिवर्तन के लिए चयन किए गए यादृच्छिक असंतुलित त्रिभुज वाले यादृच्छिक संबंधों के साथ एक पूर्ण आरेख माना जाता है। इस प्रक्रिया के अंतर्गत N नोड्स के साथ चिन्हित आरेख के विकास का अध्ययन किया जाता है और उपयोगी लिंक के स्थिर घनत्व का वर्णन करने के लिए अनुकरण किया जाता है।
संतुलन सिद्धांत को गंभीर रूप से चुनौती दी गई है, विशेष रूप से बड़ी प्रणालियों के लिए इसके आवेदन में, सैद्धांतिक आधार पर कि उपयोगी संबंध समाज को एक साथ बांधते हैं, जबकि शत्रु के दो कैंप में विभाजित समाज अत्यधिक अस्थिर होता है।[16] प्रायोगिक अध्ययनों ने भी संरचनात्मक संतुलन सिद्धांत की भविष्यवाणियों की केवल कमजोर पुष्टि प्रदान की है।[17]
प्रचक्रण ग्लास
भौतिकी में, चिन्हित रेखांकन अलोहचुंबकीय आइसिंग निदर्श के लिए एक प्राकृतिक संदर्भ है, जो प्रचक्रण ग्लास के अध्ययन के लिए उपयोजित होता है।
सम्मिश्र पद्धति
प्रारंभिक रूप से जनसंख्या जीव विज्ञान और पारिस्थितिकी में विकसित एक विश्लेषणात्मक पद्धति का उपयोग करना, लेकिन अब कई वैज्ञानिक विषयों में उपयोग किया जाता है, चिन्हित दिशा आरेख ने सम्मिश्र कारण प्रणालियों के व्यवहार के तर्क में आवेदन पाया है।[18][19] इस तरह के विश्लेषण पद्धति के दिए गए स्तरों पर प्रतिक्रिया के बारे में प्रश्नो के उत्तर देते हैं, और एक या एक से अधिक बिंदुओं पर एक पद्धति को दी गई चर प्रतिक्रियाओं की दिशा के बारे में, इस तरह के क्षोभ के चर सहसंबंध, पद्धति में विचरण का वितरण, और संवेदनशीलता या पद्धति क्षोभ के लिए विशेष चर की असंवेदनशीलता देते हैं।
डेटा गुच्छन
सहसंबंध गुच्छन समानता द्वारा डेटा के प्राकृतिक गुच्छन की रूप में है। डेटा बिंदुओं को एक आलेख के कोने के रूप में दर्शाया जाता है, जिसमें समान वस्तुओं को जोड़ने वाला एक धनात्मक किनारा और असमान वस्तुओं को जोड़ने वाला एक ऋणात्मक किनारा होता है।
तंत्रिका विज्ञान
मस्तिष्क को एक चिन्हित आरेख के रूप में माना जा सकता है जहां मस्तिष्क क्षेत्रों के गतिविधि प्रतिरुप के मध्य एककालता और प्रति एककालता धनात्मक और ऋणात्मक किनारों को निर्धारित करते हैं। इस संबंध में, मस्तिष्क संजाल की स्थिरता और ऊर्जा का पता लगाया जा सकता है।[20] इसके अलावा, हाल ही में, तंत्रिका संयोजन के गैर-तुच्छ संयोजन की पहचान करने और मस्तिष्क के समायोज्य तत्वों को उजागर करने के लिए मस्तिष्क संजाल विश्लेषण में कुंठा की अवधारणा का उपयोग किया गया है।Cite error: Invalid <ref> tag; invalid names, e.g. too many
सामान्यीकरण
एक चिन्हित आरेख एक विशेष प्रकार का लाभ आरेख है जिसमें लाभ समूह का क्रम 2 होता है। जोड़ी (G, B(Σ)) एक चिन्हित आरेख Σ द्वारा निर्धारित एक विशेष प्रकार का अभिनत आरेख है। संकेत समूह की विशेष गुण है, जो बड़े लाभ समूहों द्वारा साझा नहीं की जाती है, कि किनारे के संकेत संतुलित चक्रों के समुच्चय B(Σ) द्वारा स्विच करने के लिए निर्धारित किए जाते हैं।[21]
टिप्पणियाँ
- ↑ 1.0 1.1 Harary, Frank (1955), "On the notion of balance of a signed graph", Michigan Mathematical Journal, 2: 143–146, MR 0067468, archived from the original on 2013-04-15
- ↑ Kőnig, Dénes (1936), Akademische Verlagsgesellschaft (ed.), Theorie der endlichen und unendlichen Graphen
- ↑ 3.0 3.1 Cartwright, D.; Harary, Frank (1956). "Structural balance: a generalization of Heider's theory" (PDF). Psychological Review. 63 (5): 277–293. doi:10.1037/h0046049. PMID 13359597.
- ↑ Steven Strogatz (2010), The enemy of my enemy, The New York Times, February 14, 2010
- ↑ Zaslavsky, Thomas (1998), "A mathematical bibliography of signed and gain graphs and allied areas", Electronic Journal of Combinatorics, 5, Dynamic Surveys 8, 124 pp., MR 1744869.
- ↑ Luis Von Ahn Science of the Web Lecture 3 p. 28
- ↑ 7.0 7.1 Harary, Frank (1959), On the measurement of structural balance, Behavioral Science 4, 316–323.
- ↑ Robert P. Abelson; Milton J. Rosenberg (1958), Symbolic psycho-logic: a model of attitudinal cognition, Behavioral Science 3, 1–13.
- ↑ Aref, Samin; Mason, Andrew J.; Wilson, Mark C. (2019). "हस्ताक्षरित नेटवर्क में हताशा सूचकांक का एक मॉडलिंग और कम्प्यूटेशनल अध्ययन". arXiv:1611.09030 [cs.SI].
- ↑ Aref, Samin; Mason, Andrew J.; Wilson, Mark C. (2018), Goldengorin, Boris (ed.), "Computing the Line Index of Balance Using Integer Programming Optimisation", Optimization Problems in Graph Theory: In Honor of Gregory Z. Gutin's 60th Birthday, Springer Optimization and Its Applications (in English), Springer International Publishing, pp. 65–84, arXiv:1710.09876, doi:10.1007/978-3-319-94830-0_3, ISBN 9783319948300, S2CID 27936778
- ↑ Aref, Samin; Wilson, Mark C (2019-04-01). Estrada, Ernesto (ed.). "हस्ताक्षरित नेटवर्क में संतुलन और हताशा". Journal of Complex Networks (in English). 7 (2): 163–189. arXiv:1712.04628. doi:10.1093/comnet/cny015. ISSN 2051-1329.
- ↑ Gülpinar, N.; Gutin, G.; Mitra, G.; Zverovitch, A. (2004). "हस्ताक्षरित रेखांकन का उपयोग करके रैखिक कार्यक्रमों में शुद्ध नेटवर्क सबमैट्रिसेस निकालना". Discrete Appl. Math. 137 (3): 359–372. doi:10.1016/S0166-218X(03)00361-5.
- ↑ Zaslavsky, Thomas (1982), "Signed graphs", Discrete Applied Mathematics, 4 (1): 47–74, doi:10.1016/0166-218X(82)90033-6, hdl:10338.dmlcz/127957, MR 0676405. Erratum. Discrete Applied Mathematics, 5 (1983), 248
- ↑ Manas Joglekar, Nisarg Shah, and Ajit A. Diwan (2012), "Balanced group labeled graphs", Discrete Mathematics, vol. 312, no. 9, pp. 1542–1549.
- ↑ T. Antal, P.L. Krapivsky & S. Redner (2006) Social Balance on Networks: The Dynamics of Friendship and Enmity
- ↑ B. Anderson, in Perspectives on Social Network Research, ed. P.W. Holland and S. Leinhardt. New York: Academic Press, 1979.
- ↑ Morrissette, Julian O.; Jahnke, John C. (1967). "संरचनात्मक संतुलन के सिद्धांत में शक्ति शून्य का कोई संबंध और संबंध नहीं". Human Relations. 20 (2): 189–195. doi:10.1177/001872676702000207. S2CID 143210382.
- ↑ Puccia, Charles J. and Levins, Richard (1986). Qualitative Modeling of Complex Systems: An Introduction to Loop Analysis and Time Averaging. Harvard University Press, Cambridge, MA.
- ↑ Dambacher, Jeffrey M.; Li, Hiram W.; Rossignol, Philippe A. (2002). "पारिस्थितिक भविष्यवाणियों की अनिश्चितता का आकलन करने में सामुदायिक संरचना की प्रासंगिकता". Ecology. 83 (5): 1372–1385. doi:10.1890/0012-9658(2002)083[1372:rocsia]2.0.co;2. JSTOR 3071950.
- ↑ {{cite journal | vauthors = Saberi M, Khosrowabadi R, Khatibi A, Misic B, Jafari G | title = रेस्टिंग-स्टेट ब्रेन नेटवर्क की स्थिरता पर नकारात्मक लिंक का सामयिक प्रभाव| journal = Scientific Reports | date = January 2021 | volume = 11 | issue = 1 | page = 2176 | pmid = 33500525 | pmc = 7838299 | doi = 10.1038/s41598-021-81767-7 | bibcode = 2021NatSR..11.2176S | url = }
- ↑ Zaslavsky, Thomas (1981). "Characterizations of signed graphs". Journal of Graph Theory. 5 (4): 401–406. doi:10.1002/jgt.3190050409.
संदर्भ
- Cartwright, D.; हरारी, F. (1956), "संरचनात्मक संतुलन: हीडर के सिद्धांत का एक सामान्यीकरण", मनोवैज्ञानिक समीक्षा, 63 (5): 277–293, doi:10.1037/h0046049, PMID 13359597.
- साइडेल, J. J. (1976), "दो-ग्राफ का एक सर्वेक्षण", Colloquio Internazionale sulle Teorie Combinatorie (रोम, 1973), टोमो I, अट्टी देई कन्वेग्नी लिंसी, vol. 17, रोम: एकेडेमिया नाजियोनेल देई लिंसी, pp. 481–511, MR 0550136.
- ज़स्लावस्की, थॉमस (1998), "हस्ताक्षरित और लाभ रेखांकन और संबद्ध क्षेत्रों की एक गणितीय ग्रंथ सूची", कॉम्बिनेटरिक्स का इलेक्ट्रॉनिक जर्नल, 5, गतिशील सर्वेक्षण 8, 124 पीपी।, MR 1744869
