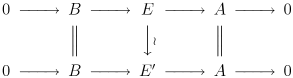एक्सट ऑपरेटर: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Construction in homological algebra}} | {{Short description|Construction in homological algebra}} | ||
गणित में, एक्सट प्रकार्यक [[मैं एक आदमी के रूप में काम करता हूं|होम प्रकार्यक]] के व्युत्पन्न प्रकार्यक हैं। [[Tor functor|टॉर प्रकार्यक]] के साथ, एक्सट [[समरूप बीजगणित| | गणित में, एक्सट प्रकार्यक [[मैं एक आदमी के रूप में काम करता हूं|होम प्रकार्यक]] के व्युत्पन्न प्रकार्यक हैं। [[Tor functor|टॉर प्रकार्यक]] के साथ, एक्सट [[समरूप बीजगणित|तुल्य बीजगणि]][[बीजगणितीय टोपोलॉजी|तीय]] की मूल अवधारणाओं में से एक है, जिसमें [[बीजगणितीय टोपोलॉजी|बीजगणितीय सांस्थितिकी]] के विचारों का उपयोग बीजगणितीय संरचनाओं के अचरों को परिभाषित करने के लिए किया जाता है। समूहों की [[समूह कोहोलॉजी|सह-समरूपता]], लाई बीजगणितीय और [[होशचाइल्ड कोहोलॉजी|साहचर्य बीजगणितीय]] सभी को एक्सट के संदर्भ में परिभाषित किया जा सकता है। यह नाम इस तथ्य से आता है कि पहला एक्सट समूह एक्सट<sup>1</sup> एक [[मॉड्यूल (गणित)|मापांक]] के [[समूह विस्तार|विस्तारण]] को दूसरे के द्वारा वर्गीकृत करता है। | ||
[[एबेलियन समूह|एबेलियन समूहों]] की विशेष स्थिति में, [[रेनहोल्ड बेयर]] (1934) द्वारा एक्सट प्रस्तुत किया गया था। इसका नाम [[सैमुअल एलेनबर्ग]] और [[सॉन्डर्स मैकलेन]] (1942) द्वारा रखा गया था और सांस्थितिकी ([[कोहोलॉजी के लिए सार्वभौमिक गुणांक प्रमेय|सह-समरूपता के लिए सार्वभौमिक गुणांक प्रमेय]]) पर अनुप्रयुक्त किया गया था। किसी भी वलय पर मापांक के लिए, एक्सट को[[ हेनरी कर्तन | हेनरी कार्टन]] और ईलेनबर्ग ने अपनी 1956 की पुस्तक तुल्य बीजगणितीय में परिभाषित किया गया था।<ref>Weibel (1999); Cartan & Eilenberg (1956), section VI.1.</ref> | [[एबेलियन समूह|एबेलियन समूहों]] की विशेष स्थिति में, [[रेनहोल्ड बेयर]] (1934) द्वारा एक्सट प्रस्तुत किया गया था। इसका नाम [[सैमुअल एलेनबर्ग]] और [[सॉन्डर्स मैकलेन]] (1942) द्वारा रखा गया था और सांस्थितिकी ([[कोहोलॉजी के लिए सार्वभौमिक गुणांक प्रमेय|सह-समरूपता के लिए सार्वभौमिक गुणांक प्रमेय]]) पर अनुप्रयुक्त किया गया था। किसी भी वलय पर मापांक के लिए, एक्सट को[[ हेनरी कर्तन | हेनरी कार्टन]] और ईलेनबर्ग ने अपनी 1956 की पुस्तक तुल्य बीजगणितीय में परिभाषित किया गया था।<ref>Weibel (1999); Cartan & Eilenberg (1956), section VI.1.</ref> | ||
| Line 6: | Line 6: | ||
== परिभाषा == | == परिभाषा == | ||
मान लीजिए कि R एक वलय और R- | मान लीजिए कि R एक वलय और R-मॉड R पर मापांक की [[श्रेणी (गणित)|श्रेणी]] है। कोई इसका अर्थ बाएं R-मापांक या दाएं R-मापांक के रूप में ले सकता है। एक नियत R-मापांक ''A'' के लिए, मान लीजिए कि R-मापांक में ''B'' के लिए ''T''(''B'') = Hom<sub>''R''</sub>(''A'', ''B'') है। (यहाँ Hom<sub>''R''</sub>(''A'', ''B'') ''A'' से B तक R-रैखिक प्रतिचित्रों का एबेलियन समूह है; यह एक R-मापांक है यदि R [[ क्रमविनिमेय अंगूठी |क्रमविनिमेय]] है)। यह R-मॉड से एबेलियन समूह Ab के वर्ग के लिए एक बाएं सटीक प्रकार्यक है और इसलिए इसमें दाएं व्युत्पन्न प्रकार्यक ''R<sup>i</sup>T'' हैं। एक्सट समूह द्वारा परिभाषित एबेलियन समूह हैं। | ||
:<math>\operatorname{Ext}_R^i(A,B)=(R^iT)(B)</math> | :<math>\operatorname{Ext}_R^i(A,B)=(R^iT)(B)</math> | ||
| Line 14: | Line 14: | ||
B पद को पदच्युत कर दें और [[कोचेन कॉम्प्लेक्स|सह श्रृंखला समष्टि]] बनाएं: | B पद को पदच्युत कर दें और [[कोचेन कॉम्प्लेक्स|सह श्रृंखला समष्टि]] बनाएं: | ||
:<math>0 \to \operatorname{Hom}_R(A,I^0) \to \operatorname{Hom}_R(A,I^1) \to \cdots | :<math>0 \to \operatorname{Hom}_R(A,I^0) \to \operatorname{Hom}_R(A,I^1) \to \cdots</math> | ||
प्रत्येक पूर्णांक i के लिए, Ext{{supsub|''i''|''R''}}(''A'', ''B'') स्थिति i पर इस समष्टि की [[चेन कॉम्प्लेक्स|सह-समरूपता]] है। यह i ऋणात्मक के लिए शून्य है। उदाहरण के लिए, Ext{{supsub|0|''R''}}(''A'', ''B'') प्रतिचित्र Hom<sub>''R''</sub>(''A'', ''I''<sup>0</sup>) → Hom<sub>''R''</sub>(''A'', ''I''<sup>1</sup>) का केंद्र है, जो Hom<sub>''R''</sub>(''A'', ''B)'' के लिए तुल्याकारी है। | प्रत्येक पूर्णांक i के लिए, Ext{{supsub|''i''|''R''}}(''A'', ''B'') की स्थिति i पर इस समष्टि की [[चेन कॉम्प्लेक्स|सह-समरूपता]] है। यह i ऋणात्मक के लिए शून्य है। उदाहरण के लिए, Ext{{supsub|0|''R''}}(''A'', ''B'') प्रतिचित्र Hom<sub>''R''</sub>(''A'', ''I''<sup>0</sup>) → Hom<sub>''R''</sub>(''A'', ''I''<sup>1</sup>) का केंद्र है, जो Hom<sub>''R''</sub>(''A'', ''B)'' के लिए तुल्याकारी है। | ||
एक वैकल्पिक परिभाषा एक नियत R-मापांक B के लिए प्रकार्यक G(A)=Hom(''A'', ''B'') का उपयोग करती है। यह एक प्रतिपरिवर्ती प्रकार्यक है, जिसे [[विपरीत श्रेणी]] (R- | एक वैकल्पिक परिभाषा एक नियत R-मापांक B के लिए प्रकार्यक G(A)=Hom(''A'', ''B'') का उपयोग करती है। यह एक प्रतिपरिवर्ती प्रकार्यक है, जिसे [[विपरीत श्रेणी]] (R-मॉड)<sup>op</sup> से Ab के लिए बाएं सटीक प्रकार्यक के रूप में देखा जा सकता है। एक्सट समूहों को दाहिने व्युत्पन्न प्रकार्यक ''R<sup>i</sup>G'' के रूप में परिभाषित किया गया है: | ||
:<math>\operatorname{Ext}_R^i(A,B)=(R^iG)(A) | :<math>\operatorname{Ext}_R^i(A,B)=(R^iG)(A)</math> | ||
अर्थात, कोई भी [[ प्रक्षेपी संकल्प |प्रक्षेपी वियोजन]] चयन करें, | अर्थात, कोई भी [[ प्रक्षेपी संकल्प |प्रक्षेपी वियोजन]] चयन करें, | ||
:<math>\cdots \to P_1 \to P_0 \to A \to 0 </math> | :<math>\cdots \to P_1 \to P_0 \to A \to 0 </math> | ||
पद A को पदच्युत कर दें, और सह श्रृंखला समष्टि बनाएं: | |||
:<math>0\to \operatorname{Hom}_R(P_0,B)\to \operatorname{Hom}_R(P_1,B) \to \cdots.</math> | :<math>0\to \operatorname{Hom}_R(P_0,B)\to \operatorname{Hom}_R(P_1,B) \to \cdots.</math> | ||
तब, Ext{{supsub|''i''|''R''}}(''A'', ''B'') स्थिति i पर इस परिसर की सह-समरूपता है। | तब, Ext{{supsub|''i''|''R''}}(''A'', ''B'') की स्थिति i पर इस परिसर की सह-समरूपता है। | ||
कार्टन और ईलेनबर्ग ने दर्शाया कि ये निर्माण प्रक्षेपी या अंतःक्षेपी वियोजन के चयन से स्वतंत्र हैं और यह कि दोनों निर्माण एक ही एक्सट समूह उत्पन्न करते हैं।<ref>Weibel (1994), sections 2.4 and 2.5 and Theorem 2.7.6.</ref> इसके अतिरिक्त, एक | कार्टन और ईलेनबर्ग ने दर्शाया कि ये निर्माण प्रक्षेपी या अंतःक्षेपी वियोजन के चयन से स्वतंत्र हैं और यह कि दोनों निर्माण एक ही एक्सट समूह उत्पन्न करते हैं।<ref>Weibel (1994), sections 2.4 and 2.5 and Theorem 2.7.6.</ref> इसके अतिरिक्त, एक नियत वलय R के लिए, एक्सट प्रत्येक चर में एक प्रकार्यक (A में प्रतिपरिवर्ती, B में सहसंयोजक) है। | ||
एक क्रमविनिमेय वलय R और R-मापांक ''A'' और B के लिए, Ext{{supsub|''i''|''R''}}(''A'', ''B'') एक R-मापांक है (Hom<sub>''R''</sub>(''A'', ''B'') इस स्थिति में एक R-मापांक है)। एक गैर-क्रमविनिमेय वलय R के लिए, Ext{{supsub|''i''|''R''}}(''A'', ''B'') सामान्यतः केवल एक एबेलियन समूह है। यदि R एक वलय S पर | एक क्रमविनिमेय वलय R और R-मापांक ''A'' और B के लिए, Ext{{supsub|''i''|''R''}}(''A'', ''B'') एक R-मापांक है, (Hom<sub>''R''</sub>(''A'', ''B'') इस स्थिति में एक R-मापांक है)। एक गैर-क्रमविनिमेय वलय R के लिए, Ext{{supsub|''i''|''R''}}(''A'', ''B'') सामान्यतः केवल एक एबेलियन समूह है। यदि R एक वलय S पर बीजगणितीय है (जिसका विशेष रूप से अर्थ है कि S क्रमविनिमेय है), तो Ext{{supsub|''i''|''R''}}(''A'', ''B'') कम-से-कम ''S''-मापांक है। | ||
== एक्सट के गुणधर्म == | == एक्सट के गुणधर्म == | ||
| Line 45: | Line 45: | ||
*यदि R एक क्रमविनिमेय वलय है और u में R एक [[शून्य भाजक]] नहीं है, तब | *यदि R एक क्रमविनिमेय वलय है और u में R एक [[शून्य भाजक]] नहीं है, तब | ||
::<math>\operatorname{Ext}_R^i(R/(u),B)\cong\begin{cases} B[u] & i=0\\ B/uB & i=1\\ 0 &\text{otherwise}\end{cases}</math> | ::<math>\operatorname{Ext}_R^i(R/(u),B)\cong\begin{cases} B[u] & i=0\\ B/uB & i=1\\ 0 &\text{otherwise}\end{cases}</math> | ||
:किसी भी R-मापांक B के लिए है। यहां ''B'' [''u''] ''B'' के ''u''-विमोटन उपसमूह {x ∈ B: ux = 0} को दर्शाता है। | :किसी भी R-मापांक B के लिए है। यहां ''B'' [''u''] ''B'' के ''u''-विमोटन उपसमूह {x ∈ B: ux = 0} को दर्शाता है। <math>\Z</math> के पूर्णांकों को R का वलय मान लेना, किसी भी [[अंतिम रूप से उत्पन्न एबेलियन समूह]] ''A'' के लिए, इस परिकलन <math>\operatorname{Ext}^1_{\Z}(A,B)</math> का उपयोग गणना करने के लिए किया जा सकता है। | ||
* पिछले उदाहरण को सामान्य करते हुए, जब कोई पहला मापांक [[जटिल शर्ट|कोज़ल]] समष्टि का उपयोग करके किसी [[नियमित अनुक्रम]] द्वारा एक क्रमविनिमेय वलय का भागफल होता है, तो कोई एक्सट समूहों की गणना कर सकता है।<ref>Weibel (1994), section 4.5.</ref> उदाहरण के लिए, यदि R | * पिछले उदाहरण को सामान्य करते हुए, जब कोई पहला मापांक [[जटिल शर्ट|कोज़ल]] समष्टि का उपयोग करके किसी [[नियमित अनुक्रम]] द्वारा एक क्रमविनिमेय वलय का भागफल होता है, तो कोई एक्सट समूहों की गणना कर सकता है।<ref>Weibel (1994), section 4.5.</ref> उदाहरण के लिए, यदि R क्षेत्रक k पर बहुपद वलय ''k''[''x''<sub>1</sub>,...,''x<sub>n</sub>''] है, तो Ext{{supsub|*|''R''}}(k,k) Ext<sup>1</sup> में n जनक पर k के ऊपर [[बाहरी बीजगणित|बाह्य बीजगणितीय]] S है। इसके अतिरिक्त, Ext{{supsub|*|''R''}}(k,k) बहुपद वलय R है; यह कोज़ल द्वैतता का एक उदाहरण है। | ||
*व्युत्पन्न प्रकार्यकों के सामान्य गुणों के अनुसार, एक्सट के लिए दो मूल सटीक अनुक्रम हैं।<ref>Weibel (1994), Definition 2.1.1.</ref> सर्वप्रथम, R-मापांक के एक छोटे सटीक अनुक्रम 0 → K → L → M → 0 | *व्युत्पन्न प्रकार्यकों के सामान्य गुणों के अनुसार, एक्सट के लिए दो मूल सटीक अनुक्रम हैं।<ref>Weibel (1994), Definition 2.1.1.</ref> सर्वप्रथम, R-मापांक के एक छोटे सटीक अनुक्रम 0 → K → L → M → 0 प्ररूप के एक लंबे सटीक अनुक्रम को प्रेरित करता है। | ||
::<math>0 \to \mathrm{Hom}_R(A,K) \to \mathrm{Hom}_R(A,L) \to \mathrm{Hom}_R(A,M) \to \mathrm{Ext}^1_R(A,K) \to \mathrm{Ext}^1_R(A,L) \to \cdots</math> | ::<math>0 \to \mathrm{Hom}_R(A,K) \to \mathrm{Hom}_R(A,L) \to \mathrm{Hom}_R(A,M) \to \mathrm{Ext}^1_R(A,K) \to \mathrm{Ext}^1_R(A,L) \to \cdots</math> | ||
: किसी भी R-मापांक ''A'' के लिए है। इसके अतिरिक्त, एक छोटे सटीक अनुक्रम 0 → ''K'' → ''L'' → ''M'' → 0 | : किसी भी R-मापांक ''A'' के लिए है। इसके अतिरिक्त, एक छोटे सटीक अनुक्रम 0 → ''K'' → ''L'' → ''M'' → 0 प्ररूप के एक लंबे सटीक अनुक्रम को प्रेरित करता है। | ||
::<math>0 \to \mathrm{Hom}_R(M,B) \to \mathrm{Hom}_R(L,B) \to \mathrm{Hom}_R(K,B) \to \mathrm{Ext}^1_R(M,B) \to \mathrm{Ext}^1_R(L,B) \to \cdots</math> | ::<math>0 \to \mathrm{Hom}_R(M,B) \to \mathrm{Hom}_R(L,B) \to \mathrm{Hom}_R(K,B) \to \mathrm{Ext}^1_R(M,B) \to \mathrm{Ext}^1_R(L,B) \to \cdots</math> | ||
: किसी भी R-मापांक B के लिए है। | : किसी भी R-मापांक B के लिए है। | ||
*एक्सट पहले चर में प्रत्यक्ष योग (संभवतः अनंत) लेता है और दूसरे चर में प्रत्यक्ष उत्पाद को उत्पादों में लेता है।<ref>Weibel (1994), Proposition 3.3.4.</ref> वह है: | *एक्सट पहले चर में प्रत्यक्ष योग (संभवतः अनंत) लेता है और दूसरे चर में प्रत्यक्ष उत्पाद को उत्पादों में लेता है।<ref>Weibel (1994), Proposition 3.3.4.</ref> वह है: | ||
| Line 61: | Line 60: | ||
\operatorname{Ext}^i_R \left(M,\prod_\alpha N_\alpha \right ) &\cong\prod_\alpha \operatorname{Ext}^i_R (M,N_\alpha) | \operatorname{Ext}^i_R \left(M,\prod_\alpha N_\alpha \right ) &\cong\prod_\alpha \operatorname{Ext}^i_R (M,N_\alpha) | ||
\end{align}</math> | \end{align}</math> | ||
* मान लीजिए कि ''A'' एक क्रमविनिमेय [[नोथेरियन रिंग|नोथेरियन वलय]] R पर | * मान लीजिए कि ''A'' एक क्रमविनिमेय [[नोथेरियन रिंग|नोथेरियन वलय]] R पर अंतिम रूप से उत्पन्न मापांक है। फिर एक्सट के स्थानीयकरण के साथ इस अर्थ में प्रारंभ होता है कि R में प्रत्येक गुणात्मक रूप से संवृत समुच्चय ''S'' के लिए, प्रत्येक R-मापांक B और प्रत्येक पूर्णांक i है।<ref>Weibel (1994), Proposition 3.3.10.</ref> | ||
::<math>S^{-1} \operatorname{Ext}_R^i(A, B) \cong \operatorname{Ext}_{S^{-1} R}^i \left (S^{-1} A, S^{-1} B \right )</math> | ::<math>S^{-1} \operatorname{Ext}_R^i(A, B) \cong \operatorname{Ext}_{S^{-1} R}^i \left (S^{-1} A, S^{-1} B \right )</math> | ||
| Line 81: | Line 80: | ||
:[[Image:EquivalenceOfExtensions.png]] | :[[Image:EquivalenceOfExtensions.png]] | ||
: | : | ||
ध्यान दें कि [[पाँच लेम्मा]] का तात्पर्य है कि मध्य शर | ध्यान दें कि [[पाँच लेम्मा]] का तात्पर्य है कि मध्य शर समरूपता है। A द्वारा B के विस्तारण को विभाजन कहा जाता है यदि यह नगण्य विस्तारण के समान है। | ||
:<math>0\to B\to A\oplus B\to A\to 0</math> | :<math>0\to B\to A\oplus B\to A\to 0</math> | ||
A द्वारा B के विस्तारण के समतुल्य वर्गों और Ext{{supsub|1|''R''}}(A, B) के तत्वों के मध्य एक-से-एक सामंजस्य है।<ref>Weibel (1994), Theorem 3.4.3.</ref> | A द्वारा B के विस्तारण के समतुल्य वर्गों और Ext{{supsub|1|''R''}}(A, B) के तत्वों के मध्य एक-से-एक सामंजस्य है।<ref>Weibel (1994), Theorem 3.4.3.</ref> नगण्य विस्तारण Ext{{supsub|1|''R''}}(A, B) के शून्य तत्व से मेल खाता है। | ||
=== विस्तारण का | === विस्तारण का बेयर योग === | ||
बेयर योग Ext{{supsub|1|''R''}}(''A'', B) पर एबेलियन समूह संरचना का एक स्पष्ट विवरण है, B द्वारा A के विस्तारण के समतुल्य वर्गों के समुच्चय के रूप में देखा जाता है।<ref>Weibel (1994), Corollary 3.4.5.</ref> अर्थात्, दो विस्तारण दिए गए, | बेयर योग Ext{{supsub|1|''R''}}(''A'', B) पर एबेलियन समूह संरचना का एक स्पष्ट विवरण है, B द्वारा A के विस्तारण के समतुल्य वर्गों के समुच्चय के रूप में देखा जाता है।<ref>Weibel (1994), Corollary 3.4.5.</ref> अर्थात्, दो विस्तारण दिए गए, | ||
| Line 101: | Line 100: | ||
:<math>0\to B\to Y\to A\to 0</math> | :<math>0\to B\to Y\to A\to 0</math> | ||
जहां पहला प्रतिचित्र<math>b \mapsto [(f(b), 0)] = [(0, f'(b))]</math> और दूसरा <math>(e, e') \mapsto g(e) = g'(e')</math> है। | जहां पहला प्रतिचित्र <math>b \mapsto [(f(b), 0)] = [(0, f'(b))]</math> और दूसरा <math>(e, e') \mapsto g(e) = g'(e')</math> है। | ||
विस्तारण की समतुल्यता [[तक]], | विस्तारण की समतुल्यता [[तक]], बेयर योग क्रमविनिमेय है और पहचान तत्व के रूप में नगण्य विस्तारण है। एक विस्तारण 0 → B → ''E'' → ''A'' → 0 का ऋणात्मक एक ही मापांक ''E'' को सम्मिलित करने वाला विस्तारण है, परन्तु समरूपता B → ''E'' के साथ इसके ऋणात्मक द्वारा प्रतिस्थापित किया गया है। | ||
== एबेलियन श्रेणियों में एक्सट का निर्माण == | == एबेलियन श्रेणियों में एक्सट का निर्माण == | ||
[[ नोबुओ योनेदा ]]ने एबेलियन समूहों Ext{{su|b='''C'''|p=''n''}}(''A'', B) को परिभाषित किया, किसी [[एबेलियन श्रेणी]] | [[ नोबुओ योनेदा ]]ने एबेलियन समूहों Ext{{su|b='''C'''|p=''n''}}(''A'', B) को परिभाषित किया, किसी [[एबेलियन श्रेणी]] C में वस्तुओं ''A'' और B के लिए; यह वियोजन के संदर्भ में परिभाषा से सहमत है यदि C के पास पर्याप्त प्रक्षेपीय या पर्याप्त अंतःक्षेपक हैं। सर्वप्रथम, Ext{{supsub|0|'''C'''}}(''A'', B) = Hom<sub>'''C'''</sub>(''A'', B) हैं। अगला, Ext{{su|b='''C'''|p=1}}(''A'', B) B द्वारा ''A'' के विस्तारण के समतुल्य वर्गों का समुच्चय है, जो बेयर योग के अंतर्गत एक एबेलियन समूह बनाता है। अंत में, उच्च एक्सट समूह Ext{{su|b='''C'''|p=''n''}}(''A'', B) को ''n''-विस्तारण के समतुल्य वर्गों के रूप में परिभाषित किया गया है, जो सटीक अनुक्रम हैं। | ||
:<math>0\to B\to X_n\to\cdots\to X_1\to A\to 0</math> | :<math>0\to B\to X_n\to\cdots\to X_1\to A\to 0</math> | ||
| Line 115: | Line 114: | ||
\xi': 0 &\to B\to X'_n\to\cdots\to X'_1\to A\to 0 | \xi': 0 &\to B\to X'_n\to\cdots\to X'_1\to A\to 0 | ||
\end{align}</math> | \end{align}</math> | ||
यदि प्रतिचित्र <math>X_m \to X'_m</math>है, {1, 2, ..., n} में सभी m के लिए ताकि प्रत्येक परिणामी वर्ग परिवर्तित हो जाए। | यदि प्रतिचित्र <math>X_m \to X'_m</math>है, {1, 2, ..., n} में सभी m के लिए है, ताकि प्रत्येक परिणामी वर्ग परिवर्तित हो जाए। | ||
यदि कोई श्रृंखला मानचित्र ξ → ξ' है जो A और B पर तत्समक है। | यदि कोई श्रृंखला मानचित्र ξ → ξ' है जो A और B पर तत्समक है। | ||
उपर्युक्त दो n-आयामों | उपर्युक्त दो n-आयामों, ''A'' पर <math>X_1</math> और <math>X'_1</math> का पुलबैक <math>X''_1</math> और B के अंतर्गत <math>X_n</math> और <math>X'_n</math> का [[पुशआउट (श्रेणी सिद्धांत)|बहिकर्षी]] <math>X''_n</math> का बेयर योग देने से बनता है,<ref>Weibel (1994), Vists 3.4.6. Some minor corrections are in the [http://www.math.rutgers.edu/~weibel/Hbook.errors.edition2.pdf errata].</ref> फिर विस्तारण का बेयर योग है। | ||
:<math>0\to B\to X''_n\to X_{n-1}\oplus X'_{n-1}\to\cdots\to X_2\oplus X'_2\to X''_1\to A\to 0</math> | :<math>0\to B\to X''_n\to X_{n-1}\oplus X'_{n-1}\to\cdots\to X_2\oplus X'_2\to X''_1\to A\to 0</math> | ||
| Line 125: | Line 124: | ||
== व्युत्पन्न श्रेणी और योनेदा उत्पाद == | == व्युत्पन्न श्रेणी और योनेदा उत्पाद == | ||
एक महत्वपूर्ण बिंदु यह है कि एबेलियन श्रेणी | एक महत्वपूर्ण बिंदु यह है कि एबेलियन श्रेणी C में एक्सट समूहों को C व्युत्पन्न श्रेणी ''D''(C) से संबंधित श्रेणी में आकारिकी के समुच्चयों के रूप में देखा जा सकता है।<ref>Weibel (1994), sections 10.4 and 10.7; Gelfand & Manin (2003), Chapter III.</ref> व्युत्पन्न श्रेणी की वस्तुएं C में वस्तुओं के परिसर हैं। विशेष रूप से, किसी के पास है | ||
:<math>\operatorname{Ext}^i_{\mathbf C}(A,B) = \operatorname{Hom}_{D({\mathbf C})}(A,B[i])</math> | :<math>\operatorname{Ext}^i_{\mathbf C}(A,B) = \operatorname{Hom}_{D({\mathbf C})}(A,B[i])</math> | ||
| Line 135: | Line 134: | ||
योनेडा उत्पाद को अधिक प्राथमिक शब्दों में भी वर्णित किया जा सकता है। i = j = 0 के लिए, गुणनफल C श्रेणी के प्रतिचित्रों का संघटन है। सामान्यतः, उत्पाद को दो योनेडा विस्तारण को एक साथ जोड़कर परिभाषित किया जा सकता है। | योनेडा उत्पाद को अधिक प्राथमिक शब्दों में भी वर्णित किया जा सकता है। i = j = 0 के लिए, गुणनफल C श्रेणी के प्रतिचित्रों का संघटन है। सामान्यतः, उत्पाद को दो योनेडा विस्तारण को एक साथ जोड़कर परिभाषित किया जा सकता है। | ||
वैकल्पिक रूप से, योनेडा उत्पाद को वियोजन के संदर्भ में परिभाषित किया जा सकता है (यह व्युत्पन्न श्रेणी की परिभाषा के समीप है)। उदाहरण के लिए, R-मापांक ''A'', ''B'', ''C'' के साथ R | वैकल्पिक रूप से, योनेडा उत्पाद को वियोजन के संदर्भ में परिभाषित किया जा सकता है (यह व्युत्पन्न श्रेणी की परिभाषा के समीप है)। उदाहरण के लिए, मान लीजिए कि R-मापांक ''A'', ''B'', ''C'' के साथ R वलय है और ''P'', ''Q'' और ''T'' के प्रक्षेपी वियोजन ''A'', ''B'', ''C'' है। फिर Ext{{supsub|''i''|''R''}}(''A'', B) को श्रृंखला प्रतिचित्र ''P'' → ''Q''[''i''] के [[चेन होमोटॉपी|श्रृंखला समस्थेयता]] कक्षाओं के समूह के साथ पहचाना जा सकता है। योनेदा उत्पाद श्रृंखला प्रतिचित्र बनाकर दिया गया है: | ||
:<math>P\to Q[i]\to T[i+j]</math> | :<math>P\to Q[i]\to T[i+j]</math> | ||
| Line 142: | Line 141: | ||
== महत्वपूर्ण विशेष स्थिति == | == महत्वपूर्ण विशेष स्थिति == | ||
*समूह सह-समरूपता <math>H^*(G,M)=\operatorname{Ext}_{\Z[G]}^*(\Z, M)</math> द्वारा परिभाषित किया गया है, जहाँ G एक समूह है, M पूर्णांकों पर G का एक [[समूह प्रतिनिधित्व]] | *समूह सह-समरूपता <math>H^*(G,M)=\operatorname{Ext}_{\Z[G]}^*(\Z, M)</math> द्वारा परिभाषित किया गया है, जहाँ G एक समूह है, M पूर्णांकों पर G का एक [[समूह प्रतिनिधित्व]] और <math>\Z[G]</math> G का [[ समूह की अंगूठी |समूह वलय]] है। | ||
* | *क्षेत्रक k और A-[[bimodule|द्विप्रतिरूपक]] M पर बीजगणितीय A के लिए, होशचाइल्ड सह-समरूपता द्वारा परिभाषित किया गया है: | ||
::<math>HH^*(A,M)=\operatorname{Ext}^*_{A\otimes_k A^{\text{op}}} (A, M)</math> | ::<math>HH^*(A,M)=\operatorname{Ext}^*_{A\otimes_k A^{\text{op}}} (A, M)</math> | ||
*लाई बीजगणितीय सह-समरूपता <math>H^*(\mathfrak g,M)=\operatorname{Ext}^*_{U\mathfrak g}(k,M)</math> द्वारा परिभाषित किया गया है, जहाँ <math>\mathfrak g</math> क्रमविनिमेय वलय k पर एक लाई बीजगणित है, M एक <math>\mathfrak g</math>-मापांक है और <math>U\mathfrak g</math> सार्वभौमिक आवृत | *लाई बीजगणितीय सह-समरूपता <math>H^*(\mathfrak g,M)=\operatorname{Ext}^*_{U\mathfrak g}(k,M)</math> द्वारा परिभाषित किया गया है, जहाँ <math>\mathfrak g</math> क्रमविनिमेय वलय k पर एक लाई बीजगणित है, M एक <math>\mathfrak g</math>-मापांक है और <math>U\mathfrak g</math> सार्वभौमिक आवृत बीजगणितीय है। | ||
* एक [[टोपोलॉजिकल स्पेस|सांस्थितिक समष्टि]] ''X'' के लिए, [[शेफ कोहोलॉजी|पूली सह-समरूपता]] को इस <math>H^*(X, A) = \operatorname{Ext}^*(\Z_X, A)</math> रूप में परिभाषित किया जा सकता है। यहाँ एक्सट को X पर एबेलियन के [[शीफ (गणित)|पुली]] की एबेलियन श्रेणी में लिया गया है और <math>\Z_X</math> स्थानीय स्थिरांक <math>\Z</math>-मूल्यवान फलन | * एक [[टोपोलॉजिकल स्पेस|सांस्थितिक समष्टि]] ''X'' के लिए, [[शेफ कोहोलॉजी|पूली सह-समरूपता]] को इस <math>H^*(X, A) = \operatorname{Ext}^*(\Z_X, A)</math> रूप में परिभाषित किया जा सकता है। यहाँ एक्सट को X पर एबेलियन समूहों के [[शीफ (गणित)|पुली]] की एबेलियन श्रेणी में लिया गया है और <math>\Z_X</math> स्थानीय स्थिरांक, <math>\Z</math>-मूल्यवान फलन की [[शीफ (गणित)|पूली]] है। | ||
*अवशिष्ट | *अवशिष्ट क्षेत्रक k के साथ क्रमविनिमेय नोथेरियन स्थानीय वलय R के लिए, <math>\operatorname{Ext}^*_R(k,k)</math> एक श्रेणीबद्ध लाई बीजगणितीय π*(R) पर k का सार्वभौमिक आवृत बीजगणितीय है, जिसे R के समस्थेयता लाई बीजगणितीय के रूप में जाना जाता है (सटीक होने के लिए, जब k की विलक्षणता 2 होती है, π*(R) को एक समायोजित लाई बीजगणितीय के रूप में देखा जा सकता है)।<ref>Sjödin (1980), Notation 14.</ref> एंड्रे-क्विलन सह-समरूपता ''D''*(''k''/''R'',''k'') से π*(R) तक श्रेणीबद्ध लाई बीजगणितीय की एक प्राकृतिक समरूपता है, जो एक समरूपता है यदि ''k'' में विलक्षणता शून्य है।<ref>Avramov (2010), section 10.2.</ref> | ||
Revision as of 06:35, 18 May 2023
गणित में, एक्सट प्रकार्यक होम प्रकार्यक के व्युत्पन्न प्रकार्यक हैं। टॉर प्रकार्यक के साथ, एक्सट तुल्य बीजगणितीय की मूल अवधारणाओं में से एक है, जिसमें बीजगणितीय सांस्थितिकी के विचारों का उपयोग बीजगणितीय संरचनाओं के अचरों को परिभाषित करने के लिए किया जाता है। समूहों की सह-समरूपता, लाई बीजगणितीय और साहचर्य बीजगणितीय सभी को एक्सट के संदर्भ में परिभाषित किया जा सकता है। यह नाम इस तथ्य से आता है कि पहला एक्सट समूह एक्सट1 एक मापांक के विस्तारण को दूसरे के द्वारा वर्गीकृत करता है।
एबेलियन समूहों की विशेष स्थिति में, रेनहोल्ड बेयर (1934) द्वारा एक्सट प्रस्तुत किया गया था। इसका नाम सैमुअल एलेनबर्ग और सॉन्डर्स मैकलेन (1942) द्वारा रखा गया था और सांस्थितिकी (सह-समरूपता के लिए सार्वभौमिक गुणांक प्रमेय) पर अनुप्रयुक्त किया गया था। किसी भी वलय पर मापांक के लिए, एक्सट को हेनरी कार्टन और ईलेनबर्ग ने अपनी 1956 की पुस्तक तुल्य बीजगणितीय में परिभाषित किया गया था।[1]
परिभाषा
मान लीजिए कि R एक वलय और R-मॉड R पर मापांक की श्रेणी है। कोई इसका अर्थ बाएं R-मापांक या दाएं R-मापांक के रूप में ले सकता है। एक नियत R-मापांक A के लिए, मान लीजिए कि R-मापांक में B के लिए T(B) = HomR(A, B) है। (यहाँ HomR(A, B) A से B तक R-रैखिक प्रतिचित्रों का एबेलियन समूह है; यह एक R-मापांक है यदि R क्रमविनिमेय है)। यह R-मॉड से एबेलियन समूह Ab के वर्ग के लिए एक बाएं सटीक प्रकार्यक है और इसलिए इसमें दाएं व्युत्पन्न प्रकार्यक RiT हैं। एक्सट समूह द्वारा परिभाषित एबेलियन समूह हैं।
एक पूर्णांक i के लिए परिभाषा के अनुसार, इसका अर्थ है: कोई अंतःक्षेपक वियोजन हैं।
B पद को पदच्युत कर दें और सह श्रृंखला समष्टि बनाएं:
प्रत्येक पूर्णांक i के लिए, Exti
R(A, B) की स्थिति i पर इस समष्टि की सह-समरूपता है। यह i ऋणात्मक के लिए शून्य है। उदाहरण के लिए, Ext0
R(A, B) प्रतिचित्र HomR(A, I0) → HomR(A, I1) का केंद्र है, जो HomR(A, B) के लिए तुल्याकारी है।
एक वैकल्पिक परिभाषा एक नियत R-मापांक B के लिए प्रकार्यक G(A)=Hom(A, B) का उपयोग करती है। यह एक प्रतिपरिवर्ती प्रकार्यक है, जिसे विपरीत श्रेणी (R-मॉड)op से Ab के लिए बाएं सटीक प्रकार्यक के रूप में देखा जा सकता है। एक्सट समूहों को दाहिने व्युत्पन्न प्रकार्यक RiG के रूप में परिभाषित किया गया है:
अर्थात, कोई भी प्रक्षेपी वियोजन चयन करें,
पद A को पदच्युत कर दें, और सह श्रृंखला समष्टि बनाएं:
तब, Exti
R(A, B) की स्थिति i पर इस परिसर की सह-समरूपता है।
कार्टन और ईलेनबर्ग ने दर्शाया कि ये निर्माण प्रक्षेपी या अंतःक्षेपी वियोजन के चयन से स्वतंत्र हैं और यह कि दोनों निर्माण एक ही एक्सट समूह उत्पन्न करते हैं।[2] इसके अतिरिक्त, एक नियत वलय R के लिए, एक्सट प्रत्येक चर में एक प्रकार्यक (A में प्रतिपरिवर्ती, B में सहसंयोजक) है।
एक क्रमविनिमेय वलय R और R-मापांक A और B के लिए, Exti
R(A, B) एक R-मापांक है, (HomR(A, B) इस स्थिति में एक R-मापांक है)। एक गैर-क्रमविनिमेय वलय R के लिए, Exti
R(A, B) सामान्यतः केवल एक एबेलियन समूह है। यदि R एक वलय S पर बीजगणितीय है (जिसका विशेष रूप से अर्थ है कि S क्रमविनिमेय है), तो Exti
R(A, B) कम-से-कम S-मापांक है।
एक्सट के गुणधर्म
यहाँ एक्सट समूहों के कुछ मूलभूत गुणधर्म और संगणनाएँ दी गई हैं।[3]
- Ext0
R(A, B) ≅ HomR(A, B) किसी भी R-मापांक A और B के लिए है।
- Exti
R(A, B) = 0 सभी i> 0 के लिए, यदि R-मापांक A प्रक्षेपी मापांक है (उदाहरण के लिए, मुफ्त मापांक ) या यदि B अंतःक्षेपक मापांक है।
- बातचीत भी रखती है:
- यदि Ext1
R(A, B) = 0 सभी B के लिए, तो A प्रक्षेपी (और इसलिए Exti
R(A, B) = 0 सभी i> 0 के लिए) है। - यदि Ext1
R(A, B) = 0 सभी A के लिए, फिर B अंतःक्षेपी (और इसलिए एक्सटi
R(A, B) = 0 सभी i> 0 के लिए) है।
- यदि Ext1
- सभी i ≥ 2 और सभी एबेलियन समूहों A और B के लिए है।[4]
- यदि R एक क्रमविनिमेय वलय है और u में R एक शून्य भाजक नहीं है, तब
- किसी भी R-मापांक B के लिए है। यहां B [u] B के u-विमोटन उपसमूह {x ∈ B: ux = 0} को दर्शाता है। के पूर्णांकों को R का वलय मान लेना, किसी भी अंतिम रूप से उत्पन्न एबेलियन समूह A के लिए, इस परिकलन का उपयोग गणना करने के लिए किया जा सकता है।
- पिछले उदाहरण को सामान्य करते हुए, जब कोई पहला मापांक कोज़ल समष्टि का उपयोग करके किसी नियमित अनुक्रम द्वारा एक क्रमविनिमेय वलय का भागफल होता है, तो कोई एक्सट समूहों की गणना कर सकता है।[5] उदाहरण के लिए, यदि R क्षेत्रक k पर बहुपद वलय k[x1,...,xn] है, तो Ext*
R(k,k) Ext1 में n जनक पर k के ऊपर बाह्य बीजगणितीय S है। इसके अतिरिक्त, Ext*
R(k,k) बहुपद वलय R है; यह कोज़ल द्वैतता का एक उदाहरण है।
- व्युत्पन्न प्रकार्यकों के सामान्य गुणों के अनुसार, एक्सट के लिए दो मूल सटीक अनुक्रम हैं।[6] सर्वप्रथम, R-मापांक के एक छोटे सटीक अनुक्रम 0 → K → L → M → 0 प्ररूप के एक लंबे सटीक अनुक्रम को प्रेरित करता है।
- किसी भी R-मापांक A के लिए है। इसके अतिरिक्त, एक छोटे सटीक अनुक्रम 0 → K → L → M → 0 प्ररूप के एक लंबे सटीक अनुक्रम को प्रेरित करता है।
- किसी भी R-मापांक B के लिए है।
- एक्सट पहले चर में प्रत्यक्ष योग (संभवतः अनंत) लेता है और दूसरे चर में प्रत्यक्ष उत्पाद को उत्पादों में लेता है।[7] वह है:
- मान लीजिए कि A एक क्रमविनिमेय नोथेरियन वलय R पर अंतिम रूप से उत्पन्न मापांक है। फिर एक्सट के स्थानीयकरण के साथ इस अर्थ में प्रारंभ होता है कि R में प्रत्येक गुणात्मक रूप से संवृत समुच्चय S के लिए, प्रत्येक R-मापांक B और प्रत्येक पूर्णांक i है।[8]
एक्सट और विस्तारण
विस्तारण की समानता
एक्सट समूह मापांक के विस्तार से उनके संबंध से अपना नाम प्राप्त करते हैं। दिए गए R-मापांक A और B, B द्वारा A का विस्तारण R-मापांक का एक छोटा सटीक अनुक्रम है।
दो विस्तारण,
एक क्रमविनिमेय आरेख होने पर समतुल्य कहा जाता है (A द्वारा B के विस्तारण के रूप में):
ध्यान दें कि पाँच लेम्मा का तात्पर्य है कि मध्य शर समरूपता है। A द्वारा B के विस्तारण को विभाजन कहा जाता है यदि यह नगण्य विस्तारण के समान है।
A द्वारा B के विस्तारण के समतुल्य वर्गों और Ext1
R(A, B) के तत्वों के मध्य एक-से-एक सामंजस्य है।[9] नगण्य विस्तारण Ext1
R(A, B) के शून्य तत्व से मेल खाता है।
विस्तारण का बेयर योग
बेयर योग Ext1
R(A, B) पर एबेलियन समूह संरचना का एक स्पष्ट विवरण है, B द्वारा A के विस्तारण के समतुल्य वर्गों के समुच्चय के रूप में देखा जाता है।[10] अर्थात्, दो विस्तारण दिए गए,
और
पहले पर पुलबैक तैयार करें,
फिर भागफल मापांक बनाएं,
E और E' का बेयर योग विस्तारण है।
जहां पहला प्रतिचित्र और दूसरा है।
विस्तारण की समतुल्यता तक, बेयर योग क्रमविनिमेय है और पहचान तत्व के रूप में नगण्य विस्तारण है। एक विस्तारण 0 → B → E → A → 0 का ऋणात्मक एक ही मापांक E को सम्मिलित करने वाला विस्तारण है, परन्तु समरूपता B → E के साथ इसके ऋणात्मक द्वारा प्रतिस्थापित किया गया है।
एबेलियन श्रेणियों में एक्सट का निर्माण
नोबुओ योनेदा ने एबेलियन समूहों Extn
C(A, B) को परिभाषित किया, किसी एबेलियन श्रेणी C में वस्तुओं A और B के लिए; यह वियोजन के संदर्भ में परिभाषा से सहमत है यदि C के पास पर्याप्त प्रक्षेपीय या पर्याप्त अंतःक्षेपक हैं। सर्वप्रथम, Ext0
C(A, B) = HomC(A, B) हैं। अगला, Ext1
C(A, B) B द्वारा A के विस्तारण के समतुल्य वर्गों का समुच्चय है, जो बेयर योग के अंतर्गत एक एबेलियन समूह बनाता है। अंत में, उच्च एक्सट समूह Extn
C(A, B) को n-विस्तारण के समतुल्य वर्गों के रूप में परिभाषित किया गया है, जो सटीक अनुक्रम हैं।
दो आयामों की पहचान करने वाले संबंध से उत्पन्न तुल्यता संबंध के अंतर्गत है।
यदि प्रतिचित्र है, {1, 2, ..., n} में सभी m के लिए है, ताकि प्रत्येक परिणामी वर्ग परिवर्तित हो जाए।
यदि कोई श्रृंखला मानचित्र ξ → ξ' है जो A और B पर तत्समक है।
उपर्युक्त दो n-आयामों, A पर और का पुलबैक और B के अंतर्गत और का बहिकर्षी का बेयर योग देने से बनता है,[11] फिर विस्तारण का बेयर योग है।
व्युत्पन्न श्रेणी और योनेदा उत्पाद
एक महत्वपूर्ण बिंदु यह है कि एबेलियन श्रेणी C में एक्सट समूहों को C व्युत्पन्न श्रेणी D(C) से संबंधित श्रेणी में आकारिकी के समुच्चयों के रूप में देखा जा सकता है।[12] व्युत्पन्न श्रेणी की वस्तुएं C में वस्तुओं के परिसर हैं। विशेष रूप से, किसी के पास है
जहां C की एक वस्तु को डिग्री शून्य में केंद्रित एक जटिल के रूप में देखा जाता है और [i] का अर्थ है। एक जटिल i चरणों को बाईं ओर स्थानांतरित करना है। इस व्याख्या से, एक द्विरेखीय प्रतिचित्र है, जिसे कभी-कभी योनेदा उत्पाद कहा जाता है:
जो केवल व्युत्पन्न श्रेणी में आकारिता की रचना है।
योनेडा उत्पाद को अधिक प्राथमिक शब्दों में भी वर्णित किया जा सकता है। i = j = 0 के लिए, गुणनफल C श्रेणी के प्रतिचित्रों का संघटन है। सामान्यतः, उत्पाद को दो योनेडा विस्तारण को एक साथ जोड़कर परिभाषित किया जा सकता है।
वैकल्पिक रूप से, योनेडा उत्पाद को वियोजन के संदर्भ में परिभाषित किया जा सकता है (यह व्युत्पन्न श्रेणी की परिभाषा के समीप है)। उदाहरण के लिए, मान लीजिए कि R-मापांक A, B, C के साथ R वलय है और P, Q और T के प्रक्षेपी वियोजन A, B, C है। फिर Exti
R(A, B) को श्रृंखला प्रतिचित्र P → Q[i] के श्रृंखला समस्थेयता कक्षाओं के समूह के साथ पहचाना जा सकता है। योनेदा उत्पाद श्रृंखला प्रतिचित्र बनाकर दिया गया है:
इनमें से किसी भी व्याख्या से, योनेदा उत्पाद साहचर्य है। फलस्वरूप, किसी भी R-मापांक A के लिए एक श्रेणीबद्ध वलय है। उदाहरण के लिए, यह समूह सह-समरूपता पर वलय संरचना देता है, चूंकि इसे के रूप में देखा जा सकता है। योनेडा उत्पाद की सहचारिता द्वारा भी: किसी भी R-मापांक A और B के लिए, पर एक मापांक है।
महत्वपूर्ण विशेष स्थिति
- समूह सह-समरूपता द्वारा परिभाषित किया गया है, जहाँ G एक समूह है, M पूर्णांकों पर G का एक समूह प्रतिनिधित्व और G का समूह वलय है।
- क्षेत्रक k और A-द्विप्रतिरूपक M पर बीजगणितीय A के लिए, होशचाइल्ड सह-समरूपता द्वारा परिभाषित किया गया है:
- लाई बीजगणितीय सह-समरूपता द्वारा परिभाषित किया गया है, जहाँ क्रमविनिमेय वलय k पर एक लाई बीजगणित है, M एक -मापांक है और सार्वभौमिक आवृत बीजगणितीय है।
- एक सांस्थितिक समष्टि X के लिए, पूली सह-समरूपता को इस रूप में परिभाषित किया जा सकता है। यहाँ एक्सट को X पर एबेलियन समूहों के पुली की एबेलियन श्रेणी में लिया गया है और स्थानीय स्थिरांक, -मूल्यवान फलन की पूली है।
- अवशिष्ट क्षेत्रक k के साथ क्रमविनिमेय नोथेरियन स्थानीय वलय R के लिए, एक श्रेणीबद्ध लाई बीजगणितीय π*(R) पर k का सार्वभौमिक आवृत बीजगणितीय है, जिसे R के समस्थेयता लाई बीजगणितीय के रूप में जाना जाता है (सटीक होने के लिए, जब k की विलक्षणता 2 होती है, π*(R) को एक समायोजित लाई बीजगणितीय के रूप में देखा जा सकता है)।[13] एंड्रे-क्विलन सह-समरूपता D*(k/R,k) से π*(R) तक श्रेणीबद्ध लाई बीजगणितीय की एक प्राकृतिक समरूपता है, जो एक समरूपता है यदि k में विलक्षणता शून्य है।[14]
यह भी देखें
- वैश्विक आयाम
- अवरोध वियोजन
- ग्रोथेंडिक समूह
- ग्रोथेंडिक स्थानीय द्वंद्व
टिप्पणियाँ
- ↑ Weibel (1999); Cartan & Eilenberg (1956), section VI.1.
- ↑ Weibel (1994), sections 2.4 and 2.5 and Theorem 2.7.6.
- ↑ Weibel (1994), Chapters 2 and 3.
- ↑ Weibeil (1994), Lemma 3.3.1.
- ↑ Weibel (1994), section 4.5.
- ↑ Weibel (1994), Definition 2.1.1.
- ↑ Weibel (1994), Proposition 3.3.4.
- ↑ Weibel (1994), Proposition 3.3.10.
- ↑ Weibel (1994), Theorem 3.4.3.
- ↑ Weibel (1994), Corollary 3.4.5.
- ↑ Weibel (1994), Vists 3.4.6. Some minor corrections are in the errata.
- ↑ Weibel (1994), sections 10.4 and 10.7; Gelfand & Manin (2003), Chapter III.
- ↑ Sjödin (1980), Notation 14.
- ↑ Avramov (2010), section 10.2.
संदर्भ
- Avramov, Luchezar (2010), "Infinite free resolutions", Six lectures on commutative algebra, Birkhäuser, pp. 1–108, doi:10.1007/978-3-0346-0329-4_1, ISBN 978-3-7643-5951-5, MR 2641236
- Baer, Reinhold (1934), "Erweiterung von Gruppen und ihren Isomorphismen", Mathematische Zeitschrift, 38 (1): 375–416, doi:10.1007/BF01170643, Zbl 0009.01101
- Cartan, Henri; Eilenberg, Samuel (1999) [1956], Homological algebra, Princeton: Princeton University Press, ISBN 0-691-04991-2, MR 0077480
- Eilenberg, Samuel; MacLane, Saunders (1942), "Group extensions and homology", Annals of Mathematics, 43 (4): 757–931, doi:10.2307/1968966, JSTOR 1968966, MR 0007108
- Gelfand, Sergei I.; Manin, Yuri Ivanovich (2003), Methods of homological algebra, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-662-12492-5, ISBN 978-3-540-43583-9, MR 1950475
- Sjödin, Gunnar (1980), "Hopf algebras and derivations", Journal of Algebra, 64: 218–229, doi:10.1016/0021-8693(80)90143-X, MR 0575792
- Weibel, Charles A. (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics. Vol. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259.
- Weibel, Charles A. (1999), "History of homological algebra" (PDF), History of topology, Amsterdam: North-Holland, pp. 797–836, ISBN 9780444823755, MR 1721123