सर्पेन्ट (सिफर): Difference between revisions
No edit summary |
No edit summary |
||
| Line 18: | Line 18: | ||
}} | }} | ||
सर्पेंट | सर्पेंट [[सममित कुंजी]] [[ब्लॉक सिफर]] है जो [[उन्नत एन्क्रिप्शन मानक प्रक्रिया]] (एईएस) प्रतियोगिता में फाइनलिस्ट था, जहां इसे [[रिजंडैल]] के बाद दूसरा स्थान दिया गया था।<ref name=":1">{{Cite journal |last1=Nechvatal |first1=J. |last2=Barker |first2=E. |last3=Bassham |first3=L. |last4=Burr |first4=W. |last5=Dworkin |first5=M. |last6=Foti |first6=J. |last7=Roback |first7=E. |date=May 2001 |title=उन्नत एन्क्रिप्शन मानक (एईएस) के विकास पर रिपोर्ट|url=https://doi.org/10.6028/jres.106.023 |journal=Journal of Research of the National Institute of Standards and Technology |volume=106 |issue=3 |pages=511–577 |doi=10.6028/jres.106.023 |issn=1044-677X |pmc=4863838 |pmid=27500035}}</ref> सर्पेंट को [[रॉस एंडरसन]], [[एली बिहम]] और [[लार्स नुडसन]] द्वारा डिज़ाइन किया गया था ।<ref>{{Cite web |title=नागिन होम पेज|url=https://www.cl.cam.ac.uk/~rja14/serpent.html |url-status=live}}</ref> | ||
अन्य उन्नत एन्क्रिप्शन मानक सबमिशन की तरह, सर्पेंट के पास 128 बिट्स का [[ब्लॉक आकार (क्रिप्टोग्राफी)]] है और 128, 192 या 256 बिट्स के प्रमुख आकार का समर्थन करता है।<ref name=":0">{{cite web | अन्य उन्नत एन्क्रिप्शन मानक सबमिशन की तरह, सर्पेंट के पास 128 बिट्स का [[ब्लॉक आकार (क्रिप्टोग्राफी)]] है और 128, 192 या 256 बिट्स के प्रमुख आकार का समर्थन करता है।<ref name=":0">{{cite web | ||
| Line 27: | Line 27: | ||
| date=2006-10-23 | | date=2006-10-23 | ||
| publisher=[[University of Cambridge Computer Laboratory]] | | publisher=[[University of Cambridge Computer Laboratory]] | ||
| access-date=2013-01-14}}</ref> [[ सिफ़र |सिफ़र]] | | access-date=2013-01-14}}</ref> [[ सिफ़र |सिफ़र]] 32-राउंड प्रतिस्थापन-क्रमपरिवर्तन नेटवर्क है जो चार 32-बिट [[वर्ड (कंप्यूटर आर्किटेक्चर)]] के ब्लॉक पर काम करता है। प्रत्येक दौर समानांतर में 32 बार आठ 4-बिट से 4-बिट [[एस-बॉक्स]] में से पर लागू होता है। सर्पेंट को डिजाइन किया गया था ताकि 32 [[ थोड़ा सा टुकड़ा |थोड़ा सा टुकड़ा]] का उपयोग करके [[समानांतर कंप्यूटिंग]] में सभी कार्यों को निष्पादित किया जा सके। यह समानता को अधिकतम करता है, लेकिन [[डेटा एन्क्रिप्शन मानक]] पर किए गए व्यापक [[क्रिप्ट विश्लेषण]] कार्य के उपयोग की भी अनुमति देता है। | ||
सर्पेंट ने सुरक्षा के लिए | सर्पेंट ने सुरक्षा के लिए रूढ़िवादी दृष्टिकोण अपनाया, बड़े सुरक्षा मार्जिन का चयन किया: डिजाइनरों ने 16 राउंड को ज्ञात प्रकार के हमले के लिए पर्याप्त माना, लेकिन 32 राउंड को क्रिप्टैनालिसिस में भविष्य की खोजों के खिलाफ बीमा के रूप में निर्दिष्ट किया।<ref>{{Cite web |title=नागिन.pdf|url=https://www.cl.cam.ac.uk/~rja14/Papers/नागिन.pdf|access-date=25 April 2022}}</ref> एईएस प्रतियोगिता पर आधिकारिक एनआईएसटी रिपोर्ट ने सर्पेंट को आरसी6 और रिजेंडेल (वर्तमान में एईएस) के पर्याप्त सुरक्षा मार्जिन के विपरीत [[मार्स (क्रिप्टोग्राफी)]] और [[ दो मछली |दो मछली]] के साथ उच्च सुरक्षा मार्जिन के रूप में वर्गीकृत किया।<ref name=":1" />फाइनल वोटिंग में, सर्पेंट के फाइनल में सबसे कम नकारात्मक वोट थे, लेकिन कुल मिलाकर दूसरा स्थान हासिल किया क्योंकि रिजेंडेल के पास काफी अधिक सकारात्मक वोट थे, निर्णायक कारक यह था कि रिजेंडेल ने कहीं अधिक कुशल सॉफ्टवेयर कार्यान्वयन की अनुमति दी थी।{{citation needed|date=June 2016}} | ||
सर्पेंट सिफर एल्गोरिथम सार्वजनिक डोमेन में है और इसका [[पेटेंट]] नहीं कराया गया है।<ref>[http://www.cl.cam.ac.uk/~rja14/serpentpr.html Serpent Holds the Key to Internet Security – Finalists in world-wide encryption competition announced] (1999)</ref> संदर्भ कोड [[सार्वजनिक डोमेन सॉफ्टवेयर]] है और अनुकूलित कोड [[GPL]] के अंतर्गत है।<ref>[http://www.cl.cam.ac.uk/~rja14/serpent.html SERPENT – A Candidate Block Cipher for the Advanced Encryption Standard ] ''"Serpent is now completely in the public domain, and we impose no restrictions on its use. This was announced on the 21st August at the First AES Candidate Conference. The optimised implementations in the submission package are now under the General Public License (GPL), although some comments in the code still say otherwise. You are welcome to use Serpent for any application. If you do use it, we would appreciate it if you would let us know!"'' (1999)</ref> इसके उपयोग के संबंध में कोई प्रतिबंध या बाधा नहीं है। नतीजतन, कोई भी लाइसेंस शुल्क का भुगतान किए बिना सर्पेंट को अपने सॉफ़्टवेयर (या हार्डवेयर कार्यान्वयन) में शामिल करने के लिए स्वतंत्र है। | सर्पेंट सिफर एल्गोरिथम सार्वजनिक डोमेन में है और इसका [[पेटेंट]] नहीं कराया गया है।<ref>[http://www.cl.cam.ac.uk/~rja14/serpentpr.html Serpent Holds the Key to Internet Security – Finalists in world-wide encryption competition announced] (1999)</ref> संदर्भ कोड [[सार्वजनिक डोमेन सॉफ्टवेयर]] है और अनुकूलित कोड [[GPL]] के अंतर्गत है।<ref>[http://www.cl.cam.ac.uk/~rja14/serpent.html SERPENT – A Candidate Block Cipher for the Advanced Encryption Standard ] ''"Serpent is now completely in the public domain, and we impose no restrictions on its use. This was announced on the 21st August at the First AES Candidate Conference. The optimised implementations in the submission package are now under the General Public License (GPL), although some comments in the code still say otherwise. You are welcome to use Serpent for any application. If you do use it, we would appreciate it if you would let us know!"'' (1999)</ref> इसके उपयोग के संबंध में कोई प्रतिबंध या बाधा नहीं है। नतीजतन, कोई भी लाइसेंस शुल्क का भुगतान किए बिना सर्पेंट को अपने सॉफ़्टवेयर (या हार्डवेयर कार्यान्वयन) में शामिल करने के लिए स्वतंत्र है। | ||
== मुख्य अनुसूची == | == मुख्य अनुसूची == | ||
सर्पेंट की शेड्यूल में 3 मुख्य चरण होते हैं। पहले चरण में यदि आवश्यक हो तो पैडिंग जोड़कर कुंजी को इनिशियलाइज़ किया जाता है। यह 256-बिट्स की लंबी कुंजियों के लिए लघु कुंजी मानचित्र बनाने के लिए किया जाता है, | सर्पेंट की शेड्यूल में 3 मुख्य चरण होते हैं। पहले चरण में यदि आवश्यक हो तो पैडिंग जोड़कर कुंजी को इनिशियलाइज़ किया जाता है। यह 256-बिट्स की लंबी कुंजियों के लिए लघु कुंजी मानचित्र बनाने के लिए किया जाता है, 1 बिट को छोटी कुंजी के अंत में 0 बिट्स के बाद जोड़ा जाता है जब तक कि छोटी कुंजी को लंबी कुंजी लंबाई में मैप नहीं किया जाता है।<ref name=":0" /> | ||
अगले चरण में, पहले से आरंभ की गई कुंजी का उपयोग करके प्रीकीज़ को प्राप्त किया जाता है। 32-बिट प्रमुख भाग XORed, FRAC जो कि [[ सुनहरा अनुपात |सुनहरा अनुपात]] का अंश है और राउंड इंडेक्स को प्रमुख भागों के साथ XORed किया जाता है, [[एकमात्र]] ऑपरेशन के परिणाम को 11 से बाईं ओर घुमाया जाता है। FRAC और राउंड इंडेक्स को इसमें जोड़ा गया था राउंड के दौरान कीज़ बिट्स का समान वितरण प्राप्त करें।<ref name=":0" /> | अगले चरण में, पहले से आरंभ की गई कुंजी का उपयोग करके प्रीकीज़ को प्राप्त किया जाता है। 32-बिट प्रमुख भाग XORed, FRAC जो कि [[ सुनहरा अनुपात |सुनहरा अनुपात]] का अंश है और राउंड इंडेक्स को प्रमुख भागों के साथ XORed किया जाता है, [[एकमात्र]] ऑपरेशन के परिणाम को 11 से बाईं ओर घुमाया जाता है। FRAC और राउंड इंडेक्स को इसमें जोड़ा गया था राउंड के दौरान कीज़ बिट्स का समान वितरण प्राप्त करें।<ref name=":0" /> | ||
| Line 89: | Line 89: | ||
सर्पेंट एस-बॉक्स 4-बिट क्रमचय हैं, और निम्नलिखित गुणों के अधीन हैं: | सर्पेंट एस-बॉक्स 4-बिट क्रमचय हैं, और निम्नलिखित गुणों के अधीन हैं: | ||
* 1-बिट इनपुट अंतर कभी भी 1-बिट आउटपुट अंतर नहीं देगा, | * 1-बिट इनपुट अंतर कभी भी 1-बिट आउटपुट अंतर नहीं देगा, अंतर विशेषता की संभावना 1:4 या उससे कम होती है।<ref name="algeb-2009" /> | ||
* रैखिक विशेषताओं की संभावना 1:2 और 1:4 के बीच होती है, इनपुट और आउटपुट बिट्स के बीच रैखिक संबंध की संभावना 1:2 और 1:8 के बीच होती है।<ref name="algeb-2009" /> | * रैखिक विशेषताओं की संभावना 1:2 और 1:4 के बीच होती है, इनपुट और आउटपुट बिट्स के बीच रैखिक संबंध की संभावना 1:2 और 1:8 के बीच होती है।<ref name="algeb-2009" /> | ||
| Line 101: | Line 101: | ||
=== प्रारंभिक क्रमचय (आईपी) === | === प्रारंभिक क्रमचय (आईपी) === | ||
प्रारंभिक क्रमचय 128 बिट्स पर | प्रारंभिक क्रमचय 128 बिट्स पर समय में बिट्स को घुमाने पर काम करता है।<syntaxhighlight lang="cpp"> | ||
for i in 0 .. 127 | for i in 0 .. 127 | ||
swap( bit(i), bit((32 * i) % 127) ) | swap( bit(i), bit((32 * i) % 127) ) | ||
| Line 108: | Line 108: | ||
=== अंतिम क्रमपरिवर्तन (एफपी) === | === अंतिम क्रमपरिवर्तन (एफपी) === | ||
अंतिम क्रमपरिवर्तन 128 बिट्स पर काम करता है जो | अंतिम क्रमपरिवर्तन 128 बिट्स पर काम करता है जो समय में बिट्स को घुमाता है।<syntaxhighlight lang="cpp"> | ||
for i in 0 .. 127 | for i in 0 .. 127 | ||
swap( bit(i), bit((2 * i) % 127) ) | swap( bit(i), bit((2 * i) % 127) ) | ||
| Line 138: | Line 138: | ||
== रिजेंडेल बनाम सर्प == | == रिजेंडेल बनाम सर्प == | ||
रिजेंडेल दस, बारह, या चौदह राउंड के साथ | रिजेंडेल दस, बारह, या चौदह राउंड के साथ प्रतिस्थापन-रैखिक परिवर्तन नेटवर्क है, जो मुख्य आकार पर निर्भर करता है, और स्वतंत्र रूप से निर्दिष्ट 128 बिट, 192 बिट या 256 बिट के प्रमुख आकार के साथ। सर्पेंट प्रतिस्थापन-क्रमपरिवर्तन नेटवर्क है जिसमें बत्तीस राउंड होते हैं, साथ ही प्रारंभिक और अंतिम क्रमचय अनुकूलित कार्यान्वयन को सरल बनाने के लिए। रिजेंडेल में गोल कार्य में तीन भाग होते हैं: गैर-रेखीय परत, रैखिक मिश्रण परत और कुंजी-मिश्रण XOR परत। सर्पेंट में राउंड फ़ंक्शन में की-मिक्सिंग एक्सओआर, समान 4×4 एस-बॉक्स के बत्तीस समानांतर अनुप्रयोग और रैखिक परिवर्तन शामिल है, अंतिम दौर को छोड़कर, जिसमें अन्य की-मिक्सिंग एक्सओआर रैखिक परिवर्तन को बदल देता है। रिजेंडेल में नॉनलाइनियर परत 8 × 8 एस-बॉक्स का उपयोग करती है जबकि सर्पेंट आठ अलग-अलग 4 × 4 एस-बॉक्स का उपयोग करता है। 32 राउंड का मतलब है कि रिजेंडेल की तुलना में सर्पेंट के पास उच्च सुरक्षा मार्जिन है; हालाँकि, 10 राउंड के साथ रिजेंडेल छोटे ब्लॉकों के लिए तेज़ और आसान है।<ref>{{cite journal | ||
| title=The Twofish Team's Final Comments on AES Selection | | title=The Twofish Team's Final Comments on AES Selection | ||
|author1=Bruce Schneier |author2=John Kelsey |author3=Doug Whiting |author4=David Wagner |author5=Chris Hall. Niels Fergusonk |author6=Tadayoshi Kohno |author7=Mike Stay | year=2000 | |author1=Bruce Schneier |author2=John Kelsey |author3=Doug Whiting |author4=David Wagner |author5=Chris Hall. Niels Fergusonk |author6=Tadayoshi Kohno |author7=Mike Stay | year=2000 | ||
| Line 147: | Line 147: | ||
== सुरक्षा == | == सुरक्षा == | ||
XSL हमला, यदि प्रभावी हो, तो सर्पेंट को कमजोर कर देगा (हालांकि उतना नहीं जितना कि यह रिजेंडेल को कमजोर करेगा, जो उन्नत एन्क्रिप्शन मानक बन गया)। हालांकि, कई क्रिप्टो विश्लेषकों का मानना है कि | XSL हमला, यदि प्रभावी हो, तो सर्पेंट को कमजोर कर देगा (हालांकि उतना नहीं जितना कि यह रिजेंडेल को कमजोर करेगा, जो उन्नत एन्क्रिप्शन मानक बन गया)। हालांकि, कई क्रिप्टो विश्लेषकों का मानना है कि बार कार्यान्वयन संबंधी विचारों को ध्यान में रखा जाता है तो [[एक्सएसएल हमला]] क्रूर बल के हमले से अधिक महंगा होगा।{{Citation needed|date=July 2010}} | ||
2000 में, कोहनो एट अल द्वारा | 2000 में, कोहनो एट अल द्वारा पेपर। सर्पेंट के 32 राउंड में से 6 के खिलाफ मीट-इन-द-बीच हमला और सर्पेंट में 32 राउंड में से 9 के खिलाफ प्रवर्धित बूमरैंग हमला प्रस्तुत करता है।<ref>{{cite journal | ||
| title=Preliminary Cryptanalysis of Reduced-Round Serpent | | title=Preliminary Cryptanalysis of Reduced-Round Serpent | ||
| url=https://www.schneier.com/paper-serpent-aes.html | | url=https://www.schneier.com/paper-serpent-aes.html | ||
|author1=Tadayoshi Kohno |author2=John Kelsey |author3=Bruce Schneier |name-list-style=amp | year=2000}}</ref> | |author1=Tadayoshi Kohno |author2=John Kelsey |author3=Bruce Schneier |name-list-style=amp | year=2000}}</ref> | ||
एली बिहाम, [[ऑर डंकलमैन]] और नाथन केलर द्वारा 2001 का | एली बिहाम, [[ऑर डंकलमैन]] और नाथन केलर द्वारा 2001 का हमला रेखीय क्रिप्ट विश्लेषण हमला प्रस्तुत करता है जो 2 के साथ सर्पेंट-128 के 32 राउंड में से 10 को तोड़ता है।<sup>118</sup> ज्ञात सादे पाठ और 2<sup>89</sup> समय, और सर्प-192/256 के 11 चक्कर 2 के साथ<sup>118</sup> ज्ञात सादे पाठ और 2<sup>187</sup> समय।<ref name=linear-2001>{{cite journal | ||
| title=Linear Cryptanalysis of Reduced Round Serpent | | title=Linear Cryptanalysis of Reduced Round Serpent | ||
|author1=Eli Biham, [[Orr Dunkelman]] |author2=Nathan Keller | |author1=Eli Biham, [[Orr Dunkelman]] |author2=Nathan Keller | ||
| Line 159: | Line 159: | ||
| publisher=[[Fast Software Encryption|FSE]] 2001 | | publisher=[[Fast Software Encryption|FSE]] 2001 | ||
|citeseerx=10.1.1.78.6148 }}</ref> | |citeseerx=10.1.1.78.6148 }}</ref> | ||
2009 के | 2009 के पेपर में देखा गया है कि सर्पेंट एस-बॉक्स का गैर-रैखिक क्रम 3 नहीं था जैसा कि डिजाइनरों द्वारा दावा किया गया था।<ref name=algeb-2009>{{cite journal | ||
| title=On Algebraic Relations of Serpent S-boxes | | title=On Algebraic Relations of Serpent S-boxes | ||
|author1=Bhupendra Singh |author2=Lexy Alexander |author3=Sanjay Burman | year= 2009 | |author1=Bhupendra Singh |author2=Lexy Alexander |author3=Sanjay Burman | year= 2009 | ||
| Line 173: | Line 173: | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[ बाघ (क्रिप्टोग्राफी) | बाघ (क्रिप्टोग्राफी)]] - | * [[ बाघ (क्रिप्टोग्राफी) | बाघ (क्रिप्टोग्राफी)]] - ही लेखक द्वारा हैश फ़ंक्शन | ||
== फुटनोट्स == | == फुटनोट्स == | ||
Revision as of 10:42, 21 May 2023
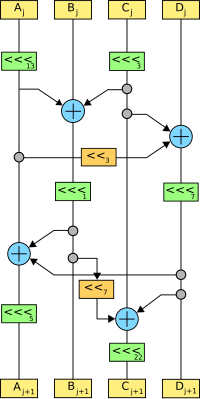
Serpent's linear mixing stage | |
| General | |
|---|---|
| Designers | Ross Anderson, Eli Biham, Lars Knudsen |
| First published | 1998-08-21 |
| Derived from | Square |
| Certification | AES finalist |
| Cipher detail | |
| Key sizes | 128, 192 or 256 bits |
| Block sizes | 128 bits |
| Structure | Substitution–permutation network |
| Rounds | 32 |
| Best public cryptanalysis | |
| All publicly known attacks are computationally infeasible, and none of them affect the full 32-round Serpent. A 2011 attack breaks 11 round Serpent (all key sizes) with 2116 known plaintexts, 2107.5 time and 2104 memory (as described in[1]). The same paper also describes two attacks which break 12 rounds of Serpent-256. The first requires 2118 known plaintexts, 2228.8 time and 2228 memory. The other attack requires 2116 known plaintexts and 2121 memory but also requires 2237.5 time. | |
सर्पेंट सममित कुंजी ब्लॉक सिफर है जो उन्नत एन्क्रिप्शन मानक प्रक्रिया (एईएस) प्रतियोगिता में फाइनलिस्ट था, जहां इसे रिजंडैल के बाद दूसरा स्थान दिया गया था।[2] सर्पेंट को रॉस एंडरसन, एली बिहम और लार्स नुडसन द्वारा डिज़ाइन किया गया था ।[3]
अन्य उन्नत एन्क्रिप्शन मानक सबमिशन की तरह, सर्पेंट के पास 128 बिट्स का ब्लॉक आकार (क्रिप्टोग्राफी) है और 128, 192 या 256 बिट्स के प्रमुख आकार का समर्थन करता है।[4] सिफ़र 32-राउंड प्रतिस्थापन-क्रमपरिवर्तन नेटवर्क है जो चार 32-बिट वर्ड (कंप्यूटर आर्किटेक्चर) के ब्लॉक पर काम करता है। प्रत्येक दौर समानांतर में 32 बार आठ 4-बिट से 4-बिट एस-बॉक्स में से पर लागू होता है। सर्पेंट को डिजाइन किया गया था ताकि 32 थोड़ा सा टुकड़ा का उपयोग करके समानांतर कंप्यूटिंग में सभी कार्यों को निष्पादित किया जा सके। यह समानता को अधिकतम करता है, लेकिन डेटा एन्क्रिप्शन मानक पर किए गए व्यापक क्रिप्ट विश्लेषण कार्य के उपयोग की भी अनुमति देता है।
सर्पेंट ने सुरक्षा के लिए रूढ़िवादी दृष्टिकोण अपनाया, बड़े सुरक्षा मार्जिन का चयन किया: डिजाइनरों ने 16 राउंड को ज्ञात प्रकार के हमले के लिए पर्याप्त माना, लेकिन 32 राउंड को क्रिप्टैनालिसिस में भविष्य की खोजों के खिलाफ बीमा के रूप में निर्दिष्ट किया।[5] एईएस प्रतियोगिता पर आधिकारिक एनआईएसटी रिपोर्ट ने सर्पेंट को आरसी6 और रिजेंडेल (वर्तमान में एईएस) के पर्याप्त सुरक्षा मार्जिन के विपरीत मार्स (क्रिप्टोग्राफी) और दो मछली के साथ उच्च सुरक्षा मार्जिन के रूप में वर्गीकृत किया।[2]फाइनल वोटिंग में, सर्पेंट के फाइनल में सबसे कम नकारात्मक वोट थे, लेकिन कुल मिलाकर दूसरा स्थान हासिल किया क्योंकि रिजेंडेल के पास काफी अधिक सकारात्मक वोट थे, निर्णायक कारक यह था कि रिजेंडेल ने कहीं अधिक कुशल सॉफ्टवेयर कार्यान्वयन की अनुमति दी थी।[citation needed]
सर्पेंट सिफर एल्गोरिथम सार्वजनिक डोमेन में है और इसका पेटेंट नहीं कराया गया है।[6] संदर्भ कोड सार्वजनिक डोमेन सॉफ्टवेयर है और अनुकूलित कोड GPL के अंतर्गत है।[7] इसके उपयोग के संबंध में कोई प्रतिबंध या बाधा नहीं है। नतीजतन, कोई भी लाइसेंस शुल्क का भुगतान किए बिना सर्पेंट को अपने सॉफ़्टवेयर (या हार्डवेयर कार्यान्वयन) में शामिल करने के लिए स्वतंत्र है।
मुख्य अनुसूची
सर्पेंट की शेड्यूल में 3 मुख्य चरण होते हैं। पहले चरण में यदि आवश्यक हो तो पैडिंग जोड़कर कुंजी को इनिशियलाइज़ किया जाता है। यह 256-बिट्स की लंबी कुंजियों के लिए लघु कुंजी मानचित्र बनाने के लिए किया जाता है, 1 बिट को छोटी कुंजी के अंत में 0 बिट्स के बाद जोड़ा जाता है जब तक कि छोटी कुंजी को लंबी कुंजी लंबाई में मैप नहीं किया जाता है।[4]
अगले चरण में, पहले से आरंभ की गई कुंजी का उपयोग करके प्रीकीज़ को प्राप्त किया जाता है। 32-बिट प्रमुख भाग XORed, FRAC जो कि सुनहरा अनुपात का अंश है और राउंड इंडेक्स को प्रमुख भागों के साथ XORed किया जाता है, एकमात्र ऑपरेशन के परिणाम को 11 से बाईं ओर घुमाया जाता है। FRAC और राउंड इंडेक्स को इसमें जोड़ा गया था राउंड के दौरान कीज़ बिट्स का समान वितरण प्राप्त करें।[4]
अंत में उपकुंजियों को पहले उत्पन्न की गई कुंजी से प्राप्त किया जाता है। इसका परिणाम कुल 33 128-बिट उपकुंजियों में होता है।[4]
अंत में कुंजी बिट्स को सही कॉलम में रखने के लिए प्रारंभिक क्रमपरिवर्तन आईपी में गोल कुंजी या उपकुंजी रखी जाती है।[4]
कुंजी अनुसूची छद्म कोड
#define FRAC 0x9e3779b9 // fractional part of the golden ratio
#define ROTL(A, n) (A << n) | (A >> (32 - n))
uint32_t key[8] // k
uint32_t words[132]; // w
uint32_t subkey[33][4] // sk
/* key schedule: get prekeys */
void w(uint32_t *w, uint32_t *k) {
uint32_t imm[140];
for (short i = 0; i < 8; i++){
imm[i]=k[i];
}
for (short i = 8; i < 140; i++) {
imm[i] = ROTL((w[i - 8] ^ w[i - 5] ^ w[i - 3] ^ w[i - 1] ^ FRAC ^ (i - 8)), 11);
w[i-8] = imm[i]
}
}
/* key schedule: get subkeys */
void k(uint32_t *w, uint32_t (*sk)[4]) {
uint8_t i, p, j, s, k;
for (i = 0; i < 33; i++) {
p = (32 + 3 - i) % 32;
for (k = 0; k < 32; k++) {
s = S[p % 8][((w[4 * i + 0] >> k) & 0x1) << 0 |
((w[4 * i + 1] >> k) & 0x1) << 1 |
((w[4 * i + 2] >> k) & 0x1) << 2 |
((w[4 * i + 3] >> k) & 0x1) << 3 ];
for (j = 0; j < 4; j++) {
sk[i][j] |= ((s >> j) & 0x1) << k;
}
}
}
}
एस-बॉक्स
सर्पेंट एस-बॉक्स 4-बिट क्रमचय हैं, और निम्नलिखित गुणों के अधीन हैं:
- 1-बिट इनपुट अंतर कभी भी 1-बिट आउटपुट अंतर नहीं देगा, अंतर विशेषता की संभावना 1:4 या उससे कम होती है।[8]
- रैखिक विशेषताओं की संभावना 1:2 और 1:4 के बीच होती है, इनपुट और आउटपुट बिट्स के बीच रैखिक संबंध की संभावना 1:2 और 1:8 के बीच होती है।[8]
- इनपुट बिट्स के कार्य के रूप में आउटपुट बिट्स का गैर-रैखिक क्रम 3 है। हालांकि ऐसे आउटपुट बिट्स पाए गए हैं जो इनपुट बिट्स के कार्य में केवल 2 का क्रम रखते हैं।[8]
डेटा एन्क्रिप्शन मानक एस-बॉक्स की 32 पंक्तियों के आधार पर सर्पेंट एस-बॉक्स का निर्माण किया गया है। इन्हें अदला-बदली प्रविष्टियों द्वारा रूपांतरित किया गया था, जिसके परिणामस्वरूप वांछित गुणों वाले सरणियों को सर्पेंट एस-बॉक्स के रूप में संग्रहीत किया गया था। यह प्रक्रिया तब तक दोहराई गई जब तक कि कुल 8 एस-बॉक्स नहीं मिल गए। इस प्रक्रिया में निम्नलिखित कुंजी का उपयोग किया गया था: "sboxesforserpent".[4]
क्रमपरिवर्तन और परिवर्तन
प्रारंभिक क्रमचय (आईपी)
प्रारंभिक क्रमचय 128 बिट्स पर समय में बिट्स को घुमाने पर काम करता है।
for i in 0 .. 127
swap( bit(i), bit((32 * i) % 127) )
अंतिम क्रमपरिवर्तन (एफपी)
अंतिम क्रमपरिवर्तन 128 बिट्स पर काम करता है जो समय में बिट्स को घुमाता है।
for i in 0 .. 127
swap( bit(i), bit((2 * i) % 127) )
रैखिक परिवर्तन (एलटी)
एक्सओआर, एस-बॉक्स, बिट शिफ्ट लेफ्ट और बिट रोटेट लेफ्ट ऑपरेशंस से मिलकर बनता है। ये ऑपरेशन 4 32-बिट शब्दों पर किए जाते हैं।
for (short i = 0; i < 4; i++) {
X[i] = S[i][B[i] ^ K[i]];
}
X[0] = ROTL(X[0], 13);
X[2] = ROTL(X[2], 3 );
X[1] = X[1] ^ X[0] ^ X[2];
X[3] = X[3] ^ X[2] ^ (X[0] << 3);
X[1] = ROTL(X[1], 1 );
X[3] = ROTL(X[3], 7 );
X[0] = X[0] ^ X[1] ^ X[3];
X[2] = X[2] ^ X[3] ^ (X[1] << 7);
X[0] = ROTL(X[0], 5 );
X[2] = ROTL(X[2], 22);
for (short i = 0; i < 4; i++) {
B[i + 1] = X[i];
}
रिजेंडेल बनाम सर्प
रिजेंडेल दस, बारह, या चौदह राउंड के साथ प्रतिस्थापन-रैखिक परिवर्तन नेटवर्क है, जो मुख्य आकार पर निर्भर करता है, और स्वतंत्र रूप से निर्दिष्ट 128 बिट, 192 बिट या 256 बिट के प्रमुख आकार के साथ। सर्पेंट प्रतिस्थापन-क्रमपरिवर्तन नेटवर्क है जिसमें बत्तीस राउंड होते हैं, साथ ही प्रारंभिक और अंतिम क्रमचय अनुकूलित कार्यान्वयन को सरल बनाने के लिए। रिजेंडेल में गोल कार्य में तीन भाग होते हैं: गैर-रेखीय परत, रैखिक मिश्रण परत और कुंजी-मिश्रण XOR परत। सर्पेंट में राउंड फ़ंक्शन में की-मिक्सिंग एक्सओआर, समान 4×4 एस-बॉक्स के बत्तीस समानांतर अनुप्रयोग और रैखिक परिवर्तन शामिल है, अंतिम दौर को छोड़कर, जिसमें अन्य की-मिक्सिंग एक्सओआर रैखिक परिवर्तन को बदल देता है। रिजेंडेल में नॉनलाइनियर परत 8 × 8 एस-बॉक्स का उपयोग करती है जबकि सर्पेंट आठ अलग-अलग 4 × 4 एस-बॉक्स का उपयोग करता है। 32 राउंड का मतलब है कि रिजेंडेल की तुलना में सर्पेंट के पास उच्च सुरक्षा मार्जिन है; हालाँकि, 10 राउंड के साथ रिजेंडेल छोटे ब्लॉकों के लिए तेज़ और आसान है।[9] इसलिए, एईएस प्रतियोगिता में रिजेंडेल को विजेता के रूप में चुना गया था।
सर्प-0 वि0 सर्प-1
मूल सर्पेंट, सर्पेंट-0, फास्ट सॉफ्टवेयर एन्क्रिप्शन पर 5वीं कार्यशाला में प्रस्तुत किया गया था, लेकिन कुछ हद तक संशोधित संस्करण, सर्पेंट-1, एईएस प्रतियोगिता में प्रस्तुत किया गया था। एईएस सबमिशन पेपर परिवर्तनों पर चर्चा करता है, जिसमें की-शेड्यूलिंग अंतर शामिल हैं।
सुरक्षा
XSL हमला, यदि प्रभावी हो, तो सर्पेंट को कमजोर कर देगा (हालांकि उतना नहीं जितना कि यह रिजेंडेल को कमजोर करेगा, जो उन्नत एन्क्रिप्शन मानक बन गया)। हालांकि, कई क्रिप्टो विश्लेषकों का मानना है कि बार कार्यान्वयन संबंधी विचारों को ध्यान में रखा जाता है तो एक्सएसएल हमला क्रूर बल के हमले से अधिक महंगा होगा।[citation needed]
2000 में, कोहनो एट अल द्वारा पेपर। सर्पेंट के 32 राउंड में से 6 के खिलाफ मीट-इन-द-बीच हमला और सर्पेंट में 32 राउंड में से 9 के खिलाफ प्रवर्धित बूमरैंग हमला प्रस्तुत करता है।[10] एली बिहाम, ऑर डंकलमैन और नाथन केलर द्वारा 2001 का हमला रेखीय क्रिप्ट विश्लेषण हमला प्रस्तुत करता है जो 2 के साथ सर्पेंट-128 के 32 राउंड में से 10 को तोड़ता है।118 ज्ञात सादे पाठ और 289 समय, और सर्प-192/256 के 11 चक्कर 2 के साथ118 ज्ञात सादे पाठ और 2187 समय।[11] 2009 के पेपर में देखा गया है कि सर्पेंट एस-बॉक्स का गैर-रैखिक क्रम 3 नहीं था जैसा कि डिजाइनरों द्वारा दावा किया गया था।[8] होंगजुन वू, हुआक्सिओनग वांग और फुओंग हा गुयेन द्वारा 2011 का हमला, रैखिक क्रिप्ट विश्लेषण का उपयोग करते हुए, 2 के साथ सर्पेंट -128 के 11 राउंड को तोड़ता है116 ज्ञात प्लेनटेक्स्ट, 2107.5 समय और 2104 मेमोरी।[1] इसी पेपर में दो हमलों का भी वर्णन है जो सर्प-256 के 12 चक्कर तोड़ते हैं। पहले 2 की आवश्यकता है118 ज्ञात सादा पाठ, 2228.8 समय और 2228 मेमोरी। दूसरे हमले के लिए 2 की आवश्यकता है116 ज्ञात सादे पाठ और 2121 मेमोरी लेकिन इसके लिए 2 की भी आवश्यकता होती है237.5 समय।
यह भी देखें
- बाघ (क्रिप्टोग्राफी) - ही लेखक द्वारा हैश फ़ंक्शन
फुटनोट्स
- ↑ 1.0 1.1 Huaxiong Wang, Hongjun Wu & Phuong Ha Nguyen (2011). "Improving the Algorithm 2 in Multidimensional Linear Cryptanalysis" (PDF). सूचना सुरक्षा और गोपनीयता. Lecture Notes in Computer Science. Vol. 6812. ACISP 2011. pp. 61–74. doi:10.1007/978-3-642-22497-3_5. ISBN 978-3-642-22496-6.
- ↑ 2.0 2.1 Nechvatal, J.; Barker, E.; Bassham, L.; Burr, W.; Dworkin, M.; Foti, J.; Roback, E. (May 2001). "उन्नत एन्क्रिप्शन मानक (एईएस) के विकास पर रिपोर्ट". Journal of Research of the National Institute of Standards and Technology. 106 (3): 511–577. doi:10.6028/jres.106.023. ISSN 1044-677X. PMC 4863838. PMID 27500035.
- ↑ "नागिन होम पेज".
{{cite web}}: CS1 maint: url-status (link) - ↑ 4.0 4.1 4.2 4.3 4.4 4.5 Ross J. Anderson (23 October 2006). "Serpent: A Candidate Block Cipher for the Advanced Encryption Standard". University of Cambridge Computer Laboratory. Retrieved 14 January 2013.
- ↑ "नागिन.pdf" (PDF). Retrieved 25 April 2022.
- ↑ Serpent Holds the Key to Internet Security – Finalists in world-wide encryption competition announced (1999)
- ↑ SERPENT – A Candidate Block Cipher for the Advanced Encryption Standard "Serpent is now completely in the public domain, and we impose no restrictions on its use. This was announced on the 21st August at the First AES Candidate Conference. The optimised implementations in the submission package are now under the General Public License (GPL), although some comments in the code still say otherwise. You are welcome to use Serpent for any application. If you do use it, we would appreciate it if you would let us know!" (1999)
- ↑ 8.0 8.1 8.2 8.3 Bhupendra Singh; Lexy Alexander; Sanjay Burman (2009). "On Algebraic Relations of Serpent S-boxes" (PDF).
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Bruce Schneier; John Kelsey; Doug Whiting; David Wagner; Chris Hall. Niels Fergusonk; Tadayoshi Kohno; Mike Stay (2000). "The Twofish Team's Final Comments on AES Selection" (PDF).
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Tadayoshi Kohno; John Kelsey & Bruce Schneier (2000). "Preliminary Cryptanalysis of Reduced-Round Serpent".
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Eli Biham, Orr Dunkelman & Nathan Keller (2001). "Linear Cryptanalysis of Reduced Round Serpent". FSE 2001. CiteSeerX 10.1.1.78.6148.
{{cite journal}}: Cite journal requires|journal=(help)
अग्रिम पठन
- Anderson, Ross; Biham, Eli; Knudsen, Lars (1998). "Cryptography – 256 bit ciphers: Reference (AES submission) implementation".
- Biham, Eli. "Serpent – A New Block Cipher Proposal for AES".
- Halbfinger, David M (5 May 2008). "In Pellicano Case, Lessons in Wiretapping Skills". The New York Times.
- Stajano, Frank (10 February 2006). "Serpent reference implementation". University of Cambridge Computer Laboratory.
बाहरी संबंध
- No URL found. Please specify a URL here or add one to Wikidata.
- 256 bit ciphers – SERPENT Reference implementation and derived code