तलीय लैमिना: Difference between revisions
(Created page with "{{Multiple issues| {{more citations needed|date=October 2021}} {{Technical|date=October 2015}} }} गणित में, एक तलीय पटल (या समतल...") |
No edit summary |
||
| Line 4: | Line 4: | ||
}} | }} | ||
गणित में, | गणित में, '''तलीय लैमिना''' (या समतल पटल) एक आकृति है जो ठोस की एक पतली, सामान्यतः एकसमान, समतल परत का प्रतिनिधित्व करती है। यह समाकलन में एक ठोस सतह के तलीय अनुप्रस्थ काट के आदर्श मॉडल के रूप में भी कार्य करती है।<ref>{{citation| first1=Tony|last1=Atkins| first2=Marcel|last2=Escudier| title=A Dictionary of Mechanical Engineering (1 ed.)| chapter=Plane lamina| chapter-url=https://www.oxfordreference.com/view/10.1093/acref/9780199587438.001.0001/acref-9780199587438-e-4614| date=2013| publisher=[[Oxford University Press]]| isbn=9780199587438| doi=10.1093/acref/9780199587438.001.0001| access-date=2021-06-08}}</ref> | ||
जड़त्व के क्षणों | जड़त्व के क्षणों या समतल आकृतियों के द्रव्यमान के केंद्र को निर्धारित करने के साथ-साथ 3डी निकायों के लिए संबंधित गणनाओं में सहायता के लिए तलीय लैमिना का उपयोग किया जा सकता है। | ||
== परिभाषा == | == परिभाषा == | ||
मूल रूप से, एक | मूल रूप से, एक तलीय लैमिना को समतल में परिमित क्षेत्र के एक आंकड़े ([[बंद सेट|सवृत समुच्चय]]) {{mvar|D}} के रूप में परिभाषित किया जाता है, जिसमें कुछ द्रव्यमान {{mvar|m}} होता है।<ref name=WAlpha/> | ||
यह स्थिर घनत्व के लिए | यह स्थिर घनत्व के लिए जड़त्व या द्रव्यमान के केंद्र के क्षणों की गणना करने में उपयोगी है क्योंकि एक पटल का द्रव्यमान उसके क्षेत्रफल के समानुपाती होता है। एक चर घनत्व की स्थिति मे कुछ (गैर-ऋणात्मक) [[सतह घनत्व]] फलन <math>\rho(x,y),</math> द्वारा दिए गए तलीय लैमिना {{mvar|D}} का द्रव्यमान {{mvar|m}} आकृति के ऊपर {{mvar|ρ}} का तलीय समाकलन है:<ref name=MathWorld/> | ||
:<math>m = \iint_D\rho(x,y)\,dx\,dy</math> | :<math>m = \iint_D\rho(x,y)\,dx\,dy</math> | ||
== गुण == | == गुण == | ||
तलीय लैमिना के द्रव्यमान के केंद्र बिंदु हैं: | |||
:<math> \left(\frac{M_y}{m},\frac{M_x}{m}\right) </math> | :<math> \left(\frac{M_y}{m},\frac{M_x}{m}\right) </math> | ||
जहाँ <math>M_y </math> y-अक्ष में संपूर्ण पटल का क्षण है और <math>M_x </math> x-अक्ष के संपूर्ण पटल का क्षण है: | |||
:<math>M_y = \lim_{m,n \to \infty}\,\sum_{i=1}^{m}\,\sum_{j=1}^{n}\,x{_{ij}}^{*}\,\rho\ (x{_{ij}}^{*},y{_{ij}}^{*})\,\Delta D = \iint_D x\, \rho\ (x,y)\,dx\,dy</math> | :<math>M_y = \lim_{m,n \to \infty}\,\sum_{i=1}^{m}\,\sum_{j=1}^{n}\,x{_{ij}}^{*}\,\rho\ (x{_{ij}}^{*},y{_{ij}}^{*})\,\Delta D = \iint_D x\, \rho\ (x,y)\,dx\,dy</math> | ||
:<math>M_x = \lim_{m,n \to \infty}\,\sum_{i=1}^{m}\,\sum_{j=1}^{n}\,y{_{ij}}^{*}\,\rho\ (x{_{ij}}^{*},y{_{ij}}^{*})\,\Delta D = \iint_D y\, \rho\ (x,y)\,dx\,dy</math> | :<math>M_x = \lim_{m,n \to \infty}\,\sum_{i=1}^{m}\,\sum_{j=1}^{n}\,y{_{ij}}^{*}\,\rho\ (x{_{ij}}^{*},y{_{ij}}^{*})\,\Delta D = \iint_D y\, \rho\ (x,y)\,dx\,dy</math> | ||
समतलीय डोमेन पर लिए गए योग और समाकलन के साथ <math>D</math> बिन्दु है। | |||
== उदाहरण == | == उदाहरण == | ||
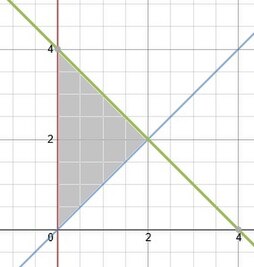
[[File:Bound region.jpg|thumb]] | [[File:Bound region.jpg|thumb|267x267px]]रेखाओ <math>x=0,</math> <math>y=x</math> और <math>y=4-x</math> द्वारा दिए गए शीर्षों के साथ एक लैमिना के द्रव्यमान का केंद्र खोजें जहां घनत्व <math>\rho\ (x,y)\,=2x+3y+2</math> के रूप में दिया गया है। | ||
इसके लिए | इसके लिए द्रव्यमान <math>m</math> और आघूर्ण <math>M_y</math> और <math>M_x</math> का पता लगाना आवश्यक है। | ||
जहां द्रव्यमान <math>m = \iint_D\rho(x,y)\,dx\,dy</math> है जिसे समान रूप से [[पुनरावृत्त अभिन्न|पुनरावृत्त समाकल]] के रूप में व्यक्त किया जा सकता है: | |||
:<math>m = \int_{x=0}^2 \int_{y=x}^{4-x} \,(2x+3y+2)\,dy\,dx</math> | :<math>m = \int_{x=0}^2 \int_{y=x}^{4-x} \,(2x+3y+2)\,dy\,dx</math> | ||
आंतरिक | आंतरिक समाकल है: | ||
:<math>\int_{y=x}^{4-x} \,(2x+3y+2)\,dy</math> | :<math>\int_{y=x}^{4-x} \,(2x+3y+2)\,dy</math> | ||
| Line 41: | Line 39: | ||
:<math>\qquad = \left[2x(4-x)+\frac{3(4-x)^2}{2}+2(4-x)\right]-\left[2x(x)+\frac{3(x)^2}{2}+2(x)\right]</math> | :<math>\qquad = \left[2x(4-x)+\frac{3(4-x)^2}{2}+2(4-x)\right]-\left[2x(x)+\frac{3(x)^2}{2}+2(x)\right]</math> | ||
:<math>\qquad = -4x^2-8x+32</math> | :<math>\qquad = -4x^2-8x+32</math> | ||
इसे बाहरी | इसे बाहरी समाकल परिणामों :के रूप में प्रयुक्त किया जा सकता है: | ||
:<math>\begin{align}m & =\int_{x=0}^2\left(-4x^2-8x+32\right)\,dx \\ | :<math>\begin{align}m & =\int_{x=0}^2\left(-4x^2-8x+32\right)\,dx \\ | ||
| Line 49: | Line 47: | ||
:<math>M_y = \iint_D x\,\rho(x,y)\,dx\,dy = \int_{x=0}^2 \int_{y=x}^{4-x} x\,(2x+3y+2)\,dy\,dx</math> | :<math>M_y = \iint_D x\,\rho(x,y)\,dx\,dy = \int_{x=0}^2 \int_{y=x}^{4-x} x\,(2x+3y+2)\,dy\,dx</math> | ||
आंतरिक | आंतरिक समाकल के साथ: | ||
:<math>\int_{y=x}^{4-x} x\,(2x+3y+2)\,dy</math> | :<math>\int_{y=x}^{4-x} x\,(2x+3y+2)\,dy</math> | ||
:<math>\qquad = \left.\left(2x^2y+\frac{3xy^2}{2}+2xy\right)\right|_{y=x}^{4-x}</math> | :<math>\qquad = \left.\left(2x^2y+\frac{3xy^2}{2}+2xy\right)\right|_{y=x}^{4-x}</math> | ||
:<math>\qquad = -4x^3-8x^2+32x</math> | :<math>\qquad = -4x^3-8x^2+32x</math> | ||
:<math>\begin{align} M_y & = \int_{x=0}^2(-4x^3-8x^2+32x)\,dx \\ | :<math>\begin{align} M_y & = \int_{x=0}^2(-4x^3-8x^2+32x)\,dx \\ | ||
| Line 66: | Line 63: | ||
& = \left.\left(-\frac{x^4}{2}+\frac{4x^3}{3}-20x^2+80x\right)\right|_{x=0}^2 \\ | & = \left.\left(-\frac{x^4}{2}+\frac{4x^3}{3}-20x^2+80x\right)\right|_{x=0}^2 \\ | ||
& = \frac{248}{3} \end{align}</math> | & = \frac{248}{3} \end{align}</math> | ||
अंत में, द्रव्यमान का केंद्र है | अंत में, द्रव्यमान का केंद्र है: | ||
:<math>\left( \frac{M_y}m, \frac{M_x}m \right) = | :<math>\left( \frac{M_y}m, \frac{M_x}m \right) = | ||
\left( \frac{\frac{80}{3}}{\frac{112}{3}}, \frac{\frac{248}{3}}{\frac{112}{3}} \right) = | \left( \frac{\frac{80}{3}}{\frac{112}{3}}, \frac{\frac{248}{3}}{\frac{112}{3}} \right) = | ||
\left( \frac 57, \frac{31}{14} \right)</math> | \left( \frac 57, \frac{31}{14} \right)</math> | ||
==संदर्भ== | ==संदर्भ== | ||
{{Reflist|refs= | {{Reflist|refs= | ||
Revision as of 10:02, 6 June 2023
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages)
(Learn how and when to remove this template message)
|
गणित में, तलीय लैमिना (या समतल पटल) एक आकृति है जो ठोस की एक पतली, सामान्यतः एकसमान, समतल परत का प्रतिनिधित्व करती है। यह समाकलन में एक ठोस सतह के तलीय अनुप्रस्थ काट के आदर्श मॉडल के रूप में भी कार्य करती है।[1]
जड़त्व के क्षणों या समतल आकृतियों के द्रव्यमान के केंद्र को निर्धारित करने के साथ-साथ 3डी निकायों के लिए संबंधित गणनाओं में सहायता के लिए तलीय लैमिना का उपयोग किया जा सकता है।
परिभाषा
मूल रूप से, एक तलीय लैमिना को समतल में परिमित क्षेत्र के एक आंकड़े (सवृत समुच्चय) D के रूप में परिभाषित किया जाता है, जिसमें कुछ द्रव्यमान m होता है।[2]
यह स्थिर घनत्व के लिए जड़त्व या द्रव्यमान के केंद्र के क्षणों की गणना करने में उपयोगी है क्योंकि एक पटल का द्रव्यमान उसके क्षेत्रफल के समानुपाती होता है। एक चर घनत्व की स्थिति मे कुछ (गैर-ऋणात्मक) सतह घनत्व फलन द्वारा दिए गए तलीय लैमिना D का द्रव्यमान m आकृति के ऊपर ρ का तलीय समाकलन है:[3]
गुण
तलीय लैमिना के द्रव्यमान के केंद्र बिंदु हैं:
जहाँ y-अक्ष में संपूर्ण पटल का क्षण है और x-अक्ष के संपूर्ण पटल का क्षण है:
समतलीय डोमेन पर लिए गए योग और समाकलन के साथ बिन्दु है।
उदाहरण
रेखाओ और द्वारा दिए गए शीर्षों के साथ एक लैमिना के द्रव्यमान का केंद्र खोजें जहां घनत्व के रूप में दिया गया है।
इसके लिए द्रव्यमान और आघूर्ण और का पता लगाना आवश्यक है।
जहां द्रव्यमान है जिसे समान रूप से पुनरावृत्त समाकल के रूप में व्यक्त किया जा सकता है:
आंतरिक समाकल है:
इसे बाहरी समाकल परिणामों :के रूप में प्रयुक्त किया जा सकता है:
इसी प्रकार दोनों क्षणों की गणना की जाती है:
आंतरिक समाकल के साथ:
और
अंत में, द्रव्यमान का केंद्र है:
संदर्भ
- ↑ Atkins, Tony; Escudier, Marcel (2013), "Plane lamina", A Dictionary of Mechanical Engineering (1 ed.), Oxford University Press, doi:10.1093/acref/9780199587438.001.0001, ISBN 9780199587438, retrieved 2021-06-08
- ↑ "Planar Laminae", WolframAlpha, retrieved 2021-03-09
- ↑ "Lamina". MathWorld. Retrieved 2021-03-09.