अधिकतम प्रवाह की समस्या

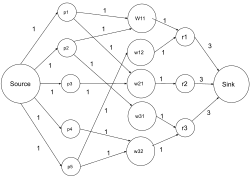अनुकूलन (गणित) में, अधिकतम प्रवाह समस्याओं में प्रवाह नेटवर्क के माध्यम से व्यवहार्य प्रवाह खोजना शामिल होता है जो अधिकतम संभव प्रवाह दर प्राप्त करता है।

अधिकतम प्रवाह समस्या को संचलन समस्या जैसे अधिक जटिल नेटवर्क प्रवाह समस्याओं के विशेष मामले के रूप में देखा जा सकता है। एसटी प्रवाह का अधिकतम मूल्य (अर्थात, ग्राफ सिद्धांत की शब्दावली से प्रवाह दिशा s से ग्राफ़ सिद्धांत की शब्दावली#दिशा t) कट (ग्राफ सिद्धांत) की न्यूनतम क्षमता के बराबर है|एसटी कट (यानी, विच्छेदित एस टी से) नेटवर्क में, जैसा कि मैक्स-फ्लो मिन-कट प्रमेय में कहा गया है।

इतिहास

अधिकतम प्रवाह समस्या पहली बार 1954 में टेड हैरिस (गणितज्ञ) | टी द्वारा तैयार की गई थी। सोवियत रेलवे यातायात प्रवाह के सरलीकृत मॉडल के रूप में ई. हैरिस और एफ.एस. रॉस।

1955 में, लेस्टर आर. फोर्ड, जूनियर और डी. आर. फुलकर्सन | डेलबर्ट आर. फुलकर्सन ने पहला ज्ञात एल्गोरिदम, फोर्ड-फुलकर्सन एल्गोरिदम बनाया। उनके 1955 के पेपर में,फोर्ड और फुलकर्सन ने लिखा है कि हैरिस और रॉस की समस्या निम्नानुसार तैयार की गई है (देखेंपी। 5):

रेल नेटवर्क पर विचार करें जो दो शहरों को कई मध्यवर्ती शहरों के माध्यम से जोड़ता है, जहां नेटवर्क के प्रत्येक लिंक में नंबर दिया गया है जो इसकी क्षमता का प्रतिनिधित्व करता है। स्थिर स्थिति की स्थिति मानते हुए, दिए गए शहर से दूसरे शहर में अधिकतम प्रवाह खोजें।

उनकी पुस्तक फ्लो इन नेटवर्क में,1962 में, फोर्ड और फुलकर्सन ने लिखा:

यह लेखकों को 1955 के वसंत में टी. ई. हैरिस द्वारा प्रस्तुत किया गया था, जिन्होंने जनरल एफ.एस. रॉस (सेवानिवृत्त) के साथ मिलकर रेलवे यातायात प्रवाह का सरलीकृत मॉडल तैयार किया था, और इस विशेष समस्या को मॉडल [11] द्वारा सुझाई गई केंद्रीय समस्या के रूप में इंगित किया।

जहां [11] हैरिस और रॉस द्वारा रेल नेट क्षमताओं के मूल्यांकन के लिए 1955 की गुप्त रिपोर्ट फंडामेंटल्स ऑफ ए मेथड को संदर्भित करता है।(देखनापी। 5).

इन वर्षों में, अधिकतम प्रवाह समस्या के विभिन्न उन्नत समाधानों की खोज की गई, विशेष रूप से एडमंड्स और कार्प और स्वतंत्र रूप से डिनिट्ज़ का सबसे छोटा संवर्द्धन पथ एल्गोरिथम; डिनिट्ज़ का ब्लॉकिंग फ्लो एल्गोरिथम; पुश-रीलेबेल अधिकतम प्रवाह एल्गोरिथम|एंड्रयू वी. गोल्डबर्ग और रॉबर्ट टार्जन का पुश-रीलेबेल एल्गोरिथम; और गोल्डबर्ग और राव का बाइनरी ब्लॉकिंग फ्लो एल्गोरिथम। शर्मन के एल्गोरिदम और केलनर, ली, ओरेचिया और सिडफोर्ड, क्रमशः, लगभग इष्टतम अधिकतम प्रवाह ज्ञात करें लेकिन केवल अप्रत्यक्ष रेखांकन में काम करें।

2013 में जेम्स बी. ओर्लिन ने वर्णन करते हुए पेपर प्रकाशित किया $O(|V||E|)$ कलन विधि।

2022 में ली चेन, रासमस किन्ग, यांग पी. लियू, रिचर्ड पेंग, मैक्सिमिलियन प्रोबस्ट गुटेनबर्ग और सुशांत सचदेवा ने लगभग-रैखिक समय एल्गोरिदम प्रकाशित किया जो चल रहा है $O(|E|^{1+o(1)})$ न्यूनतम-लागत प्रवाह समस्या के लिए|न्यूनतम-लागत प्रवाह समस्या जिसमें से अधिकतम प्रवाह समस्या विशेष मामला है। एकल स्रोत सबसे छोटी पथ समस्या | सिंगल-सोर्स शॉर्टेस्ट पाथ (एसएसएसपी) समस्या के लिए नकारात्मक भार के साथ न्यूनतम-लागत प्रवाह समस्या का और विशेष मामला लगभग-रैखिक समय में एल्गोरिथ्म भी रिपोर्ट किया गया है। दोनों एल्गोरिदम को कंप्यूटर विज्ञान की नींव पर 2022 संगोष्ठी में सर्वश्रेष्ठ पेपर माना गया।

परिभाषा

प्रवाह नेटवर्क, स्रोत एस और सिंक टी के साथ। किनारे के आगे की संख्याएँ क्षमताएँ हैं।

पहले हम कुछ अंकन स्थापित करते हैं:

• होने देना $N=(V,E)$ के साथ नेटवर्क हो $s,t\in V$ स्रोत और सिंक होने के नाते $N$ क्रमश।
• अगर $g$ के किनारों पर समारोह है $N$ फिर इसका मूल्य $(u,v)\in E$ द्वारा निरूपित किया जाता है $g_{uv}$ या $g(u,v).$

परिभाषा। किनारे की क्षमता प्रवाह की अधिकतम मात्रा है जो किनारे से गुजर सकती है। औपचारिक रूप से यह नक्शा है $c:E\to \mathbb {R} ^{+}.$ परिभाषा। प्रवाह नक्शा है $f:E\to \mathbb {R}$ जो निम्नलिखित को संतुष्ट करता है:

• क्षमता बाधा। किनारे का प्रवाह दूसरे शब्दों में इसकी क्षमता से अधिक नहीं हो सकता है: $f_{uv}\leq c_{uv}$ सभी के लिए $(u,v)\in E.$
• प्रवाह का संरक्षण। स्रोत और सिंक को छोड़कर, नोड में प्रवेश करने वाले प्रवाहों का योग उस नोड से बाहर निकलने वाले प्रवाहों के योग के बराबर होना चाहिए। या:

$\forall v\in V\setminus \{s,t\}:\quad \sum _{u:(u,v)\in E}f_{uv}=\sum _{u:(v,u)\in E}f_{vu}.$

टिप्पणी। प्रवाह विषम सममित हैं: $f_{uv}=-f_{vu}$ सभी के लिए $(u,v)\in E.$ परिभाषा। प्रवाह का मान स्रोत से सिंक तक जाने वाले प्रवाह की मात्रा है। औपचारिक रूप से प्रवाह के लिए $f:E\to \mathbb {R} ^{+}$ इसके द्वारा दिया गया है:

$|f|=\sum _{v:\ (s,v)\in E}f_{sv}-\sum _{u:\ (u,s)\in E}f_{us}.$

परिभाषा। अधिकतम प्रवाह समस्या स्रोत से सिंक तक जितना संभव हो उतना प्रवाह मार्ग है, दूसरे शब्दों में प्रवाह को ढूंढें $f_{\textrm {max}}$ अधिकतम मूल्य के साथ।

ध्यान दें कि कई अधिकतम प्रवाह मौजूद हो सकते हैं, और यदि मनमाना वास्तविक (या यहां तक ​​​​कि मनमाना तर्कसंगत) प्रवाह के मूल्यों की अनुमति है (केवल पूर्णांकों के बजाय), तो या तो अधिकतम प्रवाह होता है, या असीम रूप से कई होते हैं, क्योंकि असीम रूप से कई रैखिक संयोजन होते हैं आधार अधिकतम प्रवाह। दूसरे शब्दों में, अगर हम भेजते हैं $x$ किनारे पर प्रवाह की इकाइयाँ $u$ अधिकतम प्रवाह में, और $y>x$ प्रवाह की इकाइयाँ $u$ दूसरे अधिकतम प्रवाह में, फिर प्रत्येक के लिए $\Delta \in [0,y-x]$ हम भेज सकते हैं $x+\Delta$ इकाइयों पर $u$ और और अधिकतम प्रवाह प्राप्त करने के लिए तदनुसार शेष किनारों पर प्रवाह को रूट करें। यदि प्रवाह मान कोई वास्तविक या परिमेय संख्या हो सकती है, तो ऐसे अपरिमित रूप से अनेक होते हैं $\Delta$ प्रत्येक जोड़ी के लिए मान $x,y$.

एल्गोरिदम

निम्न तालिका अधिकतम प्रवाह समस्या को हल करने के लिए एल्गोरिदम सूचीबद्ध करती है। यहाँ, $V$ और $E$ नेटवर्क के कोने और किनारों की संख्या को निरूपित करें। मूल्य $U$ सभी क्षमताओं को पूर्णांक मानों में बदलने के बाद सबसे बड़ी धार क्षमता को संदर्भित करता है (यदि नेटवर्क में अपरिमेय संख्या क्षमताएं हैं, $U$ अनंत हो सकता है)।

Method	Complexity	Description
Linear programming		Constraints given by the definition of a legal flow. See the linear program here.
Ford–Fulkerson algorithm	$O(E^{2}U)$	As long as there is an open path through the residual graph, send the minimum of the residual capacities on that path.
Edmonds–Karp algorithm	$O(VE^{2})$	A specialization of Ford–Fulkerson, finding augmenting paths with breadth-first search.
Dinic's algorithm	$O(V^{2}E)$	In each phase the algorithms builds a layered graph with breadth-first search on the residual graph. The maximum flow in a layered graph can be calculated in $O(VE)$ time, and the maximum number of phases is $V-1$. In networks with unit capacities, Dinic's algorithm terminates in $O(\min\{V^{2/3},E^{1/2}\}E)$ time.
MKM (Malhotra, Kumar, Maheshwari) algorithm	$O(V^{3})$	A modification of Dinic's algorithm with a different approach to constructing blocking flows. Refer to the original paper.
Dinic's algorithm with dynamic trees	$O(VE\log V)$	The dynamic trees data structure speeds up the maximum flow computation in the layered graph to $O(VE\log V)$.
General push–relabel algorithm	$O(V^{2}E)$	The push relabel algorithm maintains a preflow, i.e. a flow function with the possibility of excess in the vertices. The algorithm runs while there is a vertex with positive excess, i.e. an active vertex in the graph. The push operation increases the flow on a residual edge, and a height function on the vertices controls through which residual edges can flow be pushed. The height function is changed by the relabel operation. The proper definitions of these operations guarantee that the resulting flow function is a maximum flow.
Push–relabel algorithm with FIFO vertex selection rule	$O(V^{3})$	Push-relabel algorithm variant which always selects the most recently active vertex, and performs push operations while the excess is positive and there are admissible residual edges from this vertex.
Push–relabel algorithm with maximum distance vertex selection rule	$O(V^{2}{\sqrt {E}})$	Push-relabel algorithm variant which always selects the most distant vertex from $s$ or $t$ (i.e. the highest label vertex) but otherwise proceeds as the FIFO algorithm.
Push-relabel algorithm with dynamic trees	$O\left(VE\log {\frac {V^{2}}{E}}\right)$	The algorithm builds limited size trees on the residual graph regarding to the height function. These trees provide multilevel push operations, i.e. pushing along an entire saturating path instead of a single edge.
KRT (King, Rao, Tarjan)'s algorithm	$O\left(VE\log _{\frac {E}{V\log V}}V\right)$
Binary blocking flow algorithm	$O\left(E\cdot \min\{V^{2/3},E^{1/2}\}\cdot \log {\frac {V^{2}}{E}}\cdot \log U\right)$
James B Orlin's + KRT (King, Rao, Tarjan)'s algorithm	$O(VE)$	Orlin's algorithm solves max-flow in $O(VE)$ time for $E\leq O(V^{{\frac {16}{15}}-\epsilon })$ while KRT solves it in $O(VE)$ for $E>V^{1+\epsilon }$.
Kathuria-Liu-Sidford algorithm	$E^{4/3+o(1)}U^{1/3}$	Interior point methods and edge boosting using $\ell _{p}$-norm flows. Builds on earlier algorithm of Madry, which achieved runtime ${\tilde {O}}(E^{10/7}U^{1/7})$.
BLNPSSSW / BLLSSSW algorithm	${\tilde {O}}((E+V^{3/2})\log U)$	Interior point methods and dynamic maintenance of electric flows with expander decompositions.
Gao-Liu-Peng algorithm	${\tilde {O}}(E^{{\frac {3}{2}}-{\frac {1}{328}}}\log U)$	Gao, Liu, and Peng's algorithm revolves around dynamically maintaining the augmenting electrical flows at the core of the interior point method based algorithm from [Mądry JACM ‘16]. This entails designing data structures that, in limited settings, return edges with large electric energy in a graph undergoing resistance updates.
Chen, Kyng, Liu, Peng, Gutenberg and Sachdeva's algorithm	$O(E^{1+o(1)}\log U)$	Chen, Kyng, Liu, Peng, Gutenberg and Sachdeva's algorithm solves maximum flow and minimum-cost flow in almost linear time by building the flow through a sequence of $E^{1+o(1)}$ approximate undirected minimum-ratio cycles, each of which is computed and processed in amortized $E^{o(1)}$ time using a dynamic data structure.

अतिरिक्त एल्गोरिदम के लिए, देखें Goldberg & Tarjan (1988).

इंटीग्रल फ्लो प्रमेय

अभिन्न प्रवाह प्रमेय कहता है कि

यदि प्रवाह नेटवर्क में प्रत्येक किनारे की अभिन्न क्षमता है, तो अभिन्न अधिकतम प्रवाह मौजूद है।

दावा न केवल यह है कि प्रवाह का मान पूर्णांक है, जो अधिकतम-प्रवाह न्यूनतम-कट प्रमेय से सीधे अनुसरण करता है, बल्कि यह कि 'हर किनारे' पर प्रवाह अभिन्न है। यह कई असतत गणित अनुप्रयोगों (नीचे देखें) के लिए महत्वपूर्ण है, जहां किनारे पर प्रवाह एन्कोड कर सकता है कि उस किनारे से संबंधित आइटम को सेट में शामिल किया जाना है या नहीं।

आवेदन

बहु-स्रोत बहु-सिंक अधिकतम प्रवाह समस्या

चित्र 4.1.1। एक बहु-स्रोत बहु-सिंक अधिकतम प्रवाह समस्या का एकल-स्रोत एकल-सिंक अधिकतम प्रवाह समस्या में रूपांतरण

नेटवर्क दिया $N=(V,E)$ सूत्रों के सेट के साथ $S=\{s_{1},\ldots ,s_{n}\}$ और सिंक का सेट $T=\{t_{1},\ldots ,t_{m}\}$ केवल स्रोत और सिंक के बजाय, हमें अधिकतम प्रवाह का पता लगाना है $N$. हम बहु-स्रोत बहु-सिंक समस्या को अधिकतम प्रवाह समस्या में प्रत्येक शीर्ष से जोड़ने वाले समेकित स्रोत को जोड़कर बदल सकते हैं $S$ और प्रत्येक शीर्ष से जुड़ा समेकित सिंक $T$ (सुपरसोर्स और सुपरसिंक के रूप में भी जाना जाता है) प्रत्येक किनारे पर अनंत क्षमता के साथ (चित्र देखें। 4.1.1।)।

अधिकतम कार्डिनैलिटी द्विपक्षीय मिलान

चित्र 4.3.1। अधिकतम द्विदलीय मिलान समस्या का अधिकतम प्रवाह समस्या में रूपांतरण

द्विदलीय ग्राफ दिया $G=(X\cup Y,E)$, हमें मिलान करने वाली अधिकतम कार्डिनैलिटी मिलनी है $G$, वह मिलान है जिसमें किनारों की सबसे बड़ी संभव संख्या होती है। नेटवर्क बनाकर इस समस्या को अधिकतम प्रवाह समस्या में बदला जा सकता है $N=(X\cup Y\cup \{s,t\},E')$, कहाँ

1. $E'$ किनारों को समाहित करता है $G$ से निर्देशित $X$ को $Y$.
2. $(s,x)\in E'$ प्रत्येक के लिए $x\in X$ और $(y,t)\in E'$ प्रत्येक के लिए $y\in Y$.
3. $c(e)=1$ प्रत्येक के लिए $e\in E'$ (चित्र देखें। 4.3.1)।

फिर अधिकतम प्रवाह का मान $N$ में अधिकतम मिलान के आकार के बराबर है $G$, और अधिकतम कार्डिनैलिटी मिलान उन किनारों को लेकर पाया जा सकता है जिनमें प्रवाह होता है $1$ अभिन्न अधिकतम प्रवाह में।

=== निर्देशित चक्रीय ग्राफ === में न्यूनतम पथ कवर निर्देशित विश्वकोश ग्राफ दिया $G=(V,E)$, हमें प्रत्येक शीर्ष को कवर करने के लिए पथ (ग्राफ सिद्धांत) | शीर्ष-विच्छेद पथों की न्यूनतम संख्या का पता लगाना है $V$. हम द्विदलीय ग्राफ का निर्माण कर सकते हैं $G'=(V_{\textrm {out}}\cup V_{\textrm {in}},E')$ से $G$, कहाँ

1. $V_{\textrm {out}}=\{v_{\textrm {out}}\mid v\in V\land v{\text{ has outgoing edge(s)}}\}$
2. $V_{\textrm {in}}=\{v_{\textrm {in}}\mid v\in V\land v{\text{ has incoming edge(s)}}\}$
3. $E'=\{(u_{\textrm {out}},v_{\textrm {in}})\in V_{out}\times V_{in}\mid (u,v)\in E\}$.

तभी यह दिखाया जा सकता है $G'$ मेल खाता है $M$ आकार का $m$ अगर और केवल अगर $G$ वर्टेक्स-डिसजॉइंट पाथ कवर है $C$ युक्त $m$ किनारों और $n-m$ पथ, कहाँ $n$ में शीर्षों की संख्या है $G$. इसलिए, अधिकतम कार्डिनैलिटी मैचिंग का पता लगाकर समस्या को हल किया जा सकता है $G'$ बजाय।

मान लें कि हमें मिलान मिल गया है $M$ का $G'$, और आवरण का निर्माण किया $C$ यह से। सहज रूप से, अगर दो कोने $u_{\mathrm {out} },v_{\mathrm {in} }$ में मेल खाते हैं $M$, फिर किनारा $(u,v)$ में निहित है $C$. स्पष्ट रूप से किनारों की संख्या $C$ है $m$. यह देखने के लिए $C$ वर्टेक्स-डिसजॉइंट है, निम्नलिखित पर विचार करें:

1. प्रत्येक शीर्ष $v_{\textrm {out}}$ में $G'$ या तो में बेमेल हो सकता है $M$, जिस स्थिति में कोई किनारा नहीं बचता है $v$ में $C$; या इसका मिलान किया जा सकता है, जिस स्थिति में ठीक किनारा बचता है $v$ में $C$. किसी भी मामले में, किनारे से अधिक कोई शीर्ष नहीं छोड़ता है $v$ में $C$.
2. इसी प्रकार प्रत्येक शीर्ष के लिए $v_{\textrm {in}}$ में $G'$ - यदि इसका मिलान किया जाता है, तो इसमें आने वाला किनारा होता है $v$ में $C$; अन्यथा $v$ में कोई आने वाला किनारा नहीं है $C$.

इस प्रकार किसी भी शीर्ष में दो आने वाले या दो बाहर जाने वाले किनारे नहीं होते हैं $C$, जिसका अर्थ है सभी रास्ते अंदर $C$ वर्टेक्स-डिसजॉइंट हैं।

यह दिखाने के लिए कि कवर $C$ आकार है $n-m$, हम खाली कवर से शुरू करते हैं और इसे वृद्धिशील रूप से बनाते हैं। शिखर जोड़ने के लिए $u$ कवर में, हम इसे या तो मौजूदा पथ में जोड़ सकते हैं, या उस शीर्ष पर शुरू होने वाली लंबाई शून्य का नया पथ बना सकते हैं। पूर्व का मामला जब भी लागू होता है $(u,v)\in E$ और कवर में कुछ रास्ता शुरू होता है $v$, या $(v,u)\in E$ और कुछ पथ पर समाप्त होता है $v$. बाद वाला मामला हमेशा लागू होता है। पूर्व मामले में, कवर में किनारों की कुल संख्या 1 से बढ़ जाती है और पथों की संख्या समान रहती है; बाद वाले मामले में रास्तों की संख्या बढ़ जाती है और किनारों की संख्या वही रहती है। अब यह स्पष्ट हो गया है कि सभी को कवर करने के बाद $n$ शिखर, आवरण में पथों और किनारों की संख्या का योग है $n$. इसलिए, यदि कवर में किनारों की संख्या है $m$, पथों की संख्या है $n-m$.

शीर्ष क्षमता के साथ अधिकतम प्रवाह

चित्र 4.4.1। नोड विभाजन द्वारा मूल अधिकतम प्रवाह समस्या में वर्टेक्स क्षमता बाधा के साथ अधिकतम प्रवाह समस्या का परिवर्तन

होने देना $N=(V,E)$ नेटवर्क हो। मान लीजिए कि बढ़त क्षमता के अलावा प्रत्येक नोड पर क्षमता है, यानी मैपिंग $c:V\to \mathbb {R} ^{+},$ ऐसा कि प्रवाह $f$ न केवल क्षमता की कमी और प्रवाह के संरक्षण को पूरा करना है, बल्कि वर्टेक्स क्षमता की कमी को भी पूरा करना है

$\sum _{i\in V}f_{iv}\leq c(v)\qquad \forall v\in V\backslash \{s,t\}.$

दूसरे शब्दों में, शीर्ष से गुजरने वाले प्रवाह की मात्रा इसकी क्षमता से अधिक नहीं हो सकती। अधिकतम प्रवाह खोजने के लिए $N$, हम विस्तार करके समस्या को मूल अर्थ में अधिकतम प्रवाह समस्या में बदल सकते हैं $N$. सबसे पहले, प्रत्येक $v\in V$ द्वारा प्रतिस्थापित किया जाता है $v_{\text{in}}$ और $v_{\text{out}}$, कहाँ $v_{\text{in}}$ में जाकर किनारों से जुड़ा है $v$ और $v_{\text{out}}$ से निकलने वाले किनारों से जुड़ा है $v$, फिर क्षमता असाइन करें $c(v)$ किनारे से जोड़ने के लिए $v_{\text{in}}$ और $v_{\text{out}}$ (चित्र देखें। 4.4.1)। इस विस्तारित नेटवर्क में, वर्टेक्स क्षमता की कमी को हटा दिया जाता है और इसलिए समस्या को मूल अधिकतम प्रवाह समस्या के रूप में माना जा सकता है।

=== s से t === तक पथों की अधिकतम संख्या निर्देशित ग्राफ दिया $G=(V,E)$ और दो शिखर $s$ और $t$, हमें पथों की अधिकतम संख्या ज्ञात करनी है $s$ को $t$. इस समस्या के कई रूप हैं:

1. पथ एज-डिसजॉइंट होने चाहिए। नेटवर्क बनाकर इस समस्या को अधिकतम प्रवाह समस्या में बदला जा सकता है $N=(V,E)$ से $G$, साथ $s$ और $t$ स्रोत और सिंक होने के नाते $N$ क्रमशः, और प्रत्येक किनारे की क्षमता निर्दिष्ट करना $1$. इस नेटवर्क में अधिकतम प्रवाह है $k$ अगर हैं $k$ किनारे-अलग रास्ते।

2. पथ स्वतंत्र होने चाहिए, अर्थात, वर्टेक्स-डिसजॉइंट (को छोड़कर) $s$ और $t$). हम नेटवर्क बना सकते हैं $N=(V,E)$ से $G$ वर्टेक्स कैपेसिटी के साथ, जहां सभी वर्टिकल और सभी एज की कैपेसिटी होती है $1$. तब अधिकतम प्रवाह का मान स्वतंत्र पथों की अधिकतम संख्या के बराबर होता है $s$ को $t$.

3. पथों के किनारे-विच्छेद और/या शीर्ष असंयुक्त होने के अलावा, पथों में लंबाई की बाधा भी होती है: हम केवल उन पथों की गणना करते हैं जिनकी लंबाई ठीक है $k$, या अधिक से अधिक $k$. के छोटे मूल्यों को छोड़कर, इस समस्या के अधिकांश रूप एनपी-पूर्ण हैं $k$.

बंद करने की समस्या

Main article: Closure problem

निर्देशित ग्राफ़ का बंद होना 'सी' वर्टिकल का सेट है, जैसे कोई किनारा सी नहीं छोड़ता है। क्लोजर प्रॉब्लम वर्टेक्स-वेटेड डायरेक्टेड ग्राफ में अधिकतम-वेट या न्यूनतम-वेट क्लोजर खोजने का कार्य है। अधिकतम प्रवाह समस्या में कमी का उपयोग करके इसे बहुपद समय में हल किया जा सकता है।

वास्तविक विश्व अनुप्रयोग

बेसबॉल उन्मूलन

बेसबॉल उन्मूलन समस्या के लिए नेटवर्क प्रवाह का निर्माण

बेसबॉल उन्मूलन समस्या में लीग में प्रतिस्पर्धा करने वाली n टीमें हैं। लीग सीज़न के विशिष्ट चरण में, w_i जीत और आर की संख्या है_i टीम I और r के लिए खेले जाने वाले खेलों की संख्या है_ij टीम j के विरुद्ध बचे हुए खेलों की संख्या है। टीम का सफाया कर दिया जाता है अगर उसके पास सीजन को पहले स्थान पर खत्म करने का कोई मौका नहीं है। बेसबॉल उन्मूलन समस्या का कार्य यह निर्धारित करना है कि सीजन के दौरान प्रत्येक बिंदु पर कौन सी टीम समाप्त हो जाती है। श्वार्ट्ज एक तरीका प्रस्तावित किया जो इस समस्या को अधिकतम नेटवर्क प्रवाह तक कम कर देता है। इस पद्धति में यह निर्धारित करने के लिए नेटवर्क बनाया जाता है कि टीम k समाप्त हो गई है या नहीं।

चलो जी = (वी, ई) के साथ नेटवर्क बनें s,t ∈ V क्रमशः स्रोत और सिंक है। गेम नोड जोड़ता है_ij - जो इन दो टीमों के बीच नाटकों की संख्या का प्रतिनिधित्व करता है। हम प्रत्येक टीम के लिए टीम नोड भी जोड़ते हैं और प्रत्येक गेम नोड को कनेक्ट करते हैं {i, j} i <j से V तक, और उनमें से प्रत्येक को क्षमता r के किनारे से s से जोड़ता है_ij - जो इन दो टीमों के बीच नाटकों की संख्या का प्रतिनिधित्व करता है। हम प्रत्येक टीम के लिए टीम नोड भी जोड़ते हैं और प्रत्येक गेम नोड को कनेक्ट करते हैं {i, j} दो टीम नोड्स i और j के साथ यह सुनिश्चित करने के लिए कि उनमें से जीतता है। इन किनारों पर प्रवाह मान को सीमित करने की आवश्यकता नहीं है। अंत में, किनारों को टीम नोड i से सिंक नोड टी और की क्षमता से बनाया जाता है w_k + r_k – w_i टीम i को इससे अधिक जीतने से रोकने के लिए सेट है w_k + r_k. मान लीजिए S लीग में भाग लेने वाली सभी टीमों का समुच्चय है और मान लीजिए

$r(S-\{k\})=\sum _{i,j\in \{S-\{k\}\} \atop i<j}r_{ij}$.

इस पद्धति में यह दावा किया जाता है कि टीम k को समाप्त नहीं किया जाता है यदि और केवल यदि आकार r(S - {k}) का प्रवाह मान नेटवर्क G में मौजूद है। उल्लिखित लेख में यह सिद्ध किया गया है कि यह प्रवाह मान से अधिकतम प्रवाह मान है एस से टी।

एयरलाइन शेड्यूलिंग

एयरलाइन उद्योग में बड़ी समस्या उड़ान कर्मचारियों के समय-निर्धारण की है। एयरलाइन शेड्यूलिंग समस्या को विस्तारित अधिकतम नेटवर्क प्रवाह के अनुप्रयोग के रूप में माना जा सकता है। इस समस्या का इनपुट फ़्लाइट F का सेट है जिसमें यह जानकारी होती है कि प्रत्येक फ़्लाइट कहाँ और कब प्रस्थान करती है और कब आती है। एयरलाइन शेड्यूलिंग के संस्करण में लक्ष्य अधिकतम k कर्मचारियों के साथ व्यवहार्य शेड्यूल तैयार करना है।

इस समस्या को हल करने के लिए परिबद्ध संचलन नामक संचलन समस्या की भिन्नता का उपयोग किया जाता है जो प्रवाह नेटवर्क समस्याओं का सामान्यीकरण है, किनारे प्रवाह पर निचली सीमा के अतिरिक्त बाधा के साथ।

चलो जी = (वी, ई) के साथ नेटवर्क बनें s,t ∈ V स्रोत और सिंक नोड्स के रूप में। प्रत्येक उड़ान i के स्रोत और गंतव्य के लिए, V, नोड s में दो नोड जोड़ता है_i स्रोत और नोड डी के रूप में_i उड़ान के गंतव्य नोड के रूप में i. E में निम्नलिखित किनारों को भी जोड़ा जाता है:

1. एस और प्रत्येक एस के बीच क्षमता [0, 1] वाला किनारा_i.
2. प्रत्येक डी के बीच क्षमता [0, 1] वाला किनारा_i और टी।
3. एस की प्रत्येक जोड़ी के बीच क्षमता [1, 1] वाला किनारा_i और डी_i.
4. प्रत्येक डी के बीच क्षमता [0, 1] वाला किनारा_i और एस_j, अगर स्रोत एस_j उड़ान के गंतव्य i से उचित समय और लागत के साथ पहुंच योग्य है।
5. एस और टी के बीच क्षमता [0, ∞] वाला किनारा।

उल्लिखित विधि में, यह दावा किया गया है और सिद्ध किया गया है कि एस और टी के बीच जी में के के प्रवाह मूल्य का पता लगाना अधिकतम के कर्मचारियों के साथ उड़ान सेट एफ के लिए व्यवहार्य कार्यक्रम खोजने के बराबर है। एयरलाइन शेड्यूलिंग का अन्य संस्करण सभी उड़ानों को निष्पादित करने के लिए न्यूनतम आवश्यक कर्मचारियों की तलाश कर रहा है। इस समस्या का उत्तर खोजने के लिए, द्विदलीय ग्राफ G' = (A ∪ B, E) वहाँ बनाया जाता है जहाँ प्रत्येक उड़ान की सेट A और सेट B में प्रति होती है। यदि वही विमान उड़ान i के बाद उड़ान j निष्पादित कर सकता है, i∈A से जुड़ा है j∈B. में मेल खाता है G' एफ के लिए शेड्यूल को प्रेरित करता है और स्पष्ट रूप से इस ग्राफ में अधिकतम द्विपक्षीय मिलान कर्मचारियों की न्यूनतम संख्या के साथ एयरलाइन शेड्यूल तैयार करता है।जैसा कि इस लेख के अनुप्रयोग भाग में बताया गया है, अधिकतम कार्डिनैलिटी द्विपक्षीय मिलान अधिकतम प्रवाह समस्या का अनुप्रयोग है।

परिसंचरण-मांग समस्या

कुछ कारखाने हैं जो माल का उत्पादन करते हैं और कुछ गाँव जहाँ माल पहुँचाना होता है। वे सड़कों के नेटवर्क से जुड़े हुए हैं जिनमें प्रत्येक सड़क की क्षमता है c अधिकतम माल के लिए जो इसके माध्यम से बह सकता है। समस्या यह पता लगाने की है कि क्या कोई संचलन है जो मांग को पूरा करता है। यह समस्या अधिकतम-प्रवाह समस्या में परिवर्तित हो सकती है।

1. स्रोत नोड जोड़ें s और इसके किनारों को हर फैक्ट्री नोड में जोड़ें f_i क्षमता के साथ p_i कहाँ p_i कारखाने की उत्पादन दर है f_i.
2. सिंक नोड जोड़ें t और सभी गांवों से किनारे जोड़ें v_i को t क्षमता के साथ d_i कहाँ d_i गांव की मांग दर है v_i.

बता दें कि जी = (वी, ई) यह नया नेटवर्क है। संचलन मौजूद है जो मांग को संतुष्ट करता है यदि और केवल यदि:

Maximum flow value(G) $=\sum _{i\in v}d_{i}$.

यदि कोई संचलन मौजूद है, तो अधिकतम-प्रवाह समाधान को देखने से यह उत्तर मिलेगा कि मांगों को पूरा करने के लिए किसी विशेष सड़क पर कितना माल भेजा जाना है।

कुछ किनारों पर प्रवाह पर निचली सीमा जोड़कर समस्या को बढ़ाया जा सकता है।

छवि विभाजन

बाएं

बिटमैप से निर्मित नेटवर्क। स्रोत बाईं ओर है, सिंक दाईं ओर है। किनारा जितना गहरा होता है, उसकी क्षमता उतनी ही बड़ी होती है। ए_i उच्च होता है जब पिक्सेल हरा होता है, b_i जब पिक्सेल हरा नहीं होता है। दंड पी_ij सब बराबर हैं।

क्लेनबर्ग और टार्डोस ने अपनी पुस्तक में छवि विभाजन के लिए छवि के लिए एल्गोरिथ्म प्रस्तुत किया है। वे छवि में पृष्ठभूमि और अग्रभूमि खोजने के लिए एल्गोरिथ्म प्रस्तुत करते हैं। अधिक सटीक रूप से, एल्गोरिथ्म बिटमैप को इनपुट के रूप में निम्नानुसार लेता है: a_i≥ 0 संभावना है कि पिक्सेल i अग्रभूमि से संबंधित है, b_i≥ 0 इस संभावना में कि पिक्सेल i पृष्ठभूमि से संबंधित है, और p_ijयदि दो सन्निकट पिक्सेल i और j को अग्रभूमि में और दूसरे को पृष्ठभूमि में रखा जाता है तो यह जुर्माना है। लक्ष्य निम्नलिखित मात्रा को अधिकतम करने वाले पिक्सेल के सेट के विभाजन (ए, बी) को ढूंढना है

$q(A,B)=\sum _{i\in A}a_{i}+\sum _{i\in B}b_{i}-\sum _{\begin{matrix}i,j{\text{ adjacent}}\\|A\cap \{i,j\}|=1\end{matrix}}p_{ij}$,

दरअसल, ए में पिक्सेल के लिए (अग्रभूमि के रूप में माना जाता है), हम प्राप्त करते हैं_i; बी में सभी पिक्सल के लिए (पृष्ठभूमि के रूप में माना जाता है), हम बी प्राप्त करते हैं_i. सीमा पर, दो आसन्न पिक्सेल i और j के बीच, हम p को ढीला करते हैं_ij. यह मात्रा को कम करने के बराबर है

$q'(A,B)=\sum _{i\in A}b_{i}+\sum _{i\in B}a_{i}+\sum _{\begin{matrix}i,j{\text{ adjacent}}\\|A\cap \{i,j\}|=1\end{matrix}}p_{ij}$

क्योंकि

$q(A,B)=\sum _{i\in A\cup B}a_{i}+\sum _{i\in A\cup B}b_{i}-q'(A,B).$

नेटवर्क पर प्रदर्शित न्यूनतम कट (त्रिकोण बनाम वृत्त)।

अब हम उस नेटवर्क का निर्माण करते हैं जिसके नोड पिक्सेल हैं, साथ ही स्रोत और सिंक, दाईं ओर चित्र देखें। हम स्रोत को पिक्सेल i से वजन a के किनारे से जोड़ते हैं_i. हम पिक्सेल i को वज़न b के किनारे से सिंक से जोड़ते हैं_i. हम पिक्सेल i को पिक्सेल j से वजन p के साथ जोड़ते हैं_ij. अब, यह उस नेटवर्क में न्यूनतम कटौती (या समकक्ष अधिकतम प्रवाह) की गणना करने के लिए बनी हुई है। अंतिम आंकड़ा न्यूनतम कटौती दिखाता है।

एक्सटेंशन

1. न्यूनतम-लागत प्रवाह समस्या में, प्रत्येक किनारे (u,v) का लागत-गुणांक भी होता है a_uvइसकी क्षमता के अलावा। यदि किनारे से प्रवाह f है_uv, तो कुल लागत है_uvf_uv. सबसे छोटी लागत के साथ दिए गए आकार d का प्रवाह खोजना आवश्यक है। अधिकांश प्रकारों में, लागत-गुणांक सकारात्मक या नकारात्मक हो सकते हैं। इस समस्या के लिए विभिन्न बहुपद-समय एल्गोरिदम हैं।

2. अधिकतम-प्रवाह समस्या को 'वियोगात्मक बाधाओं' द्वारा संवर्धित किया जा सकता है: नकारात्मक वियोगात्मक बाधा का कहना है कि किनारों की निश्चित जोड़ी एक साथ गैर-शून्य प्रवाह नहीं कर सकती है; सकारात्मक वियोगात्मक बाधाएँ कहती हैं कि, किनारों की निश्चित जोड़ी में, कम से कम गैर-शून्य प्रवाह होना चाहिए। नकारात्मक बाधाओं के साथ, सरल नेटवर्क के लिए भी समस्या एनपी-हार्ड हो जाती है। सकारात्मक बाधाओं के साथ, यदि आंशिक प्रवाह की अनुमति दी जाती है, तो समस्या बहुपद है, लेकिन जब प्रवाह अभिन्न होना चाहिए तो यह एनपी-हार्ड हो सकता है।

अग्रिम पठन

• Joseph Cheriyan and Kurt Mehlhorn (1999). "An analysis of the highest-level selection rule in the preflow-push max-flow algorithm". Information Processing Letters. 69 (5): 239–242. CiteSeerX 10.1.1.42.8563. doi:10.1016/S0020-0190(99)00019-8.
• Daniel D. Sleator and Robert E. Tarjan (1983). "A data structure for dynamic trees" (PDF). Journal of Computer and System Sciences. 26 (3): 362–391. doi:10.1016/0022-0000(83)90006-5. ISSN 0022-0000.
• Eugene Lawler (2001). "4. Network Flows". Combinatorial Optimization: Networks and Matroids. Dover. pp. 109–177. ISBN 978-0-486-41453-9.